Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Bond-bending isomerism of Au2I3−: competition between covalent bonding and aurophilicity†
Wan-Lu
Li‡
a,
Hong-Tao
Liu‡
b,
Tian
Jian‡
c,
Gary V.
Lopez
c,
Zachary A.
Piazza
c,
Dao-Ling
Huang
c,
Teng-Teng
Chen
c,
Jing
Su
ab,
Ping
Yang
d,
Xin
Chen
a,
Lai-Sheng
Wang
*c and
Jun
Li
 *a
*a
aDepartment of Chemistry & Key Laboratory of Organic Optoelectronics and Molecular Engineering of Ministry of Education, Tsinghua University, Beijing 100084, China. E-mail: junli@tsinghua.edu.cn
bShanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
cDepartment of Chemistry, Brown University, Providence, Rhode Island 02912, USA. E-mail: Lai-Sheng_Wang@brown.edu
dTheoretical Division T-1, Los Alamos National Laboratory, Los Alamos, NM 87544, USA
First published on 13th October 2015
Abstract
We report a joint photoelectron spectroscopy and theoretical investigation of the gaseous Au2I3− cluster, which is found to exhibit two types of isomers due to competition between Au–I covalent bonding and Au–Au aurophilic interactions. The covalent bonding favors a bent IAuIAuI− structure with an obtuse Au–I–Au angle (100.7°), while aurophilic interactions pull the two Au atoms much closer, leading to an acutely bent structure (72.0°) with an Au–Au distance of 3.08 Å. The two isomers are separated by a small barrier and are nearly degenerate with the obtuse isomer being slightly more stable. At low temperature, only the obtuse isomer is observed; distinct experimental evidence is observed for the co-existence of a combination of isomers with both acute and obtuse bending angles at room temperature. The two bond-bending isomers of Au2I3− reveal a unique example of one molecule being able to oscillate between different structures as a result of two competing chemical forces.
Introduction
The chemical and physical properties of chemical compounds are dictated by their molecular structures.1,2 A molecule usually possesses one stable structure at a given condition, because the unique geometric shape of a molecule is determined by its inherent chemical bonding. However, the concept of so-called bond-stretch isomers (BSI) was proposed some time ago, referring to two stable structures with different bond lengths on the same potential energy surface with the same spin-state.3–5 A number of experimental and theoretical studies were carried out to envisage and characterize the controversial cases of BSI.6–8 However, most of the claimed BSIs were in solid state or spin-state isomers formed with crossover of different energy surfaces.9–17 The BSI concept itself still rekindles, even though the early examples of BSI were proven as experimental artifacts.18,19In addition to the strong chemical bonding that determines molecular structures, weaker aurophilic interactions have been found in gold systems due to attractions between closed-shell AuI centers.20–31 Aurophilic interactions, which are intermediate between van der Waals forces and covalent bonding, dominate the structural chemistry of AuI compounds. Strong relativistic effects and dispersion-type electron correlations were found to be the major driving forces of aurophilicity.22,28–30,32,33
Here we report a joint photoelectron spectroscopy (PES) and quantum chemical study on the gaseous Au2I3− cluster, in which aurophilic interactions turn out to play a key role. This anion is found to have a C2v bent geometric configuration of I–Au–I–Au–I− and exhibit two near-degenerate isomers that we name as “bond-bending isomers (BBIs)”, similar to BSI, which has not been experimentally established heretofore.34,35 The two BBIs of Au2I3− reported here differ only in geometry by the bending angle (Fig. 1), owing to different mechanisms of bonding interactions. A prior study showed that the Na2Cl3− cluster has a linear ground state, because of primarily ionic interactions.36 The bent structures of Au2I3− reflect both the strong Au–I covalency37,38 and Au–Au aurophilic interactions. The obtuse isomer, which is slightly lower in energy, features a traditional chemical bonding pattern and can be viewed as two AuI moieties linked by a central iodine anion via the two Au atoms, whereas the acute isomer with a significantly shorter Au⋯Au distance features strong aurophilic interactions.
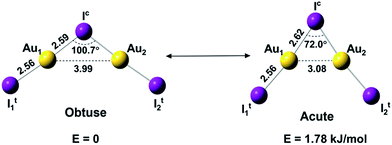 | ||
| Fig. 1 The structures and relative energies of the obtuse and acute isomers of Au2I3− at the CCSD(T)/AVTZ level. Bond lengths are in Å. | ||
Schmidbaur and Schier predicted that the [E(AuL)n] type unit could form polyhedra, due to strong aurophilic interactions,25 similar to the acute isomer of Au2I3−. Both isomers of Au2I3− are in singlet spin-states and can inter-convert easily at elevated temperatures because of the low energy barrier between them.
Experimental methods
Two different experimental apparatuses were used to obtain the photoelectron spectra of the Au2I3− cluster, which was produced by two completely different methods. It was first produced by electrospray of a 0.1 mM solution of AuI in acetonitrile, and accumulated in a room-temperature ion trap for 0.1 second before being ejected into the extraction zone of a time-of-flight mass spectrometer. The Au2I3− anions were selected by a mass gate and decelerated before being intercepted by a probe laser beam, 206 nm from a dye laser and 157 nm from an F2 excimer laser. The photoelectrons were analyzed by a 2.5 meter long magnetic-bottle electron flight tube, shortened from the original design.39 The resolution of the spectrometer was about 3% (ΔEk/Ek), i.e., about 30 meV for 1 eV electrons.In the temperature-dependent experiments, the Au2I3− clusters were produced by laser vaporization of a cold-pressed AuI target in the presence of pure He or a He carrier gas seeded with 5% Ar. The latter was shown previously to give better supersonic cooling.40 Clusters formed in the source were entrained by the carrier gas and underwent a supersonic expansion. Anions were extracted from the cluster beam and analyzed by a time-of-flight mass spectrometer. The Au2I3− anions were selected by a mass gate and decelerated before being detached by a 193 nm laser beam from an ArF excimer laser. Photoelectrons were analyzed by a magnetic-bottle analyzer with an electron energy resolution of ∼2.5% (ΔEk/Ek).41 Clusters with different resident times inside the nozzle were selected as a means to qualitatively control the cluster temperatures.42
Computational methods
Geometric structure optimizations for Au2I3− were performed using DFT with various functionals, including the generalized gradient approximation (GGA) with the PBE43 and PW91 functionals,44 the B3LYP hybrid functional,45,46 the TPSS meta-GGA functional,47,48 the TPSSh hybrid meta-GGA functional47,48 and the long-range corrected functionals49 with LC-PBE and LC-PW91 and CAM-B3LYP50 in Gaussian 09.51 Vibrational frequency calculations were carried out to verify that the structures were minima or transition states at equilibrium points of the potential energy surfaces. Zero-point energies (ZPE) were corrected based on the calculated harmonic vibrational frequencies.In as much as aurophilic interactions required sophisticated electron correlation treatment, high-level ab initio calculations were further performed to obtain accurate geometries and energies. We applied the spin-component scaled second-order perturbation theory (SCS-MP2),52 coupled clusters with single, double and perturbative triple excitations [CCSD(T)],53,54 and complete-active-space self-consistent field (CASSCF)55 methods. These ab initio electron correlation calculations were done with the MOLPRO 2008 program.56 Geometry optimizations for the acute and obtuse Au2I3− structures were both done at the SCS-MP2 and CCSD(T) level. For the neutral Au2I3 species, single-point energies of the ground and excited states were determined at the optimized anion structures using the CCSD(T) method, which accurately generated the state-specific scalar relativistic energies of all the states needed for simulating the experimental PES. Single-electron VDEs from the anion ground state to the corresponding ground and excited states of the neutral cluster were obtained using the CASSCF/CCSD(T)/SO approach. In both the Gaussian 09 and MOLPRO 2008 calculations, the Stuttgart energy-consistent relativistic pseudopotentials ECP60MDF and ECP28MDF and the corresponding valence basis sets of polarized triple-zeta level (aug-cc-pVTZ-PP) were applied for Au57,58 and I,59 respectively, which were abbreviated as AVTZ.
For chemical bonding analyses, we used the energy decomposition approach (EDA),60 various bond order indices, and electron localization function (ELF)61 using the PBE exchange–correlation functional implemented in ADF 2013.01.62 Here we applied the Slater basis sets with the quality of triple-zeta with two polarization functions (TZ2P).63 Frozen core approximation was used for the inner shells of [1s2–4f14] for Au and [1s2–4d10] for I. The scalar relativistic (SR) and spin orbit (SO) effects were taken into account by the zero-order-regular approximation (ZORA).64
In order to obtain multi-center localized orbitals, we used the Multiwfn65 codes to do adaptive natural density portioning (AdNDP) analyses.66 The atomic charges were computed via natural population analyses (NPA)67 by using NBO 3.1 (ref. 68) as implemented in Gaussian 09. The local adiabatic stretching force constants69 were calculated using a code written by the Tsinghua group.
Results
Photoelectron spectroscopy
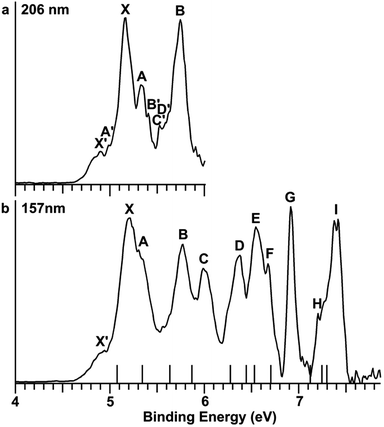
The Au2I3− anion was produced using two different methods and the experiments were carried out using two separate magnetic-bottle PES apparatuses, one equipped with an electrospray ionization (ESI) source39 and another with a laser vaporization supersonic cluster source.41 With the ESI apparatus, photoelectron spectra were taken under room temperature at two laser wavelengths, 206 nm (6.019 eV) and 157 nm (7.866 eV) (Fig. 2). The room temperature spectra were surprisingly congested. In addition to numerous intense PES features, labeled with the capital letters X and A–I, there were also weak PES features labeled as X′ and A′–D′. The weak intensities of the latter suggested that they might come from another isomer. The binding energies of all the observed features are given in Table S1,† where they are compared with the theoretical results (vide infra).In order to have a better understanding of the congested PES features, temperature-dependent experiments were carried out using a laser vaporization supersonic cluster source.41 The Au2I3− anions were selected and decelerated before being photodetached by the 193 nm (6.424 eV) radiation from an ArF excimer laser at several experimental conditions, as shown in Fig. 3. It was found previously that the residence time of clusters inside the nozzle is an important factor affecting the cluster temperature.42 Those clusters that spend more time in the nozzle experience more thermalization collisions with the carrier gas, and they are colder. The residence time of clusters in the nozzle can be controlled to obtain qualitatively hot, warm, and cold clusters.42
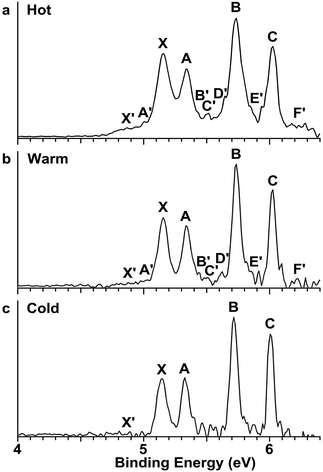 | ||
| Fig. 3 Temperature-dependent photoelectron spectra of Au2I3− at 193 nm. (a) At short residence time (hot). (b) At medium residence time (warm). (c) At long residence time (cold). | ||
Photoelectron spectra taken at 193 nm were designated as ‘hot’, ‘warm’, and ‘cold’ in Fig. 3, corresponding to three different residence times. Under the cold condition (Fig. 3c), a well-resolved spectrum with only the four intense features (X, A, B, C) was observed. Under the warm condition (Fig. 3b), weak features (X′, A′–F′) appeared and their intensities increased under the hot condition (Fig. 3a). In addition to the weak PES features observed in Fig. 2 (X′ and A′–D′), two more weak features (E′ and F′) were resolved in Fig. 3. The temperature-dependence of the weak features provided convincing evidence that they were from low-lying isomers, while the intense features were from the most stable isomer.
Geometries and energetic stabilities of the two BBIs
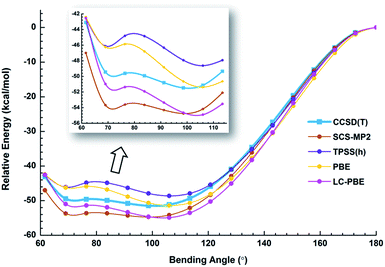
We used both density functional theory (DFT) and ab initio wave function theory (WFT) at different levels (see ESI† for details) to optimize the structures of Au2I3−. The geometries were fully optimized and the results are given in Table S2.† All levels of theory predicted a bent structure, very different from the linear alkali halide system.36 Remarkably, we found a very flat potential energy surface with two minima at almost all levels of theory. The geometric parameters at the CCSD(T) level are given in Fig. 1, showing Au1⋯Au2 distances of 3.08 Å and 3.99 Å for the acute and obtuse isomers, respectively. All the theoretical results (Table S2†) show that the bond length of Au1–Ic increases slightly in the acute isomer, while the Au1–It1 distance does not change in the two isomers. The geometric parameters obtained by SCS-MP2 agree well with the CCSD(T) calculations, as shown previously.29,70 However, the numerous DFT methods do not perform well; neither does the popular B3LYP hybrid functional, which even failed to find the acute configuration, nor the long-range corrected CAM-B3LYP functional. Comparably, TPSSh hybrid meta-GGA and PBE performed reasonably well in terms of the covalent bond between Au and I, which was also described in other gold compounds.71Because of the inherent aurophilic interactions between the two Au atoms, calculated results from the long-range corrected functionals agree with those from the ab initio coupled-cluster method. Thus, high-level quantum chemical methods are crucial in accurately characterizing these nearly degenerate isomers. The full computational results for the energy difference between the acute and obtuse isomers (ΔEA–O) are given in Table S3.† We found that the linear structure is a transition state, lying about 50 kJ mol−1 higher in energy than the two BBIs. Preliminary calculations with the SO-ZORA approach show that SO effects are important for all these species, whereas the relative energies are not affected. Fig. 4 illustrates the rather flat potential energy curve in the region of the two BBIs, which are separated by a small barrier of only 1.78 kJ mol−1 at CCSD(T) level. Such a low barrier suggests that the two BBIs can easily inter-convert. Hence, at elevated temperatures many different configurations are expected to co-exist along the bending angle, in excellent agreement with the experimental results, as shown in Table S1† (vide infra). The SCS-MP2/AVTZ calculations gave a bending angle of 80.1° for the transition state between the two BBIs. It is interesting to compare the bonding between I5− with an apical angle of 94° and the obtuse Au2I3− isomer,72,73 because Au can be viewed as a heavy halogen. However, aurophilicity also gives rise to the acute configuration for Au2I3−.
We have estimated the lifetime of the acute BBI at the upper potential well using the Wentzel–Kramers–Brillouin (WKB) escape probability.74 Using a bending frequency of 24 cm−1, we estimated a lifetime of about 104 ns for the acute BBI, which is sufficiently long-lived to be observed in the photodetachment experiments (Fig. 2 and 3a). A further possibility is that in the condensed-phase the lifetime of the acute isomer could become significantly longer so that separate BBIs could exist therein.
Discussion
Comparison of the photoelectron spectra with theoretical results
The photoelectron spectra of Au2I3− in Fig. 2 and 3 provide definitive experimental evidence for the co-existing isomers at elevated temperatures. Under the cold condition (Fig. 3c), the Au2I3− cluster resides in its electronic and vibrational ground state with the obtuse structure, giving rise to the intense PES features (X, A–I). Under the hot and warm conditions (Fig. 3a and b), the Au2I3− cluster can access the acute part of the potential energy surface, giving rise to the weak PES features (X′, A′–F′).Because the barrier between the two BBIs is low, the broad part of the potential energy curve will be accessed at high vibrational levels or high temperatures, resulting in new spectral features, in remarkable agreement with the experiment. The diffuse X′ low binding energy feature appearing in the hot spectrum by laser vaporization (Fig. 3a) or the room temperature spectrum from ESI (Fig. 2) provides unequivocal evidence for the existence of the acute configurations and for the flatness of the potential energy curve. To understand the spectral features quantitatively, we computed the vertical electron detachment energies (VDEs) of both the acute and obtuse isomers using the CASSCF/CCSD(T)/SO approach, as shown in Table S1.† This approach was shown previously to give reliable theoretical VDEs for Au-containing complexes.75–77 Theoretical VDEs of the obtuse isomer are plotted as short bars in Fig. 2b for comparison, and they are in excellent agreement with the intense spectral bands (X, A–I). The diffuse and weak low binding energy band X′ corresponds to the acute isomer. Because of the flatness of the potential energy curve, a large range of bond angles is expected to be accessed. Hence, we computed the VDEs for a broad range of bond angles from the obtuse to the acute minima, as given in Table S1.† The calculated VDE of the first detachment channel of the acute isomer increases from 4.828 eV at 72° to 5.015 eV at 90°. This result is in excellent agreement with the experimental VDE of the diffuse band X′, providing the most compelling evidence for the presence of the acute isomer and the shape of the potential energy surface at the CCSD(T) level in Fig. 4. The calculated VDEs for the higher detachment channels are also consistent with the weak features observed at higher temperatures. The excellent agreement between the theoretical VDEs and the temperature-dependent PES provide conclusive evidence for the two BBIs and the validity of the potential energy curve at the CCSD(T) level in Fig. 4.
Electronic structure and chemical bonding analyses
We performed various chemical bonding analyses to elucidate the electronic structures of the two BBIs. The chemical bonding can be glimpsed from the electron localization functions (ELFs) shown in Fig. 5. There is discernible Au–Au attraction in the acute isomer in comparison to the obtuse isomer, where no electron-pair density is localized between the two Au sites. Strong covalent bonding can be seen between the central I atom and the neighboring Au atoms in both isomers, but it is slightly stronger in the obtuse isomer. Hence, the Au–Au aurophilic interaction is in competition with the Au–I covalent bonding in the acute isomer. The molecular orbital (MO) contours are depicted for the two isomers in Fig. S2 and S3.† While the upper occupied MOs with non-bonding or anti-bonding features show little change from the obtuse to the acute isomer, the 2b1, 3a1 and 2a1 MOs of the acute isomer represent Au–Au interactions that are not present in the obtuse case. The 1b1 MOs in both isomers are dominated by Au1(5d)–Ic(5p)–Au2(5d) π-type bonding and have comparable orbital energies, as shown in Fig. S2 and S3.† Especially noteworthy is the different trend of the energy levels of the last two MOs: σg and σu for the linear configuration, a1 and b2 for the bent obtuse or acute structures (Fig. S4†). The 1σg–1a1(O)–1a1(A) orbital is considerably stabilized in the acute isomer, whereas the 1σu–1b2(O)–1b2(A) orbital is significantly destabilized in the acute isomer. The different stabilities of the 1a1 and 1b2 orbitals probably play a key role in the near degeneracy of the two isomers.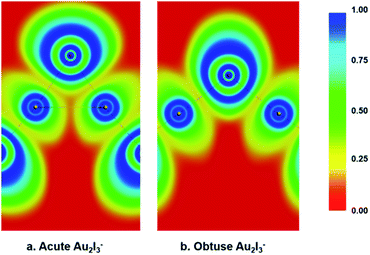 | ||
| Fig. 5 The electron localization functions (ELFs) calculated for both the acute and obtuse Au2I3− at the PBE/ZORA/TZ2P level. (a) For the acute structure. (b) For the obtuse structure. | ||
As shown in Fig. S4,† the 1a1 and 1b2 MOs in the acute isomer seem to form two types of three-center two-electron (3c–2e) bonds; one is along the C2 axis while the other is perpendicular to the C2 axis, as shown more clearly in the bonding analysis in Fig. S5c′ and d′.† This kind of three-center bonding is also found previously in OC–Th–CO,78 similar to IAu–I–AuI− or the Au2I42− complex.79 These 3c–2e orbitals are conducive to promote Au–Au aurophilic attraction, but weaken the Au–Ic interactions, resulting in the more acute angle for Au1–Ic–Au2 and elongated Au1,2–Ic bond length. However, the 1a1 and 1b2 MOs in the obtuse isomer simply represent two two-center two-electron (2c–2e) Au1,2–Ic bonds, as shown in Fig. S5c and d.† Therefore, the Au–Au aurophilic interactions in the acute isomer involve several MOs.
The calculated bond orders based on various theoretical schemes and adiabatic stretching force constants in both the acute and obtuse conformers are given in Table S4.† These results also give strong evidence that the Au(I)⋯Au(I) aurophilic attraction becomes stronger at the cost of weakening the covalent bonding between the central I and the adjacent Au in the acute isomer. All methods give a larger Au–Au bond order and a smaller Au–Ic bond order in the acute isomer relative to the obtuse isomer. The Au–Au and Au–Ic stretching frequencies show a similar trend. Table 1 provides results of the energy decomposition analysis (EDA) with SO coupling correction, showing the key role of the covalent chemical bonding interaction according to orbitals with different irreducible representations. Steric interactions in the linear, obtuse and acute isomers are almost identical. However, the orbital interactions of the b2 MOs in the obtuse isomer are 1.15 eV stronger than that in the acute isomer. On the other hand, the orbital interactions of the a1 MOs in the acute isomer are 1.04 eV more stable than the obtuse isomer, suggesting that the energy difference of these two isomers is mainly due to the energy competition between the b2 and a1 orbitals. It is also shown that the contribution of the SO coupling effect to the total bonding energy is significant (6.40 eV), but the correction is the same for the isomers with different bending angles (Table 1). Accordingly, the relative energetic stability is not influenced by the SO correction.
| Steric roleb | Orbital interactionc | Total bonding energyd | ||||||
|---|---|---|---|---|---|---|---|---|
| a1 | b1 | b2 | a2 | Sum | SR | SO | ||
| a All energies are given in eV. The SO single-point calculations are based on the spin-restricted fragments of the SR results at the equilibrium geometries. b The sum of electrostatic and Pauli interactions. c Each irreducible representation means the sum of the contributions from that orbital type. There are 11a1, 10b1, 5b2 and 4a2 orbitals that are summed up. d Sum of the steric and orbital interactions. | ||||||||
| Acute | 11.16 | −10.71 | −1.84 | −8.99 | −3.83 | −25.37 | −14.21 | −20.61 |
| Obtuse | 11.29 | −9.67 | −1.91 | −10.14 | −3.82 | −25.54 | −14.25 | −20.65 |
| Linear | 11.23 | −13.52 | −5.72 | −5.72 | −0.01 | −24.97 | −13.74 | −20.14 |
Conclusions
In summary, we have observed two bond-bending isomers for gaseous Au2I3−, which are only different by the IAu–I–AuI bond bending angles as a result of the competition between Au–I covalent bonding and Au–Au aurophilic interactions. High-level theoretical calculations showed that the acute and obtuse isomers are nearly degenerate in energy and separated by a small energy barrier with the obtuse isomer slightly lower in energy. Temperature-dependent photoelectron spectra were obtained for Au2I3−, which was produced with two completely different experimental methods, with clear evidence for the presence of these isomers. Systematic chemical bonding analyses revealed the subtle differences in the bonding interactions of the two types of structural isomers. The current finding presents a rare example of structural isomerism, akin to the long proposed concept of bond-stretching isomers.Acknowledgements
The experimental work done at Brown University was supported by the U.S. National Science Foundation (CHE-1263745). The theoretical work done at Tsinghua University was supported by NKBRSF (2011CB932400) and NSFC (21433005, 21201106, and 21221062) of China. The calculations were done using supercomputers at Tsinghua National Laboratory for Information Science and Technology and the Molecular Science Computing capability at EMSL, a National scientific user facility located at PNNL, operated for the U.S. Department of Energy by Battelle. LANL is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. DOE, under contract DE-AC52-O6NA25396.Notes and references
- P. Atkin and J. de Paula, in Atkins' physical chemistry, WH Freeman and Company, 8th edn, 2006, vol. 2, pp. 362–397 Search PubMed.
- P. Atkins, in Shriver and Atkins' inorganic chemistry, Oxford University Press, 2010, pp. 34–61 Search PubMed.
- G. Parkin, Chem. Rev., 1993, 93, 887–911 CrossRef CAS.
- Y. Jean, A. Lledos, J. K. Burdett and R. Hoffmann, J. Am. Chem. Soc., 1988, 110, 4506–4516 CrossRef CAS.
- Y. Jean, A. Lledos, J. K. Burdett and R. Hoffmann, J. Chem. Soc., Chem. Commun., 1988, 140–142 RSC.
- G. Parkin, Acc. Chem. Res., 1992, 25, 455–460 CrossRef CAS.
- J. M. Mayer, Angew. Chem., Int. Ed., 1992, 31, 286–287 CrossRef PubMed.
- J. A. Labinger, C. R. Chim., 2002, 5, 235–244 CrossRef CAS.
- P. V. Sudhakar, O. F. Guner and K. Lammertsma, J. Phys. Chem., 1989, 93, 7289–7292 CrossRef CAS.
- W. D. Stohrer and R. Hoffmann, J. Am. Chem. Soc., 1972, 94, 1661–1668 CrossRef CAS.
- M. M. Rohmer and M. Bénard, Chem. Soc. Rev., 2001, 30, 340–354 RSC.
- R. Y. Liau, A. Schier and H. Schmidbaur, Organometallics, 2003, 22, 3199–3204 CrossRef CAS.
- S. Duley, A. Chakraborty, S. Giri and P. K. Chattaraj, J. Sulfur Chem., 2010, 31, 231–246 CrossRef CAS PubMed.
- F. Zürcher and R. Nesper, Angew. Chem., Int. Ed., 1998, 37, 3314–3318 CrossRef.
- B. Molina, L. Alexandrova, R. le Lagadec, L. E. Sansores, D. Rios-Jara, F. Espinosa-Magaña and R. Salcedo, Molecules, 2011, 17, 34–47 CrossRef PubMed.
- J. E. McGrady, Angew. Chem., Int. Ed., 2000, 39, 3077–3079 CrossRef CAS.
- J. A. Boatz and M. S. Gordon, J. Phys. Chem., 1989, 93, 2888–2891 CrossRef CAS.
- G. Parkin and R. Hoffmann, Angew. Chem., 1994, 106, 1530 CrossRef CAS PubMed.
- P. Gütlich, H. A. Goodwin and D. N. Hendrickson, Angew. Chem., Int. Ed., 1994, 33, 425–427 CrossRef PubMed.
- P. Pyykkö, Chem. Soc. Rev., 2008, 37, 1967–1997 RSC.
- P. Pyykkö, Inorg. Chim. Acta, 2005, 358, 4113–4130 CrossRef PubMed.
- P. Pyykkö, Chem. Rev., 1997, 97, 597–636 CrossRef PubMed.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456 CrossRef PubMed.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370–412 RSC.
- H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931–1951 RSC.
- F. Scherbaum, A. Grohmann, B. Huber, C. Krüger and H. Schmidbaur, Angew. Chem., Int. Ed., 1988, 27, 1544–1546 CrossRef PubMed.
- N. Rösch, A. Görling, D. E. Ellis and H. Schmidbaur, Angew. Chem., Int. Ed., 1989, 28, 1357–1359 CrossRef PubMed.
- P. Pyykkö and Y. Zhao, Angew. Chem., Int. Ed., 1991, 30, 604–605 CrossRef PubMed.
- P. Pyykkö, X. G. Xiong and J. Li, Faraday Discuss., 2011, 152, 169–178 RSC.
- P. Pyykkö and N. Runeberg, Angew. Chem., Int. Ed., 2002, 41, 2174–2176 CrossRef.
- J. Muñiz, C. Wang and P. Pyykkö, Chem.–Eur. J., 2011, 17, 368–377 CrossRef PubMed.
- M. A. Rawashdeh-Omary, M. A. Omary and H. H. Patterson, J. Am. Chem. Soc., 2000, 122, 10371–10380 CrossRef CAS.
- M. Andrejić and R. A. Mata, Phys. Chem. Chem. Phys., 2013, 15, 18115–18122 RSC.
- S. R. Barua, W. D. Allen, E. Kraka, P. Jerabek, R. Sure and G. Frenking, Chem.–Eur. J., 2013, 19, 15941–15954 CrossRef CAS PubMed.
- R. Kawai and J. F. Tombrello, Phys. Rev. A, 1994, 49, 4236–4239 CrossRef CAS.
- A. N. Alexandrova, A. I. Boldyrev, Y. J. Fu, X. Yang, X. B. Wang and L. S. Wang, J. Chem. Phys., 2004, 121, 5709–5719 CrossRef CAS PubMed.
- L. S. Wang, Phys. Chem. Chem. Phys., 2010, 12, 8694–8705 RSC.
- Y. L. Wang, X. B. Wang, X. P. Xing, F. Wei, J. Li and L. S. Wang, J. Phys. Chem. A, 2010, 114, 11244–11251 CrossRef CAS PubMed.
- L. S. Wang, C. F. Ding, X. B. Wang and S. E. Barlow, Rev. Sci. Instrum., 1999, 70, 1957–1966 CrossRef CAS PubMed.
- W. Huang and L. S. Wang, Phys. Rev. Lett., 2009, 102, 153401 CrossRef.
- L. S. Wang, H. S. Cheng and J. Fan, J. Chem. Phys., 1995, 102, 9480–9493 CrossRef CAS PubMed.
- J. Akola, M. Manninen, H. Häkkinen, U. Landman, X. Li and L. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R11297 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS PubMed.
- T. Lee, W. Yang and R. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian Inc., Wallingford CT, 2009.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS PubMed.
- G. D. Purvis III and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef PubMed.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382–7387 CrossRef CAS PubMed.
- M. W. Schmidt and M. S. Gordon, Annu. Rev. Phys. Chem., 1998, 49, 233–266 CrossRef CAS PubMed.
- H. J. Werner, et al., Molpro, 2008, http://www.molpro.net Search PubMed.
- D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244 CrossRef CAS PubMed.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS PubMed.
- ADF and SCM, Theoretical Chemistry, Vrijie Universiteit, Amsterdam, The Netherlands, 2013, http://www.scm.com Search PubMed.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156 CrossRef CAS PubMed.
- E. van Lenthe, E.-J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1 Search PubMed.
- Z. Konkoli and D. Cremer, Int. J. Quantum Chem., 1998, 67, 1–9 CrossRef CAS.
- X. G. Xiong, Y. L. Wang, C. Q. Xu, Y. H. Qiu, L. S. Wang and J. Li, Dalton Trans., 2015, 44, 5535–5546 RSC.
- R. Kang, H. Chen, S. Shaik and J. Yao, J. Chem. Theory Comput., 2011, 7, 4002–4011 CrossRef CAS.
- J. Broekema, E. Havinga and E. Wiebenga, Acta Crystallogr., 1957, 10, 596 CrossRef CAS.
- S. N. Datta, C. S. Ewig and J. R. van Wazer, J. Mol. Struct., 1978, 48, 407–416 CrossRef CAS.
- M. Hotokka, T. Kindstedt, P. Pyykkö and B. O. Roos, Mol. Phys., 1984, 52, 23–32 CrossRef CAS PubMed.
- H. T. Liu, Y. L. Wang, X. G. Xiong, P. D. Dau, Z. A. Piazza, D. L. Huang, C. Q. Xu, J. Li and L. S. Wang, Chem. Sci., 2012, 3, 3286–3295 RSC.
- X. B. Wang, Y. L. Wang, J. Yang, X. P. Xing, J. Li and L. S. Wang, J. Am. Chem. Soc., 2009, 131, 16368–16370 CrossRef CAS PubMed.
- H. T. Liu, X. G. Xiong, P. D. Dau, Y. L. Wang, J. Li and L. S. Wang, Chem. Sci., 2011, 2, 2101–2108 RSC.
- J. Li, M. F. Zhou, B. E. Bursten and L. Andrews, Inorg. Chem., 2001, 2001, 5448–5460 CrossRef PubMed.
- P. Pyykkö and F. Mendizabal, Inorg. Chem., 1998, 37, 3018–3025 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary figures and tables. See DOI: 10.1039/c5sc03568f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2016 |