Open Access Article
Open Access ArticleOn the origin of high ionic conductivity in Na-doped SrSiO3†
Po-Hsiu
Chien
 a,
Youngseok
Jee
b,
Chen
Huang
c,
Riza
Dervişoğlu
a,
Youngseok
Jee
b,
Chen
Huang
c,
Riza
Dervişoğlu
 d,
Ivan
Hung
e,
Zhehong
Gan
e,
Kevin
Huang
b and
Yan-Yan
Hu
d,
Ivan
Hung
e,
Zhehong
Gan
e,
Kevin
Huang
b and
Yan-Yan
Hu
 *ae
*ae
aDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32306, USA. E-mail: hu@chem.fsu.edu
bDepartment of Mechanical Engineering, University of South Carolina, Columbia, SC 29208, USA
cDepartment of Scientific Computing, Florida State University, Tallahassee, FL 32306, USA
dInstitute for Molecules and Materials, Radboud University, Nijmegen, AJ 6525, Netherland
eCentre of Interdisciplinary Magnetic Resonance, National High Magnetic Field Laboratory, 1800 East Paul Dirac Drive, Tallahassee, FL 32310, USA
First published on 17th February 2016
Abstract
Understanding the local structure and ion dynamics is at the heart of ion conductor research. This paper reports on high-resolution solid-state 29Si, 23Na, and 17O NMR investigation of the structure, chemical composition, and ion dynamics of a newly discovered fast ion conductor, Na-doped SrSiO3, which exhibited a much higher ionic conductivity than most of current oxide ion conductors. Quantitative analyses reveal that with a small dose (<10 mol%) of Na, the doped Na integrates into the SrSiO3 structure to form NaxSr1−xSiO3−0.5x, and with >10 mol% Na doping, phase separation occurs, leading to the formation of an amorphous phase β-Na2Si2O5 and a crystalline Sr-rich phase. Variable-temperature 23Na and 17O magic-angle-spinning NMR up to 618 °C have shown significant changes in Na ion dynamics at high temperatures but little oxide ion motion, suggesting that Na ions are responsible for the observed high ionic conductivity. In addition, β-Na2Si2O5 starts to crystallize at temperatures higher than 480 °C with prolonged heating, resulting in reduction in Na+ motion, and thus degradation of ionic conductivity. This study has contributed critical evidence to the understanding of ionic conduction in Na-doped SrSiO3 and demonstrated that multinuclear high-resolution and high-temperature solid-state NMR is a uniquely useful tool for investigating ion conductors at their operating conditions.
Introduction
A new family of complex oxides with an apparent composition NaxSr1−xSiO3−0.5x (SNS hereinafter) has recently been reported as a potential solid-state oxide-ion electrolyte.1,2 The ionic conductivity of SNS with x = 0.45 reaches 0.01 S cm−1 at 500 °C, the highest among all known chemically stable oxide-ion conductors. Due to the significance of an ion conductor with high conductivity in electrochemical devices such as fuel cells, batteries, separation membranes, and sensors, SNS immediately garnered much attention and invited a number of follow-up studies after the first publication. The origin and mechanism of the ionic conduction observed in SNS were the two most discussed and debated topics. The original work by Singh et al.1 and Martinez-Coronado et al.3 with high-temperature neutron diffraction studies suggested that oxide-ion conduction via oxygen vacancies created by Na-doping was responsible for the observed high conductivity. This hypothesis appeared to be supported by Xu et al. with 29Si NMR studies on a similar system, i.e., K-doped SrSiO3.3,4 On the other hand, Bayliss et al.5 argued that SNS was virtually a mixture of a SrSiO3 phase and a glassy phase with a degrading conductivity. Their DFT calculations concluded that creation of oxygen vacancies by Na-doping was energetically prohibitive.5 The subsequent ToF-SIMS measurement revealed a very low oxygen diffusion coefficient,5 suggesting that oxide-ion conduction in SNS was indeed negligible and other ions should be responsible for the conduction. Several very recent studies further supported Bayliss's arguments on the two-phase composition and identified the glassy phase as Na2Si2O5 by 29Si NMR.6,7 Jee et al.8 also proved that the high conductivity of SNS was originated from the glassy Na2Si2O5 and the degradation of conductivity stemmed from the crystallization of the glassy Na2Si2O5 by high-temperature XRD and thermal analysis.While these early studies suggested that the glassy Na2Si2O5 phase was responsible for the high conductivity, the identity of ions responsible for high ionic conduction in the glassy Na2Si2O5 remains ambiguous. A very recent ab initio molecular dynamics simulations on the glassy Na2Si2O5 phase suggested that Na ions possess higher mobility in the structure compared with oxide ions9 and variable-temperature 23Na NMR spectroscopy and T1 relaxation time measurements demonstrated Na-ion mobility from room temperature to 350 °C.10 However, experimental evidence is necessary to explain the temperature-dependence of Na+ conduction at the operating temperature of SNS and experimental tools are needed to directly probe the O2− dynamics. It is extremely challenging to use conventional diffraction methods to obtain information on local structural defects and to be specific enough in determining chemical phases with elemental mapping methods.11
Solid-state NMR possesses unique capabilities of probing the local defect structure and ion dynamics in ion conductors.12–1929Si NMR has been previously demonstrated to help understand the silicate network in SNS and to be useful for preliminary identification of chemical phases.4–7 However, the information obtained was largely relevant to the local structural environment of SiOx, not Na+ or O2− of interest. In fact, 23Na and 17O NMR have been employed in limited studies in the area of energy materials research due to the great challenges in detection sensitivity and spectral resolution. 23Na and 17O NMR often require high magnetic field and fast sample spinning in order to achieve high spectral resolution for reliable quantification. In particular, 17O NMR is a very powerful tool for studying O2− local structure and dynamics. However, due to the low natural abundance and low gyromagnetic ratio of the 17O isotope, 17O NMR is highly challenging in data acquisition and its invaluable potential in addressing critical questions in the area of oxide ion conductors has not been fully exploited.
In this paper, we report the employment of high-resolution 23Na, 17O and 29Si NMR to track changes in the local structural environments of Na+ and O2− and the silicate framework of SNS. Careful chemical phase identification and quantification based on high-resolution NMR spectra were performed to understand the evolution in chemical phase composition when the Na content was gradually increased in SNS. Variable-temperature (VT) 23Na and 17O Magic-Angle-Spinning (MAS) NMR experiments were also carried out from room temperature to 618 °C on the sample (SNS45, i.e., x = 0.45 in the apparent composition NaxSr1−xSiO3−0.5x) with the highest ionic conductivity to probe the Na+ and O2− dynamics. This comprehensive study on chemical composition, local structure, and ion dynamics provides strong and direct experimental evidence for resolving the current debate on the origin of high ionic conductivity observed in SNS. The study is essential in that it helps assess the prospects of SNS as a potential O2− or Na+ conductor and provides guidelines for designing alternative ion conductors. It also demonstrates to the energy materials research community at large that advanced solid-state NMR is a versatile tool to address the most relevant questions in the field of ion conductors.
Results
SiOx structural frame
29Si NMR spectra of SNS0, SNS10, SNS20, SNS30, SNS40, SNS45, SNS70, and β-Na2Si2O5 were acquired to investigate the effects of Na doping on the SiOx structural frame and chemical phase composition. As shown in Fig. 1, the 29Si spectrum of SNS0 (without Na doping) shows a single sharp resonance at −85 ppm, assigned to Si3O9 sites in α-SrSiO3.4–7 With 10 mol% Na doping (SNS10), three distinct Si local environments are observed. In addition to the α-SrSiO3 resonance at −85 ppm, a broad component centred also at −85 ppm and a third peak at −77 ppm are shown. The α-SrSiO3 peak slightly broadens with the full width at half maximum (FWHM) increased from 40 Hz in SNS0 to 66 Hz in SNS10 compared with that of SNS0, suggesting long-range structural effects of Na doping. The broad resonance at −85 ppm with a FWHM of 0.93 kHz is from Si close to doped Na in the α-SrSiO3 phase, i.e. Sr(Na)SiO3 in Fig. 1, which accounts for about 1/3 of total Si amount. Significant difference in 29Si T1 relaxation times between the sharp (>10 s) and broad (<1 s) 29Si moieties is observed. The −77 ppm peak is from the Q2 site of Na2SiO3. This peak is also seen as a minor component with slight variation in percentage in other samples such as SNS40, SNS45, and synthesized β-Na2Si2O5. Na2SiO3 is readily observed due to the similar conditions for synthesis as for SNS samples.20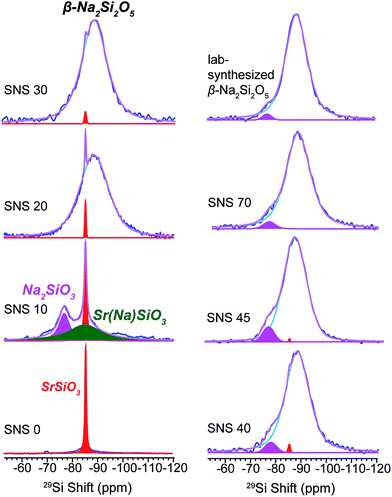 | ||
| Fig. 1 29Si MAS NMR spectra of Na-doped SrSiO3 (with apparent composition of NaxSr1−xSiO3−0.5x) with different Na contents (x = 0, 0.1, 0.2, 0.3, 0.4, 0.45 and 0.70, denoted as SNS0, SNS10, SNS20, SNS30, SNS40, SNS45 and SNS70, respectively) and lab-synthesized β-Na2Si2O5. Relevant resonance assignments, including SrSiO3 (red), SrSiO3 with Na doped within the structure (Sr(Na)SiO3, green), Na2SiO3 (magenta), and β-Na2Si2O5 (blue) are marked on the spectra. Spectral simulations are displayed together with the experimental spectra. All the NMR parameters used for the simulations are listed in Table S1.† | ||
As the Na doping content is further increased to more than 10 mol%, a broad 29Si peak centred at −89 ppm gradually replaces the α-SrSiO3 resonance (−85 ppm, sharp) and the resonance of Si close to doped Na (Sr(Na)SiO3, −85 ppm, broad). This new peak bears close resemblance to the 29Si resonance of synthesized β-Na2Si2O5, a broad peak centred at −89 ppm with a FWHM of 0.62 kHz (top right in Fig. 1). With Na content more than 40 mol%, very little change in the 29Si spectra is observed, except slight narrowing of the −89 ppm peak. The original α-SrSiO3 resonance is barely visible and the Na2SiO3 peak appears as a very minor component.
29Si NMR is a good probe for changes in the SiOx framework; however, it reveals very little information about the functional ions, i.e., Na and O ions. 23Na and 17O NMR are more direct tools for studying the structure–function relationship in ion conductors but less commonly employed due to much greater challenges in data acquisition and analysis compared with NMR of spin-1/2 nuclei such as 29Si. 23Na and 17O are both quadrupolar nuclei with non-integer spins (I = 3/2 for 23Na and 5/2 for 17O, respectively) and are thus subject to quadrupolar effects displacing resonances from their isotropic chemical positions. The strong quadrupolar interactions significantly broaden NMR spectra and thus compromise spectral resolution. Advanced capabilities, including fast sample spinning, high magnetic fields, and special techniques such as multiple-quantum MAS NMR, have been implemented to achieve high resolution. Spectral deconvolution combined with DFT NMR calculations helps to further resolve various Na and O local environments.
Fate of doped Na
23Na NMR is helpful in identifying the local structural and compositional environments of the doped Na ions, which sheds light on the underlying reasons why Na doping improves the ionic conductivity of SNS.As seen in Fig. 2, four Na resonances are observed in the 23Na NMR spectra of all SNS samples. The two resonances at high field (small chemical shifts) in the 23Na spectrum of SNS10 are from Na in the SrSiO3 phase, i.e. Sr(Na)SiO3. These two Na sites in Sr(Na)SiO3 are quite different from those in β-Na2Si2O5, which was found in SNS samples with higher Na contents. The CQ (quadrupolar couplings constant, a measure of the strength of quadrupolar couplings) values of the two Na sites in Sr(Na)SiO3 are 1.8 MHz and 0.47 MHz, respectively, while the typical CQ values of the two Na sites in crystalline β-Na2Si2O5 are 2.3 MHz.20 In SNS samples with higher Na contents (>10 mol%), these two Na resonances convert to resonances similar to those of the synthesized β-Na2Si2O5 (Fig. 2). The larger CQ values (2.4 and 4.3 MHz) of 23Na NMR resonances for the synthesized β-Na2Si2O5 (2.3 MHz), compared with those for crystalline β-Na2Si2O5, suggest significant structural disorder of the synthesized β-Na2Si2O5. It is worth noting that the synthesized β-Na2Si2O5 phase is not pure, which contains 4 mol% of crystalline Na2SiO3 and 15% NaOH. Again, it was reported previously that the synthesis condition for Na2SiO3 and β-Na2Si2O5 are very similar and co-existence of these phases were observed.20
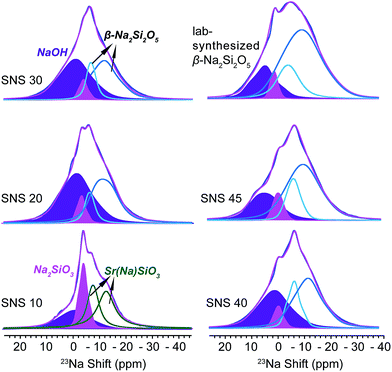 | ||
| Fig. 2 23Na MAS NMR spectra of SNS10, SNS20, SNS30, SNS40, SNS45, and lab-synthesized β-Na2Si2O5. Relevant resonance assignments, including SrSiO3 with Na doped within the structure (Sr(Na)SiO3, green), Na2SiO3 (magenta), NaOH (purple), and β-Na2Si2O5 (cyan and blue) are marked on the spectra. Spectral simulations are displayed together with the experimental spectra. All the parameters used for the simulations are listed in Table S2.† | ||
The remaining two peaks in the spectrum of SNS10 are from impurity phases, the broad peak at 8 ppm with a relatively large CQ of 3.5 MHz is assigned to NaOH, based on the 23Na NMR shift and CQ of NaOH in previous reports.21 This assignment is confirmed by comparing the 23Na NMR spectra of NaOH, SNS30, and β-Na2Si2O5 (see Fig. S1†). The peak next to the NaOH resonance is from Na2SiO3, of which the isotropic shift is −1.1 ppm and CQ 2.0 MHz. Very little variations are observed for the resonances of NaOH and Na2SiO3 in SNS samples with increasing Na contents. The content of NaOH and Na2SiO3 remains below 10 mol% in SNS samples, and fluctuates (Table S5†) without a trend, likely depending on possible temperature variations during the synthesis and exposure to H2O in the air.
Changes of O2− environments
Since SNS was designed for use as an oxide ion conductor in intermediate-temperature SOFCs, the effects of Na doping on local structural environments and dynamics of oxide ions are most relevant for its intended applications. 17O NMR is a powerful tool to probe the local environments and to investigate the dynamics of oxide ions. The extremely low sensitivity of 17O NMR renders the data acquisition very challenging. In order to obtain 17O NMR spectra with good signal-to-noise ratios for reliable interpretation, 17O-isotope enrichment of SNS samples was carried out. The sensitivity of 17O NMR was enhanced by a factor of around 180 times, which is equivalent to 0.037 mol% × 180 = 6.66 mol% 17O in the isotope-enriched samples. The 17O isotope enrichment was achieved through the isotope exchange of 16O in the sample with 17O in the 17O2 gas, and the enrichment level strongly depends on the diffusivity of oxide ions in the sample. This relatively low enrichment level (<10 mol%) suggests low O2− diffusivity in SNS (Fig. S2†).The enrichment process with careful temperature and time control does not alter the structure of pristine SNS samples, indicated by the resemblance of the 17O spectra of SNS45 with and without isotope enrichment, shown in Fig. S2.† This resemblance also suggests non-preferential enrichment of different oxygen sites and implies that all oxide ions have equally low diffusivity.
17O MAS NMR spectra of 17O-enriched SNS10, SNS30 and SNS45 samples are shown in Fig. 3. In the 17O spectrum of SNS10, the two resonances in red are assigned to α-SrSiO3. Of the two resonances, the one with an isotropic shift of 109 ppm and a CQ of 2.8 MHz is assigned to the non-bridging oxygen (nbo) sites in α-SrSiO3 and the other with a chemical shift of 79 ppm and a CQ of 3.9 MHz is from the bridging oxygen (bo) sites in α-SrSiO3.22 The ratio of the nbo to bo sites is very close to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, consistent with the crystal structure of α-SrSiO3. A very broad peak spanning over more than 250 ppm with a centre around 126 ppm is likely from the disordered O sites in the Sr(Na)SiO3 phase. The great breadth of this 17O NMR peak echoes with the large linewidth of the 29Si NMR resonance of the same phase. This phase contains about 27% of the total oxygen content. The weak and broad resonance at 66 ppm with a CQ around 8.3 MHz is assigned to NaOH. Naturally, the resonances of Na2SiO3 are seen, with the peak from the bo site at 72 ppm with a CQ of 4.7 MHz and that of the nbo site at 39 ppm with a CQ of 2.3 MHz. The ratio of these two oxygen sites is 1
1, consistent with the crystal structure of α-SrSiO3. A very broad peak spanning over more than 250 ppm with a centre around 126 ppm is likely from the disordered O sites in the Sr(Na)SiO3 phase. The great breadth of this 17O NMR peak echoes with the large linewidth of the 29Si NMR resonance of the same phase. This phase contains about 27% of the total oxygen content. The weak and broad resonance at 66 ppm with a CQ around 8.3 MHz is assigned to NaOH. Naturally, the resonances of Na2SiO3 are seen, with the peak from the bo site at 72 ppm with a CQ of 4.7 MHz and that of the nbo site at 39 ppm with a CQ of 2.3 MHz. The ratio of these two oxygen sites is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which agrees with the structure of Na2SiO3. The oxygen fraction from the impurity phases, i.e., NaOH and Na2SiO3 is less than 10 mol%.
1, which agrees with the structure of Na2SiO3. The oxygen fraction from the impurity phases, i.e., NaOH and Na2SiO3 is less than 10 mol%.
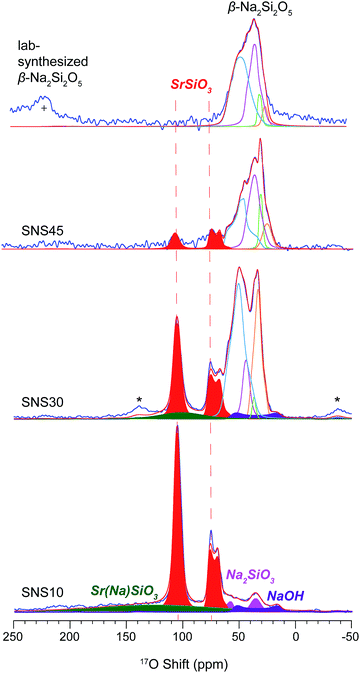 | ||
| Fig. 3 17O MAS NMR spectra of SNS10, SNS30, SNS45, and lab-synthesized β-Na2Si2O5. All the samples are 17O-isotope enriched, except the synthesized β-Na2Si2O5. Relevant resonance assignments, including SrSiO3 (red), SrSiO3 with Na doped within the structure (Sr(Na)SiO3, green), Na2SiO3 (magenta), NaOH (purple), and β-Na2Si2O5 (cyan and blue lines) are marked on the spectra. Spectral simulations (red lines) are displayed together with the experimental spectra (blue lines). All the parameters used for the simulations are listed in Table S3.† * marks the spinning sidebands. + denotes the one of the spinning sidebands from the 17O NMR resonance of ZrO2 rotor at 370 ppm. | ||
In the 17O spectrum of SNS30, the 17O peaks at 109 ppm and 80 ppm are assigned to an intermediate Sr-rich phase transformed from α-SrSiO3 due to Na doping, but with significant reduction in intensity compared with those of α-SrSiO3 in SNS10. The content of the nbo sites is reduced from 40% to 15%, while that of the bo sites from 19% to 10%. The increase in the ratio of bo sites to nbo sites from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (in SNS10) to 3
1 (in SNS10) to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (in SNS30) suggests fusion of the metasilicate structural framework. The weak broad Sr(Na)SiO3 resonance is also observed with the position shifted to higher field by 25 ppm (from 126 ppm in SNS10 to 101 ppm in SNS30). Our DFT calculations also show 17O resonances of O sites close to Na appearing at a higher field than those of O sites further away from Na (Fig. S4†) The content of Sr(Na)SiO3 is decreased from 27% in SNS10 to 6% in SNS30. At the expense of Sr-rich phases, the percentage of the β-Na2Si2O5-like phase grows, manifested by multiple resonances between 10–65 ppm. Four 17O environments are resolved with spectral analysis based on typical CQ and shifts from our DFT calculations and previous reports.23 The 63 ppm resonance with a CQ of 4.5 MHz is very similar to the 17O NMR signature of one of the bo sites in β-Na2Si2O5 (Fig. 3 and Table S3†). The other bo site (with a shift of 47 ppm and a CQ of 2.7 MHz) has a smaller shift and CQ compared with the corresponding site in β-Na2Si2O5. The resonances with shifts of 40 and 39 ppm and CQ values of 3.3 MHz and 2.1 MHz, respectively, are assigned to nbo sites of this β-Na2Si2O5-like phase.
2 (in SNS30) suggests fusion of the metasilicate structural framework. The weak broad Sr(Na)SiO3 resonance is also observed with the position shifted to higher field by 25 ppm (from 126 ppm in SNS10 to 101 ppm in SNS30). Our DFT calculations also show 17O resonances of O sites close to Na appearing at a higher field than those of O sites further away from Na (Fig. S4†) The content of Sr(Na)SiO3 is decreased from 27% in SNS10 to 6% in SNS30. At the expense of Sr-rich phases, the percentage of the β-Na2Si2O5-like phase grows, manifested by multiple resonances between 10–65 ppm. Four 17O environments are resolved with spectral analysis based on typical CQ and shifts from our DFT calculations and previous reports.23 The 63 ppm resonance with a CQ of 4.5 MHz is very similar to the 17O NMR signature of one of the bo sites in β-Na2Si2O5 (Fig. 3 and Table S3†). The other bo site (with a shift of 47 ppm and a CQ of 2.7 MHz) has a smaller shift and CQ compared with the corresponding site in β-Na2Si2O5. The resonances with shifts of 40 and 39 ppm and CQ values of 3.3 MHz and 2.1 MHz, respectively, are assigned to nbo sites of this β-Na2Si2O5-like phase.
The 17O spectrum of SNS45 is dominated by peaks primarily from the β-Na2Si2O5 phase, accounting for about 88% of the total O content. The remaining O comes from the Sr-rich phase. The β-Na2Si2O5 phase in SNS45 resembles very closely the synthesized β-Na2Si2O5, suggested by similar 17O resonances. The two resonances at lower field with shifts of 58 ppm and 41 ppm and CQ values of 5.0 MHz and 4.0 MHz, respectively, are from the bo sites in β-Na2Si2O5. The remaining two peaks with shifts of 30 ppm and 25 ppm and CQ values of 2.1 MHz and 2.3 MHz, respectively, are from the nbo sites in β-Na2Si2O5. The 17O peaks in the spectrum of synthesized β-Na2Si2O5 are slightly broader than those of the β-Na2Si2O5 phase in SNS45, indicating an increased degree in structural disorder.
The resonances from the Sr-rich phase at 109 ppm and 79 ppm are again reduced not only in peak intensity but also in the ratio of nbo-to-bo (from 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in SNS30 to 1
2 in SNS30 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in SNS45). The decrease in the ratio of nbo sites to bo sites indicates further fusion of the silicate framework. The 29Si and 17O signatures of this Sr-rich phase do not match those of Sr2SiO4 as proposed in previous report.10
1 in SNS45). The decrease in the ratio of nbo sites to bo sites indicates further fusion of the silicate framework. The 29Si and 17O signatures of this Sr-rich phase do not match those of Sr2SiO4 as proposed in previous report.10
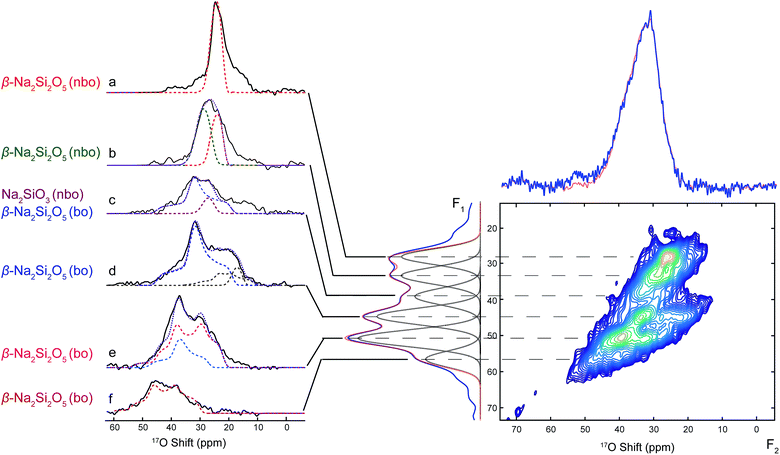
Due to second-order quadrupolar broadening, the resolution of 1D 17O NMR spectra is often insufficient for distinguishing individual oxide sites, despite that high magnetic field and fast MAS have been employed in the 1D 17O NMR data acquisition. In order to achieve higher resolution, two-dimensional multiple quantum magic-angle spinning (MQMAS) NMR experiments were implemented to separate quadrupolar coupling effects from chemical shift interactions. Therefore, 1D 17O projection NMR spectra with highest possible resolution could be obtained in the indirect dimension (F1 dimension or isotropic dimension). The quadrupolar pattern for each isotropic site can be extracted in the direct dimension (F2 dimension) for more accurate determination of quadrupolar parameters, which contains rich structural information.
The MQMAS NMR spectrum shown in Fig. 4 was acquired on 17O-enriched SNS45. In the indirect (F1) dimension of the sheared 2D MQMAS NMR spectrum, a projection spectrum was obtained with six resonances shown at their isotropic shift positions. The corresponding quadrupolar pattern (Fig. 4a–f) for each resonance was extracted by taking a cross section along the F2 dimension at the respective isotropic shift position, which reveals information on the local environment of each oxygen site. The short 17O T2 relaxation times limit the resolution of the isotropic spectrum; therefore, overlap between the isotropic peaks in the F1 dimension is observed. As a result, the corresponding quadrupolar patterns are also overlapped to certain extent. Nevertheless, it is still possible to more clearly resolve individual O sites with MQMAS than with regular 1D 17O MAS NMR. The isotropic shifts of the O sites are determined from the projection spectrum in F1 dimension and the corresponding quadrupolar coupling parameters are obtained from simulations of the cross sections in F2. Among the six components, the two at 28 ppm (Fig. 4a, red dashed line) and 32 ppm (Fig. 4b, green dashed line) are from the nbo sites in β-Na2Si2O5; and the small quadrupolar couplings of 2.5 MHz and 2.8 MHz are close to our DFT calculations (Table S8†). Fig. 4d (navy blue dashed line), Fig. 4e (violet red and dodger blue lines), and Fig. 4f (dark red) show the quadrupolar patterns of the bo sites in β-Na2Si2O5 with isotropic shifts at 45 ppm, 51 ppm and 58 ppm, respectively. Two of the three bo sites have similar CQ (4.5 and 4.1 MHz) while the third site with the isotropic shift of 58 ppm has a larger CQ of 5.2 MHz. All the five oxygen sites in β-Na2Si2O5 have been resolved with the MQMAS experiment and the results of spectral analysis assisted with simulations are consistent with our DFT NMR calculations (Table S8†).
Quantified evolution in SiOx, Na, and O
Quantification of different chemical phases in SNS samples has been carried out based on the 29Si, 23Na, and 17O NMR spectra. The results are summarized in Fig. 5, S4, and Tables S4–S6.† Although the accuracy of NMR quantification for quadrupolar nuclei is often compromised by different relaxation behaviours, it is still helpful to qualitatively follow the trend of phase evolution with increasing Na doping content in SNS. Quantification based on 29Si, 23Na, and 17O NMR consistently indicates the same pattern of phase transition accompanied by structural transformation. The changes in the content of the three major phases, i.e., α-SrSiO3 (including SrSiO3-derived phases), Sr(Na)SiO3, and β-Na2Si2O5, found in SNS upon increasing the Na doping content is illustrated in Fig. 5. It is shown that with little (<10 mol%) or no Na doping, α-SrSiO3 is the dominant phase (> mol50%). As the Na doping amount is increased to 10 mol% (SNS10), the phase fraction of α-SrSiO3 drops dramatically while the fraction of the intermediate phase Sr(Na)SiO3 reaches its maximum. With further increase in Na-content to 20 mol%, α-SrSiO3 continuously decreases to less than 10 mol%. Gradual conversion from the intermediate phase Sr(Na)SiO3 to β-Na2Si2O5 is observed. In SNS samples with more than 20 mol% Na doping, β-Na2Si2O5 becomes the dominant component among the three major phases.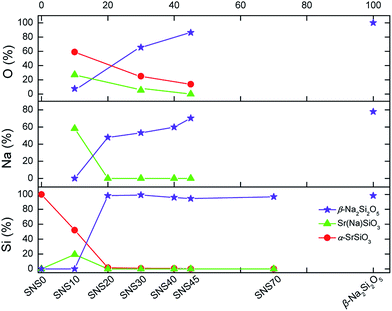 | ||
| Fig. 5 Quantification of Si, Na, and O in various chemical phases in SNS samples based on the area integral of the 29Si, 23Na, and 17O NMR spectra in Fig. 1–3. | ||
The complete quantification results, including impurity phases such as NaOH and Na2SiO3 and more detailed classification of various Na and O sites within the same phases, are documented in Tables S5 and S6 and plotted in Fig. S4.† A close examination of the evolution of various Na and O sites reveals information on gradual structure transition. Take the full quantification data from 23Na NMR as an example first, the initial dose of Na goes into the pristine structure α-SrSiO3 to form Sr(Na)SiO3. The ratio of the two Na sites in Sr(Na)SiO3 is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Further addition of Na leads to the formation of β-Na2Si2O5 and the ratio of the two Na sites in β-Na2Si2O5 stays nearly constant, i.e., 1
1. Further addition of Na leads to the formation of β-Na2Si2O5 and the ratio of the two Na sites in β-Na2Si2O5 stays nearly constant, i.e., 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, similar to that in the lab-synthesized β-Na2Si2O5. From the detailed quantification of 17O NMR, we can also gain additional information regarding the structural changes. In the initial structure of α-SrSiO3, the ratio of the nbo and bo is 2
3, similar to that in the lab-synthesized β-Na2Si2O5. From the detailed quantification of 17O NMR, we can also gain additional information regarding the structural changes. In the initial structure of α-SrSiO3, the ratio of the nbo and bo is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The vanishing rates of these two O sites are quite different. The nbo sites disappearing much faster than the bo sites as Na is added into SNS, which brings the ratio of nbo and bo close to 1
1. The vanishing rates of these two O sites are quite different. The nbo sites disappearing much faster than the bo sites as Na is added into SNS, which brings the ratio of nbo and bo close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in SNS45.
1 in SNS45.
Na and O ion dynamics
The dynamics of Na+ and O2− have been probed via the changes in 23Na and 17O NMR spectral lineshape of SNS45 over a broad temperature range from room temperature (RT) to 618 °C. In 23Na and 17O MAS NMR, the spectral broadening is mainly due to the different orientations of crystallites in the powder sample, quadrupolar coupling, and dipolar coupling.24 Ion motions at elevated temperatures average out some of the interactions and this motional effect manifests in the spectra as the narrowing of the peaks.23Na variable-temperature NMR spectra in Fig. 6a reveal gradual changes in Na+ dynamics as the temperature is increased. At RT, a Gaussian lineshape is observed, broadened due to random crystallite orientations and 23Na quadrupolar and dipolar couplings. As the temperature was increased to 419 °C, continuous narrowing of the peak occurs. Meanwhile, the transition from a Gaussian to a Lorentzian shape is seen. The linewidth of a solid-state NMR resonance is determined by homogeneous and/or inhomogeneous broadening. Inhomogeneous broadening is often resulted from a distribution of local structural environments of the nuclei and leads to a Gaussian lineshape. Homogeneous broadening is usually caused by the relaxation of the nuclear polarization. Ion dynamics modulates the local magnetic field and introduces perturbation to various spin–spin and spin–lattice interactions, and this perturbation further manifests as exponential decay of the magnetization. The Fourier transform of an exponential decay yields Lorentzian lineshapes. More often than not, the lineshapes of NMR resonances are a combination of Gaussian and Lorentzian with one of them shown as the predominant feature. In the case of SNS, at low temperature, the Na ion dynamics is slow, and the relaxation of the magnetization is also relatively slow (as seen from T1 relaxation time constant measurements of 23Na NMR),10 thus inhomogeneous broadening yields the observed Gaussian lineshape. The increase in temperature allows faster Na ion motions. On one hand, Na ion motion reduces inhomogeneous broadening by averaging out the orientation difference in local structural environments; on the other hand, faster Na ion motion leads to more rapid relaxation of 23Na magnetization thus increased homogeneous broadening.10 Therefore, diminishing inhomogeneous broadening and increasing homogeneous broadening give rise to a transition from a Gaussian to a Lorentzian lineshape of the 23Na resonance at high temperatures. Further increase in temperature from 419 °C up to 618 °C returns 23Na resonances back to a Gaussian shape with increased peak width. Upon slow cooling of the sample to RT, another spectrum was acquired, which overlays completely with the spectrum collected before variable-temperature experiments. 17O NMR (Fig. 6b) shows little or no change in the peak shape or width as the temperature was increased from RT to 618 °C. The 17O NMR spectra acquired before and after heating are very similar.
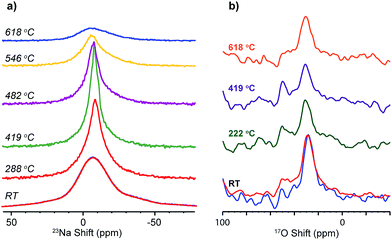 | ||
| Fig. 6 Variable high-temperature (a) 23Na, and (b) 17O solid-state MAS NMR spectra of SNS45, acquired at a spinning speed of 5 kHz. | ||
Discussion
Multinuclear high-resolution solid-state MAS NMR characterizations of the SNS series provide useful insights into the composition, structure, and ion dynamics of this fast ion conductor. 29Si, 23Na, and 17O NMR have clearly and consistently revealed the gradual changes in chemical phase composition and structure with increasing Na doping amount. These gradual changes correlate well with the continuous improvement in ionic conductivity up to 45 mol% Na doping (SNS45).With Na doping less than 10 mol% in SNS, the initial dose of Na incorporates into the α-SrSiO3 structure to form a structurally disordered phase Sr(Na)SiO3, i.e. NaxSr1−xSiO3−0.5x. Approximately 46% of the original α-SrSiO3 structure is affected by Na doping with 54% remaining crystalline. The disordered Sr(Na)SiO3 and crystalline α-SrSiO3 phases co-exist but are spatially separated. The spatial separation of Sr(Na)SiO3 and α-SrSiO3 is indicated by the significant difference in 29Si T1 relaxation times of Sr(Na)SiO3 (<1 s) and α-SrSiO3 (>10 s) resonances. This agrees with previous ToF-SIMS mapping of an analogous compound Sr0.8K0.2Si0.5Ge0.5Si2.9 showing an inhomogeneous elemental distribution.5 α-SrSiO3 remains crystalline as shown by its sharp peak in 29Si NMR and the two well-defined quadrupolar patterns in 17O NMR. The area integral ratio of the two oxygen peaks representing the two oxygen sites (nbo and bo) in α-SrSiO3 is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, consistent with its crystal structure, which also supports that this phase remains largely unaffected by small amount of Na doping. In Sr(Na)SiO3, strictly speaking, Na does not simply occupy the position of Sr; instead it takes up two inequivalent chemical sites. The local environments of these two Na sites, although bearing a certain degree of resemblance to the two Na sites in β-Na2Si2O5, are better defined compared to those in β-Na2Si2O5, as indicated by the relatively narrower linewidth. Also, the occupancy ratio of the two sites in Sr(Na)SiO3 obtained from 23Na NMR is close to 1
1, consistent with its crystal structure, which also supports that this phase remains largely unaffected by small amount of Na doping. In Sr(Na)SiO3, strictly speaking, Na does not simply occupy the position of Sr; instead it takes up two inequivalent chemical sites. The local environments of these two Na sites, although bearing a certain degree of resemblance to the two Na sites in β-Na2Si2O5, are better defined compared to those in β-Na2Si2O5, as indicated by the relatively narrower linewidth. Also, the occupancy ratio of the two sites in Sr(Na)SiO3 obtained from 23Na NMR is close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, while in the synthesized β-Na2Si2O5, the ratio of the two Na sites is found to be 1
1, while in the synthesized β-Na2Si2O5, the ratio of the two Na sites is found to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. Therefore, Sr(Na)SiO3 is an intermediate phase from α-SrSiO3 to β-Na2Si2O5. The conductivity measurements of SNS showed that even with only 10 mol% Na doping, four orders of magnitude increase in ionic conductivity is observed compared with crystalline α-SrSiO3.7 Based on the analysis above, the source of the ionic conductivity boost is likely from the 46% disordered Sr(Na)SiO3 phase with very little contribution from the 54% crystalline α-SrSiO3 phase.
3. Therefore, Sr(Na)SiO3 is an intermediate phase from α-SrSiO3 to β-Na2Si2O5. The conductivity measurements of SNS showed that even with only 10 mol% Na doping, four orders of magnitude increase in ionic conductivity is observed compared with crystalline α-SrSiO3.7 Based on the analysis above, the source of the ionic conductivity boost is likely from the 46% disordered Sr(Na)SiO3 phase with very little contribution from the 54% crystalline α-SrSiO3 phase.
With Na doping content between 10–40 mol% in SNS, the crystalline α-SrSiO3 phase continues to diminish and the remaining crystalline phase transforms to an intermediate Sr-rich phase, meanwhile a gradual phase transition from Sr(Na)SiO3 to β-Na2Si2O5 occurs. In this region, the α-SrSiO3 phase decreases to less than 10% of its original quantity. Continuous fusion of the SiOx framework in the Sr-rich phase is suggested by the increased ratio of bo to nbo sites in 17O NMR. The Sr-rich phase still remains crystalline and isolated, as evidenced by the sharp resonance in 29Si NMR and the well-defined quadrupolar 17O NMR patterns. The β-Na2Si2O5 phase grows at the expense of both α-SrSiO3 and Sr(Na)SiO3. The transition from Sr(Na)SiO3 to β-Na2Si2O5 is much faster than that from α-SrSiO3 to Sr(Na)SiO3. Therefore, Sr(Na)SiO3 is hardly visible in SNS30 and beyond. As manifested in the gradual changes in the 23Na and 17O NMR resonances, the structural adjustment from Sr(Na)SiO3 to β-Na2Si2O5, occurs via a gradual instead of a one-step process. The shifts of the two Na peaks continuously move downfield close to those in β-Na2Si2O5. Also, the 23Na quadrupolar coupling constants are gradually increased to match those in β-Na2Si2O5. The increase in quadrupolar coupling constants is a strong indication of structural disorder, which is promoted by the addition of Na into SNS. 17O NMR data also clearly illustrates the progressive changes from a different perspective. 17O NMR indicates that Sr(Na)SiO3 first converts to a “β-Na2Si2O5-like” phase with approximately equal amount of bo and nbo (terminal) sites while in the synthesized β-Na2Si2O5 sample, there is much greater representation of bo than that of nbo; this indicates a re-adjustment of the SiOx framework to facilitate the phase transition. The “β-Na2Si2O5-like” phase has a more ordered structure compared with the synthesized β-Na2Si2O5, as suggested by the relatively smaller 17O CQ parameters of the “β-Na2Si2O5-like” resonances. In this region, the ionic conductivity continues to see significant improvement as the Na content is increased. This closely follows the trend of the continuous decrease in the content of the crystalline Sr-rich phase and increase in the fraction of structurally disordered component, i.e. the “β-Na2Si2O5-like” phase.
With increasing Na content more than 40 mol% in SNS, a small decrease in the content and minimal structural changes of the Sr-rich phase are observed. Both 29Si and 17O NMR spectra suggest a Si2O5 network. In addition to the Sr-rich phase, NMR signatures of the dominant phase formed in SNS are very similar as those of the synthesized β-Na2Si2O5. The improvement in ionic conductivity beyond 40 mol% Na doping is very limited, which echoes with only small changes in composition or structure of the SNS composites.
Overall, Na doping into SrSiO3 leads to formation of structurally disordered phases including Sr(Na)SiO3 and β-Na2Si2O5 and a crystalline Sr-rich phase. The content of Sr(Na)SiO3 and β-Na2Si2O5 correlates well with the change in the total ionic conductivity of SNS. No significant changes in structure or composition, thus ionic conductivity, have been observed for compositions with more than 40 mol% Na doping.
Na+ and O2− motions are probed by the variable high-temperature MAS NMR. The narrowing of 23Na NMR peaks and the lineshape transformation from Gaussian to Lorentzian from RT to 419 °C indicate increase in Na+ motions, consistent with a most recent 23Na variable-temperature study over a range from room temperature to 350 °C.10 Then with the temperature increased beyond 480 °C, the 23Na peaks are broadened again accompanied by the return of a Gaussian lineshape. This unusual behaviour, deviating from expected further increase in Na ion motions with higher temperature, is likely caused by the onset of a crystallization process at high temperatures, which inevitably slows down the Na+ ion motions. This is consistent with the recent degradation studies of amorphous Na2Si2O5 at temperatures higher than 500 °C, which shows the transformation of amorphous Na2Si2O5 to crystalline Na2Si2O5 based on the high-temperature XRD data and decreased ionic conductivity was observed as a result of the phase transition.8 On the other hand, no motional narrowing of the 17O resonance was observed with temperature increased up to 618 °C, suggesting minimal O2− motion. Based on the analysis above, it is likely that mainly Na ions are responsible for the high ionic conductivity measured at temperatures below 500 °C. This finding contradicts the earlier studies suggesting O2− conduction in this material,1,2 but agrees with recent reports showing that the material is virtually a mixture of amorphous Na2Si2O5 and crystalline SrSiO3;5–8 the former has been predicted as a Na+ conductor by MD simulations9 and NMR measurements.10
It is worth noting that sufficient ion dynamics is a necessary condition for good ion conduction. Ion dynamics include both local motion and long-range diffusional motion, and only the diffusional motion effectively contributes to ion conduction. The ion diffusivity can often be measured by pulse field gradient (PFG) NMR. However, due to very short relaxation times on the order of milliseconds of 23Na NMR resonance for SNS,10 the estimated diffusivity based on the measured ion conductivity1,2 is below the limit of the state-of-the-art PFG NMR for reliable detection (please refer to ESI† for detailed explanation).
Conclusion
The changes in structure, phase composition, and ion dynamics of a fast-ion conductor SNS with varying Na content have been probed with advanced solid-state NMR techniques. Detailed data analyses reveal that initial Na addition to the crystalline α-SrSiO3 phase leads to the formation of a structurally disordered intermediate phase Sr(Na)SiO3 and further increase in Na content promotes the gradual transformation of Sr(Na)SiO3 to a “β-Na2Si2O5-like” phase accompanied by fusion of the SiOx network in the Sr-rich phase. Eventually β-Na2Si2O5 appears as the dominant phase in SNS samples with >40 mol% Na doping. The decrease in the content of crystalline α-SrSiO3 and increase in that of Sr(Na)SiO3 and β-Na2Si2O5 contribute to the significantly increased ionic conductivity in SNS. Variable-temperature 23Na and 17O NMR experiments reveal increased Na+ motion but little O2− motion as the temperature was increased from RT to 480 °C. Above ∼480 °C, the Na+ motion slows down likely due to early-stage crystallization, consistent with ionic conductivity measurements. Therefore, Na ions have been identified as the major charge carriers and are responsible for the observed high ionic conductivity of this material. The insights gained from careful investigations of the local structural environments and dynamics of potential charge carriers in SNS help clearly resolve the long-standing debate regarding the origin of high ionic conductivity observed in SNS. This study identifies SNS as a Na+ conductor instead of an O2− conductor, which means its application in intermediate-temperature SOFCs may not be suitable. It also confirms that the majority of doped Na does not replace Sr in the structure, but rather it resides in an amorphous β-Na2Si2O5 phase. This research demonstrates that high-resolution high-temperature NMR can be a very powerful tool in addressing critical questions such as phase transition and ion transport in ion conductors.Experimental section
Materials
SNS samples with x = 0, 0.1, 0.2, 0.3, 0.4, 0.45 and 0.7 in the apparent composition NaxSr1−xSiO3−0.5x were synthesized following the procedure detailed in previous studies,1,2 and denoted as SNS0, SNS10, SNS30, SNS40, SNS45 and SNS70, respectively. β-Na2Si2O5 was also made and used as a model material for phase identification in this study. The starting materials Na2CO3 (99.9%, Fisher Scientific, USA) and SiO2 (99.9%, Alfa Aesar, USA) in the respective molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 were first mixed in a high-energy mechanical mixer (8000M Mixer/Mill®, SPEX® SamplePrep, USA) in the presence of ethanol. The dried mixture was pelletized at 5 MPa and calcined at 800 °C for 10 h. The pre-calcined pellets were then broken into fine particles of 1–2 μm in diameter with a high-energy vibrational mill (Micronizing Mill, McCrone, USA). After pelletizing again at a pressure of 75 MPa, the sample was eventually sintered at 900 °C for 10 h and gradually cooled down to room temperature with a rate of 2 °C min−1.
2 were first mixed in a high-energy mechanical mixer (8000M Mixer/Mill®, SPEX® SamplePrep, USA) in the presence of ethanol. The dried mixture was pelletized at 5 MPa and calcined at 800 °C for 10 h. The pre-calcined pellets were then broken into fine particles of 1–2 μm in diameter with a high-energy vibrational mill (Micronizing Mill, McCrone, USA). After pelletizing again at a pressure of 75 MPa, the sample was eventually sintered at 900 °C for 10 h and gradually cooled down to room temperature with a rate of 2 °C min−1.
The 17O-enrichment of SNS samples was carried out by heating the SNS powder in a closed quartz tube filled with 17O2 gas atmosphere (70%, Cambridge Isotope Laboratories) at 600 °C for 24 h followed by gradually cooling down to room temperature.
Solid-state NMR characterization
29Si NMR spectra were acquired on a Bruker DRX-300 spectrometer at a Larmor frequency of 59.6 MHz using a Bruker 4 mm MAS probe spinning at 10 kHz. A rotor-synchronized spin-echo pulse sequence was employed. The 90° pulse length was 4.5 μs and the recycle delay was 2 s. A recycle delay of 100 s was also used when the crystalline phase SrSiO3 is present to ensure accurate quantification. The 29Si NMR shift of 4,4-dimethyl-4-silapentane-1-sulfonic acid at 0 ppm was used as the chemical shift reference.To minimize broadening effects of quadrupolar couplings and to gain high resolution and sensitivity, 23Na and 17O NMR spectra were acquired on a Bruker DRX-830 spectrometer with a home-built 3.2 mm low-E and high-sensitivity MAS probe.25 The Larmor frequency for 23Na is 219.6 MHz and for 17O is 112.6 MHz.
All 23Na NMR measurements were carried out with a rotor-synchronized spin–echo pulse sequence at a MAS rate of 18 kHz. For the series of SNS samples and β-Na2Si2O5, the solid 90° pulse length was 1.5 μs and the recycle delay was 0.5 s. All the 23Na shifts were referenced to that of a 1 M NaCl solution at 0 ppm.
17O MAS NMR experiments were carried out using the home-built 3.2 mm MAS probe spinning at a frequency of 18 kHz. A rotor-synchronized spin–echo pulse sequence was applied to 17O-enriched SNS samples (SNS10, SNS30, and SNS45) and lab-synthesized β-Na2Si2O5. The solid 90° pulse length was 2 μs and the recycle delay was 10 s. All of the 17O shifts were referenced to H2O(l) (0 ppm). The MQMAS spectrum of 17O-enriched SNS45 was collected using a shifted-echo sequence using a home-built 4 mm single channel probe with a spinning speed of 10 kHz.26 All r.f. pulse lengths were optimized on the SNS45 sample. The recycle delay was 1 s and a total of 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 scans were acquired for each of the 12 rotor-synchronized t1 increments.
200 scans were acquired for each of the 12 rotor-synchronized t1 increments.
Variable high-temperature 23Na and 17O MAS NMR experiments were carried out with a rotor-synchronized spin-echo pulse sequence at a MAS speed of 5 kHz, using a Bruker 7 mm laser-absorption MAS probe on a Bruker Avance-600 spectrometer. Recycle delays of 1 s for both 23Na and 17O were used. Temperature was calibrated based on the temperature dependence of the 79Br chemical shift of KBr.27
The spectral analyses and simulations of all 1D spectra were performed using the Topspin (v 3.2) software. MQMAS spectral processing and simulations were carried out with a MATLAB (v 8.5.1) script.
Acknowledgements
Y.-Y. Hu and P.-H. Chien acknowledge support from the National Science Foundation under Grant No. 1508404. K. Huang and Y. Lee acknowledge the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy for support under Award number DE-AR0000492.Notes and references
- P. Singh and J. B. Goodenough, J. Am. Chem. Soc., 2013, 135, 10149 CrossRef CAS PubMed.
- T. Wei, P. Singh, Y. Gong, J. B. Goodenough, Y. Huang and K. Huang, Energy Environ. Sci., 2014, 7, 1680 CAS.
- R. Martinez-Coronado, P. Singh, J. Alonso-Alonso and J. B. Goodenough, J. Mater. Chem. A, 2014, 2, 4355 CAS.
- J. Xu, X. Wang, H. Fu, C. M. Brown, X. Jing, F. Liao, F. Lu, X. Li, X. Kuang and M. Wu, Inorg. Chem., 2014, 53, 6962 CrossRef CAS PubMed.
- R. D. Bayliss, S. N. Cook, S. Fearn, J. A. Kilner, C. Greaves and S. J. Skinner, Energy Environ. Sci., 2014, 7, 2999 CAS.
- C. Tealdi, L. Malavasi, I. Uda, C. Ferrara, V. Berbenni and P. Mustarelli, Chem. Commun., 2014, 50, 14732 RSC.
- I. R. Evans, J. S. O. Evans, H. G. Davies, A. R. Haworth and M. L. Tate, Chem. Mater., 2014, 26, 5187 CrossRef CAS.
- Y. Jee, X. Zhao and K. Huang, Chem. Commun., 2015, 51, 9640 RSC.
- X. Lei, Y. Jee and K. Huang, J. Mater. Chem. A, 2015, 3, 19920 CAS.
- J. R. Peet, C. M. Widdifield, D. C. Apperley, P. Hodgkinson, M. R. Johnson and I. R. Evans, Chem. Commun., 2015, 51, 17163 RSC.
- R. D. Bayliss, S. N. Cook, D. O. Scanlon, S. Fearn, J. Cabana, C. Greaves, J. A. Kilner and S. J. Skinner, J. Mater. Chem. A, 2014, 2, 17919 CAS.
- F. Blanc, D. S. Middlemiss, Z. Gan and C. P. Grey, J. Am. Chem. Soc., 2011, 133, 17662 CrossRef CAS PubMed.
- F. Blanc, M. Leskes and C. P. Grey, Acc. Chem. Res., 2013, 46, 1952 CrossRef CAS PubMed.
- R. Dervişoğlu, D. S. Middlemiss, F. Blanc, L. A. Holmes, Y.-L. Lee, D. Morgan and C. P. Grey, Phys. Chem. Chem. Phys., 2014, 16, 2597 RSC.
- M. T. Dunstan, F. Blanc, M. Avdeev, G. J. McIntyre, C. P. Grey and C. D. Ling, Chem. Mater., 2013, 25, 3154 CrossRef CAS.
- Y. Yamazaki, F. Blanc, Y. Okuyama, L. Buannic, J. C. Lucio-Vega, C. P. Grey and S. M. Haile, Nat. Mater., 2013, 12, 647 CrossRef CAS PubMed.
- G. Kim, F. Blanc, Y.-Y. Hu and C. P. Grey, J. Phys. Chem. C, 2013, 117, 6504 CAS.
- L. Buannic, F. Blanc, D. S. Middlemiss and C. P. Grey, J. Am. Chem. Soc., 2012, 134, 14483 CrossRef CAS PubMed.
- R. Dervişoğlu, D. S. Middlemiss, F. Blanc, Y.-L. Lee, D. Morgan and C. P. Grey, Chem. Mater., 2015, 27, 3861 CrossRef PubMed.
- X. Xue and J. F. Stebbins, Phys. Chem. Miner., 1993, 20, 297 CrossRef CAS.
- S. F. Dec, G. E. Maciel and J. J. Fitzgerald, J. Am. Chem. Soc., 1990, 112, 9069 CrossRef CAS.
- H. K. C. Timken, S. E. Schramm, R. J. Kirkpatrick and E. Oldfield, J. Phys. Chem., 1987, 91, 1054 CrossRef CAS.
- T. Charpentier, S. Ispas, M. Profeta, F. Mauri and C. J. Pickard, J. Phys. Chem. B, 2004, 108, 4147 CrossRef CAS.
- A. M. George, P. Richet and J. F. Stebbins, Am. Mineral., 1998, 83, 1277 CrossRef CAS.
- (a) P. L. Por'kov, W. Mao, J. A. Kitchen, Z. Gan, J. Trebosc, J. P. Amoureux and W. W. Brey, Presented at the 54th Experimental NMR Conference, Pacific Grove, CA, April, 2013 Search PubMed; (b) Z. Gan, P. L. Gor'kov, W. W. Brey, P. J. Sideris and C. P. Grey, J. Magn. Reson., 2009, 200, 2 CrossRef CAS PubMed.
- (a) A. Medek, J. S. Harwood and L. Frydman, J. Am. Chem. Soc., 1995, 117, 12779 CrossRef CAS; (b) Z. Gan and H.-T. Kwak, J. Magn. Reson., 2004, 168, 346 CrossRef CAS PubMed.
- K. R. Thurber and R. Tycko, J. Magn. Reson., 2009, 196, 84 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: NMR spectra, deconvolution results, and DFT calculations. See DOI: 10.1039/c5sc04270d |
| This journal is © The Royal Society of Chemistry 2016 |