Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Water vs. cucurbituril rim: a fierce competition for guest solvation†
Xiaoxi
Ling
 ,
Stefan
Saretz
,
Lifeng
Xiao
,
John
Francescon
and
Eric
Masson
*
,
Stefan
Saretz
,
Lifeng
Xiao
,
John
Francescon
and
Eric
Masson
*
Department of Chemistry and Biochemistry, Ohio University, Athens, Ohio 45701, USA. E-mail: masson@ohio.edu
First published on 17th February 2016
Abstract
The impact of remote substituents on the affinity of cucurbit[n]urils (CB[n]) towards a homologous series of guests, which differ from one another only by a single substituent, and adopt the same geometry within the cavity of the macrocycle, is presented for the first time, and is used to decipher the competition between water and the carbonylated portal of CB[7] for the stabilization of positively charged guests. Binding affinities of CB[7] towards substituted N-benzyl-trimethylsilylmethylammonium cations relative to the unsubstituted member (X = H) range from 0.9 (X = CH3) to 3.1 (X = SO2CF3), and correlate very precisely with a linear combination of Swain–Lupton field/inductive (F; 67%) and resonance (R; 33%) parameters tabulated for each substituent. We show that this subtle sensitivity results exclusively from the balance between two competing mechanisms, on which the substituents exert an approximately 11 times greater impact: (1) the solvation of the ammonium unit and its immediate surroundings by water in the free guests, and (2) the coulombic attraction between the ammonium unit and the rim of CB[7] in the complexes.
Introduction
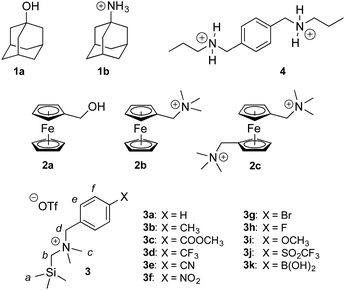
Cucurbiturils1–3 form notoriously tight complexes with organic guests, especially when the latter fit well within the cavity of the macrocycle. Optimal packing coefficients (i.e. the ratios of the volumes of the guest and of the host cavity) range from 50 to 60%,4 in agreement with Rebek's “55% solution”.5 In that case, nanomolar binding affinities are commonly measured for neutral species interacting with cucurbit[7]uril (CB[7]).6–8 The coulombic interaction between a positively charged substituent and one of the carbonylated portals of CB[n]s generally results in a 103 to 104-fold increase in binding affinity. For example, 1-adamantanol (1a) and 1-adamantylammonium (1b) display binding affinities of 2.3 × 1010 and 1.7 × 1014 M−1 towards CB[7] in water, respectively.6 Similarly, substituted ferrocenes 2a, 2b and 2c bind increasingly tightly to CB[7] as one, then both CB[7] portals interact with a positively charged substituent (see Chart 1; affinities of 3.2 × 109, 4.1 × 1012 and 3.0 × 1015 M−1, respectively).6 As a corollary, the pKa of ammonium cations generally increases by 2–4 units upon CB[n] encapsulation, as the affinity of the corresponding neutral amine towards the macrocycle is 102 to 104-fold weaker than the ammonium cation.9–13 Yet, this 4–5 kcal mol−1 increase in binding affinity per CB/positive substituent interaction measured in aqueous solution pales in comparison to the corresponding gain in free energy in the gas phase,6 and the precise quantification of each contribution and penalty to the binding free energy in solution remains difficult. In the 2a–2c series for example, the orientation of the ferrocene unit inside CB[7] is not steady, the magnitude or mere existence of hydrogen bonding between ferrocene methanol (2a) and the rim of the macrocycle is unclear, and the solvation energy of each guest is widely different. In this study, we circumvent these limitations by examining and rationalizing the binding affinities of CB[7] towards a homologous series of substituted N-benzyl-trimethylsilylmethylammonium cations (3a–3k; see Chart 1). In that case, the position of the trimethylsilyl unit inside the cavity of CB[7] and of the ammonium group at the rim remain steady throughout the series, and binding affinities are solely regulated by the electron-donating or withdrawing substituents at the remote para-position of the benzyl group and the accompanying solvation contributions.Results and discussion
Silanes 3a–3k were prepared from N,N-dimethyl-(trimethylsilyl)methylamine and the corresponding benzyl halides in acetone, followed by anion exchange with silver or barium triflate. Upon interaction with CB[7], the 1H nuclear magnetic resonance (NMR) signals of the trimethylsilyl units undergo a large upfield shift (consistently 0.69 ppm throughout the series of guests 3, thereby confirming their steady arrangement inside the cavity of the macrocycle; see Fig. 1, spectra a and b). They also show that the trimethylsilyl group quantitatively outcompetes the benzyl unit for CB[7] interaction (see Fig. 1 for an optimized structure of complex 3e·CB[7]).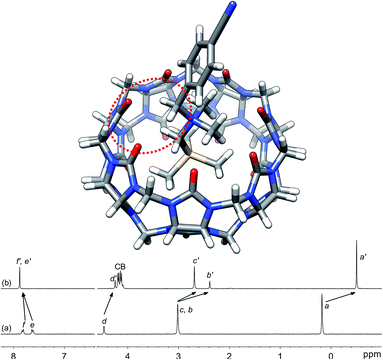 | ||
| Fig. 1 Optimized structure of complex 3e·CB[7] calculated at the TPSS-D3(BJ)/def2-SVP level with the COSMO solvation model. The interaction between the benzylic hydrogens and the CB[7] rim is highlighted with the dotted red ellipse. 1H NMR spectra of (a) silane 3e (X = CN), (b) complex 3e·CB[7]. See Chart 1 for numbering. | ||
The relative binding affinities of silanes 3 towards CB[7] were determined by 1H NMR spectroscopy in a series of competition experiments using xylylene diammonium 4 as the reference guest; its CB[7] affinity is on par with silanes 3, and its concentration as free and bound species was monitored using the signals of the two propyl tails (see ESI† section). The binding affinities of silanes 3 towards CB[7] relative to analog 3a range from 0.9 (in the case of X = CH3) to 3.1 (X = SO2CF3). The absolute binding affinity of silane 3a reached 1.5 × 1012 M−1, as determined by isothermal titration calorimetry (see ESI† section for the binding isotherms). The binding affinity was too high to be determined by direct titration, thus L-phenylalanine was used as a relay guest (i.e. the titration was carried out using silane 3a and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of CB[7] and L-phenylalanine; the binding affinity of the latter is 8.8 × 105 M−1 in water).
1 complex of CB[7] and L-phenylalanine; the binding affinity of the latter is 8.8 × 105 M−1 in water).
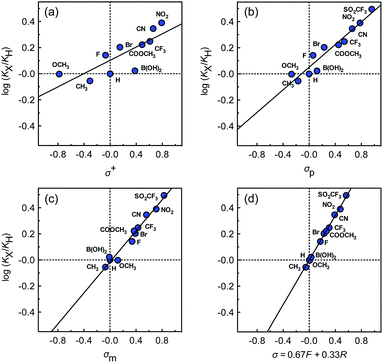
The binding affinities of silanes 3 (KX) towards CB[7] relative to the unsubstituted member 3a (KH) were plotted as a function of Hammett parameters σ+, σp and σm to assess the impact of the substituents on the affinities (see Fig. 2a–c).14 Hammett parameters reflect a combination of field, inductive and resonance substituent effects, with a bias towards field/induction in the case of σm and towards resonance for σ+, while both effects are evenly balanced in the case of σp.14 For each of these parameters, coefficients of determination r2 were 0.646, 0.923 and 0.971, respectively. The fact that outliers are visibly present in each correlation indicates that both field (or induction) and resonance effects affect binding affinities, but not precisely in the ratios built into the σp, σm and σ+ series of parameters. A near flawless linear relationship (r2 = 0.997; see Fig. 2d) could yet be obtained using a linear combination of Swain–Lupton field/inductive (F) and resonance (R) parameters that are derived from the Hammett parameters, and aim at treating both effects independently (see eqn (1); the h parameter accounts for all other effects);14,15
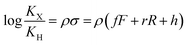 | (1) |
While we expected the binding affinities to be affected by field and induction effects, the magnitude of the resonance term (33%) is surprising, and indicates a pronounced interaction between the benzylic methylene group, whose electrostatic potential is affected by resonance through the aromatic ring, and the carbonylated rim of CB[7] (see Fig. 1, interaction highlighted in red).
That electron-withdrawing substituents would increase binding affinities by bolstering the density of positive charge at the ammonium center and the interaction with the CB[7] portal seems intuitive. A closer evaluation reveals otherwise: as the only difference between the members of the 3·CB[7] complexes is a remote aryl substituent, differences in binding affinities are due to the changes in relative stabilization of the ammonium group by water and the CB[7] rim along the homologous series. Had ammonium solvation by water been more sensitive to substituent effects than CB[7] binding, electron-withdrawing groups would have weakened CB[7] binding! In order to decipher this competition between water and the CB[7] rim for ammonium interaction, we determined substituent effects (1) on the solvation of the free guests, (2) on the solvation of complexes 3·CB[7], and (3) on the affinity of silanes 3 towards CB[7] in the gas phase.
The conformations of silanes 3 were screened using density functional theory (DFT) at the TPSS-D3(BJ)/def2-TZVP level.16,17 The “W-shaped” conformation as depicted in Fig. 1 was consistently the most stable one throughout the series of silanes 3. Solvation energies ΔGsolv(X) were then calculated with the COSMO18,19 and IEFPCM20–22 models. In order to limit the determination of the solvation to the ammonium unit (and the 4 surrounding methyl or methylene groups), we separate the solvation energy into 4 terms:
| ΔGsolv(X) = ΔGSisolv + ΔGNsolv(X) + ΔGPhsolv(X) + ΔGCorrsolv | (2) |
| ΔΔGNsolv(X) = ΔΔGsolv(X) − ΔΔGPhsolv(X) | (3) |
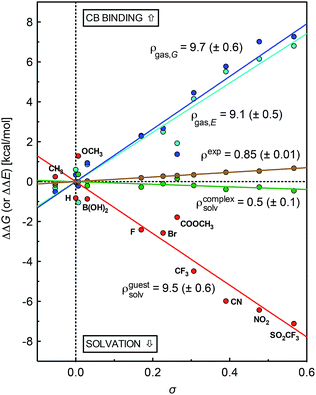
A plot of relative solvation energies of the ammonium unit as a function of the linear combination of Swain–Lupton parameters σ = 0.67F + 0.33R displays very good linearity, with a sensitivity factor ρguestsolv of 9.5 ± 0.6 (see Fig. 3, red dots and regression line; the sensitivity factor is obtained from the slope of the regression line after dividing by 1.364 (RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10) to convert relative energies into decimal logarithms of equilibrium constants). A very similar sensitivity factor was calculated using the IEFPCM solvation model and single-point energies calculated at the M05-2X/6-31G(d) level (ρguestsolv = 9.2 ± 0.6).
10) to convert relative energies into decimal logarithms of equilibrium constants). A very similar sensitivity factor was calculated using the IEFPCM solvation model and single-point energies calculated at the M05-2X/6-31G(d) level (ρguestsolv = 9.2 ± 0.6).
The conformations of complexes 3·CB[7] were then screened at the TPSS-D3(BJ)/def2-SVP level with the COSMO solvation model, and the total energies and solvation energies of the most stable conformers were obtained with def2-TZVP basis sets in single-point calculations (see ESI† for details; the guest adopts a “W-shaped” conformation throughout the series of silanes 3, see Fig. 1). Solvation energies of the CB[7]-bound ammonium units relative to the reference complex 3a·CB[7] were determined as described in eqn (3), and plotted as a function of parameter σ (see Fig. 3, green dots and regression line). Excellent linearity was again observed, but this time with a near-zero substituent sensitivity factor (ρcomplexsolv = 0.5 ± 0.1). This indicates that (1) the carbonylated rim of CB[7] efficiently weakens the density of positive charge around the ammonium unit (and thereby lowers its solvation energy), (2) the field effect of the benzyl substituent does not propagate as far as the periphery of CB[7], and (3) surprisingly, CB[7] shields the ammonium group from virtually any water solvation. The binding affinity of CB[7] towards guests 3 were then calculated in the gas phase using the TPSS-D3(BJ)/def2-SVP-optimized structures discussed above, after single-point calculations with def2-TZVP basis sets. Enthalpic and entropic contributions were obtained after vibrational analysis at the TPSS-D3(BJ)/def2-SVP level, using Grimme's treatment for low vibrational frequencies (see ESI† for details).23
The gas phase affinities of guests 3 towards CB[7], relative to reference guest 3a, were then plotted as a function of the linear combination of Swain–Lupton parameters σ = 0.67F + 0.33R. Very good linearity was obtained for both the electronic component of the binding affinity and the relative binding free energies after enthalpic and entropic corrections, albeit with a slightly larger error in the latter case (see cyan and blue dots with the corresponding regression lines, respectively); sensitivity to the benzyl substituents are ρgas,E = 9.1 ± 0.5 and ρgas,G = 9.7 ± 0.6.
The sensitivity of binding affinities to substituents calculated in the gas phase is thus approximately 11 times greater than the one measured in aqueous solution. This is reminiscent of the 6.6-fold difference obtained by Taft and coworkers when comparing the gas and aqueous phase acidities of meta- and para-substituted phenols.24
Sensitivity factors pertaining to solvation and CB[7] binding are strikingly similar, and highlight the fierce competition between water and the rim of CB[7] for ammonium binding. The cumulative sensitivity factor ρcalc can be calculated using eqn (4), and is equal to 0.6 (±0.9), in excellent agreement with the sensitivity determined experimentally (ρ = 0.85 ± 0.01).
| ρcalc = ρgas,G − (ρguestsolv − ρcomplexsolv) | (4) |
We also note that while DFT calculations accurately predict the trend in binding affinities along the series of silanes 3, they fail to predict accurate absolute free energies of binding. Whereas a free energy of −16.9 kcal mol−1 is determined for CB[7] binding to reference silane 3a experimentally, calculations greatly underestimate the free energy and return −3.7 kcal mol−1 with the COSMO solvation model, and −9.5 kcal mol−1 with the IEFPCM model. In fact, we find this negative result rather reassuring: as shown by Nau, Biedermann and coworkers4,25–27 the ejection of high energy water from the cavity of CB[n]s is the main driving force of the binding event, and continuum solvation models like COSMO or IEFPCM are expected to overestimate the solvation energy of the empty macrocycle. However, this result contrasts with the more accurately computed binding affinities obtained by Inoue and Gilson6 (±4 kcal mol−1), as well as Grimme and coworkers28 (±2 kcal mol−1) using continuum solvation models. Yet, in the latter case, the authors compared affinities calculated in water with affinities determined experimentally in a 0.10 M sodium phosphate buffer adjusted to pH 7.4.29 The high concentration of sodium cations (0.30 M) competing for CB[7] binding is expected to lower the affinities of the guests by 200 to 1000-fold compared to those in pure water.30 Therefore, calculations underestimate binding affinities by an additional 3–4 kcal mol−1 bias, which the authors have not taken into account. In the present study, it is not currently possible for us to assess which portion of the 7–13 kcal mol−1 discrepancy between calculated and experimental free energies is due to the ejection of high-energy water from the cavity, and to the error caused by our computational choices.
Finally, we wanted to test whether enthalpy or entropy variations were mainly responsible for the increase in CB[7] binding affinity along the series of silanes 3. Kaifer, Isaacs, Kim, Inoue and Gilson6,8 show that an increase in solvation entropy is responsible for the improved binding affinities measured along the series of guests 1 and 2 (see Chart 1). We had already determined the thermodynamic parameters for the interaction between CB[7] and guest 3a, therefore we carried out another series of titrations with guest 3f (X = NO2). Binding affinities were 1.5 (±0.1) × 1012 and 3.2 (±0.2) × 1012 M−1, respectively. This result is in excellent agreement with the 2.5-fold difference between the two guests measured by competitive NMR titrations. Although the difference in binding affinities is small, the high quality of the ITC titration fitting allows a very accurate evaluation of the enthalpic and free energy parameters (−15.45 (±0.03) and −16.63 (±0.02) kcal mol−1 in the case of silane 3a; −15.45 (±0.03) and −17.07 (±0.03) kcal mol−1 for silane 3f). As the enthalpic terms are identical for both silanes, the difference in binding affinity is again solely due to the entropic term (TΔS = 1.43 (±0.04) and 1.87 (±0.04) kcal mol−1, respectively), in agreement with the studies mentioned above.
Conclusions
Exploiting substituent effects in a quantitative manner is a classic method available in the physical organic chemist toolbox to study reaction mechanisms, yet to the best of our knowledge this is the first time it has been used to decipher the various forces at play in CB[n]/guests interactions. By varying a remote para-substituent in a series of N-benzyl-trimethylsilylmethylammonium cations 3, and thereby leaving the trimethylsilyl CB[n]-binding unit in a steady position inside the cavity of the macrocycle throughout the series, the role of the ammonium unit on the binding process, and how water solvation and interactions with the carbonylated CB[7] rim affected it, could be treated separately from the rest of the structure. We showed that the mild impact of the substituent on binding affinities in water is essentially due to a barely tilted balance between two competing mechanisms that are affected by substituent changes to a much greater extent, by approximately 11-fold compared to the combined effect: (1) the solvation of the ammonium unit and its immediate surroundings by water in the free guests, and (2) the coulombic attraction between the ammonium unit and the CB[7] portal in the complexes. The solvation of the complexes is barely affected by substituents, and does not play a major role in the competition, as the CB[7] rim annihilates most of the positive charge around the ammonium unit, and the macrocycle seems to shield the ammonium group from most water solvation. Beyond these fundamental aspects of CB[n] recognition, this study is also intended as a guide to fine-tune the binding affinities of guests in CB[n]-based self-assembling systems.Acknowledgements
This work was supported by the Department of Chemistry and Biochemistry, the College of Arts and Sciences and the Vice President for Research at Ohio University. We thank the Ohio Supercomputer Center (OSC) in Columbus for its generous allocation of computing time.References
- J. Lagona, P. Mukhopadhyay, S. Chakrabarti and L. Isaacs, Angew. Chem., Int. Ed., 2005, 44, 4844–4870 CrossRef CAS PubMed.
- E. Masson, X. Ling, R. Joseph, L. Kyeremeh-Mensah and X. Lu, RSC Adv., 2012, 2, 1213–1247 RSC.
- W. A. Freeman, W. L. Mock and N. Y. Shih, J. Am. Chem. Soc., 1981, 103, 6044 CrossRef.
- W. M. Nau, M. Florea and K. I. Assaf, Isr. J. Chem., 2011, 51, 559–577 CrossRef CAS.
- S. Mecozzi and J. J. Rebek, Chem.−Eur. J., 1998, 4, 1016–1022 CrossRef CAS.
- S. Moghaddam, C. Yang, M. Rekharsky, Y. H. Ko, K. Kim, Y. Inoue and M. K. Gilson, J. Am. Chem. Soc., 2011, 133, 3570–3581 CrossRef CAS PubMed.
- S. Liu, C. Ruspic, P. Mukhopadhyay, S. Chakrabarti, P. Y. Zavalij and L. Isaacs, J. Am. Chem. Soc., 2005, 127, 15959–15967 CrossRef CAS PubMed.
- M. V. Rekharsky, T. Mori, C. Yang, Y. H. Ko, N. Selvapalam, H. Kim, D. Sobransingh, A. E. Kaifer, S. Liu, L. Isaacs, W. Chen, S. Moghaddam, M. K. Gilson, K. Kim and Y. Inoue, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20737–20742 CrossRef CAS PubMed.
- M. Shaikh, S. Dutta Choudhury, J. Mohanty, A. C. Bhasikuttan, W. M. Nau and H. Pal, Chem.–Eur. J., 2009, 15, 12362–12370 CrossRef CAS PubMed.
- N. Saleh, A. L. Koner and W. M. Nau, Angew. Chem., Int. Ed., 2008, 47, 5398–5401 CrossRef CAS PubMed.
- M. Shaikh, J. Mohanty, A. C. Bhasikuttan, V. D. Uzunova, W. M. Nau and H. Pal, Chem. Commun., 2008, 3681–3683 RSC.
- I. W. Wyman and D. H. Macartney, Org. Biomol. Chem., 2010, 8, 247–252 CAS.
- A. Praetorius, D. M. Bailey, T. Schwarzlose and W. M. Nau, Org. Lett., 2008, 10, 4089–4092 CrossRef CAS PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- C. G. Swain and E. C. Lupton Jr, J. Am. Chem. Soc., 1968, 90, 4328–4337 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Klamt and G. Schueuermann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504 CrossRef PubMed.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 CrossRef PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- M. Fujio, R. T. McIver and R. W. Taft, J. Am. Chem. Soc., 1981, 103, 4017–4029 CrossRef CAS.
- F. Biedermann, W. M. Nau and H. J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171 CrossRef CAS PubMed.
- F. Biedermann, M. Vendruscolo, O. A. Scherman, A. De Simone and W. M. Nau, J. Am. Chem. Soc., 2013, 135, 14879–14888 CrossRef CAS PubMed.
- F. Biedermann, V. D. Uzunova, O. A. Scherman, W. M. Nau and A. De Simone, J. Am. Chem. Soc., 2012, 134, 15318–15323 CrossRef CAS PubMed.
- R. Sure, J. Antony and S. Grimme, J. Phys. Chem. B, 2014, 118, 3431–3440 CrossRef CAS PubMed.
- L. Cao and L. Isaacs, Supramol. Chem., 2014, 26, 251–258 CrossRef CAS.
- W. Ong and A. E. Kaifer, J. Org. Chem., 2004, 69, 1383–1385 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Preparation and characterization of guests 3a–3k and their precursors; determination of binding affinities by competitive NMR titrations and ITC; computational procedures and data; Cartesian coordinates of the optimized structure of complexes 3a·CB[7] and 3e·CB[7]. See DOI: 10.1039/c5sc04475h |
| This journal is © The Royal Society of Chemistry 2016 |