Observation of quantum dynamical resonances in near cold inelastic collisions of astrophysical molecules

Abstract

This mini review summarizes experimental findings of quantum dynamical resonances in inelastic collisions at energies equivalent to temperatures of a few to a few tens of Kelvin, corresponding to physical conditions prevailing in dense molecular clouds of the interstellar medium. Information obtained is thus relevant to collision energy transfer modelling in such media. Crossed-beam scattering experiments performed at Bordeaux university for inelastic collisions of important astrophysical molecules such as CO with H₂ or He and O₂ with H₂ are described. The peaks that show up in the collision energy dependence of the state-to-state integral cross sections for the lowest rotational excitation transitions reveal the quantum nature of such processes. They are ascribed as shape and Feshbach resonances by comparison with the results of close coupling quantum mechanical calculations performed concomitantly on accurate potential energy surfaces.

---

Michel Costes and Christian Naulin

The long-standing collaboration at Bordeaux University between Michel Costes, CNRS Director of Research, and Christian Naulin, Professor, sums up to sixty years of experience in crossed molecular beam scattering. They were pioneers to demonstrate the efficiency of pulsed beam technology for reaction dynamics studies, in years when all reactive scattering studies were implemented with continuous beam sources. At the end of the 90's, their interest on reactions between neutral species which may occur in the cold molecular clouds of the interstellar medium pushed them to develop a crossed-beam apparatus attaining collision energies corresponding to temperatures as low as 30 Kelvin. Their ongoing research project, for which they improved the low collision energy range of the apparatus by an order of magnitude, is targeted on the search of quantum effects in molecular collisions, reactive and inelastic.

Introduction

In recent years, many ingenious physics experiments have allowed to generate beams or samples of atoms and molecules moving with very low velocities in the laboratory.^1–5 The frontier for the knowledge of chemical kinetics and dynamics has been pushed towards the so-called cold and ultracold regimes characterized by temperatures below 1 K and 1 mK, respectively. These conditions are recognized as ideal to observe the quantum nature of molecular collisions since, (i) the angular momentum becomes severely constrained eventually reaching the limit l = 0 where only s-wave scattering takes place, and (ii) the de Broglie wavelength associated with relative velocity becomes comparable to or even greater than the size of the reactants.^6–8 However, such temperatures achieved in the laboratory are unnatural: the temperature of the cosmic background radiation is T = 2.8 K and as far as is known, only one place in the universe, the Boomerang Nebula, falls below.⁹ Note that the dense molecular clouds of the interstellar medium, which are at the origin of star formation and are giant ultra low density reactors where efficient gas phase chemistry and molecular energy transfer occur, are characterized by temperatures below 50 K with the cold cores reaching temperatures as low as 5–10 K.¹⁰

The temperature range T = 1–50 K immediately above the cold regime that we define as near cold is entirely appropriate for the observation of quantum effects in molecular collisions, in particular for inelastic processes. Collision energies of a few cm⁻¹ (T = 1 K is roughly equivalent to 12.5 J mol⁻¹ or 1 cm⁻¹ since 〈E_T〉 = 3/2k_BT for a thermalized distribution of velocities) are far above pure s-wave scattering but the opening of a restricted number of partial waves has one advantage. Opposed to s-wave scattering where only Feshbach resonances may occur, scattering with angular momentum l > 0 creates centrifugal barriers which may be responsible for shape (orbiting) resonances.^11,12 In fact, all quantum-mechanical (QM) studies of rotational (de)excitation of simple molecules of astrophysical interest such as CO, O₂, CN, C₂, C₃, OH, NO, H₂O and NH₃, by inelastic collisions with H₂ molecules or He atoms – which are fundamental collision processes that occur in dense molecular clouds – establish the existence of shape and Feshbach resonances.^13–33 When occurring in the near cold energy regime, the resonance signatures are not completely blurred by partial wave averaging: they can still be distinguished as peaks in the collision energy dependent state-to-state integral cross sections (ICSs). This happens in particular in the vicinity of the thresholds of the lowest molecular rotational excitations. However, the characteristics of these quantum dynamical resonances, i.e. their position in energy, magnitude and width, strongly depend on the topology of the multidimensional potential energy surface (PES) employed to describe the van der Waals interaction between the colliding partners. The results can appear strikingly different with even slight modifications of the PES, in particular in the long-range part of the potential where the molecules approach together and in the region of the van der Waals well. Experimental observation of resonances is thus likely to provide a stringent test for the accuracy of the PES. Such quantum effects proved nonetheless very difficult to detect³⁴ and could only be seen recently.^{24,25,27–29,33} The findings obtained in our laboratory are described in this mini review.

Experimental approach

In a collision between two species sharing a reduced mass μ, the relative velocity v_r and the relative translational energy (collision energy) E_T depend on the respective velocities v₁ and v₂ and the crossing angle χ:

E_T = ½μv_r² = ½μ(v₁² + v₂² − 2v₁v₂ cos χ) (1)

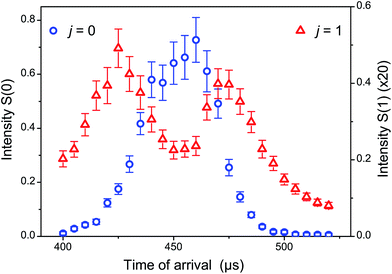
Obtaining collision energies in the near cold regime with low energy spread as provided by supersonic beams in crossed-beam scattering experiments is not straightforward. In inelastic scattering of astrophysical molecules such as CO, O₂ and other species with H₂ and He, the reduced mass which falls below 2 a.m.u with H₂ (4 a.m.u with He) constitutes a favourable factor, but stringent and interrelated constraints apply on the respective values of v₁, v₂, and χ. Obviously, the standard crossed-beam configuration with χ = 90° is inadequate and a drastic reduction of the beam intersection angle is necessary. However, as χ is reduced, matched velocities v₁ ≈ v₂ are needed to attain a minimal E_T = μv₁²(1 − cos χ). Molecules like CO, O₂ and others can be conveniently seeded at low concentration in Ne with the nozzle maintained near room temperature. A velocity v₁ around 800 m s⁻¹, a high speed ratio and efficient cooling of the molecule to its ground rotational state (j = 0) are obtained with these operating conditions (see Fig. 1). However, equivalent velocities for H₂ or He beams can only be reached with the nozzle cooled well below liquid nitrogen temperature.

Fig. 1 Temporal profiles of a CO beam (0.3% CO in Ne at 300 K) in the beam crossing region. REMPI intensities (arbitrary units) for CO j = 0 and 1 rotational states obtained with (E¹Π, v = 0 ← X¹Σ_g⁺, v = 0) S(0) (blue circles) and S(1) (red triangles) transitions. The profiles are the result of efficient CO–Ne inelastic collisions which occur in the supersonic expansion of the carrier gas immediately after the pulsed nozzle. The scattering experiment is synchronized around 450 μs, in the coldest part of the molecular beam estimated at T_rot = 1 K where the ratio of number densities of CO (j = 0) versus CO (j = 1) is the highest. The beam velocity is v₁ = 789 ± 7 m s⁻¹ and the speed ratio v₁/δv₁ ≥ 28. Reprinted from Nat. Chem., 2015, 7, 349–353. Copyright 2015 Macmillan Publishers Ltd.

Our experiments at Bordeaux University utilize a variable beam intersection angle to achieve convenient scanning and control of the collision energy (see Fig. 2). The apparatus incorporates two fast-pulsed valves (Even-Lavie type) that can be cooled down to low temperatures.³⁵ Each pulsed valve is mounted on a helium closed-cycle cryostat with fine tuning and control of the temperature to adjust the beam velocity. The primary beam (CO, O₂) is fixed (defining χ = 0) and can also provide radical species by laser photolysis or dielectric barrier discharge. The secondary beam (H₂ or He) is rotatable step by step in the whole χ = 0–90° angular range. The wedged-shaped chamber which houses the H₂ (He) beam source sets an effective minimum value χ = 12.5° for scattering experiments hence a minimum E_T around 3.5 cm⁻¹ (or 3.5 K). The energy resolution δE_T also is a critical parameter. With typical velocity spreads below 4%, it mainly depends on the collision angle spread due to the divergence of the molecular beams.^25,37 At E_T = 3.5 cm⁻¹, δE_T is ca. 1 cm⁻¹ for all the inelastic processes described hereafter.

Fig. 2 Open view of the scattering chamber. The O₂ beam originates from a first supersonic nozzle situated in a separated and differentially pumped volume (not shown) above the collision chamber; the H₂ beam originates from a second nozzle situated inside the wedged-shaped chamber, (also differentially pumped) attached to the rotatable lid. In this configuration, the probe laser beam propagates perpendicular to the symmetry plane of the molecular beams; ionized species (REMPI) are detected by REMPI via the TOF-MS.

Detection of the molecules is achieved in the beam crossing region by resonance-enhanced multiphoton ionisation (REMPI) with the laser propagating perpendicular to the scattering plane. A two stages Wiley–Mac Laren time-of-flight mass spectrometer (TOF MS) which has specially cut plates to allow the beams to pass through is positioned in the beam scattering plane at χ = 135°. The placement of the TOF MS in the beam scattering plane with the laser beam perpendicular to it is not usual in crossed-beam scattering. It results from the choice of scanning χ with one source fixed and the other one rotatable. Indeed, the rotation of the relative velocity vector during the scan would induce an undesirable variable Doppler shift of the absorption wavelength if the laser was propagating within the scattering plane.

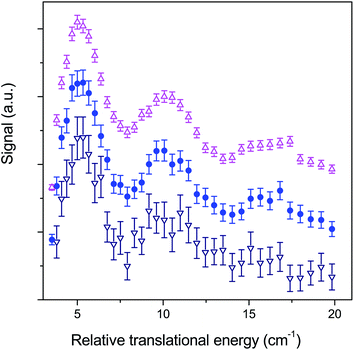
The major advantage of the apparatus is the possibility to repetitively and quickly scan the energy across resonance features with fixed beam conditions, yielding rapidly good statistical uncertainties. As an example, Fig. 3 shows the excitation function for O₂ + H₂ inelastic scattering. Each individual scan is recorded between χ = 30° and 12.5° with −0.5° decrement and 100 laser shots per angle in less than 400 s. Long term drifts are thus drastically reduced and all data are normalized to their sum (all samples at all angles) for each scan, allowing all scans recorded under the same conditions to be accumulated. Thus, the statistical uncertainties mainly due to laser pulse energy and wavelength jitter fluctuations rapidly improve with summation of a reasonable number of scans.

Fig. 3 Signal statistical fluctuations as a function of the number of scans n for O₂ (N = 1, j = 0) + H₂ (j = 0) → O₂ (N = 1, j = 1) + H₂ (j = 0) inelastic collisions. Lower triangles: n = 4; filled circles: n = 12; upper triangles: n = 40. The three excitation functions are shifted vertically for clarity. Note that the fluctuations (given at 95% of the confidence interval) vary as n^−1/2 as expected.

A benchmark system: CO + H₂

The modelling of the physical and chemical processes occurring in dense molecular clouds aims to bring the predicted line intensities of the molecular species in agreement with the observations. Since inelastic collisions compete with radiative processes in altering populations of molecular rovibrational levels, the estimation of molecular abundances from spectral line data analysis requires the knowledge of inelastic collision cross sections and rates with the most abundant interstellar species, H₂ and He. The system to consider in priority is CO + H₂. Carbon monoxide is the second most abundant molecule in the interstellar medium with a density of ca. 10⁻⁴ with respect to H₂ and is widely used to determine the temperature in dense molecular clouds and other objects through transitions in the millimetre wavelength range. Quantum scattering calculations have established the strong influence of the PES on the resonance structures apparent in the ICSs and the subsequent effect on the thermal rate coefficients.¹⁴

We first performed a crossed-beam experiment realizing CO (j = 0) + para-H₂ (j = 0) → CO (j = 1) + para-H₂ (j = 0) inelastic collisions in the vicinity of the energetic threshold of the CO (j = 0 → j = 1) transition at 3.85 cm⁻¹.²⁴ Time-independent QM calculations (close coupling) were run on the most accurate available PES at that time, designated as V₀₄. The V₀₄ PES, calculated by the coupled-cluster method with single, double and non-iterative triple excitations (CCSD(T)) is based on a 5-dimensional grid of ab initio points including the dependence on the H–H separation while the C–O separation is fixed, averaged over monomer vibrational modes and fitted as a 4-dimensional rigid-rotor surface.³⁶ A qualitative agreement, in particular the three undulations revealing the resonance behaviour was found between experiment and theory, albeit after applying a multiplying factor f = 1.05 to the PES. However, in this work, we had missed an important experimental bias: the effect of the mean interaction time between the CO and H₂ pulsed beams which depends on the beam divergences and on the beam crossing angle χ. This effect produces an asymmetric collision energy spread around the nominal value calculated with eqn (1) with its mean value slightly higher than the nominal one. When corrected from this effect the agreement with theory became much better.³⁷

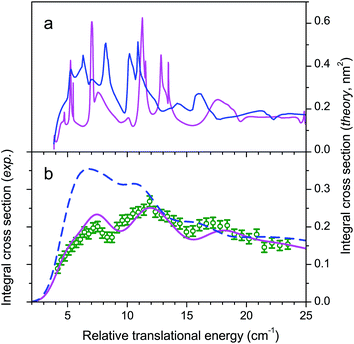
We then conducted additional experiments on CO (j = 0) + para-H₂ (j = 0) → CO (j = 2) + para-H₂ (j = 0) and CO (j = 0) + normal-H₂ → CO (j = 1) + normal-H₂, the normal-H₂ being a mixture of 25% para-H₂ (j = 0) and 75% ortho-H₂ (j = 1).²⁸ The whole set of experimental state-to-state ICSs was compared with theoretical ones obtained by using a newly developed PES, V₁₂.^38,39 The V₁₂ PES computed with inclusion of complete triple and non-iterative quadruple excitations (CCSDT(Q)) is based on a full 6-dimensional grid of ab initio points, again averaged over monomer vibrational modes and fitted as a 4-dimensional rigid-rotor surface. Despite very subtle differences with V_04, not exceeding 1 cm⁻¹ in the depth of the well, V₁₂ was found to increase the agreement between experiment and theory for the IR spectrum of the ortho-H₂–CO complex from 0.1 cm⁻¹ to 0.01 cm⁻¹.^38,39 The agreement is found excellent for the CO (j = 0) + para-H₂ (j = 0) → CO (j = 2) + para-H₂ (j = 0) and CO (j = 0) + normal-H₂ → CO (j = 1) + normal-H₂ cross sections as demonstrated by Fig. 4 and 5. It also becomes fair with the previously obtained CO (j = 0) + para-H₂ (j = 0) → CO (j = 1) + para-H₂ (j = 0) results, although some mismatch in the respective maxima and minima of the three undulations is still observed (see. Fig. 6).

Fig. 4 Experimental and theoretical cross sections for CO (j = 0, 1) + H₂ (j = 0) → CO (j = 2) + H₂ (j = 0) inelastic collisions. (a) Theoretical ICSs calculated with V₁₂ PES for both possible transitions 0 → 2 (solid blue line) and 1 → 2 (dashed red line); (b) theoretical ICSs convoluted with the experimental collision energy spread: total ICS (solid magenta line) calculated with a 10% relative population of the j = 1, corresponding to a rotational temperature of 1.6 K: CO j = 1–2 (dash-dotted red line) and 0–2 (dashed blue line) contributions; experimental data (open circles) in arbitrary units; v₁ = 941 m s⁻¹, v₂ = 943 m s⁻¹, χ varied from 37.5° to 17.5° by −0.5° decrements. Reprinted from Astrophys. J. Lett., 2015, 799, L9. Copyright 2015 IOP Publishing.

Fig. 5 Experimental and theoretical cross sections for CO (j = 0) + normal-H₂ → CO (j = 1) + normal-H₂ inelastic collisions. (a) Theoretical ICSs calculated with V₁₂ PES for para- (solid blue line) and ortho-H₂ (solid red line); (b) theoretical ICSs convoluted with the experimental collision energy spread (solid magenta line),with a 25% relative population of para-H₂ (dashed blue line) and 75% of ortho-H₂ (dash-dotted red line); experimental data (open circles) in arbitrary units; v₁ = 992 m s⁻¹, v₂ = 971 m s⁻¹, χ varied from 33° to 12.5° by −0.5° decrements. Reprinted from Astrophys. J. Lett., 2015, 799, L9. Copyright 2015 IOP Publishing.

Fig. 6 Experimental and theoretical cross sections for CO (j = 0) + H₂ (j = 0) → CO (j = 1) + H₂ (j = 0) inelastic collisions. (a) Theoretical ICSs calculated with V₁₂ PES (magenta solid line) and with the 6-dimensional PES, V6D (solid blue line); (b) theoretical ICSs convoluted with the experimental collision energy spread: V₁₂ PES (magenta solid line) and V6D PES (dashed blue line); experimental data (open circles) in arbitrary units; v₁ = 941 m s⁻¹, v₂ = 943 m s⁻¹, χ varied from 37.5° to 17.5° by −0.5° decrements. Adapted from Astrophys. J. Lett., 2015, 799, L9, copyright 2015 IOP Publishing; and Nat. Comm., 2015, 6, 6629, copyright 2015 Macmillan Publishers Ltd.

Comparison has also been made recently between our CO (j = 0) + para-H₂ (j = 0) → CO (j = 1) + para-H₂ (j = 0) experiments and quantum dynamics in full dimensionality obtained with a 6-dimensional PES, V6D, calculated with the CCSD(T)-F12b method.³⁰ Unfortunately, the comparison was achieved with our uncorrected experimental data of ref. 24. When the corrected data is considered, a poor agreement is obtained. In particular, theory does not reproduce the three experimental undulations apparent in the experimental cross sections (see Fig. 6). It can be concluded that the determinant factor for an accurate description of the collision is not the full dimensionality, but the very high-level of accuracy required for the calculation of the grid of ab initio points and of the long-range part of the potential. It can also be concluded that it is the excitation of the lowest rotational transition CO (j = 0 → 1) with para-H₂ (j = 0) which, with less partial wave averaging, really constitutes the principal test of the PES. Indeed, the resonance pattern is averaged when using normal-H₂ by the 25% para-H₂ (j = 0) and 75% ortho-H₂ (j = 1) summation and becomes too congested for excitation of CO (j = 0 → 2) with para-H₂ (j = 0).

A perfect system: CO + He

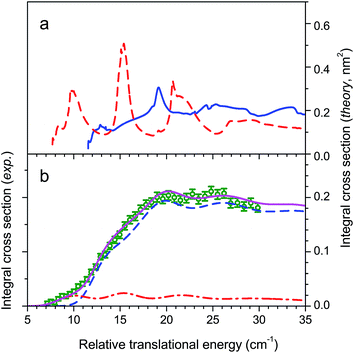
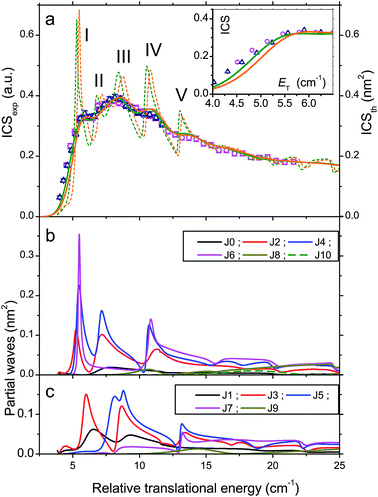
If collisions of CO with He are not as important as those with H₂ for astrophysical modelling as a consequence of a ratio of column densities [He]/[H₂] = 0.1, they nonetheless constitute a system of choice for testing theory. Fig. 7 compares our experimental ICSs for CO (j = 0) + He → CO (j = 1) + He in the threshold region with theoretical ones obtained by close-coupling calculations performed with two different PESs.²⁹ The two PESs had been previously calculated (i) with symmetry-adapted perturbation theory (SAPT) and (ii) at the singles and doubles coupled cluster level with perturbative triples and extrapolation to the complete basis set (CCSD(T)/CBS).^40,41 It can be seen in panel (a) that the ICSs obtained with the two PESs are very similar and that the experimental data are in very good agreement with the theoretical ICSs curves convoluted over the collision energy spread.

Fig. 7 Experimental and theoretical cross sections for CO (j = 0) + He → CO (j = 1) + He inelastic collisions. (a) The experimental ICSs (in arbitrary units) displayed as open circles and open triangles result from two sets of experiments (circles, v₁ = 738 m s⁻¹, v₂ = 695 m s⁻¹, χ varied from 30° to 12.5° by −0.5° decrements; upper triangles v₁ = 699 m s⁻¹, v₂ = 695 m s⁻¹, χ varied from 22.5° to 12.5° by −0.5° decrements), with vertical error bars representing the statistical fluctuations at a 95% confidence interval. To facilitate comparison of experiment to theory, the total calculated ICSs (dashed curves) are convoluted (solid curves) with the experimental resolution resulting from the velocity spread and angular divergence of the beams: orange and green curves were calculated using the CCSD(T)/CBS and SAPT PESs. To allow for comparison, data are normalised relative to the ICS calculated with the SAPT PES: this results in a rescaling of the CCSD(T)/CBS ICSs displayed by a factor of 0.975. The main peaks labelled I, II, III, IV and V correspond to the resonances discussed in the text. (b) and (c) Partial cross sections from QM calculations using the CCSD(T)/CBS PES, for even and odd values of total angular momentum J. Reprinted from Nat. Chem., 2015, 7, 349–353. Copyright 2015 Macmillan Publishers Ltd.

Many strong resonances occur for collision energies in the vicinity of the energetic threshold of the j = 1 channel, but unlike CO + H₂ for which the resonance pattern is too rich to ascribe the three undulations to specific resonances, this becomes possible here. The five peaks labelled I, II, III, IV, and V respectively mainly result from overlapped contributions of partial waves with total angular momentum J = 2 to 6 shown in panels (b) for even J values and (c) for odd values. The collision energy spread does not allow for full resolution of the peaks but I, III and IV are still discernible in the experimental ICSs and V can be distinguished as a shoulder. Peak II, which is a feature of lower intensity, is smoothed in the experimental bump of peak III.

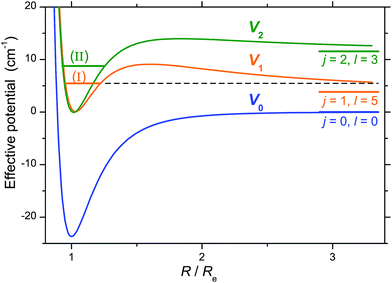
Characterization of the resonances was achieved by generating scattering wave functions for specific values of total angular momentum J, orbital angular momentum l and rotational state j. When on resonance, the scattering wave functions show large contributions in the region of the van der Waals well. For example, at E_T = 5.48 cm⁻¹ (peak I), partial waves with J = 4 and 6 and l = 5 correlate with j = 1 which is open at this energy (E_j=1 = 3.85 cm⁻¹): tunnelling through the centrifugal barrier gives rise to a shape resonance (Fig. 8). At E_T = 8.76 cm⁻¹ (peak III), partial waves with J = 3 and 5 and l = 3 correlate with j = 2 which is an asymptotically closed channel (E_j=2 = 11.54 cm⁻¹). When the collision partners approach the region of the van der Waals well, CO ephemerally accesses the j = 2 state which is energetically allowed only at these distances, but closed at larger values. As the collision partners move off, the transient CO (j = 2) molecules relax back to the open j = 1 state as a Feshbach resonance (Fig. 8). Other calculations establish the nature of all resonances, three shape and five Feshbach in the J = 2 to 6 partial waves.

Fig. 8 Effective potentials illustrating shape and Feshbach resonances. The effective potentials for CO–He collisions are schematically represented for j = 0, l = 0 (V₀), j = 1, l = 5 (V₁) and j = 2, l = 3 (V₂). R_e is the position of the minimum of the well. Also the quasi-bound states corresponding to the dominant contributions in the wavefunctions at E_T = 5.48 cm⁻¹ and E_T = 8.76 cm⁻¹ are represented. Resonances occur when the incident energy coincides with such a state. Two different situations can occur. For the V₁ curve, the quasi-bound state (I) is below the centrifugal barrier, but above the dissociation limit: in this case, the complex can access this state by tunnelling through the centrifugal barrier, and then decay to j = 1, resulting in the rotational excitation of CO. This is known as a shape (or orbiting) resonance. For the V₂ curve, state (II) is below the dissociation limit: in that case, the complex can ephemerally access this state which is energetically allowed at small distances. It cannot dissociate in its j = 2 state since this is not energetically allowed. It can, however, decay to j = 1; this is known as a Feshbach resonance. Reprinted from Nat. Chem., 2015, 7, 349–353. Copyright 2015 Macmillan Publishers Ltd.

As stated above, the agreement between experiment and theory is very good. In particular the mismatch between experiment and theory on the sharp rise of the ICS in the threshold region does not exceed 0.2 cm⁻¹ with the SAPT potential. It is particularly refreshing to see that for this system, a PES calculated in 1997 yields perfect results.

An ideal system: O₂ + H₂

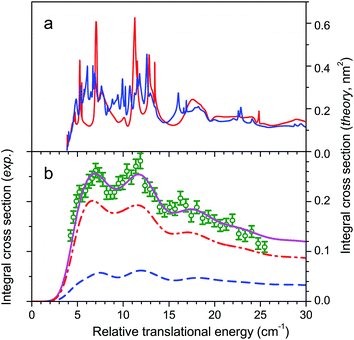
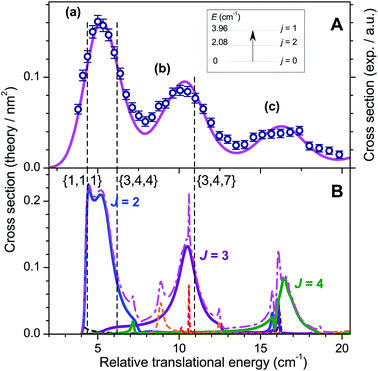
Molecular oxygen is elusive in dense molecular clouds but an accurate knowledge of the inelastic collision cross sections and rates with H₂ is needed for a precise determination of its abundance. The ground electronic state of O₂ is X³Σ_g⁻ and the rotational manifold comprises only odd values of the rotational angular momentum N. Each rotational level is split into 3 spin components due to the vectorial coupling of N with spin S = 1: anti parallel j = N − 1, perpendicular j = N and parallel j = N + 1. The ground-state is N = 1, j = 0 followed by N = 1, j = 2 at E_1,2 = 2.08 cm⁻¹ and N = 1, j = 1 at E_1,1 = 3.96 cm⁻¹. The inelastic collision O₂ (N = 1, j = 0) + H₂ (j = 0) → O₂ (N = 1, j = 1) + H₂ (j = 0) is an ideal system for observing scattering resonances. Indeed, semi classical propensity rules in rotationally inelastic collisions of diatomic molecules in ³Σ electronic states have established that the transition from O₂ (N = 1, j = 0) to O₂ (N = 1, j = 1) is forbidden.⁴² Thus, scattering cannot occur classically and, if any, should only arise from quantum dynamical resonances.⁴³

The results of our experiments displayed in Fig. 9 demonstrate this behaviour.²⁵ The QM calculations show that three well-separated partial waves J = 2, 3 and 4 contribute significantly to the ICSs at these energies, those of the other opened ones J = 1, 5, 6, 7 and 8 remaining marginal. As a result, the three partial waves appear as three resolved peaks (a), (b) and (c) in the experimental ICSs.

Fig. 9 Experimental and theoretical cross sections for O₂ (N = 1, j = 0) + H₂ (j = 0) → O₂ (N = 1, j = 1) + H₂ (j = 0) inelastic collisions. (A) Experimental data (open circles with error bars representing the statistical uncertainties at 95% of the confidence interval) in arbitrary units; v₁ = 957 m s⁻¹, v₂ = 951 m s⁻¹, each point corresponds to 40 consecutive scans of χ acquired between 30° and 12.5° with −0.5° decrement and 100 laser shots per angle; theoretical ICSs convoluted with the experimental collision energy spread (solid line). Inset: energy level diagram and excitation scheme of O₂ in the N = 1 state. (B) Theoretical results: partial waves J = 2, 3 and 4 (solid lines); partial waves J = 1 and J = 5–7 (dashed lines); integral cross section (dashed-dotted line). Positions of the bound and quasi-bound states labelled by quantum numbers N, j, l responsible for the resonances in J = 2 and 3 partial waves are shown by vertical dashed lines. Reprinted from Science, 2013, 341, 1094–1096.

Adiabatic-bender potentials associated with J = 2, 3 and 4 partial waves and correlating with the O₂ (N = 1, j = 1) a + H₂ (j = 0) opened channel or the O₂ (N = 3, j = 2, 3, 4) + H₂ (j = 0) closed channels are shown to support quasi-bound states. These ephemeral states labelled by quantum numbers N, j, l reveal the nature of the peaks. Hence peak (a) results from a shape resonance in the threshold region (E_1,1,1 = 4.37 cm⁻¹) and a Feshbach resonance at higher energies (E_3,3,4 = 6.19 cm⁻¹), while peak (b) is a pure Feshbach resonance (E_3,4,7 = 10.97 cm⁻¹) and peak (c) a composite of six Feshbach resonances (E_3,4,8 = 15.3 cm⁻¹, E_3,2,4 = 15.9 cm⁻¹, E_3,2,2 = 16.6 cm⁻¹, E_3,2,6 = 16.8 cm⁻¹, E_3,3,6 = 16.8 cm⁻¹ and E_3,4,4 = 17.1 cm⁻¹).

As for CO + H₂, the level of accuracy of the PES plays a dominant role. Originally, the 4-dimensional ab initio PES treating O₂ and H₂ as rigid rotors had been obtained at the CCSD(T) level.⁴⁴ However, as shown in Fig. 10, this level is insufficient to reproduce the experimental resonance pattern. Calculations performed at a higher level of theory on ab initio points in the region of the van der Waals well suggested that 5% of correlation energy was missing in this region.²⁵ The f = 1.05 multiplying factor applied to the PES indeed gives the nice match with experiment as displayed in Fig. 9.

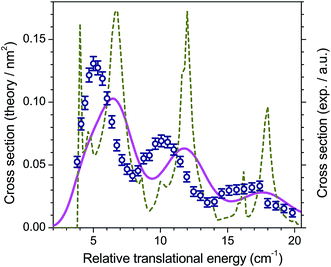Fig. 10 Experimental and theoretical integral cross sections for O₂ (N = 1, j = 0) + H₂ (j = 0) → O₂ (N = 1, j = 1) + H₂ (j = 0) inelastic collisions. Experimental data (open circles; as in Fig. 9), compared to convoluted (solid line) and non convoluted (dashed line) theoretical ICSs obtained with the original (uncorrected) PES of ref. 44.

Conclusions and outlook

The experimental observation of quantum dynamical resonances for the lowest rotational excitation transitions of astrophysical molecules in inelastic collisions with H₂ or He occurring in the near cold regime constitutes a stringent test for theoretical calculations. Thanks to that, the description of inelastic collisions based on ab initio PESs and QM scattering calculations can reach a remarkable level of precision for small systems, as emphasized by the CO + H₂, CO + He and O₂ + H₂ results. It becomes possible to accurately calculate the relevant collisional (de-)excitation rates for inclusion into models describing astrophysical systems, such as cold interstellar clouds.^27–29

The experiments in Bordeaux will be pursued with other species like H₂O molecules and C atoms. It is indeed possible to generate a cold beam of ground-state C(³P₀) atoms almost free of C(³P₁) and C(³P₂) components by passing CO diluted in Ne through a dielectric barrier discharge coupled with the Even-Lavie pulsed-valve.⁴⁵ Spin–orbit collisional excitation of C(³P₀) to the upper components C(³P₁) and C(³P₂) can thus be investigated. The search for scattering resonances is also a constant goal for crossed-beam scattering experiments in Nijmegen by van de Meerakker and co-workers with Stark decelerated OH and NH₃ beams^22,23,31,32 and successful detection has just been obtained for NO + He collisions³³ at E_Ts between 13 and 19 cm⁻¹. Finally, merged beams (χ = 0), which are the prime configuration to attain sub-Kelvin temperatures, could bring important contributions in the field. The technique, largely employed in the past for ion–molecule reactions, has been recently implemented in Rehovot by Narevicius and co-workers^46–48 and in Lausanne by Osterwalder and co-workers^45,49–51 for reactions between neutral species. Experiments in Rehovot on Penning ionization reactions of He(2³S₁) with H₂, HD, D₂ have clearly identified shape resonances occurring in the near cold and cold regimes.^46,47 Experiments in Lausanne on He(2³S₁) with NH₃ have also detected shape resonances at E_Ts between 1 and 100 cm⁻¹.⁵⁰ While the Rehovot experiment uses a magnetic quadrupole guide to clean and bend the metastable He(2³S₁) beam before merging it with a straight H₂ beam, the Lausanne apparatus incorporates in addition of the magnetic quadrupole guide an electric hexapole guide to clean and bend the NH₃ beam. An experiment combining an electric hexapole guide (NH₃) and a straight H₂ (He) beam could realize the ultimate choice for inelastic collisions of astrophysical molecules in the near cold regime.

Acknowledgements

The authors gratefully acknowledge the Agence Nationale de la Recherche (contracts ANR-BLAN-2006-0247 and ANR-12-BS05-0011-02), the Conseil Régional d'Aquitaine (contract 2007.1221) and the Programme National Physique et Chimie du Milieu Interstellaire for financial support.

References

1. M. T. Bell and T. P. Softley, Mol. Phys., 2009, 107, 99–132.
2. O. Dulieu and C. Gabbanini, Rep. Prog. Phys., 2009, 72, 086401.
3. B. Friedrich and J. M. Doyle, ChemPhysChem, 2009, 10, 604–623.
4. B. K. Stuhl, M. T. Hummon and J. Ye, Annu. Rev. Phys. Chem., 2014, 65, 501–518.
5. S. Y. T. van de Meerakker, H. L. Bethlem, N. Vanhaecke and G. Meijer, Chem. Rev., 2012, 112, 4828–4878.
6. C. Buggle, J. Léonard, W. von Klitzing and J. T. M. Walraven, Phys. Rev. Lett., 2004, 93, 173202.
7. N. R. Thomas, N. Kjærgaard, P. S. Julienne and A. C. Wilson, Phys. Rev. Lett., 2004, 93, 173201.
8. S. Ospelkaus, K.-K. Ni, D. Wang, M. H. G. de Miranda, B. Neyenhuis, G. Quéméner, P. S. Julienne, J. L. Bohn, D. S. Jin and J. Ye, Science, 2010, 327, 853–857.
9. R. Sahai and L.-A. Nyman, Astrophys. J., 1997, 487, L155–L159.
10. E. Herbst and J. T. Yates Jr, Chem. Rev., 2013, 113, 8707–8709.
11. A. Schutte, D. Bassi, F. Tommasini and G. Scoles, Phys. Rev. Lett., 1972, 29, 979–982.
12. J. P. Toennies, W. Welz and G. Wolf, J. Chem. Phys., 1979, 71, 614–642.
13. C. Cecchi-Pestellini, E. Bodo, N. Balakrishnan and A. Dalgarno, Astrophys. J., 2002, 571, 1015–1020.
14. M. Wernli, P. Valiron, A. Faure, L. Wiesenfeld, P. Jankowski and K. Szalewicz, Astron. Astrophys., 2006, 446, 367–372.
15. B. Yang, E. Perera, N. Balakrishnan, R. C. Forrey and P. C. Stancil, J. Phys. B: At. Mol. Opt. Phys., 2006, 39, S1229–S1239.
16. B. Yang and P. C. Stancil, J. Chem. Phys., 2007, 126, 154306.
17. D. Ben Abdallah, K. Hammami, F. Najar, N. Jaidane, Z. Ben Lakhdar, M. L. Senent, G. Chambaud and M. Hochlaf, Astrophys. J., 2008, 686, 379–383.
18. F. Najar, D. Ben Abdallah, N. Jaidane, Z. Ben Lakhdar, G. Chambaud and M. Hochlaf, J. Chem. Phys., 2009, 130, 204305.
19. F. Lique, J. Chem. Phys., 2010, 132, 044311.
20. F. Lique, A. Spielfiedel, N. Feautrier, I. F. Schneider, J. Kłos and M. H. Alexander, J. Chem. Phys., 2010, 132, 024303.
21. Y. Scribano, A. Faure and L. Wiesenfeld, J. Chem. Phys., 2010, 133, 231105.
22. K. B. Gubbels, Q. Ma, M. H. Alexander, P. J. Dagdigian, D. Tanis, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, J. Chem. Phys., 2012, 136, 144308.
23. K. B. Gubbels, S. Y. T. van de Meerakker, G. C. Groenenboom, G. Meijer and A. van der Avoird, J. Chem. Phys., 2012, 136, 074301.
24. S. Chefdeville, T. Stoecklin, A. Bergeat, K. M. Hickson, C. Naulin and M. Costes, Phys. Rev. Lett., 2012, 109, 023201.
25. S. Chefdeville, Y. Kalugina, S. Y. T. van de Meerakker, C. Naulin, F. Lique and M. Costes, Science, 2013, 341, 1094–1096.
26. Y. Kalugina, J. Kłos and F. Lique, J. Chem. Phys., 2013, 139, 074301.
27. F. Lique, Y. Kalugina, S. Chefdeville, S. Y. T. van de Meerakker, M. Costes and C. Naulin, Astron. Astrophys., 2014, 567, A22.
28. S. Chefdeville, T. Stoecklin, C. Naulin, P. Jankowski, K. Szalewicz, A. Faure, M. Costes and A. Bergeat, Astrophys. J. Lett., 2015, 799, L9.
29. A. Bergeat, J. Onvlee, C. Naulin, A. van der Avoird and M. Costes, Nat. Chem., 2015, 7, 349–353.
30. B. Yang, P. Zhang, X. Wang, P. C. Stancil, J. M. Bowman, N. Balakrishnan and R. C. Forrey, Nat. Commun., 2015, 6, 6629.
31. Q. Ma, A. van der Avoird, J. Loreau, M. H. Alexander, S. Y. T. van de Meerakker and P. J. Dagdigian, J. Chem. Phys., 2015, 143, 044312.
32. H. C. Schewe, Q. Ma, N. Vanhaecke, X. Wang, J. Kłos, M. H. Alexander, S. Y. T. van de Meerakker, G. Meijer, A. van der Avoird and P. J. Dagdigian, J. Chem. Phys., 2015, 142, 204310.
33. S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790.
34. D. W. Chandler, J. Chem. Phys., 2010, 132, 110901.
35. D. Pentlehner, R. Riechers, B. Dick, A. Slenczka, U. Even, N. Lavie, R. Brown and K. Luria, Rev. Sci. Instrum., 2009, 80, 043302.
36. P. Jankowski and K. Szalewicz, J. Chem. Phys., 2005, 123, 104301.
37. C. Naulin and M. Costes, Int. Rev. Phys. Chem., 2014, 33, 427–446.
38. P. Jankowski, A. R. W. McKellar and K. Szalewicz, Science, 2012, 336, 1147–1150.
39. P. Jankowski, L. A. Surin, A. Potapov, S. Schlemmer, A. R. W. McKellar and K. Szalewicz, J. Chem. Phys., 2013, 138, 084307.
40. T. G. A. Heijmen, R. Moszynski, P. E. S. Wormer and A. van der Avoird, J. Chem. Phys., 1997, 107, 9921–9928.
41. K. A. Peterson and G. C. McBane, J. Chem. Phys., 2005, 123, 084314 ( Erratum , 2006 , 124 , 229901 ).
42. M. H. Alexander and P. J. Dagdigian, J. Chem. Phys., 1983, 79, 302–310.
43. P. Casavecchia and M. H. Alexander, Science, 2013, 341, 1076–1077.
44. Y. Kalugina, O. D. Alpizar, T. Stoecklin and F. Lique, Phys. Chem. Chem. Phys., 2012, 14, 16458–16466.
45. J. Jankunas, K. S. Reisyan and A. Osterwalder, J. Chem. Phys., 2015, 142, 104311.
46. A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234–238.
47. E. Lavert-Ofir, Y. Shagam, A. B. Henson, S. Gersten, J. Klos, P. S. Zuchowski, J. Narevicius and E. Narevicius, Nat. Chem., 2014, 6, 332–335.
48. Y. Shagam, A. Klein, W. Skomorowski, R. Yun, V. Averbukh, C. P. Koch and E. Narevicius, Nat. Chem., 2015, 7, 921–926.
49. J. Jankunas, B. Bertsche, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2014, 140, 244302.
50. J. Jankunas, K. Jachymski, M. Hapka and A. Osterwalder, J. Chem. Phys., 2015, 142, 164305.
51. J. Jankunas and A. Osterwalder, Annu. Rev. Phys. Chem., 2015, 66, 241–262.

---