Open Access Article
Open Access ArticleSymmetry of octa-coordination environment has a substantial influence on dinuclear TbIII triple-decker single-molecule magnets†
Keiichi
Katoh
*,
Brian K.
Breedlove
and
Masahiro
Yamashita
*
Department of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aramaki Aza Aoba, Aoba-ku, Sendai, Miyagi 980-8578, Japan. E-mail: kkatoh@m.tohoku.ac.jp
First published on 29th March 2016
Abstract
Single-molecule magnet (SMM) properties of terbium(III)-phthalocyaninato and porphyrinato mixed ligand triple-decker complexes, [(TTP)Tb(Pc)Tb(TTP)] (1) and [(Pc)Tb(Pc)Tb(TTP)] type (2), were studied and were compared with those of the TbIII homoleptic triple-decker complex [(obPc)Tb(obPc)Tb(obPc)] (3) in order to elucidate the relationship between octa-coordination environments and SMM properties (TbIII = terbium(III), TTP2− = tetraphenylporphyrinato, Pc2− = phthalocyaninato, obPc2− = 2,3,9,10,16,17,23,24-octabutoxyphthalocyaninato). By combining TTP2− and Pc2− with TbIII ions, it is possible to make three octa-coordination environments: SP–SP, SAP–SP and SAP–SAP sites, where SAP is square-antiprismatic and SP is square-prismatic. The direction and magnitude of the ligand field (LF) strongly affect the magnetic properties. Complexes 2 and 3, which have SAP–SAP sites, undergo dual magnetic relaxation processes in the low temperature region in a direct current magnetic field. On the other hand, 1, which has an SP–SP environment, undergoes a single magnetic relaxation process, indicating that the octa-coordination environments strongly influence the SMM properties. The SMM behaviour of dinuclear TbIII SMMs 1–3 were explained by using X-ray crystallography and static and dynamic susceptibility measurements. This work shows that the SMM properties can be fine-tuned by introducing different octa-coordination geometries with the same TbIII–TbIII distances.
Introduction
The field involving single-molecule magnets (SMMs) began in 1993 with the synthesis of Mn12 clusters.1 In recent years, mononuclear metal complexes, not just polynuclear ones, have also been reported.2 In other words, slow magnetic relaxation processes are observed for SMMs regardless of the type and number of metal ions in the complexes under certain conditions. In general, in crystals, d and/or f electrons forming the electronic states reflect the symmetry of the crystals. As a result, the crystal field (CF) or ligand field (LF) directly influences the magnetic properties. Recently, a few groups have published reviews on lanthanide(III) (LnIII)-based SMMs,2 which have several distinctive features, including slow magnetic relaxation and quantum tunnelling of the magnetization (QTM). Although the reviews show that molecular design is important to bring about SMM behaviour, controlling the magnetic relaxation pathway is still challenging. Since the tunneling gap (Δtunnel) is dependent on the establishment of QTM, most studies have focused on the influence of the spin–spin interactions and nuclear spins.2 However, because molecular spintronics based on SMMs, which exhibit new quantum phenomena, will be the next generation devices,3 it is necessary to elucidate completely the magnetic relaxation processes of the SMMs used.In 2003, the terbium(III)-phthalocyaninato stacked complex (TBA)+[TbPc2]− (TbIII = terbium(III), Pc2− = phthalocyaninato, TBA+ = tetrabutylammonium) was reported to exhibit SMM behaviour, which originates from the ligand field (LF).4 The magnetic properties of rare-earth metal ions are strongly related to the charge density distribution.2 TbIII and DyIII ions exhibit uniaxial magnetic anisotropies of the easy axis, and splitting of the ground state multiplets is caused by the LF at the axial position. In this case, the energy gap between the ground and first excited states is associated with the energy barrier for the reversal of the magnetization (Δ), thereby causing slow relaxation of the magnetization. Consequently, the direction and magnitude of the LF strongly affect the magnetic properties.1–4
Although lanthanide(III)-phthalocyaninato double-decker (LnPc2) SMMs have been studied in detail, little is known about Ln2Pc3. Ishikawa and co-workers have reported a series of studies on the magnetic properties of the LnIII-Pc triple-decker complex [(Pc)Ln(Pc)Ln(obPc)] (obPc2− = 2,3,9,10,16,17,23,24-octabutoxyphthalocyaninato; LnIII = Tb, Dy, and Y), which are the first reports on the dynamic magnetism of a coupled 4f system.5 More recently, we have reported that the TbIII-Pc triple-decker SMM Tb2(obPc)3 (3) shows dual magnetic relaxation processes in the low temperature region in a dc magnetic field (Hdc).6 The dual magnetic relaxation behaviour has been observed not only for 3 but also for the spatially closed TbIII-Pc quadruple- and quintuple-decker complexes.7 This is clear evidence that the magnetic relaxation mechanism depends heavily on the f–f interactions between the TbIII ions in the dinuclear systems. Several SMMs with dual magnetic relaxation processes have been reported, and it has been shown that dual magnetic relaxation processes are observed for SMMs regardless of the type and number of metal ions in the complexes.8 It is well known that the magnetic relaxation rates reflect the local molecular symmetry and are extremely sensitive to tiny distortions in the coordination geometries. Our results suggest that the dual magnetic relaxation properties in the TbIII-Pc multiple-decker systems have a magic number of “two”, i.e., the number of metal sites.7 However, further experiments are required to corroborate this hypothesis.
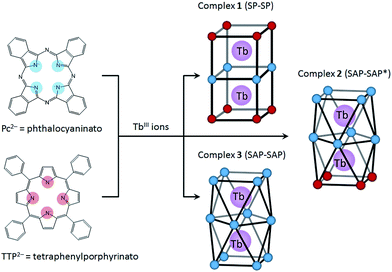
In this study, we focused on a porphyrin (H2Por) ligand, which has a cyclic structure with four pyrroles in common with a phthalocyanine (H2Pc). In the case of H2Por, the four pyrroles in the macrocycle are linked by methine groups, whereas H2Pc has a four isoindole molecules, which are pyrrole molecules fused with benzene rings, linked with nitrogen atoms. Both have planar structures with the π-conjugation spread over the entire molecule. However, the stacked coordination environments in complexes are significantly different depending on the presence or absence of π-electron repulsion. It is well-known that porphyrins form multiple-decker complexes when coordinated to lanthanide ions. A number of studies on LnIII-Por2− and LnIII-Por2−/Pc2− mixed multiple-decker type SMMs have been reported.9 From previous research, when using Por2− ligands, the SMM properties are not as same as those of Pc2− complexes due to the LF potential of coordination geometry. In addition, contractions of the square-antiprismatic (SAP) coordination environment affect the LF of the LnIII ions, which in turn affects the SMM properties.4,9a However, not only the effects of the ground state for different octa-coordination geometries but also dual magnetic relaxation processes have not been methodically discussed. In order to simplify the discussion, therefore, we designed dinuclear TbIII triple-decker complexes with different octa-coordination environments but with similar intramolecular TbIII–TbIII distances (∼0.36 nm). The combination of Por2− and Pc2− with LnIII ions can give rise to three different octa-coordination environments (Scheme 1).
Herein we present the results of studies on the SMM properties of dinuclear TbIII triple-decker mixed ligands complexes [(TTP)Tb(Pc)Tb(TTP)] (1) and [(Pc)Tb(Pc)Tb(TTP)] (2) (Scheme 1). The relationship between the octa-coordination environment and SMM properties of 1 and 2 are discussed in comparison to Tb2(obPc)3 (3).6 The SMM behaviours of dinuclear TbIII complexes 1–3 were explained by using X-ray crystallography and static and dynamic susceptibility measurements. This work shows that the SMM properties can be fine-tuned by introducing different octa-coordination geometries while maintaining the same TbIII–TbIII distances.
Experimental
All reagents were purchased from Wako chemicals, Tokyo Chemical Industry (TCI), and Sigma Aldrich and used without further purification. The compounds were prepared following reported procedures with slight modifications.10Synthesis of [(TTP)Tb(Pc)Tb(TTP)] (1) and [(Pc)Tb(Pc)Tb(TTP)] (2)10
Tb(acac)3·4H2O (180 mg, 0.40 mmol) and H2TTP (tetraphenylporphyrin) (150 mg, 0.25 mmol) were added to dry 1,2,4-trichlorobenzene (40 mL). The solution was refluxed under argon for 4 h. After cooling, Li2Pc (158 mg, 0.60 mmol) was added to the mixture. Then the solution was refluxed for 12 h. After cooling, the reaction mixture was added to n-hexane (500 mL). The obtained solid was purified by using column chromatography on silica gel with chloroform as the eluent. [(TTP)Tb(Pc)Tb(TTP)] (1) was obtained from a deep brownish red fraction, which was the first fraction, by removing the solvent, and [(Pc)Tb(Pc)Tb(TTP)] (2) was obtained from the dark green second fraction. Column chromatography (C-200 silica gel, Wako and Sephadex G-10, Pharmacia Biotech) was used to remove the remaining impurities. Dark red fine block crystals of 1 were obtained from chloroform/n-hexane (50 mg). ESI-MS: m/z (%): 2055.46605 (100) [M+]; elemental analysis calcd (%) for C120H72N16Tb2·3.5CHCl3: C 59.97, H 3.08, N 9.06; found: C 60.03, H 3.21, N 8.89. Black fine needle crystals of 2 were obtained from chloroform/n-hexane (40 mg). ESI-MS: m/z (%): 1855.30261 (100) [M+]; elemental analysis calcd (%) for C108H60N20Tb2·CHCl3: C 63.09, H 2.96, N 13.50; found: C 62.91, H 3.28, N 13.36.Physical property measurements
UV-Vis-NIR spectra for chloroform solutions of 1 and 2 were acquired on a SHIMADZU UV-3100PC in a quartz cell with a pathlength of 1 cm at 298 K (Fig. S1†). IR spectroscopy was performed on KBr pellets on a Jasco FT/IR-4200 spectrometer at 298 K (Fig. S2†). Electrospray ionization mass spectroscopy and elemental analyses were performed at the Research and Analytical Centre for Giant Molecules, Tohoku University. Magnetic susceptibility measurements were performed on Quantum Design SQUID magnetometers MPMS-3. Direct current (dc) measurements were performed in the temperature (T) range of 1.8–300 K and in dc magnetic fields (Hdc) of −70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 to 70
000 to 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe. Alternating current (ac) measurements were performed in the ac frequency (ν) range of 1–996 Hz with an ac field amplitude of 3 Oe in the presence of a dc field (zero–6000 Oe). Measurements were performed on randomly oriented powder samples of 1–3, which were placed in gel capsules and fixed with n-eicosane to prevent them from moving during measurements. All data were corrected for the sample holder, n-eicosane, and diamagnetic contributions from the molecules by using Pascal's constants.
000 Oe. Alternating current (ac) measurements were performed in the ac frequency (ν) range of 1–996 Hz with an ac field amplitude of 3 Oe in the presence of a dc field (zero–6000 Oe). Measurements were performed on randomly oriented powder samples of 1–3, which were placed in gel capsules and fixed with n-eicosane to prevent them from moving during measurements. All data were corrected for the sample holder, n-eicosane, and diamagnetic contributions from the molecules by using Pascal's constants.
X-Ray crystal structure analysis
A single crystal was mounted on a loop rod coated with Paratone-N (HAMPTON RESEARCH). Data collection was performed on a Rigaku Saturn 724+ CCD diffractometer with graphite-monochromated Mo-Kα radiation (λ = 0.71069 Å) at T = −180 ± 1 °C. An empirical absorption correction based on azimuthal scans of several reflections was applied. The data were corrected for Lorentz and polarization effects. All non-hydrogen atoms were refined anisotropically using a least-squares method, and hydrogen atoms were fixed at calculated positions and refined using a riding model. SHELXL-97 was used for structure refinement, and the structure was expanded using Fourier techniques.12a The weighting scheme was based on counting statistics. Full-matrix least-squares refinements on F2 based on unique reflections with unweighted and weighted agreement factors of R = ∑||Fo| − |Fc||/∑|Fo| (I > 2.00σ(I)), and wR = [∑w(Fo2 − Fc2)2/∑w(Fo2)2]1/2 were performed. Powder X-ray diffraction (PXRD) patterns of crushed polycrystalline samples of 1 and 2, loaded into capillaries (diameter: 0.8 mm, length: 80 mm, Hilgenderg) with their mother liquor, were collected at 298 K using a Rigaku X-ray diffractometer (AFC-7R/LW) operated at 50 kV and 300 mA in the diffraction angle (2θ) range of 3–60° in steps of 0.02° at 2 s per step (Fig. S3†). Visualization and analysis of the crystal structures and PXRD patterns were simulated from the single crystal data by using Mercury 3.0.12bResults and discussion
Synthesis and electronic structure
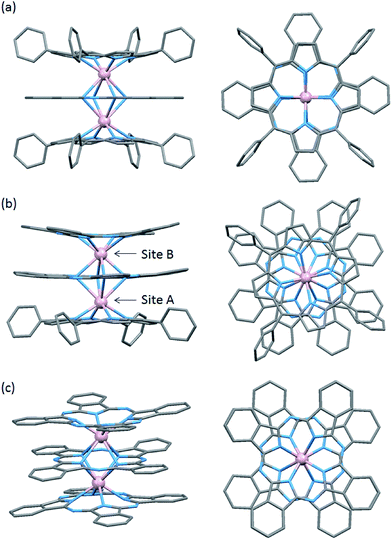
The structures of 1–3 are shown in Fig. 1 with several octa-coordination geometries for TbIII dinuclear systems. In our studies, we used a tetraphenylporphyrinato (TTP2−) ligand with a phthalocyaninato (Pc2−) ligand because it has a high solubility, making crystallization easier.10 In order to control the spin orientation in the molecules, we designed 1–3 so that the two TbIII ions were along the anisotropy axis. Mixed ligand triple-decker complexes 1 and 2 were synthesized in one-step using Tb(acac)3·nH2O, H2TTP and Li2Pc following a procedure reported by Weiss and co-workers.10 On the other hand, triple-decker 3 was synthesized in one step starting from Tb(acac)3·4H2O and H2obPc following a procedure reported by Takahashi and co-workers.11 Por2− and Pc2− can form neutral triple-decker complexes composed of two TbIII ions and three obPc2− ligands ([(obPc)Tb(obPc)Tb(obPc)] (3)) and in Por2−:Pc2− ratios of 1:2 ([(Pc)Tb(Pc)Tb(Por)] (2)) and 2:1 ([(Por)Tb(Pc)Tb(Por)] (1)) with closed shell π electron systems.5,6,9–11Triple-decker complexes 1–3 are soluble in most organic solvents, except for alcohols and n-hexane. A chloroform solution of 1–3 showed 3–6 prominent absorption bands in the wavelength range of 250–1200 nm (Fig. S1†). The absorption spectrum of 1, which has an inner Pc2− ligand strongly interacting with the two outer TTP2− ligands, were similar to those of the [(TTP)Ln(Pc)Ln(TTP)] analogues and, therefore, were assigned on the basis of a previous report.10 The strong absorption bands at 419 nm were assigned to be Soret (S) bands, and the weak absorptions at 493 and 553 nm were assigned to be the Q bands of the TTP2− ligands with a large contribution from the former tetrapyrroles, respectively. The bands at 353 (S band) and 606 nm (Q band) were attributed to the Pc2− ligand. Furthermore, the weak broad bands in the near-IR region (850–1100 nm) were assigned to be electronic transitions between the dianionic ligands.
The absorption spectrum of 2 was similar to that of 1, but the absorption intensities and peak positions were different. From experimental and theoretical studies, this is clear evidence that excitonic interactions between the two Pc2−/Por2− chromophores depend heavily on the molecular structures, in which the ligands are stacked in a staggered face-to-face fashion.10 The strong absorption bands at 341 nm with shoulders at 324 nm, and the weak absorptions at 617 and 669 nm were assigned to be S and Q bands of the Pc2− ligands, respectively. The bands at 418 (S band) and those at 522 and 604 nm (Q bands) were attributed to the TTP2− ligand. Furthermore, the broad band at 737 nm was assigned to be electronic transitions between the dianionic ligands. In IR spectra of 1 and 2, three strong peaks at 1330, 1062, 728 cm−1, which were attributed to the Pc2− ligand, were observed (Fig. S2†).
In the case of 3, the two absorption bands at 290 and 356 nm were assigned to be the S bands of the obPc2− ligands,11 and those at 577 and 655 nm were assigned to be the Q bands of the obPc2− ligands.
Crystal structure and octa-coordination geometry
To evaluate the effects of the coordination geometry around the TbIII ion in the triple-decker complexes 1–3, contractions of their octa-coordination environments were investigated by using single-crystal X-ray diffraction analysis (Fig. 1). The longitudinally contracted SAP coordination environment shares an edge with an undistorted complex, i.e., there is a twist angle (φ) between the upper and the lower Pc2− ligands (Fig. S4†). Selected crystallographic data for 1–3 are compiled in Table S1.† The data clearly show that contractions of the octa-coordination environment have an influence on the LF of the LnIII ions, which affects the SMM properties.4,9,13Complex 1, shown in Fig. 1a, crystallized with chloroform in the crystal lattice in the tetragonal space group I4/m, which has a SP (quasi-D4h) coordination environment (Scheme 1 and Fig. S4d†). Complex 1 has two TbIII ions, which a Pc2− ligand coordinated between them. The inner Pc2− ligand with four isoindole-nitrogen donor atoms (Niso) and a center of symmetry strongly interacts with the two outer TTP2− ligands. The center of the square formed by the four pyrrolic nitrogens of the Pc2− ligand form a crystallographically imposed inversion center, making the two TbIII ions and outer TTP2− ligands equivalent. In addition, the inner Pc2− ligand of 1 is located on a mirror plane. The intramolecular TbIII–TbIII distance was determined to be 0.372 nm (TbIII–TbIII distance was determined to be 0.352 nm in 3).6φ between the outer TTP2− ligands and the inner Pc2− ligand was determined to be 3.62°. Thus, the two TbIII sites in 1 have a slightly distorted SP geometry (Fig. 1a). The TbIII ions are unevenly spaced between the outer TTP2− and inner Pc2− ligands with distances of 0.239 nm (3: 0.234–0.237 nm)6 from the mean plane of the four Niso of the outer TTP2− ligands and 0.268 nm (3: 0.258–0.262 nm)6 from the mean plane of the four Niso of the inner Pc2− ligand.
Crystal-packing diagrams of 1 are shown in Fig. S5.† The intermolecular TbIII⋯TbIII distance along the a and c axes were determined to be 1.431 and 1.364 nm, respectively. Each molecule of 1 is rather well separated from neighboring molecules due to the tetraphenyl groups of TTP2− ligands and chloroform molecules as crystal solvents. Furthermore, PXRD patterns for 1 at 293 K are similar to those simulated from X-ray single crystallographic data for 1 at 93 K (Fig. S3-1†).
Recently, Jiang and co-workers have reported the [(Por)Ln(Pc)Ln(Por)] type triple-decker SMM {(TCIPP)Dy[Pc(OBNP)4]Dy(TCIPP)}, which has DyIII ions in SAP (φ ≈ 7°) and SAP* (φ ≈ 42°) environments (TClPP = meso-tetrakis(4-chlorophenyl)porphyrinato; Pc(OBNP)4 = tetrakis(dinaphtho[1,2-e:1′,2′-g]-1,4-dioxocine)[2,3-b;2′,3′-k;2′′,3′′-t;2′′′,3′′′-c′]phthalocyaninato).9e The coordination environments are completely different from those in 1, which has two TbIII ions in the slightly distorted SP environments (φ ≈ 4°).
On the other hand, complex 2, shown in Fig. 1b, crystallized with chloroform in the crystal lattice in the monoclinic space group P21/c. 2 has a SAP (quasi-D4d) coordination environment (Scheme 1 and Fig. S4e†), and it has two TbIII ions and an inner Pc2− ligand, which strongly interact with each other. The TbIII–TbIII distance in 2 was determined to be 0.363 nm, and φ between the outer Pc2− ligands and the center Pc2− one was determined to be 38.40° (site B = SAP*). On the other hand, φ between the outer TTP2− ligands and the inner Pc2− one was determined to be 13.80° (site A = SAP). The TbIII ions are unevenly spaced between the outer TTP2− and inner Pc2− ligands with distances of 0.237–0.240 nm from the mean plane of the four Niso of the outer TTP2− ligands and 0.270–0.274 nm from the mean plane of the four Niso of the inner Pc2− one. On the other hand, the TbIII ions are unevenly spaced between the outer Pc2− and inner Pc2− ligands with distances of 0.235–0.237 nm from the mean plane of the four Niso of the outer Pc2− ligands and 0.257–0.260 nm from the mean plane of the four Niso of the center Pc2− one. The distance between the TbIII ions and Niso of 1–3 are essentially the same.
Crystal-packing diagrams of 2 are shown in Fig. S6.† The closest intermolecular TbIII⋯TbIII distance along the c axis was determined to be 1.162 nm. Each molecule of 2 is rather well separated from neighboring molecules due to the four phenyl groups of the TTP2− ligands and chloroform as crystal solvents. PXRD patterns of 2 at 293 K were similar to the patterns simulated from X-ray single crystallographic data of 2 at 93 K (Fig. S3-2†).
A number of studies on [(Pc)Ln(Pc)Ln(Por)] mixed ligand triple-decker type SMMs have been reported.9a,9d Ishikawa and co-workers reported the triple-decker complex {(Pc)Tb(Pc)Tb[T(p-OMe)PP]} [T(p-OMe)PP = 5,10,15,20-tetra(p-methoxyphenyl)porphyrinato], in which the TbIII ions are in SP (φ ≈ 1°) and SAP (φ ≈ 45°) environments.9a Jiang and co-workers reported the triple-decker complex {(TClPP)Dy[Pc(OPh)8]Dy[Pc(OPh)8]} [Pc(OPh)8 = 2,3,9,10,16,17,23,24-octa(phenoxyl)phthalocyaninato] with DyIII ions in SAP (φ ≈ 10°) and SAP* (φ ≈ 25°) environments.9d From a comparison of the reported complexes, in 2, the TbIII ions have SAP (φ ≈ 14°) and SAP* (φ ≈ 38°) environments, and the octa-coordination environments are completely different from those in 1 (SP–SP). In other words, both TbIII sites in 2 exhibit slightly distorted SAP geometries with independent environments (Fig. 1b). Viewed from another direction, site A (φ ≈ 14°) appears to have a slightly distorted SP environment. Thus, the SMM properties cannot be predicted solely from the crystal structure, and it is necessary to study the SMM properties in detail (see Magnetic properties section).
We have already reported a crystal structure of 3.6 Complex 3 crystallized with ethanol in the crystal lattice in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) , as shown in Fig. 1c. Complex 3 has two TbIII ions sandwiched between three obPc2− ligands with four Niso donor atoms and a center of symmetry. The intramolecular TbIII–TbIII distance was determined to be 0.352 nm. φ between the outer obPc2− ligands and the inner one was determined to be 32°. This means that both TbIII sites in 3 have the same slightly distorted SAP geometry (quasi-D4d). The intermolecular TbIII⋯TbIII distance along the a axis was determined to be 1.098 nm. Each molecule of 3 is rather well separated from neighbouring molecules due to the n-butoxy chains. This is supported by the dc and ac magnetic measurements on an isomorphous sample of 3 diluted with diamagnetic Y2(obPc)3, which show that the intermolecular magnetic interactions are negligible. In other words, the magnetic properties of 1–3 are due to intramolecular TbIII–TbIII interactions and the symmetry of the octa-coordination geometry (vide infra). Selected molecular geometry information for dinuclear LnIII triple-decker mixed ligand complexes are listed in Table 1.
, as shown in Fig. 1c. Complex 3 has two TbIII ions sandwiched between three obPc2− ligands with four Niso donor atoms and a center of symmetry. The intramolecular TbIII–TbIII distance was determined to be 0.352 nm. φ between the outer obPc2− ligands and the inner one was determined to be 32°. This means that both TbIII sites in 3 have the same slightly distorted SAP geometry (quasi-D4d). The intermolecular TbIII⋯TbIII distance along the a axis was determined to be 1.098 nm. Each molecule of 3 is rather well separated from neighbouring molecules due to the n-butoxy chains. This is supported by the dc and ac magnetic measurements on an isomorphous sample of 3 diluted with diamagnetic Y2(obPc)3, which show that the intermolecular magnetic interactions are negligible. In other words, the magnetic properties of 1–3 are due to intramolecular TbIII–TbIII interactions and the symmetry of the octa-coordination geometry (vide infra). Selected molecular geometry information for dinuclear LnIII triple-decker mixed ligand complexes are listed in Table 1.
| Complexes | Ln–Ln distance/nm | φ A/° | φ B/° | Site geometry |
|---|---|---|---|---|
| a This work; see main text in this manuscript. | ||||
| [(TTP)Tb(Pc)Tb(TTP)] 1a | 0.372 | 4 | 4 | SP–SP |
| [(Pc)Tb(Pc)Tb(TTP)] 2a | 0.363 | 14 | 38 | SAP–SAP* |
| [(obPc)Tb(obPc)Tb(obPc)] 36 | 0.352 | 32 | 32 | SAP–SAP |
| {(Pc)Tb(Pc)Tb[T(p-OMe)PP]}9a | 0.360 | 1 | 45 | SP–SAP |
| {(TCIPP)Dy[Pc(OBNP)4]Dy(TCIPP)}9e | 0.371 | 7 | 42 | SAP–SAP* |
| {(TCIPP)Dy[Pc(OPh)8]Dy[Pc(OPh)8]}9d | 0.361 | 10 | 25 | SAP–SAP* |
Static magnetic properties
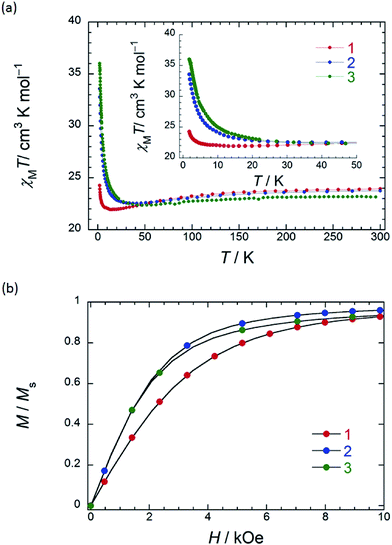
In order to understand the SMM properties of 1 (SP–SP) and 2 (SAP–SAP*), we compared them with those of SMM 3 (SAP–SAP).6 The dc magnetic susceptibilities (χM) of powder samples of 1 and 2 were measured in the temperature (T) range of 1.8–300 K in a dc magnetic field (Hdc) of 500 Oe by using a superconducting quantum interference device (SQUID) magnetometer.The χMT value at 300 K (23.6 cm3 K mol−1) corresponds to two free TbIII ions (7F6, S = 3, L = 3, g = 4/3) (Fig. 2a). The χM of 1 obeyed the Curie–Weiss law, giving a Curie constant (C) of 23.3 cm3 K mol−1 with a positive Weiss constant (θ) of 0.15 K over the T range of 180–300 K (Fig. S7a†). With a decrease in T, the χMT value of 1 gradually increased and reached ∼25 cm3 K mol−1 at 1.8 K. In the case of 2, the χMT value at 300 K (23.6 cm3 K mol−1) corresponds to two free TbIII ions (Fig. 2a). The χM obeyed the Curie–Weiss law, giving a C value of 23.6 cm3 K mol−1 with a positive θ of 0.02 K over the entire T range (Fig. S7b†). With a decrease in T, the χMT value of 2 slightly increased and reached 34 cm3 K mol−1 at 1.8 K. The behaviour of χMT clearly shows that the magnetic behaviour depends heavily on the magnetic dipole–dipole interactions between the TbIII ions in the molecule under 10 K. Behaviour similar to those of triple-decker 3 was observed, as shown in Fig. 2a.6χMT versus T plots for 3 increased with a decrease in T and reached a maximum of 36 cm3 K mol−1 at 1.8 K, which indicates the existence of ferromagnetic interactions between the TbIII ions.5–71 has a lower χMT value at 1.8 K than 2 and 3 do. The deviation in the χMT values occur due to a combination of a few factors, such as the intermetallic TbIII–TbIII distance, LF effects with significant magnetic anisotropy, and/or depopulation of the excited states.2b–e,g,h,5–7,9a
To understand the deviation in the χMT value of 1, we first studied the influence of the TbIII–TbIII distance. The intramolecular TbIII–TbIII distance of complexes 1–3 were determined to be in the range of 0.352–0.372 nm, indicating that there were strong magnetic interactions between TbIII ions in the molecules. This is clear evidence that the χMT value of TbIII dinuclear systems depends heavily on the magnetic dipole–dipole (f–f) interactions between the TbIII ions.5–7 Therefore, the ferromagnetic dipole–dipole interactions (Dij ∝ 1/rij3, where rij is the distance between spin i and j) between the TbIII ions in 1 are similar to those in triple-decker complex 3 because rij between the TbIII ions of 1 (0.372 nm) is similar to that of 3 (0.352 nm) (ca. 1/1.1).6 In other words, the χMT value of 1 cannot be explained solely on the basis of the TbIII–TbIII distance, and it is possible that the magnetic anisotropies of 1–3 are due to the octa-coordination geometries of the TbIII ions.
Next, we focused on the different octa-coordination environments of 1–3. To study the effects on the magnetic properties of the triple-decker complexes, contractions of the coordination environments in 1 and 2 were investigated. From XRD analysis, it was determined that the octa-coordination geometries of 1 (SP–SP), 2 (SAP–SAP*), and 3 (SAP–SAP) had pseudo-4-fold axes (direction of the uniaxial magnetic anisotropy) perpendicular to the tetrapyrrole rings. In addition, contractions of the SAP coordination environments affect the LF of the LnIII ions, which affects the SMM properties.4,9a,13 It has been reported that the LF parameters (Bqk) of an ideal SAP coordination geometry with D4d symmetry is different from Bqk of an SP coordination geometry with D4h symmetry.4,9a,13 Differences in the SMM properties are thought to be due to the presence or absence of particular off-diagonal LF terms. Thus, SAP geometry only occurs in the terms B02 (α2A02r2), B04 (α4A04r4) and B06 (α6A06r6), which are LF parameters for the axial anisotropy, where the αkAqkrk are LF parameters.13 The LF Hamiltonian can be written as ĤLF = ∑∑kq=−k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BqkOqk, where Oqk are spin operators.13 On the other hand, SP geometry not only contributes to the LF of axial parameters but also to the terms B44 (α4A44r4) and B46 (α6A46r6), which are LF parameters for the transverse anisotropy. The fourth-range extradiagonal parameters (B44 and B46) enable mixing between the ground state of the |+6〉 and |−6〉 doublet in a zero magnetic field.4,9a,13 It exerts a greater effect on both the hyperfine structure of the ground state and the ground state multiplets structure.
BqkOqk, where Oqk are spin operators.13 On the other hand, SP geometry not only contributes to the LF of axial parameters but also to the terms B44 (α4A44r4) and B46 (α6A46r6), which are LF parameters for the transverse anisotropy. The fourth-range extradiagonal parameters (B44 and B46) enable mixing between the ground state of the |+6〉 and |−6〉 doublet in a zero magnetic field.4,9a,13 It exerts a greater effect on both the hyperfine structure of the ground state and the ground state multiplets structure.
There have been many attempts to elucidate the relationship between the coordination geometry and LF parameters both experimentally and theoretically. The LF parameters have been shown to have a significant influence on the ground state multiplets structure and magnetic anisotropy. The effects of the LF parameters on the uniaxial anisotropy are described below.
Gatteschi and co-workers have reported that the twist angle (φ) has a big effect on the ground state and the first excited state of the octa-coordination geometries with C4 symmetry axes for LnIII complexes, since the structures deviate from D4d symmetry. This deviation appears in the fourth-range extradiagonal parameters, and the distortion has an effect on both axial and transverse parameters, which has been shown by using theoretical calculations.13e In addition, the angles (α) between the C4 axis and the direction of LnIII–Niso coordination bond have a strong influence on the LF parameters.13f
Ishikawa and co-workers have reported that the values of the energy barrier for the reversal of the magnetization (Δ) of the ground state multiplets of [TbPc2]+/− complexes are changed depending on the difference in the closest Pc–Pc distance.4 Longitudinal contraction of the SAP structure causes the changes in Δ and increases the LF splitting of the ground multiplets of LnIII ions in the cation structure.4i Furthermore, Ishikawa and co-workers have reported the LF parameters of the YIII–TbIII triple-decker complex [(Pc)Y(Pc)Tb(obPc)] which has quasi-D4d geometry like 3.5c They do not report φ for the TbIII site, but it should be ca. 32° on the basis of the structure of a similar complex.5d The value of A02r2 decreases with a decrease in φ from 414 cm−1 for [TbPc2]− with φ ≈ 45° to 293 cm−1 for [(Pc)Y(Pc)Tb(obPc)] with φ ≈ 32°. It should be noted that the A44r4 dramatically increases from 10 to 863 cm−1, and A46r6 increases from a negligible value to 357 cm−1.4,5c,13j The Δ value for [(Pc)Y(Pc)Tb(obPc)] with φ ≈ 32° has been determined to be 300 cm−1 from the LF parameters.5c On the other hand, Δ for [TbPc2]− with φ ≈ 45° has been determined to be ca. 420 cm−1 from the LF parameters.4 Theoretical calculations support the relationship between the LF parameters and Δ.13g,h Furthermore, they demonstrate that they can reversibly switch between the non-SMM protonated form [TbH(TTP)2] with a hepta-coordinate environment to the SMM deprotonated form [Tb(TTP)2]− (H-DBU)+ with D4d symmetry.9b They argue that the change in SMM properties is due to the off-diagonal LF term and/or that the lowest energy level is no longer Jz = ±6 in the hepta-coordinate environment. Therefore, there is a loss of uniaxial anisotropy, and [TbH(TTP)2] does not exhibit SMM behaviour.
Recently, Chibotaru, Tong and co-workers have reported strong evidence for the relationship between the symmetry and Δ of SMMs.13g They demonstrated that when Δ of an DyIII SMM was decreased by changing symmetry from quasi-D5h to quasi-Oh. They report that Δ changes by two orders of magnitude between the quasi-D5h (305 cm−1) and quasi-Oh structures (negligible value). The axial parameters B02 and B04 of quasi-D5h structure are large, whereas the values of the non-axial parameters B22, B44 and B34 of quasi-Oh structure are the same or slightly larger than those of the axial ones. In addition, the DyIII site in the quasi-D5h structure exhibits very strong axial magnetic anisotropy. On the other hand, the DyIII site in the quasi-Oh structure shows weak axial magnetic anisotropy due to the non-axial parameters. In other words, the uniaxial anisotropy of the quasi-D5h structure is stronger than that of quasi-Oh structure on the basis of the g tensor.
Considering the above research results, it is possible that the transverse anisotropy parameters (Bqk; q ≠ 0) have an effect on the uniaxial magnetic anisotropies and the ground state multiplets structure. The coefficient values show that there are interactions between the metal orbitals and the ligands, and they can be determined experimentally.2,4,5,9,13 However, we discuss this point in the section “Dynamic magnetic properties”.
In order to qualitatively estimate the magnetic anisotropy, reduced magnetization measurements were performed on 1 (SP–SP), 2 (SAP–SAP*), and 3 (SAP–SAP) (Fig. S8-1†). If molecules have large magnetic anisotropies, M versus HT−1 plots do not overlap on a single curve, and they did not show saturation at high fields (up to 70 kOe).1,2M of 3 was not synchronised, whereas those of 2 and 1 slightly unaligned, indicating the presence of significant magnetic anisotropy.13h To elucidate the ground state of 1–3, as shown in Fig. 2b, we focused on the initial increase in M in a weak dc magnetic field (M versus H). M of 1 gradually increased, whereas those of 2 and 3 sharply increased. The M–H curve reflects the overall effect of the LF and magnetic interactions. As the ground states are rather differently mixed, it is very difficult to infer the strength of the magnetic interactions in various LFs from the M data which have strong magnetic anisotropies. It is indicated that the ground state of 1 is different from that of 2 and 3. This result agrees with other information concerning the ground state (see Dynamic magnetic properties and Magnetic relaxation mechanism). For diluted samples of 1–3, behaviour similar to that of 1–3 (powder sample) were observed, thus confirming that the magnetic properties were not due to the intermolecular TbIII⋯TbIII interactions, as shown in Fig. S9.†6,7 Therefore, the different magnetic behaviours observed for 1–3 is thought to be due to the symmetry of the octa-coordination environment.4–6,9,13 Below, the relationship between the symmetry of coordination environments and the ν dependence of the ac susceptibilities are discussed.
Dynamic magnetic properties
To elucidate the details of the relaxation dynamics, ac magnetic susceptibility measurements were performed on powder samples of 1 (SP–SP) and 2 (SAP–SAP*) in a 3 Oe oscillating ac field. The in-phase (χM′) and out-of-phase (χM′′) signals changed in different T ranges depending on the ν in the range of 1–996 Hz, indicating that 1 and 2 are SMMs (Fig. 3 and 4, S10–S28†). The values of the energy barrier for the reversal of the magnetization (Δ) and pre-exponential factor (τ0: the average relaxation time in response to thermal fluctuation) can be estimated from Arrhenius equation: τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δ/kBT),1,2 where τ is the magnetic relaxation time, kB is Boltzmann constant. This linear relation between ln(τ) and T−1 indicates that the Orbach process (spin–phonon interaction which approximately corresponds to the Δ for thermal relaxation for the reversal of the magnetic moment) is dominant in high-T ranges. This method is highly credible for the high-T region.
exp(Δ/kBT),1,2 where τ is the magnetic relaxation time, kB is Boltzmann constant. This linear relation between ln(τ) and T−1 indicates that the Orbach process (spin–phonon interaction which approximately corresponds to the Δ for thermal relaxation for the reversal of the magnetic moment) is dominant in high-T ranges. This method is highly credible for the high-T region.
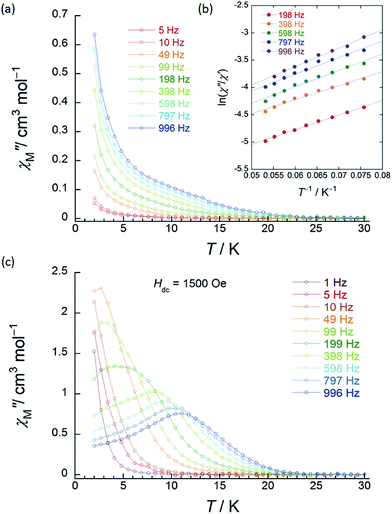 | ||
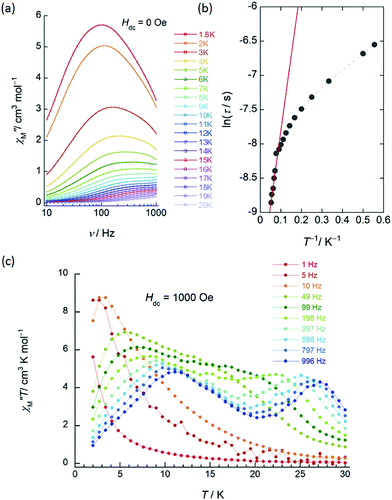
| Fig. 3 Frequency (ν) and temperature (T) dependence of the ac magnetic susceptibilities (χM′′: out-of-phase) of 1 (SP–SP). The measurements were performed in a 3 Oe ac magnetic field at the indicated frequencies in an Hdc of (a) zero. The solid lines are guides for eyes. (b) χM′′/χM′ versus T−1 (13–18 K) plot at the given ν (198–996 Hz) of the ac susceptibility data by using the Kramers–Kronig equation (eqn (S1)–(S3)†). The solid lines were fitted as described in Table S2.† (c) ν dependence of χM′′ versus T in an Hdc of 1500 Oe. The solid lines are guides for eyes. | ||
χ M′′ versus T plots for both 1 and 2 in the ν range of 1–996 Hz barely showed any tailing, and the expected maximum value due to blocking could not be observed down to 1.8 K in an applied Hdc of zero (Fig. 3a, S10 and S11†). The χM′′ did not disappear in the T region below 2 K, indicating that the magnetic moment was not frozen and that a different relaxation process, which is likely a ground state QTM process, became dominant in the low-T region. Since we have no basis for comparing Δ and τ0 in a zero Hdc, we determined Δ for 1 and 2 from χM′′/χM′ versus T−1 (13–18 K) plots of the ac susceptibility data at various ν (198–996 Hz) by using the Kramers–Kronig equation (eqn (S1)–(S3)† and Fig. 4b).14 By fitting the data, the Δ was determined to be 18–24 cm−1 with τ0 = 10−6 to 10−7 s for 1 and 36–38 cm−1 with τ0 ≈ 10−6 s for 2 in a zero Hdc. The estimated parameters for 1 and 2 are summarized in Tables S2 and S3,† respectively.
In the case of 1 (SP–SP), in detailed Hdc dependent ac magnetic susceptibility (χM′ and χM′′) measurements at ν of 996 Hz in the T range of 2–30 K, χM′′ showed a single maximum at 11 K in an Hdc of 1500 Oe (Fig. 3c and S12†). The shapes of the peaks of 1 drastically changed, and the peaks shifted to the low-T side when an Hdc large enough to suppress QTM was applied. The χM′ and χM′′ peaks were clearly shifted in different T ranges dependent on the ν (1–996 Hz) in Hdc of 1500 and 3000 Oe, indicating that 1 is a field-induced SMM (Fig. S13†).
In contrast to 1, 2 (SAP–SAP*) showed clear Hdc field dependent character and two χM′′ peaks appeared at 11 K and 27 K at 996 Hz and did not show Hdc dependence in the range of 250–5000 Oe, indicating that 2 is a field-induced SMM (Fig. S14 and S15†). However, a χM′′ peak top for 2 was not clearly observed in the measured T range (Fig. S15b†). In order to clarify the T dependence, we prepared χM′T and χM′′T graphs (Fig. 4c and S16†). The shape of the two peaks of 2 were drastically different from those of 1 and clearly shifted in different T ranges depending on ν in an Hdc of 1000 Oe.
This behaviour is similar to those of other dinuclear TbIII complexes with slightly different structures relative to 2, such as {(Pc)Tb(Pc)Tb[T(p-OMe)PP]} and [(Pc)Tb(Pc)Tb(obPc)], with different coordination environments around the asymmetric TbIII sites reported by Ishikawa and co-workers.5,9a Our results clearly show that the two TbIII ion sites (SAP and SAP* sites) are inequivalent and are in agreement with the structure of 2 (SAP–SAP*) determined using XRD and the ac susceptibility measurements. From a χM′′T versus T plot, the intensity of the χM′′ peak top at 27 K (the SAP* site of 2) was lower in an Hdc of 3000 Oe. On the other hand, the intensity of the χM′′ peak top at 11 K (the SAP site of 2) showed ν dependence, and this behaviour is similar to that observed in a χM′′T versus T plot for 2 in a zero Hdc (Fig. S17 and S18†). It was attributed to an Orbach process, which was observed when an Hdc large enough to suppress QTM (τ ≈ 10−4 s) was applied. The Orbach process for the SAP* environment is inhibited by fast QTM and/or direct magnetic relaxation process (τ ≈ 10−3 s).13g,15 See the details in “the Magnetic relaxation mechanism” section.
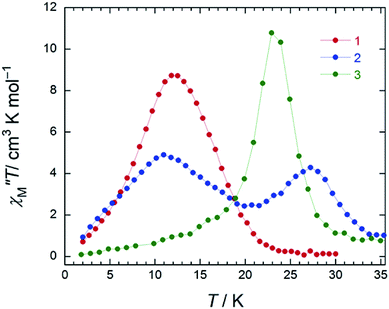
In the case of 3 (SAP–SAP), in a χM′′ versus T plot at ν of 996 Hz, only a single peak around 24 K was observed in an Hdc of zero.6 These results indicate that the two χM′′T peak top T values (11 and 27 K) at 996 Hz for 2 with an SAP–SAP* site correspond to a state that is a combination of 1 with an SP–SP site (11 K) and 3 with an SAP–SAP site (24 K), respectively (Fig. 5). Thus, it is important to study the properties of dinuclear TbIII triple-decker type SMMs on the bases of crystal structure features, such as molecular contractions, i.e., LF and CF of the central metal ions.
To elucidate the details of the relaxation dynamics of 1 and 2, the ν dependence of the χM′ and χM′′ signals in the range of 10–996 Hz were studied at each T. Argand plots (χM′′ versus χM′) for 1 were partially semicircular in shape in an Hdc of zero in the T range of 4–16 K (Fig. S19†). In the case of the χM′′ signals for 1 in the range of 10–996 Hz, the expected maximum value due to blocking could not be observed down to 1.8 K in an applied Hdc of zero (Fig. S19b†). On the contrary, below 10 K, a small shoulder peak in the range of 10–100 Hz was observed. A χM′′ peak top T of 5 K was observed when Hdc > 200 Oe (Fig. S20b†). The shape of the χM′′ peaks for 1 drastically changed and shifted to the low-ν side when an Hdc large enough to suppress QTM was applied, which will be described in detail below (Fig. 8).
The obtained τ values of 1 are plotted as a function of T−1 in Fig. S21.† We observed QTM (T-independent regime for τ) with a fast τ below 10 K. These results confirm that QTM via the presence of off-diagonal LF terms in SP–SP environments is not suppressed in sharp contrast to that of 3 (SAP–SAP).6 Ishikawa and co-workers have reported that the ground state of an SP site has a high probability of QTM in comparison to an SAP one due to the presence of off-diagonal LF terms.4,9a,13 In the above case, the τ values at 5 K for 1–3 in an Hdc of zero follow the order: 1 with SP–SP site (4.1 × 10−5 s) < 2 with SAP–SAP* sites (5.6 × 10−4 s) < 3 with SAP–SAP sites (1.8 × 10−2 s) (Table S4†). This coordination relationship is also reflected in the τ of the QTM process at low-T region.
In order to study the field-induced SMM properties, the ν dependence of the χM′ and χM′′ signals for 1 in the range of 10–996 Hz were measured at each T (4–16 K) in Hdc of 1500 and 3000 Oe (Fig. S22 and S23†). From Argand plots in Hdc of 1500 and 3000 Oe, which were made using a generalized Debye model (eqn (S4)–(S6)†), the magnetic relaxations of 1 with SP–SP geometry showed a single component process.16 The obtained τ values are plotted as a function of T−1 in Fig. S24.† The T-independent regime for QTM was restrained, and there were clear signs of the T-dependent regime for the Orbach process. The Δ was estimated from a χM′′ versus ν plot to be 32 cm−1, and a τ0 value of 3.97 × 10−6 s was obtained from an Arrhenius plot using τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Δ/kBT) for 1 in an Hdc of 1500 and 3000 Oe in the T range of 11–16 K (Fig. S24†). These results confirm that the QTM is suppressed in an Hdc and that the direct process is enhanced. This is clear evidence that τ of 1 depends heavily on T and Hdc.
exp(Δ/kBT) for 1 in an Hdc of 1500 and 3000 Oe in the T range of 11–16 K (Fig. S24†). These results confirm that the QTM is suppressed in an Hdc and that the direct process is enhanced. This is clear evidence that τ of 1 depends heavily on T and Hdc.
On the other hand, as shown in Fig. S25,† Argand plots for 2 were semicircular in an Hdc of zero in the T range of 1.8–20 K and could be analyzed using a generalized Debye model (eqn (S4)–(S6)†).16 The obtained τ values of 2 are plotted as a function of T−1 in Fig. 4b. We did not observe pure QTM (T-independent regime for τ), and the T-dependent regime for τ occurred under 10 K. These results confirm that pure QTM via the SAP–SAP* environments of 2 is suppressed as it is in 3 with SAP–SAP sites.6 The solid line represents a least-squares fit by using an Arrhenius equation with the following kinetic parameters: Δ = 15 cm−1 and τ0 = 4.8 × 10−5 s (Fig. 4b). These values have similar orders of magnitude as those obtained by using the Kramers–Kronig equation (Table S3†).
On the other hand, the T-dependent regime for τ in the low-T region appears to involve thermally assisted QTM via a doublet ground state, a direct process and/or a Raman process, which are difficult to separate from each other.13d,15 Together with the Arrhenius plot of the data from χM′′T versus T (Fig. S16b†) and χM′′ versus ν plots for 2 in an Hdc of 1000 Oe (Fig. 4c and S26†), Δ was estimated to be 60 cm−1 with τ0 of 3.48 × 10−6 s (SAP site: blue circle in Fig. 6) and 162 cm−1 with 3.16 × 10−8 s (SAP* site: red open circle in Fig. 6) in the T range of 18–29 K. Furthermore, Argand plots for 2 were partially semicircular in shape for the magnetic relaxation process in an Hdc of 3000 Oe in the T range of 4–17 K (Fig. S27†). Similar irregularity was observed in the Argand plots when T < 6 K but in an applied Hdc > 500 Oe (Fig. S28†).
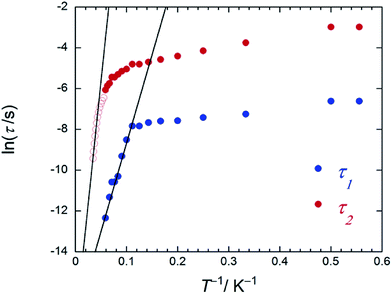 | ||
| Fig. 6 An Arrhenius plot of 2 (SAP–SAP*), where the magnetic relaxation time τ (blue and red circles) were obtained from χM′′ versus ν plots (Fig. S26b†) at T between 1.8 and 20 K in an Hdc of 1000 Oe and the red open circles were obtained from peak top T of χM′′T versus T plots (Fig. 4c) at T between 22 and 27 K in an Hdc of 1000 Oe. τ was obtained from the least-squares fitting using a generalized Debye model (eqn (S4)–(S6)†) and an extended Debye model (eqn (S8)–(S10)†). | ||
In order to elucidate the relationship between the geometry and LF, we examined the correlation between the twist angle (φ) and Δ (Fig. 7). Δ versus φ plots for 1–3 and [TbPc2]− complex showed linear relationships. Above 10 K, the lowest excitation in the energy gap between the ground and first excited state levels of each SMM are approximately the same magnitude as the obtained Δ values because the intramolecular TbIII–TbIII interactions have little effect on the LF (Fig. S29†). As previously stated, the molecular geometry is related to the mixing of off-diagonal LF terms.4,5,9,13 In other words, the degree of mixing of the off-diagonal LF terms increases from the D4d ([TbPc2]− complex with φ ≈ 45°) to D4h (1 with φ ≈ 4°). Thus, Δ for the D4h geometry becomes narrower than that for the D4d one due to the influence of LF parameters. This agrees with earlier studies.2,4,5,9,13i,j In addition, there is a slight deviation from linearity in the plot of Δ due to distortions in the molecular geometry, such as longitudinal contraction of the coordination environment.4e,i Selected geometry and SMM information for 1–3 and related SMM are listed in Table S5.†
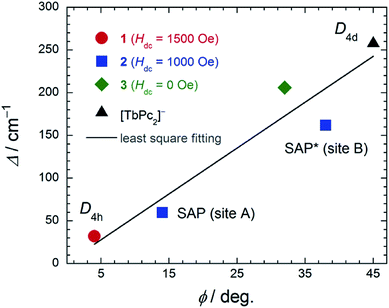 | ||
| Fig. 7 The relationship between the twist angle (φ) and the energy barrier for the reversal of the magnetization (Δ). The experimental data for [TbPc2]− complex with D4d geometry from ref. 4c and 3 from ref. 7e. In order to suppress QTM, we applied an Hdc for 1 and 2 (see main text). The solid line is a guide for eyes. | ||
Magnetic relaxation mechanism
The magnetic relaxation processes in dc magnetic fields can be explained by applying the Landau–Zener–Stükelberg (LZS) model of the ground state ±Jz levels.1,2,17 Probability P of the adiabatic change can be obtained from the relationship between Δtunnel and the magnetic field sweep rate. The fast spin reversal between the ±Jz levels due to the adiabatic process is QTM. Relaxation via a direct process causes the release of a phonon (hω) when the spin flips in a nonadiabatic process. The probability of nonadiabatic process (1 − P) shows that the spin is not maintained with changes in the magnetic field sweep rate. This is thought to be the basis for the magnetic relaxation mechanism of 1–3 in the low-T region.In a previous study on SMM 3 (SAP–SAP), we determined the ground state from the magnetic heat capacity (Cm) in an Hdc (Fig. S30†).6 When two TbIII ions are in close proximity to each other, ferromagnetic (|±6, ±6〉) and antiferromagnetic states (|±6, ∓6〉) form, and these states are energetically separated by the f–f interactions between the TbIII ions. Broadening of the Cm peak with an increase in Hdc shows that the Jz = |−6, −6〉, |+6, +6〉 and Jz = |−6, +6〉, |+6, −6〉 energy levels of the dinuclear TbIII system are split by Zeeman energy. The magnetic axes of the ground state at the TbIII sites are parallel to each other and have ferromagnetic dipole–dipole interactions among the magnetic moments (Jz = |±6, ±6〉). The dependence of the Cm of 3 on Hdc aligned along the magnetic easy axis could be reproduced theoretically (Fig. S30d†). The degenerate Jz = |±6, ±6〉 is split into Jz = |−6, −6〉 and Jz = |+6, +6〉 in an Hdc (Zeeman splitting). Thus, the crossing point at around ±4000 Oe is due to level crossing of the Jz = |±6, ∓6〉 state and Jz = |+6, +6〉 state. Furthermore, in the micro-SQUID experiments, 3 clearly exhibited a butterfly-shaped hysteresis loop with the field applied along the easy magnetization axis (Fig. S30b†).6 In the up sweep, the magnetization jump around ±3500 Oe is due to level crossing of the doublet ground state between the Jz = |±6, ∓6〉 state and Jz = |+6, +6〉 state.
Ishikawa and co-workers have obtained the Zeeman plots, where in the presence of the nuclear spin of Iz = ±3/2, ±1/2 with Jz = ±6 of the dinuclear TbIII system, pure QTM in an Hdc of zero is forbidden because of the absence of mixing between the |±6, ∓6〉 and |±6, ±6〉 states.9a Therefore, there is no crossover between the QTM and direct processes. At around ±3500 Oe, although QTM is possible, the direct process is a possible relaxation pathway in such a strong Hdc at low-T (Fig. 8c and S30b†). Therefore, we have reported that 3 shows pure QTM and a direct process in Hdc of around 3500 Oe, which is consistent with the Zeeman diagrams. Furthermore, we can explain the dual magnetic relaxation mechanism of 2 (SAP–SAP*) using Zeeman diagrams.
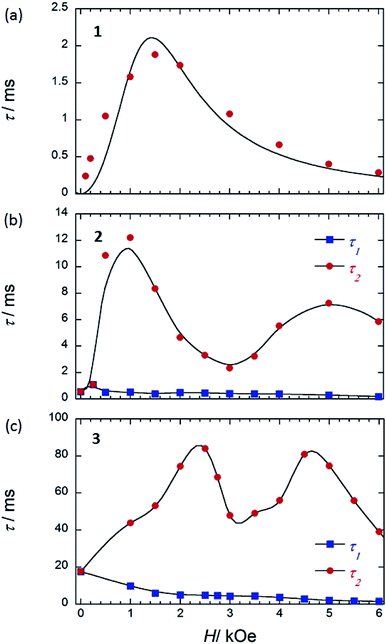 | ||
| Fig. 8 τ versus H for (a) 1 (SP–SP), (b) 2 (SAP–SAP*), and (c) 3 (SAP–SAP)6 at 5 K. τ was obtained from the least-squares fitting using an extended Debye model (eqn (S8)–(S10) and Fig. S20 and S28†). The order of the maximum values of τ (red circle) are different from each other. See main text. The solid lines are guides for eyes. | ||
On the other hand, below 18 K, the Argand plots for 2 showed two sets of irregular semicircular shapes for the dual magnetic relaxation processes in an Hdc of 1000 Oe (Fig. S26†). In other words, the magnetic relaxation splits from a one-component system into a two-component system (τ1: high-frequency part and τ2: low-frequency part) in an Hdc similar to the case of 3. In order to understand the different relaxation mechanisms corresponding to the two observed peaks, an extended Debye model (eqn (S8)–(S10)†) was used to fit the values of τ1 and τ2.6,8aτ1 and τ2 are plotted as a function of T−1 in Fig. 6. There are two different T regions. Above 18 K, the relaxation follows a thermally-activated mechanism, such as the Orbach process, whereas at lower temperatures (<10 K), a gradual crossover to a T-independent regime for τ1 and T-dependent regime for τ2 occurs. Similar behaviour was observed for 3 (SAP–SAP), and this is clear evidence that the magnetic relaxation mechanism depends heavily on the ground state properties of the TbIII ions in the dinuclear systems below 10 K (Fig. 2).6,7
To corroborate the relationship between the dual magnetic relaxation process in the dinuclear TbIII complexes 1–3 in the low-T region and the octa-coordination environments, the ν dependence of χM′ and χM′′ in the range of 10–996 Hz were conducted at 5 K in several Hdc.6,7 In the case of the Argand plots for 2 in an Hdc up to 6000 Oe at 5 K (Fig. S28†), the magnetic relaxation splits from a one-component system into a two-component system (τ1 and τ2). τ1 (∼10−4 s) did not change in the range of 0–6000 Oe. On the other hand, τ2 fluctuated with an “M” shaped curve (Fig. 8b) in the same ν range. τ2 increased from 250 Oe and became a maximum of ∼10−2 s in an Hdc of 1000 Oe (Hτ2,max). These results confirm that the QTM is suppressed in an Hdc of 1000 Oe, and the direct process is enhanced. When Hdc > 1000 Oe, the magnitude of τ2 decreased to a minimum value (∼10−3 s) in Hdc of ∼3000 Oe (Hτ2,min). Then τ2 began to increase again to a second maximum in an Hdc of 5000 Oe, followed by another decrease. These results confirm that the QTM is induced in the Hdc range of 1000–5000 Oe, and the direct process and QTM are enhanced due to Zeeman splitting of Jz = |±6, ±6〉 and level crossing of the doublet ground state between the Jz = |±6, ∓6〉 state and Jz = |+6, +6〉 state around 3000 Oe, respectively. The two levels of the lines in the energy diagrams are broadened because the coupled states are finely split by hyperfine coupling (I–J) and the interactions between the spins (f–f), which are due to absorption and/or emission of phonons (spin–phonon interactions).4,6 Thus, the width of level crossing of the doublet ground state between the Jz = |±6, ∓6〉 and Jz = |+6, +6〉 states expanded in the Hdc range of 1000–5000 Oe.7e Therefore, we believe that the magnetic relaxation process in an Hdc can be explained using Zeeman diagrams. By comparing the Hdc dependence of τ for the dinuclear TbIII system, we found that the octa-coordination geometries with SAP–SAP* and SAP–SAP sites affected the Hdc regions where QTM was active.
In contrast to 2 and 3 (Fig. 8b and c), 1 with SP–SP sites exhibited only a single magnetic relaxation process (Fig. 8a), which could be described by using a generalized Debye model (eqn (S4)–(S6)†). The order of τ (10−4 s) increased from 250 Oe, reaching a maximum value of ∼10−3 s in an Hdc of 1500 Oe (Hτ,max). These results confirm that the QTM is suppressed in an Hdc = 1500 Oe and that the direct process is enhanced. When Hdc > 1500 Oe, the order of magnitude of τ decreased to a minimum value of ∼10−4 s in an Hdc of 6000 Oe. These results confirm that the QTM is suppressed up to an Hdc of 6000 Oe and that the direct process is enhanced. The ground state properties of 1 are completely different from those of 2 and 3. The ground state of 2 and 3 undergo a level crossing to give rise to a dual magnetic relaxation phenomenon, whereas 1 does not (Fig. 8a and S30†). This is consistent the differences in the values of Δtunnel in the ground states of the SP and SAP environments.9a The differences are due to the differences in the ground state brought about by the symmetry of octa-coordination geometries and can be explained on the bases of the Zeeman diagrams.
Conclusions
The relationship between the octa-coordination environment and the SMM properties of 1 (SP–SP) and 2 (SAP–SAP*) with different octa-coordination environments are discussed in comparison to 3 (SAP–SAP). The SMM behaviours of the three complexes were explained by using X-ray crystallography and static and dynamic susceptibility measurements.The relaxation dynamics of 1 and 2 indicate that they are field-induced SMMs because the QTM is enhanced by the presence of off-diagonal LF terms (Bqk; q ≠ 0). Both 2 and 3 undergo dual magnetic relaxation processes in an Hdc, whereas 1 undergoes only a single magnetic relaxation process. The differences are due to the differences in the ground state of the respective octa-coordination geometries and can be explained on the bases of the Zeeman diagrams. Thus, the dual magnetic relaxation properties of dinuclear TbIII complexes can be tuned by changing the strength of the mixing of fourth-range extradiagonal parameters using the octa-coordination environments, and thus, we must carefully design the dinuclear TbIII triple-decker complexes to control the dual magnetic relaxation mechanisms.
In addition, we demonstrated that there was a linear relationship between the twist angle (φ) and the energy barrier for the reversal of the magnetization (Δ). Qualitatively, this result is consistent with the degree of the mixing of off-diagonal LF terms due to the symmetry of the octa-coordination environment. Detailed theoretical calculations will make it possible to fully elucidate the relationship between LF and SMM properties in detail.
Finally, the dual magnetic relaxation mechanisms are related the two energy gap in the doublet ground state in the dinuclear TbIII ions with ferromagnetic dipolar interactions and the octa-coordination geometry because the SAP–SAP sites have axial components in the LF terms and because the SP–SP sites have not only the axial LF terms but also the off-diagonal LF terms.
Acknowledgements
This work was financially supported by a Grant-in-Aid for Scientific Research (S) (Grant No. 20225003, MY) and Grant-in-Aid for Young Scientists (B) (grant No. 24750119, KK) and Scientific Research (C) (grant No. 15K05467, KK) from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) and CREST, JST, Japan.Notes and references
- (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS; (b) R. Sessoli and D. Gatteschi, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef PubMed; (c) D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, U.K., 2006 Search PubMed.
- (a) X.-Y. Wang, C. Avendaño and K. R. Dunbar, Chem. Soc. Rev., 2011, 40, 3212 Search PubMed; (b) J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078 RSC; (c) Molecular Cluster Magnets (World Scientific Series in Nanoscience and Nanotechnology-Vol. 3), ed. R. E. P. Winpenny, World Scientific Publishing Co. Pte. Ltd., USA, 2011 Search PubMed; (d) D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed; (e) F. Habib and M. Murugesu, Chem. Soc. Rev., 2013, 42, 3278 RSC; (f) K. S. Pedersen, J. Bendix and R. Clérac, Chem. Commun., 2014, 50, 4396 RSC; (g) Introduction to Molecular Magnetism: From Transition Metals to Lanthanides, ed. C. Benelli and D. Gatteschi, Wiley-VCH, Germany, 2015 Search PubMed; (h) Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VCH, Germany, 2015 Search PubMed; (i) A. A., Molecular Nanomagnets and Related Phenomena, Struct. Bonding, 2015, 164 Search PubMed; (j) S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655 RSC.
- (a) A. Candini, S. Klyatskaya, M. Ruben, W. Wernsdorfer and M. Affronte, Nano Lett., 2011, 11, 2634 CrossRef CAS PubMed; (b) M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502 CrossRef CAS PubMed; (c) S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Muller and B. Barbara, Nature, 2008, 453, 203 CrossRef CAS PubMed; (d) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179 CrossRef CAS PubMed; (e) E. Burzurí, F. Luis, B. Barbara, R. Ballou, E. Ressouche, O. Montero, J. Campo and S. Maegawa, Phys. Rev. Lett., 2011, 107, 097203 CrossRef PubMed; (f) W. Wernsdorfer and R. Sessoli, Science, 1999, 284, 133 CrossRef CAS PubMed; (g) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS PubMed.
- (a) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed; (b) N. Ishikawa, M. Sugita and W. Wernsdorfer, Angew. Chem., Int. Ed., 2005, 44, 2931 CrossRef CAS PubMed; (c) N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Phys. Chem. B, 2004, 108, 11265 CrossRef CAS; (d) N. Ishikawa, Polyhedron, 2007, 26, 2147 CrossRef CAS; (e) S. Takamatsu and N. Ishikawa, Polyhedron, 2007, 26, 1859 CrossRef CAS; (f) N. Ishikawa, M. Sugita, T. Okubo, N. Tanaka, T. Iino and Y. Kaizu, Inorg. Chem., 2003, 42, 2440 CrossRef CAS PubMed; (g) N. Ishikawa, J. Phys. Chem. A, 2003, 107, 5831 CrossRef CAS; (h) N. Ishikawa and Y. Kaizu, Coord. Chem. Rev., 2002, 226, 93 CrossRef CAS; (i) S. Takamatsu, T. Ishikawa, S. Koshihara and N. Ishikawa, Inorg. Chem., 2007, 46, 7250 CrossRef CAS PubMed.
- (a) N. Ishikawa, S. Otsuka and Y. Kaizu, Angew. Chem., Int. Ed., 2005, 44, 731 CrossRef CAS PubMed; (b) N. Ishikawa, T. Iion and Y. Kaizu, J. Am. Chem. Soc., 2002, 124, 11440 CrossRef CAS PubMed; (c) N. Ishikawa, T. Iino and Y. Kaizu, J. Phys. Chem. A, 2002, 106, 9543 CrossRef CAS; (d) Y. Lan, S. Klyatskaya, M. Ruben, O. Fuhr, W. Wernsdorfer, A. Candini, V. Corradini, A. L. Rizzini, U. del Pennino, F. Troiani, L. Joly, D. Klar, H. Wende and M. Affrontef, J. Mater. Chem. C, 2015, 3, 9794 RSC.
- K. Katoh, T. Kajiwara, M. Nakano, Y. Nakazawa, W. Wernsdorfer, N. Ishikawa, B. K. Breedlove and M. Yamashita, Chem.–Eur. J., 2011, 17, 117 CrossRef CAS PubMed.
- (a) K. Katoh, H. Isshiki, T. Komeda and M. Yamashita, Coord. Chem. Rev., 2011, 255, 2124 CrossRef CAS; (b) K. Katoh, Y. Horii, N. Yasuda, W. Wernsdorfer, K. Toriumi, B. K. Breedlove and M. Yamashita, Dalton Trans., 2012, 41, 13582 RSC; (c) T. Morita, K. Katoh, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 13555 CrossRef CAS PubMed; (d) M. Damjanovic, K. Katoh, M. Yamashita and M. Enders, J. Am. Chem. Soc., 2013, 135, 14349 CrossRef CAS PubMed; (e) Y. Horii, K. Katoh, N. Yasuda, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2015, 54, 3297 CrossRef CAS PubMed.
- (a) N. Domingo, F. Luis, M. Nakano, M. Muntó, J. Gómez, J. Chaboy and N. Ventosa, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 214404–214411 CrossRef; (b) D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem.–Eur. J., 2011, 17, 4700 CrossRef CAS PubMed; (c) Y.-N. Guo, G.-F. Xu, P. Gamez, L. Zhao, S.-Y. Lin, R. Deng, J. Tang and H.-J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538 CrossRef CAS PubMed; (d) S.-D. Jiang, B.-W. Wang, H.-L. Sun, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133, 4730 CrossRef CAS PubMed; (e) M. Gonidec, F. Luis, À. Vílchez, J. Esquena, D. B. Amabilino and J. Veciana, Angew. Chem., Int. Ed., 2010, 49, 1623 CrossRef CAS PubMed; (f) H. Wang, T. Liu, K. Wang, C. Duan and J. Jiang, Chem.–Eur. J., 2012, 18, 7691 CrossRef CAS PubMed; (g) D. Pinkowicz, M. Ren, L.-M. Zheng, S. Sato, M. Hasegawa, M. Morimoto, M. Irie, B. K. Breedlove, G. Cosquer, K. Katoh and M. Yamashita, Chem.–Eur. J., 2014, 20, 12502 CrossRef CAS PubMed; (h) F. Pointillart, T. Guizouarn, B. Lefeuvre, S. Golhen, O. Cador and L. Ouahab, Chem.–Eur. J., 2015, 21, 16929 CrossRef CAS PubMed.
- (a) S. Sakaue, A. Fuyuhiro, T. Fukuda and N. Ishikawa, Chem. Commun., 2012, 48, 5337 RSC; (b) D. Tanaka, T. Inose, H. Tanaka, S. Lee, N. Ishikawa and T. Ogawa, Chem. Commun., 2012, 48, 7796 RSC; (c) H. Wang, K. Wang, J. Tao and J. Jiang, Chem. Commun., 2012, 48, 2973 RSC; (d) J. Kan, H. Wang, W. Sun, W. Cao, J. Tao and J. Jiang, Inorg. Chem., 2013, 52(15), 8505 CrossRef CAS PubMed; (e) K. Wang, S. Zeng, H. Wang, J. Dou and J. Jiang, Inorg. Chem. Front., 2014, 1, 167 RSC.
- (a) D. Chabach, M. Lachkar, A. De Cian, J. Fischer and R. Weiss, New J. Chem., 1992, 16, 431 CAS; (b) T.-H. Tran-Thi, T. A. Mattiolit, D. Chabach, A. De Cian and R. Weiss, J. Phys. Chem., 1994, 98, 8279 CrossRef CAS.
- (a) K. Takahashi, M. Itoh, Y. Tomita, K. Nojima, K. Kasuga and K. Isa, Chem. Lett., 1993, 1915 CrossRef CAS; (b) K. Kasuga, M. Ando, H. Morimoto and M. Isa, Chem. Lett., 1986, 1095 CrossRef CAS; (c) A. De Cian, M. Moussavi, J. Fischer and R. Weiss, Inorg. Chem., 1985, 24, 3162 CrossRef CAS; (d) J. L. Paillaud, M. Drillon, A. De Cian, J. Fischer, R. Weiss and G. Villeneuve, Phys. Rev. Lett., 1991, 67, 244 CrossRef CAS PubMed.
- (a) G. M. Sheldrick, SHELX-97, Program for Crystal Structure Analysis, Universität Göttingen, Germany, 1997 Search PubMed; (b) C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453 CrossRef CAS.
- (a) D. Schmitt, J. Phys., 1986, 47, 677 CrossRef; (b) J. Sievers, Z. Phys. B: Condens. Matter Quanta, 1982, 45, 289 CrossRef CAS; (c) K. W. H. Stevens, Proc. Phys. Soc., London, Sect. A, 1952, 65, 209 CrossRef; (d) A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, London, 1970 Search PubMed; (e) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC; (f) C. Görller-Walrand and K. Binnemans, Handbook on the physics and chemistry of rare earths, ed. K. A. Gschneidner Jr and E. LeRoy, Elsevier, Amsterdam, 1996, 23, p. 121 Search PubMed; (g) J.-L. Liu, Y.-C. Chen, Y.-Z. Zheng, W.-Q. Lin, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M.-L. Tong, Chem. Sci., 2013, 4, 3310 RSC; (h) X.-C. Huang, V. Vieru, L. F. Chibotaru, W. Wernsdorfer, S.-D. Jiang and X.-Y. Wang, Chem. Commun., 2015, 51, 10373 RSC; (i) J. J. Baldovi, J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Dalton Trans., 2012, 41, 13705 RSC; (j) L. F. Chibotaru, Struct. Bonding, 2015, 164, 185 CrossRef CAS.
- (a) F. Luis, J. Bartolomé, J. F. Fernández, J. Tejada, J. M. Hernández, X. X. Zhang and R. Ziolo, Phys. Rev. B: Condens. Matter, 1997, 55, 11448 CrossRef CAS; (b) J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014430 CrossRef; (c) J. Ferrando-Soria, D. Cangussu, M. Eslava, Y. Journaux, R. Lescouëzec, M. Julve, F. Lloret, J. Pasán, C. Ruiz-Pérez, E. Lhotel, C. Paulsen and E. Pardo, Chem.–Eur. J., 2011, 17, 12482 CrossRef CAS PubMed; (d) I. A. Gass, B. Moubaraki, S. K. Langley, S. R. Batten and K. S. Murray, Chem. Commun., 2012, 48, 2089 RSC.
- (a) I. Waller, Z. Phys., 1932, 79, 370 CrossRef; (b) J. H. Van Vleck, J. Chem. Phys., 1939, 7, 72 CrossRef CAS; (c) J. H. Van Vleck, Phys. Rev., 1940, 57, 426 CrossRef CAS; (d) R. de and L. Kronig, Physica, 1939, 6, 33 CrossRef; (e) R. Orbach, Proc. Phys. Soc., 1961, 77, 821 CrossRef CAS; (f) C. B. P. Finn, R. Orbach and W. P. Wolf, Proc. Phys. Soc., 1961, 77, 261 CrossRef CAS; (g) R. L. Carlin, Magnetochemistry, Springer, Berlin, 1986 Search PubMed.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341 CrossRef CAS.
- (a) L. D. Landau, Phys. Z. Sowjetunion, 1932, 2, 46 CAS; (b) C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696 CrossRef; (c) E. C. G. Stückelberg, Helv. Phys. Acta, 1932, 5, 369 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 989974 for 1 and 1041202 for 2. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5sc04669f |
| This journal is © The Royal Society of Chemistry 2016 |