Open Access Article
Open Access ArticleGenetic engineering of inorganic functional modular materials
Yi
Li
 and
Jihong
Yu
*
and
Jihong
Yu
*
State Key Laboratory of Inorganic Synthesis and Preparative Chemistry, Jilin University, Qianjin Street 2699, Changchun 130012, China. E-mail: jihong@jlu.edu.cn
First published on 29th March 2016
Abstract
Since the launch of the Materials Genome Initiative by the US government in 2011, many computer techniques have been developed to predict the structures and properties of advanced materials, providing important guidance for laboratory experimentation and a promising new direction for future materials innovation. However, lots of inorganic materials are difficult for computers to process because of their complex three-dimensionally extended structures. Fortunately, many of these materials are built from well-defined stacking layer modules, and the stacking sequences of their layer modules unambiguously determine their three-dimensional structures. Such one-dimensional stacking sequence representation is naturally accessible for computer processing, easing the problems not only of structure elucidation, but also in the enumeration, evaluation, and screening of a large number of unknown materials with desired properties. More importantly, with the aid of various computational methods, we may reveal the relationship between the stacking sequences and the properties of these materials, which is a key prerequisite for function-led targeted synthesis. This Minireview covers the most recent progress in this emerging area.
Introduction
The recent advances in science and technology, the rapid growth of various industries, and the improvement in the quality of our daily life, largely rely on the discovery of new functional materials. Unfortunately, today's materials innovation still relies primarily on researchers' scientific intuition and trial-and-error experimentation. Owing to the rapid development in both hardware and software, computers have been increasingly involved in our daily scientific activity, and their potential to accelerate materials innovation has been widely recognised. In 2011, the US government launched the Materials Genome Initiative aiming to develop high-throughput computer methods and data-sharing systems to complement and fully leverage existing experimental research on advanced materials.1–3 In particular, the incorporation of various computational techniques in materials innovation has recently achieved noteworthy success in predicting the structures and properties of various types of unknown materials.4–19 However, the extremely high computational overheads make these techniques only applicable to a very small number of materials. Therefore, high-throughput computational techniques for the enumeration, evaluation, and screening of a large number of unknown materials are highly desired.Inorganic functional materials usually have complex three-dimensionally extended crystalline structures. Because the computational cost rises exponentially with the structural complexity, in silico predictions of the structures and the properties of inorganic functional materials are usually challenging. Fortunately, many inorganic materials can be viewed as the result of the sequential stacking of well-defined layer modules. Every unique way of layer stacking determines a specific modular structure. If each type of layer module is assigned a predefined letter, then the manner of layer stacking, as well as the corresponding three-dimensional modular structure, can be written as a sequence of letters. By enumerating all possible stacking sequences of specific layer modules, we can restore the atomic models for all corresponding materials, known and unknown. Via various computational approaches, we may reveal the relationship between a material’s stacking sequence and its properties, so that we can perform high-throughput structure evaluation for these models and identify the most promising synthetic candidates with desired properties. With the development of various synthetic techniques, function-led synthesis of these modular materials can be achieved.
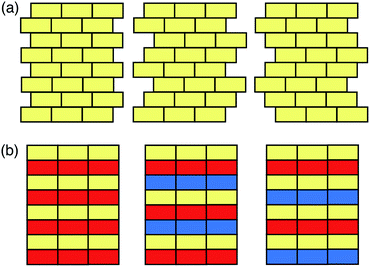
In this Minireview, we will discuss the computational approaches recently developed for the prediction of the structures and properties of inorganic materials by enumerating their stacking sequences. Here we only consider inorganic functional materials whose atomic structures can be unambiguously determined, and the layer modules in these materials are bound together through strong chemical bonds. These materials include a variety of metals, minerals, and synthetic inorganic compounds that have been widely used as catalysts, semiconductors, battery cathodes, capacitors, etc. Following the conventional nomenclature,20,21 here we categorise the modular structures into two groups: the polytypic series and the polysomatic series. A polytypic series is a group of structures that are all built by chemically and structurally identical layer modules. Each member in this polytypic series is a polytype, and different polytypes differ only in the spatial arrangement of the layer modules (Fig. 1a). In contrast, the polysomatic series are formed by polysomes, each of which is built by chemically and/or structurally distinct layer modules. Besides stacking sequences, the chemical compositions may also be different among polysomes (Fig. 1b).
Polytypic series
Close-packed structures
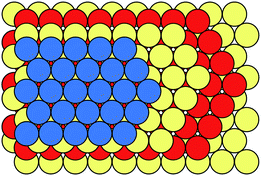
Many metals, alloys, and inorganic compounds exhibit close-packed structures. A close-packed structure is built by the stacking of identical layers of atoms. Every atom in these layers is in contact with six of its neighbours in the same layer, so these layers have a symmetry of 6mm and they are often referred to as hexagonal close-packed layers (Fig. 2). Each layer has two types of triangular voids for atoms in adjacent layers to occupy. If we name the beginning layer “A”, the next layer would be named “B” or “C” depending on which voids it occupies. Notice that layers A, B, and C are chemically and structurally identical; they only differ in their relative positions (Fig. 2). The stacking of these layers can be described as a sequence of letters A, B, and C, and the length of the stacking sequence represents the periodicity of the layer stacking. Because all of the layers are close packed, there are no identical successive letters in their stacking sequences. Different polytypes correspond to different stacking sequences. For instance, a stacking sequence of [AB] represents a hexagonal close-packed (hcp) polytype, where each layer's neighbours are identical; [ABC] represents a cubic close-packed (ccp) or face-centred cubic (fcc) polytype, where each layer's neighbours are distinct. [AB] and [ABC] are the two basic structures of close packing; all other close-packed polytypes can be viewed as combinations of hexagonal and cubic close packing. “Hexagonality”, defined as the proportion of hexagonal close packing in a given close-packed polytype, has been found to be related to many of the physical and chemical properties of close-packed structures. There are many other types of notations used in the literature for close-packed structures,22 which are beyond the topic of this Minireview and won't be discussed here.Because of the correspondence between polytypes and their stacking sequences, we can generate all close-packed structures by enumerating all the possible stacking sequences. In theory, close packing of N layers would produce 2N−1 polytypes. Most of these polytypes are equivalent among one another, so we have to avoid or remove them during enumeration in order to keep the distinct polytypes only. Taking advantage of many sophisticated algorithms that have been proposed so far, we can now enumerate an astronomical number of close-packed polytypes with a periodicity over 100.23–25 However, it is practically impossible to perform expensive chemical computations for all of these polytypes. Therefore, current studies in high-level computational evaluation of close-packed structures usually involve no more than 100 polytypes.26–33
Gold, like many other metals, takes the [ABC] polytype (fcc) as the most stable structure under ambient conditions. When pressure increases, gold may exhibit different structures. In 2013, Ishikawa and coworkers performed first-principles calculations to study the variation of the structure of gold under high pressures.34 They built 48 distinct close-packed polytypic structures of gold with a periodicity of 12, including [AB]6, [ABC]4, [ABAC]3, [ABCACB]2, and [ABABABACACAC], etc. Through periodic DFT calculations under various pressures up to 1400 GPa, they found that gold would undergo a series of phase transitions from an fcc structure to an hcp structure with the increase of pressure: [ABC]4 → [ABCACB]2 → [ABAC]3 → [ABABABACACAC] → [AB]6. Interestingly, the hexagonality of these five polytypic structures exhibited a step-by-step increase in accordance with the pressure: 0.0 → 0.3333 → 0.5 → 0.8333 → 1.0. In contrast, previous calculations on iron in the earth's inner core showed a different trend.35 At pressures up to 400 GPa, the hcp structure was the most stable polytype of iron, whereas the fcc structure was the least stable one. The enthalpy of the iron polytypes increased with the decrease of the hexagonality. This indicates that even identical stacking sequences may induce completely different properties in different systems. Any stacking information derived from one system should be double-checked when it is going to be applied to another system.
More complex close packing can be found in multimetallic systems. In 2015, Grau-Crespo and coworkers studied the structure of palladium multilayers grown on the (001) surface of rhenium.36 Because the lattice parameters of Pd and Re were similar, they neglected the strain between the lattices of Pd and Re and assumed the Pd layers to be closely stacked on the surface of the Re support. It was already known that the (001) layers of Re took the hcp stacking (ABAB). To find out the stacking scheme of Pd over the Re support, Grau-Crespo and coworkers enumerated the possible stacking of no more than four Pd layers over the hcp-stacking Re layers. Because of the existence of another metal, the close packing of Pd over Re would have many more polytypes than the close packing of individual metals. They discovered two close-packed polytypes for one Pd layer over Re, four polytypes for two Pd layers, eight polytypes for three Pd layers, and four polytypes for four Pd layers. Periodic DFT calculations revealed that the most stable stacking sequences for one, two, three, and four Pd layers over Re were ABABa, ABABac, ABABacb, and ABABacba, respectively (“ABAB” represents the hcp stacking of Re; the lowercase letters represent the stacking of Pd). These results agreed well with the experimental observation that the first layer of Pd continued the hcp sequence of Re, whereas the second and the subsequent layers all preferred the fcc structure. Based on these results, Grau-Crespo and coworkers calculated the electronic structures of this bimetallic system and revealed a significant amount of charge transfer from Re to Pd, mainly localised at the interface layers.36
Besides metals, many close-packed inorganic compounds, such as SiC,28,30,37 III–V compounds,27–29,31,32 and various metal oxides,33,38 have recently been computationally investigated. In 2014, Fisher and coworkers conducted a first-principles study of LiCoO2, a family of widely used lithium-ion battery cathode materials.39 The three-dimensional structure of LiCoO2 can be viewed as the result of the close packing of O layers; Li and Co cations alternately occupy the interstitial octahedral voids between the adjacent O layers. Because the locations of the Li and Co cations are both defined by the close-packed O layers, all possible LiCoO2 models could be built by enumerating the stacking of O layers solely. Fisher and coworkers enumerated all possible stacking of 2, 4, 6, 8, 10, and 12 O layers and built over 100 atomic models with the stoichiometry of LiCoO2. Via periodic DFT calculations, they found that the most stable polytypes built by 2, 4, 6, 8, 10, and 12 O layers were [AB], [ABAC], [ABCABC], [ABCACBAC], [ABCABCABAC], and [ABCABCACBACB], respectively. The lattice stabilities of these six polytypes followed the order of [ABCABC] > [ABCABCACBACB] > [ABCABCABAC] > [ABCACBAC] > [ABAC] > [AB], which agreed with the order of the cell voltages calculated assuming full delithiation. These results were consistent with the experimental observations. Interestingly, the orders of stability and cell voltages of these polytypes were the exact opposite of the order of their hexagonality. Knowing this relationship, the stability and cell voltage of more complex LiCoO2 polytypes could be estimated without expensive first-principles calculations.
Zeolites
Besides the close packing that renders dense materials, other ways of layer stacking may lead to porous or open-framework structures. Zeolites are a family of porous materials that have been widely used in petroleum refining, the petrochemical industry, and in the fine chemical industry, as catalysts, adsorbents, and ion-exchangers.40 The three-dimensional frameworks of zeolites are built exclusively from corner-sharing TO4 tetrahedra (T denotes tetrahedrally coordinated Si, Al, or P, etc.). The different ways in which the TO4 tetrahedra are connected lead to a wide variety of zeolite structures.41 To date, there are over 200 distinct zeolite framework types discovered in nature or by synthesis.42–44 Besides, millions of hypothetical zeolite frameworks have been predicted as potential synthetic candidates through various computational methods.45–51 Many zeolite structures can be described by the stacking of layer modules.52–56 In the days when computers were not popular, many unknown zeolite structures were predicted by manipulating the stacking of several of the most frequently observed layer modules.57–61 On the other hand, synthetic chemists recently discovered that new zeolite structures, even those deemed “unfeasible” according to conventional evaluation criteria, could be realised by controlling the assembly, disassembly, and reassembly of some known layer modules of zeolites.62–67 This breakthrough in synthesis has drawn attention back to zeolite structures that are built by layer stacking. Among them, ABC-6 zeolites are a group of important representatives.ABC-6 zeolites are built by the hexagonal stacking of identical 6-ring layers, where each 6-ring is built of six corner-sharing TO4 tetrahedra. Since these 6-ring layers are hexagonally stacked, there are three possible positions for them to occupy. Following the notation used for close-packed structures, the 6-ring layers at these three positions are named A, B, and C, respectively (Fig. 3). This is where the name “ABC-6” comes from. To date, there are 30 distinct ABC-6 polytypes discovered. Different from the close-packed structures where no successive layers are identical, ABC-6 polytypes allow their constituent layers to be stacked directly upon themselves, i.e., the stacking sequences of ABC-6 polytypes may contain “AA”, “BB”, or “CC”. Thus, ABC-6 zeolites may have, in theory, many more polytypes than close-packed structures with the same stacking periodicity (Fig. 3). In the early 1980s, Smith and Bennett counted the possible operations between successive 6-ring layers in ABC-6 zeolites and got 941 distinct stacking sequences with periodicities of ≤11.68 In 2015, Yu and coworkers enumerated the ABC-6 stacking sequences directly and reached a periodicity up to 16.69 After removal of all chemically infeasible ones,70 they found 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292 distinct ABC-6 stacking sequences. In comparison, hexagonal close packing of ≤16 layers leads to only 901 polytypes.23 From the 84
292 distinct ABC-6 stacking sequences. In comparison, hexagonal close packing of ≤16 layers leads to only 901 polytypes.23 From the 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292 enumerated ABC-6 stacking sequences, they built up the corresponding atomic models and refined them via a classical molecular mechanics approach.
292 enumerated ABC-6 stacking sequences, they built up the corresponding atomic models and refined them via a classical molecular mechanics approach.
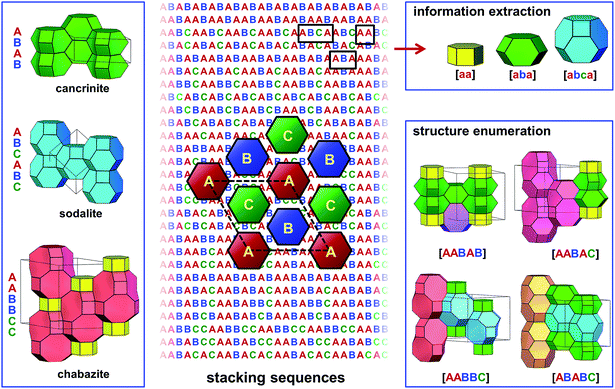 | ||
| Fig. 3 Enumeration of ABC-6 polytypes and interpretation of ABC-6 stacking sequences. This figure shows the structures of cancrinite, sodalite and chabazite (left), the schematic drawing of the three types of six-ring layers (middle), some constituent cages determined from the stacking sequences (top right), and four enumerated ABC-6 structures comprised of five stacking layers (bottom right). This figure was taken from ref. 69. | ||
The next step was high-throughput property prediction for all the enumerated polytypes. In ABC-6 zeolites, there exist various types of well-defined polyhedral cages in molecular dimensions, as well as interconnecting channels running along several directions. These cages and channels provide suitable void space for the adsorption, diffusion, and reaction of various types of guest species, being the most important structural features for ABC-6 zeolites. Yu and coworkers developed a high-throughput decoding program to extract this key structural information directly from the stacking sequences of ABC-6 structures (Fig. 3). With this computer program, they analysed all 84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 292 enumerated ABC-6 stacking sequences, and for each corresponding ABC-6 polytype, they got the key information about the constituent cages and channels. Furthermore, they identified 1127 ABC-6 polytypes as the most realisable synthetic candidates among all the enumerated ones, because they were built by no more than four types of cages, just as all already-realised ABC-6 zeolites were. Under conventional hydrothermal conditions, Yu and coworkers successfully realised two of their synthetic targets, confirming the reliability of their predictions. Knowing the constituent cages of an ABC-6 polytype would have another advantage. Many chemical properties of ABC-6 zeolites, such as the catalytic activity for a specific reaction, were difficult to predict directly for all the ABC-6 polytypes because of the high computational overheads. Yu and coworkers showed that the number of ABC-6 cage types was very limited in comparison with the total number of ABC-6 polytypes. It was possible to calculate the catalytic performance for all the ABC-6 cages through first-principles calculations. When this was done, the catalytic activity of all the ABC-6 polytypes could be estimated immediately by checking their constituent cages and the calculated catalytic properties thereof.
292 enumerated ABC-6 stacking sequences, and for each corresponding ABC-6 polytype, they got the key information about the constituent cages and channels. Furthermore, they identified 1127 ABC-6 polytypes as the most realisable synthetic candidates among all the enumerated ones, because they were built by no more than four types of cages, just as all already-realised ABC-6 zeolites were. Under conventional hydrothermal conditions, Yu and coworkers successfully realised two of their synthetic targets, confirming the reliability of their predictions. Knowing the constituent cages of an ABC-6 polytype would have another advantage. Many chemical properties of ABC-6 zeolites, such as the catalytic activity for a specific reaction, were difficult to predict directly for all the ABC-6 polytypes because of the high computational overheads. Yu and coworkers showed that the number of ABC-6 cage types was very limited in comparison with the total number of ABC-6 polytypes. It was possible to calculate the catalytic performance for all the ABC-6 cages through first-principles calculations. When this was done, the catalytic activity of all the ABC-6 polytypes could be estimated immediately by checking their constituent cages and the calculated catalytic properties thereof.
Polysomatic series
Perovskite structures
The perovskite structure is adopted by many compounds, being one of the best-known structure types. The general chemical formula for perovskite compounds is ABX3, where “A” and “B” are two very different cations and “X” is an anion. The ideal symmetry for a perovskite structure is cubic, with A cations sitting at the lattice body centres, B cations at the lattice vertices, and X anions at the midpoints of the lattice edges. Alternatively, the perovskite structure can be described as the alternate stacking of [AX] and [BX2] square layer modules along the [100] direction, or the alternate stacking of [AX3] and [B] hexagonal layer modules along the [111] direction.71 With various chemical substitutions at the A, B, and X sites, perovskite-related compounds have exhibited a wide variety of polysomes with intriguing electrical, magnetic, dielectric, optical, and catalytic properties.72,73In 2013, Rosseinsky and coworkers developed an “extended module materials assembly” (EMMA) approach for the design of functional inorganic materials built from layer modules. Via this approach, new perovskite compounds, as well as their physical and chemical properties, can be predicted.74 To design new perovskite compounds that can be used as solid oxide fuel-cell (SOFC) cathodes, Rosseinsky and coworkers started with YBa2CaFe5O13, an already-known perovskite compound with oxygen vacancies. To reproduce this perovskite structure, they chose three types of “A” layer ([Y4], [Ba4O4], and [Ca4O4]) and two types of “B” layer ([Fe4O4] and [Fe4O8]) (Fig. 4a). Considering the restriction of A–B alternation and the stoichiometry of this known material, Rosseinsky and coworkers enumerated the combinations of these layer modules and obtained 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 polysomes, each of which contained 184 atoms per unit cell. After initial structure relaxation via a fast force-field approach, they found three polysomes (Fig. 4c) significantly lower in energy than the others (Fig. 4b). To improve the precision of their ranking, they performed periodic DFT calculations on these three polysomes and found the one with the lowest DFT energy corresponded to the known experimental structure of YBa2CaFe5O13. This test on an already-known material confirmed the viability of this EMMA approach.
190 polysomes, each of which contained 184 atoms per unit cell. After initial structure relaxation via a fast force-field approach, they found three polysomes (Fig. 4c) significantly lower in energy than the others (Fig. 4b). To improve the precision of their ranking, they performed periodic DFT calculations on these three polysomes and found the one with the lowest DFT energy corresponded to the known experimental structure of YBa2CaFe5O13. This test on an already-known material confirmed the viability of this EMMA approach.
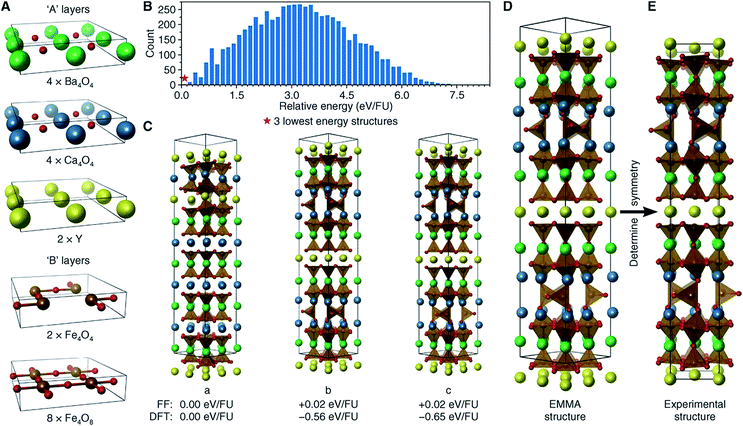 | ||
| Fig. 4 Reproducing the structure of YBa2Ca2Fe5O13via EMMA. (A) The layer modules. (B) A histogram showing the force-field energies of all enumerated polysomes. (C) The three lowest-energy polysomes predicted from initial force-field calculations, together with their force-field and DFT relative energies. (D) The final polysome predicted via EMMA. (E) The refined experimental structure. Atoms are coloured as follows: yellow, Y; green, Ba; blue, Ca; brown, Fe; and red, O. Reprinted with permission from ref. 74. Copyright 2013 The American Association for the Advancement of Science. | ||
The next step was to find a new material with improved performance as an SOFC cathode. Towards this end, Rosseinsky and coworkers substituted a small amount of Cu2+ for Fe3+ to enhance the electronic conductivity of the new material. They got a phase with an idealized composition of Y2Ba2Ca4Fe7.5Cu0.5O21. To determine the structure of this new phase, they performed another EMMA calculation using the layer modules in the above test and one additional B-type layer module, i.e., [Fe3CuO8], to represent the introduction of copper in the experiment. A total of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 640 polysomes for Y2Ba2Ca4Fe7.5Cu0.5O21 were enumerated. After the initial force-field relaxation, one Y2Ba2Ca4Fe7.5Cu0.5O21 polysome was found to be much more stable than all the others. Later DFT calculations confirmed this result. The EMMA-predicted structure was then used as the initial structural model for further Rietveld refinement against powder X-ray diffraction data. The final refined structure was in excellent agreement with the one predicted from the EMMA approach. The new material has the desired enhanced electronic conductivity, which was encoded in the choice of EMMA modules.
640 polysomes for Y2Ba2Ca4Fe7.5Cu0.5O21 were enumerated. After the initial force-field relaxation, one Y2Ba2Ca4Fe7.5Cu0.5O21 polysome was found to be much more stable than all the others. Later DFT calculations confirmed this result. The EMMA-predicted structure was then used as the initial structural model for further Rietveld refinement against powder X-ray diffraction data. The final refined structure was in excellent agreement with the one predicted from the EMMA approach. The new material has the desired enhanced electronic conductivity, which was encoded in the choice of EMMA modules.
In 2014, Darling and coworkers extended the EMMA approach to a group of B-site deficient materials with perovskite structures (AnBn−δO3n, 0 < δ < n).75 Different from the previous work that enumerated the stacking of [AO] and [BO3] layers along the [100] direction, the authors enumerated the stacking of [AO3] layers and interstitial [B] layers along the [111] direction of the cubic unit cell, which was equivalent to the [001] direction of the transformed hexagonal unit cell. Their goal was to generate hexagonal perovskite structures with the general formula of Ban(Co,Nb)n−δO3n, which are a group of excellent dielectric materials. They chose four types of layer modules in this EMMA process, including one type of A-layer ([BaO3]) and three types of B-layer ([Co], [Nb], and the vacancy layers). To generate the structures of known materials Ba3CoNb2O9, Ba5Nb4O15, and Ba8CoNb6O24, Darling and coworkers enumerated all the possible stacking sequences with lengths of 3, 5, and 8 (in reference to A-type layers), and obtained 3, 5, and 448 polysomes, respectively. After force-field relaxations and DFT calculations, the most stable polysomes were all confirmed to be the experimental structures of the three known materials. Interestingly, the Ba8CoNb6O24 structure was equivalent to a Ba3CoNb2O9 block stacked on a Ba5Nb4O15 block. Based on these results, Darling and coworkers went on to predict unknown Ban(Co,Nb)n−δO3n structures with longer stacking sequences. Using the same layer modules but in different compositions and stacking periodicity, they enumerated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 395 Ba11Co2Nb8O33 and 54
395 Ba11Co2Nb8O33 and 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 054 Ba13CoNb10O39 polysomes, respectively. After force-field and DFT relaxations, the most stable Ba11Co2Nb8O33 polysome was equivalent to a double Ba3CoNb2O9 block stacked on a Ba5Nb4O15 block, whereas the most stable Ba13CoNb10O39 polysome was equivalent to a Ba3CoNb2O9 block stacked on a double Ba5Nb4O15 block. This implied that the predicted polysomes might be realisable through the layer-by-layer growth of known materials.
054 Ba13CoNb10O39 polysomes, respectively. After force-field and DFT relaxations, the most stable Ba11Co2Nb8O33 polysome was equivalent to a double Ba3CoNb2O9 block stacked on a Ba5Nb4O15 block, whereas the most stable Ba13CoNb10O39 polysome was equivalent to a Ba3CoNb2O9 block stacked on a double Ba5Nb4O15 block. This implied that the predicted polysomes might be realisable through the layer-by-layer growth of known materials.
Misfit layer compounds
Misfit layer compounds are built from at least two types of layer modules whose basic periodicities do not coincide along one or two directions. Such materials have exhibited intriguing physical and chemical properties, showing their potential to be used as high-performance semiconductors, superconductors, thermoresistant composites, etc.76 Most of the currently known misfit layer compounds are synthetic chalcogenides built from the stacking of two different types of layer modules (Fig. 5). One module has the formula of [MX], where “M” is Sn, Pb, Bi, Sb, a rare earth metal, etc., and “X” is S, Se, Te, etc. This module is two-atoms thick and exhibits a distorted NaCl structure type. Here we call it the M-module. The other module is the T-module, which has the formula of [TX2], where “T” can be Ti, V, Cr, Nb, Ta, Mo, W, etc. This T-module is three-atoms thick, with a layer of T atoms sandwiched by two layers of X atoms. Given δ as the misfit between the M- and T-modules, the general formula of the misfit layer structures built by the stacking of m of the M-modules and t of the T-modules can be written as [[MX]1+δ]m[TX2]t.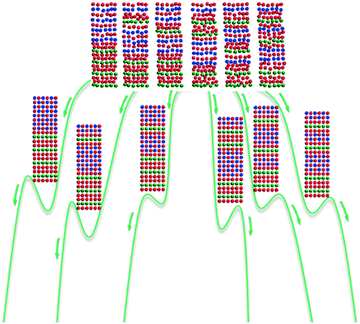 | ||
| Fig. 5 Formation of six metastable polysomes of [[PbSe]1.14]4[NbSe2]4 from initial reactants upon annealing. The green lines are the schematic representations of the free energy pathways for the six corresponding reactions. Atoms are coloured as follows: blue, Pb; green, Nb; and red, Se. Reprinted with permission from ref. 77. Copyright 2015 John Wiley and Sons. | ||
Different from the strict A–B alternation in the perovskite polysomes, the stacking of the M- and T-modules in misfit layer compounds does not have this restriction. Therefore, even a small number of layer modules could lead to over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 incommensurate metastable polysomes.77 Today's state-of-the-art synthetic techniques allow researchers to precisely control the self-assembly of these layer modules. Therefore, these misfit layer compounds can be synthesised in a more designed way than other conventional inorganic materials.78,79 For instance, four M-modules and four T-modules could have six distinct ways of stacking, including [MMMMTTTT], [MMMTTTMT], [MMMTTMTT], [MMTTTMT], [MMTTMTMT], and [MMTMTTMT]. On the basis of these stacking sequences, in 2015, Johnson and coworkers prepared all six polysomes of [[PbSe]1.14]4[NbSe2]4via low-temperature annealing (Fig. 5), which was the first report of the targeted synthesis of extended inorganic polysomes through a nonepitaxial growth technique.77 Through a similar approach, Johnson and coworkers also prepared the six polysomes of [[SnSe]1+δ]4[NbSe2]4 (δ = 0.14–0.16).80 The electrical properties measurement revealed metallic behaviour for all six polysomes. More importantly, the authors found that the charge transfer between constituent modules depended primarily on the number of successive [SnSe] layers, whereas the carrier mobility mainly depended on the number of successive [NbSe2] layers. Since the constituent modules may have different functions, these misfit layer compounds can be designed to optimise their performance by wisely choosing the ratios and stacking sequences of various types of constituent modules.
000 incommensurate metastable polysomes.77 Today's state-of-the-art synthetic techniques allow researchers to precisely control the self-assembly of these layer modules. Therefore, these misfit layer compounds can be synthesised in a more designed way than other conventional inorganic materials.78,79 For instance, four M-modules and four T-modules could have six distinct ways of stacking, including [MMMMTTTT], [MMMTTTMT], [MMMTTMTT], [MMTTTMT], [MMTTMTMT], and [MMTMTTMT]. On the basis of these stacking sequences, in 2015, Johnson and coworkers prepared all six polysomes of [[PbSe]1.14]4[NbSe2]4via low-temperature annealing (Fig. 5), which was the first report of the targeted synthesis of extended inorganic polysomes through a nonepitaxial growth technique.77 Through a similar approach, Johnson and coworkers also prepared the six polysomes of [[SnSe]1+δ]4[NbSe2]4 (δ = 0.14–0.16).80 The electrical properties measurement revealed metallic behaviour for all six polysomes. More importantly, the authors found that the charge transfer between constituent modules depended primarily on the number of successive [SnSe] layers, whereas the carrier mobility mainly depended on the number of successive [NbSe2] layers. Since the constituent modules may have different functions, these misfit layer compounds can be designed to optimise their performance by wisely choosing the ratios and stacking sequences of various types of constituent modules.
Considering the vast number of possible polysomes, finding a high-throughput method to predict the properties of yet-to-be-prepared misfit layer compounds becomes very important. Towards this end, Johnson and coworkers created a simplistic model to predict the properties of complex polysomes by calculating the weighted sums of the properties of their constituent building blocks.80 For instance, the polysome [MMMTTMTT] can be viewed as the combination of two smaller building blocks, i.e., [MMMTT] and [MTT]. Given the properties of polysomes [MMMTT] and [MTT], measured or calculated, the properties of polysome [MMMTTMTT] can be estimated by summing up the corresponding properties of polysomes [MMMTT] and [MTT]. For [[SnSe]1+δ]4[NbSe2]4 polysomes, this model predicted the carrier concentrations reasonably well, but did a poorer job on the resistivity prediction. Therefore, a more sophisticated high-throughput theoretical method is highly needed to predict the specific properties among the many potential misfit layer polysomes that can be prepared.
MAX phases
The MAX phases are a family of hexagonal carbides or nitrides with a general formula of Mn+1AXn, where “M” is an early transition metal (Sc, Ti, Zr, Mo, etc.), “A” is a group 13 to 16 element (Al, Ga, Si, P, etc.), and “X” is C or N. Owing to their thermodynamically stable modular layered structures and the metal-like nature of their bonding, MAX phases are not only electrically and thermally conductive like metals, but also elastically rigid and lightweight like ceramics. Among all known MAX phases, Al-containing structures are of particular interest because of their exceptional oxidation resistance. More importantly, MXenes, a new family of two-dimensional materials possessing hydrophilicity, conductivity, and extremely high capacitance, can be prepared by selectively etching the Al layers in MAX phases.81,82Understanding the influence of layer stacking on the stability of MAX phases is key for the prediction and targeted synthesis of these materials. In 2015, Barsoum and coworkers studied the stabilities of two recently synthesised MAX phases, i.e., Mo2TiAlC2 and Mo2Ti2AlC3.83 The general manner of layer stacking in the unit cell of Mo2TiAlC2 is [AMXMXMAMXMXM], and in Mo2Ti2AlC3 is [AMXMXMXMAMXMXMXM], where “A” layers are formed by Al atoms, “X” layers by C atoms, and “M” layers by either Mo or Ti atoms. By enumerating the distributions of Mo and Ti, Barsoun and coworkers built 6 possible polysomes for Mo2TiAlC2 and 20 polysomes for Mo2Ti2AlC3 (Fig. 6). Meanwhile, they also built some ordered structural models with different Mo/Ti ratios and some disordered models with Mo and Ti randomly distributed over the M-sites. DFT calculations revealed that the ordered polysomes consistent with the experimental structures were the most stable ones (the leftmost structures in Fig. 6) in comparison with their competing phases. In these most stable polysomes, the Mo layers sandwich both the Al and Ti layers (for instance, [MoAlMo] and [MoCTiCMo]). More importantly, the authors found that the Mo atoms surrounded by C atoms in a face-centred configuration ([CMoC]) were a big contribution to the high formation energy in the unstable polysomes. This should be the driving force leading to the M-layer ordering observed in the experiment. Notice that both of these favoured and disfavoured configurations could be directly extracted from the stacking sequences of these polysomes. In more complex MAX systems that may have larger unit cells and many more polysomes to evaluate, we may instantly prescreen the infeasible polysomes with disfavoured stacking sequences and conduct computationally expensive first-principles calculations only on those with favoured stacking sequences.
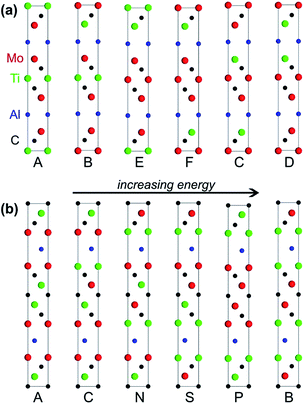 | ||
| Fig. 6 (a) All six possible Mo2TiAlC2 polysomes and (b) six of the 20 possible Mo2Ti2AlC3 polysomes sorted from the most stable on the left to the least stable on the right. Reprinted with permission from ref. 83. Copyright 2015 AIP Publishing LLC. | ||
Summary and outlook
The past few years have seen rapid developments in materials science with the aid of various computational and informatics tools. These tools not only help us understand the experimental observations on a theoretical level, but also provide predictive information on unknown materials and properties. Since the pioneer scientists started to elucidate the simplest crystal structures a century ago, many three-dimensionally extended solid structures have been described as the stacking of layer modules. The advantage of this representation is not only the simplification of complex structures, but also its convenience to build topological relations among similar polymorphs. More importantly, it significantly eases the problems of structure predictions, which is a prerequisite for function-led materials innovation. Although the stacking sequences of inorganic materials still cannot be “engineered” in a way we manipulate the DNA of organisms, recent progress in this field has shed some light towards this direction.The next challenge is to develop a general routine for high-throughput structure evaluation, through which we can quickly estimate the physical and chemical properties of a large number of predicted structures and pick out the ones with desired properties as our synthetic targets. This requires a significant enhancement in the efficiency of our current computational tools. The developing distributed computing techniques might be one of the solutions. These techniques aim to divide complex computational tasks into many smaller ones and solve them among a group of networked but loosely coupled computers. These computers, which can be located at different places all over the world, form a grid. In theory, there is no upper limit for the number or size of the grids. Everyday, millions of computer owners voluntarily donate their computing resources to several huge grids to help scientists solve computationally intensive problems. Actually, some of the computational tasks in materials science have recently been solved via these new techniques.84–87 We can envisage that with the development of computer hardware and internet algorithms, distributed computing will play a more important role in materials innovation in the near future. An alternative solution could be the data mining techniques, which include a variety of computer algorithms that are capable of “learning” the already-known experimental and computational facts stored in databases, discovering the hidden structure-property patterns, and making predictions on the properties of complex structures that are currently experimentally or computationally inaccessible. We are now in the era of “big data”; we create an enormous amount of experimental and computational data every day. Data mining techniques process these data in a purely mathematical manner without touching the deepest physical and chemical theories that require intensive computations. Therefore, data mining techniques are capable of making analyses, evaluations, and predictions much quicker than any conventional computational chemistry approach. Being an important part of the Materials Genomes Initiative, data mining techniques have already shown their potential in high-throughput structure and property predictions for a large number of advanced materials.88–95 We have shown in this Minireview that it is possible to estimate specific properties directly from the stacking sequences in some cases. With the aid of various data mining techniques (especially the “text mining” techniques), we may soon find some general models to estimate more complex properties from the stacking sequences of inorganic modular materials. When large-scale structure evaluation and property prediction become possible we will be able to identify the most promising synthetic targets according to our functional needs from a large number of theoretical candidates and experimentally realise them with the aid of various state-of-the-art synthetic techniques.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 21320102001 and 21273098) and the State Basic Research Project of China (Grant No. 2014CB931802). Y. L. acknowledges the support of the Program for New Century Excellent Talents in University (NCET-13-0246).References
- Materials Genome Initiative, http://www.whitehouse.gov/mgi, 2016.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- C. M. Simon, J. Kim, D. A. Gomez-Gualdron, J. S. Camp, Y. G. Chung, R. L. Martin, R. Mercado, M. W. Deem, D. Gunter, M. Haranczyk, D. S. Sholl, R. Q. Snurr and B. Smit, Energy Environ. Sci., 2015, 8, 1190–1199 CAS.
- A. R. Oganov, R. Martoňák, A. Laio, P. Raiteri and M. Parrinello, Nature, 2005, 438, 1142–1144 CrossRef CAS PubMed.
- J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913 CrossRef CAS PubMed.
- S. M. Woodley and R. Catlow, Nat. Mater., 2008, 7, 937–946 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- A. L. Dzubak, L.-C. Lin, J. Kim, J. A. Swisher, R. Poloni, S. N. Maximoff, B. Smit and L. Gagliardi, Nat. Chem., 2012, 4, 810–816 CrossRef CAS PubMed.
- K. Yang, W. Setyawan, S. Wang, M. Buongiorno Nardelli and S. Curtarolo, Nat. Mater., 2012, 11, 614–619 CrossRef CAS PubMed.
- L.-C. Lin, A. H. Berger, R. L. Martin, J. Kim, J. A. Swisher, K. Jariwala, C. H. Rycroft, A. S. Bhown, M. W. Deem, M. Haranczyk and B. Smit, Nat. Mater., 2012, 11, 633–641 CrossRef CAS PubMed.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Chem. Rev., 2013, 113, 8261–8323 CrossRef CAS PubMed.
- J. Kim, A. Maiti, L.-C. Lin, J. K. Stolaroff, B. Smit and R. D. Aines, Nat. Commun., 2013, 4, 1694 CrossRef PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- Y. J. Colón and R. Q. Snurr, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- P. Bai, M. Y. Jeon, L. Ren, C. Knight, M. W. Deem, M. Tsapatsis and J. I. Siepmann, Nat. Commun., 2015, 6, 5912 CrossRef CAS PubMed.
- A. G. Slater and A. I. Cooper, Science, 2015, 348, aaa8075 CrossRef PubMed.
- C. R. A. Catlow, Interdiscip. Sci. Rev., 2015, 40, 294–307 CrossRef.
- R. Gautier, X. Zhang, L. Hu, L. Yu, Y. Lin, T. O. L. Sunde, D. Chon, K. R. Poeppelmeier and A. Zunger, Nat. Chem., 2015, 7, 308–316 CrossRef CAS PubMed.
- G. B. Bokij, K. Boll-Dornberger, J. M. Cowley, S. Ďurovič, H. Jagodzinski, P. Krishna, P. M. De Wolff, B. B. Zvyagin, D. E. Cox and P. Goodman, et al. , Acta Crystallogr., Sect. A: Found. Crystallogr., 1984, 40, 399–404 CrossRef.
- D. R. Veblen, Am. Mineral., 1991, 76, 801–826 CAS.
- International Tables for Crystallography. Volume C. Mathematical, Physical and Chemical Tables, ed. E. Prince, Kluwer Acad. Publ., Dordrecht, 3rd edn, 2004 Search PubMed.
- E. Estevez-Rams, C. Azanza Ricardo and B. Aragón Fernández, Z. Kristallogr., 2005, 220, 692–695 Search PubMed.
- J. E. Iglesias, Z. Kristallogr., 2006, 221, 237–245 CAS.
- J. E. Iglesias, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 178–194 CrossRef PubMed.
- C. Raffy, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 075201 CrossRef.
- K. Kobayashi and S. Komatsu, J. Phys. Soc. Jpn., 2008, 77, 084703 CrossRef.
- J. Johansson, J. Bolinsson, M. Ek, P. Caroff and K. A. Dick, ACS Nano, 2012, 6, 6142–6149 CrossRef CAS PubMed.
- A. Belabbes, C. Panse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075208 CrossRef.
- T. Ito, T. Akiyama and K. Nakamura, J. Cryst. Growth, 2013, 362, 207–210 CrossRef CAS.
- M. B. Smirnov, A. O. Koshkin, S. V. Karpov, B. V. Novikov, A. N. Smirnov, I. V. Shtrohm, G. E. Cirlin, A. D. Bouravleuv and Y. B. Samsonenko, Phys. Solid State, 2013, 55, 1220–1230 CrossRef CAS.
- F. Bechstedt and A. Belabbes, J. Phys.: Condens. Matter, 2013, 25, 273201 CrossRef PubMed.
- D. Zagorac, J. C. Schön, J. Zagorac and M. Jansen, RSC Adv., 2015, 5, 25929–25935 RSC.
- T. Ishikawa, K. Kato, M. Nomura, N. Suzuki, H. Nagara and K. Shimizu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214110 CrossRef.
- T. Ishikawa, T. Tsuchiya and J. Tsuchiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 212101 CrossRef.
- J. Ontaneda, R. A. Bennett and R. Grau-Crespo, J. Phys. Chem. C, 2015, 119, 23436–23444 CAS.
- F. Mercier and S. Nishizawa, J. Cryst. Growth, 2012, 360, 189–192 CrossRef CAS.
- Y. Kim, H. Lee and S. Kang, J. Mater. Chem., 2012, 22, 12874–12881 RSC.
- C. A. J. Fisher, A. Kuwabara, H. Moriwake, H. Oki, K. Kohama and Y. Ikuhara, Phys. Status Solidi RRL, 2014, 8, 545–548 CrossRef CAS.
- M. E. Davis, Nature, 2002, 417, 813–821 CrossRef CAS PubMed.
- Y. Li and J. Yu, Chem. Rev., 2014, 114, 7268–7316 CrossRef CAS PubMed.
- J. Yu and R. Xu, Acc. Chem. Res., 2010, 43, 1195–1204 CrossRef CAS PubMed.
- Z. Wang, J. Yu and R. Xu, Chem. Soc. Rev., 2012, 41, 1729–1741 RSC.
- J. Li, A. Corma and J. Yu, Chem. Soc. Rev., 2015, 44, 7112–7127 RSC.
- C. Mellot Draznieks, J. M. Newsam, A. M. Gorman, C. M. Freeman and G. Férey, Angew. Chem., Int. Ed., 2000, 39, 2270–2275 CrossRef.
- Y. Li, J. Yu, D. Liu, W. Yan, R. Xu and Y. Xu, Chem. Mater., 2003, 15, 2780–2785 CrossRef CAS.
- M. M. J. Treacy, I. Rivin, E. Balkovsky, K. H. Randall and M. D. Foster, Microporous Mesoporous Mater., 2004, 74, 121–132 CrossRef CAS.
- Y. Li, J. Yu, Z. Wang, J. Zhang, M. Guo and R. Xu, Chem. Mater., 2005, 17, 4399–4405 CrossRef CAS.
- G. Férey, C. Mellot-Draznieks, C. Serre and F. Millange, Acc. Chem. Res., 2005, 38, 217–225 CrossRef PubMed.
- Y. Li, J. Yu, R. Xu, C. Baerlocher and L. B. McCusker, Angew. Chem., Int. Ed., 2008, 47, 4401–4405 CrossRef CAS PubMed.
- R. Pophale, P. A. Cheeseman and M. W. Deem, Phys. Chem. Chem. Phys., 2011, 13, 12407–12412 RSC.
- Z.-B. Yu, Y. Han, L. Zhao, S. Huang, Q.-Y. Zheng, S. Lin, A. Córdova, X. Zou and J. Sun, Chem. Mater., 2012, 24, 3701–3706 CrossRef CAS.
- T. Willhammar, J. Sun, W. Wan, P. Oleynikov, D. Zhang, X. Zou, M. Moliner, J. Gonzalez, C. Martínez, F. Rey and A. Corma, Nat. Chem., 2012, 4, 188–194 CrossRef CAS PubMed.
- M. Moliner, T. Willhammar, W. Wan, J. González, F. Rey, J. L. Jorda, X. Zou and A. Corma, J. Am. Chem. Soc., 2012, 134, 6473–6478 CrossRef CAS PubMed.
- D. Xie, L. B. McCusker, C. Baerlocher, S. I. Zones, W. Wan and X. Zou, J. Am. Chem. Soc., 2013, 135, 10519–10524 CrossRef CAS PubMed.
- T. Willhammar and X. Zou, Z. Kristallogr., 2013, 228, 11–27 CAS.
- J. V. Smith, Chem. Rev., 1988, 88, 149–182 CrossRef CAS.
- D. E. Akporiaye and G. D. Price, Zeolites, 1989, 9, 23–32 CrossRef CAS.
- D. E. Akporiaye, Zeolites, 1992, 12, 197–201 CrossRef CAS.
- M. Trachta, O. Bludský, J. Čejka, R. E. Morris and P. Nachtigall, ChemPhysChem, 2014, 15, 2972–2976 CrossRef CAS PubMed.
- M. Trachta, P. Nachtigall and O. Bludský, Catal. Today, 2015, 243, 32–38 CrossRef CAS.
- W. J. Roth, P. Nachtigall, R. E. Morris, P. S. Wheatley, V. R. Seymour, S. E. Ashbrook, P. Chlubná, L. Grajciar, M. Položij, A. Zukal, O. Shvets and J. Čejka, Nat. Chem., 2013, 5, 628–633 CrossRef CAS PubMed.
- W. J. Roth, P. Nachtigall, R. E. Morris and J. Čejka, Chem. Rev., 2014, 114, 4807–4837 CrossRef CAS PubMed.
- P. S. Wheatley, P. Chlubná-Eliášová, H. Greer, W. Zhou, V. R. Seymour, D. M. Dawson, S. E. Ashbrook, A. B. Pinar, L. B. McCusker, M. Opanasenko, J. Čejka and R. E. Morris, Angew. Chem., Int. Ed., 2014, 53, 13210–13214 CrossRef CAS PubMed.
- P. Eliášová, M. Opanasenko, P. S. Wheatley, M. Shamzhy, M. Mazur, P. Nachtigall, W. J. Roth, R. E. Morris and J. Čejka, Chem. Soc. Rev., 2015, 44, 7177–7206 RSC.
- R. E. Morris and J. Čejka, Nat. Chem., 2015, 7, 381–388 CrossRef CAS PubMed.
- M. Mazur, P. S. Wheatley, M. Navarro, W. J. Roth, M. Položij, A. Mayoral, P. Eliášová, P. Nachtigall, J. Čejka and R. E. Morris, Nat. Chem., 2016, 8, 58–62 CrossRef CAS PubMed.
- J. V. Smith and J. M. Bennett, Am. Mineral., 1981, 66, 777–788 CAS.
- Y. Li, X. Li, J. Liu, F. Duan and J. Yu, Nat. Commun., 2015, 6, 8328 CrossRef CAS PubMed.
- Y. Li, J. Yu and R. Xu, Angew. Chem., Int. Ed., 2013, 52, 1673–1677 CrossRef CAS PubMed.
- J. Darriet and M. A. Subramanian, J. Mater. Chem., 1995, 5, 543–552 RSC.
- Nat. Mater., 2014, 13, 837 Search PubMed.
- J. Alaria, P. Borisov, M. S. Dyer, T. D. Manning, S. Lepadatu, M. G. Cain, E. D. Mishina, N. E. Sherstyuk, N. A. Ilyin, J. Hadermann, D. Lederman, J. B. Claridge and M. J. Rosseinsky, Chem. Sci., 2014, 5, 1599–1610 RSC.
- M. S. Dyer, C. Collins, D. Hodgeman, P. A. Chater, A. Demont, S. Romani, R. Sayers, M. F. Thomas, J. B. Claridge, G. R. Darling and M. J. Rosseinsky, Science, 2013, 340, 847–852 CrossRef CAS PubMed.
- K. A. Bradley, C. Collins, M. S. Dyer, J. B. Claridge, G. R. Darling and M. J. Rosseinsky, Phys. Chem. Chem. Phys., 2014, 16, 21073–21081 RSC.
- A. Meerschaut, Curr. Opin. Solid State Mater. Sci., 1996, 1, 250–259 CrossRef CAS.
- M. Esters, M. B. Alemayehu, Z. Jones, N. T. Nguyen, M. D. Anderson, C. Grosse, S. F. Fischer and D. C. Johnson, Angew. Chem., Int. Ed., 2015, 54, 1130–1134 CrossRef CAS PubMed.
- C. L. Heideman, S. Tepfer, Q. Lin, R. Rostek, P. Zschack, M. D. Anderson, I. M. Anderson and D. C. Johnson, J. Am. Chem. Soc., 2013, 135, 11055–11062 CrossRef CAS PubMed.
- D. B. Moore, M. Beekman, S. Disch and D. C. Johnson, Angew. Chem., Int. Ed., 2014, 53, 5672–5675 CrossRef CAS PubMed.
- M. B. Alemayehu, M. Falmbigl, K. Ta and D. C. Johnson, ACS Nano, 2015, 9, 4427–4434 CrossRef CAS PubMed.
- M. Ghidiu, M. R. Lukatskaya, M.-Q. Zhao, Y. Gogotsi and M. W. Barsoum, Nature, 2014, 516, 78–81 CAS.
- M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005 CrossRef CAS PubMed.
- B. Anasori, M. Dahlqvist, J. Halim, E. J. Moon, J. Lu, B. C. Hosler, E. N. Caspi, S. J. May, L. Hultman, P. Eklund, J. Rosén and M. W. Barsoum, J. Appl. Phys., 2015, 118, 094304 CrossRef.
- S. A. French, R. Coates, D. W. Lewis and C. R. A. Catlow, J. Solid State Chem., 2011, 184, 1484–1491 CrossRef CAS.
- J. Hachmann, R. Olivares-Amaya, S. Atahan-Evrenk, C. Amador-Bedolla, R. S. Sánchez-Carrera, A. Gold-Parker, L. Vogt, A. M. Brockway and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2011, 2, 2241–2251 CrossRef CAS.
- Q. Xing and E. Blaisten-Barojas, Concurrency Comput. Pract. Ex., 2013, 25, 2157–2169 CrossRef.
- M. J. Harvey and G. De Fabritiis, J. Chem. Inf. Model., 2015, 55, 909–914 CrossRef CAS PubMed.
- C. C. Fischer, K. J. Tibbetts, D. Morgan and G. Ceder, Nat. Mater., 2006, 5, 641–646 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- J. C. Snyder, M. Rupp, K. Hansen, K.-R. Müller and K. Burke, Phys. Rev. Lett., 2012, 108, 253002 CrossRef PubMed.
- G. Pilania, C. Wang, X. Jiang, S. Rajasekaran and R. Ramprasad, Sci. Rep., 2013, 3, 2810 Search PubMed.
- M. Fernandez, P. G. Boyd, T. D. Daff, M. Z. Aghaji and T. K. Woo, J. Phys. Chem. Lett., 2014, 5, 3056–3060 CrossRef CAS PubMed.
- A. G. Kusne, T. Gao, A. Mehta, L. Ke, M. C. Nguyen, K.-M. Ho, V. Antropov, C.-Z. Wang, M. J. Kramer, C. Long and I. Takeuchi, Sci. Rep., 2014, 4, 6367 CrossRef PubMed.
- J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050 CrossRef CAS.
- V. Botu and R. Ramprasad, Int. J. Quantum Chem., 2015, 115, 1074–1083 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |