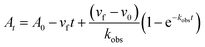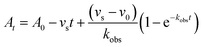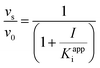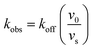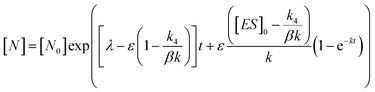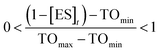DOI:
10.1039/C6SC01000H
(Edge Article)
Chem. Sci., 2016,
7, 5945-5954
Correlating drug–target kinetics and in vivo pharmacodynamics: long residence time inhibitors of the FabI enoyl-ACP reductase†
Received
3rd March 2016
, Accepted 20th May 2016
First published on 25th May 2016
Abstract
Drug–target kinetics enable time-dependent changes in target engagement to be quantified as a function of drug concentration. When coupled to drug pharmacokinetics (PK), drug–target kinetics can thus be used to predict in vivo pharmacodynamics (PD). Previously we described a mechanistic PK/PD model that successfully predicted the antibacterial activity of an LpxC inhibitor in a model of Pseudomonas aeruginosa infection. In the present work we demonstrate that the same approach can be used to predict the in vivo activity of an enoyl-ACP reductase (FabI) inhibitor in a model of methicillin-resistant Staphylococcus aureus (MRSA) infection. This is significant because the LpxC inhibitors are cidal, whereas the FabI inhibitors are static. In addition P. aeruginosa is a Gram-negative organism whereas MRSA is Gram-positive. Thus this study supports the general applicability of our modeling approach across antibacterial space.
Introduction
Despite advances in genomics and bioinformatics that have identified a large number of novel drug targets across disease space,1,2 target-based strategies have resulted in very few new drugs.3–5 Barriers to success include the growing realization that genetic essentiality does not necessarily equate to druggability, and thus not all essential proteins are actually good targets for drug discovery. In addition, the lack of success suggests that our ability to predict efficacy and selectivity in humans at early stages of drug discovery is inadequate, highlighting the need for improved methods for correlating in vitro and in vivo measurements of drug activity. In the present work we demonstrate that the integration of drug–target kinetics into a mechanistic mathematical model that links drug pharmacokinetics (PK) and in vitro antibacterial activity can be used to predict in vivo drug efficacy (PD).
Traditionally, the selection and optimization of drug leads is heavily reliant on thermodynamic parameters such as IC50 and Kd values. However, these equilibrium parameters are insufficient to predict efficacy and selectivity in the dynamic in vivo environment where drug and target are not at equilibrium.6–11 As a consequence, drug–target residence time (tR = 1/koff) has emerged as a key parameter in lead optimization in which kinetic parameters are used to drive drug discovery.7,8,11 This strategy exploits rapid in vivo clearance to achieve efficacy and selectivity via prolonged dissociation rates from the drug target.
We have developed a mechanistic PK/PD model which is capable of predicting in vivo efficacy based on in vitro drug–target kinetic parameters.12 This model successfully predicted the antibacterial activity of a Pseudomonas aeruginosa LpxC (paLpxC) inhibitor in a mouse model of infection. To evaluate the generality of our approach, we have now used the model to analyze the antibacterial activity of inhibitors that target the enoyl-ACP reductase (FabI) enzyme in the Gram-positive bacterium Staphylococcus aureus (saFabI).13–15 The saFabI-inhibitors are static inhibitors of S. aureus growth in contrast to the paLpxC-inhibitors which display cidal activity against the Gram-negative pathogen P. aeruginosa. However, despite these major differences in mechanism and organism, the model is able to fit the time-dependent antibacterial activity of a series of saFabI inhibitors at the cellular level, and also to simulate the efficacy of two selected FabI inhibitors in an animal infection model. By comparing the relationship between target inhibition and activity in these two different systems, we are able to gain insight into target vulnerability, which characterizes the degree of inhibition required to elicit the desired pharmacodynamic (PD) response.16,17
Results
Long residence time inhibitors of saFabI
To evaluate the applicability of the PK/PD model described previously to other systems,12 we have now used the model to analyze the in vitro and in vivo activity of inhibitors of the S. aureus FabI enzyme (saFabI) from the bacterial type II fatty acid biosynthesis pathway. Our saFabI inhibitor program has generated several series of compounds including those based on the diphenyl ether scaffold that are time-dependent enzyme inhibitors, a selection of which have excellent in vitro activity and efficacy in animal models of infection. For the purposes of this work, we selected four compounds, PT55, PT447, PT119 and SKTS1 with a wide range of residence-times (Fig. 1 and Table 1). PT119, PT55 and PT447 have been described previously.18,19SKTS1 was designed to explore a hitherto unaddressed region of the binding pocket with the ultimate goal of further increasing affinity and residence time. The binding mode obtained by docking suggests new interactions with Ala97 mediated by nearly ideal hydrogen bonds (Fig. 2). Since SKTS1 had a predicted IC50 of 1 nM, which is ∼200-fold lower than the corresponding value for the parent molecule 5-hexyl-2-phenoxyphenol (yellow portion of SKTS1 in Fig. 2), we selected this molecule for synthesis and further investigation.
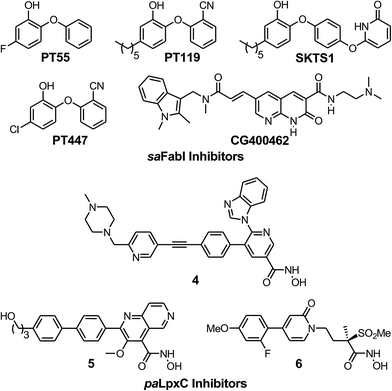 |
| | Fig. 1 The saFabI and paLpxC inhibitors used in this work. The saFabI inhibitors PT55, PT119 and PT447 have been described in Chang et al.18 and Wang et al.,19 and the paLpxC inhibitors in Walkup et al.12SKTS1 is described in the present work. | |
Table 1 Kinetic and cellular parameters for inhibitors of saFabI
| Inhibitor |
K
appi (nM) |
MIC (μM) |
t
R (h) 37 °C |
PAEa (h) 37 °C |
|
Post-antibiotic effect (PAE) values are reported at 4x MIC.
|
|
PT55
|
1970 |
39 |
0.04 |
0.25 ± 0.21 |
|
PT447
|
114 |
8 |
0.5 |
0.91 ± 0.11 |
|
PT119
|
89 |
2 |
1.78 |
1.03 ± 0.17 |
|
SKTS1
|
46 |
10 |
5.75 |
2.04 ± 0.18 |
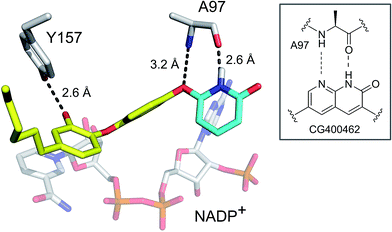 |
| | Fig. 2 Rational design of SKTS1. The putative binding mode of SKTS1 derived from our docking study is shown within the saFabI protein structure (selected residues and the cofactor are depicted as gray sticks). The diphenyl ether scaffold of SKTS1 is indicated in yellow while the novel 6-hydroxypyridin-2(1H)-one modification is highlighted in cyan. The inset highlights the underlying concept that drove the design of SKTS1. | |
K
appi values were determined by progress curve analysis followed by global fitting of the data to eqn (1)–(4). All four compounds showed one-step inhibition (Scheme 1), consistent with previous reports for this series of inhibitors.18 The dissociation rate constants were then determined at 37 °C using a jump dilution assay, in which the compounds were incubated overnight with saFabI at a concentration above their Ki values, after which reaction mixtures were diluted 1000-fold into the reaction buffer containing excess substrate. This approach yielded residence times of 0.04, 0.5, 1.78 and 5.75 h for PT55, PT447, PT119 and SKTS1, respectively. In Table 1 it can also be seen that Kappi decreases ∼40-fold as residence time increases 140-fold, and thus the increase in the life-time of the drug–target complex results primarily from ground state stabilization in addition to a modest change in transition state stability.18
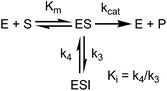 |
| | Scheme 1
saFabI inhibition. | |
In vitro PAE data analysis: correlation between PAE and tR
We next determined the time-dependent antibacterial activity of each saFabI inhibitor at the whole cell level by measuring the post-antibiotic effect (PAE), which is the persistent suppression of bacterial growth following antibiotic wash-out.20 In each case, a longer PAE was observed as the drug concentration increased except for SKTS1 where the PAE reached a maximum at 4x MIC. PT55, a saFabI inhibitor with a very short residence time (0.04 h) had the shortest PAE (0.25 h), whilst the PAE increased with residence time for the other compounds (Table 1). The relationship between PAE and residence time (tR) is shown graphically in Fig. 3, where we also present data for the paLpxC inhibitors reported previously.12 In each case a positive slope is observed, indicating that prolonged antibacterial activity at low drug concentration is coupled to the life-time of the drug–target complex. In contrast, no correlation was observed between MIC and residence time.
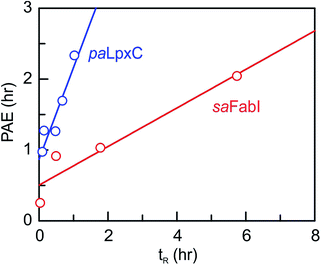 |
| | Fig. 3 Correlation between residence time (tR) and post-antibiotic effect (PAE). Data for paLpxC inhibitors (blue) are from ref. 12. The PAE and tR values were determined at 37 °C and the PAE values obtained at 4x MIC have been plotted. In each case the data have been fit to a straight line with slope values of 0.27 (saFabI) and 1.3 (paLpxC). | |
In vitro PAE data analysis: PK/PD model fitting
In order to integrate drug–target kinetics into predictions of in vivo drug activity, we previously derived a PK/PD model in which time-dependent changes in target engagement are directly related to inhibition of bacterial growth.12 This model had to be modified slightly for use with the saFabI inhibitors which follow an uncompetitive one-step mechanism in contrast to the paLpxC inhibitors which bind to their target via a competitive two-step mechanism. The derivation of the PK/PD model is outlined in the Methods section (eqn (5)) and described in detail in the ESI (eqn (S14)†).| | 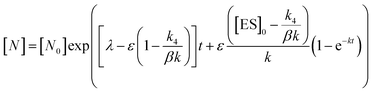 | (eqn 5 S14) |
Eqn (5) relates the bacterial cell count ([N], CFU mL−1) to the rate of logarithmic cell growth (λ) minus the maximum rate of inhibitor-induced cell death (ε) multiplied by a factor that integrates time-dependent changes in the amount of the enzyme forms that cannot sustain growth ([E] and [EI] in Scheme 1). In eqn (5), k4 is the rate constant for breakdown of the enzyme-inhibitor complex (ESI†), β = 1 + Km/[S], where M = Km/[S], and κ is a more complex function that includes the concentration of inhibitor (drug) ([I]) at the target as well as the thermodynamic affinity of the inhibitor for the enzyme (Ki in Scheme 1). Since the intracellular drug concentration is not known, we use a permeability factor (pm) to relate the concentration of drug in the media (or the free fraction drug concentration in plasma) to the intracellular drug concentration.
In order to use eqn (5) for predictions of in vivo drug activity, we first fit the PAE data using the equation to obtain values for M and pm. The progress curve kinetics (Table 1) yield a seed value for k4 and a value for the apparent Ki (Kappi) which was used as input for Ki. λ (kgrowth) was an experimental value and ε (kkillmax) was assumed to be similar to λ since the saFabI inhibitors are static. Finally, M was assigned a value of unity given the general assumption that the substrate concentration is usually around the value of Km. Non-linear regression was used to perform global fits of data to the PK/PD model, and excellent fits to the experimental data were obtained (Fig. 4) with the output parameters showing only small changes from the input seed values (Table 2), thus validating the ability of the model to correlate saFabI inhibition with in vitro antibacterial activity.
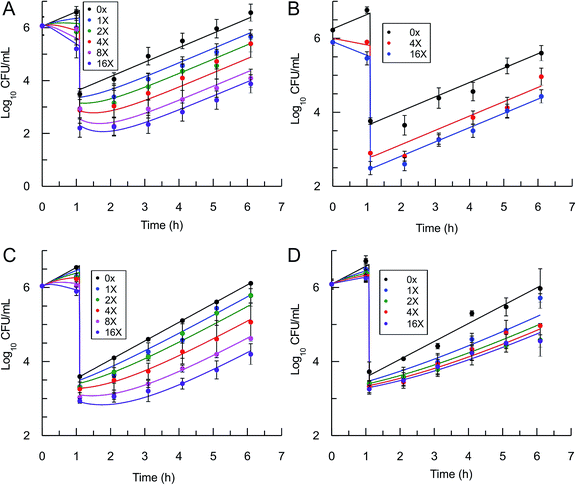 |
| | Fig. 4 Post-antibiotic effect of the saFabI inhibitors against S. aureus. The recovery of bacterial growth after 1 h exposure and compound washout was measured at various concentrations of inhibitor up to 16x MIC. Experimental data points represent mean values from triplicate, independent measurements and error bars represent 1 s.d. of the log10 CFU mean. Solid lines are the result of global fitting to the PK/PD model (Table 2). A: PT119, B: PT55, C: PT447, D: SKTS1. | |
Table 2
In vitro PAE model fitting: input and output parameters for PT119, PT55, PT447 and SKTS1
| Parameter |
PT119
|
PT55
|
PT447
|
SKTS1
|
| Input value |
Output value |
Ratio |
Input value |
Output value |
Ratio |
Input value |
Output value |
Ratio |
Input value |
Output value |
Ratio |
|
The saFabI inhibitors are bacteriostatic agents in vitro and thus the value of kkillmax is similar to the bacterial growth rate (kgrowth).
The input value for pm/Ki has been chosen randomly within a large constraint range (1/100–100).
|
|
k
4 (min−1) |
0.009 |
0.016 |
1.8 |
0.43 |
0.36 |
0.8 |
0.033 |
0.017 |
0.5 |
0.0033 |
0.0038 |
1.2 |
|
λ (kgrowth) (log10 h−1) |
1.2 |
1.2 |
1.0 |
1.2 |
1.2 |
1.0 |
1.2 |
1.2 |
1.0 |
1.0 |
1.1 |
1.1 |
|
ε (kkillmax) (log10 h−1)a |
1.8 |
2.1 |
1.2 |
1.8 |
1.8 |
1.0 |
1.6 |
1.7 |
1.5 |
1.0 |
0.9 |
0.8 |
|
K
appi (μM) |
0.089 |
0.098 |
1.1 |
1.97 |
1.81 |
0.92 |
0.11 |
0.17 |
0.74 |
0.05 |
0.04 |
0.74 |
|
p
m/Kappi (μM−1)b |
0.05 |
0.041 |
0.82 |
0.05 |
0.017 |
0.3 |
0.05 |
0.01 |
0.2 |
0.05 |
0.059 |
1.2 |
|
M(Km/[S]) |
1.0 |
0.45 |
0.45 |
1.0 |
0.88 |
0.88 |
1.0 |
0.80 |
0.80 |
1.0 |
1.82 |
1.8 |
|
R
2
|
0.95 |
0.97 |
0.97 |
0.98 |
Predicting in vivo efficacy of PT55 and PT119 using the mechanistic PD model
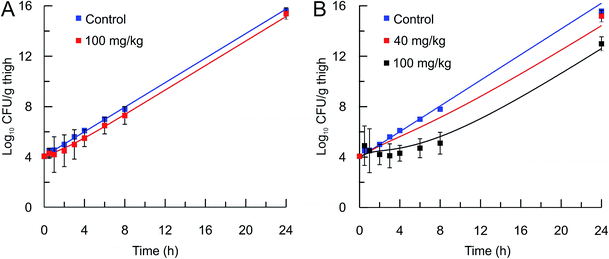
The mechanistic PK/PD model was then used to predict the in vivo activity of two compounds, PT55 and PT119, that differ significantly in their residence times on saFabI (0.04 and 1.78 h, respectively). The pharmacokinetic (PK) parameters of these compounds in mice were calculated after the administration of a 40 or 100 mg kg−1 dose of each compound and the use of a single-compartmental PK model (Table 3). The pharmacodynamic activity of each compound was also evaluated after administration of a single dose (40 mg kg−1 or 100 mg kg−1) to mice infected with MRSA by collecting the infected thighs at different time points and plating on Mueller Hinton II agar containing 5% sheep blood. The free fraction of each drug at multiple time-points was then used as input for the PK/PD model to predict drug efficacy. Importantly, this approach was able to replicate the observed change in bacterial load following administration of both drugs (Table 4 and Fig. 5).
Table 3 Pharmacokinetic parameters for PT55 and PT119 in micea
|
In vivo
|
Volume of distribution (Vd), L kg−1 |
Clearance (CL), L h−1 kg−1 |
Half-life (T1/2), h |
Absorption rate (ka), h−1 |
AUC/MIC (h μg mL−1)/(μg mL−1) |
t
max (h) |
C
max (ng mL−1) |
In vitro data: PT55, free fraction of drug (fu) = 0.05, clog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 3.24; PT119, fu = 0.01, clog P = 3.24; PT119, fu = 0.01, clog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 5.44.
From Wang et al.19 P = 5.44.
From Wang et al.19
|
|
PT55 100 mg kg−1 |
33 ± 13 |
20 |
1.3 ± 0.7 |
3.5 ± 2.5 |
0.5 |
0.75 |
1200 ± 1100 |
|
PT119 100 mg kg−1 |
40 ± 12 |
7.4 |
3.8 ± 2.4 |
1.7 ± 1.0 |
9.4 |
1 |
760 ± 540 |
|
PT119 40 mg kg−1b |
96 |
10.8 |
6.2 |
0.77 |
3.5 |
4 |
280 |
Table 4
In vivo efficacy model fitting: input and output parameters for PT55 and PT119
| Parameter |
PT55
|
PT119
|
| Input value |
Output value |
Ratio |
Input value |
Output value |
Ratio |
|
The bacterial growth rate (kgrowth) is assumed to be ∼3-fold lower that that observed for in vitro growth conditions which most likely reflects nutrient limitation in vivo.12
The input value for pm/Ki has been chosen randomly within a large constraint range (1/100–100).
|
|
k
4 (min −1) |
0.42 |
0.42 |
1.0 |
0.009 |
0.022 |
2.4 |
|
λ (kgrowth)a (log10 h−1) |
0.37 |
0.73 |
2.0 |
0.37 |
0.66 |
1.8 |
|
ε (kkillmax) (log10 h−1) |
1.2 |
1.5 |
1.2 |
1.2 |
1.67 |
1.4 |
|
K
appi (μM) |
1.97 |
1.97 |
1.0 |
0.089 |
0.18 |
2.0 |
|
p
m/Ki (μM−1)b |
0.01 |
0.04 |
4.0 |
0.01 |
0.001 |
0.1 |
|
M(Km/[S]) |
1 |
0.2 |
0.2 |
1 |
0.1 |
0.1 |
|
R
2
|
0.99 |
0.98 |
 |
| | Fig. 5
In vivo efficacy and pharmacodynamic modeling of PT55 and PT119. In vivo S. aureus MRSA BAA 1762 CFU thigh tissue burden after a single sc dose of the vehicle (blue square) or (A) PT55 at 100 mg kg−1 (red square) or (B) PT119 at 40 mg kg−1 (red squares), or PT119 at 100 mg kg−1 (black squares). Solid lines represent the mechanistic PD simulations using the biochemical parameters from Table 2 and the PK parameters from Table 3. Note that the 40 mg kg−1 data set is an efficacy study and only one time point was collected. | |
Minimum and maximum target occupancy required for antibacterial activity
To estimate TOmin and TOmax we added a slope function to the PK/PD model in Mathematica. Subsequently, the parameters resulting from global fitting to the original PK/PD model were used as inputs for this new model. We analyzed three of the saFabI inhibitors described in this work and three paLpxC inhibitors reported previously (Table 5).12 The resulting relationship between target occupancy and antibacterial activity for these two systems has been plotted in Fig. 6 where it can be seen that lower values of paLpxC occupancy are required for activity (TOmin 29%, TOmax 48%) compared to saFabI (TOmin 39%, TOmax 76%). Thus paLpxC, is more vulnerable than saFabI consistent with the correlation between drug–target residence time and PAE in both systems (Fig. 3).
Table 5 Minimum (TOmin) and maximum (TOmax) values of target occupancy of the saFabI and paLpxC inhibitorsa
|
saFabI |
PT447
|
PT119
|
SKTS1
|
Average |
| 16x |
4x |
16x |
8x |
4x |
4x |
|
The output parameters from PK/PD modeling of the saFabI inhibitors PT119, PT447 and SKTS1 (Table 2) and of the paLpxC inhibitors 4–6,12 were used as input for the TO PK/PD model to fit the PAE phase for each compound at specific inhibitor concentrations. The average values of TOmin and TOmax for all the inhibitors of each target were used to generate the plot shown in Fig. 5.
|
| TOmin |
0.43 |
0.42 |
0.33 |
0.33 |
0.33 |
0.49 |
0.39 ± 0.07 |
| TOmax |
0.78 |
0.8 |
0.68 |
0.72 |
0.71 |
0.84 |
0.76 ± 0.06 |
|
paLpxC |
4
|
5
|
6
|
Average |
| 4x |
8x |
4x |
16x |
4x |
16x |
| TOmin |
0.20 |
0.17 |
0.27 |
0.36 |
0.38 |
0.36 |
0.29 ± 0.09 |
| TOmax |
0.50 |
0.48 |
0.50 |
0.43 |
0.48 |
0.48 |
0.48 ± 0.03 |
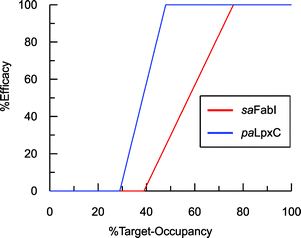 |
| | Fig. 6 Correlation between target-occupancy and efficacy for the saFabI and paLpxC inhibitors. | |
Discussion
The ultimate goal of target-based drug discovery is the prediction of in vivo efficacy from early in vitro parameters. In theory, a kinetics-driven approach works in tandem with the dynamic in vivo environment, circumventing the traditional requirement for a stable pharmacokinetic profile by relying on drug–target kinetics to attain prolonged efficacy.7,8,11 We believe that the kinetics-based approach to drug discovery provides several key advantages. First, the pharmacokinetic exposure requirement for efficacy is governed by multiple factors which can be easily measured using in vitro assays (tR, Ki), thus providing a more robust set of parameters for lead optimization than traditional methods that rely on thermodynamic measures alone. Second, there is a suggestion that prolonged target binding results in a higher barrier to resistance.7,21 This would also apply to efflux-mediated resistance, which is particularly relevant in difficult Gram-negative pathogens.4 Third, the kinetics-driven approach has the potential to improve therapeutic indices by maximizing target engagement using minimal compound exposure. Selectivity can be achieved between similarly potent on- and off-targets via modulation of the transition-state barrier.
To provide an experimental framework for evaluating the relevance of drug–target kinetics to in vivo drug activity, we previously described a mechanistic PK/PD model that coupled in vitro kinetic measurements of drug–target binding with drug PK to predict drug PD. This approach was able to model the in vitro PAE for a series of paLpxC inhibitors and to predict the activity of one of these inhibitors in a mouse model of P. aeruginosa infection.12 LpxC catalyzes the first committed step in the biosynthesis of lipopolysaccharide, an essential component of the Gram-negative bacterial cell wall. To evaluate the ability of this model to predict drug activity in other systems, we chose to study inhibitors of the FabI enzyme in the Gram-positive bacterium S. aureus. FabI is a component of the bacterial type II fatty acid biosynthesis pathway, and inhibitors of saFabI have a static effect on bacterial growth in contrast to the paLpxC inhibitors which are cidal. The paLpxC inhibitors show a correlation between residence time on the enzyme and the magnitude of the PAE observed following compound washout.12 Thus we first selected several saFabI inhibitors with a range of residence times, and determined the drug–target kinetic parameters and PAE values at 37 °C (Table 1). As observed in the LpxC system, the PAE resulting from the saFabI inhibitors increases as residence time increases, indicating that prolonged antibacterial activity at low drug concentration is coupled to the life-time of the drug–target complex. However, in Fig. 3 it can be seen that a steeper correlation exists between residence-time and PAE for the paLpxC inhibitors (slope 1.3) compared to that of saFabI inhibitors (slope 0.27), indicating that drug–target residence time in the LpxC system is translated more strongly to the time-dependent efficacy than in the FabI system.
The molecular factors that control the coupling between extended target engagement and time-dependent drug activity play a direct role in determining the sensitivity of a specific target to intervention. In this regard, the rate of protein synthesis will play a key role since the production of new target will dilute the impact of extended target engagement at low drug concentration,22 and Narberhaus et al. have reported that paLpxC is highly stable and thus turns over relatively slowly in P. aeruginosa.23 In addition, the LpxC inhibitors are cidal whereas the FabI inhibitors are static, and growth recovery after exposure to cidal drugs is expected to depend on both the rate of drug–target dissociation and the rate of recovery from downstream events resulting from target engagement. As a result, the PAE depends on both the duration of drug–target interaction as well as the time required for physiological recovery of the process(es) involved in the cidality response. In contrast, static agents are envisioned to induce a dormant growth state, and therefore recovery in this case is anticipated to be primarily dependent upon the rate of drug–target dissociation.
The slope of the tR PAE correlation is an indication of the vulnerability of each target to engagement – and thus LpxC is a more vulnerable target than FabI under the in vitro growth conditions employed for determining the PAE values. It is also possible to access a more quantitative assessment of target vulnerability by using the model fitting to estimate the minimum and maximum levels of engagement that provide the thresholds for the observed antibacterial activity. As demonstrated in the in vitro PAE measurements, higher concentrations of drug, expressed as fold-MIC, normally result in longer PAEs. This relationship exists because increased drug concentration leads to higher levels of target-occupancy, and that the time required for recovery from the effect of target engagement is longer at higher levels of occupancy. Although global fitting to the PK/PD model calculates the relative target-occupancies at each drug concentration, this process does not explicitly generate the target-occupancy at each drug concentration at the end of the exposure time, nor the minimum and maximum target-occupancy (TOmin and TOmax, respectively) that set the threshold limits for the correlation between target occupancy and efficacy which is hypothesized to be linear. This modeling exercise is analogous to the normal sigmoidal correlation that is assumed to exist between drug concentration and effect, where the central section of the sigmoidal curve, which has the largest slope, is approximately linear.24,25 All non-mechanistic traditional PK/PD models use the Hill equation to predict drug efficacy based on the drug concentration at the site of activity.24,26–28 According to this logic, a similar sigmoidal relationship is expected to exist between target-occupancy and drug efficacy.
Estimates of TOmin and TOmax were obtained for inhibitors of saFabI and paLpxC at individual compound concentrations (Table 5). The average values for the TOmin and TOmax values for all the inhibitors of each enzyme are plotted in Fig. 6 where it can be seen that values for both TOmin and TOmax are lower for paLpxC compared to saFabI, demonstrating that paLpxC is a more vulnerable target than saFabI. Classification of target vulnerability in the early stages of the drug development pipeline, based on drug–target binding kinetics and PAE measurements, is likely to reduce the rate of attrition in clinical trials and is also likely to provide valuable information for developing suitable dosing strategies. Specifically, for those drugs that interact with a non-vulnerable target or that have a short residence-time, high concentrations of drug will have to be maintained thus reducing the safety window. Conversely, drugs that target vulnerable targets and also have a long residence time, can be dosed less frequently leading to an increase in the therapeutic window. We note, however, that this vulnerability analysis has been conducted based on antibacterial activity measured in culture. While valuable, it is important to note that a similar correlation developed using in vivo efficacy data would be significantly more appropriate since growth conditions, including pressure from the immune system, can alter target vulnerability. In this regard the saFabI inhibitor PT119 has promising in vivo efficacy despite poor bioavailability and high protein binding (>99%), and the conclusion from the in vitro data analysis that suggest FabI is a low vulnerability target.
Conclusions
In this report, we have been able to model in vivo efficacy data for two S. aureus FabI inhibitors using the approach that was used previously for an inhibitor of LpxC.12 Given the high quality fits of the model to both the FabI and LpxC inhibitors, it is important to note the differences between these two compound series. In addition to targeting very different enzymes and metabolic pathways (FabI, fatty acid biosynthesis; LpxC, cell envelope), the compounds differ in their mode of inhibition (LpxC, competitive inhibition; FabI, uncompetitive inhibition), type of slow-onset inhibition (one-step for FabI and two-step for LpxC inhibition), static time–kill profile (FabI, bacteriostatic; LpxC, bactericidal) and organism that they target (S. aureus, Gram-positive; P. aeruginosa, Gram-negative). Collectively, these data sets provide a strong argument for the general applicability of the time-dependent pharmacodynamic model.
Experimental
Material and methods
Compounds.
The FabI inhibitors PT119, PT55 and PT447 (Fig. 1) were available from previous studies.18SKTS1 was purchased from COSMIC Discoveries (Hyderabad, India) after commissioned synthesis. Cell growth media (Mueller-Hinton broth/agar and Mueller-Hinton agar + 5% defibrinated sheep blood) and chemicals were obtained from commercial vendors.
Design of SKTS1.
The rational design of saFabI inhibitors with improved affinity and/or residence time was based on several structures of the target in complex with NADP+ and different diphenyl ether inhibitors.18,29 In order to learn which substituents on the diphenyl ether scaffold might improve enzyme-inhibitor interactions, hot-spot analyses of the saFabI binding pocket were performed using the program GRID (version 22, Molecular Discovery, Pinner, United Kingdom) and the knowledge-based DrugScoreX potentials (G. Neudert and G. Klebe, University of Marburg, Germany).30,31 These studies demonstrated that partially lipophilic moieties contacting the Ala97 carbonyl oxygen with a hydrogen-bond donor might be suitable to extend the diphenyl ether scaffold at the 4′-position. Additionally inspired by comparisons with the ligand CG400462 (ref. 32) (Fig. 1) and a crystal structure of Bacillus cereus FabI in complex with a related indole naphthyridinone compound (PDB-code: 3OJF), we postulated that introduction of a 6-hydroxypyridin-2(1H)-one group at the 4′-position might lead to favorable interactions with the active site (SKTS1). Together with additional candidates for synthesis, SKTS1 was docked into the saFabI binding pocket using our validated docking protocol as described in Schiebel et al.14,33 Briefly, FlexX (version 3.1.3, BioSolveIT, Sankt Augustin, Germany)34 was first used to dock SKTS1 into the available saFabI structures, followed by scoring with DrugScoreX. The putative binding mode and most suitable receptor (in the case of SKTS1: PDB-code 4D42) were then selected via visual inspection of the top-ranked binding poses. Finally, IC50 values were estimated using a FabI-specific empirical scoring function that builds on SFCscore descriptors and was developed specifically for this purpose.35SKTS1 was selected for synthesis due to its high predicted affinity, low log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value and reasonable interactions with the protein. Purity of SKTS1 was confirmed by HPLC and NMR. 1H NMR (400 MHz, acetone-d6) δ ppm 0.87–0.94 (m, 3H), 1.28–1.41 (m, 6H), 1.58–1.68 (m, 2H), 2.55–2.61 (m, 2H), 6.35 (dd, J = 13.87, 7.84 Hz, 2H), 6.73 (dd, J = 8.16, 2.01 Hz, 1H), 6.89–6.95 (m, 4H), 7.06 (d, J = 9.16 Hz, 2H), 7.64 (t, J = 7.91 Hz, 1H). ESI-MS (m/z): calculated for C23H24NO4 [M − H]− 378.2; found 378.1 [M − H]−. High resolution MS (m/z): calculated for C23H25NO4H [M + H]+ 380.1856; found 380.1855 [M + H]+; calculated for C23H24NO4 [M − H]− 378.1711; found 378.1717 [M − H]−.
P value and reasonable interactions with the protein. Purity of SKTS1 was confirmed by HPLC and NMR. 1H NMR (400 MHz, acetone-d6) δ ppm 0.87–0.94 (m, 3H), 1.28–1.41 (m, 6H), 1.58–1.68 (m, 2H), 2.55–2.61 (m, 2H), 6.35 (dd, J = 13.87, 7.84 Hz, 2H), 6.73 (dd, J = 8.16, 2.01 Hz, 1H), 6.89–6.95 (m, 4H), 7.06 (d, J = 9.16 Hz, 2H), 7.64 (t, J = 7.91 Hz, 1H). ESI-MS (m/z): calculated for C23H24NO4 [M − H]− 378.2; found 378.1 [M − H]−. High resolution MS (m/z): calculated for C23H25NO4H [M + H]+ 380.1856; found 380.1855 [M + H]+; calculated for C23H24NO4 [M − H]− 378.1711; found 378.1717 [M − H]−.
Bacterial strains.
The Staphylococcus aureus strains RN4220 and MRSA BAA 1762 were used for the microbiology experiments described below.
MIC measurements.
MIC values were determined with the microbroth dilution assay according to the Clinical and Laboratory Standards Institute methods for antimicrobial susceptibility tests for aerobically growing bacteria.36
Post-antibiotic effect (PAE).
A starter culture of the antibiotic-sensitive S. aureus strain RN4220 was grown to log phase (OD600 = 0.5; 108 CFU mL−1) and diluted 100-fold into cation-adjusted Mueller-Hinton (CAMH) media containing either drug or an equal volume of DMSO. Cultures were then shaken at 37 °C for 1 h after which both treated and untreated cells were diluted 1000-fold in fresh CAMH media and again incubated at 37 °C. Regrowth was monitored by removing aliquots (0.1 mL) of culture at hourly intervals and plating serial dilutions on Mueller-Hinton agar containing sheep blood. The number of CFUs was then counted following overnight incubation of plates at 37 °C. The post-antibiotic effect was calculated as the time in hours required for the number of compound-treated cells (CFUs) to increase 1 log10 above the count immediately after dilution minus the time in hours required for the number of cfu’s in the control culture to increase by 1 log10 above the count immediately after the dilution.20
Compound pharmacokinetics.
Pharmacokinetic (PK) studies were conducted in CD-1 mice via subcutaneous (sc) administration of the test agents in a vehicle of 40% H2O/40% EtOH/20% PEG-400. Plasma samples were collected from animals at eight distinct time points (5 min, 15 min, 30 min, 1 h, 2 h, 4 h, 8 h and 24 h post-injection). Three mice were used per time point.19 Plasma concentrations for each sample were determined by LC/MS/MS using a calibration curve, and the PK parameters were calculated with WinNonlin (Pharsight Corporation, Mountain View, CA, USA). All animals used in this study were maintained in accordance with the American Association for Accreditation of Laboratory Animal Care criteria. The experimental protocol for both the PK studies and the pharmacodynamics studies (below) was approved by the Institutional Animal Care and Use Committee (IACUC) at Stony Brook University. The animal studies were performed under the protocol “In vivo pharmacokinetic and pharmacodynamic evaluation of novel antibacterial agents” (IACUC #383230).
Plasma protein binding.
The free fraction of PT55 and PT119 in plasma was determined by rapid equilibrium dialysis using a Thermo Scientific™ Single-Use RED Plate. A solution of each compound was prepared in mouse plasma to match the Cmax determined in the PK study (1.82 μg mL−1 for PT55 and 0.79 μg mL−1 for PT119). Then 200 μL of each solution was transferred to the plasma chamber of the Thermo Scientific™ Single-Use RED Plate and PBS was placed in the corresponding buffer chamber. The plate was sealed and incubated at 37 °C on an orbital shaker at ∼250 rpm for 4 h. Subsequently, the amount of compound in the plasma and buffer samples was determined by LC/MS/MS and the free fraction was calculated by taking the ratio of compound concentration in the buffer and plasma chambers.
Pharmacodynamics.
For pharmacodynamic studies, six-week old, specific-pathogen free, male Swiss Webster mice weighing 27 g to 32 g (Taconic) were used. Mice were rendered neutropenic with IP doses of cyclophosphamide (150 mg kg−1, uid), 4 and 1 day before the infection challenge. Infection was induced by injection of S. aureus, MRSA (BAA 1762, 106 CFU in 50 μL of saline) into the left thigh muscle (IM). Infected neutropenic mice were given a single dose of vehicle or one of the antibacterial agents 1 h post infection by SC injection in the back of the neck. Mice were euthanized by CO2 inhalation at 24 h (efficacy), or at different time points post infection (in vivo PAE). Muscle tissue from the infected thighs was collected, weighed and homogenized in 2 mL of saline. Serial dilutions of each homogenized sample were plated on Mueller Hinton II agar containing 5% difibrinated sheep blood. The bacterial burden per gram of thigh muscle was calculated from the number of viable bacteria following overnight incubation at 37 °C on agar media.19
Mechanistic PK/PD model for saFabI inhibition.
To minimize complexity we have used the simple inhibition mechanism shown in Scheme 1 to derive the appropriate PK/PD model for inhibition of saFabI. paLpxC is a single substrate enzyme and inhibitors bind to paLpxC through a competitive two-step induced-fit mechanism.12 In contrast, saFabI catalyzes the NADPH-dependent reduction of an enoyl-ACP substrate through a ternary complex mechanism, and the saFabI inhibitors bind through a one-step mechanism to the E-NADP+ product complex formed during substrate turnover.18 Thus, the ES complex presented in Scheme 1 represents all saFabI enzyme-complexes capable of binding to the inhibitor. On this basis, we derived a mechanistic PK/PD model (eqn (1), (S14)†) that incorporates one-step uncompetitive inhibition (see ESI†).12| | 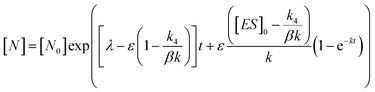 | (eqn 5 S14) |
Global fitting of in vitro and in vivo antibacterial activity.
In vitro cellular PAE data were obtained at a range of drug concentrations, from 1x MIC to 16x MIC. The PAE data at each drug concentration (three replicates), expressed as CFU mL−1 as a function of time, were then globally fit to eqn (5) using initial estimates of the parameters Kappi, k4, M (= Km/[S]), pm/Ki, kgrowth and kkillmax. The analysis takes the initial inhibitor concentration as an input value which is assumed to remain constant until the dilution step. The program returns fitted values for these parameters as well as an R2 value.
In vivo time dependent antibacterial activity was simulated using eqn (5) and using the fitted values from the cellular PAE analysis as input values. In this case the input drug concentration as function of time was obtained from the PK analysis.12
Estimation of TOmin and TOmax using a new mechanistic tool.
To provide estimates of the minimum (TOmin) and maximum (TOmax) target occupancy required for antibacterial activity, a slope factor (eqn (6)) was added to the PK/PD models used to analyze the inhibition of paLpxC (Walkup et al.)12 and saFabI (this work) (see ESI eqn (S15)†). TOmin is the minimum target occupancy required for activity below which no activity is observed, whereas TOmax is the maximum occupancy, above which no further increase in activity is observed. Between TOmin and TOmax a linear correlation is assumed to exist between occupancy and drug activity.| | 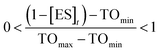 | (eqn 6 S16) |
The PAE data sets for the paLpxC inhibitors 4, 5 and 6 (Fig. 1),11 and the saFabI inhibitors PT119, PT447 and SKTS1, were globally fit to the respective PK/PD models using MATLAB. The resulting output values for the kinetic parameters, kgrowth, kkill and the permeability factor were used as inputs for the TO PK/PD model. The input values were fixed at their initial values and the change in CFU mL−1 as a function of time for the PAE phase was analyzed by the TO PK/PD model in Mathematica to find the best fit for each individual concentration of each compound enabling values of TOmin, TOmax and the initial value for [ES]t, at the beginning of the PAE phase, to be determined.
Conflict of interest
The authors declare no competing financial interest.
Acknowledgements
This research was funded by NIH/NIGMS (PJT GM102864), and, in part, by the Deutsche Forschungsgemeinschaft DFG (SFB630 to C.A.S and C.K.).
Notes and references
- D. Becker, M. Selbach, C. Rollenhagen, M. Ballmaier, T. F. Meyer, M. Mann and D. Bumann, Nature, 2006, 440, 303–307 CrossRef CAS PubMed.
- R. Guimera and L. A. Nunes Amaral, Nature, 2005, 433, 895–900 CrossRef CAS PubMed.
- M. N. Gwynn, A. Portnoy, S. F. Rittenhouse and D. J. Payne, Ann. N. Y. Acad. Sci., 2010, 1213, 5–19 CrossRef PubMed.
- D. J. Payne, M. N. Gwynn, D. J. Holmes and D. L. Pompliano, Nat. Rev. Drug Discovery, 2007, 6, 29–40 CrossRef CAS PubMed.
- C. Walsh, Nat. Rev. Microbiol., 2003, 1, 65–70 CrossRef CAS PubMed.
- R. A. Copeland, Future Med. Chem., 2011, 3, 1491–1501 CrossRef CAS PubMed.
- R. A. Copeland, D. L. Pompliano and T. D. Meek, Nat. Rev. Drug Discovery, 2006, 5, 730–739 CrossRef CAS PubMed.
- H. Lu and P. J. Tonge, Curr. Opin. Chem. Biol., 2010, 14, 467–474 CrossRef CAS PubMed.
- P. J. Tummino and R. A. Copeland, Biochemistry, 2008, 47, 8465 CrossRef CAS.
- R. Zhang and F. Monsma, Curr. Opin. Drug Discovery Dev., 2009, 12, 488–496 CAS.
- R. A. Copeland, Nat. Rev. Drug Discovery, 2016, 15, 87–95 CrossRef CAS PubMed.
- G. K. Walkup, Z. You, P. L. Ross, E. K. Allen, F. Daryaee, M. R. Hale, J. O'Donnell, D. E. Ehmann, V. J. Schuck, E. T. Buurman, A. L. Choy, L. Hajec, K. Murphy-Benenato, V. Marone, S. A. Patey, L. A. Grosser, M. Johnstone, S. G. Walker, P. J. Tonge and S. L. Fisher, Nat. Chem. Biol., 2015, 11, 416–423 CrossRef CAS PubMed.
- H. J. Li, C. T. Lai, P. Pan, W. Yu, N. Liu, G. R. Bommineni, M. Garcia-Diaz, C. Simmerling and P. J. Tonge, ACS Chem. Biol., 2014, 9, 986–993 CrossRef CAS PubMed.
- J. Schiebel, A. Chang, S. Shah, Y. Lu, L. Liu, P. Pan, M. W. Hirschbeck, M. Tareilus, S. Eltschkner, W. Yu, J. E. Cummings, S. E. Knudson, G. R. Bommineni, S. G. Walker, R. A. Slayden, C. A. Sotriffer, P. J. Tonge and C. Kisker, J. Biol. Chem., 2014, 289, 15987–16005 CrossRef CAS PubMed.
- P. Pan, S. E. Knudson, G. R. Bommineni, H. J. Li, C. T. Lai, N. Liu, M. Garcia-Diaz, C. Simmerling, S. S. Patil, R. A. Slayden and P. J. Tonge, ChemMedChem, 2014, 9, 776–791 CrossRef CAS PubMed.
- D. Czock and F. Keller, J. Pharmacokinet. Pharmacodyn., 2007, 34, 727–751 CrossRef CAS PubMed.
- J. Gabrielsson, O. Fjellstrom, J. Ulander, M. Rowley and P. H. Van Der Graaf, Curr. Top. Med. Chem., 2011, 11, 404–418 CrossRef CAS PubMed.
- A. Chang, J. Schiebel, W. Yu, G. R. Bommineni, P. Pan, M. V. Baxter, A. Khanna, C. A. Sotriffer, C. Kisker and P. J. Tonge, Biochemistry, 2013, 52, 4217–4228 CrossRef CAS PubMed.
- H. Wang, Y. Lu, L. Liu, S. W. Kim, J. M. Hooker, J. S. Fowler and P. J. Tonge, Eur. J. Med. Chem., 2014, 88, 66–73 CrossRef CAS PubMed.
- R. W. Bundtzen, A. U. Gerber, D. L. Cohn and W. A. Craig, Rev. Infect. Dis., 1981, 3, 28–37 CrossRef CAS PubMed.
- K. E. Hightower, R. Wang, F. Deanda, B. A. Johns, K. Weaver, Y. Shen, G. H. Tomberlin, H. L. Carter III, T. Broderick, S. Sigethy, T. Seki, M. Kobayashi and M. R. Underwood, Antimicrob. Agents Chemother., 2011, 55, 4552–4559 CrossRef CAS PubMed.
- A. Lewandowicz, P. C. Tyler, G. B. Evans, R. H. Furneaux and V. L. Schramm, J. Biol. Chem., 2003, 278, 31465–31468 CrossRef CAS PubMed.
- S. Langklotz, M. Schakermann and F. Narberhaus, J. Bacteriol., 2011, 193, 1090–1097 CrossRef CAS PubMed.
- R. C. Li, S. W. Lee and C. H. Kong, J. Antimicrob. Chemother., 1997, 40, 39–45 CrossRef CAS PubMed.
- L. Liu, J. Di Paolo, J. Barbosa, H. Rong, K. Reif and H. Wong, J. Pharmacol. Exp. Ther., 2011, 338, 154–163 CrossRef CAS PubMed.
- R. C. Li, Antimicrob. Agents Chemother., 1996, 40, 2306–2310 CAS.
- B. V. de Araujo, A. Diniz, E. C. Palma, C. Buffe and T. Dalla Costa, J. Antibiot., 2011, 64, 439–446 CrossRef PubMed.
- F. Del Bene, M. Germani, G. De Nicolao, P. Magni, C. E. Re, D. Ballinari and M. Rocchetti, Cancer Chemother. Pharmacol., 2009, 63, 827–836 CrossRef CAS PubMed.
- J. Schiebel, A. Chang, H. Lu, M. V. Baxter, P. J. Tonge and C. Kisker, Structure, 2012, 20, 802–813 CrossRef CAS PubMed.
- H. F. Velec, H. Gohlke and G. Klebe, J. Med. Chem., 2005, 48, 6296–6303 CrossRef CAS PubMed.
- P. J. Goodford, J. Med. Chem., 1985, 28, 849–857 CrossRef CAS PubMed.
- H. S. Park, Y. M. Yoon, S. J. Jung, I. N. Yun, C. M. Kim, J. M. Kim and J. H. Kwak, Int. J. Antimicrob. Agents, 2007, 30, 446–451 CrossRef CAS PubMed.
- J. Schiebel, A. Chang, B. Merget, G. R. Bommineni, W. Yu, L. A. Spagnuolo, M. V. Baxter, M. Tareilus, P. J. Tonge, C. Kisker and C. A. Sotriffer, Biochemistry, 2015, 54, 1943–1955 CrossRef CAS PubMed.
- M. Rarey, B. Kramer, T. Lengauer and G. Klebe, J. Mol. Biol., 1996, 261, 470–489 CrossRef CAS PubMed.
- C. A. Sotriffer, P. Sanschagrin, H. Matter and G. Klebe, Proteins, 2008, 73, 395–419 CrossRef CAS PubMed.
-
F. R. Cockerill, M. A. Wilkler, J. Alder, M. N. Dudley, G. M. Eliopoulos, M. J. Ferraro, D. J. Hardy, J. A. Hindler, J. B. Patel, M. Powell, J. M. Swenson, R. B. Thomson, M. M. Traczewski, J. D. Turnidge, M. P. Weinstein and B. L. Zimmer, Clinical and Laboratory Standards Institute (CLSI), 2012, p. 32 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Derivation of PK/PD models. See DOI: 10.1039/c6sc01000h |
| ‡ These authors contributed equally to this work. |
| § Present address: Institute of Pharmaceutical Chemistry, Philipps-Universität Marburg, Marbacher Weg 6, D-35032 Marburg, Germany. |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

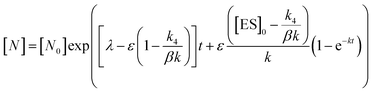

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 3.24; PT119, fu = 0.01, clog
P = 3.24; PT119, fu = 0.01, clog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 5.44.
b From Wang et al.19
P = 5.44.
b From Wang et al.19

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value and reasonable interactions with the protein. Purity of SKTS1 was confirmed by HPLC and NMR. 1H NMR (400 MHz, acetone-d6) δ ppm 0.87–0.94 (m, 3H), 1.28–1.41 (m, 6H), 1.58–1.68 (m, 2H), 2.55–2.61 (m, 2H), 6.35 (dd, J = 13.87, 7.84 Hz, 2H), 6.73 (dd, J = 8.16, 2.01 Hz, 1H), 6.89–6.95 (m, 4H), 7.06 (d, J = 9.16 Hz, 2H), 7.64 (t, J = 7.91 Hz, 1H). ESI-MS (m/z): calculated for C23H24NO4 [M − H]− 378.2; found 378.1 [M − H]−. High resolution MS (m/z): calculated for C23H25NO4H [M + H]+ 380.1856; found 380.1855 [M + H]+; calculated for C23H24NO4 [M − H]− 378.1711; found 378.1717 [M − H]−.
P value and reasonable interactions with the protein. Purity of SKTS1 was confirmed by HPLC and NMR. 1H NMR (400 MHz, acetone-d6) δ ppm 0.87–0.94 (m, 3H), 1.28–1.41 (m, 6H), 1.58–1.68 (m, 2H), 2.55–2.61 (m, 2H), 6.35 (dd, J = 13.87, 7.84 Hz, 2H), 6.73 (dd, J = 8.16, 2.01 Hz, 1H), 6.89–6.95 (m, 4H), 7.06 (d, J = 9.16 Hz, 2H), 7.64 (t, J = 7.91 Hz, 1H). ESI-MS (m/z): calculated for C23H24NO4 [M − H]− 378.2; found 378.1 [M − H]−. High resolution MS (m/z): calculated for C23H25NO4H [M + H]+ 380.1856; found 380.1855 [M + H]+; calculated for C23H24NO4 [M − H]− 378.1711; found 378.1717 [M − H]−.