Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
In situ small-angle X-ray scattering studies of sterically-stabilized diblock copolymer nanoparticles formed during polymerization-induced self-assembly in non-polar media†
Matthew J.
Derry
*a,
Lee A.
Fielding‡
 a,
Nicholas J.
Warren
a,
Charlotte J.
Mable
a,
Andrew J.
Smith
b,
Oleksandr O.
Mykhaylyk
*a and
Steven P.
Armes
*a
a,
Nicholas J.
Warren
a,
Charlotte J.
Mable
a,
Andrew J.
Smith
b,
Oleksandr O.
Mykhaylyk
*a and
Steven P.
Armes
*a
aDepartment of Chemistry, The University of Sheffield, Dainton Building, Brook Hill, Sheffield, South Yorkshire S3 7HF, UK. E-mail: s.p.armes@sheffield.ac.uk; o.mykhaylyk@sheffield.ac.uk; m.derry@sheffield.ac.uk
bDiamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot, Oxfordshire OX11 0DE, UK
First published on 18th April 2016
Abstract
Reversible addition–fragmentation chain transfer (RAFT) dispersion polymerization of benzyl methacrylate (BzMA) is utilized to prepare a series of poly(stearyl methacrylate)–poly(benzyl methacrylate) (PSMA–PBzMA) diblock copolymer nano-objects at 90 °C directly in mineral oil. Polymerization-induced self-assembly (PISA) occurs under these conditions, with the resulting nanoparticles exhibiting spherical, worm-like or vesicular morphologies when using a relatively short PSMA13 macromolecular chain transfer agent (macro-CTA), as confirmed by transmission electron microscopy (TEM) and small-angle X-ray scattering (SAXS) studies. Only kinetically-trapped spherical nanoparticles are obtained when using longer macro-CTAs (e.g. PSMA18 or PSMA31), with higher mean degrees of polymerization (DPs) for the PBzMA core-forming block simply producing progressively larger spheres. SAXS is used for the first time to monitor the various morphological transitions that occur in situ during the RAFT dispersion polymerization of BzMA when targeting either spheres or vesicles as the final copolymer morphology. This powerful characterization technique enables the evolution of particle diameter, mean aggregation number, number of copolymer chains per unit surface area (Sagg) and the distance between adjacent copolymer chains at the core–shell interface (dint) to be monitored as a function of monomer conversion for kinetically-trapped spheres. Moreover, the gradual evolution of copolymer morphology during PISA is confirmed unequivocally, with approximate ‘lifetimes’ assigned to the intermediate pure sphere and worm morphologies when targeting PSMA13–PBzMA150 vesicles. Within vesicle phase space, the membrane thickness (Tm) increases monotonically with PBzMA DP. Furthermore, a combination of dynamic light scattering (DLS), TEM and post mortem SAXS studies indicate that the lumen volume is reduced while the overall vesicle dimensions remain essentially constant. Thus the constrained vesicles grow inwards, as recently reported for an aqueous PISA formulation. This suggests a universal vesicle growth mechanism for all PISA formulations.
Introduction
It has been known for more than fifty years that diblock copolymers self-assemble to form well-defined nanoparticles when dispersed in a selective solvent for one of the blocks.1–4 For example, there is a vast range of literature describing the micellar self-assembly of polystyrene-based block copolymers in non-polar media: spherical morphologies are obtained in most cases,5–11 but examples of worm-like (or cylindrical)9–13 and vesicular11 morphologies have also been reported. More recently, metal-containing diblock copolymers have been utilized for the formation of cylindrical micelles in n-alkanes.14–16 The commercial potential for diblock copolymer nanoparticles dispersed in non-polar solvents was highlighted by Zheng et al., who reported that spherical nanoparticles of approximately 40 nm diameter offer enhanced boundary lubrication performance when dispersed in base oil.17 Moreover, self-assembled block copolymer nanoparticles have been shown to act as effective dispersants for diesel soot, which in turn minimizes wear and hence improves engine efficiency and long-term performance.18,19Recently, there has been considerable interest in the development of polymerization-induced self-assembly (PISA), particularly using reversible addition–fragmentation chain transfer (RAFT)20–22 dispersion polymerization.23–27 PISA provides an efficient and versatile route to diblock copolymer nanoparticles directly at high solids without the need for post-polymerization processing, making this approach amenable to scale-up.28 Most of the PISA literature has focused on optimizing aqueous26,29–40 or alcoholic41–53 formulations. In contrast, there are relatively few examples of suitable PISA formulations conducted in non-polar solvents such as n- or iso-alkanes.54–62 Charleux and co-workers evaluated dithiobenzoate and trithiocarbonate RAFT chain transfer agents (CTAs) for the polymerization of methyl acrylate in iso-dodecane.54,55 However, broad molecular weight distributions and low blocking efficiencies (i.e. inefficient re-initiation of the macro-CTA) were achieved, suggesting rather poor control. Fielding et al.57 reported reasonably well-controlled RAFT polymerizations for the synthesis of poly(lauryl methacrylate)–poly(benzyl methacrylate) (PLMA–PBzMA) diblock copolymer nanoparticles in n-heptane via PISA. In this case, either spheres, worms or vesicles could be obtained provided that the PLMA stabilizer block was sufficiently short to enable efficient sphere–sphere fusion to occur during PISA. The construction of a phase diagram facilitated reproducible targeting of the worm phase, with these highly anisotropic nanoparticles forming free-standing gels in n-heptane at 20 °C.57 Derry et al.28 recently revisited this RAFT dispersion polymerization formulation and developed a highly convenient ‘one-pot’ protocol for the synthesis of PLMA-PBzMA spheres in mineral oil at high solids. This work highlights the potential industrial relevance of such PISA formulations.
Small-angle X-ray scattering (SAXS) techniques have been employed to characterize nanoparticle morphologies obtained by various PISA formulations.38,48,58,62–70 In particular, thermally-induced micelle-to-unimer64,65 and worm-to-sphere58,64,65 transitions have been studied, as well as the evolution of vesicle dimensions on increasing the mean degree of polymerization (DP) of the core-forming block.67 Most notably for non-polar formulations, heating a free-standing PLMA–PBzMA worm gel in n-dodecane to 160 °C resulted in the formation of a free-flowing dispersion of spheres.58 This change in copolymer morphology was attributed to ingress of hot solvent leading to surface plasticization of the core-forming PBzMA block, as indicated by variable-temperature 1H NMR studies. Such solvation lowers the packing parameter30 and hence drives the worm-to-sphere transition, which was confirmed by transmission electron microscopy (TEM) studies.58 SAXS was particularly useful for characterizing this specific formulation, since the reduction in the mean worm contour length (Lw) could be monitored on heating from 20 °C (Lw ≈ 600 nm) to 90 °C (Lw ≈ 350 nm), with spherical nanoparticles of ∼17 nm diameter being observed at 160 °C. In related work, Lowe and co-workers used TEM and dynamic light scattering (DLS) to demonstrate a worm-to-sphere transition for PSMA–PPPMA nanoparticles in n-tetradecane59 and n-octane,61 with 1H NMR spectroscopy confirming a similar surface plasticization effect for the core-forming PPPMA block on heating to 95 °C. Recently, SAXS has been utilized to characterize microphase separation within block copolymer microparticles,71 with time-resolved studies being conducted during the synthesis of poly(methyl methacrylate)–poly(benzyl methacrylate) (PMMA–PBzMA) block copolymers via RAFT dispersion polymerization in supercritical CO2.72
Herein we report the PISA synthesis of poly(stearyl methacrylate)–poly(benzyl methacrylate) (PSMA–PBzMA) diblock copolymer nano-objects directly in mineral oil (see Scheme 1). We demonstrate that PSMA offers significant advantages over PLMA in terms of both blocking efficiency and control during the RAFT dispersion polymerization of BzMA. A detailed phase diagram is constructed for this new dispersion polymerization formulation using TEM, while DLS and SAXS are utilized to characterize the nanoparticle dispersions. In particular, we utilize a synchrotron source to conduct SAXS studies of the in situ evolution of the copolymer morphology during PISA. SAXS provides remarkably detailed insights regarding the sphere-to-worm and worm-to-vesicle transitions during this non-aqueous PISA formulation and also sheds new light on the mechanism of in situ vesicle growth.
Results and discussion
Synthesis of macro-CTAs
RAFT solution polymerization of stearyl methacrylate (SMA) was conducted in toluene at 70 °C using cumyl dithiobenzoate (CDB) as a CTA. Three PSMA macro-CTAs were characterized using 1H NMR spectroscopy and the mean degree of polymerization (DP) was calculated to be 13, 18 or 31 (see ESI, Table S1†). Each homopolymerization was quenched at 72% to 76% conversion in order to avoid monomer-starved conditions, thus ensuring the retention of RAFT end-groups.73,74 This is usually required for high blocking efficiencies and hence well-defined PSMA–PBzMA diblock copolymers. Each PSMA macro-CTA had a polydispersity (Mw/Mn) of ≤1.24, which is consistent with previous studies reporting well-controlled RAFT syntheses under these conditions.57 A typical kinetic study of the synthesis of a PSMA31 macro-CTA via RAFT solution polymerization was conducted (Fig. S3a†). After an initial induction period, first-order kinetics were observed prior to quenching at 72% conversion after 10 h. Gel permeation chromatography (GPC) analysis indicated a linear evolution of molecular weight with conversion (Fig. S3b†).PSMA18–PBzMAx and PSMA31–PBzMAx diblock copolymer spheres
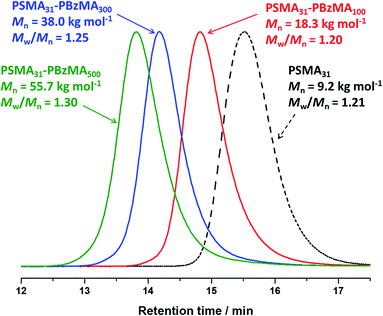
BzMA monomer was polymerized using two of the low polydispersity PSMA macro-CTAs (DP = 18, or 31) in turn via RAFT dispersion polymerization (see ESI, Table S2†). In all cases, ≥97% BzMA conversion was achieved within 5 h at 90 °C, as judged by 1H NMR spectroscopy. Only spherical morphologies were obtained when using a longer PSMA stabilizer block (DP = 18 or 31). This indicates that the upper limit PSMA DP for access to higher order morphologies (i.e. worms or vesicles) is relatively low for this PISA formulation in mineral oil. Longer PSMA stabilizer blocks confer enhanced steric stabilization, which prevents the efficient 1D fusion of multiple spheres and therefore the formation of anisotropic worms. Similar observations were reported for PLMA–PBzMA diblock copolymers prepared via RAFT dispersion polymerization of BzMA in n-heptane,57n-dodecane58 and mineral oil.28 In these earlier studies, the upper limit PLMA stabilizer DP which allowed access to higher order morphologies was 16–18. Given the relative molecular volumes of the LMA (C12 side-chain) and SMA (C18 side-chain) repeat units, it is reasonable that using PSMA18 only allows access to spheres. Clearly, PSMA13 has a comparable molecular volume to that of PLMA18, which is why using the former macro-CTA allows access to worms and vesicles, as well as spheres.Compared to related RAFT dispersion polymerization syntheses conducted in non-polar media,54–58 the present PSMA–PBzMA formulation enables relatively narrow molecular weight distributions to be obtained even when targeting PBzMA DPs as high as 500, which corresponds to an experimentally determined Mn of ∼56 kg mol−1 (Fig. 1). GPC analysis of PSMA31–PBzMAx (x ≤ 500) diblock copolymers in THF eluent indicates Mw/Mn values ranging between 1.19 and 1.30, which suggests good RAFT control. Also, the unimodal nature of these curves and the clear shift from the original PSMA31 macro-CTA indicates relatively high blocking efficiencies. In contrast, relatively broad molecular weight distributions (Mw/Mn > 1.50) were reported by Fielding et al. when targeting x values above 300 for PLMA37–PBzMAx diblock copolymers via closely-related PISA syntheses conducted in n-heptane.57 However, it is not yet understood why simply using a PSMA macro-CTA instead of a PLMA macro-CTA leads to significantly better pseudo-living character during the dispersion polymerization of BzMA.
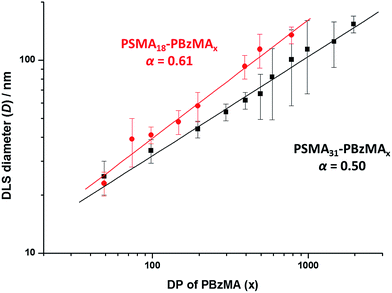
A series of spherical nanoparticles with tunable diameters was conveniently prepared in mineral oil at 20% w/w solids simply by varying the target DP of the core-forming PBzMA block when using a PSMA macro-CTA with a sufficiently high DP. For example, PSMA18–PBzMAx spheres ranging from 23 to 135 nm diameter (as judged by DLS) were obtained when targeting x values of 50 to 800. Similarly, well-defined PSMA31–PBzMAx spheres of 25 to 154 nm diameter were produced for x = 50 to 2000. The mean sphere diameter, D, is related to the mean DP of the core-forming block, x, by a scaling exponent, α, as indicated by the equation D ∼ kxα where k is a constant.75,76Fig. 2 shows double-logarithmic plots of D, as judged by DLS, against x for each series of PSMA18–PBzMAx and PSMA31–PBzMAx spheres. A clear relationship is observed in each case, which enables the corresponding scaling exponent (α) to be determined. This parameter provides important information regarding the behavior of the PBzMA core-forming chains. For the PSMA31–PBzMAx series we find that α = 0.50, which corresponds to unperturbed PBzMA chains.75,76,80 According to the literature, such low α values suggest weak segregation (and minimal solvation).75,76,80 On the other hand, we find that α = 0.61 for the PSMA18–PBzMAx series, indicating that the PBzMA chains are more stretched and may have a finite degree of solvation. This means that, for a given PBzMAx block (where x > 50), larger spheres are always obtained when using the shorter PSMA18 stabilizer block. For example, DLS studies indicate that spheres obtained when targeting a core-forming PBzMA DP of 400 are larger when using the PSMA18 macro-CTA (93 nm) compared to the PSMA31 macro-CTA (62 nm).
In situ SAXS studies of the PISA synthesis of PSMA31–PBzMA2000 spheres
A synchrotron X-ray source was used to acquire SAXS patterns in situ during the PISA synthesis of PSMA31–PBzMA2000 diblock copolymer spheres at 90 °C in mineral oil at 10% w/w solids. The sample cell was a 2 mm glass capillary and scattering patterns were recorded every 2 min for 120 min (Fig. 3). The onset of micellization occurs when the growing PBzMA chains become sufficiently long to induce nucleation.26,27 This occurred within around 2 min of the polymerization, as indicated by the presence of a local minimum at q ∼ 0.23 nm−1 (where q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ is the length of the scattering vector, λ is the wavelength of X-ray radiation and θ is one-half of the scattering angle). The characteristic length scale corresponding to this feature is the mean core radius of the spherical diblock copolymer nanoparticles (Rs), which was observed to be 15 nm. Since the PISA synthesis was conducted at 10% w/w solids, it was necessary to incorporate an appropriate structure factor81 into a well-known spherical micelle model77–79 in order to obtain satisfactory fits to the SAXS patterns.
θ/λ is the length of the scattering vector, λ is the wavelength of X-ray radiation and θ is one-half of the scattering angle). The characteristic length scale corresponding to this feature is the mean core radius of the spherical diblock copolymer nanoparticles (Rs), which was observed to be 15 nm. Since the PISA synthesis was conducted at 10% w/w solids, it was necessary to incorporate an appropriate structure factor81 into a well-known spherical micelle model77–79 in order to obtain satisfactory fits to the SAXS patterns.
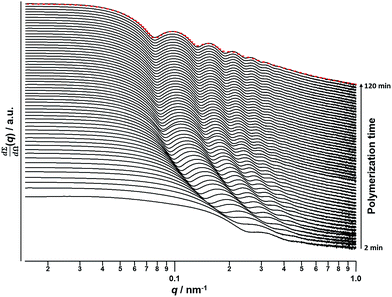 | ||
| Fig. 3 SAXS patterns obtained in situ during the PISA synthesis of PSMA31–PBzMA2000 diblock copolymer spheres at 90 °C in mineral oil at 10% w/w solids. Red dashes indicate the data fit to the final SAXS pattern recorded after 120 min using a spherical micelle model.77–79 | ||
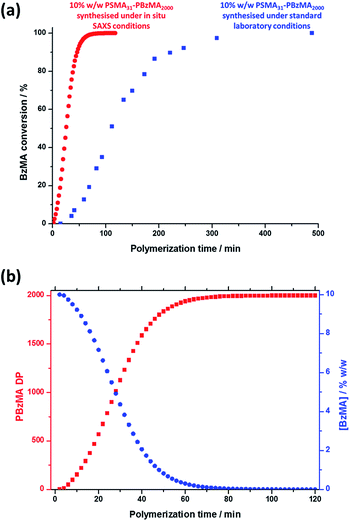
Monitoring this minimum as it shifts to lower q (larger radii) as the BzMA polymerization proceeded provides useful information regarding the kinetics of nanoparticle growth. However, in order to fit the SAXS data shown in Fig. 3 to a spherical micelle model,77–79 the instantaneous BzMA conversion is required, since this in turn determines the mean DP and hence the molecular volume occupied by a single growing core-forming (PBzMA) block within the sphere is given by Vs = (DPPBzMAMn,BzMA)/(NAρ), where Mn,BzMA corresponds to the molecular weight of the one BzMA unit within the PBzMA block and ρ is the density of PBzMA. No further change in the SAXS patterns shown in Fig. 3 was taken to signify the end of the polymerization. Unfortunately, the BzMA polymerization was complete within 120 min during the in situ SAXS studies, whereas around 500 min was required for the same formulation in a typical laboratory-scale synthesis (∼20 mL reaction volume) conducted using an oil bath and stirrer hot plate. A possible reason for this significant increase in polymerization rate could be additional radical species generated by the intense X-ray photon flux provided by the synchrotron source.82,83 The ∼125 μL reaction volume of the capillary used for the SAXS studies precludes sampling of the polymerizing reaction mixture. Instead, intermediate BzMA conversions were calculated by renormalizing the kinetic data set obtained for the laboratory-scale synthesis. More specifically, a sigmoid function was used to calculate intermediate BzMA conversions (see Fig. 4a and ESI†) since this best described the conversion vs. time curve.84 The resulting BzMA conversions were subsequently used to calculate the instantaneous PBzMA DP during the PISA synthesis (see Fig. 4b, red data). It must be noted that due to the nature of the renormalization using the sigmoid function, the predicted kinetic data for the in situ SAXS measurements are a smooth representation of the somewhat scattered experimental data obtained under standard laboratory conditions.
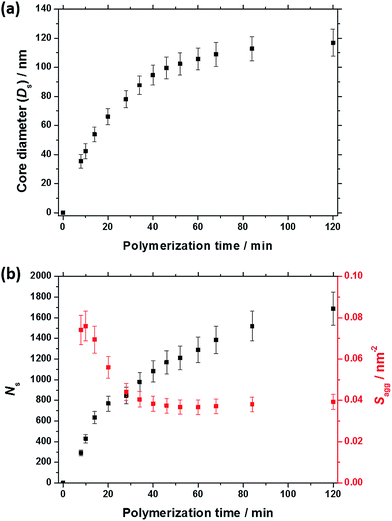
As expected, the spherical core diameter of the growing nanoparticles (Ds) increases monotonically with polymerization time (see Fig. 5a and Table 1). At the end of the BzMA polymerization, at least six minima are visible in the final scattering pattern (120 min, Fig. 3), indicating a relatively narrow size distribution for the resulting PSMA31–PBzMA2000 spheres. Data fitting for various SAXS patterns during the RAFT dispersion polymerization of PSMA31–PBzMA2000 spheres indicated essentially no solvent associated with the core-forming PBzMA block, which is consistent with the PSMA31–PBzMAx data set shown in Fig. 2. Moreover, 1H NMR studies of the latter laboratory-scale syntheses (data not shown) confirmed that the volume fraction of solvent within the core domain (xsol) is essentially zero. Thus, when fitting SAXS patterns recorded during the polymerization, the mean number of copolymer chains per sphere (Ns) was calculated based solely on the volume fraction of BzMA monomer within the core domain (φBzMA), Rs and Vs as shown below.
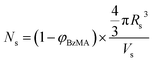 | (1) |
| Time/min | BzMA conversion/% | PBzMA DP | V s/nm3 | D s/nm | φ BzMA | N s | S agg/nm−2 | d int/nm |
|---|---|---|---|---|---|---|---|---|
| 8 | 5.0 | 99 | 25 ± 2 | 35 ± 5 | 0.691 | 292 ± 28 | 0.074 ± 0.007 | 3.7 ± 0.4 |
| 10 | 7.8 | 155 | 39 ± 4 | 42 ± 5 | 0.586 | 429 ± 41 | 0.076 ± 0.007 | 3.6 ± 0.3 |
| 14 | 14.7 | 294 | 73 ± 7 | 54 ± 5 | 0.437 | 633 ± 60 | 0.069 ± 0.007 | 3.8 ± 0.4 |
| 20 | 28.4 | 569 | 141 ± 13 | 66 ± 6 | 0.282 | 769 ± 73 | 0.056 ± 0.005 | 4.2 ± 0.4 |
| 28 | 50.8 | 1015 | 252 ± 24 | 78 ± 6 | 0.147 | 845 ± 80 | 0.044 ± 0.004 | 4.8 ± 0.5 |
| 34 | 66.8 | 1335 | 331 ± 32 | 88 ± 6 | 0.083 | 978 ± 93 | 0.040 ± 0.004 | 5.0 ± 0.5 |
| 40 | 79.3 | 1587 | 394 ± 37 | 95 ± 7 | 0.042 | 1082 ± 103 | 0.038 ± 0.004 | 5.1 ± 0.5 |
| 46 | 87.9 | 1758 | 436 ± 41 | 100 ± 8 | 0.018 | 1168 ± 111 | 0.037 ± 0.004 | 5.2 ± 0.5 |
| 52 | 93.2 | 1864 | 463 ± 44 | 102 ± 8 | 0.004 | 1210 ± 115 | 0.037 ± 0.003 | 5.2 ± 0.5 |
| 60 | 97.0 | 1939 | 481 ± 46 | 106 ± 8 | 0.000 | 1289 ± 122 | 0.037 ± 0.003 | 5.2 ± 0.5 |
| 68 | 98.7 | 1973 | 490 ± 47 | 109 ± 8 | 0.000 | 1385 ± 132 | 0.037 ± 0.004 | 5.2 ± 0.5 |
| 84 | 99.8 | 1995 | 495 ± 47 | 113 ± 8 | 0.000 | 1519 ± 144 | 0.038 ± 0.004 | 5.1 ± 0.5 |
| 120 | 100 | 2000 | 496 ± 47 | 117 ± 9 | 0.000 | 1688 ± 160 | 0.039 ± 0.004 | 5.0 ± 0.5 |
Values for φBzMA were estimated via centrifugation of selected dispersions of PSMA31–PBzMAx spheres (obtained at full BzMA conversion via laboratory-scale syntheses) to which varying amounts of BzMA monomer and additional mineral oil had been added in order to replicate specific intermediate BzMA conversions during the synthesis of PSMA31–PBzMA2000 spheres in the in situ SAXS studies. Firstly, the BzMA–swollen PSMA31–PBzMAx spheres were heated at 90 °C for 1 h and then centrifuged at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 1 to 10 h at 20 °C to ensure complete sedimentation of the spheres. Since centrifugation was not possible at 90 °C, it is assumed that the amount of BzMA monomer within the PBzMA cores is the same at 20 °C and 90 °C. Each supernatant was then analyzed for its BzMA content against an internal standard (triethoxymethylsilane) via1H NMR spectroscopy (see ESI† for further details). The experimentally-determined values of φBzMA at particular BzMA conversions were then fitted to a logarithmic decay function (R2 > 0.95), which was subsequently utilized to calculate φBzMA values for all entries in Table 1via interpolation. Eqn (1) was then used to calculate the corresponding Ns values. According to the SAXS fittings, the uncertainty in Rs is small, hence the error in Ns is dominated by that associated with Vs, which is in turn dictated by the molecular weight distribution (MWD) of the growing core-forming PBzMA block. Given that the PSMA31 stabilizer block is relatively short, this MWD is approximately the same as that of the diblock copolymer. However, since the in situ SAXS experiments were conducted on such a small scale, it was not feasible to determine the copolymer MWD at intermediate times during the polymerization. Therefore, the maximum error in Vs at any given time during the polymerization was estimated from the final MWD obtained for the laboratory-scale synthesis of the equivalent PSMA31–PBzMA2000 spheres. The unimodal MWD determined by THF GPC was fitted to a Gaussian model to determine its standard deviation (see ESI†), which was found to be approximately 9.5%. Since the PISA synthesis conducted under in situ SAXS conditions proceeded much faster than standard laboratory conditions, it is possible that a broader MWD is observed for the copolymers synthesized in the former case. However, several recent reports of PISA syntheses conducted in non-polar solvents indicate that there is no correlation between copolymer MWD and the final copolymer morphology – even highly polydisperse copolymer chains (Mw/Mn > 2.0) can self-assemble to give well-defined nano-objects.85,86
000 rpm for 1 to 10 h at 20 °C to ensure complete sedimentation of the spheres. Since centrifugation was not possible at 90 °C, it is assumed that the amount of BzMA monomer within the PBzMA cores is the same at 20 °C and 90 °C. Each supernatant was then analyzed for its BzMA content against an internal standard (triethoxymethylsilane) via1H NMR spectroscopy (see ESI† for further details). The experimentally-determined values of φBzMA at particular BzMA conversions were then fitted to a logarithmic decay function (R2 > 0.95), which was subsequently utilized to calculate φBzMA values for all entries in Table 1via interpolation. Eqn (1) was then used to calculate the corresponding Ns values. According to the SAXS fittings, the uncertainty in Rs is small, hence the error in Ns is dominated by that associated with Vs, which is in turn dictated by the molecular weight distribution (MWD) of the growing core-forming PBzMA block. Given that the PSMA31 stabilizer block is relatively short, this MWD is approximately the same as that of the diblock copolymer. However, since the in situ SAXS experiments were conducted on such a small scale, it was not feasible to determine the copolymer MWD at intermediate times during the polymerization. Therefore, the maximum error in Vs at any given time during the polymerization was estimated from the final MWD obtained for the laboratory-scale synthesis of the equivalent PSMA31–PBzMA2000 spheres. The unimodal MWD determined by THF GPC was fitted to a Gaussian model to determine its standard deviation (see ESI†), which was found to be approximately 9.5%. Since the PISA synthesis conducted under in situ SAXS conditions proceeded much faster than standard laboratory conditions, it is possible that a broader MWD is observed for the copolymers synthesized in the former case. However, several recent reports of PISA syntheses conducted in non-polar solvents indicate that there is no correlation between copolymer MWD and the final copolymer morphology – even highly polydisperse copolymer chains (Mw/Mn > 2.0) can self-assemble to give well-defined nano-objects.85,86
N s gradually increased with polymerization time, as indicated in Fig. 5b (black data). This is not unexpected in view of recent observations made by both Jones et al.70 and Zhang and co-workers87 for non-aqueous PISA formulations. Nevertheless, it provides the first direct experimental evidence that the mean number of copolymer chains per nanoparticle increases during PISA syntheses. Likely mechanisms are either efficient fusion between monomer-swollen spheres and/or continuous aggregation of molecularly-dissolved copolymer chains.70 The latter seems more likely to occur during the early stages of the polymerization (just after nucleation), rather than in the latter stages. The average number of copolymer chains per unit surface area (Sagg) during the polymerization was calculated using eqn (2) below.
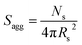 | (2) |
Interestingly, Sagg values (Fig. 5b, red data) decrease from 0.075 nm−2 to a limiting value of approximately 0.04 nm−2 after around 40 min, suggesting an optimum surface packing density of copolymer chains within the sterically-stabilized PSMA31–PBzMA2000 spherical nanoparticles.70
The average distance between adjacent chains at the core–shell interface (dint) was calculated using eqn (3) below.76
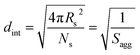 | (3) |
For small spheres (i.e., Ds = 35.4 nm), dint was calculated to be 3.67 nm after 8 min (or 5.0% BzMA conversion, which corresponds to PSMA31–PBzMA99). This is comparable to that reported by Förster et al.76 for similar-sized polystyrene–poly(4-vinyl pyridine) block copolymer micelles, for which dint was found to be 3.20 nm. Subsequently, dint increased up to 5.04 nm at full conversion (i.e., PSMA31–PBzMA2000; Ds = 116.9 nm), indicating that copolymer chains with longer core-forming PBzMA blocks occupy a larger surface area at the core–shell interface.
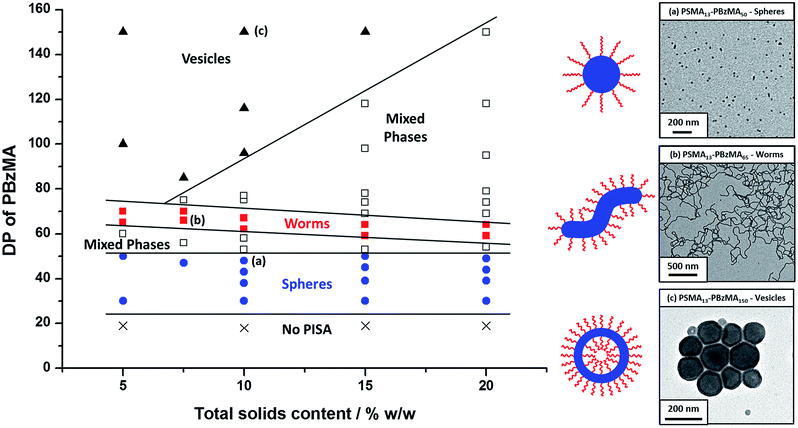
PSMA13–PBzMAx block copolymer syntheses and corresponding phase diagram
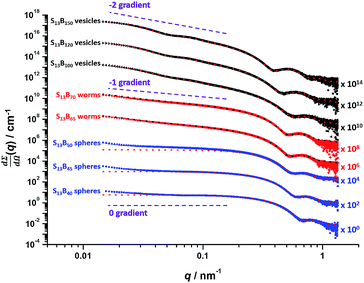
Utilizing a shorter PSMA13 macro-CTA to target PBzMA core-forming block DPs of 20 to 150 at various copolymer concentrations enabled access to spherical, worm-like and vesicular morphologies at relatively low copolymer concentrations (≥5% w/w solids). In contrast, well-defined vesicular morphologies were only obtained at copolymer concentrations of at least 12.5% w/w solids for the PISA synthesis of PLMA–PBzMA diblock copolymer nanoparticles, whereas somewhat higher copolymer concentrations (≥17.5% w/w solids) were required to access a pure worm phase.28,57,58 A detailed phase diagram was constructed for the present PSMA13–PBzMAx formulation, with diblock copolymer morphologies assigned via post mortem TEM studies (see Fig. 6). Such phase diagrams are essential to ensure reproducible targeting of the desired copolymer morphology. Thus spheres were obtained at all copolymer concentrations investigated (5–20% w/w) when targeting PBzMA block DPs of 30 to 50. As reported for related PISA formulations,26,28,34,45,46,57,58,62 the worm phase space is relatively narrow and is bounded by mixed phase regions. As expected, pure vesicles were obtained by targeting asymmetric PSMA13–PBzMAx diblock copolymers (i.e. x > 80). However, for PBzMA DPs of up to 150 this phase appears to be confined to copolymer concentrations of 5–15% w/w solids, with mixed phases being obtained at 20% w/w solids. It is perhaps worth emphasizing that the ability to prepare vesicles at copolymer concentrations as low as 5% w/w solids is an important advantage for in situ SAXS studies (see later). This is because lower copolymer concentrations minimize structural effects arising from inter-particle interactions.Post mortem SAXS patterns recorded for 1.0% w/w dispersions of eight PSMA13–PBzMAx diblock copolymer nano-objects (originally prepared at 10% w/w solids; see phase diagram in Fig. 6) are depicted in Fig. 7. Each of the three examples of spherical nanoparticles exhibit an approximate zero gradient at low q, as expected.88 Some deviations from zero gradient observed at low q values could be associated with an aggregation of the spherical micelles. The local minimum observed for each scattering curve at q ≈ 0.5–0.7 nm−1 gradually shifted to lower q on increasing the mean PBzMA DP from 40 to 50, indicating a progressive increase in the sphere dimensions. This is consistent with previously reported PISA syntheses conducted using a fixed stabilizer block DP, where increasing the core-forming block DP led to larger spherical nanoparticles.33,57 According to theory, rigid rods should exhibit a limiting gradient of −1 at low q.88 However, TEM studies (see Fig. 6b) suggest that these particular worms exhibit appreciable flexibility. Nevertheless, the SAXS patterns recorded for PSMA13–PBzMA65 and PSMA13–PBzMA70 worms in Fig. 7 do indeed exhibit gradients of approximately −1 at low q. For these two copolymer dispersions, the local minimum observed at q ≈ 0.5–0.6 nm−1 is associated with the mean worm width. Vesicular morphologies were also confirmed for PSMA13–PBzMA100–150, since SAXS patterns indicated a slope of approximately −2 at low q for these three dispersions. For such hollow spheres, there are two characteristic local minima. Firstly, the minimum observed at q ≈ 0.4–0.6 nm−1 is associated with the vesicle membrane thickness (Tm), which increases monotonically as higher PBzMA DPs are targeted. Secondly, the local minimum observed at q ≈ 0.04–0.05 nm−1 is characteristic of the overall vesicle dimensions. Interestingly, this parameter remains relatively constant (109 ± 5 nm) for the series of three PSMA13–PBzMA100–150 vesicles prepared at 10% w/w solids shown in Fig. 6.
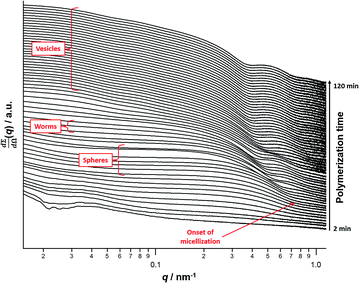
In situ SAXS studies of the PISA synthesis of PSMA13–PBzMA150 vesicles
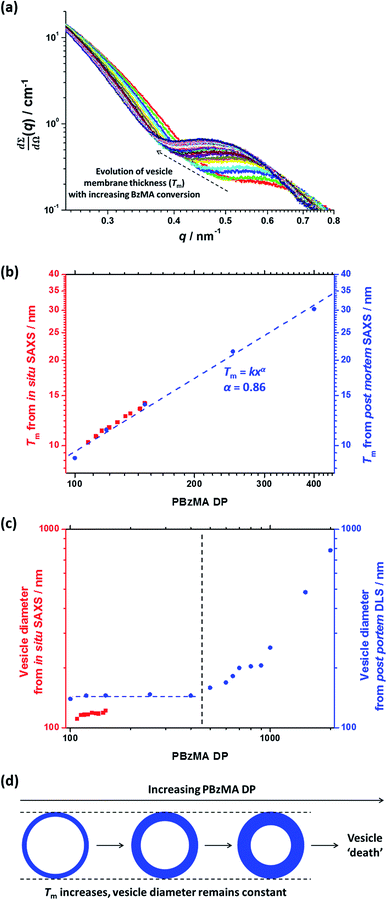
A series of in situ SAXS patterns were also recorded when targeting PSMA13–PBzMA150 vesicles at 10% w/w solids in mineral oil. This core-forming block DP was chosen to guarantee access vesicle space (see Fig. 6) while maximizing the time scales for the existence of the intermediate sphere and worm phases. Inspecting Fig. 8, this strategy was clearly successful since the full range of copolymer morphologies is observed, from initially soluble copolymer chains through to the final vesicular morphology via intermediate spherical and worm-like nanoparticles.35 Again, the polymerization kinetics required renormalization prior to detailed data analyses (see Fig. S4†). In this case, a significantly longer polymerization time (and hence a somewhat higher BzMA conversion) is required for the onset of micellization. Inspecting Fig. 6, it is clear that the critical DP for the core-forming PBzMA block required to induce nucleation is around 30. This is because PSMA13–PBzMA20 diblock copolymers do not self-assemble in mineral oil at 90 °C, whereas PSMA13–PBzMA30 diblock copolymer spheres are observed under these conditions. Thus approximately 20% BzMA conversion is required to trigger in situ self-assembly for this particular PSMA13–PBzMA150 PISA formulation. In contrast, when targeting PSMA31–PBzMA2000 diblock copolymer spheres (Fig. 3), a BzMA conversion of only ∼1.5% is required to achieve the same critical PBzMA DP for micellar nucleation. Spherical nanoparticles are formed just after the onset of micellization, as confirmed by the approximately zero gradient at low q.88 However, just 10 min after nucleation this low q gradient tends towards −1, indicating that the nascent spherical nanoparticles undergo multiple 1D fusion events leading to the formation of highly anisotropic worms. This second morphology is relatively short-lived (∼6 min), which is consistent with the narrow worm phase space observed in the phase diagram (Fig. 6). A mixed phase of worms and vesicles is apparent from 46 to 56 min. This corresponds to a PBzMA DP of 76 to 104 and is consistent with the mixed phase region observed in Fig. 6. Informed by these in situ studies, multiple aliquots were taken from the same polymerization conducted under standard laboratory conditions, with particular attention being paid to the above DP interval. TEM analyses confirmed that vesicles are formed from worms via octopi (see Fig. S7b†) and jellyfish (see Fig. S5c and S5d†) intermediates. Such transient structures were also reported by Blanazs and co-workers35 for an aqueous PISA formulation when targeting vesicles as the final copolymer morphology. This provides the first experimental evidence of octopi and jellyfish intermediates for a non-polar PISA formulation and suggests that the worm-to-vesicle morphology transition via such structures is likely to be universal for all vesicles prepared via PISA syntheses. Finally, well-defined vesicles are present as a pure phase in the latter stages of the polymerization (∼58–120 min), as indicated by the slope of −2 at low q.For this particular in situ SAXS study (see Fig. 8), the experimental protocol used to renormalize the polymerization kinetics can be validated by comparing the PBzMA DP ranges within which pure spheres, worms and vesicles are observed to those indicated within the phase diagram shown in Fig. 6 (see Table 2). The generally good agreement between the upper and lower DPs at which each pure morphology is observed provides strong evidence that the analytical approach employed to renormalize the kinetic data is indeed valid. It is also worth emphasizing that the relatively well-defined phase boundaries shown in Fig. 6 enable a particularly robust comparison. SAXS patterns assigned to pure vesicles exhibit two local minima: one is a rather subtle feature at q ≈ 0.04–0.07 nm−1 representing the overall vesicle dimensions and the other is a more pronounced feature at q ≈ 0.3–0.7 nm−1 that is associated with the vesicle membrane thickness (Tm).67Fig. 9a shows selected SAXS patterns taken from Fig. 8 over a much narrower q range in order to better illustrate the evolution in Tm at q ≈ 0.3–0.7 nm−1. A pure vesicle phase is observed after 58 min, with subsequent data fits indicating that Tm increases monotonically from 10.3 nm to 14.1 nm for PBzMA DPs ranging from 108 to 150 (see Fig. 9b, red data and Table 3). There is also an apparent increase in the outer core radius (Rout) with increasing PBzMA DP (see Table 3) but this rather modest difference appears to be within the relatively large error associated with these data.
| Pure copolymer morphology | PBzMA DP indicated by phase diagram | PBzMA DP indicated by in situ SAXS studies | |
|---|---|---|---|
| Spheres | Lower limit boundary | 25 ± 5 | 29 ± 3 |
| Spheres | Upper limit boundary | 51 ± 1 | 48 ± 4 |
| Worms | Lower limit boundary | 60 ± 1 | 59 ± 5 |
| Worms | Upper limit boundary | 70 ± 1 | 70 ± 6 |
| Vesicles | Lower limit boundary | 93 ± 2 | 108 ± 4 |
| Time/min | BzMA conversion/% | PBzMA DP | V m/nm3 | R out/nm | T m/nm | R in/nm |
|---|---|---|---|---|---|---|
| 58 | 72.3 | 108 | 27 ± 0.9 | 53 ± 18 | 10 ± 1.6 | 43 ± 18 |
| 60 | 75.4 | 113 | 28 ± 1.0 | 56 ± 19 | 11 ± 1.6 | 45 ± 19 |
| 62 | 78.2 | 117 | 29 ± 1.0 | 56 ± 19 | 11 ± 1.6 | 45 ± 19 |
| 64 | 80.7 | 122 | 30 ± 1.0 | 56 ± 19 | 12 ± 1.6 | 44 ± 19 |
| 68 | 85.2 | 128 | 32 ± 1.1 | 57 ± 20 | 12 ± 1.8 | 45 ± 20 |
| 72 | 88.9 | 134 | 33 ± 1.1 | 57 ± 20 | 13 ± 1.8 | 44 ± 20 |
| 76 | 91.8 | 138 | 34 ± 1.2 | 57 ± 19 | 13 ± 1.9 | 44 ± 19 |
| 88 | 97.1 | 146 | 36 ± 1.2 | 57 ± 20 | 14 ± 2.0 | 44 ± 20 |
| 120 | 100 | 150 | 37 ± 1.3 | 59 ± 20 | 14 ± 2.2 | 45 ± 21 |
Precise knowledge of the dimensions of the growing vesicles is important, because in principle this enables the vesicle growth mechanism to be deduced. For example, Warren et al.67 reported that the overall diameter of poly(glycerol monomethacrylate)–poly(2-hydroxypropyl methacrylate) (PGMA–PHPMA) vesicles prepared via RAFT aqueous dispersion polymerization remained constant while Tm increased when targeting higher PHPMA DPs. This indicates that the constrained vesicles grow inwards, with the thickening membrane leading to a reduction in the vesicle lumen volume. In order to elucidate the growth mechanism for the PSMA13–PBzMAx vesicles described in this work, much higher PBzMA DPs must be targeted. Consequently, PSMA13–PBzMAx vesicles with PBzMA DPs up to 2000 (prepared at 10% w/w solids on a 5.0 mL scale) were subjected to post mortem analysis using DLS, TEM and SAXS (see ESI†). DLS studies indicated that the overall vesicle diameter remained essentially constant (140–145 nm) for PBzMA DPs of between 100 and 400 (see Fig. 9c, blue data). For reference, the corresponding SAXS data reported in Table 3 for the in situ SAXS studies are also shown in Fig. 9c. The apparent discrepancy between these two data sets simply reflects the intensity-average and volume-average vesicle diameters reported by DLS and SAXS respectively. DLS diameters progressively increased for PBzMA DPs between 500 and 2000, while the corresponding size distributions significantly broadened for PBzMA DPs above 900. These data suggest that the vesicles become unstable for PBzMA DPs greater than 400, as similarly reported by Warren et al. for PGMA–PHPMA vesicles.67 TEM studies (see Fig. S8a†) support these DLS data: vesicles with narrow size distributions and approximately constant diameters were observed for PBzMA DPs up to 400. This indicates that the apparent modest increase in overall vesicle dimensions observed in the in situ SAXS studies (see Table 3) is actually an artefact. Moreover, the vesicle membrane thickness increases with PBzMA DP over this range, which suggests a similar ‘inward growth’ mechanism. Importantly, there is excellent agreement between the in situ and post mortem Tm data sets shown in Fig. 9b, which supports the validity of our kinetics renormalization approach. Furthermore, large, ill-defined species are observed by TEM for PBzMA DPs above 500 (see vertical dashed line in Fig. 9c). This is consistent with observations made by Warren et al.,67 who reported loss of the vesicular morphology for PHPMA DPs above 1000. In view of these observations, further post mortem SAXS studies were undertaken to monitor the evolution of the PSMA13–PBzMAx morphology (see red data set in Fig. 9c and also S8b†). It should be noted that these additional SAXS measurements were performed using an in-house NanoStar instrument, rather than a synchrotron X-ray source. Thus the accessible q range was only sufficient to allow the evolution in Tm to be monitored; no information regarding the overall vesicle dimensions could be obtained. Tm increased monotonically from 9 nm to 30 nm on increasing the target PBzMA DP from 100 to 400. These data were fitted to the power law Tm = kxα where k is a constant and x is the PBzMA DP. The α exponent was calculated to be 0.86, which is consistent with that reported by Warren et al.67 for post mortem SAXS analysis of PGMA–PHPMA vesicles (α = 0.79). For PBzMA DPs above 400, the Tm feature at around q = 0.2 nm−1 to 0.6 nm−1 becomes increasingly indistinct. This indicates the gradual loss of the vesicular morphology, which is consistent with the corresponding TEM studies. Since the DLS data indicate approximately the same overall vesicle dimensions for PBzMA DPs of 100–400, this indicates that the ‘inward growth’ mechanism is valid for both aqueous and non-polar media (see Fig. 9d). This is important, because it implies a generic vesicle growth mechanism for all PISA formulations. This is perfectly reasonable, because Warren et al. showed that this hitherto unrecognized mechanism is the only means by which the vesicles can lower their total surface area, and hence reduce their overall free energy.67
In the case of vesicles, different equations are required for the calculation of mean aggregation number per vesicle (Nv), Sagg and dint, as indicated below (see eqn (4)–(6)). By definition, the volume fraction of BzMA monomer within the core domain (φBzMA) at full conversion must be zero. Moreover, the SAXS data fits suggest that the volume fraction of solvent within the PBzMA chains forming the vesicle membrane (xsol) is close to zero. In this case, Nv for the final PSMA13–PBzMA150 vesicles can be calculated using eqn (4) below.
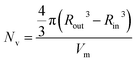 | (4) |
As for the earlier in situ SAXS studies conducted when targeting PSMA31–PBzMA2000 spheres, the leading error in the calculation of Nv is the MWD of the core-forming PBzMA block, which dictates the error in Vm. From the GPC data obtained for PSMA13–PBzMA150 vesicles prepared on a laboratory scale, the standard deviation in Vm was estimated to be 3.4% using the same method used for the spheres (see ESI†). Sagg and dint for the PSMA13–PBzMA150 vesicles are subsequently calculated using eqn (5) and (6), respectively.
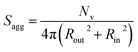 | (5) |
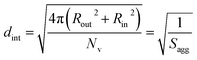 | (6) |
The Nv value calculated for PSMA13–PBzMA150 vesicles at full conversion was 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 ± 400, with the corresponding Sagg determined to be 0.187 ± 0.006 nm−2 and the average distance between adjacent copolymer chains at the core–shell interface (dint) was 2.31 ± 0.08 nm. These data somewhat differ to those calculated for related aqueous67 and alcoholic48 PISA formulations, where dint is (retrospectively) calculated to be 3.1–3.4 nm. However, the solvent volume fraction within the vesicle membrane was found to be more than 0.35 in these earlier literature examples compared to essentially zero in the present work. This indicates that the copolymer chains are more densely packed in the current non-polar PISA formulation. Notably, the value of dint calculated for these vesicles is comparable to that determined for densely-packed polybutadiene–poly(L-lysine) block copolymer chains within vesicle membranes formed in saline solution (dint = 2.4 nm at pH 10.3).89 The Sagg and dint values calculated for PSMA13–PBzMA150 vesicles can also be compared to those for PSMA31–PBzMA2000 spheres (Sagg = 0.039 ± 0.004 nm−2, dint = 5.04 ± 0.48 nm). It is evident that the copolymer chains are packed more densely within the PSMA13–PBzMA150 vesicles compared to the PSMA31–PBzMA2000 spheres. This is likely to be the result of the differing interfacial curvatures associated with each copolymer morphology, but the significant difference in target DP for the core-forming PBzMA blocks may also be a factor.
700 ± 400, with the corresponding Sagg determined to be 0.187 ± 0.006 nm−2 and the average distance between adjacent copolymer chains at the core–shell interface (dint) was 2.31 ± 0.08 nm. These data somewhat differ to those calculated for related aqueous67 and alcoholic48 PISA formulations, where dint is (retrospectively) calculated to be 3.1–3.4 nm. However, the solvent volume fraction within the vesicle membrane was found to be more than 0.35 in these earlier literature examples compared to essentially zero in the present work. This indicates that the copolymer chains are more densely packed in the current non-polar PISA formulation. Notably, the value of dint calculated for these vesicles is comparable to that determined for densely-packed polybutadiene–poly(L-lysine) block copolymer chains within vesicle membranes formed in saline solution (dint = 2.4 nm at pH 10.3).89 The Sagg and dint values calculated for PSMA13–PBzMA150 vesicles can also be compared to those for PSMA31–PBzMA2000 spheres (Sagg = 0.039 ± 0.004 nm−2, dint = 5.04 ± 0.48 nm). It is evident that the copolymer chains are packed more densely within the PSMA13–PBzMA150 vesicles compared to the PSMA31–PBzMA2000 spheres. This is likely to be the result of the differing interfacial curvatures associated with each copolymer morphology, but the significant difference in target DP for the core-forming PBzMA blocks may also be a factor.
Conclusions
In summary, a range of sterically-stabilized PSMA–PBzMA diblock copolymer nano-objects have been prepared via RAFT dispersion polymerization in mineral oil. Improved control over the copolymer molecular weight distribution is achieved compared to previously reported PISA syntheses conducted in non-polar media, with relatively narrow molecular weight distributions (Mw/Mn ≤ 1.30) being achieved even when targeting PBzMA DPs of up to 500. As expected, only spherical nanoparticles were obtained when using relatively long PSMA18 or PSMA31 macro-CTAs. In both cases, a log–log plot indicated a linear correlation between the mean sphere diameter (as judged by DLS) and the core-forming PBzMA DP. PSMA31–PBzMAx spheres indicated a scaling exponent of 0.50, suggesting essentially non-solvated PBzMA chains within the core-forming PBzMA block, whereas a scaling exponent of 0.61 was obtained for PSMA18–PBzMAx spheres, suggesting a finite degree of solvation for the PBzMA chains in this case. In contrast, using a relatively short PSMA13 macro-CTA allows the synthesis of spherical, worm-like or vesicular morphologies. Construction of a detailed phase diagram for PSMA13–PBzMAx diblock copolymers confirmed that pure spheres, worms or vesicles could be obtained at relatively low solids concentrations. This is important, because it facilitates in situ SAXS studies of the formation of PSMA31–PBzMA2000 spheres and PSMA13–PBzMA150 nano-objects at 10% w/w solids. However, the rate of BzMA polymerization during such scattering experiments is significantly faster than that observed under normal laboratory conditions. Thus the latter kinetic data sets require renormalization to enable detailed analysis of the in situ SAXS data. When targeting PSMA31–PBzMA2000 spheres, a systematic increase in core diameter (Ds) and mean aggregation number (Ns) are clearly discernible during the BzMA polymerization, with the final scattering pattern indicating the formation of near-monodisperse PSMA31–PBzMA2000 spheres. Interestingly, the number of copolymer chains per unit surface area (Sagg) decreased rapidly during the initial stages of the polymerization until a limiting value of ∼0.038 nm−2 is attained. This indicated that the mean distance between copolymer chains at the core–shell interface (dint) at full conversion was approximately 5.0 nm. When targeting PSMA13–PBzMA150 vesicles, characteristic scattering patterns for the dissolved copolymer chains, intermediate spheres and worms, and the final vesicle morphology were obtained. Importantly, revisiting the phase diagram constructed for this formulation enabled validation of the renormalization protocol adopted for analysis of the kinetic data. More specifically, the mean PBzMA DPs corresponding to the various phase boundaries were in relatively good agreement with the upper and lower DPs assigned to the corresponding pure phases indicated by analysis of the in situ SAXS patterns. Within the mixed phase space, it was shown that vesicles are formed from worms via octopi and jellyfish intermediates as first reported for an aqueous PISA formulation. Combined DLS, TEM and SAXS studies indicate that the overall vesicle dimensions remain relatively constant as the vesicle membrane gradually thickens with increasing PBzMA DP until so-called vesicle ‘death’ (or break-up) occurs. These observations indicate an ‘inward growth’ mechanism, as recently reported for an aqueous PISA formulation. This suggests that a generic vesicle growth mechanism is most likely applicable for PISA syntheses.Acknowledgements
We are grateful to Diamond Light Source for providing synchrotron beam time and thank the personnel of I22 for their assistance. Lubrizol Corporation Ltd is thanked for funding a PhD studentship for MJD. EPSRC is thanked for a Platform grant (EP/J007846/1) to support LAF, OOM, NJW and SPA also acknowledges an ERC Advanced Investigator grant (PISA 320372) to support both himself and CJM.Notes and references
- S. Krause, J. Phys. Chem., 1964, 68, 1948–1955 CrossRef CAS.
- Z. Tuzar and P. Kratochvil, Adv. Colloid Interface Sci., 1976, 6, 201–232 CrossRef CAS.
- R. K. O'Reilly, C. J. Hawker and K. L. Wooley, Chem. Soc. Rev., 2006, 35, 1068–1083 RSC.
- M. Antonietti and S. Förster, Adv. Mater., 2003, 15, 1323–1333 CrossRef CAS.
- L. J. M. Vagberg, K. A. Cogan and A. P. Gast, Macromolecules, 1991, 24, 1670–1677 CrossRef CAS.
- L. F. Zhang and A. Eisenberg, Science, 1995, 268, 1728–1731 CAS.
- G. Mountrichas, M. Mpiri and S. Pispas, Macromolecules, 2005, 38, 940–947 CrossRef CAS.
- S. Y. Choi, F. S. Bates and T. P. Lodge, J. Phys. Chem. B, 2009, 113, 13840–13848 CrossRef CAS PubMed.
- J. Tao, S. Stewart, G. J. Liu and M. L. Yang, Macromolecules, 1997, 30, 2738–2745 CrossRef CAS.
- G. J. Liu, J. F. Ding, L. J. Qiao, A. Guo, B. P. Dymov, J. T. Gleeson, T. Hashimoto and K. Saijo, Chem.–Eur. J., 1999, 5, 2740–2749 CrossRef CAS.
- N. Ouarti, P. Viville, R. Lazzaroni, E. Minatti, M. Schappacher, A. Deffieux and R. Borsali, Langmuir, 2005, 21, 1180–1186 CrossRef CAS PubMed.
- M. Lazzari, D. Scalarone, C. Vazquez-Vazquez and M. A. Lopez-Quintela, Macromol. Rapid Commun., 2008, 29, 352–357 CrossRef CAS.
- J. B. Gilroy, T. Gadt, G. R. Whittell, L. Chabanne, J. M. Mitchels, R. M. Richardson, M. A. Winnik and I. Manners, Nat. Chem., 2010, 2, 566–570 CrossRef CAS PubMed.
- J. A. Massey, K. Temple, L. Cao, Y. Rharbi, J. Raez, M. A. Winnik and I. Manners, J. Am. Chem. Soc., 2000, 122, 11577–11584 CrossRef CAS.
- X. Wang, G. Guerin, H. Wang, Y. Wang, I. Manners and M. A. Winnik, Science, 2007, 317, 644–647 CrossRef CAS PubMed.
- T. Gaedt, N. S. Ieong, G. Cambridge, M. A. Winnik and I. Manners, Nat. Mater., 2009, 8, 144–150 CrossRef CAS PubMed.
- R. Zheng, G. Liu, M. Devlin, K. Hux and T.-C. Jao, Tribol. Trans., 2009, 53, 97–107 CrossRef.
- D. J. Growney, O. O. Mykhaylyk and S. P. Armes, Langmuir, 2014, 30, 6047–6056 CrossRef CAS PubMed.
- D. J. Growney, O. O. Mykhaylyk, L. Middlemiss, L. A. Fielding, M. J. Derry, N. Aragrag, G. D. Lamb and S. P. Armes, Langmuir, 2015, 31, 10358–10369 CrossRef CAS PubMed.
- J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Aust. J. Chem., 2005, 58, 379–410 CrossRef CAS.
- G. Moad, E. Rizzardo and S. H. Thang, Acc. Chem. Res., 2008, 41, 1133–1142 CrossRef CAS PubMed.
- B. Charleux, G. Delaittre, J. Rieger and F. D'Agosto, Macromolecules, 2012, 45, 6753–6765 CrossRef CAS.
- M. J. Monteiro and M. F. Cunningham, Macromolecules, 2012, 45, 4939–4957 CrossRef CAS.
- J.-T. Sun, C.-Y. Hong and C.-Y. Pan, Polym. Chem., 2013, 4, 873–881 RSC.
- N. J. Warren and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 10174–10185 CrossRef CAS PubMed.
- M. J. Derry, L. A. Fielding and S. P. Armes, Prog. Polym. Sci., 2016, 52, 1–18 CrossRef CAS.
- M. J. Derry, L. A. Fielding and S. P. Armes, Polym. Chem., 2015, 6, 3054–3062 RSC.
- Z. An, Q. Shi, W. Tang, C.-K. Tsung, C. J. Hawker and G. D. Stucky, J. Am. Chem. Soc., 2007, 129, 14493–14499 CrossRef CAS PubMed.
- A. Blanazs, S. P. Armes and A. J. Ryan, Macromol. Rapid Commun., 2009, 30, 267–277 CrossRef CAS PubMed.
- J. Rieger, C. Grazon, B. Charleux, D. Alaimo and C. Jérôme, J. Polym. Sci., Part A: Polym. Chem., 2009, 47, 2373–2390 CrossRef CAS.
- S. Boisse, J. Rieger, K. Belal, A. Di-Cicco, P. Beaunier, M.-H. Li and B. Charleux, Chem. Commun., 2010, 46, 1950–1952 RSC.
- Y. Li and S. P. Armes, Angew. Chem., Int. Ed., 2010, 49, 4042–4046 CrossRef CAS PubMed.
- S. Sugihara, A. Blanazs, S. P. Armes, A. J. Ryan and A. L. Lewis, J. Am. Chem. Soc., 2011, 133, 15707–15713 CrossRef CAS PubMed.
- A. Blanazs, J. Madsen, G. Battaglia, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2011, 133, 16581–16587 CrossRef CAS PubMed.
- G. Liu, Q. Qiu, W. Shen and Z. An, Macromolecules, 2011, 44, 5237–5245 CrossRef CAS.
- A. Blanazs, A. J. Ryan and S. P. Armes, Macromolecules, 2012, 45, 5099–5107 CrossRef CAS.
- N. J. Warren, O. O. Mykhaylyk, D. Mahmood, A. J. Ryan and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 1023–1033 CrossRef CAS PubMed.
- C. A. Figg, A. Simula, K. A. Gebre, B. S. Tucker, D. M. Haddleton and B. S. Sumerlin, Chem. Sci., 2015, 6, 1230–1236 RSC.
- J. Tan, H. Sun, M. Yu, B. S. Sumerlin and L. Zhang, ACS Macro Lett., 2015, 4, 1249–1253 CrossRef CAS.
- W.-M. Wan and C.-Y. Pan, Polym. Chem., 2010, 1, 1475–1484 RSC.
- W.-M. Wan, X.-L. Sun and C.-Y. Pan, Macromol. Rapid Commun., 2010, 31, 399–404 CrossRef CAS PubMed.
- W. Cai, W. Wan, C. Hong, C. Huang and C. Pan, Soft Matter, 2010, 6, 5554–5561 RSC.
- C.-Q. Huang and C.-Y. Pan, Polymer, 2010, 51, 5115–5121 CrossRef CAS.
- E. R. Jones, M. Semsarilar, A. Blanazs and S. P. Armes, Macromolecules, 2012, 45, 5091–5098 CrossRef CAS.
- M. Semsarilar, E. R. Jones, A. Blanazs and S. P. Armes, Adv. Mater., 2012, 24, 3378–3382 CrossRef CAS PubMed.
- M. Semsarilar, E. R. Jones and S. P. Armes, Polym. Chem., 2014, 5, 195–203 RSC.
- C. Gonzato, M. Semsarilar, E. R. Jones, F. Li, G. J. P. Krooshof, P. Wyman, O. O. Mykhaylyk, R. Tuinier and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 11100–11106 CrossRef CAS PubMed.
- Y. Pei and A. B. Lowe, Polym. Chem., 2014, 5, 2342–2351 RSC.
- Y. W. Pei, N. C. Dharsana, J. A. Van Hensbergen, R. P. Burford, P. J. Roth and A. B. Lowe, Soft Matter, 2014, 10, 5787–5796 RSC.
- B. Karagoz, C. Boyer and T. P. Davis, Macromol. Rapid Commun., 2014, 35, 417–421 CrossRef CAS PubMed.
- B. Karagoz, L. Esser, H. T. Duong, J. S. Basuki, C. Boyer and T. P. Davis, Polym. Chem., 2014, 5, 350–355 RSC.
- S. Dong, W. Zhao, F. P. Lucien, S. Perrier and P. B. Zetterlund, Polym. Chem., 2015, 6, 2249–2254 RSC.
- L. Houillot, C. Bui, M. Save, B. Charleux, C. Farcet, C. Moire, J.-A. Raust and I. Rodriguez, Macromolecules, 2007, 40, 6500–6509 CrossRef CAS.
- L. Houillot, C. Bui, C. Farcet, C. Moire, J.-A. Raust, H. Pasch, M. Save and B. Charleux, ACS Appl. Mater. Interfaces, 2010, 2, 434–442 CAS.
- J. A. Raust, L. Houillot, M. Save, B. Charleux, C. Moire, C. Farcet and H. Pasch, Macromolecules, 2010, 43, 8755–8765 CrossRef CAS.
- L. A. Fielding, M. J. Derry, V. Ladmiral, J. Rosselgong, A. M. Rodrigues, L. P. D. Ratcliffe, S. Sugihara and S. P. Armes, Chem. Sci., 2013, 4, 2081–2087 RSC.
- L. A. Fielding, J. A. Lane, M. J. Derry, O. O. Mykhaylyk and S. P. Armes, J. Am. Chem. Soc., 2014, 136, 5790–5798 CrossRef CAS PubMed.
- Y. Pei, L. Thurairajah, O. R. Sugita and A. B. Lowe, Macromolecules, 2015, 48, 236–244 CrossRef CAS.
- Y. Pei, J.-M. Noy, P. J. Roth and A. B. Lowe, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 2326–2335 CrossRef CAS.
- Y. Pei, O. R. Sugita, L. Thurairajah and A. B. Lowe, RSC Adv., 2015, 5, 17636–17646 RSC.
- A. P. Lopez-Oliva, N. J. Warren, A. Rajkumar, O. O. Mykhaylyk, M. J. Derry, K. E. B. Doncom, M. J. Rymaruk and S. P. Armes, Macromolecules, 2015, 48, 3547–3555 CrossRef CAS.
- A. Blanazs, R. Verber, O. O. Mykhaylyk, A. J. Ryan, J. Z. Heath, C. W. I. Douglas and S. P. Armes, J. Am. Chem. Soc., 2012, 134, 9741–9748 CrossRef CAS PubMed.
- V. J. Cunningham, L. P. D. Ratcliffe, A. Blanazs, N. J. Warren, A. J. Smith, O. O. Mykhaylyk and S. P. Armes, Polym. Chem., 2014, 5, 6307–6317 RSC.
- M. K. Kocik, O. O. Mykhaylyk and S. P. Armes, Soft Matter, 2014, 10, 3984–3992 RSC.
- C. J. Mable, N. J. Warren, K. L. Thompson, O. O. Mykhaylyk and S. P. Armes, Chem. Sci., 2015, 6, 6179–6188 RSC.
- N. J. Warren, O. O. Mykhaylyk, A. J. Ryan, M. Williams, T. Doussineau, P. Dugourd, R. Antoine, G. Portale and S. P. Armes, J. Am. Chem. Soc., 2015, 137, 1929–1937 CrossRef CAS PubMed.
- Y. Kang, A. Pitto-Barry, H. Willcock, W. D. Quan, N. Kirby, A. M. Sanchez and R. K. O'Reilly, Polym. Chem., 2015, 6, 106–117 RSC.
- X. W. Zhang, S. Boisse, C. Bui, P. A. Albouy, A. Brulet, M. H. Li, J. Rieger and B. Charleux, Soft Matter, 2012, 8, 1130–1141 RSC.
- E. R. Jones, O. O. Mykhaylyk, M. Semsarilar, M. Boerakker, P. Wyman and S. P. Armes, Macromolecules, 2016, 49, 172–181 CrossRef CAS PubMed.
- J. Jennings, M. Beija, A. P. Richez, S. D. Cooper, P. E. Mignot, K. J. Thurecht, K. S. Jack and S. M. Howdle, J. Am. Chem. Soc., 2012, 134, 4772–4781 CrossRef CAS PubMed.
- D. Hermida-Merino, G. Portale, P. Fields, R. Wilson, S. P. Bassett, J. Jennings, M. Dellar, C. Gommes, S. M. Howdle, B. C. M. Vrolijk and W. Bras, Rev. Sci. Instrum., 2014, 85, 093905 CrossRef PubMed.
- P. Cacioli, D. G. Hawthorne, R. L. Laslett, E. Rizzardo and D. H. Solomon, J. Macromol. Sci., Chem., 1986, 23, 839–852 CrossRef.
- M. Rodlert, E. Harth, I. Rees and C. J. Hawker, J. Polym. Sci., Part A: Polym. Chem., 2000, 38, 4749–4763 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS PubMed.
- S. Foörster, M. Zisenis, E. Wenz and M. Antonietti, J. Chem. Phys., 1996, 104, 9956–9970 CrossRef.
- J. S. Pedersen and M. C. Gerstenberg, Macromolecules, 1996, 29, 1363–1365 CrossRef CAS.
- J. S. Pedersen and P. Schurtenberger, Macromolecules, 1996, 29, 7602–7612 CrossRef CAS.
- J. S. Pedersen, J. Appl. Crystallogr., 2000, 33, 637–640 CrossRef CAS.
- G. Battaglia and A. J. Ryan, J. Am. Chem. Soc., 2005, 127, 8757–8764 CrossRef CAS PubMed.
- J. S. Pedersen, J. Chem. Phys., 2001, 114, 2839–2846 CrossRef CAS.
- S. J. Tseng, C.-C. Chien, Z.-X. Liao, H.-H. Chen, Y.-D. Kang, C.-L. Wang, Y. Hwu and G. Margaritondo, Soft Matter, 2012, 8, 1420–1427 RSC.
- M. H. Qiao, F. Q. Yan, W. S. Sim, J. F. Deng and G. Q. Xu, Surf. Sci., 2000, 460, 67–73 CrossRef CAS.
- M. A. Winnik, R. Lukas, W. F. Chen, P. Furlong and M. D. Croucher, Makromol. Chem., Macromol. Symp., 1987, 10–11, 483–501 CrossRef CAS.
- V. J. Cunningham, S. P. Armes and O. M. Musa, Polym. Chem., 2016, 7, 1882–1891 RSC.
- L. P. D. Ratcliffe, B. E. McKenzie, G. M. D. Le Bouëdec, C. N. Williams, S. L. Brown and S. P. Armes, Macromolecules, 2015, 48, 8594–8607 CrossRef CAS.
- Y. Su, X. Xiao, S. Li, M. Dan, X. Wang and W. Zhang, Polym. Chem., 2014, 5, 578–587 RSC.
- O. Glatter and O. Kratky, Small-angle X-ray Scattering, Academic Press, London, 1982 Search PubMed.
- R. Sigel, M. Łosik and H. Schlaad, Langmuir, 2007, 23, 7196–7199 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental details including in situ SAXS measurements; synthesis and characterization of (co)polymers; kinetic study for the synthesis of a PSMA31 macro-CTA; data modelling for in situ SAXS experiments including kinetic renormalization, determination of BzMA monomer within the nanoparticle cores and estimation of the standard deviation in the molecular weight distribution; example 2D SAXS patterns; TEM images of octopi and jellyfish; DLS, TEM and SAXS analyses of PSMA13–PBzMAx vesicles; SAXS models used for spherical micelles and vesicles. See DOI: 10.1039/c6sc01243d |
| ‡ Present address: The School of Materials, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. |
| This journal is © The Royal Society of Chemistry 2016 |