 Open Access Article
Open Access ArticleCoupled wave-packets for non-adiabatic molecular dynamics: a generalization of Gaussian wave-packet dynamics to multiple potential energy surfaces†
Alexander
White
 *ab,
Sergei
Tretiak
abc and
Dmitry
Mozyrsky
a
*ab,
Sergei
Tretiak
abc and
Dmitry
Mozyrsky
a
aTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM, USA. E-mail: alwhite@lanl.gov; serg@lanl.gov; mozyrsky@lanl.gov
bCenter for Nonlinear Studies, USA
cCenter for Integrated Nanotechnologies, USA
First published on 25th April 2016
Abstract
Accurate simulation of the non-adiabatic dynamics of molecules in excited electronic states is key to understanding molecular photo-physical processes. Here we present a novel method, based on a semi-classical approximation, that is as efficient as the commonly used mean field Ehrenfest or ad hoc surface hopping methods and properly accounts for interference and decoherence effects. This novel method is an extension of Heller's thawed Gaussian wave-packet dynamics that includes coupling between potential energy surfaces. By studying several standard test problems we demonstrate that the accuracy of the method can be systematically improved while maintaining high efficiency. The method is suitable for investigating the role of quantum coherence in the non-adiabatic dynamics of many-atom molecules.
1 Introduction
First principles-based molecular dynamics (MD) is becoming an important tool for understanding properties of complex molecular systems.1–3 Unfortunately, the cost of exact dynamics, by direct calculation of the time-dependent Schrödinger equation (TDSE), scales exponentially with the dimensionality (i.e. number of atoms) of the system.4–10 Thus, for large systems one often approximates that the nuclei of a molecule propagate via classical equations of motion and calculates forces (due to coulombic interaction) via quantum chemistry methods. In doing so one typically relies on the Born–Oppenheimer approximation, where electrons remain in the same electronic quantum state |n(x)〉 with energy, E(n)(x), that parametrically depends on nuclear coordinates, x = (x1, …, xN)T.11 Thus, the nuclei propagate on a single potential energy surface (PES). For molecules in the ground electronic state, and at low temperatures, this situation often holds due to a sufficiently wide gap between the PES of the ground and excited electronic states. However, for certain nuclear configurations, common when the molecule is in an excited electronic state due to absorption of energy (e.g. a photon), the gaps can become small or even vanish. In these regions, where the nuclear-electronic coupling is the same order as the energy gap, non-adiabatic behavior is expected.12 This creates a superposition of electronic states, with different forces acting on the nuclei.Since the full TDSE is numerically intractable for high dimensions, approximations for the non-adiabatic molecular dynamics (NAMD) must be made. The simplest approximation is to average over the electronic degree of freedom (DOF), a mean-filed approximation, to determine the force on the nuclei.13,14 This is known as the Ehrenfest approximation. Like any mean-field approximation, it breaks down when there is non-negligible correlation between the dynamical DOF (the nuclear) and the averaged DOF (the electronic), i.e. if the components of the nuclear wavefunction separate depending on which PES they propagate. In an attempt to correct for this problem, while maintaining efficiency and simplicity, Tully proposed the surface hopping method,15 most commonly used with the fewest-switching procedure (FSSH).16 In this method a swarm of classical trajectories propagate on an initial PES, with a finite probability to hop to a coupled PES in regions of non-adiabatic coupling. This method is ad hoc, and is only strictly accurate in the same limit as the Ehrenfest approximation.17,18 This incomplete treatment of the nuclear-electron correlation has two well known symptoms: the interference problem, where the incorrect phase of the nuclear wavefunction leads to incorrect levels of constructive/deconstructive interference, and the decoherence problem, where the separation of the nuclear wavefunction is improperly accounted for. Both problems were pointed out by Tully himself.16 These two methods, Ehrenfest and FSSH, are by far the most commonly used in the simulation of NAMD.19–31
Many attempts have been made to improve upon the basic foundation of these two methods, while retaining the independence of trajectories.17,18,32–40 Quantum coherence effects require first-principles mixed quantum-classical or semi-classical methods, which allow interference between trajectories. These methods are typically applied only in small, or reduced, systems due to inefficiency and/or complexity.41–54 Wave-packet methods, such as ab initio multiple spawning,55 non-adiabatic Herman–Kluk frozen Gaussians,56 and non-adiabatic matching pursuit/split-operator Fourier transform,57 to name a few, provide a more accurate alternative to surface hopping and Ehrenfest methods. Additional complexities and computational costs are involved, but they also benefit from direct calculation of the wavefunction, and thus a clear, unambiguous, route to expectation values.
An ideal NAMD method would have certain properties. It should (1) be based on localized dynamics, i.e. based on real-space trajectories, (2) use only local parameters easily calculated from common electronic structure methods, i.e. PES and electronic wavefunction, (3) require no empirical or ad hoc treatments, (4) include proper treatment of electron-nuclear coupling, (5) be at least as efficient as surface hopping, and (6) be systematically improvable. The coupled wave-packets for non-adiabatic dynamics method, presented in this paper, satisfies each of these conditions. Similar to ab initio multiple spawning, it is built on a framework of branching, due to non-adiabatic coupling, Gaussian wave-packets. These wave-packets form a Gaussian basis for the nuclear wavefunction. The method is systematically improvable, capable of converging to the exact solution, and accurately accounts for decoherence and interference effects. Efficiency is retained, relative to Ehrenfest and FSSH, even when very high accuracy is required.
2 Extension of thawed Gaussian approximation to multiple PES
To build a new NAMD method, which satisfies the first and second conditions, one must start from a sound foundation for these real-spaced trajectories. The closest analog to a classical particle, and thus real local trajectory, for a quantum system is a localized wave-packet, or superposition of wave-packets.58The use of complex multi-dimensional Gaussian wave-packets (GWP):
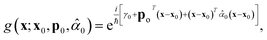 | (1) |
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) 0, complex phase γ0) of the GWP, assuming the PES is locally quadratic around x0, the thawed Gaussian approximation (TGA). The key of this method is that the phase-space center of the wave-packet moves by classical mechanics. That classical point is “dressed” in the semi-classical width and phase.59,66
0, complex phase γ0) of the GWP, assuming the PES is locally quadratic around x0, the thawed Gaussian approximation (TGA). The key of this method is that the phase-space center of the wave-packet moves by classical mechanics. That classical point is “dressed” in the semi-classical width and phase.59,66
In the adiabatic limit, the dynamics can be formally described in the framework of quantum mechanical description of the nuclei, Ψ(x,t) = eiH(x)tΨ(x,0) (here and in the following we set ħ = 1 unless stated otherwise),
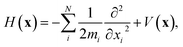 | (2) |
The non-adiabatic dynamics can similarly be obtained from a quantum mechanical description of the nuclei, |Ψ(x,t)〉 = eiĤ(x)t|Ψ(x,0)〉. Now the nuclei's potential energy operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (x) and the wavefunction |Ψ(x,t)〉 are M × M Hermitian matrix and M component vector respectively, where M is the number of relevant electronic states. For simplicity we will consider a situation with two levels crossing, i.e., with M = 2. This is the most common situation, typically more complex problems with multiple PESs and crossings can be modeled as consecutive transitions through well separated regions of coupling between two locally adjacent PESs. Furthermore, an extension to the M > 2 situation is straightforward. We assume that the initial state is a single Gaussian localized on the first PES, |Ψ(x,0)〉 = N(1)0g(1)(x;x(1)0,p(1)0,
(x) and the wavefunction |Ψ(x,t)〉 are M × M Hermitian matrix and M component vector respectively, where M is the number of relevant electronic states. For simplicity we will consider a situation with two levels crossing, i.e., with M = 2. This is the most common situation, typically more complex problems with multiple PESs and crossings can be modeled as consecutive transitions through well separated regions of coupling between two locally adjacent PESs. Furthermore, an extension to the M > 2 situation is straightforward. We assume that the initial state is a single Gaussian localized on the first PES, |Ψ(x,0)〉 = N(1)0g(1)(x;x(1)0,p(1)0,![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) (1)0)|1[x(1)0]〉, where |1[x(1)0]〉 an eigenstate of
(1)0)|1[x(1)0]〉, where |1[x(1)0]〉 an eigenstate of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (x) corresponding to the first PES evaluated at x(1)0 and N(1)0 is the real amplitude of the otherwise normalized state |Ψ(x,0)〉. Here and in the following the superscripts indicate the electronic state or PES. Non-Gaussian states can be treated as linear superpositions of finite number of Gaussians due to the linearity of the TDSE.
(x) corresponding to the first PES evaluated at x(1)0 and N(1)0 is the real amplitude of the otherwise normalized state |Ψ(x,0)〉. Here and in the following the superscripts indicate the electronic state or PES. Non-Gaussian states can be treated as linear superpositions of finite number of Gaussians due to the linearity of the TDSE.
We again split the evolution operator operator e−iĤt into slices e−iĤεe−iĤε… and now introduce a basis resolution 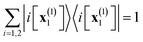 between the first and the second slices (the subscripts here and below indicate the time steps). The point x(1)1 is the location of the classical trajectory to be specified below. This is not to be confused with representation of unity used in the traditional Born–Oppenheimer expansion
between the first and the second slices (the subscripts here and below indicate the time steps). The point x(1)1 is the location of the classical trajectory to be specified below. This is not to be confused with representation of unity used in the traditional Born–Oppenheimer expansion 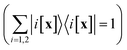 ).67 The use of the prior basis set, which is locally defined by the center of the wave-packet, as compared to the later, which is defined non-locally, by the variable x, is a subtle but crucial deviation from previously derived path-integral GWP dynamics.68,69 The use of a local eigenfunction is in line with a Gaussian wave-packet or trajectory based approach, since the Gaussian wave-packet is fully defined by localized quantities. Physically, introduction of the basis resolution corresponds to projecting the wave-packet on the new, slightly shifted basis of the eigenstates of V at the new average position of the wave-packet at time ε. The new wave-packet will mostly remain in the electronic state |1[x(1)1]〉 with a small (∝ε) transfer to |2[x(1)1]〉. After some calculation one gets66
).67 The use of the prior basis set, which is locally defined by the center of the wave-packet, as compared to the later, which is defined non-locally, by the variable x, is a subtle but crucial deviation from previously derived path-integral GWP dynamics.68,69 The use of a local eigenfunction is in line with a Gaussian wave-packet or trajectory based approach, since the Gaussian wave-packet is fully defined by localized quantities. Physically, introduction of the basis resolution corresponds to projecting the wave-packet on the new, slightly shifted basis of the eigenstates of V at the new average position of the wave-packet at time ε. The new wave-packet will mostly remain in the electronic state |1[x(1)1]〉 with a small (∝ε) transfer to |2[x(1)1]〉. After some calculation one gets66
| |Ψ(x,ε)〉 = N(1)1g(1)(x)|1[x(1)1]〉 + εN(2)1g(2)(x)|2[x(1)1]〉. | (3) |
The change in the wave-packet g(1)(x) in eqn (3) (i.e., after a single time step) is infinitesimal with the same form as the Heller GWP dynamics, leading to equations of motion for the multistate case:
ẋ0(1) = p0(1)![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) −1 −1 | (4) |
| ṗ(1)0 = −〈1[x(1)0]|∂xV(x0)|1[x(1)0]〉, |
The weight, N(1)1 = N(1)0, is unchanged.
The wave-packet g(2)(x) “hopped” to PES 2. It has the same classical position as the original wave-packet, x(2)1 = x(1)0, but different momentum: p(2)1 is such that p(2)1 − p(1)0 is parallel to the non-adiabatic coupling vector d12(x(1)0) = 〈2[x(1)0]|∂x|1[x(1)0]〉, and its absolute value satisfies the energy conservation condition, 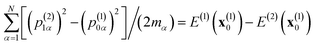 .66,70 This rescaled momentum, and thus the idea of “hopping”, is a direct consequence of the projection onto local electronic basis functions. This can be seen in detail in the full derivation presented in the ESI.†66 The parameters α(2) and N(2)1 are related to the coefficients of g(1)(x) as
.66,70 This rescaled momentum, and thus the idea of “hopping”, is a direct consequence of the projection onto local electronic basis functions. This can be seen in detail in the full derivation presented in the ESI.†66 The parameters α(2) and N(2)1 are related to the coefficients of g(1)(x) as
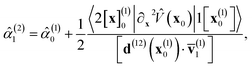 | (5) |
where v(1)0α = p(1)0α/mα,
![[v with combining macron]](https://www.rsc.org/images/entities/b_char_0076_0304.gif) (1)1 = (v(1)0 + v(2)1)/2 and Δv(1)0 = (v(1)0 − v(2)1)/2. Note that the parameters of the spawned wave-packet, e.g.eqn (5), change discontinuously at the moment of the hop. In practice we only keep the linear term in the expansion of V(x), affecting eqn (4) and (5), since for realistic systems calculation of the quadratic term can be very costly.
(1)1 = (v(1)0 + v(2)1)/2 and Δv(1)0 = (v(1)0 − v(2)1)/2. Note that the parameters of the spawned wave-packet, e.g.eqn (5), change discontinuously at the moment of the hop. In practice we only keep the linear term in the expansion of V(x), affecting eqn (4) and (5), since for realistic systems calculation of the quadratic term can be very costly.
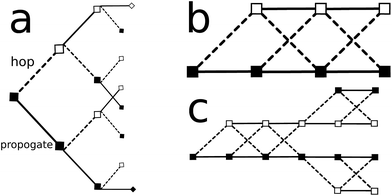
At the next time step each of the wave-packets propagates and spawns again, according to eqn (3)–(5) (with a replacement 1 → 2 for the wave-packet on the second PES). After each time step the total number of the wave-packets doubles. Such process can be viewed as branching on a tree, shown in Fig. 1a. This branching tree can be evaluated by a Monte-Carlo approach48,50,71 which becomes too computationally expensive in systems with multiple level crossings.
An alternative way to represent the branching tree is to group terms with the same number of hops. In the continuous limit the resulting wavefunction can be written as
Here the first term in the right hand side is the wave-packet that did not hop, while the single integral term, is the sum over the wave-packets that hopped only once at time t1, etc. Note that all the integrals are time-ordered, which insures the convergence of the series for finite t. A full derivation is available in the ESI.†66
3 Coupled wave-packets
Here we propose a new approach based on the wave-packet reconstruction after each spawning event. The approach is schematically shown in Fig. 1b. That is, after two time steps, described in eqn (3)–(5), one creates two wave-packets, on each PES, which will give rise to four more, etc. We note, however, that if each pair of the wave-packets on the same surface has close coordinates and momenta, one can replace each pair by a single GWP, with slightly shifted parameters. We parameterize the new Gaussian by calculating the expectation values of![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) ,
, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2,
2, ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 2 of the superposition. 〈
2 of the superposition. 〈![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 〉 and 〈
〉 and 〈![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 〉 are taken as the position and momentum of the reconstructed wave-packet, while 〈
〉 are taken as the position and momentum of the reconstructed wave-packet, while 〈![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2〉 and 〈
2〉 and 〈![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 2〉 directly give the new complex width. The new phase and weight, γ and N, are determined by maximizing the overlap of the new wave-packet with the superposition, under the constraint that N2 is the same as the density of the superposition.66 Approximations are made in order to decouple the calculation of 〈
2〉 directly give the new complex width. The new phase and weight, γ and N, are determined by maximizing the overlap of the new wave-packet with the superposition, under the constraint that N2 is the same as the density of the superposition.66 Approximations are made in order to decouple the calculation of 〈![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 〉 and 〈
〉 and 〈![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) 〉 from the explicit form of the wavefunction, i.e.
〉 from the explicit form of the wavefunction, i.e. ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) .66 Thus, as with Heller's equations, the trajectories of the GWPs remains independent of the phase and width. At the next step the procedure is repeated, again we have only two GWP and so on. The process repeats until the overlap, O12, between the Gaussians within each pair becomes intolerable, O12 < Omin. At this point, or if the non-adiabatic coupling drops below its own threshold, the “coupling” between the GWPs stops and each is treated independently, thus new branching is allowed. This coarse branching, schematically shown in Fig. 1c, significantly reduces or eliminates the exponential growth of the number of wave-packets. We call this approximation coupled wave-packets for non-adiabatic molecular dynamics (CW-NAMD).
.66 Thus, as with Heller's equations, the trajectories of the GWPs remains independent of the phase and width. At the next step the procedure is repeated, again we have only two GWP and so on. The process repeats until the overlap, O12, between the Gaussians within each pair becomes intolerable, O12 < Omin. At this point, or if the non-adiabatic coupling drops below its own threshold, the “coupling” between the GWPs stops and each is treated independently, thus new branching is allowed. This coarse branching, schematically shown in Fig. 1c, significantly reduces or eliminates the exponential growth of the number of wave-packets. We call this approximation coupled wave-packets for non-adiabatic molecular dynamics (CW-NAMD).
As the two wave-packets separate in position space, their electronic bases will become non-orthogonal. Formally this must be taken into account by considering the required basis rotations when reconstruction occurs. These rotations lead to a correction, but it is small and does not affect the results presented in this article.66
4 Results
Fig. 2 shows scattering probabilities for the standard Tully test problems II and III, Fig. 2d and e. These problems are frequently used to test new methods of non-adiabatic dynamics because they specifically probe the interference (Tully II) and decoherence (Tully III) questions directly. We compare the CW-NAMD results, with Omin = 0, to the standard fewest switching surface hopping (FSSH) and the mean-field Ehrenfest method as well as direct calculation of the time-dependent Schrödinger equation.16 When branching does not occur, the computational cost of the CW-NAMD method is similar to Ehrenfest (i.e. there is one force calculation per surface per time point), and is much lower than surface hopping. Fig. 2a and b demonstrates that for sufficiently high momentum the CW-NAMD method produces the correct scattering results. The CW-NAMD does not suffer from the interference or decoherence errors of Ehrenfest or FSSH. This can be observed by comparing the position of the peaks of the Stueckelberg oscillations72 in Fig. 2a and the lack of false oscillations in the reflected probabilities in Fig. 2b. Unlike Ehrenfest, CW-NAMD produces the correct momenta and positions of the wave-packets on the upper and lower surface (see Fig. 2f). However at low momenta, the total scattering probability is not conserved and may be poorly estimated. This is evident in both Tully-II (see Fig. 2a, 3b) and Tully-I (Fig. 3a). This can be corrected by allowing the coupled GWPs to branch, i.e. set Omin > 0.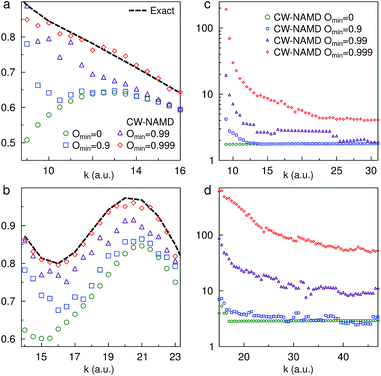 | ||
Fig. 3 (a and b) Comparison of low momentum transmission probabilities, on lower surface, with different values of Omin, compared to exact solution, for Tully I (II). Initial conditions as in Fig. 2 (except xinitial = −5 a.u. for Tully I). (c and d) Number of “effective” trajectories for Tully I (II) calculation with different values of Omin. Dynamics are run for a total time of 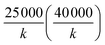 a.u. for Tully I (II). a.u. for Tully I (II). | ||
We compare the low momentum results for Tully I (II) with different values of Omin in Fig. 3a and b. The difference between exact and CW-NAMD solutions is systematically improved by increasing Omin. The increased cost can be seen in Fig. 3c and d. In direct dynamics simulations the bottleneck is typically the calculation of the PES gradients (forces). Trajectory methods like FSSH, require one force calculation per time step per trajectory. Thus we define an “effective” number of trajectories, by determining the total number of force calculations (summed over all branches) divided by the total number of time steps for the simulation, to compare the cost of a branching scheme to that of a trajectory based methods (i.e. FSSH). We see a growth of the number of trajectories required with increased Omin, however the cost of CW-NAMD is still lower than the 2000 trajectories used to calculate the FSSH result (Fig. 2b). In the limit Omin = 1 we recover the full branching tree (Fig. 1a). Lower values of Omin result in a coarse-grained tree (Fig. 1c). To prevent overgrowth of the tree, we place hard-limits on the spawning rate and utilize pruning procedures to discard irrelevant branches.66
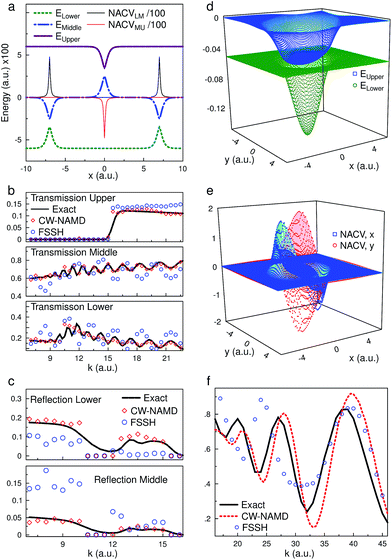
To further test the capabilities of this new algorithm we apply the method to the three level, three crossing Model X problem (Fig. 4a–c).18 As is common in realistic systems there are multiple interfering pathways, reflection on multiple surfaces, and sharply changing potentials. The wave-packet is initialized on the middle surface, with an initial width, αinitial = ik2/1600, which is four times smaller (broader wave-packet in position space) than for the Tully test suite. There are four district regions of the momentum dependence: (1) when energy is too low for a classical particle to pass the peak in the middle PES (k < 11), (2) when the particle can pass but does not have energy to hop to the upper surface (k < 12), (3) when it can hop but cannot escape the well (k < 16), and (4) when it can transmit on the upper surface. The CW-NAMD method accurately describes scattering probabilities for all regions. The region between k = 12 and k = 16 is especially difficult to simulate for trajectories based methods, due to the many oscillations inside the upper well, and seems numerically infeasible for Monte-Carlo methods.50,71 FSSH results are also shown. The FSSH method shows breakdown at lower momentum due to over-coherence and incorrect phase interference.18
Finally, accuracy in non-separable multidimensional PESs is key for application to realistic molecular systems. Such a model, introduced by Shenvi et al.,73 involves two coupled nuclear degrees of freedom in a non-trivial geometry (Fig. 4d) with significant non-adiabatic coupling in both directions (Fig. 4e). As in Tully II, strong Stueckelberg oscillations are present in the scattering probabilities. Fig. 4f shows the probability of transmission on the lower surface as a function of initial momentum in the x direction (k), there is no initial momentum in the y direction. Even in the free-thawed Gaussian approximation the oscillations are qualitatively more accurate with CW-NAMD than with FSSH. At very high momentums the FSSH result converges to the CW-NAMD result. In this regime the difference in integrated forces on the two PES are negligible compared to the initial momentum. Quantitative deviation from the exact result is due to the break down the Thawed Gaussian Approximation, the width of the wave-packet being of similar size to the PES well. This is further discussed in the following section.
5 Discussion and Conclusion
CW-NAMD is based on the thawed Gaussian approximation, which is known to be accurate only for short times, unless the PES is harmonic or linear. In practice we have approximated even further, by only keeping the linear expansion in V(x). The linear expansion, and indeed the full TGA is appropriate when imag[![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e101.gif) 0] ≫ ∂x2
0] ≫ ∂x2![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) (x0), essentially when the wave-packet is narrower in position than the variance of the potential. When this does not hold error will accumulate over time, thus limiting the procedure to short-time dynamics. However, TGA can be systematically improved through time-slicing procedures, which allow for the broadened wave-packets to be reconstructed from narrower, in position space, wave-packets.74,75 This can be done by Monte-Carlo sampling or gradient-descent,57,76 and adds an additional source of branching which interfaces well with the CW algorithm. By reducing the over-complete basis, the number of trajectories can be kept to the minimum necessary for an accurate description.44,57,75,76 Inclusion of this time-slicing procedure is a goal for the continued development of the CW-NAMD method.
(x0), essentially when the wave-packet is narrower in position than the variance of the potential. When this does not hold error will accumulate over time, thus limiting the procedure to short-time dynamics. However, TGA can be systematically improved through time-slicing procedures, which allow for the broadened wave-packets to be reconstructed from narrower, in position space, wave-packets.74,75 This can be done by Monte-Carlo sampling or gradient-descent,57,76 and adds an additional source of branching which interfaces well with the CW algorithm. By reducing the over-complete basis, the number of trajectories can be kept to the minimum necessary for an accurate description.44,57,75,76 Inclusion of this time-slicing procedure is a goal for the continued development of the CW-NAMD method.
The CW-NAMD method is similar in spirit to the ab initio multiple spawning (AIMS) method developed by Martinez et al.55,77,78 Both involve approximate solution to an infinitely branching tree, of GWPs. However, in practice AIMS is usually based on the so called independent first generation, where an initial sampling of non-interfering frozen Gaussian wave-packets are propagated. Note that subsequently spawned packets do interfere and full interference can be considered as well.55 CW-NAMD uses thawed GWPs, which can be expanded to improve accuracy, and considers the full superposition of GWPs. For AIMS the “spawning” procedure is based on well-reasoned but empirical considerations.79 The branching procedure in CW-NAMD has a simple numerical control parameter, Omin. In AIMS, coupling between spawned wave-packets results in an equation of motion for complex pre-factors (weight and phase), but, unlike CW-NAMD, does not result in shifts of the other Gaussian parameters.
In conclusion, the new CW-NAMD method is a highly efficient and accurate method of simulating non-adiabatic dynamics applicable to realistic molecular systems. CW-NAMD consistently accounts for decoherence and interference between different dynamical pathways. It can be as efficient as the Ehrenfest method in the high momentum limit, moreover it accurately describes the dynamics of branching wave-packets. In the low momentum limit the method can be systematically improved by increase the rate of allowed branching via the user controlled accuracy threshold, Omin. Combined with filtering of insignificant branches, the method is more accurate and more efficient than the standard FSSH. In our test problems we observe numerical cost of CW-NAMD ranging from about 2(M) to 1000 trajectories depending on initial momentum and desired accuracy. This needs to be compared with the number of effective trajectories in other methods: 2(M) (Ehrenfest), (2 − 10) × 103 (FSSH), (2 − 10) × 104 (Monte-Carlo approaches).
The development of CW-NAMD opens new avenues for future research. On the technical development side, this includes more advance branching criterion, manipulation of the electronic bases, optimization of the reconstruction and branch pruning procedures, as well as the introduction of time-slicing. In regards to application, the CW-NAMD opens a path towards investigation of the role of quantum coherent effects in the non-adiabatic dynamics of large scale molecular systems.
Acknowledgements
We acknowledge support of the U.S. Department of Energy through the Los Alamos National Laboratory (LANL) LDRD Program. LANL is operated by Los Alamos National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy under Contract No. DE-AC52-06NA25396. We also acknowledge the LANL Institutional Computing (IC) Program provided computational resources. This work was supported in part by the Center for Nonlinear Studies (CNLS) and the Center for Integrated Nanotechnology (CINT) at LANL.References
- D. Marx, J. Hutter, Ab initio Molecular Dynamics, Cambridge University Press, 2009 Search PubMed.
- M. E. Tuckerman, J. Phys.: Condens. Matter, 2002, 14, R1297 CrossRef CAS.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS PubMed.
- M. Feit, J. Fleck and A. Steiger, J. Comput. Phys., 1982, 47, 412–433 CrossRef CAS.
- H. Tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967–3971 CrossRef CAS.
- T. J. Park and J. C. Light, J. Chem. Phys., 1986, 85, 5870–5876 CrossRef CAS.
- R. Kosloff, Annu. Rev. Phys. Chem., 1994, 45, 145–178 CrossRef CAS.
- D. Neuhauser, J. Chem. Phys., 1994, 100, 9272–9275 CrossRef CAS.
- C. Xie, J. Ma, X. Zhu, D. H. Zhang, D. R. Yarkony, D. Xie and H. Guo, J. Phys. Chem. Lett., 2014, 5, 1055–1060 CrossRef CAS PubMed.
- B. Jiang and H. Guo, Phys. Rev. Lett., 2015, 114, 166101 CrossRef PubMed.
- M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- H. S. W. Massey, Rep. Prog. Phys., 1949, 12, 248 CAS.
- P. Ehrenfest, Zeitschrift Physik, 1927, 45, 455–457 CrossRef.
- S.-I. Sawada, A. Nitzan and H. Metiu, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 851–867 CrossRef CAS.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- J. C. Tully, J. Chem. Phys., 1990, 93, 1061–1071 CrossRef CAS.
- J. E. Subotnik, J. Chem. Phys., 2010, 132, 134112 CrossRef PubMed.
- J. E. Subotnik, J. Phys. Chem. A, 2011, 115, 12083–12096 CrossRef CAS PubMed.
- S. V. Kilina, D. S. Kilin and O. V. Prezhdo, ACS Nano, 2009, 3, 93–99 CrossRef CAS PubMed.
- K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2014, 10, 789–804 CrossRef CAS PubMed.
- L. Wang, R. Long and O. V. Prezhdo, Annu. Rev. Phys. Chem., 2015, 66, 549–579 CrossRef CAS PubMed.
- S. Choi, R. Onofrio and B. Sundaram, Phys. Rev. E, 2015, 92, 042907 CrossRef PubMed.
- P. Goyal, C. A. Schwerdtfeger, A. V. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. B, 2015, 119, 2758–2768 CrossRef CAS PubMed.
- A. S. Petit and J. E. Subotnik, J. Chem. Theory Comput., 2015, 11, 4328–4341 CrossRef CAS PubMed.
- L. Du and Z. Lan, J. Chem. Theory Comput., 2015, 11, 1360–1374 CrossRef CAS PubMed.
- W. Ouyang, W. Dou and J. E. Subotnik, J. Chem. Phys., 2015, 142, 084109 CrossRef PubMed.
- W. Dou, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2015, 142, 084110 CrossRef PubMed.
- W. Dou, A. Nitzan and J. E. Subotnik, J. Chem. Phys., 2015, 142, 234106 CrossRef PubMed.
- M. Galperin and A. Nitzan, J. Phys. Chem. Lett., 2015, 6, 4898–4903 CrossRef CAS PubMed.
- E. R. Bittner and P. J. Rossky, J. Chem. Phys., 1995, 103, 8130–8143 CrossRef CAS.
- C. Zhu, S. Nangia, A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2004, 121, 7658–7670 CrossRef CAS PubMed.
- M. J. Bedard-Hearn, R. E. Larsen and B. J. Schwartz, J. Chem. Phys., 2005, 123, 234106 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, J. Chem. Phys., 2013, 138, 224111 CrossRef PubMed.
- A. V. Akimov and O. V. Prezhdo, Phys. Rev. Lett., 2014, 113, 153003 CrossRef PubMed.
- L. Wang and O. V. Prezhdo, J. Phys. Chem. Lett., 2014, 5, 713–719 CrossRef CAS PubMed.
- A. E. Sifain, L. Wang and O. V. Prezhdo, J. Chem. Phys., 2015, 142, 224102 CrossRef PubMed.
- L. Wang, A. E. Sifain and O. V. Prezhdo, J. Phys. Chem. Lett., 2015, 6, 3827–3833 CrossRef CAS PubMed.
- D. J. Trivedi and O. V. Prezhdo, J. Phys. Chem. A, 2015, 119, 8846–8853 CrossRef CAS PubMed.
- H.-D. Meyera and W. H. Miller, J. Chem. Phys., 1979, 70, 3214–3223 CrossRef.
- M. Thoss and G. Stock, Phys. Rev. A, 1999, 59, 64–79 CrossRef CAS.
- R. Kapral, Annu. Rev. Phys. Chem., 2006, 57, 129–157 CrossRef CAS PubMed.
- X. Chen and V. S. Batista, J. Chem. Phys., 2006, 125, 124313 CrossRef PubMed.
- W. H. Miller, J. Phys. Chem. A, 2009, 113, 1405–1415 CrossRef CAS PubMed.
- V. A. Rassolov and S. Garashchuk, Phys. Rev. A, 2005, 71, 032511 CrossRef.
- N. Zamstein and D. J. Tannor, J. Chem. Phys., 2012, 137, 22A518 Search PubMed.
- V. N. Gorshkov, S. Tretiak and D. Mozyrsky, Nat. Commun., 2013, 4, 2144 Search PubMed.
- A. R. Menzeleev, F. Bell and T. F. Miller, J. Chem. Phys., 2014, 140, 064103 CrossRef PubMed.
- A. J. White, V. N. Gorshkov, R. Wang, S. Tretiak and D. Mozyrsky, J. Chem. Phys., 2014, 141, 184101 CrossRef PubMed.
- N. Makri, Int. J. Quantum Chem., 2015, 115, 1209–1214 CrossRef CAS.
- S. K. Min, F. Agostini and E. K. U. Gross, Phys. Rev. Lett., 2015, 115, 073001 CrossRef PubMed.
- W. C. Pfalzgraff, A. Kelly and T. E. Markland, J. Phys. Chem. Lett., 2015, 6, 4743–4748 CrossRef CAS PubMed.
- C. C. Martens, J. Chem. Phys., 2015, 143, 141101 CrossRef PubMed.
- T. J. Martinez, M. Ben-Nun and R. D. Levine, J. Chem. Phys., 1996, 100, 7884–7895 CrossRef CAS.
- M. F. Herman and E. Kluk, Chem. Phys., 1984, 91, 27–34 CrossRef CAS.
- Y. Wu, M. F. Herman and V. S. Batista, J. Chem. Phys., 2005, 122, 114114 CrossRef PubMed.
- P. A. M. Dirac, The Principles of Quantum Mechanics, Oxford University Press, 1958 Search PubMed.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1981, 75, 2923–2931 CrossRef CAS.
- D. Huber and E. J. Heller, J. Chem. Phys., 1987, 87, 5302–5311 CrossRef CAS.
- R. D. Coalson and M. Karplus, J. Chem. Phys., 1990, 93, 3919–3930 CrossRef CAS.
- A. K. Pattanayak and W. C. Schieve, Phys. Rev. E, 1994, 50, 3601–3615 CrossRef CAS.
- E. Kluk, M. F. Herman and H. L. Davis, J. Chem. Phys., 1986, 84, 326–334 CrossRef CAS.
- B. Gu and S. Garashchuk, J. Phys. Chem. A DOI:10.1021/acs.jpca.5b10029.
- See ESI†.
- M. Baer, Beyond Born–Oppenheimer, Wiley-Interscience, 2006 Search PubMed.
- S. Krempl, M. Winterstetter, H. Plöhn and W. Domcke, J. Chem. Phys., 1994, 100, 926–937 CrossRef CAS.
- R. D. Coalson, J. Chem. Phys., 1996, 100, 7896–7902 CrossRef CAS.
- M. F. Herman, J. Chem. Phys., 1984, 81, 754–763 CrossRef CAS.
- A. J. White, V. N. Gorshkov, S. Tretiak and D. Mozyrsky, J. Chem. Phys., 2015, 143, 014115 CrossRef PubMed.
- E. C. G. Stueckelberg, Helv. Phys. Acta, 1932, 5, 370–423 Search PubMed.
- N. Shenvi, J. E. Subotnik and W. Yang, J. Chem. Phys., 2011, 135, 024101 CrossRef PubMed.
- F. Grossmann, Phys. Rev. Lett., 2000, 85, 903–907 CrossRef CAS PubMed.
- X. Kong, A. Markmann and V. S. Batista, J. Phys. Chem. A, 2016 DOI:10.1021/acs.jpca.5b12192.
- Y. Wu and V. S. Batista, J. Chem. Phys., 2003, 118, 6720–6724 CrossRef CAS.
- M. Ben-Nun, J. Quenneville and T. J. Martinez, J. Phys. Chem. A, 2000, 104, 5161–5175 CrossRef CAS.
- T. J. Martinez, Acc. Chem. Res., 2006, 39, 119–126 CrossRef CAS PubMed.
- B. G. Levine, J. D. Coe, A. M. Virshup and T. J. Martinez, Chem. Phys., 2008, 347, 3–16 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed derivation of the CW-NAMD method and a step-by-step description of the algorithm. See DOI: 10.1039/c6sc01319h |
| This journal is © The Royal Society of Chemistry 2016 |

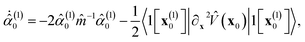
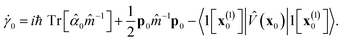
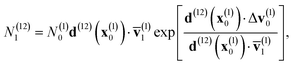
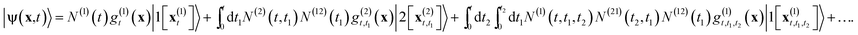
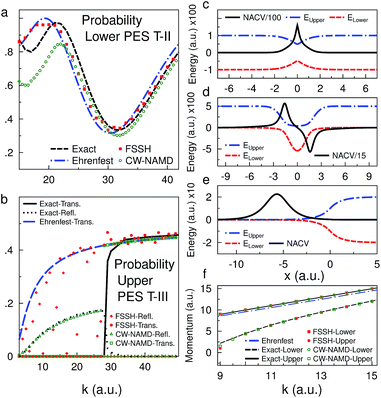
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 trajectories) results are compared.
000 trajectories) results are compared.