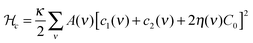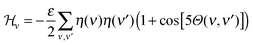Membrane invagination induced by Shiga toxin B-subunit: from molecular structure to tube formation

Abstract

The bacterial Shiga toxin is composed of an enzymatically active A-subunit, and a receptor-binding homopentameric B-subunit (STxB) that mediates intracellular toxin trafficking. Upon STxB-mediated binding to the glycolipid globotriaosylceramide (Gb₃) at the plasma membrane of target cells, Shiga toxin is internalized by clathrin-dependent and independent endocytosis. The formation of tubular membrane invaginations is an essential step in the clathrin-independent STxB uptake process. However, the mechanism by which STxB induces these invaginations has remained unclear. Using a combination of all-atom molecular dynamics and Monte Carlo simulations we show that the molecular architecture of STxB enables the following sequence of events: the Gb₃ binding sites on STxB are arranged such that tight avidity-based binding results in a small increment of local curvature. Membrane-mediated clustering of several toxin molecules then creates a tubular membrane invagination that drives toxin entry into the cell. This mechanism requires: (1) a precise molecular architecture of the STxB binding sites; (2) a fluid bilayer in order for the tubular invagination to form. Although, STxB binding to the membrane requires specific interactions with Gb₃ lipids, our study points to a generic molecular design principle for clathrin-independent endocytosis of nanoparticles.

---

Introduction

The hydrophobic nature of a plasma membrane's interior makes it impermeable to ions and large water-soluble molecules. The plasma membrane thereby separates the cellular cytoplasm from the external environment. However, the cell also needs to communicate with its external environment and transport substances in and out of the cell. For this, the plasma membrane must be selectively permeable. To resolve this problem, cells use a number of mechanisms. The uptake of macromolecules and large particles from the surrounding medium is accomplished by endocytosis. Endocytic processes can be hijacked by bacteria, viruses and toxins, typically causing disease in animals and humans.^1–4 The bacterial Shiga toxin and Shiga-like toxins are examples of pathogenic toxins that use endocytosis for their entry into host cells. They are members of the AB₅ family of protein toxins that are associated with human pathologies like dysentery, diarrhea, and hemolytic uremic syndrome. A single catalytic A-subunit associates with a homopentameric B-subunit (STxB). The A-subunit modifies ribosomal RNA in target cells and thereby causes inhibition of protein biosynthesis, while STxB is responsible for binding of the toxin to the host cell membrane. Each STxB molecule has 15 binding sites for the glycosphingolipid (GSL) globotriaosylceramide (Gb₃), the cellular toxin receptor.^5,6Via interactions with these receptor molecules, Shiga toxin enters cells by clathrin-dependent⁷ and independent endocytosis.^5,8,9

In the absence of the A-subunit, STxB still forms a pentameric unit¹⁰ and its internalization ability remains unaffected,¹¹ even if the uptake pathway might be modulated by the A-subunit.¹² When membrane scission is inhibited by different means, STxB localizes to tubular invaginations that are induced by the protein^5,8,9,11 suggesting a model in which the toxin drives the initial step of its uptake into cells, i.e. the formation of a deep and narrow invaginated membrane domain, the endocytic pit.¹³ Indeed, STxB induces tubular membrane invaginations on giant unilamellar vesicles (GUV) in the absence of any cytosolic machinery.⁵ Interestingly, several pathogenic^14,15 or cellular lectins¹⁶ share with STxB the capacity to induce membrane invaginations in interaction with defined GSL species, indicating that this could be a general mechanism (reviewed in ref. 17).

A specific Gb₃ acyl chain composition is required for STxB to induce tubular membrane invaginations. Binding of STxB to Gb₃ with saturated acyl chains (Gb₃:C22:0; denoted hereafter by S-Gb₃) does not lead to the formation of invaginations, whereas invaginations form upon STxB binding to Gb₃ with unsaturated acyl chains (Gb₃:C22:1; denoted by U-Gb₃).⁵ In the case of the related cholera toxin that like Shiga toxin induces membrane bending via interactions with its cellular receptor, the GSL GM₁, it was shown that unsaturated GM₁ acyl chain species indeed favored cellular infection.¹⁴ The mechanisms by which these lectins drive membrane bending have not yet been determined.

Formation of inward tubular invaginations has previously been studied by use of computer simulation.^18–20 These studies were performed using spherical inclusions (or spherical caps) that induce a high curvature imprint onto the membrane,^19,20 in contradistinction to the STxB protein which is flat. The cited simulations also do not incorporate specific information about the molecular structure of the proteins. By contrast, molecular structure is a key element in the STxB system.⁵

Here, we first use all-atom molecular dynamics (MD) simulations to characterize at the atomistic length scale the effect of binding a single STxB protein to a bilayer containing Gb₃ lipids. Subsequently, we feed these results into a Monte Carlo (MC) simulation of a triangulated surface model²¹ to study the macroscopic conformational behaviour of the membrane with many STxB proteins. The results of these multi-scale simulations reveal conditions in which STxB can induce tubular membrane invaginations. Of note, these conditions are in agreement with results in the experimental literature.

Methods

Two distinct simulation techniques, at two different length scales were used to investigate this process. At the atomistic length scale we exploited all-atom MD simulation, and for the macroscopic length scale MC simulation of a triangulated surface was used. Details of each technique are discussed below.

Molecular dynamic simulations

We performed all-atom MD simulations of STxB and STxB mutant W34A binding to a DOPC bilayer containing 15 Gb₃ lipids (in the system containing the STxB mutant only 10 Gb₃ lipids are presented, because the W34A mutant binds at most to 10 Gb₃⁵) in the upper monolayer (either U-Gb₃ or S-Gb₃). As a control, STxB binding to a pure DOPC bilayer was also simulated. Additionally, trajectories from our previous work,²² where 16 Gb₃ lipids were presented in the upper monolayer, were analysed as two extra control simulations to investigate the effect of Gb₃ inhomogeneity on bilayer curvature. Initially, all 15 Gb₃ binding sites on STxB (or 10 binding sites of W34A) were occupied by their Gb₃ binding partners. The simulations were performed using GROMACS^23,24 and the CHARMM36 force field.^25,26 The Gb₃ parameters were obtained from ref. 22. The systems were solvated using the TIP3P water model.²⁷ STxB is a charged protein (1 e⁻ per monomer), so Na⁺ and Cl⁻ ions were added to a physiological concentration of about 150 mmol to neutralize the system. Electrostatic interactions were treated with particle-mesh Ewald (PME) with a short-range cutoff at 1.2 nm, and van der Waals interactions were switched off between 1.0 nm to 1.2 nm. The system temperature was kept constant at 37 °C using Nose–Hoover temperature coupling.^28,29 Bonds containing hydrogen atoms were constrained using the LINCS algorithm.³⁰ Parrinello–Rahman barostat pressure coupling³¹ was applied to all systems after equilibrating them with the Berendsen pressure coupling.³² Finally, the leap frog integrator was used with a time step of 2 fs.

Monte Carlo

The large scale conformational properties of the membrane are governed by its curvature elasticity and the lateral organization of the membrane, and only a few model parameters are involved. To explore these properties, we performed MC simulations of a closed, fluid triangulated surface consisting of 2030 vertices and hence 4056 triangles, in which vertices diffuse according to the usual bond-flip MC move. This method allows us to determine the tangent plane and curvature tensor on each vertex, as described in detail in ref. 21. A STxB protein is modelled as an in-plane vector field on a vertex with five-fold rotational symmetry that induces local curvature on the surface of the membrane. The total system energy consists of two parts: (1) membrane elastic bending energy. (2) Vector field interactions.

(1) Membrane elastic energy: this part of the energy is described by a discretized form of the Helfrich Hamiltonian

where the sum is over all vertices, κ is the bending modulus of the membrane, A(ν) is the area associated with vertex ν, η(ν) is a binary function returning the value 1 if ν holds a protein, and 0 otherwise, C₀ is the local curvature induced by a protein on the vertex ν (this will be obtained from MD simulation results), and c₁(ν) and c₂(ν) are the principal curvatures, respectively.²¹

(2) The vector field interaction energy: STxB proteins cluster upon binding to a membrane whereas in the absence of a membrane they remain unassociated. This indicates that a membrane mediated interaction is required for clustering. However, the source of this clustering force is still elusive.⁵ We modelled this membrane mediated interaction by the following energy function

where the sum is over neighboring vertices. ε is the interaction strength between proteins, and Θ(ν,ν′) is the angle difference between two vectors after parallel transport.²¹ The first term of this equation includes a short-range attraction between the proteins that reflects the clustering tendency of STxB when bound to cellular or model membranes, and the cos[5Θ(ν,ν′)] term in the equation reflects the anisotropic interaction due to pentagonal shape (5 fold symmetry) of STxB. The strength of this attraction, ε, is a parameter in our model. To complete the STxB model in the MC simulation, we fix the MC length scale (a) using the value of the induced local curvature by STxB (C₀), which is given in nm⁻¹. In order to do this, we consider the area associated to a vertex to be equal to the area of one STxB (Fig. 1). A_ν = A_stxb, a ≈ 6.65 nm. This can also be used to make an estimate of the total vesicle area A_tot ∼ 0.1 μm².

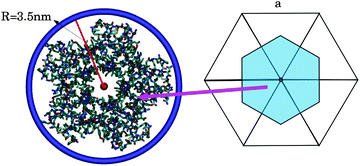Fig. 1 (left) The smallest ring that wraps around STxB has a radius of 3.5 nm. (right) The area associated to a vertex (on average a vertex is surrounded by 6 triangles in a spherical topology).

MD systems

DOPC–STxB system was built by symmetrically placing 338 DOPC lipids on two parallel lattices and equilibrating the system by a 50 ns simulation. Then STxB was placed at a close distance from the bilayer surface and the new system was equilibrated for another 50 ns while the STxB backbone was restrained.

Systems containing a protein and Gb₃ lipids: complexes of 15 U-Gb₃ lipids with one STxB protein, 15 S-Gb₃ lipids with one STxB protein, or of 10 U-Gb₃ lipids with one mutant STxB–W34A protein were prepared in such a way that the carbohydrate moiety of each Gb₃ lipid was close to one of the protein binding sites (the structure in ref. 6 was mapped). Simultaneously, a DOPC bilayer was made by symmetrically placing 364 DOPC lipids on two parallel lattices. Then we embedded the Gb₃–protein complex in the upper mono-layer of the bilayer and removed 15 DOPC lipids so that Gb₃ lipids did not touch any remaining DOPC lipids. This configuration was equilibrated by a 150 ns simulation while imposing position restraints on both the STxB backbone and the Gb₃ atoms. Next we re-equilibrated the system for another 50 ns simulation while the position restraint was imposed only on the protein backbone. After equilibration, the position restraint on the protein was removed and simulations were continued for 400 ns. In addition, for each system of S-Gb₃–DOPC–STxB or U-Gb₃–DOPC–STxB, 4 replicas were simulated for 200 ns. Details of the systems can be found in Table 1.

Table 1 Details of simulated systems

Systems	DOPC/Gb3/STxB/W34A	Na/Cl	Solvent	Time (ns)
S-Gb3–DOPC–STxB	349/15/1/0	90/85	33 475	400
S-Gb3–DOPC–STxB 4 replicas	349/15/1/0	90/85	33 475	200
U-Gb3–DOPC–STxB	349/15/1/0	87/82	32 989	400
U-Gb3–DOPC–STxB 4 replicas	349/15/1/0	87/82	32 989	200
DOPC–STxB	338/0/1/0	70/65	27 152	400
U-Gb3–DOPC–W34A	344/10/0/1	80/75	31 594	400

---

MC systems

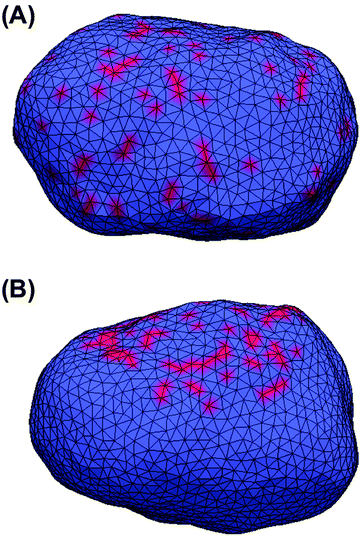
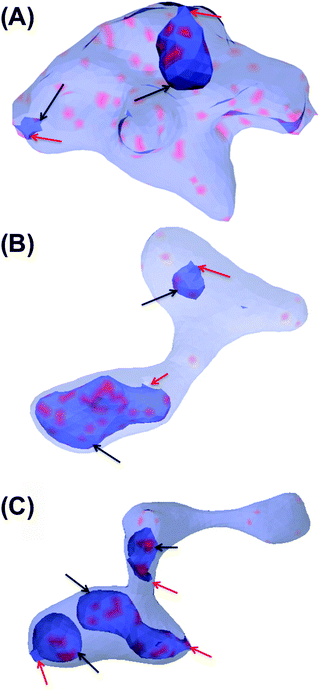
All MC simulations were performed on a vesicle containing 2030 vertices. A percentage P_v of the vesicle surface was initially covered by STxB proteins with properties described in the Method section (P_v varies between the different simulations). Initial systems were built by randomly distributing STxB proteins on the surface of the vesicle (Fig. 2A). Also, in order to boost simulation performance, some initial systems were built by randomly distributing STxB proteins on a small patch containing 20% of the vesicle surface (Fig. 2B). In order to increase the sampling accuracy, simulations were performed on 24 replicas for each set of parameters.

Fig. 2 Initial states of MC simulations. Red represents vertices that own a protein. (A) Proteins are randomly distributed over the whole surface of the vesicle. (B) Proteins are randomly distributed on a small patch of the vesicle surface.

Results and discussion

STxB induces local curvature

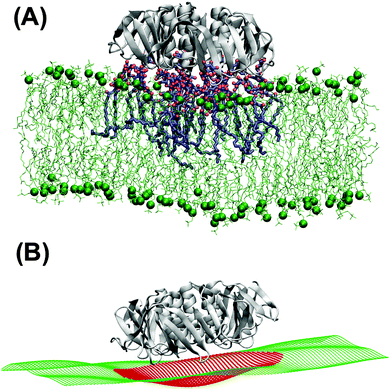
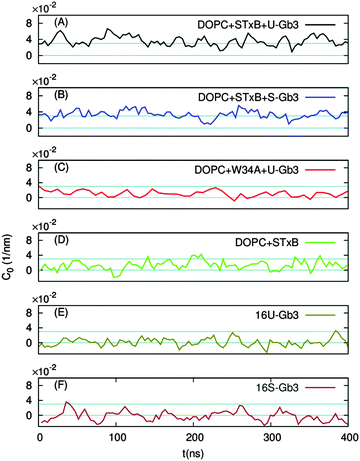
Independently of the Gb₃ saturation level, after 200 ns simulation time, the majority of the replica simulations show that 13 (out of 15) Gb₃ lipids remain in the proximity of the correct STxB binding site positions.⁶ Such configurations are reached within 100 ns simulation and the analysis is performed after this equilibration time. Two of these replicas (one for each Gb₃ type) were continued to 400 ns.

Fig. 3A shows the last snapshot for the U-Gb₃–DOPC–STxB system. The snapshot shows that STxB induces a small increment of local curvature on the surface of the bilayer. Fig. 3B shows a clearer representation of the induced curvature that is obtained by fitting the surface to a series of Legendre functions as described next.

Fig. 3 (A) U-Gb₃–DOPC–STxB complex. Upon binding to Gb₃, STxB induces local curvature. (B) Reconstruction of the bilayer surface (in A) by fitting a series of Legendre polynomials to the positions of the phosphor atom of DOPC lipid in order to better display the local curvature induced by STxB.

To differentiate the toxin particle-induced curvature from thermally-induced random deformations of the bilayer surface, we calculated the local bilayer curvature induced by STxB over time. Since we are going to use this data in MC simulations we are specifically interested in the local bilayer curvature in the area under STxB molecules. First, the membrane surface is obtained by fitting the phosphorus atom coordinates of the DOPC lipids to a series of Legendre polynomials as 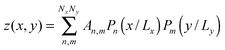where P_n is the nth Legendre polynomial, L_x and L_y are simulation box side lengths in the x and y directions (Here N_x = N_y = 6 has been used). Since the curvatures of the bilayers are small (Fig. 3B), the linear approximation for mean curvature, C(x,y), can be used: 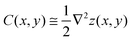. The local curvature per unit area underneath of the STxB is defined as 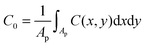where A_p is the projected area of STxB on membrane plane. In this formulation, an inward/outward bending will be represented by a positive/negative C₀.

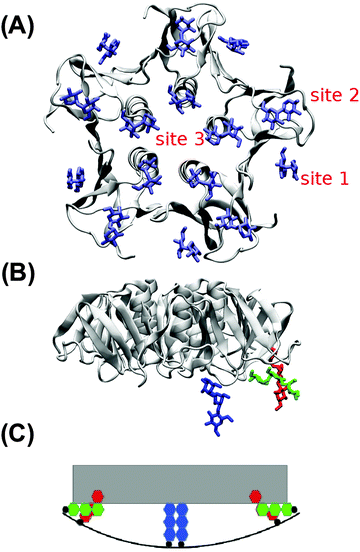
In the absence of Gb₃ lipids (the pure DOPC–STxB system), bilayer deformations were solely due to thermal fluctuations of the membrane surface, and C₀ fluctuated around zero (Fig. 4D), the time average of the local curvature was 〈C₀〉 = 0.011 ± 0.003 nm⁻¹ (errors are estimated using block averaging). However, binding of STxB to either S-Gb₃ or U-Gb₃ induces an inward curvature (Fig. 4A and B: values from the replica simulations can be found in the ESI,† Table S1). The time averages of the local curvature were: 〈C₀〉 = 0.034 ± 0.004 nm⁻¹ in the presence of S-Gb₃, and 〈C₀〉 = 0.035 ± 0.003 nm⁻¹ in presence of U-Gb₃ lipid. Accordingly, the presence of Gb₃ lipids is a prerequisite for STxB to induce an inward curvature, and Gb₃ lipid chain saturation plays a secondary role. The value of 〈C₀〉 was strongly affected by the number of bound Gb₃ lipids. For example, in a simulation where STxB remained bound to 10 Gb₃, 〈C₀〉 reduced to 0.028 ± 0.003 nm⁻¹ (Fig. S1C, ESI†). Therefore we conclude that STxB induces local curvature on the surface of a bilayer upon binding to either of the Gb₃ types whose magnitude is in the range 0 < C₀ < 0.035 nm⁻¹. STxB is a nearly flat protein, and it is expected that the induced curvature arises from molecular details of the STxB–Gb₃ binding. When STxB binds Gb₃ lipids, the head group sugars are oriented differently with respect to the membrane normal and protrude from the membrane to different heights (Fig. 5A). The Gb₃ lipid head groups that bind to site 3, which is located approximately in the middle of the bottom face of STxB, are normal to the protein surface. Therefore, the sphingosine backbones of these lipids stay at a larger distance from the protein face compared to sphingosine backbones of Gb₃ lipids which bind to the peripheral sites 1 and 2 (Fig. 5B). Thus, the impact of STxB on the surface of a bilayer containing Gb₃ is similar to that of a convex object and, upon binding, the pentamer imposes its geometry on the membrane (Fig. 5C). This indicates that STxB binding site 3 plays a crucial role in inducing local curvature. To test this hypothesis we performed an MD simulation with the Shiga toxin mutant W34A, in which binding site 3 is inactivated. In this case, binding of STxB to the membrane did not induce any local curvature (〈C₀〉 = 0.01 ± 0.006 nm⁻¹: see Fig. 4C).

Fig. 4 The local membrane curvature C₀ as a function of time. STxB binding to a bilayer containing U-Gb₃ (A) or S-Gb₃ (B) species induces local curvature. STxB–W34A in which Gb₃ binding site 3 is mutated fails to induce local curvature (C). In the absence of Gb₃ lipids, no curvature is induced (D). In the absence of STxB, the presence of 16 U-Gb₃ (E) or 16 S-Gb₃ (F) species in the upper monolayer does not induce membrane bending. Very clearly, STxB binding is required for induction of local curvature.

Fig. 5 (A) STxB holds 15 Gb₃ binding sites. Gb₃ head groups are shown in blue. (B) Height mismatch and orientation difference among different STxB binding sites imprints an increment of local curvature onto the bilayer. Gb₃ head groups in binding sites 1, 2 and 3 are represented in red, green and blue, respectively. (C) Schematic view of Gb₃ carbohydrate moieties at different STxB binding sites. The gray object is STxB and the red, green, and blue hexagons represent Gb₃ sugar moieties in the binding sites 1, 2 and 3, respectively.

An alternative explanation of the inward curvature might be the transbilayer inhomogeneity in the lipid distribution, induced by STxB binding. To investigate whether this effect plays an important role in the observed local curvature, we analysed the trajectories from our previous work where such inhomogeneity exists in the absence of STxB.²² 16 Gb₃ lipids were positioned in a patch in the upper monolayer of a bilayer system composed of DOPC. If a change in lipid distribution results in an inward local curvature, the inward local curvature should be observed even in the absence of STxB. However, the results show that Gb₃ clustering in the absence of STxB does not induce any significant membrane bending (see Fig. 4E, F and Table S1, ESI†), and can not explain the observed inward local curvature induced by STxB. Therefore a specific STxB–Gb₃ complex is required for induction of local inward curvature.

STxB induces tubular invaginations in MC simulations

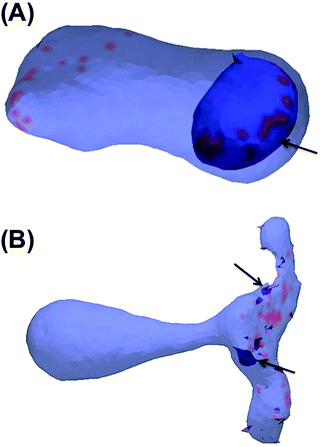
In this section, the cooperative effects of STxB binding to the vesicle membrane on the geometrical conformations of the membrane were investigated using MC simulations. The bending rigidity of a DOPC lipid bilayer is around 20k_BT.³³ However, Gb₃ gives rise to a significant ordering of the bilayer.²² Therefore we have chosen 6 different values for bending rigidity, κ = 10, 20, 30, 40, 50, 60k_BT to cover the relevant value for the DOPC/Gb₃ mixture. Proteins were randomly distributed on the surface of the vesicle (P_v = 5%, 10%, and 20%). Three different values of the protein–protein interaction strength, ε = 0.5, 1, 2k_BT, were tested. Despite the small local curvature induced by STxB (small compared to N-BAR domain proteins³⁴) and despite the relatively weak interaction among them, the fields still drive the vesicle to form long and narrow tubular invaginations (Fig. 6A (κ = 60k_BT), Fig. 6B and C (κ = 30k_BT) and Fig. S2, ESI†), which are covered by STxB proteins. For ε ≤ 0.5k_BT, no stable tube formation was observed, while for ε ≥ 1k_BT stable tubes were observed for all compositions. An interesting aspect of the tube morphology is the formation of a narrow neck that connects the tube to the surface of the vesicle. Although at first sight such a neck formation seems to be energetically unfavourable, theoretical calculations on catenoid-like surfaces show that this configuration can in fact form with very low energy cost³⁵ (the mean curvature of the catenoid being zero). The formation of the neck is important because it may assist scission, e.g. by dynamin.⁵

Fig. 6 Tubular invagination induced by STxB on a vesicle whose surface is 20% (A) and 10% (B and C) covered by a curvature-inducing field that represents membrane-bound STxB proteins. Blue color shows the free surface of the membrane, and red indicates the areas where proteins are present. The vesicles are partially transparent so that the tubular invaginations (indicated by black arrows) can be seen. The lack of a volume constraint gives rise to a variety of vesicle shapes. However, the membrane surface is smooth except on the neck of the invaginations. The inside of the invagination regions are topologically connected to the outside of the vesicle via narrow necks. These narrow necks are indicated by red arrows.

STxB mutant (W34A) fails to induces tubular invagination

In order to investigate the role of the induced local curvature on the formation of tubular invaginations, we performed 32 different simulations for ε = 0.5, 1, 2, 3k_BT and different random number seeds with proteins that induce zero local curvature (C₀ = 0). In none of these cases was a significant deformation in the morphology of the vesicles observed (ESI,† Fig. S3) although clustering was observed for ε ≥ 1k_BT. Thus, we conclude that tubular invaginations do not form in the absence of a local STxB-induced curvature. This result combined with the finding of the MD simulations, that no local curvature is induced by STxB mutant W34A (Fig. 4C), is consistent with experimental observation that this mutant does not induce tubular invaginations.⁵

Gb₃ acyl chain saturation

The MD simulations have revealed that STxB induces a small local curvature on the surface of a fluid bilayer in interaction with both S-Gb₃ and U-Gb₃. However, experiments have shown that tubular invaginations on GUVs only form with U-Gb₃.⁵ So far we have simulated fluid vesicles, based on the definition of the Hamiltonian and the possibility of link flips in the MC moves. According to our previous simulations of a protein-free DOPC–Gb₃ system, we predicted that membranes containing a high concentration of S-Gb₃ are not in the liquid phase.²² Membranes in an ordered phase cannot be described by the Helfrich Hamiltonian. However, the importance of the membrane fluidity can be studied by removing the link flips in MC moves. It was observed that tubular invaginations did not form under these conditions (not shown). We hence strengthen the hypothesis proposed in ref. 22 that local increase in S-Gb₃ concentration due to STxB clustering results in ordering of the bilayer, and therefore STxB is unable to induce tubular invaginations on a bilayer containing S-Gb₃.

Effect of the different values of induced local curvature

So far we have shown that inclusions that induce a local curvature of C₀ ≈ 0.035 nm⁻¹ (or in MC length scale: C₀ ≈ 0.24a⁻¹) and cluster via membrane-mediated interactions drive the formation of tubular membrane invaginations with narrow necks that connect them to the vesicle surface (Fig. 6). We further investigated whether upper and lower limits exist for C₀. We have systematically varied the value of C₀ in the interval of C₀ = [0.01a⁻¹ : 0.6a⁻¹] with an increment of 0.01 (initial configuration was built as Fig. 2B). The results show that the lower limit is C₀ = 0.09a⁻¹ (C₀ = 0.013 nm⁻¹) and above this value, inclusions induce a tubular membrane invaginations as shown in Fig. 7A. However, regarding the upper limit, we need to be more cautious. For 〈C₀〉 = 0.55a⁻¹ (C₀ = 0.083 nm⁻¹) only small inward budding (Fig. 7B) was observed. However, this curvature radius is in a range that is close to the coarse graining length scale (R ∼ a), and the MC model may not apply any more. Therefore further investigation is required to determine the upper limit of C₀.

Fig. 7 (A) Tubular invaginations are formed for small values of induced local curvature (C₀ = 0.1a⁻¹/0.015 nm⁻¹). (B) Small and polymer like buds are formed for large values of induced local curvature (C₀ = 0.6a⁻¹/0.92 nm⁻¹).

Conclusions

We have combined simulation techniques on atomistic and macroscopic length scales to study the formation of tubular membrane invaginations upon STxB binding to a lipid bilayer system. Our results suggest a pathway for cellular entry that can be exploited by any protein or manufactured nanoparticle that binds tightly to the plasma membrane and induces a small increment of inward-oriented local curvature. The important features of the STxB–Gb₃ complex for invagination are: (1) Gb₃ interacts with different orientations and distances from the normal plane of the membrane with its binding sites on STxB. This allows STxB to induce a small increment of local curvature. (2) Binding site 3 of STxB plays a crucial role for the induction of local curvature, providing an explanation for the decreased ability of Shiga toxin molecules that are mutated at this site to induce membrane invagination and enter cells.^5,36 (3) Clustering of STxB molecules drives the formation of tubular invaginations with narrow necks only in fluid bilayers. This mechanism may also operate for other cargoes that share this fundamental building plan.

Acknowledgements

The authors gratefully acknowledge funding from the European Community's Seventh Framework Programme (FP7/2007–2013) under the grant agreement number TRANSPOL-264399, and Horizon 2020 Framework Programme under the grant agreement number H2020-MSCA-ITN-2014, BIOPOL project. The funding by Agence Nationale pour la Recherche (ANR-11 BSV2 014 03, ANR-14-CE14-0002-02 and ANR-14-CE16-0004-03), Human Frontier Science Program grant RGP0029-2014, and European Research Council advanced grant (project 340485) is also acknowledged. H. K. is funded by Lundbeckfonden. Some parts of the computations were carried out on the Horseshoe clusters at the SDU node for the Danish Center for Scientific Computing (DCSC). We also acknowledge computer resources allocated to the PRACE-2IP project (FP7 RI-283493) resource ARCHER based on the United Kingdom at http://https://www.archer.ac.uk/. We thank Mie Thorborg Pedersen for assisting with figure presentation.

References

1. M. Bonazzi and P. Cossart, FEBS Lett., 2006, 580, 2962–2967.
2. P. Cossart and P. J. Sansonetti, Science, 2004, 304, 242–248.
3. L. Pelkmans and A. Helenius, Curr. Opin. Cell Biol., 2003, 15, 414–422.
4. D. Tran, J. L. Carpentier, F. Sawano, P. Gorden and L. Orci, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7957–7961.
5. W. Romer, L. Berland, V. Chambon, K. Gaus, B. Windschiegl, D. Tenza, M. R. Aly, V. Fraisier, J. C. Florent, D. Perrais, C. Lamaze, G. Raposo, C. Steinem, P. Sens, P. Bassereau and L. Johannes, Nature, 2007, 450, 670–675.
6. H. Ling, A. Boodhoo, B. Hazes, M. D. Cummings, G. D. Armstrong, J. L. Brunton and R. J. Read, Biochemistry, 1998, 37, 1777–1788.
7. S. U. Lauvrak, S. Walchli, T. G. Iversen, H. H. Slagsvold, M. L. Torgersen, B. Spilsberg and K. Sandvig, Mol. Biol. Cell, 2006, 17, 1096–1109.
8. W. Romer, L. L. Pontani, B. Sorre, C. Rentero, L. Berland, V. Chambon, C. Lamaze, P. Bassereau, C. Sykes, K. Gaus and L. Johannes, Cell, 2010, 140, 540–553.
9. H. F. Renard, M. Simunovic, J. Lemiere, E. Boucrot, M. D. Garcia-Castillo, S. Arumugam, V. Chambon, C. Lamaze, C. Wunder, A. K. Kenworthy, A. A. Schmidt, H. T. McMahon, C. Sykes, P. Bassereau and L. Johannes, Nature, 2015, 517, 493–496.
10. M. E. Fraser, M. M. Chernaia, Y. V. Kozlov and M. N. James, Nat. Struct. Biol., 1994, 1, 59–64.
11. A. Donohue-Rolfe, M. Jacewicz and G. T. Keusch, Mol. Microbiol., 1989, 3, 1231–1236.
12. M. L. Torgersen, S. U. Lauvrak and K. Sandvig, FEBS J., 2005, 272, 4103–4113.
13. L. Johannes, C. Wunder and P. Bassereau, Cold Spring Harbor Perspect. Biol., 2014, 6, a016741.
14. H. Ewers, W. Romer, A. E. Smith, K. Bacia, S. Dmitrieff, W. Chai, R. Mancini, J. Kartenbeck, V. Chambon, L. Berland, A. Oppenheim, G. Schwarzmann, T. Feizi, P. Schwille, P. Sens, A. Helenius and L. Johannes, Nat. Cell Biol., 2010, 12, 11–18 ; sup pp. 11–12.
15. G. E. Rydell, L. Svensson, G. Larson, L. Johannes and W. Romer, Biochim. Biophys. Acta, 2013, 1828, 1840–1845.
16. R. Lakshminarayan, C. Wunder, U. Becken, M. T. Howes, C. Benzing, S. Arumugam, S. Sales, N. Ariotti, V. Chambon, C. Lamaze, D. Loew, A. Shevchenko, K. Gaus, R. G. Parton and L. Johannes, Nat. Cell Biol., 2014, 16, 595–606.
17. L. Johannes, R. G. Parton, P. Bassereau and S. Mayor, Nat. Rev. Mol. Cell Biol., 2015, 16, 311–321.
18. B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Muller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464.
19. A. Saric and A. Cacciuto, Phys. Rev. Lett., 2012, 109, 188101.
20. A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102.
21. N. Ramakrishnan, P. B. Sunil Kumar and J. H. Ipsen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041922.
22. W. Pezeshkian, V. V. Chaban, L. Johannes, J. Shillcock, J. H. Ipsen and H. Khandelia, Soft Matter, 2015, 11, 1352–1361.
23. S. Pronk, S. Pall, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854.
24. H. J. C. Berendsen, D. Vanderspoel and R. Vandrunen, Comput. Phys. Commun., 1995, 91, 43–56.
25. P. Bjelkmar, P. Larsson, M. A. Cuendet, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2010, 6, 459–466.
26. J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell, Jr. and R. W. Pastor, J. Phys. Chem. B, 2010, 114, 7830–7843.
27. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
28. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697.
29. S. Nose, Mol. Phys., 1984, 52, 255–268.
30. B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
31. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
32. H. J. C. Berendsen, J. P. M. Postma, W. F. Vangunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
33. Y. Lyatskaya, Y. Liu, S. Tristram-Nagle, J. Katsaras and J. F. Nagle, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 011907.
34. P. D. Blood and G. A. Voth, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15068–15072.
35. B. Fourcade, L. Miao, M. Rao, M. Wortis and R. K. Zia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5276–5286.
36. D. J. Bast, L. Banerjee, C. Clark, R. J. Read and J. L. Brunton, Mol. Microbiol., 1999, 32, 953–960.

---

Footnote

† Electronic supplementary information (ESI) available: Three figures and one table. See DOI: 10.1039/c6sm00464d

---