Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-equimolar discrete compounds in binary chiral systems of organic substances†
Elena N.
Kotelnikova
 a,
Anton I.
Isakov
a and
Heike
Lorenz
*b
a,
Anton I.
Isakov
a and
Heike
Lorenz
*b
aDepartment of Crystallography, Saint Petersburg State University, Universitetskaya emb. 7/9, 199034 Saint Petersburg, Russia
bMax Plank Institute for Dynamics of Complex Technical Systems, Sandtorstrasse 1, 39106 Magdeburg, Germany. E-mail: lorenz@mpi-magdeburg.mpg.de; Tel: +49 391 6110 293
First published on 23rd March 2017
Abstract
Since knowledge on the occurrence of non-equimolar discrete compounds in binary systems containing chiral molecules is very limited, this study reviews and systematizes the current state of investigating such systems and summarizes the results on two example systems studied in detail by the authors. In particular, the identification and verification of the non-equimolar discrete compounds compared to other discrete solid phases occurring in the two systems are discussed by presenting the results of related SCXRD, PXRD, TRPXRD, DSC, IR, and HSM studies. The (S)-malic acid–(R)-malic acid system has been found to contain non-equimolar 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3
3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stable (S3R and SR3) and metastable (3S1R and 1S3R) discrete compounds, along with the equimolar compounds RSI and RSII (known monoclinic modifications) and the recently discovered RSIII modification. Polymorphic transformations of the discrete phases are debated, and the crystal structure of the stable compound S3R is identified (S. G. P1). The L-valine–L-isoleucine system has been stated to contain a non-equimolar 2
1 stable (S3R and SR3) and metastable (3S1R and 1S3R) discrete compounds, along with the equimolar compounds RSI and RSII (known monoclinic modifications) and the recently discovered RSIII modification. Polymorphic transformations of the discrete phases are debated, and the crystal structure of the stable compound S3R is identified (S. G. P1). The L-valine–L-isoleucine system has been stated to contain a non-equimolar 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 discrete compound, V2I, that could independently be proven by the ternary solubility diagram in water and its crystal structure solved (S. G. C2). The results obtained are discussed in conjunction with the findings reported in the literature. In order to systematize the variety of terms used for the description of discrete phases in binary chiral systems of organic substances, a systematization of equimolar and non-equimolar compounds based on chemical and crystallographic characteristics is proposed.
1 discrete compound, V2I, that could independently be proven by the ternary solubility diagram in water and its crystal structure solved (S. G. C2). The results obtained are discussed in conjunction with the findings reported in the literature. In order to systematize the variety of terms used for the description of discrete phases in binary chiral systems of organic substances, a systematization of equimolar and non-equimolar compounds based on chemical and crystallographic characteristics is proposed.
1. Introduction
When studying the limits of solid solutions and the polymorph diversity of organic compounds, several geometric and chemical factors are taken into account, such as dimensions, shape, and symmetry of a molecule, as well as the type of intermolecular bonding.1–3 In the last decades, further geometrical (stereochemical) factors – the molecule chirality and its configuration4 – have been found to be essential for the analysis of molecular packing in crystal structures of enantiomeric compounds.5,6 An avalanche-like growing interest in a rather abundant class of organic substances that contain chiral molecules is prompted by their numerous applications in the pharmaceutical industry, medicine, biochemistry7–11 and even in geology,12–16 where they are used, for example, for sediment rock dating; the last method is based on interrelations between levorotatory and dextrorotatory enantiomers in fossilized organic matter.13,16 Industrial use and treatment of biochemically active chiral compounds requires development and improvement of synthesis techniques and also of methods for chiral resolution and purification. This requires, in its turn, a fundamental knowledge and understanding of the phase equilibria and crystal chemistry in chiral systems.6–20The three general types of phase diagrams known for chiral systems are shown in Fig. 1 (upper part).5,21 These are diagrams containing a eutectic (Fig. 1a), a binary compound (Fig. 1b), and (complete) solid solutions (Fig. 1c). The exact type of phase diagram is determined by the nature of the equimolar (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) mixture of enantiomers. The diagram of the first type corresponds to a physical mixture of enantiomers, or conglomerate, S + R; the second type to a binary compound (racemic compound5), RS; and the third type to a solid solution, S,R. Schematic representations of the equimolar compositions that correspond to the three types mentioned are illustrated in Fig. 1 (bottom part). The maximum of the liquidus line of the racemic compound can lie above or below the melting points of the enantiomers or even be equal to them (Fig. 1b). So, the diagrams of the second type can be further divided into three subtypes.5,6,22 Analogous subtypes are allocated for the diagrams containing solid solutions (Fig. 1c). According to J. Jacques et al.,5 a majority of binary systems (∼90%) belongs to the second type, while the first type systems are much less frequent (∼10%), with the third type being the rarest.
1) mixture of enantiomers. The diagram of the first type corresponds to a physical mixture of enantiomers, or conglomerate, S + R; the second type to a binary compound (racemic compound5), RS; and the third type to a solid solution, S,R. Schematic representations of the equimolar compositions that correspond to the three types mentioned are illustrated in Fig. 1 (bottom part). The maximum of the liquidus line of the racemic compound can lie above or below the melting points of the enantiomers or even be equal to them (Fig. 1b). So, the diagrams of the second type can be further divided into three subtypes.5,6,22 Analogous subtypes are allocated for the diagrams containing solid solutions (Fig. 1c). According to J. Jacques et al.,5 a majority of binary systems (∼90%) belongs to the second type, while the first type systems are much less frequent (∼10%), with the third type being the rarest.
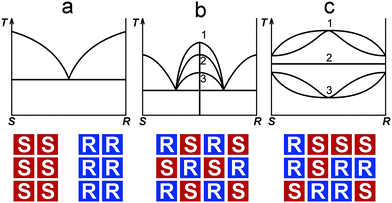 | ||
| Fig. 1 Three basic types of phase diagrams characterizing binary systems formed by S- and R-enantiomers. At the top: diagrams of the systems containing a conglomerate (a), a racemic compound (b), and solid solutions (c). Subtypes 1, 2, and 3 of racemic compounds have melting points that lie above, are equal to, or lie below the melting points of the enantiomers; subtypes 1, 2, and 3 of the solid solutions are presented in the following order: a non-ideal solution having a maximum, an ideal solution, and a non-ideal solution having a minimum.5At the bottom: schematic representations of molecular packing in the equimolar phases corresponding to the diagrams above. | ||
A diagram of each type may be further complicated due to polymorphism of the system components and/or equimolar compounds. Moreover, the diagrams of the first two types can be additionally diversified due to the formation of limited solid solutions.19 For example, in very recent work,23 C. Brandel et al. described the complex behavior of the diprophylline enantiomers, a system where solid solutions form in addition to the polymorphism of both the equimolar compound and the enantiomer.23 Possible phase diagram arrangements that can result from such complications are discussed in detail by G. Coquerel.6 However, all the diagrams presented there correspond to binary systems of the same group, viz. systems consisting of enantiomers of the same chemical compound.
In the published literature, there are sparse data on two other groups of binary systems containing chiral molecules. One group includes systems of diastereomers and the other systems of enantiomers of different compounds. Examples of our investigations of the solid phases existing in binary systems of the three above groups are summarized in Table 1.
| Molecular components | System | Number of chiral centers | Solid phase characteristics | Ref. |
|---|---|---|---|---|
| Designations: E3ClMA – ethanolamine salt of 3-chloromandelic acid; Thr and aThr – threonine and allo-threonine; Val – valine; Ile – isoleucine. | ||||
| Systems of enantiomers of the same compound | ||||
| Enantiomers | (S)-E3ClMA–(R)-E3ClMA | 1 and 1 | Eutectic mixture and limited solid solutions | 24, 25 |
| Enantiomers | (S)-Malic acid–(R)-malic acid | 1 and 1 | Equimolar (RS) and non-equimolar (S3R and SR3) discrete compounds and limited solid solutions | 26, 27, 28, 29 |
| Enantiomers | L-Thr–D-Thr (L-aThr–D-aThr) | 2 and 2 | Eutectic mixture | 30 |
| Systems of diastereomers of the same compound | ||||
| Diastereomers | D-Thr–L-aThr (L-Thr–D-aThr) | 2 and 2 | Eutectic mixtures | 31 |
| Diastereomers | L-Thr–L-aThr (D-Thr–D-aThr) | 2 and 2 | Complete miscibility | 32, 33 |
| The system of enantiomers of different compounds | ||||
| Enantiomers of different compounds | L-Val–L-Ile (D-Val–D-Ile) | 1 and 2 | Non-equimolar discrete compound (V2I) and limited solid solutions | 34, 35 |
The three systems of the first group24–30 contain enantiomers of the same compound. The system formed by the S- and R-enantiomers of the ethanolamine salt of 3-chloromandelic acid (E3ClMA) is an example of a eutectic system with partial miscibility between the components.24,25 The system of malic acid S- and R-enantiomers belongs to the type 2 systems showing different polymorphs of the racemic compound and limited solid solutions.26–29 Moreover, the system is complicated by the presence of two non-equimolar discrete compounds, S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1
R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3
3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.29 The system of L- and D-enantiomers of threonine is a eutectic system free from solid solutions.30 Two shown systems of the second group are formed by diastereomers of the same compound. D- and L-allo-diastereomers of threonine form a eutectic system,31 where, in contrast to the L- and D-threonine system, the eutectic point must be shifted from the equimolar composition. L- and L-allo-diastereomers of threonine show full miscibility in the solid state,32,33 and the phase diagram is asymmetric due to different components' melting points/solubilities.32 The third groups' system studied consists of enantiomers of different compounds: L-valine and L-isoleucine. This system is characterized by the occurrence of a non-equimolar discrete compound Val
1.29 The system of L- and D-enantiomers of threonine is a eutectic system free from solid solutions.30 Two shown systems of the second group are formed by diastereomers of the same compound. D- and L-allo-diastereomers of threonine form a eutectic system,31 where, in contrast to the L- and D-threonine system, the eutectic point must be shifted from the equimolar composition. L- and L-allo-diastereomers of threonine show full miscibility in the solid state,32,33 and the phase diagram is asymmetric due to different components' melting points/solubilities.32 The third groups' system studied consists of enantiomers of different compounds: L-valine and L-isoleucine. This system is characterized by the occurrence of a non-equimolar discrete compound Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile = 2
Ile = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and limited solid solutions.34,35
1 and limited solid solutions.34,35
Polymorphism of enantiomers and their equimolar compounds is rather common among chiral systems.6 However, the systems (S)-malic acid–(R)-malic acid and L-valine–L-isoleucine show relatively rarely reported additional phase behaviours as limited solid solutions and, in particular, non-equimolar discrete compounds. Both, as well as literature data concerning these and similar systems, will be presented in this paper. A discrete compound as used here is a solid phase with fixed stoichiometry (equimolar or not but stoichiometric) having a crystal structure different from the compound components and, hence, clearly differs from solid solutions.
The paper is structured as follows. After introducing in section 2 the materials and experimental methods used in our own studies, in section 3, the systems of enantiomers of the same compound containing non-equimolar discrete phases are reviewed and followed by a detailed discussion of the (S)-malic acid–(R)-malic acid example. Section 4 refers to the systems of enantiomers of different compounds containing equimolar and non-equimolar discrete solid phases with a special emphasis on the L-Val–L-Ile system. For both exemplary systems, particular focus is set on discrete compounds described recently. In section 5, a systematization of the discrete compounds occurring in binary chiral systems of organic substances is suggested. Finally, the main results are summarized, and conclusions are drawn.
2. Materials and methods
2.1 Materials
2.2 Experimental techniques
3. Systems of enantiomers of the same compound containing non-equimolar discrete phases
3.1 Overview
A list of enantiomeric systems, which are found to contain equimolar, as well as non-equimolar discrete compounds («anomalous racemates»), is presented in Table 2. Published data on the formation of non-equimolar discrete compounds in chiral systems is not always reliable, in particular, when the study is only based on melting point/DSC analyses, and the crystal structure of the compounds is not deciphered. A brief description of some systems is presented below.Ratio S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
Compounds | Crystal structure; methods of research | Ref. |
|---|---|---|---|
| a This work. | |||
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
2,4-Dimethylglutaric acid | Not determined; melt phase diagram | 36, 37 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
Tetramisole (6-phenyl-2,3,5,6-tetrahydroimidazo[2,1-b][1,3]thiazole) | Not determined; DSC, PXRD | 38 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
3-Hydroxy-4-(2,4,5-trifluorophenyl)butanoic acid | Not determined; DSC, PXRD, HPLC | 21 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
Carvone (2-methyl-5-(prop-1-en-2-yl)cyclohex-2-en-1-one) | Not determined; DSC | 39 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
4-Methyl-7-methylenetricyclo[7.2.1.01,5]dodecan-12-one oxime | Determined | 40 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
Bicyclic bis-lactam derivative BBL7 | Determined | 41 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
Exo-trans-exo-(13R,24R)-14,23-dioxaoctacyclo (25.3.0.02,5.03,29.04,8.06,10.09,13.024,28) triacontane-15,22-dione | Determined | 42 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
1-(Hydroxymethyl)-4,10-dimethyl-3-oxatricyclo[5.2.1.02,4]decan-10-ol | Determined | 43 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
2-Diisopropylcarbamoyl-3-methylpentane-3,4-diol | Determined | 44 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
rac-2,2′-di(Ethoxycarbonyl)-6,6′,7,7′-tetramethoxy-1,1′,2,2′,3,3′,4,4′-octahydro-1,1′-bisisoquinoline | Determined | 45 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
(E)-3,4-Di-t-butyl-1,1,2,2-tetrakis(trimethylsilyl)-1,2-disilacyclobutane | Determined | 46 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
trans-(1RS,3RS)-2-N,N′-Dimethylaminomethyl-1,3-dithiolane-1,3-dioxide | Determined | 47 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
3-Propyl-4-(p-toluenesulfonylamino)-1,2-diselenolane | Determined | 48 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
3-(2-tert-Butylphenoxy)-propane-1,2-diol | Determined | 49 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
6-(Dimethoxymethylene)-dibenzo(d,k)tricyclo(5.2.2.03,7)undeca-4,10-dien-8-one | Determined | 50 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
Malic acid | Determined;a PXRD, DSC, SCXRD, TRPXRD, IR, HSM | 29, 37, anda |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. They found that the homogeneous precipitate obtained via such crystallization has a unique optical activity value. Its angle of optical rotation [α]D was +/−7.2°, while the same parameter for the enantiomers was +/−22°. On this basis, they stated that the compound in question could crystallize in the racemic form and two additional compounds 1
2. They found that the homogeneous precipitate obtained via such crystallization has a unique optical activity value. Its angle of optical rotation [α]D was +/−7.2°, while the same parameter for the enantiomers was +/−22°. On this basis, they stated that the compound in question could crystallize in the racemic form and two additional compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 2
2 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Quite recently (2015), A. A. Bredikhin et al.52 proved in a reinvestigation via IR spectra, SCXRD and PXRD analysis, and solubility data that no additional compounds exist in the system. Taking this into account, we did not include the system in Table 2.
1. Quite recently (2015), A. A. Bredikhin et al.52 proved in a reinvestigation via IR spectra, SCXRD and PXRD analysis, and solubility data that no additional compounds exist in the system. Taking this into account, we did not include the system in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. The authors53 assumed that the matter analyzed was a solid solution. Later, J. E. Tabora et al.21 mentioned that the existence of unit cells with 1
3. The authors53 assumed that the matter analyzed was a solid solution. Later, J. E. Tabora et al.21 mentioned that the existence of unit cells with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3
3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 populations in the crystal structure of racemic naringenin can be indirect evidence of the presence of 1
1 populations in the crystal structure of racemic naringenin can be indirect evidence of the presence of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 phases in the system. In our opinion, this crystal structure can be regarded as a partially disordered racemate since the authors21 showed it to be centrosymmetric (present authors' note: pseudo-centrosymmetric).
3 phases in the system. In our opinion, this crystal structure can be regarded as a partially disordered racemate since the authors21 showed it to be centrosymmetric (present authors' note: pseudo-centrosymmetric).
As a result, Table 2 contains 16 systems with non-equimolar discrete compounds of which we have knowledge. It should be mentioned that crystal structures of four of the listed compounds have not yet been clarified.21,36–39 For example, paper21 reports the results of the crystallization of different mixtures of the 3-hydroxy-4-(2,4,5-trifluorophenyl)butanoic acid enantiomers from toluene solutions. In the ternary phase diagram, two additional eutonics and a maximum in-between were detected. The composition S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1
R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, corresponding to the maximum, showed both a unique melting point and X-ray powder pattern, leading to the conclusion that it is a discrete compound.
3, corresponding to the maximum, showed both a unique melting point and X-ray powder pattern, leading to the conclusion that it is a discrete compound.
Thus, the compounds found in the systems discussed must be further investigated since a final conclusion can be drawn only after depicting their crystal structures. For this reason, the detection of such compounds can be considered completely valid only for 12 (ref. 29, 40–50) of the systems shown in Table 2. Among them, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 1
2 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 compounds are reported for eight and three cases, respectively; for one system, a 1
3 compounds are reported for eight and three cases, respectively; for one system, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 compound is described. Beside our research on the malic acid system in section 3.2, two examples shall be briefly mentioned.
5 compound is described. Beside our research on the malic acid system in section 3.2, two examples shall be briefly mentioned.
R. G. Kostyanovsky et al.41 determined crystal structures for two chiral compounds belonging to the group of bicyclic bis-lactam (BBL). There, compound BBL7 is composed of three different, independent homochiral chains: two of them comprising molecules of the same chirality, –R–R–R–, while the third contains molecules of chirality –S–S–S–. Therefore, it could be classified as a compound of an S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1
R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 type. A. A. Bredikhin et al.49 studied the 3-(2-tert-butylphenoxy)-propane-1,2-diol system and found an additional peak in the DSC curve for the composition with an S
2 type. A. A. Bredikhin et al.49 studied the 3-(2-tert-butylphenoxy)-propane-1,2-diol system and found an additional peak in the DSC curve for the composition with an S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R ratio close to 1
R ratio close to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. SCXRD analysis of that sample allowed identification of a discrete phase and its crystal structure.
3. SCXRD analysis of that sample allowed identification of a discrete phase and its crystal structure.
3.2 The system (S)-malic acid–(R)-malic acid
In addition to the racemic compound, the presence of “anomalous racemates” in the malic acid system was firstly reported in paper.37 The authors studied some enantiomeric compositions using HSM and plotted the phase diagram. Besides the maximum corresponding to the racemic compound (RSI, the only modification known at that time), they found additional inflexion points of the liquidus line at compositions S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 3
1 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. They also found that the sample crystallized from aqueous solution with the composition S
1. They also found that the sample crystallized from aqueous solution with the composition S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1
R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 was characterized by a unique diffraction pattern. Later, the authors of other work63 discovered a second monoclinic polymorph of the racemic compound (RSII). They assumed that the inflexions of the liquidus line discovered by previous authors resulted from the intersections of two liquidus lines belonging to the different polymorphs of the racemic compound, which, consequently, could not be proof of the anomalous racemates existence. For many years, this point of view has prevailed. Later, H. Kaemmerer et al.26 carried out experiments to verify that the racemic forms RSI and RSII are monotropically related. They showed that the lower melting form RSII undergoes a polymorphic phase transition to RSI by storage at room temperature. The DSC data also proved monotropy in accordance with the heat-of-fusion rule.64 DSC and DTA studies on S- and RS-malic acid have been also reported by other authors.65
3 was characterized by a unique diffraction pattern. Later, the authors of other work63 discovered a second monoclinic polymorph of the racemic compound (RSII). They assumed that the inflexions of the liquidus line discovered by previous authors resulted from the intersections of two liquidus lines belonging to the different polymorphs of the racemic compound, which, consequently, could not be proof of the anomalous racemates existence. For many years, this point of view has prevailed. Later, H. Kaemmerer et al.26 carried out experiments to verify that the racemic forms RSI and RSII are monotropically related. They showed that the lower melting form RSII undergoes a polymorphic phase transition to RSI by storage at room temperature. The DSC data also proved monotropy in accordance with the heat-of-fusion rule.64 DSC and DTA studies on S- and RS-malic acid have been also reported by other authors.65
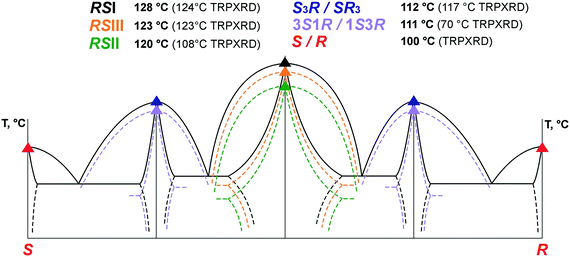
Phase diversity in the (S)-malic acid–(R)-malic acid system. The system of malic acid enantiomers appeared to be more complex than it seemed before. Firstly, along with the known monoclinic modifications RSI and RSII, a third modification of the racemic compound RSIII can be formed. Secondly, in addition to the equimolar compound RS, non-equimolar discrete phases with the ratio S
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 occur that thirdly, can crystallize as stable S3R (SR3) and metastable 3S1R (1S3R) modifications. Moreover, the discovery of additional discrete phases necessitated further adjusting the limits of solid solutions in this system.
3 occur that thirdly, can crystallize as stable S3R (SR3) and metastable 3S1R (1S3R) modifications. Moreover, the discovery of additional discrete phases necessitated further adjusting the limits of solid solutions in this system.
Equimolar discrete compounds. PXRD studies of samples of the racemic compounds crystallized from various solvents showed27 that the polymorphic diversity of the RS compound depends, first of all, upon the crystallization medium and the crystallization rate (ESI:†Table 1). The influence of some other crystallization conditions is discussed in details in the paper.27 Phase distribution of the crystallization products according to the crystallization time (ESI:†Table 1) correlates with estimation of the stability of the various phases based on DSC data.
Non-equimolar discrete compounds. A PXRD study of samples with an enantiomer ratio of S
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (1
1 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) allowed the determination of stable S3R (SR3) and metastable modifications 3S1R (1S3R) of 3
3) allowed the determination of stable S3R (SR3) and metastable modifications 3S1R (1S3R) of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
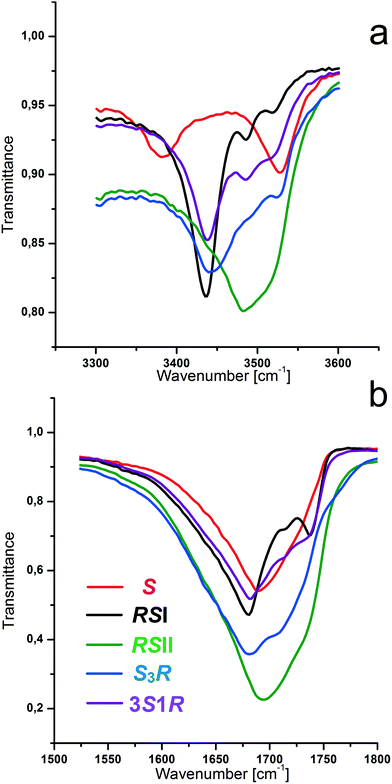
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 discrete compounds in the system.66 As for the racemic compound, the diversity of the polymorphic modifications of these compounds depends upon the crystallization medium and the crystallization rate (ESI:†Table 1). The presence of the non-equimolar discrete phases in the system was also confirmed by IR-spectroscopy, DSC and HSM studies. We obtained IR spectra of the malic acid equimolar and non-equimolar compounds in the area of 4000–400 cm−1. Fig. 2a and b show the IR spectra of S-enantiomer, racemic compounds RSI and RSII and non-equimolar S3R and 3S1R discrete phases in the diagnostic ranges of 3600–3300 cm−1 and 1740–1630 cm−1. It can be seen that each of the phases S, RSI, RSII, SR3, and 3S1R, of malic acid has its own spectrum that allows for the use of IR-spectroscopy for their identification. The results for the known racemic and enantiomer phases agree with data reported in the works26,63 and do not contradict other literature findings.67
3 discrete compounds in the system.66 As for the racemic compound, the diversity of the polymorphic modifications of these compounds depends upon the crystallization medium and the crystallization rate (ESI:†Table 1). The presence of the non-equimolar discrete phases in the system was also confirmed by IR-spectroscopy, DSC and HSM studies. We obtained IR spectra of the malic acid equimolar and non-equimolar compounds in the area of 4000–400 cm−1. Fig. 2a and b show the IR spectra of S-enantiomer, racemic compounds RSI and RSII and non-equimolar S3R and 3S1R discrete phases in the diagnostic ranges of 3600–3300 cm−1 and 1740–1630 cm−1. It can be seen that each of the phases S, RSI, RSII, SR3, and 3S1R, of malic acid has its own spectrum that allows for the use of IR-spectroscopy for their identification. The results for the known racemic and enantiomer phases agree with data reported in the works26,63 and do not contradict other literature findings.67
Phase relationships in the (S)-malic acid–(R)-malic acid system. The TRPXRD method showed that the racemic phases RSI and RSIII do not undergo polymorph transformations until the substances reached their melting points at 124 °C and 123 °C, respectively. However, heating a sample of an RSI + RSIII mixture resulted in a homogenization at 110–123 °C to form RSI and the subsequent melting of the latter at 124 °C. In addition, a slurry experiment where a RSI + RSIII mixture was slurried in an acetonitrile solution for 1 month also showed RSI to be stable and RSIII to be metastable. Upon heating, the RSII phase transforms into RSI at a temperature of 106–108 °C. The experiments confirmed stability of the RSI phase, the obvious metastability of RSII, and the less obvious metastability of RSIII at ambient temperature.
Fig. 3 shows the DSC melting curves for the three racemic phases and the non-equimolar S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 modifications of malic acid. The melting temperatures increased in the order 3S1R, S3R, RSII, RSIII, RSI. Based on the heat-of-fusion rule,64 the monotropic relationships between the polymorphs RSI, RSII and RSIII of the racemic compound as well as the polymorphs S3R and 3S1R of the non-equimolar discrete compounds could be proven (Fig. 3).
1 modifications of malic acid. The melting temperatures increased in the order 3S1R, S3R, RSII, RSIII, RSI. Based on the heat-of-fusion rule,64 the monotropic relationships between the polymorphs RSI, RSII and RSIII of the racemic compound as well as the polymorphs S3R and 3S1R of the non-equimolar discrete compounds could be proven (Fig. 3).
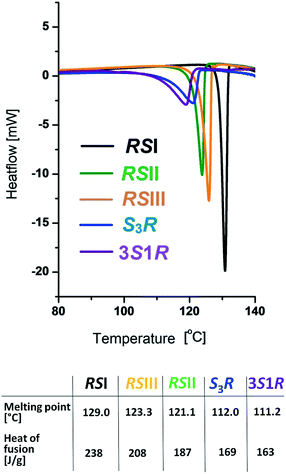 | ||
| Fig. 3 DSC curves and derived melting data of the racemic compounds RSI, RSII, and RSIII and the S3R and 3S1R compounds of malic acid. | ||
Thermomicroscopic (HSM) investigations of the S-enantiomer, racemic compounds RSI and RSII, physical mixtures of enantiomers S + R with the proportions of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for the components, and the non-equimolar discrete compounds S3R and 3S1R were performed (ESI:†Fig. 1). Close to the DSC results, the heating of the enantiomer and racemates RSI and RSII did not lead to any noticeable changes until melting of the substances. Instead of powders, in experiments with a 1
3 for the components, and the non-equimolar discrete compounds S3R and 3S1R were performed (ESI:†Fig. 1). Close to the DSC results, the heating of the enantiomer and racemates RSI and RSII did not lead to any noticeable changes until melting of the substances. Instead of powders, in experiments with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 physical mixture of enantiomers S + R, we used two homochiral crystallites obtained by quenching the melt of the corresponding enantiomers (ESI:†Fig. 1a). The interaction between the enantiomers starts at the contact area of the two grains and leads to the formation of racemic compound. This correlates with the fact that the crystallization of a melt containing two enantiomers provides the compound RSII (ESI:†Table 1). Experiments with the 3
1 physical mixture of enantiomers S + R, we used two homochiral crystallites obtained by quenching the melt of the corresponding enantiomers (ESI:†Fig. 1a). The interaction between the enantiomers starts at the contact area of the two grains and leads to the formation of racemic compound. This correlates with the fact that the crystallization of a melt containing two enantiomers provides the compound RSII (ESI:†Table 1). Experiments with the 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 physical mixture (S + R) were run with powders (ESI:†Fig. 1b). They resulted in the formation of the discrete compound that finally melts. After recrystallization, a crystallite was taken, which was the metastable discrete phase 3S1R, and analyzed (ESI:†Fig. 1c). A visible transformation of the metastable into the stable phase, 3S1R → S3R, was not observed. The substance melted and recrystallized after removal of the heat.
1 physical mixture (S + R) were run with powders (ESI:†Fig. 1b). They resulted in the formation of the discrete compound that finally melts. After recrystallization, a crystallite was taken, which was the metastable discrete phase 3S1R, and analyzed (ESI:†Fig. 1c). A visible transformation of the metastable into the stable phase, 3S1R → S3R, was not observed. The substance melted and recrystallized after removal of the heat.
The thorough study of the malic acid system resulting in identification of various modifications of the equimolar and non-equimolar discrete phases as well as the limits of solid solutions in two of the systems28 facilitates compiling a schematic representation of the phase diagram (Fig. 4). It is based on the data obtained by the PXRD, TRPXRD, DSC, HSM, IR, and SCXRD methods mentioned. The given melting points originate from both the DSC and TRPXRD results. The limits of solid solutions were allocated using the results of a PXRD study of molten mixtures (ESI:†Fig. 2). When compared with the known diagrams of the second type5,21 (see Fig. 1), the diagram of the malic acid system is very complex with the following characteristics. 1) The racemic compound can form three polymorphic modifications, with two of them already known26,58–60,63,65 (RSI and RSII), and the third one (RSIII) discovered by the present authors.27 2) Non-equimolar discrete compounds with the ratio S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 3
R = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (ref. 29) are formed in the system. 3) The non-equimolar discrete compounds can crystallize in stable (S3R and SR3) and metastable (3S1R and 1S3R) modifications. 4) Studies of the detected discrete phases allow determination of the areas of solid solutions in this system, which are found in the vicinity of all the discrete phases.28
3 (ref. 29) are formed in the system. 3) The non-equimolar discrete compounds can crystallize in stable (S3R and SR3) and metastable (3S1R and 1S3R) modifications. 4) Studies of the detected discrete phases allow determination of the areas of solid solutions in this system, which are found in the vicinity of all the discrete phases.28
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R ratio of 75
R ratio of 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25% obtained from an acetonitrile solution via an isothermal evaporation method was studied by means of SCXRD. The crystal structure data and structure refinement of the compound are presented in ESI:†Table 2. The powder X-ray diffraction pattern calculated using the structural data (ESI:†Fig. 3a) is consistent with the experimental diffractogram of the stable compound S3R (ESI:†Fig. 3b) and differs from the pattern of the metastable compound 3S1R (ESI:†Fig. 3c). ESI:†Table 3 shows the triclinic cell parameters of the compound S3R in comparison to the other discrete phases in the system.
25% obtained from an acetonitrile solution via an isothermal evaporation method was studied by means of SCXRD. The crystal structure data and structure refinement of the compound are presented in ESI:†Table 2. The powder X-ray diffraction pattern calculated using the structural data (ESI:†Fig. 3a) is consistent with the experimental diffractogram of the stable compound S3R (ESI:†Fig. 3b) and differs from the pattern of the metastable compound 3S1R (ESI:†Fig. 3c). ESI:†Table 3 shows the triclinic cell parameters of the compound S3R in comparison to the other discrete phases in the system.
| Systems | Methods of research | Crystal structure | Ref. |
|---|---|---|---|
| (+)-Chlorosuccinic acid–(−)-bromosuccinic acid | Melt phase diagram | Not determined | 68 |
| (+)-Mercaptosuccinic acid–(−)-methylsuccinic acid | Melt phase diagram | Not determined | 69 |
| (−)-Dilactic acid–(+)-2,4-dimethylglutaric acid | Melt phase diagram | Not determined | 70 |
| (−)-Thiodilactic acid–(+)-2,4-dimethylglutaric acid | Melt phase diagram | Not determined | 70 |
| (+)-2-Methylglutaric acid–(−)-2,4-dimethylglutaric acid | Melt phase diagram | Not determined | 36 |
| (+)-m-Methoxyphenoxypropionic acid–(−)-m-bromophenoxypropionic acid | SCXRD | Determined | 71 |
| (S)-2-(3-Bromophenoxy)propionic acid–(R)-2-(3-methoxyphenoxy)propionic acid | SCXRD | Determined | 72 |
| (R)-2-(2,4-Dichlorophenyl)propanoic acid–(S)-2-(2-chloro-4-nitrophenyl)propanoic acid | SCXRD | Determined | 73 |
| (R)-N-(4-Methylbenzoyl)-R-methylbenzylamine–(S)-N-(4-nitrobenzoyl)-R-methylbenzylamine | SCXRD | Determined | 74 |
| (S)-2-(2,4,5-Trichloroanilino)propanoic acid–(R)-2-(2,4,5-trichlorophenoxy)propanoic acid | SCXRD | Determined | 75 |
| (R)-N-(2-Chlorobenzoyl)methylbenzylamine–(S)-N-(2-bromobenzoyl)methylbenzylamine | SCXRD | Determined | 76 |
| (S,S)-2,8-Dichloro-6H,12H-5,11-methanodibenzo[b,f][1,5]diazocine–(R,R)-2,8-dibromo-6H,12H-5,11-methanodibenzo[b,f][1,5]diazocine | SCXRD | Determined | 77 |
| L-Malic–L-tartaric acid | SCXRD | Determined | 78 |
| L-Malic–D-tartaric acid | SCXRD | Determined | 79 |
| D-Valine–L-isoleucine | SCXRD | Determined | 80 |
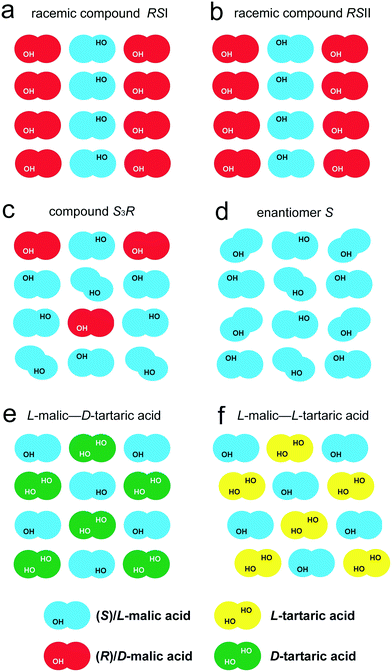
Fig. 5 presents the crystal structure of the compound S3R in projections on the planes ab (a), bc (b), and ac (c). It might be described as an arrangement of molecular chains of two types. Chains of the first “enantiomeric” type are composed of molecules of the same chirality –S–S–S–S–, while chains of the second “racemic” type include alternating molecules of both chiralities –S–R–S–R–.
ESI:†Fig. 4 shows projections of the crystal structures of racemate RSI, racemate RSII, S-enantiomer, and compound S3R onto the ab and bc planes. The most interesting for analysis of these crystal structures are their projections on the ac plane depicted in Fig. 6. It can be seen that the neighbor molecules within the chains are interlinked via hydrogen bonds in all the crystal structures of RSI (Fig. 6a), RSII (Fig. 6b), S (Fig. 6c), and S3R (Fig. 6d). For a convenient description, two opposite edges of the molecules will be designated here as a “head” and a “tail”, where the head is the end of the molecule, which is closer to the side OH group, while the opposite end is, correspondingly, the tail.
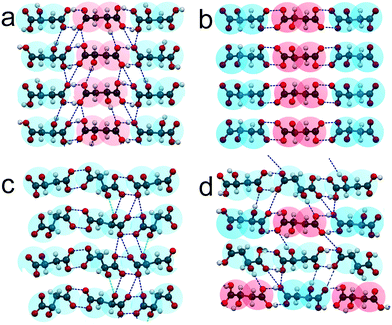 | ||
| Fig. 6 Crystal structures of the racemic compounds RSI (a) and RSII (b), enantiomer S (c), and compound S3R (d) of malic acid in projections upon the ac plane. The color designations of the S- and R-molecules are the same as in Fig. 5. | ||
In the crystal structures of racemate RSI, S-enantiomer and compound S3R, the neighbor molecules have “head-to-head, tail-to-tail” connections. Molecules of different chiralities are characterized by the same conformation in the case of RSI chains and “racemic” chains of S3R. Alternatively, molecules of the same chirality in the case of enantiomer chains and “enantiomeric” chains of S3R are characterized by two conformations; this allows interlinking of such molecules. The crystal structure of RSII contains “head-to-tail” arrangements of molecules. As for RSI, the molecules are also characterized by different chiralities and by the same conformation.
In the crystal structures of all the malic acid compounds, the hydrogen bonds between neighbor molecules are conducted by the edge COOH groups. Two COOH groups belonging to neighbor molecules form carboxylic dimers (dimer ring). The differences in H-bond topography between various compounds (RSI, RSII, S, and S3R) are due to the number of such contacts linking the molecules of the neighbor chains. In the case of RSI (Fig. 6a), there is an alternating number of H-bonds that connect the carboxylic rings corresponding to the neighbor chains. Carboxylic rings forming four contacts alternate with those forming six contacts. In Fig. 6, the contacts connecting the carboxylic dimers, as well as the contacts forming the dimers, are shown by the blue dashed lines. In the case of RSII (Fig. 6b), there are no hydrogen bonds between the neighbor chains. In the case of the S-enantiomer (Fig. 6c), only half of the carboxylic rings are connected to those of a neighbor chain. There are five H-bonds per one ring. Moreover, there are two H-bonds on both sides from the ring that connect the pendant OH groups of the molecules corresponding to the neighbor chains. The contacts are shown by green dashed lines. In the case of S3R (Fig. 6d), there are rings of four types. This is due to molecular chains of two types alternating in the crystal structure – enantiomeric and racemic. In the enantiomeric chains, there are alternating dimers with three and two contacts with the neighbor chains. In the racemic chains, there are alternating dimers forming two and four such contacts.
For convenience, the crystal structures described are schematically shown in Fig. 7(a–d). The use of different colors enables distinguishing S- and R-enantiomer molecules, and the OH groups are indicated to recognize the “tails” and the “heads” of the molecules. The molecule shape reflects its conformation – a straight shape corresponds to the “racemic” conformation, while the slanted shape corresponds to the “enantiomeric” conformation. This representation shows the principle packing of molecular chains of two types in the crystal structure of the compound S3R. The crystal structure is a combination of the racemate RSI chains and S-enantiomer chains.
4. Systems of enantiomers of different compounds containing equimolar and non-equimolar discrete phases
4.1 Systems of enantiomers of different compounds containing equimolar discrete phases
In the available literature, there are a considerable number of publications reporting systems composed of enantiomers of different compounds. Some of these systems belong to the type two (see Fig. 1) since their equimolar compositions are discrete compounds. Fifteen examples of such systems are presented in Table 3,36,68–80 and for ten of the related compounds, the crystal structures were determined using SCXRD. Almost all the represented enantiomeric molecules have only one chiral center, the exceptions being (−)-dilactic acid, (+)-2,4-dimethylglutaric acid and tartaric acid molecules with two equal chiral centers, i.e., the carbon atoms with the chiral centers have the same substituents.70The most interesting for our discussion are three systems: L-malic acid–L-tartaric acid,78L-malic acid–D-tartaric acid79 and D-valine–L-isoleucine,80 while malic acid and L-valine–L-isoleucine are, in turn, the subjects of our studies (see Table 1).
The first two systems differ from each other only in the type of chirality of tartaric acid as the second component. It should be noted that malic and tartaric acids have non-coinciding directions of rotation for the polarized light plane, which are L(−) and D(+) for malic acid and L(+) and D(−) for tartaric acid. The configuration difference of the tartaric acid molecule is reflected in the structure of the resulting binary compounds. The compound formed in the L-malic acid–D-tartaric acid system has the space group P21, while the one in the L-malic acid–L-tartaric acid system is characterized by the space group P1. The schematic representations of the molecular packing in the equimolar compounds of the above systems and selected discrete phases in the system of malic acid enantiomers are shown in Fig. 7(e and f) and (a–d), respectively. The third system, D-valine–L-isoleucine, differs from the one we studied only in having a different chirality in valine. This discrepancy determines the differences in the molecular compositions of the discrete compounds formed in the corresponding systems. A comparative analysis of their crystal structures is given in section 4.2.
L-Malic acid–D-tartaric acid system (Fig. 7e) is denoted L–D′. In the molecular chains of the LD′ binary compound of this system, the malic acid molecules only have the “racemic” conformation. In contrast to the chain arrangements in malic acid RSI and RSII (Fig. 7a and b), the neighbor chains are shifted relative to each other by one molecule in the direction of their elongation. This shift results in the molecules having a staggered arrangement (Fig. 7e). The tartaric acid molecule contains two side OH groups, while malic acid only has one. Hence, the neighbor molecular chains in the crystal structure of tartaric acid form more hydrogen bonds than the chains in the crystal structure of the malic acid racemate RSI.
L-Malic acid–L-tartaric acid system (Fig. 7f) is denoted L–L′. Similar to the LD′ compound, in the molecular chains of the LL′ discrete compound, the malic acid molecules only have the “racemic” conformation, and the neighbor chains are shifted, forming a staggered arrangement. The difference is that the “heads” of the malic acid molecules in the neighbor chains of the binary compound LL′ are directed to the same direction (Fig. 7f), while in the LD′ compound, they face the opposite sides (Fig. 7e).
4.2 Systems of enantiomers of different compounds containing non-equimolar discrete phases: the example of L-Val–L-Ile
We are aware of the existence of only three such systems containing non-equimolar discrete phases (Table 4). Two of them have been studied by means of melting point measurements,36,70 and both are cited in Table 3 since they also include equimolar compounds. According to work,5 these systems tend to form non-equimolar discrete compounds because they involve 2,4-dimethylglutaric acid as a component. The crystal structures of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 discrete compounds have not been determined; their presence was indicated by additional inflexion points in the liquidus lines. Molecules constituting both systems have different chiralities. Each of the molecular components of the system (−)-dilactic acid–(+)-2,4-dimethylglutaric acid has two equal chiral centers, while the molecules of the system (+)-2-methylglutaric acid–(−)-2,4-dimethylglutaric acid possess (with one and two) different numbers of chiral centers.
3 discrete compounds have not been determined; their presence was indicated by additional inflexion points in the liquidus lines. Molecules constituting both systems have different chiralities. Each of the molecular components of the system (−)-dilactic acid–(+)-2,4-dimethylglutaric acid has two equal chiral centers, while the molecules of the system (+)-2-methylglutaric acid–(−)-2,4-dimethylglutaric acid possess (with one and two) different numbers of chiral centers.
| Systems | Ratio | Methods of research | Crystal structure | Ref. |
|---|---|---|---|---|
| (+)-2,4-Dimethylglutaric acid–(−)-dilactic acid | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Melt phase diagram | Not determined | 70 |
| (−)-2,4-Dimethylglutaric acid–(+)-2-methylglutaric acid | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Melt phase diagram | Not determined | 36 |
| L-Valine–L-isoleucine | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
SCXRD, PXRD, TRPXRD | Determined | 34, 35 |
The principal feature distinguishing the L-valine–L-isoleucine system from those discussed above is the same – the L-chirality (configuration) of its components. The valine molecule has one chiral center; isoleucine contains two unequal chiral centers that differ from the (−)-dilactic and (+)-2,4-dimethylglutaric acid molecules, which have equal chiral centers (Table 4).
At least since 1933,81 studies of solubility of Ile and Val in combination, and of individual solubilities of Val82,83 and Ile84,85 have been performed. The equilibria between the solid and liquid phases in the ternary system L-Val–L-Ile–water were studied by I. Kurosawa et al.86 (HPLC and PXRD) and by D. Binev et al.87 (HPLC). H. Koolman and R. Rousseau88 investigated (SCXRD) the effect of small amounts of Val admixture on the growth and morphology of Ile crystals. The detailed correlation to our findings is discussed in work,34 where most of our results for the L-Val–L-Ile system using HPLC (11 samples), PXRD (13 compositions), and SCXRD methods are published. First data obtained by TRPXRD was recently reported.35
According to the PXRD data, the limits of solid solutions in the system L-Val–L-Ile are rather limited. The system has been found to contain a non-equimolar discrete compound V2I with the ratio Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile = 2
Ile = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (∼66 mol% Val). According to this, three areas of solid solutions (ss) originating from valine ssV (>70 mol% Val), isoleucine ssI (<10 mol% Val), and discrete compound ssV2I (60–68 mol% Val) were distinguished; also, two-phase regions were identified consisting of solid solutions ssI + ssV2I (10–60 mol% Val) and ssV2I + ssV (68–70 mol% Val). The results agree well with that obtained by independent HPLC studies. As shown in Fig. 8, the ternary phase diagram of the system L-Val–L-Ile–water contains a local solubility minimum that corresponds to the composition of ∼66 mol% Val and is positioned in-between two eutonics laying asymmetrically left and right from it. Such behavior of the solubility curve is characteristic for systems containing a binary discrete compound.22,89 Although the absolute solubility data (obtained by different methods) differ slightly from each other, they clearly indicate the local solubility minimum close to the 2
1 (∼66 mol% Val). According to this, three areas of solid solutions (ss) originating from valine ssV (>70 mol% Val), isoleucine ssI (<10 mol% Val), and discrete compound ssV2I (60–68 mol% Val) were distinguished; also, two-phase regions were identified consisting of solid solutions ssI + ssV2I (10–60 mol% Val) and ssV2I + ssV (68–70 mol% Val). The results agree well with that obtained by independent HPLC studies. As shown in Fig. 8, the ternary phase diagram of the system L-Val–L-Ile–water contains a local solubility minimum that corresponds to the composition of ∼66 mol% Val and is positioned in-between two eutonics laying asymmetrically left and right from it. Such behavior of the solubility curve is characteristic for systems containing a binary discrete compound.22,89 Although the absolute solubility data (obtained by different methods) differ slightly from each other, they clearly indicate the local solubility minimum close to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Val
1 Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile composition and verify the presence of the related V2I compound in the system.
Ile composition and verify the presence of the related V2I compound in the system.
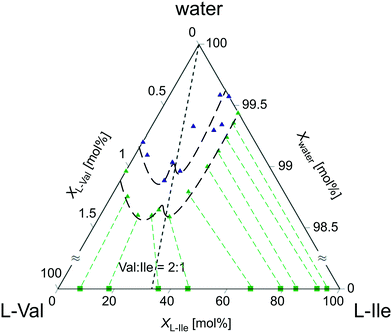 | ||
| Fig. 8 Ternary phase diagram (50 °C) of the system L-Val–L-Ile–water. Green and blue triangles denote solubility data obtained by evaporation and cooling methods, respectively. Note that the solubilities occupy only the upper 1.5 mol% of the diagram. Green squares denote the compositions of the corresponding solids obtained from HPLC compositional analyses. Isotherm line is just to guide the eye (part of the data was published in former work34). | ||
The monoclinic cells of Val and Ile (space group P21) (Fig. 9a and b) are characterized by two crystallographically independent positions of the molecules.90–94 Molecules occupying both positions have the same conformation. The monoclinic cell of V2I (space group C2) (Fig. 9c) is characterized by four independent positions of the molecules, each of which have mixed populations, i.e., can be occupied by either a Val or Ile molecule. The parameter a of the V2I monoclinic cell is doubled in comparison to the corresponding parameters c of Val and Ile monoclinic cells (due to different unit cell orientations). The empirical formula of compound V2I calculated on the basis of structural data corresponds to the Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile ratio of ∼60
Ile ratio of ∼60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and is practically confirmed by the composition of the sample studied (66 mol% Val). The calculated powder X-ray diffraction pattern shows good agreement with the experimentally obtained one.34
40 and is practically confirmed by the composition of the sample studied (66 mol% Val). The calculated powder X-ray diffraction pattern shows good agreement with the experimentally obtained one.34
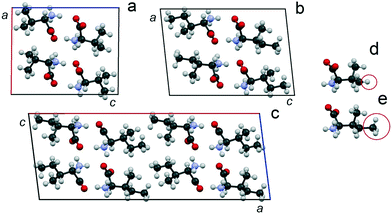 | ||
| Fig. 9 Projections of the monoclinic cells of Val (a), Ile (b) and the discrete compound V2I (c) on the ac plane34 as well as levorotatory molecules of Val (d) and Ile (e). Atoms C, O, N, and H are colored in black, red, blue, and gray, respectively. The H atom of Val and CH3 group of Ile are circled. The projections of the monoclinic cells of Val and Ile are plotted using structural data from CSD (identifiers LVALIN01 and LISLEU02, respectively).94 | ||
Similar to the crystal structures of Val90,92,94 and Ile,91,93,94 the crystal structure of the discrete compound V2I is layered. Molecules in the three crystal structures are combined in H-bonded dimer molecules, and dimers form molecular layers also via H-bonds. The layers interact with each other by van der Waals forces. The Val and Ile dimers are elongated along the c axis, and the layers are connected by axes 21. However, the dimers in the crystal structure of V2I are elongated along the a axis, and the layers are connected by axes 21 and 2. The difference in the azimuthal arrangement of the molecular layers can be seen easily if the doubled unit cell of Ile and the unit cell of V2I are compared (see ESI:†Fig. 5 and work34).
Components of the system D-Val–L-Ile are known in the literature80 and were mentioned before (Table 3). They differ from those of the system L-Val–L-Ile only by the configuration of the valine molecules. These systems exemplify the effect of the different chiralities of the molecules forming a binary system. In the first system,80 an equimolar discrete compound VI (Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile = 1
Ile = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is formed, while in the second system, a non-equimolar discrete compound V2I (Val
1) is formed, while in the second system, a non-equimolar discrete compound V2I (Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile = 2
Ile = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) is formed. The crystal structures of both compounds are characterized by alternating azimuthally non-equivalent molecular layers and by doubled unit cells including two layers in corresponding translation. Wherein, the compound VI crystallizes in the space group P21, and the compound V2I in the space group C2.
1) is formed. The crystal structures of both compounds are characterized by alternating azimuthally non-equivalent molecular layers and by doubled unit cells including two layers in corresponding translation. Wherein, the compound VI crystallizes in the space group P21, and the compound V2I in the space group C2.
Schematic representations of the molecular packing in the crystal structures of Val, Ile, V2I, and VI are shown in Fig. 10 for comparison. Molecules with L-configuration and the coordinates y and y + 1/2 at the b axis of the unit cell are shown in blue and light blue colors, respectively; molecules with D-configuration are in green. Different shapes of the Val and Ile molecules reflect the fact that in comparison to Val, the edge H atom is replaced by a CH3 group in Ile. The group is shown by an additional rear circle. Partial coloring of the circle in the case of V2I symbolizes the partial (33%) occupation of the site by a rear CH3 group.
5. Systematization of discrete compounds formed in binary chiral systems of organic substances
The term “racemate” or “racemic modification” was introduced as early as the 2nd half of the 19th century after L. Pasteur's well-known experiments to describe an enantiomer mixture containing equimolar amounts of the components. However, this definition does not reveal the nature of the mixture itself. In the published literature, there are plenty of terms used for discrete phases in related systems, e.g., true racemates, false conglomerates, quasiracemates, anomalous racemates, anomalous quasiracemates, anomalous conglomerates, cocrystals, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, and others. The importance of knowledge about the variety of solid phases in chiral systems (e.g., for pharmaceutical and food industries) as well as the great scope of acquired data made the following questions emerge: Which particular type of compound is implied when one of the above definitions is used? How do they relate to each other?
1 complexes, and others. The importance of knowledge about the variety of solid phases in chiral systems (e.g., for pharmaceutical and food industries) as well as the great scope of acquired data made the following questions emerge: Which particular type of compound is implied when one of the above definitions is used? How do they relate to each other?
We have attempted to systematize the data on discrete compounds in such systems, and the results are compiled in Table 5. The systematization is not aimed at changing the terminology but clarifying what is exactly meant under the terms mentioned. To make the systematics viable, it is necessary to define the border lines covering the types of compounds that can be included.
Equimolar discrete compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 1
|
||||||
|---|---|---|---|---|---|---|
| Homomolecular (racemic) compounds | Heteromolecular compounds | |||||
| Centrosymmetric | Non-centrosymmetric | Pseudo-centrosymmetric | Non-centrosymmetric | |||
| S and R molecules are connected via other symmetry elements | Independent S and R molecules | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Complexes104 1 Complexes104 |
Quasiracemates105 | Cocrystals79 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes106,108 1 complexes106,108 |
|
| Racemic compounds (true racemates)5 | Racemic compounds (true racemates)5 | Kryptoracemates101 (= false conglomerates102) | ||||
Enantiomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
Enantiomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
Enantiomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R R |
Diastereomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa (R Sa (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra) and S Ra) and S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra (R Ra (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa) Sa) |
Enantiomers of different substances S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R′ (S′ R′ (S′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) R) |
Enantiomers of different substances S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R′ (S′ R′ (S′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) and S R) and S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S′ (R′ S′ (R′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) R) |
Diastereomers of different substances |
| e.g.: Malic acid RSI29 | e.g.: Malic acid RSII29 | e.g.: SR-Allylglycine103 |
e.g. (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa): L-Isoleucine–L-allo-isoleucine104 Sa): L-Isoleucine–L-allo-isoleucine104 |
e.g.: L-Isoleucine–D-valine80 |
e.g. (L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L′): L-Malic acid–L-tartaric acid78 L′): L-Malic acid–L-tartaric acid78 |
e.g. (R′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa): D-Norleucine–L-allo-isoleucine106 Sa): D-Norleucine–L-allo-isoleucine106 |
e.g. (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra): L-Isoleucine–D-allo-isoleucine104 Ra): L-Isoleucine–D-allo-isoleucine104 |
e.g. (L![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D′): L-Malic acid–D-tartaric acid79 D′): L-Malic acid–D-tartaric acid79 |
e.g. (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra′): L-Phenylalanine–D–allo-isoleucine108 Ra′): L-Phenylalanine–D–allo-isoleucine108 |
||||
Non-equimolar discrete compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) N N
|
||||||
|---|---|---|---|---|---|---|
| Homomolecular compounds | Heteromolecular compounds | |||||
| Anomalous racemates51 (= anomalous conglomerates52,107) | Diastereomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa (R Sa (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra) and S Ra) and S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra (R Ra (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa) = 1 Sa) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and N N and N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Anomalous quasiracemates37 | Enantiomers of different substances S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S′ (R S′ (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R′) = 1 R′) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N or N N or N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Diastereomers of different substances S′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra (R′ Ra (R′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa) and S Sa) and S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra′ (R Ra′ (R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa′) = 1 Sa′) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N or N N or N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
||
Enantiomers S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1 R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N and N N and N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Enantiomers of different substances S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R′ (S′ R′ (S′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R) = 1 R) = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N or N N or N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
|||||
e.g.: Malic acid S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R = 1 R = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 3 3 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (ref. 29) 1 (ref. 29) |
No examples found |
e.g. (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R′): Dilactic acid–dimethylglutaric acid = 1 R′): Dilactic acid–dimethylglutaric acid = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (ref. 70) 3 (ref. 70) |
e.g. (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S′): L-Valine–L-isoleucine = 2 S′): L-Valine–L-isoleucine = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (ref. 34) 1 (ref. 34) |
No examples found | ||
First, it is applicable only to chiral compounds that are “true” organic substances (known to contain a selected number of chemical elements95) and, therefore, excludes organometallic compounds. Second, the systematization is proposed only for compounds formed in true binary systems, i.e., substances composed of only two molecular species. That is why it does not encompass compounds containing solvent molecules. For example, E. Wachter et al.96 recently described the crystal structure of a PF6− salt of [Ru(2,9-dimethyl-1,10-phenanthroline)2(dipyrido[3,2-d:2′,3′-f]quinoxaline)]2+ with the enantiomer ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. However, the crystal structure of this compound incorporates molecules of the solvents (acetone, diethyl ether, and water) in addition to the organometallic component. Third, we only consider hydrogen and van der Waals-bonded crystals where the molecular components are related to each other as enantiomers or quasi-enantiomers (including diastereomers).97 Furthermore, attention should be paid to the term “cocrystals,” which is frequently used in relation to pharmaceuticals with the potential to improve their physicochemical properties.98 A broadly accepted definition of the term comprises substances composed of two or more neutral molecular components at definite stoichiometric amounts, which are characterized by structural homogeneity and the absence of solvate molecules in their crystal structure.99,100 Therefore, related compounds include binary donor–acceptor complexes and crystals with hydrogen bonds.99 Consequently, the term cocrystal has a rather broad definition, especially considering chiral and achiral compounds. Accordingly, only cocrystals containing chiral components and only two of them find proper positions in our systematization.
4. However, the crystal structure of this compound incorporates molecules of the solvents (acetone, diethyl ether, and water) in addition to the organometallic component. Third, we only consider hydrogen and van der Waals-bonded crystals where the molecular components are related to each other as enantiomers or quasi-enantiomers (including diastereomers).97 Furthermore, attention should be paid to the term “cocrystals,” which is frequently used in relation to pharmaceuticals with the potential to improve their physicochemical properties.98 A broadly accepted definition of the term comprises substances composed of two or more neutral molecular components at definite stoichiometric amounts, which are characterized by structural homogeneity and the absence of solvate molecules in their crystal structure.99,100 Therefore, related compounds include binary donor–acceptor complexes and crystals with hydrogen bonds.99 Consequently, the term cocrystal has a rather broad definition, especially considering chiral and achiral compounds. Accordingly, only cocrystals containing chiral components and only two of them find proper positions in our systematization.
The systematization in Table 5 is based on the following two principles. Principle 1: Classification according to the composition of the compound: 1) division into two major groups, viz.: equimolar and non-equimolar discrete compounds (at top and bottom of Table 5), and 2) further division into two subgroups, viz.: homomolecular and heteromolecular compounds, i.e., compounds composed of molecules of the same or different substances. Principle 2: Classification within each one of the four resulting subgroups according to 1) compound stereochemistry (enantiomers or diastereomers) and 2) crystallographic features. Each subsection in the table provides particular examples. The references given there correspond to the original publications with the authors' definitions.
Homomolecular (racemic) compounds
Homomolecular (racemic) compounds can be divided into centrosymmetric and non-centrosymmetric compounds.Centrosymmetric compounds of this group are represented only by racemic compounds or true racemates.5 They form the most abundant and most frequently studied group. In the compounds, molecules form dimers, wherein a dextrorotatory molecule is connected to a levorotatory one via an inversion center. One of the feasible examples is racemic malic acid of the RSI modification.27–29
Non-centrosymmetric compounds of this group are much less frequently occurring and can be divided into three subgroups. The first one is also represented by racemic compounds. S and R molecules do not form dimers here; they are combined via other symmetry elements instead of an inversion center. It includes the RSII modification of racemic malic acid discussed before.27–29 The second subgroup consists of kryptoracemates,101 also known as false conglomerates.102 In compounds of this type, S and R molecules occupy independent crystallographic positions, i.e., they are not connected via symmetry elements. According to the authors,101 about 180 substances form compounds of this type. The third subgroup is comprised of compounds named 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes,104 where the components are diastereomers of the same substance and can have either the same chirality (S
1 complexes,104 where the components are diastereomers of the same substance and can have either the same chirality (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa and R
Sa and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra) or different chiralities (S
Ra) or different chiralities (S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ra and R
Ra and R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Sa). Diastereomeric molecules forming such pairs cannot be related via symmetry elements.
Sa). Diastereomeric molecules forming such pairs cannot be related via symmetry elements.
Heteromolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1
Heteromolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cannot be centrosymmetric by definition. However, they can also be classified into two subgroups: pseudo-centrosymmetric and non-centrosymmetric ones.
1 cannot be centrosymmetric by definition. However, they can also be classified into two subgroups: pseudo-centrosymmetric and non-centrosymmetric ones.
Pseudo-centrosymmetric compounds of this type are known to be reported as quasiracemates.105 They contain enantiomer molecules of different substances (see Table 3). However, structural differences between the molecules are rather insignificant, and, usually, they differ only by one atom or a small group of atoms. In some works,97 the term “quasienantiomers” is used for such molecules. In a crystal structure, a pair of such molecules usually forms a dimer, wherein the molecules are connected to each other via a pseudo-inversion center.
Non-centrosymmetric compounds of this group can be subdivided into two subgroups. One of them would include cocrystals,79i.e., the system components are enantiomers of different substances. The other one contains 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes,97,106 wherein the system components are diastereomers of different compounds.
1 complexes,97,106 wherein the system components are diastereomers of different compounds.
Homomolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) N
N
Homomolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N (Table 5, bottom part) can formally be classified into two subgroups. One of them contains anomalous racemates51 or anomalous conglomerates.52,107 Both terms were introduced to define non-equimolar compounds formed by enantiomers. Compounds of this type have not been found yet among diastereomeric pairs. Systems containing anomalous racemates are rather rare and scarcely studied, and most publications, with a couple of minor exceptions, are devoted to compounds of enantiomer pairs with the enantiomer ratio of 1
N (Table 5, bottom part) can formally be classified into two subgroups. One of them contains anomalous racemates51 or anomalous conglomerates.52,107 Both terms were introduced to define non-equimolar compounds formed by enantiomers. Compounds of this type have not been found yet among diastereomeric pairs. Systems containing anomalous racemates are rather rare and scarcely studied, and most publications, with a couple of minor exceptions, are devoted to compounds of enantiomer pairs with the enantiomer ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (see Table 2). Examples include the stable S3R and metastable 3S1R modifications of malic acid described above.
3 (see Table 2). Examples include the stable S3R and metastable 3S1R modifications of malic acid described above.
Heteromolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) N
N
Heteromolecular compounds 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N (Table 5, bottom part) form the rarest group, and the number of reported studies of such compounds is very limited. Technically, three subgroups can be distinguished. The first one was named anomalous quasiracemates50 and contains compounds of enantiomer molecules of different substances. The term has been introduced to denote 1
N (Table 5, bottom part) form the rarest group, and the number of reported studies of such compounds is very limited. Technically, three subgroups can be distinguished. The first one was named anomalous quasiracemates50 and contains compounds of enantiomer molecules of different substances. The term has been introduced to denote 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N compounds formed in addition to quasiracemates in systems of components of different chiralities. The second subgroup (no name yet) includes compounds occurring in systems of components of the same chirality; such systems do not produce quasiracemates. A representative of this subgroup, compound V2I, has been depicted above. The third subgroup (also no name yet) is comprised of compounds formed by diastereomers of different substances. We know only three systems forming 1
N compounds formed in addition to quasiracemates in systems of components of different chiralities. The second subgroup (no name yet) includes compounds occurring in systems of components of the same chirality; such systems do not produce quasiracemates. A representative of this subgroup, compound V2I, has been depicted above. The third subgroup (also no name yet) is comprised of compounds formed by diastereomers of different substances. We know only three systems forming 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N heteromolecular compounds (see Table 4), and they belong to the first and second subgroups.
N heteromolecular compounds (see Table 4), and they belong to the first and second subgroups.
According to statistical data,96 the occurrence of non-equimolar discrete compounds among substances with chiral molecules is negligible, being 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. If so, is their study practical? We think that it is. Their physicochemical properties (beneficial, harmful, or neutral) have not been sufficiently investigated yet. We suppose that this may change in the future provided the examinations of chiral systems (enantiomers and diastereomers) are performed using a combination of precision methods. Both systems that we investigated can serve as good examples.
000. If so, is their study practical? We think that it is. Their physicochemical properties (beneficial, harmful, or neutral) have not been sufficiently investigated yet. We suppose that this may change in the future provided the examinations of chiral systems (enantiomers and diastereomers) are performed using a combination of precision methods. Both systems that we investigated can serve as good examples.
6. Summary
Information on non-equimolar discrete compounds in binary systems of chiral organic substances, which is available in the literature, has been reviewed and systematized, including the rate of occurrence of such systems and the current state of knowledge in the field.For the systems (S)-malic acid–(R)-malic acid and L-valine–L-isoleucine, as examples representing different types of binary systems, the crystal structures of the non-equimolar discrete compounds were analyzed on the basis of comprehensive experimental studies. The results obtained were compared with the data reported in the literature for these two and other similar systems.
The (S)-malic acid–(R)-malic acid system was shown to form 1) an equimolar compound, which could occur in three modifications; two of these, the RSI and RSII modifications, have been known for some time, while the third form, RSIII, was discovered and described by the present authors, and 2) the non-equimolar stable (S3R and SR3) and metastable (3S1R and 1S3R) compounds with ratios S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) R equal to 3
R equal to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, correspondingly. Crystallization conditions resulting in the formation of a particular modification of both equimolar and non-equimolar compounds have been ascertained, and the polymorphic transformations between the discrete phases have been studied. The data obtained were used to plot a schematic representation of the system phase diagram. The (triclinic) crystal structure of the non-equimolar discrete compound S3R has been identified and compared to those of the S-enantiomer and the racemic compounds RSI and RSII. At present, information on the crystal structures of non-equimolar discrete compounds is available only for a dozen systems of enantiomers of the same compound of which we have knowledge (including our data).
3, correspondingly. Crystallization conditions resulting in the formation of a particular modification of both equimolar and non-equimolar compounds have been ascertained, and the polymorphic transformations between the discrete phases have been studied. The data obtained were used to plot a schematic representation of the system phase diagram. The (triclinic) crystal structure of the non-equimolar discrete compound S3R has been identified and compared to those of the S-enantiomer and the racemic compounds RSI and RSII. At present, information on the crystal structures of non-equimolar discrete compounds is available only for a dozen systems of enantiomers of the same compound of which we have knowledge (including our data).
For the L-valine–L-isoleucine system, the occurrence of a non-equimolar compound V2I with the Val![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ile ratio of 2
Ile ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 could be proven. The solubility diagram plotted for the ternary L-valine–L-isoleucine–water system exhibits two eutonics located on both sides from the local solubility minimum, which corresponds to the composition of compound V2I. The (monoclinic) crystal structure of the V2I compound has been determined and compared to those of the system components L-Val, L-Ile and the equimolar compound formed in the D-Val–L-Ile system. To the best of our knowledge, this is the only available information on the crystal structure of a non-equimolar compound in a system of enantiomers of different substances and, at the same time, the only example of a binary compound where these enantiomers are of the same chirality.
1 could be proven. The solubility diagram plotted for the ternary L-valine–L-isoleucine–water system exhibits two eutonics located on both sides from the local solubility minimum, which corresponds to the composition of compound V2I. The (monoclinic) crystal structure of the V2I compound has been determined and compared to those of the system components L-Val, L-Ile and the equimolar compound formed in the D-Val–L-Ile system. To the best of our knowledge, this is the only available information on the crystal structure of a non-equimolar compound in a system of enantiomers of different substances and, at the same time, the only example of a binary compound where these enantiomers are of the same chirality.
Based on the results of the study, a systematization of discrete compounds occurring in binary chiral systems of organic substances was proposed. This was motivated by the great scope of the acquired knowledge and the variety of terms used in the literature. The presented systematics define chemical and crystallographic characteristics of the discrete compounds that can be ascertained when using a particular term. To increase its applicability, the types of compounds covered with the systematization were defined. Of course, we do not consider this systematization as complete and all-encompassing. New materials are steadily appearing that might fill the still empty places in the systematization table and support a deeper understanding of the structure–property relationships within the systems studied.
Acknowledgements
The investigations were performed using equipment of the Saint Petersburg State University Resource Centers “X-ray diffraction studies” and “Geomodel” and equipment of the MPI Magdeburg PCF lab. The authors thank S. Muenzberg, Dr. S. Bocharov, Dr. A. A. Zolotarev Jr., and Dr. L. Yu. Kryuchkova for collaboration. The authors appreciate the financial support provided by the Saint Petersburg State University Foundation (NIR 2/15, project 3.38.243.2015), the Russian Foundation for Basic Research (Projects 16-05-00837-a and 16-29-11727-ofi_m), and the DAAD and Saint Petersburg State University common program «Dmitrij Mendeleev» (personal grant given to A. I. Isakov in 2014). Open Access funding provided by the Max Planck Society.Notes and references
- A. I. Kitaygorodsky, Molecular crystals, Nauka, Moscow, 1971, p. 424(Rus) Search PubMed.
- A. I. Kitaygorodsky, Mixed crystals, Nauka, Moscow, 1983, p. 280(Rus) Search PubMed.
- J. Bernstein, Polymorphism in Molecular Crystals, Oxford Univ. Press, New York, 2002, p. 428 Search PubMed.
- M. Nogradi, Stereochemistry, Basic concepts and applications, Pergamon press, Oxford, 1981, p. 283 Search PubMed.
- J. Jacques, A. Collet and S. H. Wilen, Enantiomers, Racemates and Resolutions, J. Wiley & Sons, New York, 1st edn, 1981, p. 233 Search PubMed.
- G. Coquerel, Review on the heterogeneous equilibria between condensed phases in binary systems of enantiomers, Enantiomer, 2000, 5(5), 481–489 CAS.
- G.-Q. Lin, J.-G. Zhang and J.-F. Cheng, Overview of Chirality and Chiral Drugs, in Chiral Drugs: Chemistry and Biological Action, ed. G.-Q. Lin, Q.-D. You and J.-F. Cheng, John Wiley & Sons, Hoboken (NJ), 2011, p. 456 Search PubMed.
- D. J. Giron, Polymorphism in the pharmaceutical industry, J. Therm. Anal. Calorim., 2001, 64, 37–60 CrossRef CAS.
- H. Murakami, From Racemates to Single Enantiomers – Chiral Synthetic Drugs over the last 20 year, Top. Curr. Chem., 2006, 269, 273–299 CrossRef.
- A. A. Bredikhin, Z. A. Bredikhina and D. V. Zakharychev, Crystallization of chiral compounds: thermodynamical, structural and practical aspects, Mendeleev Commun., 2012, 22, 171–180 CrossRef CAS.
- G. Desiraju, Crystal engineering: from molecule to crystal, J. Am. Chem. Soc., 2013, 135(17), 9952–9967 CrossRef CAS PubMed.
- J. Bada, S. Diego and L. Jolla, Amino acid racemization reactions and their geochemical implications, Naturwissenschaften, 1975, 62(3), 71–79 CrossRef CAS.
- J. Bada, M. Man and E. Shou, Decomposition of hydroxy amino acids in foraminiferal test; kinetics, mechanism and geochronological implications, Earth Planet. Sci. Lett., 1978, 41(1), 67–76 CrossRef CAS.
- J. Robins, M. Jones and E. Matisoo-Smith, Amino Acid Racemization Dating in New Zealand: An overview and Bibliography, Auckland Univ, Auckland, 2001, p. 34 Search PubMed.
- S. Killops and V. Killops, Introduction to organic geochemistry, Blackwell Publishing, Oxford, 2005, p. 393 Search PubMed.
- T. De Torres, J. E. Ortiz, I. Arribas, A. Delgado, R. Julia and J. A. Martın-Rubı, Geochemistry of Persististrombus latus Gmelin from the Pleistocene Iberian Mediterranean realm, Lethaia, 2010, 43, 149–163 CrossRef.
- H. Lorenz, A. Perlberg, D. Sapoundjiev, M. P. Elsner and A. Seidel-Morgenstern, Crystallization of enantiomers, Chem. Eng. Process., 2006, 45, 863–873 CrossRef CAS.
- R. M. Kellogg, B. Kaptein and T. R. Vries, Dutch Resolution of Racemates and the Roles of Solid Solution Formation and Nucleation Inhibition, Top. Curr. Chem., 2007, 269, 159–197 CrossRef CAS PubMed.
- H. Lorenz, Solubility and solution equilibria in crystallization, in Crystallization – Basic concepts and industrial applications, ed. W. Beckmann, Wiley-VCH, Weinheim, 2013 Search PubMed.
- C. Brandel, Y. Amharar, J. Rollinger, U. Griesser, Y. Cartigny, S. Petit and G. Coquerel, Impact of Molecular Flexibility on Double Polymorphism, Solid Solutions and Chiral Discrimination during Crystallization of Diprophylline Enantiomers, Mol. Pharmaceutics, 2013, 10, 3850–3861 CrossRef CAS PubMed.
- J. E. Tabora, J. Corry, R. Osifchin, J. V. Lepore, O. A. Davidson and M. P. Thien, Identification and characterization of an anomalous racemate, Fluid Phase Equilib., 2007, 258, 140–147 CrossRef CAS.
- V. Ya. Anosov, M. I. Ozerova and Yu. Ya. Fialkov, Fundamentals of physical – chemical analysis, Nauka, Moscow, 1976, p. 503(Rus) Search PubMed.
- C. Brandel, Y. Cartigny, G. Coquerel, J. H. ter Horst and S. Petit, Prenucleation Self-Assembly and Chiral Discrimination Mechanisms during Solution Crystallization of Racemic Diprophylline, Chem. – Eur. J., 2016, 22(45), 16103–16112 CrossRef CAS PubMed.
- N. Wermester, E. Aubin, M. Pauchet, S. Coste and G. Coquerel, Preferential crystallization in an unusual case of conglomerate with partial solid solutions, Tetrahedron: Asymmetry, 2007, 18(7), 821–831 CrossRef CAS.
- N. V. Taratin, H. Lorenz, E. N. Kotelnikova, A. E. Glikin, A. Galland, V. Dupray, G. Coquerel and A. Seidel-Morgenstern, Mixed Crystals in Chiral Organic Systems: A Case Study on (R)- and (S)-Ethanolammonium 3-Chloromandelate, Cryst. Growth Des., 2012, 12, 5882–5888 CAS.
- H. Kaemmerer, H. Lorenz, S. N. Black and A. Seidel-Morgenstern, Study of System Thermodynamics and the Feasibility of Chiral Resolution of the Polymorphic System of Malic Acid Enantiomers and Its Partial Solid Solutions, Cryst. Growth Des., 2009, 9(4), 1851–1862 CAS.
- A. I. Isakov, E. N. Kotelnikova, L. Yu. Kryuchkova and H. Lorenz, Effect of crystallization conditions on polymorphic diversity of malic acid RS-racemate, Trans. Tianjin Univ., 2013, 19(2), 86–91 CrossRef CAS.
- A. I. Isakov, E. N. Kotelnikova, L. Yu. Kryuchkova and H. Lorenz, Isomorphism and polymorphism in the system of malic acid enantiomers on the basis of X-ray and high-temperature X-ray diffractometry, in BIWIC 2013 – 20th International Workshop on Industrial Crystallization, ed. H. Qu, J. Rantanen and C. Malwade, Univ. of Southern Denmark, Odense, 2013, pp. 395–402 Search PubMed.
- A. I. Isakov, E. N. Kotelnikova and H. Lorenz, Non-Equimolar Discrete Phases Formed in the System of Malic Acid Enantiomers, Chem. Eng. Technol., 2015, 38(6), 1047–1052 CrossRef CAS.
- D. Sapoundjiev, H. Lorenz and A. Seidel-Morgenstern, Solubility of chiral threonine species in water/ethanol mixture, J. Chem. Eng. Data, 2006, 51(5), 1562–1566 CrossRef CAS.
- N. V. Taratin, D. Binev, H. Lorenz, A. Seidel-Morgenstern and E. N. Kotelnikova, Characterization and limits of solid solutions in binary systems of threonine diastereomers according to X-ray diffraction data, in Proc. of the III Intern. Conf. Crystallogenesis and Mineralogy, Institute of Geology and Mineralogy, Novosibirsk, 2013, pp. 341-I–341-II Search PubMed.
- D. Binev, N. Taratin, E. Kotelnikova, A. Seidel-Morgenstern and H. Lorenz, Solubility Equilibria and Crystallographic Characterization of the L-Threonine/L-allo-Threonine System, Part 1: Solubility Equilibria in the Threonine Diastereomeric System, Cryst. Growth Des., 2014, 14, 367–373 CAS.
- N. Taratin, H. Lorenz, D. Binev, A. Seidel-Morgenstern and E. Kotelnikova, Solubility Equilibria and Crystallographic Characterization of the L-Threonine/L-allo-Threonine System, Part 2: Crystallographic Characterization of Solid Solutions in the Threonine Diastereomeric System, Cryst. Growth Des., 2015, 15, 137–144 CAS.
- A. I. Isakov, E. N. Kotelnikova, S. Muenzberg, S. N. Bocharov and H. Lorenz, Solid Phases in the System L-Valine – L-Isoleucine, Cryst. Growth Des., 2016, 16, 2653–2661 CAS.
- A. I. Isakov, E. N. Kotelnikova, S. N. Bocharov, A. A. Zolotarev Jr. and H. Lorenz, Thermal deformations of the crystal structures of L-valine, L-isoleucine and discrete compound V2I, in BIWIC 2016 – 23rd International Workshop on Industrial Crystallization, ed. H. Lorenz and H. Buchholz, Cuvillier Verlag, Göttingen, 2016, pp. 7–12 Search PubMed.
- A. Fredga, The steric relationships of optically active α-methylglutaric acid, Ark. Kemi, Mineral. Geol., 1947, 24A(32), 1–10 Search PubMed.
- M. Andersson, A. Fredga and B. Jerslev, Anomalous Racemates of Malic Acid, Acta Chem. Scand., 1966, 20, 1060–1063 CrossRef CAS.
- L. Toke, M. Acs, E. Fogassy, F. Faigl, S. Gal and J. Sztatisz, A new anomalous racemate, Acta Chim. Acad. Sci. Hung., 1979, 102, 59–65 CAS.
- H. E. Gallis, P. J. Van Ekeren, J. C. Van Miltenburg and H. A. J. Oonk, Mixtures of d- and l-carvone: IV. Transformation from a solid solution to a racemic compound, Thermochim. Acta, 1999, 326(1–2), 83–90 CrossRef CAS.
- M. Harmata, P. Rashatasakhon and C. L. Barnes, Intramolecular [4+3] cycloadditions – Stereochemical issues in the cycloaddition reactions of cyclopentenyl cations – A synthesis of (+)-dactylol, Can. J. Chem., 2006, 84(10), 1456–1469 CrossRef CAS.
- R. G. Kostyanovsky, K. A. Lyssenko, D. A. Lenev and I. A. Bronzova, Competitive H-bonding in bicyclic bis-lactams: self-assembly in nanotubes or in unbalanced chiral threefold interpenetrated diamondoid network, Tetrahedron: Asymmetry, 2002, 13, 2697–2701 CrossRef CAS.
- R. Chebolu, W. Zhang and E. Galoppini, Copper(I)-catalyzed intramolecular photocycloadditions of dicyclopentadiene derivatives linked by removable tethers, Tetrahedron Lett., 2000, 41(16), 2831–2834 CrossRef CAS.
- L. Chen, X. Zhang and A. Schultz, An efficient approach to bridged-bicyclic rings via intramolecular diazo ketone insertion, Tetrahedron Lett., 2002, 43(26), 4711–4715 CrossRef CAS.
- E. Vedejs and W. Kruger, Diastereoselective Osmylation and Hydroboration of β,γ-Unsaturated N,N-Diisopropylamides and Acid-Catalyzed Conversion to δ-Lactones, J. Organomet. Chem., 1999, 64(13), 4790–4797 CAS.
- S. Busato, D. C. Craig, Z. M. A. Zudeh and R. W. Read, New N-acyl, N-alkyl, and N-bridged derivatives of rac-6,6′,7,7′-tetramethoxy-1,1′,2,2′,3,3′,4,4′-octahydro-1,1′-bisisoquinoline, Tetrahedron, 2003, 59(4), 461–472 CrossRef CAS.
- C. Krempner, H. Reinke and H. Oehme, Synthesis of Transient Silenes by a Modified Peterson Reaction, Eur. J. Inorg. Chem., 1995, 128(2), 143–149 CAS.
- Z. Gültekin and T. Hökelek, Crystal Structure of trans-(1RS,3RS)-2-N,N′-Dimethylaminomethyl-1,3-dithiolane-1,3-dioxide, Anal. Sci., 2006, 22, x9–x10 CrossRef.
- D. Sureshkumar, S. Koutha and S. Chandrasekaran, A New Selena-Aza-Payne-Type Rearrangement of Aziridinylmethyl Tosylates Mediated by Tetraselenotungstate, Eur. J. Org. Chem., 2007, 27, 4543–4551 CrossRef.
- A. A. Bredikhin, Z. A. Bredikhina, V. G. Novikova, A. V. Pashagin, D. V. Zakharychev and A. T. Gubaidullin, Three different types of chirality-driven crystallization within the series of uniformly substituted phenyl glycerol ethers, Chirality, 2008, 20(10), 1092–1103 CrossRef CAS PubMed.
- M. J. Heileman and H. W. Moore, Generation and intramolecular cyclization of (2-ethenylphenyl)bisketenes. Synthesis of benzofuranones, Tetrahedron Lett., 1998, 39(22), 3643–3646 CrossRef CAS.
- M. Bergmann and M. Lissitzin, Die überzähligen Stereoisomeren der γ-Amino-β-oxy-buttersäure, Ber. Dtsch. Chem. Ges., 1930, 63(2), 310–313 CrossRef.
- A. A. Bredikhin, Z. A. Bredikhina, D. V. Zakharychev, A. I. Samigullina and A. T. Gubaidullin, 4-Benzoylamino-3-hydroxybutyric Acid, Historically First “Anomalous Racemate”: Reinvestigation, Cryst. Growth Des., 2015, 15(3), 1362–1373 CAS.
- P. J. Cox, M. Jaspars, Y. Kumarasamy, L. Nahar and S. D. Sarker, An anomalous racemate of naringenin at 120 K, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2003, 59, o46–o48 CAS.
- H. Lorenz and A. Seidel-Morgenstern, Processes To Separate Enantiomers, Angew. Chem., Int. Ed., 2014, 53(5), 1218–1250 CrossRef CAS PubMed.
- CSD files (identifier): COFRUK10, DLMALC11 and DLMALC.
- ICDD Powder Diffraction File (card): 42-1702, 46-1864 and 31-1776.
- J. Van Loock, W. Van Havere and A. Lenstra, The structure of (plus or minus)-malic acid, Bull. Soc. Chim. Belg., 1981, 90, 161–166 CAS.
- P. Van der Sluis and J. Kroon, The Structure of (±)-malic acid, (±)-C4H6O5, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41(6), 956–959 CrossRef.
- P. Van der Sluis and J. Kroon, Structure of (-)-Malic Acid, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45(9), 1406–1408 CrossRef.
- R. Ceolin, H. Szwarc and F. Lepage, On the dimorphism of DL-malic acid, Thermochim. Acta, 1990, 158, 347–352 CrossRef CAS.
- H. Fjaer and E. J. Samuelsen, Order-disorder in the linear chain structure of terephthalic acid, studied by Raman scattering, J. Phys. C: Solid State Phys., 1986, 19(30), 5945–5956 CrossRef CAS.
- R. Srinivasa Gopalan, P. Kumaradhas, G. U. Kulkarni and C. N. R. Rao, An experimental charge density study of aliphatic dicarboxylic acids, J. Mol. Struct., 2000, 521(1), 97–106 CrossRef CAS.
- M. Kuhnert-Brandstätter and L. Friedl, Zur Frage der Existenz anomaler Racemate, Microchim. Acta, 1977, 68, 507–516 CrossRef.
- A. Burger and R. Ramberger, On the polymorphism of pharmaceuticals and other molecular crystals. I Theory of thermodynamic rules, Microchim. Acta, 1979, 72, 259–271 CrossRef.
- V. N. Danilin, L. V. Borovskaya, L. F. Pyshnaya and L. S. Smirnova, Malic acid study by DSC and DTA, Physical-chemical analysis of the properties of multicomponent systems, 2007, vol. 5, pp. 18–20(Rus) Search PubMed.
- A. I. Isakov, E. N. Kotelnikova and H. Lorenz, Phases with discrete compositions formed in the system of malic acid enantiomers, in BIWIC 2014 - 21st International Workshop on Industrial Crystallization, ed. J. Coquerel, Y. Cartigny and N. Couvrat, Univ. of Rouen, Rouen, 2014, pp. 42–49 Search PubMed.
- H. Barańska, J. Kuduk-Jaworska, R. Szostak and A. Romaniewska, Vibrational spectra of racemic and enantiomeric malic acids, J. Raman Spectrosc., 2003, 34, 68–76 CrossRef.
- M. Centnerszwer, Über Schmelzpunkte von Gemengen optischer Antipoden, Z. Phys. Chem., 1899, 29, 715–725 CAS.
- A. Fredga, Über den konfigurativen Zusammenhang zwischen optisch aktiver Methyl-bernsteinsäure und Thioäpfelsäure, Ark. Kemi, Mineral. Geol., 1942, 15B(23), 1–6 CAS.
- A. Fredga, Über den konfigurativen Zusammenhang zwischen optisch aktiver Milchsäure und Thiomilchsäure, Ark. Kemi, Mineral. Geol., 1940, 14B(12), 1–10 CAS.
- I. L. Karle and J. Karle, The Crystal Structure of the Quasi-Racemate from (+)-m-Methoxyphenoxypropionic Acid and (–)-m-Bromophenoxypropionic Acid, J. Am. Chem. Soc., 1966, 88(1), 24–27 CrossRef CAS.
- M. E. Breen, S. L. Tameze, W. G. Dougherty, W. S. Kassel and K. A. Wheeler, Structural Studies of Enantiomers, Racemates, and Quasiracemates. 2-(3-Bromophenoxy)propionic Acid and 2-(3-Methoxyphenoxy)propionic Acid, Cryst. Growth Des., 2008, 8(10), 3863–3870 CAS.
- M. S. Hendi, R. E. Davis, V. M. Lynch and K. A. Wheeler, Structural studies of enantiomers, racemates, and quasiracemates. 2-(2,4-dichlorophenyl)propanoic acid and 2-(2-chloro-4-nitrophenyl)propanoic acid, Cryst. Eng., 2001, 4, 11–24 CrossRef CAS.
- M. S. Hendi, P. Hooter, R. E. Davis, V. M. Lynch and K. A. Wheeler, Structural Studies of Enantiomers, Racemates, and Quasiracemates: N-(4-Methylbenzoyl)methylbenzylamine and N-(4-Nitrobenzoyl)methylbenzylamine, Cryst. Growth Des., 2004, 4(1), 95–101 CAS.
- S. L. Fomulu, M. S. Hendi, R. E. Davis and K. A. Wheeler, Structural Studies of Enantiomers, Racemates, and Quasiracemates. 2-(2,4,5-Trichloroanilino)propanoic Acid and 2-(2,4,5-Trichlorophenoxy)propanoic Acid, Cryst. Growth Des., 2002, 2(6), 637–644 CAS.
- S. L. Fomulu, M. S. Hendi, R. E. Davis and K. A. Wheeler, Structural Studies of Enantiomers, Racemates, and Quasiracemates. N-(2-Chlorobenzoyl)methylbenzylamine and N-(2-Bromobenzoyl)methylbenzylamine, Cryst. Growth Des., 2002, 2(6), 645–651 CAS.
- J. T. Cross, N. A. Rossi, M. Serafin and K. A. Wheeler, Tröger's base quasiracemates and crystal packing tendencies, CrystEngComm, 2014, 16, 7251–7258 RSC.
- C. B. Aakeröy, T. I. Cooke and M. Nieuwenhuyzen, The crystal structure of the molecular cocrystal L-malic acid L-tartaric acid (1/1), Supramol. Chem., 1996, 7(2), 153–156 CrossRef.
- M. D. Eddleston, M. Arhangelskis, T. Fričšić and W. Jones, Solid state grinding as a tool to aid enantiomeric resolution by cocrystallization, Chem. Commun., 2012, 48, 11340–11342 RSC.
- B. Dalhus and C. H. Görbitz, Molecular aggregation in crystalline 1:1 complexes of hydrophobic D- and L-amino acids. I. The L-isoleucine series, Acta Crystallogr., Sect. B: Struct. Sci., 1999, 55(3), 424–431 Search PubMed.
- M. S. Dunn, F. J. Ross and L. E. Read, The solubility of the amino acids in water, J. Biol. Chem., 1933, 103, 579–595 CAS.
- T. E. Needham Jr., A. N. Paruta and R. J. Gerraughty, Solubility of Amino Acids in Pure Solvent Systems, J. Pharm. Sci., 1971, 60(4), 565–567 CrossRef CAS.
- C. Zhang, B. Liu, X. Wang and H. Wang, Measurement and Correlation of the Solubilities of L-Valine in Water, Ethanol, N,N-Dimethylformamide, Acetone, and Isopropyl Alcohol between (293.15 and 343.15) K, J. Chem. Eng. Data, 2014, 59(9), 2704–2708 CrossRef CAS.
- R. C. Zumstein and R. W. Rousseau, Solubility of L-isoleucine in and Recovery of L-isoleucine from Neutral and Acidic Aqueous Solutions, Ind. Eng. Chem. Res., 1989, 28(8), 1226–1231 CrossRef CAS.
- J. C. Givand, A. S. Teja and R. W. Rousseau, Effect of relative solubility on amino acid crystal purity, AIChE J., 2001, 47(12), 2705–2712 CrossRef CAS.
- I. Kurosawa, A. S. Teja and R. W. Rousseau, Solubility measurements in the l-Isoleucine + l-Valine + Water System at 298 K, Ind. Eng. Chem. Res., 2005, 44, 3284–3288 CrossRef CAS.
- D. Binev, S. Wloch, E. Temmel, H. Lorenz and A. Seidel-Morgenstern, Mixed crystal formation and fractional crystallization of selected amino acids, in Proc. of the 19th International Workshop on Industrial and Pharmaceutical Crystallization, Deajeon, 2012, pp. 127–135 Search PubMed.
- H. C. Koolman and R. W. Rousseau, Effects of isomorphic compounds on the purity and morphology of L-isoleucine crystals, AIChE J., 1996, 42(1), 147–153 CrossRef CAS.
- A. E. Glikin, Polymineral-Metasomatic Crystallogenesis, Springer Science + Business Media B. V., Heidelberg, 2009, p. 312 Search PubMed.
- K. Torii and Y. Iitaka, The crystal structure of L-valine, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1317–1326 CrossRef CAS PubMed.
- K. Torii and Y. Iitaka, The crystal structure of L-isoleucine, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 2237–2246 CrossRef CAS.
- C. H. Gorbitz and B. Dalhus, L-Isoleucine, Redetermination at 120 K, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52(6), 1464–1466 CrossRef.
- B. Dalhus and C. H. Gorbitz, Crystal Structures of Hydrophobic Amino Acids. I. Redeterminations of L-Methionine and L-Valine at 120 K, Acta Chem. Scand., 1996, 50, 544–548 CrossRef CAS.
- CSD files (identifiers): LVALIN01 and LISLEU02.
- P. M. Zorky, The symmetry of molecules and crystal structures, Moscow University, Moscow, 1986, p. 232(Rus) Search PubMed.
- E. Wachter, E. C. Glazer, S. Parkin and C. P. Brock, An exeptional 5:4 enantiomeric structure, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 223–231 CAS.
- Q. Zhang and D. P. Curran, Quasienantiomers and Quasiracemates: New Tools for Identification, Analysis, Separation, and Synthesis of Enantiomers, Chem. – Eur. J., 2005, 11, 4866–4880 CrossRef CAS PubMed.
- T. Fričšić and W. Jones, Benefits of cocrystallisation in pharmaceutical materials science: an update, J. Pharm. Pharmacol., 2010, 62, 1547–1559 CrossRef PubMed.
- C. B. Aakeröy and D. J. Salmon, Building co-crystals with molecular sense and supramolecular sensibility, CrystEngComm, 2005, 7(72), 439–448 RSC.
- G. Springuel, K. Robeyns, B. Norberg, J. Wouters and T. Leyssens, Cocrystal formation between chiral compounds: how cocrystals differ from salts, Cryst. Growth Des., 2014, 14(8), 3996–4004 CAS.
- L. Fábián and C. P. Brock, A list of organic kryptoracemates, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66(1), 94–103 Search PubMed.
- R. Bishop and M. L. Scudder, Multiple Molecules in the Asymmetric Unit (Z′ > 1) and the Formation of False Conglomerate Crystal Structures, Cryst. Growth Des., 2009, 9(6), 2890–2894 CAS.
- B. Dalhus and C. H. Görbitz, Non-centrosymmetric racemates: space-group frequencies and conformational similarities between crystallographically independent molecules, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56(4), 715–719 CAS.
- B. Dalhus and C. H. Görbitz, Structural relationships in crystals accommodating different stereoisomers of 2-amino-3-methylpentanoic acid, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56(4), 720–727 CAS.
- A. Fredga, Proc. of the The Svedberg, Uppsala and Stockholm, Sweden, 1944, p. 261 Search PubMed.
- B. Dalhus and C. H. Görbitz, Molecular aggregation in selected crystalline 1:1 complexes of hydrophobic D- and L-amino acids. II. The D-norleucine series, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55(8), 1105–1112 Search PubMed.
- A. T. Gubaidullin, A. I. Samigullina, Z. A. Bredikhina and A. A. Bredikhin, Crystal structure of chiral ortho-alkyl phenyl ethers of glycerol: true racemic compound, normal, false and anomalous conglomerates within the single five-membered family, CrystEngComm, 2014, 16, 6716–6729 RSC.
- C. H. Görbitz, K. Rissanen, A. Valkonen and A. Husabø, Molecular aggregation in selected crystalline 1:1 complexes of hydrophobic D- and L-amino acids. IV. The L-phenylalanine series, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65(6), o267–o272 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 5 Figures and 3 Tables. CCDC 1501884 and 1468938 contain the supplementary crystallographic data for this paper. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce02209j |
| This journal is © The Royal Society of Chemistry 2017 |