Reply to the ‘Comment on “1,4-Diazabicyclo[2.2.2]octane-based disalts showing non-centrosymmetric structures and phase transition behaviors”’ by M. Szafrański, CrystEngComm, 2017, 19, DOI: 10.1039/C6CE01469K
Xiang-Bin
Han
and
Wen
Zhang
 *
*
Ordered Matter Science Research Center, Southeast University, Nanjing 211189, Jiangsu, China. E-mail: zhangwen@seu.edu.cn
First published on 9th December 2016
Abstract
This Letter is a reply to the preceding comment by Szafrański. We suggest that other probabilities could exist besides Szafrański's assertion on the phase transitions of the crystals and point out how the present experiments and conclusions can be solidified by additional investigations.
We appreciate Szafrański's valuable comment1 because it raised some timely and critical issues regarding the field of structural phase transitions that were not addressed in our work.2 Szafrański reported an extended study of molecular crystals 1 and 2 and asserted that the phase transitions in 1 and 2 should be of the second-order (continuous) type. Therefore, he specified that the low-temperature phase (LTP) structures must be a subgroup (the space group P1 was selected) of Pca21 in the high-temperature phase within Landau's theory.3 This then affords a probable explanation for the seemingly isosymmetric and continuous phase transitions in 1 and 2. However, further careful investigation of the properties of 1 and 2 is necessary, paying particular attention to the following points.
Szafrański draws his key conclusion regarding the type of phase transition simply on the criterion of there being a thermal hysteresis in the transition temperature (Ttr) upon heating and cooling, as shown in the DSC curves. In general, according to Ehrenfest's classification, there is zero hysteresis for a continuous transition.4 However, a seemingly zero hysteresis does not only indicate a continuous transition. The trick is that the experimentally recorded “zero” might not be a real zero but a finite value close to zero.5 Therefore, other probabilities could exist besides Szafrański's assertion (Fig. 1). For example, weak first-order transitions are probably difficult to experimentally distinguish from continuous transitions because the size of the discontinuity, which is not determined by Landau's theory, may be hard to detect.6–8 Moreover, in some reported pressure-induced isosymmetric phase transitions, the obtained quasi continuity is tentatively ascribed to being close to the critical point.9 That is, the very subtle discontinuity effect is covered by a seemingly continuous change in volume. As shown in Fig. 1, the combination of crystallographic isosymmetry and continuity is just the example that has been claimed to violate the phenomenological mean-field Landau theory.
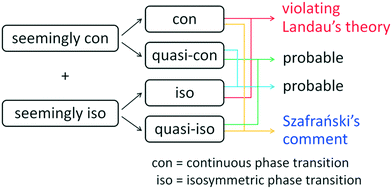 | ||
| Fig. 1 Combinations of seeming isosymmetry and continuity for a structural phase transition. Note: our work does not classify the order of the phase transitions in 1 and 2. | ||
The selection of the P1 space group is a matter of some debate. Szafrański made his choice mainly by evaluating the reliability factor (R) of the diffraction data. In fact, an incorrect lower space group often yields a better R value than a correct higher space group. From the crystallographic viewpoint, the systematic absence of the LTP diffraction data (in the original data set, without basis transformation) of 2 at 203 K clearly reveals the existence of the glide plane b along the c-axis and the screw axis 21 along the b-axis (Table 1). Therefore, the correct subspace group in the LTP is still uncertain, even within Landau's theory. Furthermore, the model of the anions in the LTP can hardly reflect the real situation, e.g., it cannot tell us the difference between dynamic and static disorders. This fact, conversely, impairs the validity of the Boltzmann equation, which we discuss below.
| b-- | c-- | n-- | 21-- | -c- | -a- | -n- | -21- | --a | --b | --n | --21 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | 358 | 350 | 346 | 14 | 268 | 277 | 279 | 13 | 222 | 212 | 210 | 16 |
| N (I > 3 s) | 299 | 250 | 277 | 10 | 219 | 220 | 233 | 0 | 106 | 1 | 107 | 8 |
| 〈I〉 | 41.9 | 6.3 | 42.7 | 57.5 | 63.9 | 77.2 | 47.0 | 0.1 | 35.4 | 0.2 | 37.4 | 7.7 |
| 〈I/s〉 | 10.8 | 6.9 | 10.3 | 14.1 | 12.4 | 12.3 | 12.2 | 0.4 | 8.8 | 0.6 | 9.3 | 6.2 |
We would like to clarify the variable-temperature cell parameters of 1, of which two were reported in our work (Fig. 2). Szafrański supposed that the diffraction data at 233 K must be wrongly assigned. This is not the case. As shown in Fig. 2, a few abnormal cell parameters would indicate either a first-order characteristic of the phase transition or a testing error due to being near Ttr. A further careful investigation is needed.
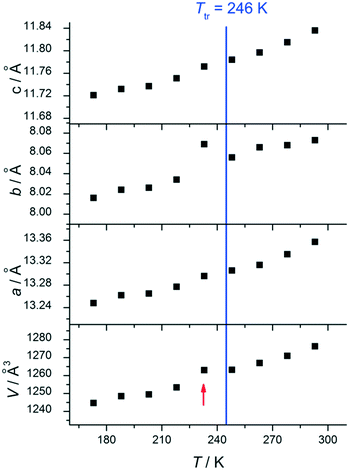 | ||
| Fig. 2 Temperature dependence of the cell parameters of 1. The arrow points to the data collected at 233 K. | ||
Furthermore, to analyze the DSC data, Szafrański suggested that the onset temperature should be used to characterize Ttr. Here we emphasize another as yet unmentioned point, i.e., the extrapolation of the measurements at various scan rates to the zero rate in order to exclude the rate dependence. Consider the Boltzmann equation, ΔS = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(W/W0), where ΔS is the entropy change, R is the gas constant, and W/W0 is the ratio of the respective numbers of microstates. Szafrański used this equation as a basis for justifying his structural solution of the order–disorder transition. However, this equation is generally unsuitable for order–disorder structural phase transitions in the solid state because of its oversimplification of the intermolecular interactions and correlations.10 It is thus unreasonable to clarify the transition mechanism based on the conclusions drawn from the equation. In addition, it is interesting that the “ferroelastic domain structure” was mentioned in the comment. We suggest further studies to demonstrate the switching of the domains because “A crystal is said to be ferroelastic if, strictly speaking, a ferroelastic hysteresis has been observed”.11
ln(W/W0), where ΔS is the entropy change, R is the gas constant, and W/W0 is the ratio of the respective numbers of microstates. Szafrański used this equation as a basis for justifying his structural solution of the order–disorder transition. However, this equation is generally unsuitable for order–disorder structural phase transitions in the solid state because of its oversimplification of the intermolecular interactions and correlations.10 It is thus unreasonable to clarify the transition mechanism based on the conclusions drawn from the equation. In addition, it is interesting that the “ferroelastic domain structure” was mentioned in the comment. We suggest further studies to demonstrate the switching of the domains because “A crystal is said to be ferroelastic if, strictly speaking, a ferroelastic hysteresis has been observed”.11
In summary, Szafrański's valuable comment affords a probable explanation for the seemingly isosymmetric and continuous phase transitions in 1 and 2. However, we believe that the present results do not exclude other probabilities. Further investigation is needed to solidify the findings of the experiments and the conclusions of both reports, which are clearly still preliminary.
References
- M. Szafrański, CrystEngComm, 2017, 19 10.1039/c6ce01469k.
- X.-B. Han, P. Hu, C. Shi and W. Zhang, CrystEngComm, 2016, 18, 1563–1569 RSC.
- A. Christy, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 753–757 CrossRef.
- G. Jaeger, Arch. Hist. Exact Sci., 1998, 53, 51–81 CrossRef.
- Liquid crystals: Experimental Study of Physical Properties and Phase Transitions, ed. S. Kumar, Cambridge University Press, Cambridge, UK, 2001 Search PubMed.
- I. Swainson, R. Hammond, J. Cockcroft and R. Weir, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174109 CrossRef.
- J. Arvanitidis, K. Papagelis, S. Margadonna, K. Prassides and A. N. Fitch, Nature, 2003, 425, 599–602 CrossRef CAS PubMed.
- T. Apih, A. Gregorovič, V. Žagar and J. Seliger, J. Phys. Chem. C, 2016, 120, 9992–10000 CAS.
- D. Paliwoda, K. Kowalska, M. Hanfland and A. Katrusiak, J. Phys. Chem. Lett., 2013, 4, 4032–4037 CrossRef CAS.
- E. I. Kozliak, J. Chem. Educ., 2007, 84, 493–498 CrossRef CAS.
- E. Salje, Ferroelectrics, 1990, 104, 111–120 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |
