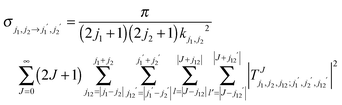Comparative experimental and theoretical study of the rotational excitation of CO by collision with ortho- and para-D2 molecules
Received
16th September 2016
, Accepted 16th November 2016
First published on 17th November 2016
Abstract
A joint crossed beam and quantum mechanical investigation of the rotationally inelastic collisions of CO with ortho- and para-D2 molecules is reported. A new 4D potential energy surface (PES) averaged over the ground vibrational states of D2 and CO is used to calculate the rovibrational bound states of the ortho-D2–CO complexes. Close coupling calculations are then performed in the rigid rotor approximation for ortho- and para-D2 colliding with CO for the experimentally investigated transition of CO (j = 0 → 1) and for collision energies ranging from 0.1 to 25 cm−1. The agreement between theory and experiment is found to be very good for both the bound state energies of the ortho-D2–CO complexes and for the inelastic scattering cross-sections showing that the free rotation of two rigid rotors is a very good model of the D2–CO system in this low collision energy domain.
1. Introduction
Because CO is the second most abundant molecule after H2 in the interstellar medium (ISM), its collisions with H21–4 and He5 have been extensively theoretically studied in recent years. CO is widely used as a tracer of physical conditions in galactic and extragalactic sources and such studies require knowing accurately the rates of the CO excitation and relaxation by inelastic collisions with H2. The accuracy of the calculated rates depends critically on the quality of the potential energy surface (PES) used to perform the Close Coupling calculations. This is the reason why several models of the H2–CO PES were developed6,7 with an increasing level of sophistication. Recently two full six-dimensional PESs were thus obtained1,2 and it was shown in particular that rigid-rotor calculations based on the vibrationally averaged PES (i.e. averaged over the vibrations of H2 and CO) gave results almost indistinguishable from full-dimensional scattering calculations.1 The quality of the PES in the study of Jankowski and coworkers was demonstrated by the good agreement obtained with the crossed beam inelastic cross-sections measured for H2–CO at collision energies8,9 below 30 cm−1 and by the excellent comparison with the experimental infrared and microwave spectra of the H2–CO van der Waals complex.7 These experimental studies were the first performed in this domain of low collision energies where all the details of the PES appear in the structures of the cross-sections. In the present work we report a joint experimental and theoretical study of the D2–CO rotationally inelastic collision for the same transitions in the [4–25] cm−1 collision energy range. This study is complemented by the computation of the bound states of the ortho-D2–CO (oD2–CO) complex, which are compared to available experimental data.10 The D2–CO and H2–CO systems differ in many aspects such as their relative masses, the position of their center of mass and the values of the vibrational frequencies and the rotational constant of D2 and H2. The rotational constant and vibrational frequencies of D2 are, for example, respectively, about one half and two third of those of H2. Consequently, the new PES which is used here to describe the D2–CO system is distinct from that used successfully for H2–CO,7 as it is obtained by averaging the six-dimensional ab initio data7 over the ground vibrational wave functions of CO and D2. This paper is organized as follows. In Section 2, the PES is presented and used to calculate the bound states of the oD2–CO complex. A brief account of the parameters of the Close Coupling calculations is also given in the same section. The experimental part is presented in Section 3 and the comparison between theory and experiment is discussed in Section 4 while a few conclusions of this study are given Section 5.
2. Theory
A. Potential energy surface
In our previous studies of collisions of H2 and CO, we used the 2012 four-dimensional interaction energy surface of H2–CO.7 This surface is based on the 6D grid of ab initio points which are used to compute the interaction energies averaged over the particular vibrations of the H2 and CO molecules. The resulting averaged energies are fitted to obtain the analytic representation of the 4D surface. Such an approach is an alternative to the averaging of the full-dimensional surface over the vibrational states of the fragments, but does not require the full-dimensional fit.11 Very recently, three of the authors of the present paper published a new 6D PES for H2–CO,1 which could in principle be used for performing scattering calculations for D2–CO. However, as the D2–CO project was started before the 6D surface was ready, a new 4D PES based on the 6D ab initio data6 was specially designed for the present study. The vibrationally averaged energies have been calculated using the Taylor-expansion method,11 also employed for H2–CO.7 Within this approach we need to know the averaged values of the H2 and CO intramolecular distances and their squares. For the ground vibrational states of both molecules, if r and s denote the H–H and C–O distances, respectively, the corresponding values are found to be 〈r〉 = 1.434562 Bohr, 〈r2〉 = 2.077687 Bohr, 〈s〉 = 2.13989 Bohr, and 〈s2〉 = 4.58320 Bohr.
Since the bound-state and scattering calculations require an expansion of the angular dependence of the PES into products of spherical harmonics, the 4D CO–D2 potential had to be refitted. The analytic fit was employed to generate interaction energies on a grid of 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries in R, θ1, θ2 and ϕ, as in previous studies on H2–CO3 where θ1 and θ2 are, respectively, the polar angles between the CO and DD interatomic distances and the R Jacobi vector while ϕ is the Jacobi azimuthal angle. A total of 29 values of R (in Bohr) were thus used in the range [3.00–15.00]. This radial grid was combined with 3000 random angular geometries. The PES was refitted using a spherical harmonics expansion including all anisotropies up to l1 = 10 for CO and l2 = 6 for H2 (where the integer indices l1 and l2 refer to θ1 and θ2 dependencies), resulting in 142 angular terms. The RMS residual was found to be lower than 0.1 cm−1 for R > 5.00 Bohr. The most significant terms were selected using a self-consistent Monte-Carlo estimator, resulting in a final set of 60 expansion functions with anisotropies up to l1 = 7 and l2 = 6. A cubic spline radial interpolation of the expansion coefficients was finally performed over the whole intermolecular distance range and was smoothly connected using a switching function to standard extrapolation (exponential and power laws at short-range and long-range, respectively). The resulting D2–CO PES is very similar to the H2–CO one as can be seen in Fig. 1. The global minimum energy of the new surface is −93.048 cm−1 and is obtained for the linear arrangement D–D⋯C–O and for an intermolecular distance R equal to 7.908 Bohr. The corresponding values for the H2–CO complex are, respectively, equal to −94.096 cm−1 and 7.911 Bohr. The values of the energies and intermolecular distances associated with the other linear geometry H–H⋯O–C are also very close for the two systems. Their values are found to be −73.336 cm−1 and 7.160 Bohr for D2–CO and −73.738 cm−1 and 7.168 Bohr for H2–CO. The D2–CO surface is then slightly shallower than the H2–CO one by about 1.1% at the global minimum and 0.5% at the local one. We conclude from this comparison that the lower zero point energy of D2 compared to H2 and the small differences of the vibrationally averaged distances of these two molecules lead to only very small differences of the interaction energy surfaces. Also, the differences if any between the results involving these two systems will then result only from the differences between the diatom rovibrational energies and wave functions and from those between the reduced masses and positions of the center of masses.
000 geometries in R, θ1, θ2 and ϕ, as in previous studies on H2–CO3 where θ1 and θ2 are, respectively, the polar angles between the CO and DD interatomic distances and the R Jacobi vector while ϕ is the Jacobi azimuthal angle. A total of 29 values of R (in Bohr) were thus used in the range [3.00–15.00]. This radial grid was combined with 3000 random angular geometries. The PES was refitted using a spherical harmonics expansion including all anisotropies up to l1 = 10 for CO and l2 = 6 for H2 (where the integer indices l1 and l2 refer to θ1 and θ2 dependencies), resulting in 142 angular terms. The RMS residual was found to be lower than 0.1 cm−1 for R > 5.00 Bohr. The most significant terms were selected using a self-consistent Monte-Carlo estimator, resulting in a final set of 60 expansion functions with anisotropies up to l1 = 7 and l2 = 6. A cubic spline radial interpolation of the expansion coefficients was finally performed over the whole intermolecular distance range and was smoothly connected using a switching function to standard extrapolation (exponential and power laws at short-range and long-range, respectively). The resulting D2–CO PES is very similar to the H2–CO one as can be seen in Fig. 1. The global minimum energy of the new surface is −93.048 cm−1 and is obtained for the linear arrangement D–D⋯C–O and for an intermolecular distance R equal to 7.908 Bohr. The corresponding values for the H2–CO complex are, respectively, equal to −94.096 cm−1 and 7.911 Bohr. The values of the energies and intermolecular distances associated with the other linear geometry H–H⋯O–C are also very close for the two systems. Their values are found to be −73.336 cm−1 and 7.160 Bohr for D2–CO and −73.738 cm−1 and 7.168 Bohr for H2–CO. The D2–CO surface is then slightly shallower than the H2–CO one by about 1.1% at the global minimum and 0.5% at the local one. We conclude from this comparison that the lower zero point energy of D2 compared to H2 and the small differences of the vibrationally averaged distances of these two molecules lead to only very small differences of the interaction energy surfaces. Also, the differences if any between the results involving these two systems will then result only from the differences between the diatom rovibrational energies and wave functions and from those between the reduced masses and positions of the center of masses.
 |
| | Fig. 1 Comparison between the contour plots of the H2–CO and D2–CO PES. The angles θ1 and θ2 are, respectively, the polar angles between the CO and DD interatomic distances and the R Jacobi vector while the Jacobi azimuthal angle ϕ is set to zero. For each point associated with the two Jacobi angles θ1 and θ2 the intermolecular distance R is optimized to give the lowest energy. Contour lines are equally spaced by 2 cm−1. | |
B. Bound state calculations
A first interesting test of the quality of the D2–CO PES can be done by performing the calculations of the bound states of the system as they were experimentally determined recently.10 We use a close coupling approach to compute the rovibrational energy levels of the CO–D2 complex using our didimat code according to the approach proposed by Danby12 and Hutson13 for the R-matrix and log-derivative propagators, respectively. Briefly, our code solves the rovibrationally inelastic Close Coupling equations in the space fixed frame using the Jacobi coordinates.14 The angular basis set is made of the usual coupled representation |j12lJMε〉 which provides eigenfunctions of the angular momenta ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 12 =
12 = ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 1 +
1 + ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 2,
2, ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) ,
, ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) =
= ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 12 +
12 + ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) and of both Jz and the parity operator Π, where
and of both Jz and the parity operator Π, where ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 1 and
1 and ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 2 are the rotational angular momenta of H2 and CO,
2 are the rotational angular momenta of H2 and CO, ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) is the relative angular momentum of the fragments,
is the relative angular momentum of the fragments, ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) is the total angular momentum of the system and Jz is its projection along the z space fixed axis. The vibrational levels of the van der Waals complex are calculated by performing calculations using a rigid rotor description of both D2 and CO for all the values of the total angular momentum J and parity ε leading to bound states. We used the ground vibrationally averaged rotational constants for both molecules15 (B = 29.9037 cm−1 for D2 and B = 1.9225 cm−1 for CO). The convergence of the bound levels of the CO–D2 complex with respect to the CO and D2 rotational basis was tested. Fifteen rotational states were included in the basis set describing the CO molecule while for ortho-D2 we included two rotational states. The maximum propagation distance was 50 Bohr. The calculations were performed for two values of the propagator step size (0.1 and 0.05 Bohr) and the values of the bound state energies were obtained from a Richardson extrapolation as suggested by Hutson.13 The results of this approach are compared to the experimental results in the study of Potapov et al.10 in Table 1. As can be seen in this table the agreement between theory and experiment is found to be excellent with the maximum difference between the calculated and measured bound state energies of 0.024 cm−1 and a global root mean square equal to 0.008 cm−1. This result shows that the model of the free rotation of two rigid rotors suggested by Potapov et al.10 offers a good description of the D2–CO system. If we now compare the bound states of the oD2–CO complex to those calculated and measured for pH2–CO we notice that the density of bound states is significantly higher for oD2–CO than for pH2–CO. Since the PES is very similar, this result is a simple consequence of the change in the reduced mass of the two complexes.
is the total angular momentum of the system and Jz is its projection along the z space fixed axis. The vibrational levels of the van der Waals complex are calculated by performing calculations using a rigid rotor description of both D2 and CO for all the values of the total angular momentum J and parity ε leading to bound states. We used the ground vibrationally averaged rotational constants for both molecules15 (B = 29.9037 cm−1 for D2 and B = 1.9225 cm−1 for CO). The convergence of the bound levels of the CO–D2 complex with respect to the CO and D2 rotational basis was tested. Fifteen rotational states were included in the basis set describing the CO molecule while for ortho-D2 we included two rotational states. The maximum propagation distance was 50 Bohr. The calculations were performed for two values of the propagator step size (0.1 and 0.05 Bohr) and the values of the bound state energies were obtained from a Richardson extrapolation as suggested by Hutson.13 The results of this approach are compared to the experimental results in the study of Potapov et al.10 in Table 1. As can be seen in this table the agreement between theory and experiment is found to be excellent with the maximum difference between the calculated and measured bound state energies of 0.024 cm−1 and a global root mean square equal to 0.008 cm−1. This result shows that the model of the free rotation of two rigid rotors suggested by Potapov et al.10 offers a good description of the D2–CO system. If we now compare the bound states of the oD2–CO complex to those calculated and measured for pH2–CO we notice that the density of bound states is significantly higher for oD2–CO than for pH2–CO. Since the PES is very similar, this result is a simple consequence of the change in the reduced mass of the two complexes.
Table 1 Comparison between calculated and experimentally determined10 energy levels (in cm−1) of the oD2–CO complex. The energies are given relative to the ground level (−25.558 cm−1) while the differences with the experimental values are given in parentheses
|
J
|
(j,l) |
| (0, j) |
(1, J − 1) |
(1, J) |
(1, J + 1) |
| 0 |
|
|
|
6.984 (0.005) |
| 1 |
0.610 (0.001) |
3.420 (−0.009) |
3.586 (−0.009) |
7.692 (0.005) |
| 2 |
1.827 (0.001) |
4.365 (−0.007) |
4.840 (−0.008) |
9.083 (0.004) |
| 3 |
3.644 (0.003) |
5.813 (−0.007) |
6.713 (−0.006) |
11.120 (0.005) |
| 4 |
6.050 (0.004) |
7.781 (−0.006) |
9.192 (−0.005) |
13.857 (0.024) |
| 5 |
9.030 (0.006) |
10.273 (−0.005) |
12.262 (−0.003) |
16.988 (0.001) |
| 6 |
12.567 (0.009) |
13.282 (−0.005) |
15.900 (0.001) |
20.264 (−0.001) |
| 7 |
16.633 (0.012) |
16.789 (−0.006) |
20.074 (0.003) |
24.953 (0.002) |
| 8 |
21.195 (0.017) |
20.760 (−0.006) |
24.739 (0.002) |
|
| 9 |
|
25.142 (−0.011) |
|
|
C. Scattering calculations
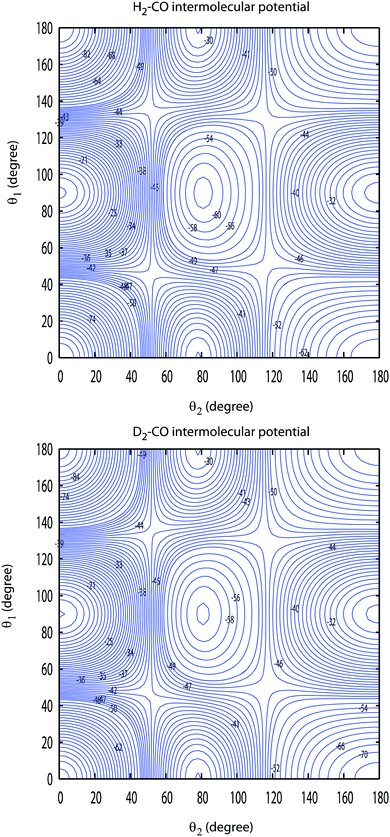
The rigid rotor Close Coupling calculations were performed using our DIDIMAT code16 which was first applied to the H2–HF collisions and used in our previous studies of H2–CO,1 or H2–CS.17 This code solves the Close Coupling equations in the space fixed frame using an R-matrix18 or a log derivative propagator.19 The T matrix elements are obtained and used to calculate the cross-sections for the transitions from an initial set of rotational levels of D2 and CO labeled by the quantum numbers (j1 = jD2, j2 = jCO) to a final set labeled by the quantum numbers (j1′ = jD2′, j2′ = jCO′):
The magnitude of the wave vector is defined by 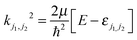 , with εj1j2 being the eigenenergy associated with a given set of initial rotational state (j1, j2) of D2 and CO, E the total energy and μ the relative mass of the system.
, with εj1j2 being the eigenenergy associated with a given set of initial rotational state (j1, j2) of D2 and CO, E the total energy and μ the relative mass of the system.
Full Close Coupling calculations were performed using the rigid rotor approximation for collision energies ranging from 10−2 up to 50 cm−1 and with the rotational constants given in the Bound state calculations section. The rotational basis set was the same as the one used for the bound state calculations. The propagation along the intermolecular coordinate was carried out using the log derivative propagator and a step size of 0.1 a0. The convergence of the cross-sections as a function of the maximum intermolecular distance and the total angular momentum was checked for each collision energy. The minimum propagation distance was 2.8 a0 while the maximum propagation distance was always greater than or equal to 50 a0.
3. Experimental
The integral cross-section (ICS) for collisional excitation of CO by para-H2 and normal-H2 has been observed for the j = 0 → 1 and 0 → 2 transitions. Using the same apparatus as the one described in the previous study, we measured the ICS corresponding to the CO j = 0 → 1 excitation induced by collisions with ortho- and normal-D2. The collision induced population enhancement of the j = 1 level was probed as a function of the collision energy using the (2 + 1) resonance-enhanced multiphoton ionisation via the (E1Π, v = 0 ← X1Σg+, v = 0) S(1) transition at 46474.8 cm−1 (215.17 nm).20 The initial residual population at the j = 1 level was offset by shot-to-shot background subtraction when triggering the probe laser and the CO beam at 10 Hz with the D2 beam at 5 Hz. The ICSs were recovered from the measured intensities IREMPI:| | 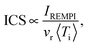 | (1) |
where vr stands for the relative velocity and 〈Ti〉 for the mean interaction time.
The relative translational energy reads:
| | 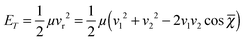 | (2) |
where
μ and
vi (
i = 1, 2) are the reduced mass and the velocities of the collision partners, respectively. The mean crossing angle,
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif)
, generally differs from the actual beam axis angle,
χ0 for reasons discussed in the ESI of
ref. 21. Briefly, it was shown that for nearly thermo-neutral processes, the detected species propagate almost in phase with the reactants, with two consequences. First, the mean crossing angle
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif)
is shifted from the beam axis angle
χ0, with Δ
χ =
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif)
−
χ0; this shift and the crossing angle spread δ
χ both depend upon the beam axis angle, as shown in
Fig. 2a. Second, the interaction time increases at decreasing crossing angles. This effect is more pronounced when using beams of matched velocities and for heavy–light collisions, which is the case here. The energy resolution (which depends on velocity and crossing angle spreads) and mean interaction time as a function of collision energy are displayed in
Fig. 2b. These effects are detailed for the O
2 + H
2 inelastic collisions in the supplementary materials of
ref. 21.
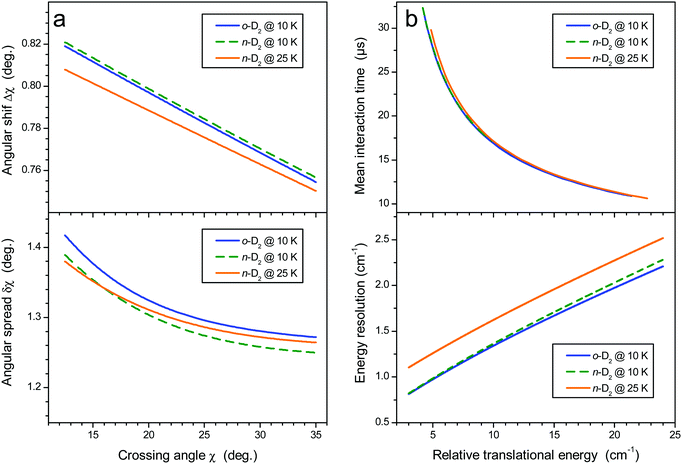 |
| | Fig. 2 (a) Crossing angle shift (upper panel) and spread (lower panel). (b) Mean interaction time for all experimental sets (upper panel) and energy resolution (lower panel). | |
4. Results and discussion
(a) Theory
The results of Close Coupling calculations are presented in Fig. 3 and 4 for the rotational excitation of CO (jCO = 0 → 1), respectively, in collisions with oD2 and pD2. The partial wave expansions of these cross-sections are also represented in the same figures. Many shape and Feshbach resonances appear in these two figures. The density of the resonances is larger than for the collisions of pH2 + CO as was noticed in the previous paragraph for the density of the bound states of oD2–CO compared to those of pH2–CO. This is mainly due to the change in the relative mass which is almost doubled when one moves from H2–CO to D2–CO, thus requiring more partial waves to get the convergence of the cross-sections. Also, if at low collision energy it is often possible to attribute a single partial wave to a given resonance, this task becomes more and more difficult at higher energy.
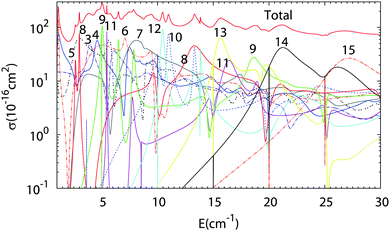 |
| | Fig. 3 Partial wave expansion of the CO (j = 0 → 1) rotational excitation cross-section in collisions with oD2 as a function of the collision energy. The curves are labeled by the value of the total angular momentum quantum number J. | |
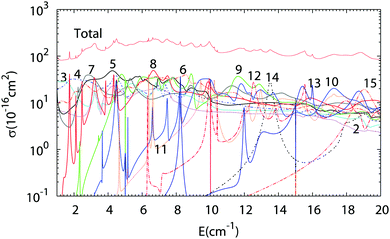 |
| | Fig. 4 Partial wave expansion of the CO (j = 0 → 1) rotational excitation cross-section in collisions with pD2 as a function of the collision energy. The curves are labeled by the value of the total angular momentum quantum number J. | |
The results of our Close Coupling calculations are then compared in Fig. 5 and 6 for the rotational excitation of CO (j = 0 → 1) in collisions with oD2/pH2 and pD2/oH2, respectively. For all these calculations the same number of rotational states was used for each fragment, respectively, 15 states for CO and 2 states for pD2, oD2, pH2 and oH2. The results for para-H2 and ortho-H2 are those of our previous study. As can be seen in these figures the cross-sections with D2 are significantly larger than those with H2. This result is expected, as the mass of D2 is twice that of H2 giving more strength to the inelastic collisions involving D2. Furthermore, the density of the resonances is larger than for the collisions of pH2 + CO as expected from the larger density of bound states in the D2–CO complex. This is again mainly due to the change in the reduced mass, which is almost doubled when turning from H2–CO to D2–CO, thus requiring more partial waves to get the convergence of the cross-sections.
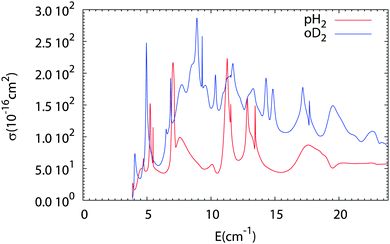 |
| | Fig. 5 Comparison of the rotational excitation cross-section of CO (j = 0 → 1) in collisions with pH2 (see ref. 1) and oD2 as a function of collision energy. | |
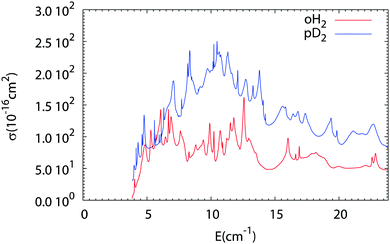 |
| | Fig. 6 Comparison of the rotational excitation cross-section of CO (j = 0 → 1) in collisions with oH2 and pD2 as a function of collision energy. | |
(b) Experiment
The comparison between experiment and theory for the CO (j = 0 → 1) excitation by collisions with ortho-D2 is displayed in Fig. 7. In a similar manner the results obtained for CO (j = 0 → 1) excitation by collisions with normal-D2 are displayed in Fig. 8. The theoretical ICSs calculated for ortho- and para-D2 are given in the top panel (a), while experimental data are displayed in the bottom panel (b), along with the theoretical ICS convoluted with experimental energy distribution to allow for comparison. The total ICS is the sum of both ortho and para contributions weighted by their statistical relative populations: 2/3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3, respectively. In both cases of para D2 and normal D2 colliding with CO the agreement between theory and experiment is very good confirming once again the good quality of the new PES. These results show again that the rigid rotor approximation combined with a specific vibrational averaging of the PES1 is working well for this system and that the model of the free rotation of D2 and CO suggested by Potapov et al.10 offers a good description of the D2–CO system. In other words CO and D2 are so weakly bound that they almost freely rotate independently. The results presented here for the benchmark D2–CO system demonstrate that theory and experiment have reached a high level of refinement. Just like bound states, inelastic cross-sections can now be probed with spectroscopic resolution and they provide very useful and complementary information on the interactions between individual molecules.
1/3, respectively. In both cases of para D2 and normal D2 colliding with CO the agreement between theory and experiment is very good confirming once again the good quality of the new PES. These results show again that the rigid rotor approximation combined with a specific vibrational averaging of the PES1 is working well for this system and that the model of the free rotation of D2 and CO suggested by Potapov et al.10 offers a good description of the D2–CO system. In other words CO and D2 are so weakly bound that they almost freely rotate independently. The results presented here for the benchmark D2–CO system demonstrate that theory and experiment have reached a high level of refinement. Just like bound states, inelastic cross-sections can now be probed with spectroscopic resolution and they provide very useful and complementary information on the interactions between individual molecules.
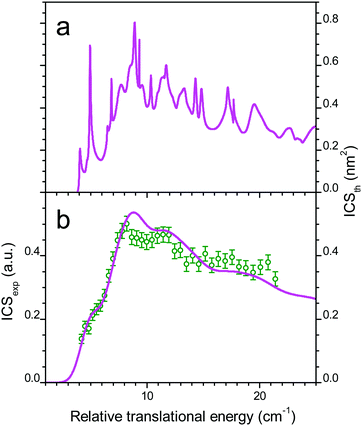 |
| | Fig. 7 Collisional energy dependence of the integral cross-sections for CO excitation to j = 1 by collisions with ortho-D2. (a) Theoretical ICS and (b) experimental data in arbitrary units, obtained when crossing the CO:Ne beam (#1 in Table 2) from a first pulsed nozzle with a beam of neat ortho-D2 from a second nozzle (beam #4, crossing angle χ = 30–12.5° with −0.5° decrement: open circles). Theoretical ICS convoluted with the experimental collision energy spread (solid line). | |
Table 2 Characteristics of the molecular beams used in the determination of the integral cross-sections
| Beam |
Gas mixture |
T
(K) |
v
(ms−1) |
δvHWEb (ms−1) |
S
|
γ
0
(μs) |
δχe (deg.) |
|
Temperature set point of the cold head. The effective temperature of the pulsed valve is limited by losses due to thermal radiation. At the lowest set point of 10 K, the effective nozzle temperature deduced from the D2 beam velocity is 35 K higher.
Peak velocities, v, and velocity spreads, δvHWE, are deduced from temporal profiles recorded at the crossing point (detecting CO by REMPI and D2 by CO signal depletion), and at a distance d = 393.3 mm downstream (with a fast-ionization gauge inserted perpendicular to the molecular beam). Both profiles were fitted to Gaussian functions, with peak positions t0 and t1 and half-width at 1/e (HWE), γ0 and γ1, yielding the peak velocities v = d/(t1 − t0), and the velocity spreads δvHWE from the pulse broadening.
Speed ratio S ≈ v/δvHWE (Gaussian limit of the Maxwell–Boltzmann distribution).
Pulse width HWE at the crossing point.
Angular divergence (HWE).
|
| #1 CO |
CO:0.004/Ne:0.996 |
230 |
697 ± 5 |
19.8 |
≥35 |
28.3 |
0.9 |
| #2 n-D2 |
Neat |
25 |
763 ± 5 |
46.5 |
≥15 |
14.4 |
2.0 |
| #3 n-D2 |
Neat |
10 |
728 ± 5 |
48.6 |
≥15 |
16 |
2.0 |
| #4 o-D2 |
Neat |
10 |
732 ± 5 |
43.5 |
≥16 |
14.2 |
2.0 |
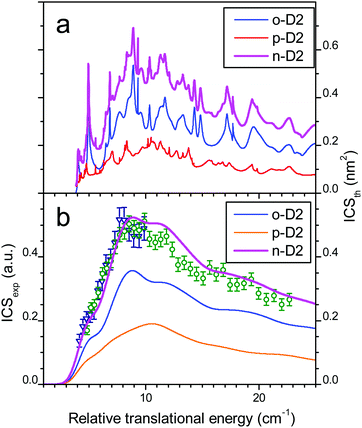 |
| | Fig. 8 Collisional energy dependence of the integral cross-sections for CO excitation to j = 1 by collisions with normal-D2. (a) Theoretical ICSs calculated for CO + normal-D2 (magenta solid line), with contributions of ortho-D2 (blue solid line) and para-D2 (orange solid line). (b) Experimental data in arbitrary units, obtained when crossing the CO:Ne beam (#1 in Table 2) from a first pulsed nozzle with a beam of neat normal-D2 from a second nozzle (beam #2, crossing angle χ = 30–12.5° with −0.5° decrement: open circles; beam #3; χ = 20–12.5° with −0.5° decrement: open triangles). Theoretical ICSs convoluted with the experimental collision energy spread: total ICS (solid line), ortho- (dashed line) and para-D2 (dashed-dotted line) contributions. | |
5. Conclusion
A joint experimental and theoretical study of the CO (j = 0 → 1) inelastic cross-section in collision with D2 was presented. The new 4 D PES obtained by averaging the original model of Jankowski et al.7 over the vibrational level of D2 was shown to differ only slightly from the one averaged over the vibrational level of H2. The present results were compared with those obtained previously for the collisions of H2 with CO.1 The cross-sections for the rotationally inelastic transition of CO (0 → 1) in collisions with D2 were found to be always greater than those involving H2. This result was shown to be essentially due to the ratio of the relative masses of these two collisional systems which is roughly equal to two. More partial waves are then needed to converge the cross-sections involving D2 and these supplementary contributions increase significantly the magnitude of the cross-sections. The agreement between theory and experiment is found to be excellent and demonstrates the validity of the rigid rotor approximation for this system in this domain of collision energy. The computed bound state energies of the oD2–CO were also found to be in excellent agreement with the available experimental data in the study of Potapov et al.10 showing that the model of the free rotation of two rigid rotors suggested by Potapov et al. offers a good description of the D2–CO system. In other words CO and D2 are so weakly bound that they almost freely rotate independently. The results presented here for this benchmark D2–CO system demonstrate that theory and experiment have reached a high level of refinement. Just like bound states, inelastic cross-sections can now be probed with spectroscopic resolution and they provide very useful and complementary information on the interactions between individual molecules.
Acknowledgements
This work has been supported by the “Agence Nationale de la Recherche” (ANR-HYDRIDES, contract ANR-12-BS05-0011-01) and by the CNRS national program “Physico-Chimie du Milieu Interstellaire”. Computer time for this study was provided by the Mésocentre de Calcul Intensif Aquitain computing facilities of Université de Bordeaux and Université de Pau et des Pays de l’Adour.
References
- A. Faure, P. Jankowski, T. Stoecklin and K. Szalewicz, Sci. Rep., 2016, 6, 28849 CrossRef PubMed.
- B. H. Yang,
et al.
, Nat. Commun., 2015, 6, 6629 CrossRef CAS PubMed.
- M. Wernli, P. Valiron, A. Faure, L. Wiesenfeld, P. Jankowski and K. Szalewicz, Astron. Astrophys., 2006, 446, 367 CrossRef CAS.
- D. R. Flower, Mon. Not. R. Astron. Soc., 2008, 425, 1350 CrossRef.
- J. P. Reid, C. J. S. M. Simpson, H. M. Quiney and J. M. Hutson, J. Chem. Phys., 1995, 103, 2528 CrossRef CAS.
- P. Jankowski and K. Szalewicz, J. Chem. Phys., 2005, 123, 104301 CrossRef PubMed.
- P. Jankowski, A. R. W. McKellar and K. Szalewicz, Science, 2012, 336, 1147 CrossRef CAS PubMed.
- S. Chefdeville, T. Stoecklin, C. Naulin, P. Jankowski, K. Szalewicz, A. Faure, M. Costes and A. Bergeat, Astrophys. J., Lett., 2015, 799, L9 CrossRef CAS.
- S. Chefdeville, T. Stoecklin, A. Bergeat, K. M. Hickson, C. Naulin and M. Costes, Phys. Rev. Lett., 2012, 109, 023201 CrossRef PubMed.
- A. V. Potapov, V. A. Panfilov, A. A. Dolgov, L. A. Surin and B. S. Dumesh, Opt. Spectrosc., 2009, 106, 655 CrossRef CAS.
- P. Jankowski, J. Chem. Phys., 2004, 121, 1655 CrossRef CAS PubMed.
- G. Danby, J. Phys. B: At. Mol. Phys., 1983, 16, 3393 CrossRef CAS.
- J. M. Hutson, Comput. Phys. Commun., 1994, 84, 1 CrossRef CAS.
- S. Green, J. Chem. Phys., 1975, 62, 2271 CrossRef CAS.
-
K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules, Van Nostrand, New York, 1987 Search PubMed.
- G. Guillon, T. Stoecklin, A. Voronin and P. Halvick, J. Chem. Phys., 2008, 129, 104308 CrossRef CAS PubMed.
- O. Denis-Alpizar, T. Stoecklin, P. Halvick and M. L. Dubernet, J. Chem. Phys., 2013, 139, 204304 CrossRef PubMed.
- G. A. Parker, T. G. Schmalz and J. C. Light, J. Chem. Phys., 1980, 73, 1757 CrossRef CAS.
- D. E. Manolopoulos, J. Chem. Phys., 1986, 85, 6425 CrossRef CAS.
- M. A. Hines, H. A. Michelsen and R. N. Zare, J. Chem. Phys., 1990, 93, 8557 CrossRef CAS.
- S. Chefdeville, Y. Kalugina, S. Y. T. van de Meerakker, C. Naulin, F. Lique and M. Costes, Science, 2013, 341, 1094 CrossRef CAS PubMed.
|
| This journal is © the Owner Societies 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
S. B.
Morales
ab and
M.
Costes
ab
ab,
S. B.
Morales
ab and
M.
Costes
ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 geometries in R, θ1, θ2 and ϕ, as in previous studies on H2–CO3 where θ1 and θ2 are, respectively, the polar angles between the CO and DD interatomic distances and the R Jacobi vector while ϕ is the Jacobi azimuthal angle. A total of 29 values of R (in Bohr) were thus used in the range [3.00–15.00]. This radial grid was combined with 3000 random angular geometries. The PES was refitted using a spherical harmonics expansion including all anisotropies up to l1 = 10 for CO and l2 = 6 for H2 (where the integer indices l1 and l2 refer to θ1 and θ2 dependencies), resulting in 142 angular terms. The RMS residual was found to be lower than 0.1 cm−1 for R > 5.00 Bohr. The most significant terms were selected using a self-consistent Monte-Carlo estimator, resulting in a final set of 60 expansion functions with anisotropies up to l1 = 7 and l2 = 6. A cubic spline radial interpolation of the expansion coefficients was finally performed over the whole intermolecular distance range and was smoothly connected using a switching function to standard extrapolation (exponential and power laws at short-range and long-range, respectively). The resulting D2–CO PES is very similar to the H2–CO one as can be seen in Fig. 1. The global minimum energy of the new surface is −93.048 cm−1 and is obtained for the linear arrangement D–D⋯C–O and for an intermolecular distance R equal to 7.908 Bohr. The corresponding values for the H2–CO complex are, respectively, equal to −94.096 cm−1 and 7.911 Bohr. The values of the energies and intermolecular distances associated with the other linear geometry H–H⋯O–C are also very close for the two systems. Their values are found to be −73.336 cm−1 and 7.160 Bohr for D2–CO and −73.738 cm−1 and 7.168 Bohr for H2–CO. The D2–CO surface is then slightly shallower than the H2–CO one by about 1.1% at the global minimum and 0.5% at the local one. We conclude from this comparison that the lower zero point energy of D2 compared to H2 and the small differences of the vibrationally averaged distances of these two molecules lead to only very small differences of the interaction energy surfaces. Also, the differences if any between the results involving these two systems will then result only from the differences between the diatom rovibrational energies and wave functions and from those between the reduced masses and positions of the center of masses.
000 geometries in R, θ1, θ2 and ϕ, as in previous studies on H2–CO3 where θ1 and θ2 are, respectively, the polar angles between the CO and DD interatomic distances and the R Jacobi vector while ϕ is the Jacobi azimuthal angle. A total of 29 values of R (in Bohr) were thus used in the range [3.00–15.00]. This radial grid was combined with 3000 random angular geometries. The PES was refitted using a spherical harmonics expansion including all anisotropies up to l1 = 10 for CO and l2 = 6 for H2 (where the integer indices l1 and l2 refer to θ1 and θ2 dependencies), resulting in 142 angular terms. The RMS residual was found to be lower than 0.1 cm−1 for R > 5.00 Bohr. The most significant terms were selected using a self-consistent Monte-Carlo estimator, resulting in a final set of 60 expansion functions with anisotropies up to l1 = 7 and l2 = 6. A cubic spline radial interpolation of the expansion coefficients was finally performed over the whole intermolecular distance range and was smoothly connected using a switching function to standard extrapolation (exponential and power laws at short-range and long-range, respectively). The resulting D2–CO PES is very similar to the H2–CO one as can be seen in Fig. 1. The global minimum energy of the new surface is −93.048 cm−1 and is obtained for the linear arrangement D–D⋯C–O and for an intermolecular distance R equal to 7.908 Bohr. The corresponding values for the H2–CO complex are, respectively, equal to −94.096 cm−1 and 7.911 Bohr. The values of the energies and intermolecular distances associated with the other linear geometry H–H⋯O–C are also very close for the two systems. Their values are found to be −73.336 cm−1 and 7.160 Bohr for D2–CO and −73.738 cm−1 and 7.168 Bohr for H2–CO. The D2–CO surface is then slightly shallower than the H2–CO one by about 1.1% at the global minimum and 0.5% at the local one. We conclude from this comparison that the lower zero point energy of D2 compared to H2 and the small differences of the vibrationally averaged distances of these two molecules lead to only very small differences of the interaction energy surfaces. Also, the differences if any between the results involving these two systems will then result only from the differences between the diatom rovibrational energies and wave functions and from those between the reduced masses and positions of the center of masses.![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 12 =
12 = ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 1 +
1 + ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 2,
2, ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) ,
, ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) =
= ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 12 +
12 + ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) and of both Jz and the parity operator Π, where
and of both Jz and the parity operator Π, where ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 1 and
1 and ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) 2 are the rotational angular momenta of H2 and CO,
2 are the rotational angular momenta of H2 and CO, ![[l with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006c_20d1.gif) is the relative angular momentum of the fragments,
is the relative angular momentum of the fragments, ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) is the total angular momentum of the system and Jz is its projection along the z space fixed axis. The vibrational levels of the van der Waals complex are calculated by performing calculations using a rigid rotor description of both D2 and CO for all the values of the total angular momentum J and parity ε leading to bound states. We used the ground vibrationally averaged rotational constants for both molecules15 (B = 29.9037 cm−1 for D2 and B = 1.9225 cm−1 for CO). The convergence of the bound levels of the CO–D2 complex with respect to the CO and D2 rotational basis was tested. Fifteen rotational states were included in the basis set describing the CO molecule while for ortho-D2 we included two rotational states. The maximum propagation distance was 50 Bohr. The calculations were performed for two values of the propagator step size (0.1 and 0.05 Bohr) and the values of the bound state energies were obtained from a Richardson extrapolation as suggested by Hutson.13 The results of this approach are compared to the experimental results in the study of Potapov et al.10 in Table 1. As can be seen in this table the agreement between theory and experiment is found to be excellent with the maximum difference between the calculated and measured bound state energies of 0.024 cm−1 and a global root mean square equal to 0.008 cm−1. This result shows that the model of the free rotation of two rigid rotors suggested by Potapov et al.10 offers a good description of the D2–CO system. If we now compare the bound states of the oD2–CO complex to those calculated and measured for pH2–CO we notice that the density of bound states is significantly higher for oD2–CO than for pH2–CO. Since the PES is very similar, this result is a simple consequence of the change in the reduced mass of the two complexes.
is the total angular momentum of the system and Jz is its projection along the z space fixed axis. The vibrational levels of the van der Waals complex are calculated by performing calculations using a rigid rotor description of both D2 and CO for all the values of the total angular momentum J and parity ε leading to bound states. We used the ground vibrationally averaged rotational constants for both molecules15 (B = 29.9037 cm−1 for D2 and B = 1.9225 cm−1 for CO). The convergence of the bound levels of the CO–D2 complex with respect to the CO and D2 rotational basis was tested. Fifteen rotational states were included in the basis set describing the CO molecule while for ortho-D2 we included two rotational states. The maximum propagation distance was 50 Bohr. The calculations were performed for two values of the propagator step size (0.1 and 0.05 Bohr) and the values of the bound state energies were obtained from a Richardson extrapolation as suggested by Hutson.13 The results of this approach are compared to the experimental results in the study of Potapov et al.10 in Table 1. As can be seen in this table the agreement between theory and experiment is found to be excellent with the maximum difference between the calculated and measured bound state energies of 0.024 cm−1 and a global root mean square equal to 0.008 cm−1. This result shows that the model of the free rotation of two rigid rotors suggested by Potapov et al.10 offers a good description of the D2–CO system. If we now compare the bound states of the oD2–CO complex to those calculated and measured for pH2–CO we notice that the density of bound states is significantly higher for oD2–CO than for pH2–CO. Since the PES is very similar, this result is a simple consequence of the change in the reduced mass of the two complexes.
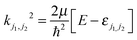 , with εj1j2 being the eigenenergy associated with a given set of initial rotational state (j1, j2) of D2 and CO, E the total energy and μ the relative mass of the system.
, with εj1j2 being the eigenenergy associated with a given set of initial rotational state (j1, j2) of D2 and CO, E the total energy and μ the relative mass of the system.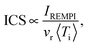
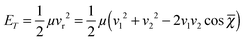
![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) , generally differs from the actual beam axis angle, χ0 for reasons discussed in the ESI of ref. 21. Briefly, it was shown that for nearly thermo-neutral processes, the detected species propagate almost in phase with the reactants, with two consequences. First, the mean crossing angle
, generally differs from the actual beam axis angle, χ0 for reasons discussed in the ESI of ref. 21. Briefly, it was shown that for nearly thermo-neutral processes, the detected species propagate almost in phase with the reactants, with two consequences. First, the mean crossing angle ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) is shifted from the beam axis angle χ0, with Δχ =
is shifted from the beam axis angle χ0, with Δχ = ![[small chi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d8.gif) − χ0; this shift and the crossing angle spread δχ both depend upon the beam axis angle, as shown in Fig. 2a. Second, the interaction time increases at decreasing crossing angles. This effect is more pronounced when using beams of matched velocities and for heavy–light collisions, which is the case here. The energy resolution (which depends on velocity and crossing angle spreads) and mean interaction time as a function of collision energy are displayed in Fig. 2b. These effects are detailed for the O2 + H2 inelastic collisions in the supplementary materials of ref. 21.
− χ0; this shift and the crossing angle spread δχ both depend upon the beam axis angle, as shown in Fig. 2a. Second, the interaction time increases at decreasing crossing angles. This effect is more pronounced when using beams of matched velocities and for heavy–light collisions, which is the case here. The energy resolution (which depends on velocity and crossing angle spreads) and mean interaction time as a function of collision energy are displayed in Fig. 2b. These effects are detailed for the O2 + H2 inelastic collisions in the supplementary materials of ref. 21.



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1/3, respectively. In both cases of para D2 and normal D2 colliding with CO the agreement between theory and experiment is very good confirming once again the good quality of the new PES. These results show again that the rigid rotor approximation combined with a specific vibrational averaging of the PES1 is working well for this system and that the model of the free rotation of D2 and CO suggested by Potapov et al.10 offers a good description of the D2–CO system. In other words CO and D2 are so weakly bound that they almost freely rotate independently. The results presented here for the benchmark D2–CO system demonstrate that theory and experiment have reached a high level of refinement. Just like bound states, inelastic cross-sections can now be probed with spectroscopic resolution and they provide very useful and complementary information on the interactions between individual molecules.
1/3, respectively. In both cases of para D2 and normal D2 colliding with CO the agreement between theory and experiment is very good confirming once again the good quality of the new PES. These results show again that the rigid rotor approximation combined with a specific vibrational averaging of the PES1 is working well for this system and that the model of the free rotation of D2 and CO suggested by Potapov et al.10 offers a good description of the D2–CO system. In other words CO and D2 are so weakly bound that they almost freely rotate independently. The results presented here for the benchmark D2–CO system demonstrate that theory and experiment have reached a high level of refinement. Just like bound states, inelastic cross-sections can now be probed with spectroscopic resolution and they provide very useful and complementary information on the interactions between individual molecules.