Open Access Article
Open Access ArticleA butterfly motion of formic acid and cyclobutanone in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h2_char_2009.gif) 1 hydrogen bonded molecular cluster†
1 hydrogen bonded molecular cluster†
Luca
Evangelisti
a,
Lorenzo
Spada
a,
Weixing
Li
a,
Susana
Blanco
b,
Juan Carlos
López
b,
Alberto
Lesarri
 *b,
Jens-Uwe
Grabow
c and
Walther
Caminati
*a
*b,
Jens-Uwe
Grabow
c and
Walther
Caminati
*a
aDipartimento di Chimica “G. Ciamician” dell'Università, Via Selmi 2, I-40126 Bologna, Italy. E-mail: walther.caminati@unibo.it
bDepartamento de Química Física y Química Inorgánica, Facultad de Ciencias, Universidad de Valladolid, E-47011 Valladolid, Spain. E-mail: lesarri@qf.uva.es
cInstitut für Physikalische Chemie und Elektrochemie, Lehrgebiet A, Gottfried-Wilhelm-Leibniz-Universität, Callinstrasse 3A, D-30167 Hannover, Germany
First published on 16th November 2016
Abstract
Upon supersonic expansion, formic acid and cyclobutanone (CBU) form a molecular cluster in which the two constituent molecules, linked by OH⋯O and CH⋯O hydrogen bonds, undergo a rapid interconversion between two equivalent forms. The tunneling motion takes place through the rupture and reformation of the C–H⋯O hydrogen bond between the carbonyl oxygen of HCOOH and one of the two hydrogen atoms of the methylenic group adjacent to the cyclobutanone keto group. From the microwave spectra, tunneling energy splittings (ΔE01) have been determined for the parent (1122.756(3) MHz), DCOOH⋯CBU (1084.538(1) MHz) and HCOOD⋯CBU (1180.282(4) MHz) isotopic species. From these splittings, the potential barrier to interconversion has been calculated to be B2 = 39.7(5) cm−1. The tunneling pathway is an asymmetric butterfly-like motion between the two moieties of the adduct, with a barrier at a configuration in which the ring plane of cyclobutanone is coplanar with formic acid.
Introduction
A number of complexes of carboxylic acids have been investigated by high resolution spectroscopy, providing information on the non-bonding interactions which link the constituent molecules,1–27 on the Ubbelohde effect related to the OH → OD isotopic substitution, on occasionally occurring conformational equilibria, and – most noticeably – on the internal dynamics of large amplitude motions.With respect to internal dynamics, useful information is obtained when splittings of the rotational transitions, due to tunneling motions connecting equivalent minima, are observed in high resolution (typically microwave) spectra. From these splittings it is generally possible to determine the potential energy barrier connecting equivalent minima. This kind of splitting has been measured for internal motions such as: (i) double proton transfer in dimers of carboxylic acids with a suitable symmetry;3–7 (ii) internal rotation of a light symmetric group (i.e. a CH3 group);1,5,18 (iii) inversion of an asymmetric group (e.g. a hydroxyl or carboxylic acid) connecting two equivalent minima11,12,14,19 or (iv) internal motion of water in hydrated forms of carboxylic acids.15–21
Here we report the direct observation in the jet-cooled spectra of huge rotational splittings arising from a relative motion of a partner as heavy as cyclobutanone (CBU) with respect to formic acid (FA) in their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (FA–CBU). The tunneling pathway and the potential energy function of the motion have been derived from the experimental values for the ΔE01 splittings of some isotopologues, as described below.
1 complex (FA–CBU). The tunneling pathway and the potential energy function of the motion have been derived from the experimental values for the ΔE01 splittings of some isotopologues, as described below.
Methods
Experimental
Samples of HCOOH, HCOOD, DCOOH and CBU were obtained commercially (Aldrich) and used without further purification. The rotational spectra of the FA⋯CBU isotopologues have been recorded in two different laboratories:(a) Bologna. Measurements were performed between 6 and 18.5 GHz using a high-Q pulse-excitation Fourier transform microwave (FTMW) spectrometer described elsewhere,28 based on the pioneering designs of Flygare29 and Grabow.30 Adducts were formed by flowing helium (∼5 atm) through two stainless steel reservoirs containing, respectively, CBU at room temperature, and FA (or isotopologues) at 273 K, and running the resulting gaseous mixture through a pulsed nozzle. Rotational frequencies were determined after the Fourier transform of 8k-data point time domain free induction decays, recorded with 40 ns sampling intervals. The pulsed molecular beam was introduced along the axis of a Fabry–Pérot resonator. Consequently, each observed transition appeared as a Doppler doublet, and the rest frequency was determined as the arithmetic mean of the frequencies of the two Doppler components. The accuracy of frequency measurements is estimated to be better than 3 kHz.
(b) Valladolid. The rotational spectrum of the parent species was initially recorded with a broadband direct-digital chirp-pulse FTMW spectrometer covering the frequency range of 2–8 GHz, which follows Pate's design.31 In this spectrometer a 5 μs chirp pulse created using an arbitrary waveform generator is amplified to 20 W and radiated perpendicular to the propagation of the jet expansion through a horn antenna. A molecular transient emission spanning 40 μs is then detected through a second horn, recorded with a digital oscilloscope and Fourier-transformed to the frequency domain. Sample preparation was similar to Bologna, with optimal conditions requiring a backing pressure of ca. 4 atm and neon as the carrier gas. The accuracy of the frequency measurements is better than 15 kHz.
Computational
Information on the most stable geometries, and conformational and dissociation energies of the dimer was predicted computationally using both density functional theory (B3LYP assisted with empirical dispersion terms using the Grimme D3 scheme) and ab initio methods (MP2). All calculations used Pople's 6-311++G(d,p) basis set and were implemented in the Gaussian 09 program.32Results and discussion
To get an initial guess on the shapes and relative energies of the plausible isomers of FA-CBU, we performed geometry optimizations comparing the performance of the MP2 and B3LYP-D3 methods. The two subunits are expected to assume a nearly co-planar arrangement in the complex. MP2 predictions suggest two energetically close minima, with the CBU ring slightly distorted (up or down) from planarity, while the B3LYP-D3 calculation predicts a single minimum, with the CBU ring nearly planar in the complex. Actually, the ring puckering of isolated CBU has a double minimum potential energy function with a small barrier close to 5 cm−1 at the planar ring.33 In this case the ground vibrational state lies above the barrier, corresponding to an effective planar ring. It is well-known that MP2 tends to overestimate ring-puckering barriers while B3LYP underestimates them. In particular, MP2 suggests ring-puckering distortions when it is not the case (even for benzene). In addition, in previous investigations of complexes of CBU with water34 and trifluoromethane,35 MP2 suggested two conformers differing in the distortion of the CBU ring, but only one was found, with CBU effectively being planar. For this reason, we followed the prediction of the B3LYP-D3 calculation. The rotational constants, the values of the dipole moment components and the absolute energy for the most stable conformer are reported in Table 1.The rotational spectrum was first recorded for the parent species with a chirp-excitation microwave spectrometer in the frequency range of 2–8 GHz. Unfortunately, the spectrum was weak and considerably perturbed in that frequency region. We could reliably assign three transitions, 202 ← 101, 303 ← 202, and 404 ← 303, split into two component lines associated with the two inversion sublevels of the vibrational ground state. We then recorded the 6–18.5 GHz region using the pulse-excitation microwave spectrometer. We measured 31 μa- and 6 μb-type transitions, displaying two intra-state tunneling components split up to 10 MHz. Finally, once good spectral predictions were iteratively obtained, 6 additional μc-transitions were measured, with the two components evenly spaced by ca. 2245 MHz. The latter lines were identified as inter-state transitions, so the separation between the two components is about the double of the energy separation of the two inversion sublevels.
All rotational transitions have been satisfactorily fitted using the following two-state coupled Hamiltonian:
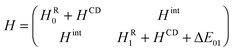 | (1) |
| Hint = Fbc × (PbPc + PcPb) + Fac × (PaPc + PcPa) | (2) |
| HCOOH⋯CBU | DCOOH⋯CBU | HCOOD⋯CBU | |
|---|---|---|---|
| a Uncertainties in parentheses in units of the last digit. b Values in brackets have been held fixed at the values of the parent species. c Root-mean-square deviation of the fit. d Number of transitions in the fit. | |||
| A 0/MHz | 4151.912(9)a | 4139.417(9) | 4119.26(1) |
| A 1/MHz | 4151.222(9) | 4138.707(10) | 4118.54(1) |
| B 0/MHz | 988.452(2) | 961.557(2) | 983.636(2) |
| B 1/MHz | 988.562(2) | 961.671(2) | 983.745(2) |
| C 0/MHz | 843.447(4) | 823.406(5) | 838.570(5) |
| C 1/MHz | 843.683(4) | 823.627(5) | 838.816(5) |
| D J/kHz | 0.596(1) | 0.565(2) | 0.586(1) |
| D JK/kHz | −0.86(4) | −1.04(7) | −0.91(5) |
| D K/kHz | 11(1) | [11]b | 11(2) |
| d 1/kHz | 0.039(1) | 0.037(2) | 0.040(1) |
| d 2/kHz | −0.016(1) | −0.016(5) | −0.014(1) |
| ΔE01/MHz | 1122.756(3) | 1084.538(5) | 1180.282(5) |
| F bc/MHz | 5.2261(2) | 4.9179(7) | 5.2584(2) |
| F ac/MHz | 15.5(5) | 16.4(5) | 14.0(6) |
| σ /kHz | 5.1 | 5.2 | 4.5 |
| N | 84 | 54 | 74 |
Additionally, we could assign the spectra of the two mono-deuterated species DCOOH⋯CBU and HCOOD⋯CBU, using ca. 99% enriched samples of DCOOH and HCOOD, respectively. The measured transition frequencies were fitted using the same procedure described for the parent species. The results of the fits are reported in the second and third columns of Table 2. No effects of the hyperfine quadrupole structure of the D atom (I = 1) have been satisfactorily resolved. All the measured transition frequencies are given in the ESI† (Tables S1–S3).
Using the isotopic data, we report the Kraitchman substitution coordinates39 of the two hydrogen atoms of the FA unit (H5 and H4) in Table 3. The atom numbering and the principal inertial axes system of the complex are shown in Fig. 1. The derived atomic positions are in good agreement with the theoretical values.
| r s | r e | r 0 | ||
|---|---|---|---|---|
| a Calculated from the partial r0 structure (see the text). b Uncertainties in parenthesis in units of the last digit. | ||||
| H4 | |a|/Å | 1.584(2)b | 1.4549 | 1.4991 |
| |b|/Å | 0.989(3) | 1.0365 | 1.0635 | |
| |c|/Å | 0.06(5) | 0.1812 | 0.1806 | |
| H5 | |a|/Å | 3.7785(8) | 3.7924 | 3.7720 |
| |b|/Å | 0.579(6) | 0.5712 | 0.6365 | |
| |c|/Å | 0.22(2) | 0.0682 | 0.1247 | |
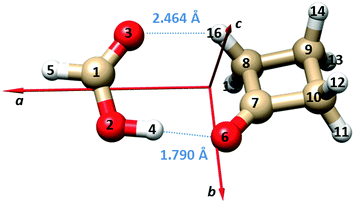 | ||
| Fig. 1 Principal inertial axes and atom numbering of the observed dimer of FA⋯CBU. The bond lengths of the two hydrogen bonds are also given. | ||
The B3LYP-D3/6-311++G(d,p) structures of the two equivalent energy minima and the transition state on the potential energy surface connecting the two minima (see Fig. 2 and the following paragraph) are reported in the ESI† (Tables S4 and S5). Adjusting the theoretical values of the structural parameters rO6–O2, ∠O6O2C1 and ∠O6O2–C1O3 from 2.7475 Å, 111.0° and −2.2° to 2.7800 Å, 109° and 0.4°, respectively, let us obtain an effective structure reproducing the experimental rotational constants within a few MHz. The bond lengths of the two hydrogen bonds corresponding to this geometry are: rO6–H4 = 1.790 Å and rO3–H16 = 2.464 Å, respectively. These values are also shown in Fig. 1, and are in line with the values for “conventional” O–H⋯O and weak C–H⋯O hydrogen bonds.
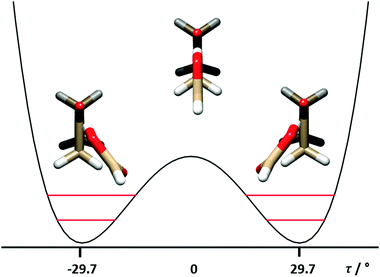 | ||
| Fig. 2 The tunneling motion in FA–CBU is due to the internal rotation around the C7O6–O2C1 (τ) dihedral angle, accompanied by structural relaxation of some other parameters. | ||
The three determined splittings ΔE01 are related to the height B2 of the potential barrier connecting the two equivalent minima depicted in Fig. 2, and to the specific pathway of the tunnelling motion. As expected, ΔE01(DCOOH⋯CBU) = 1084.538 MHz is smaller than ΔE01(HCOOH⋯CBU) = 1122.756 MHz, because the reduced mass of the motion is higher for DCOOH⋯CBU. However, unexpectedly, ΔE01(HCOOD⋯CBU) = 1180.282 MHz is larger than the value of the parent species. This is probably related to the Ubbelohde effect,40 often observed in the complexes of carboxylic acids,8–14 and related to the change in the bond length of the O–H⋯O hydrogen bond upon H → D substitution.
For this reason, we relied only on the former two ΔE01 values to calculate the potential energy surface of the intermolecular motion. According to the theoretical calculations, B2 is a function of the dihedral angle C7O6–O2C1 (τ), which is the main parameter describing the relative motion of the two subunits. However, other structural parameters undergo considerable changes as a function of τ, influencing the reduced mass of the motion. The latter depends not only on τ with respect to the rigid moieties, but also on the dynamic structural relaxation which takes place during the complex's large amplitude motion.
Meyer's flexible model41 is especially suitable to determine potential energy surfaces from rotational and vibrational experimental data. As justified by the theoretical predictions, we describe the large amplitude motion along the dihedral angle τ with any structural relaxations in other co-ordinates of the dimer constrained into a one-dimensional function of τ. The double minimum potential can then be parameterized and described using the following function:
| V(τ) = B2[1 − (τ/τ0)2]2, | (3) |
| ∠C8C7–O6O2/° = 12.0·(τ/τ0) | (4) |
| ∠O6O2–C1O3/° = −2.2·(τ/τ0) | (5) |
| ∠C7O6O2/° = 126.7 − 3·(τ/τ0)2 | (6) |
| Tunneling splittings | Obs. | Calc. |
|---|---|---|
| ΔE01(HCOOH⋯CBU)/MHz | 1122.8 | 1119.8 |
| ΔE01(DCOOH⋯CBU)/MHz | 1084.5 | 1079.6 |
| Potential energy parameters | |
|---|---|
| B 2 = 39.7(5) cm−1 | τ 0 = 29.7° |
| Structural relaxation parameters |
|---|
| ∠C8C7–O6O2/° = 12.0·(τ/τ0) |
| ∠O6O2–C1O3/° = 10·(τ/τ0) |
| ∠C7O6O2/° = 126.7–3.0·(τ/τ0)2 |
In the flexible model calculations, the τ coordinate has been probed in the ±60° range and solved into 41 mesh points.41 Going back to the HCOOD⋯CBU isotopologue, a barrier of about 1 cm−1 lower is suitable to reproduce the ΔE01 splitting adhering to the parametrization used for the two former isotopologues. Using this model, the experimental ratios Fac/Fbc are also reproduced using the Eckart axis system of Pickett and Strauss.42
The positive value (+10°) of the relaxation parameter for O6O2–C1O3 suggests that the tunneling is due to an asymmetric butterfly motion of the two moieties with respect to each other, with the displacement with respect to the planarity of the O6 atom being much smaller that that of the C8 atom.
The dissociation energy of the complex, ED, has been calculated at the MP2 and B3LYP-D3 levels to be 40.7 kJ mol−1 and 47.9 kJ mol−1, respectively. In order to obtain a comparable experimental estimate, it is necessary to approximate ED from the centrifugal distortion parameter DJ within the so-called pseudo diatomic approximation43 combined with a Lennard-Jones type potential.44 This approximation is valid when the intermolecular stretching motion leading to the dimer dissociation is almost parallel to the a-axis of the complex. In the present case such a procedure leads to an ED value of 9.7 kJ mol−1, which is plausibly an underestimated value. While the theoretical values are not necessarily correct, the large discrepancy with the pseudodiatomic model results indicates that this model probably fails in this case, both because of the non-co-linearity of the dissociative stretching mode with the a-axis and the fact that DJ contains contributions from other vibrational motions.
Conclusion
The experimental observation of large tunneling splittings for three isotopologues of the adduct FA⋯CBU allowed describing the inversion pathway and the potential energy surface along the C7O6–O2C1 dihedral angle. This is one of the first times that the relative motion of two relatively large molecules constituting a heterodimer is characterized quantitatively from the tunnelling splitting measured in the complex's rotational spectrum. The two subunits are linked through a conventional O–H⋯O hydrogen bond, which acts as a fulcrum for a butterfly-like motion that lets the O3 oxygen alternate between a C–H⋯O contact (or weak hydrogen bond) with the hydrogen atoms H15 or H16, corresponding to the two equivalent minima.Acknowledgements
We thank the Italian MIUR (PRIN project 2010ERFKXL_001) and the University of Bologna (RFO) for financial support. We also thank funding from the Spanish MINECO-FEDER (CTQ2015-68148-C2-2-P) and the Junta de Castilla y León (UNVA-13-3E-2103).References
- L. Martinache, W. Kresa, M. Wegener, U. Vonmont and A. Bauder, Microwave Spectra and Partial Substitution Structure of Carboxylic Acid Bimolecules, Chem. Phys., 1990, 148, 129–140 CrossRef CAS.
- S. Antolinez, H. Dreizler, V. Storm, D. H. Sutter and J. L. Alonso, The Microwave Spectrum of the Bimolecule Trifluoroacetic Acid⋯Cyclopropanecarboxylic Acid, Z. Naturforsch., A: Phys. Sci., 1997, 52, 803–806 CrossRef CAS.
- I. Kalkman, C. Vu, M. Schmitt and W. L. Meerts, Tunneling Splittings in the S0 and S1 States of the Benzoic Acid Dimer Determined by High-Resolution UV Spectroscopy, ChemPhysChem, 2008, 9, 1788–1797 CrossRef CAS PubMed.
- A. M. Daly, K. O. Douglass, L. C. Sarkozy, J. L. Neill, M. T. Muckle, D. P. Zaleski, B. H. Pate and S. G. Kukolich, Microwave Measurements of Proton Tunneling and Structural Parameters for the Propiolic Acid–Formic Acid Dimer, J. Chem. Phys., 2011, 135, 154304 CrossRef PubMed.
- M. C. D. Tayler, B. Ouyang and B. J. Howard, Unraveling the Spectroscopy of Coupled Intramolecular Tunneling Modes: A Study of Double Proton Transfer in the Formic–Acetic Acid Complex, J. Chem. Phys., 2011, 134, 054316 CrossRef PubMed.
- G. Feng, L. B. Favero, A. Maris, A. Vigorito, W. Caminati and R. Meyer, Proton Transfer in Homodimer of Carboxylic Acids: The Rotational Spectrum of the Dimer of Acrylic Acid, J. Am. Chem. Soc., 2012, 134, 19281–19286 CrossRef CAS PubMed.
- L. Evangelisti, P. Ecija, E. J. Cocinero, F. Castaño, A. Lesarri, W. Caminati and R. Meyer, R. Proton Tunneling in Heterodimers of Carboxylic Acids: A Rotational Study of the Benzoic Acid–Formic Acid Bi-Molecule, J. Phys. Chem. Lett., 2012, 3, 3770–3775 CrossRef CAS PubMed.
- G. Feng, Q. Gou, L. Evangelisti, Z. Xia and W. Caminati, Conformational Equilibria in Carboxylic Acid Bimolecules: A Rotational Study of Acrylic Acid–Formic Acid, Phys. Chem. Chem. Phys., 2013, 15, 2917–2922 RSC.
- Q. Gou, G. Feng, L. Evangelisti and W. Caminati, Conformational Equilibria in Bimolecules of Carboxylic Acids: A Rotational Study of Fluoroacetic Acid–Acrylic Acid, J. Phys. Chem. Lett., 2013, 4, 2838–2842 CrossRef CAS.
- Q. Gou, G. Feng, L. Evangelisti and W. Caminati, A Rotational Study of cis and trans Acrylic Acid–Trifluoroacetic Acid, J. Phys. Chem. A, 2013, 117, 13500–13503 CrossRef CAS PubMed.
- Q. Gou, G. Feng, L. Evangelisti and W. Caminati, Conformers of Dimers of Carboxylic Acids in the Gas Phase: A Rotational Study of Difluoroacetic Acid–Formic Acid, Chem. Phys. Lett., 2014, 591, 301–305 CrossRef CAS.
- G. Feng, Q. Gou, L. Evangelisti and W. Caminati, Frontiers in Rotational Spectroscopy: Shapes and Tunneling Dynamics of the Four Conformers of the Acrylic Acid–Difluoroacetic Acid Adduct, Angew. Chem., Int. Ed., 2014, 53, 530–534 CrossRef CAS PubMed.
- L. Evangelisti, G. Feng, Q. Gou and W. Caminati, The Rotational Spectrum of Formic Acid⋯Fluoroacetic Acid, J. Mol. Spectrosc., 2014, 299, 1–5 CrossRef CAS.
- Q. Gou, G. Feng, L. Evangelisti and W. Caminati, Conformational Equilibria and Large Amplitude Motions in Dimers of Carboxylic Acids: The Rotational Spectrum of Acetic Acid–Difluoroacetic acid, ChemPhysChem, 2014, 15, 2977–2984 CrossRef CAS PubMed.
- D. Priem, T.-K. Ha and A. Bauder, Rotational Spectra and Structures of Three Hydrogen-Bonded Complexes between Formic Acid and Water, J. Chem. Phys., 2000, 113, 169–175 CrossRef CAS.
- B. Ouyang, T. G. Starkey and B. J. Howard, High-Resolution Microwave Studies of Ring-Structured Complexes between Trifluoroacetic Acid and Water, J. Phys. Chem. A, 2007, 111, 6165–6175 CrossRef CAS PubMed.
- B. Ouyang and B. J. Howard, High-Resolution Microwave Spectroscopic and ab initio Studies of Propanoic Acid and Its Hydrates, J. Phys. Chem. A, 2008, 112, 8208–8214 CrossRef CAS PubMed.
- B. Ouyang and B. J. Howard, The Monohydrate and Dihydrate of Acetic Acid: A High-Resolution Microwave Spectroscopic Study, Phys. Chem. Chem. Phys., 2009, 11, 366–373 RSC.
- B. Ouyang and B. J. Howard, Hydrates of trans- and gauche-Difluoroacetic Acids: A High-Resolution Microwave Spectroscopic Study, J. Phys. Chem. A, 2010, 114, 4109–4117 CrossRef CAS PubMed.
- E. G. Schnitzler and W. Jäger, The Benzoic Acid–Water Complex: A Potential Atmospheric Nucleation Precursor Studied Using Microwave Spectroscopy and ab initio Calculations, Phys. Chem. Chem. Phys., 2014, 16, 2305–2314 RSC.
- G. Feng, Q. Gou, L. Evangelisti, L. Spada, S. Blanco and W. Caminati, Hydrated Forms of Fluoroacetic Acid: A Rotational Study”, Phys. Chem. Chem. Phys., 2016, 18, 23651–23656 RSC.
- A. Vigorito, Q. Gou, C. Calabrese, S. Melandri, A. Maris and W. Caminati, How CO2 Interacts with Carboxylic Acids: A Rotational Study of Formic Acid–CO2, ChemPhysChem, 2015, 16, 2961–2967 CrossRef CAS PubMed.
- Q. Gou, L. B. Favero, S. S. Bahamyirou, Z. N. Xia and W. Caminati, Interactions between Carboxylic Acids and Aldehydes: A Rotational Study of HCOOH–CH2O, J. Phys. Chem. A, 2014, 118, 10738–10741 CrossRef CAS PubMed.
- A. M. Daly, B. A. Sargus and S. G. Kukolich, Microwave Spectrum and Structural Parameters for the Formamide–Formic Acid Dimer, J. Chem. Phys., 2010, 133, 174304 CrossRef PubMed.
- L. Evangelisti, L. Spada, W. Li, A. Ciurlini, J.-U. Grabow and W. Caminati, Shape of the Adduct Formic Acid–Dimethyl Ether: A Rotational Study, J. Phys. Chem. A, 2016, 120, 2863–2867 CrossRef CAS PubMed.
- R. B. Mackenzie, C. T. Dewberry and K. R. Leopold, The Trimethylamine-Formic Acid Complex: Microwave Characterization of a Prototype for Potential Precursors to Atmospheric Aerosol, J. Phys. Chem. A, 2016, 120, 2268–2273 CrossRef CAS PubMed.
- L. Spada, Q. Gou, B. M. Giuliano and W. Caminati, Interactions between Carboxylic Acids and Heteroaromatics: A Rotational Study of Formic Acid–Pyridine, J. Phys. Chem. A, 2016, 120, 5094–5098 CrossRef CAS PubMed.
- W. Caminati, A. Millemaggi, J. L. Alonso, A. Lesarri, J. C. López and S. Mata, Molecular Beam Fourier Transform Microwave Spectrum of the Dimethylether–Xenon Complex: Tunnelling Splitting and 131Xe Quadrupole Coupling Constants, Chem. Phys. Lett., 2004, 392, 1–6 CrossRef CAS.
- T. J. Balle and W. H. Flygare, Fabry–Perot Cavity Pulsed Fourier Transform Microwave Spectrometer with a Pulsed Nozzle Particle Source, Rev. Sci. Instrum., 1981, 52, 33–45 CrossRef CAS.
- J.-U. Grabow, W. Stahl and H. Dreizler, A Multioctave Coaxially Oriented Beam-Resonator Arrangement Fourier-Transform Microwave Spectrometer, Rev. Sci. Instrum., 1996, 67, 4072–4084 CrossRef CAS.
- J. L. Neill, S. T. Shipman, L. Alvarez-Valtierra, A. Lesarri, Z. Kisiel and B. H. Pate, Rotational Spectroscopy of Iodobenzene and Iodobenzene-Neon with a Direct-Digital 2–8 GHz Chirped-Pulse Fourier Transform Microwave Spectrometer, J. Mol. Spectrosc., 2011, 269, 21–29 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
- J. L. Alonso, R. Spielh, A. Guarnieri, J. C. López and A. Lesarri, The Centimeter and Millimeter Microwave Spectrum of Cyclobutanone, J. Mol. Spectrosc., 1992, 156, 341–359 CrossRef CAS.
- S. Melandri, A. Maris, B. M. Giuliano and W. Caminati, Water-Ketones Hydrogen Bonding: The Rotational Spectrum of Cyclobutanone–Water, J. Chem. Phys., 2005, 123, 164304 CrossRef PubMed.
- P. Ottaviani, W. Caminati, L. B. Favero, S. Blanco, J. C. López and J. L. Alonso, Molecular Beam Rotational Spectrum of Cyclobutanone-Trifluoromethane: Nature of Weak CH⋯O
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and CH⋯F Hydrogen Bonds, Chem. – Eur. J., 2006, 12, 915–920 CrossRef CAS PubMed.
C and CH⋯F Hydrogen Bonds, Chem. – Eur. J., 2006, 12, 915–920 CrossRef CAS PubMed. - H. M. Pickett, Vibration–Rotation Interactions and the Choice of Rotating Axes for Polyatomic Molecules, J. Chem. Phys., 1972, 56, 1715–1723 CrossRef CAS.
- H. M. Pickett, The Fitting and Prediction of Vibration–Rotation Spectra with Spin Interactions, J. Mol. Spectrosc., 1991, 148, 371–377 CrossRef CAS . Current versions are described and available at URL: http://spec.jpl.nasa.gov.
- J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier, New York/Amsterdam, 1977, vol. 6, pp. 1–89 Search PubMed.
- J. Kraitchman, Determination of Molecular Structure from Microwave Spectroscopic Data, Am. J. Phys., 1953, 21, 17–25 CrossRef CAS.
- A. R. Ubbelohde and K. J. Gallagher, Acid–Base Effects in Hydrogen Bonds in Crystals, Acta Crystallogr., 1955, 8, 71–83 CrossRef CAS.
- R. Meyer, Flexible Models for Intramolecular Motion, a Versatile Treatment and Its Application to Glyoxal, J. Mol. Spectrosc., 1979, 76, 266–300 CrossRef CAS.
- H. M. Pickett and H. L. Strauss, Conformational structure, energy, and inversion rates of cyclohexane and some related oxanes, J. Am. Chem. Soc., 1970, 92, 7281–7290 CrossRef.
- D. J. Millen, Determination of Stretching Force Constants of Weakly Bound Dimers from Centrifugal Distortion Constants, Can. J. Chem., 1985, 63, 1477–1479 CrossRef CAS.
- S. E. Novick, S. J. Harris, K. C. Janda and W. Klemperer, Structure and Bonding of KrClF: Intermolecular Force Fields in van der Waals Molecules, Can. J. Phys., 1975, 53, 2007–2015 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–S5 with the rotational transition frequencies and the MP2/6-311++G(d,p) optimized structure of the complex. See DOI: 10.1039/c6cp06941j |
| This journal is © the Owner Societies 2017 |