Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Surface-specific vibrational spectroscopy of the water/silica interface: screening and interference†
Jan
Schaefer
 ,
Grazia
Gonella
,
Grazia
Gonella
 ,
Mischa
Bonn
,
Mischa
Bonn
 and
Ellen H. G.
Backus
and
Ellen H. G.
Backus
 *
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128, Mainz, Germany. E-mail: backus@mpip-mainz.mpg.de
First published on 13th June 2017
Abstract
Surface-specific vibrational sum-frequency generation spectroscopy (V-SFG) is frequently used to obtain information about the molecular structure at charged interfaces. Here, we provide experimental evidence that not only screening of surface charges but also interference limits the extent to which V-SFG probes interfacial water at sub-mM salt concentrations. As a consequence, V-SFG yields information about the ∼single monolayer interfacial region not only at very high ionic strength, where the surface charge is effectively screened, but also for pure water due to the particularly large screening length at this low ionic strength. At these low ionic strengths, the large screening lengths cause destructive interference between contributions in the surface region. A recently proposed theoretical framework near-quantitatively describes our experimental findings by considering only interference and screening. However, a comparison between NaCl and LiCl reveals ion specific effects in the screening efficiency of different electrolytes. Independent of electrolyte, the hydrogen bonding strength of water right at the interface is enhanced at high electrolyte concentrations.
Introduction
In contact with water, mineral surfaces may accumulate an excess of positive or negative charges, which in turn affects the arrangement of interfacial water molecules. Through interaction with the associated DC electric field, interfacial water layers form the so-called electric double layer (EDL) which consists of the near-surface, highly ordered Stern layer, and the more diffuse outer water layers. It is clear that interfacial chemistry, relevant for many geological and industrial processes, is affected by the reaction of dipolar interfacial molecules, in particular water, to the surface field. The distance-dependent potential associated to such an electric field is typically described by the Gouy–Chapman–Stern model, assuming an exponential decay of the potential away from the surface through the diffuse layer, while the Stern layer is characterized by a linear drop in analogy to a dielectric capacitor.Associated parameters such as surface potential, surface charge density and Debye screening length are challenging to access experimentally. Besides potentiometric titration,1,2 Atomic Force Microscopy3 and X-ray Photoelectron Spectroscopy,4,5 also non-linear spectroscopy techniques have been demonstrated to be a useful tool for studying these kind of interfaces.6–18 As such, we employed Vibrational Sum Frequency Generation (V-SFG) spectroscopy for interrogating those interfacial properties, since it allows for probing vibrational states of interfacial molecules with sub-micrometer sensitivity and selectivity towards the symmetry-broken interfacial layers (given by the additional symmetry selection rule underlying V-SFG processes). Using this technique, we study how the presence of ions changes the composition of the EDL for water at a mineral surface. Specifically, we aim to understand to which depth water interacts with the surface electric field and if the intermolecular structure of interfacial water is affected differently by the presence of ions than that of bulk water. For this purpose, we investigated the silica/water interface with varying electrolyte content. Around neutral pH, the silica surface is covered by silanol groups which are mostly deprotonated, generating a negatively charged surface as the point of zero charge (pzc) is pH 2.1,14
V-SFG spectra of neutral interfaces are commonly discussed by invoking the second-order non-linear susceptibility χ(2) of involved media. Based on symmetry arguments, χ(2) is zero for centro-symmetric materials. This makes V-SFG a sensitive probe for the first few molecular layers of e.g. water at interfaces, as only at the interface centro-symmetry is broken. Moreover, χ(2) is proportional to molecular order and molecular number density. However, as discussed previously,6,10,19–21 this description does not suffice in presence of charged interfaces since surface charges may induce an extra DC electric field, EDC, which, in addition to the IR- and VIS- fields, EIR and EVIS, also acts on non-linear active molecules in the proximity of the surface. This gives rise to an additional third order (χ(3)) contribution to the V-SFG response which depends on the penetration depth of the DC field and may even exceed the χ(2)-response. As a consequence, the generated V-SFG signal contains a χ(2) contribution from directly bonded interfacial molecules and a χ(3) contribution from up to ∼1 μm away from the surface for low ion concentrations.15 In contrast to χ(2), not only oriented but also isotropic water may contribute to χ(3) signal, i.e. χ(3)aniso and χ(3)iso, where the anisotropic term reflects the DC-field induced orientation of near-surface water, and the isotropic term the contribution from bulk-like, randomly oriented water. As such, the V-SFG intensity of charged interfaces does not purely reflect the degree of interfacial order but is a convolution of field induced reorientation and polarization:6,10,22
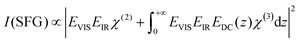 | (1) |
| χ(3) = χ(3)aniso + χ(3)iso | (2) |
It is clear from eqn (1) that the V-SFG intensity of such systems depends strongly on the number of molecules interacting with the DC electric field. That number is determined by the strength and decay length of that field, which, in turn are defined by the charge density at the surface and the Debye screening length of the solution. With increasing bulk ion concentration, the surface charges are increasingly shielded, resulting in reduced penetration depths of the DC field. Conversely, with increasing Debye length (i.e. decreasing bulk ion concentration) an increasing number of molecules contribute, resulting in a higher V-SFG signal. For a given surface charge, the probing depth can thus be tuned by varying the ionic content in the solution.
As the V-SFG signal of charged interfaces is thus composed of a complex interplay between the bonded interfacial layer χ(2) and the diffuse layer χ(3) response, it is a priori not clear how these contributions are convoluted in the V-SFG spectrum. For the silica/water interface, the correlation between V-SFG intensity and bulk ion concentration has been studied experimentally for aqueous sodium chloride solutions between 10−4 M and 4 M.10 The decrease of the V-SFG intensity with increasing electrolyte concentration has mainly been attributed to Debye screening due to the presence of electrolyte. However, a second electrolyte concentration-dependent effect has been proposed, based on theoretical considerations and direct observation by second harmonic scattering.15,23 At very low electrolyte concentrations, the probing depth can be limited by phase matching of the V-SFG probe. Hence, as the penetration depth of the DC field exceeds the coherence length, the signal intensity is expected to be increasingly depleted due to destructive interference between contributions from sufficiently spatially separated non-linear active molecules.15 For particularly large penetration depths, the third order contribution vanishes completely and only the field-independent V-SFG response of the bonded interfacial layer (χ(2)) survives.15 The V-SFG intensity may thus not necessarily increase with number of molecules affected by the DC field as has been generally assumed,6,7,10,20,24,25 but decreases if the DC field reaches the magnitude of the coherence length of the probed non-linear process.15,17
Here, we provide new insights into the sparsely studied regime of low ionic strength ([NaCl] < 5 × 10−4 M) for which we observe an inverted dependence between ionic strength and the V-SFG signal intensity in accordance with theoretical predictions.15 We demonstrate experimentally that V-SFG spectroscopy provides interfacial layer sensitivity to the silica/water interface both for pure water and for highly concentrated (>1 M) NaCl solutions. Furthermore, we show that the overall concentration dependence of the V-SFG intensity is similar for monovalent cations of different radii, however they seem to differ in their screening efficiency. Moreover, we observe significant redshifts of the O–H stretch signal for high electrolyte concentration, which can only be rationalized by invoking surface-specific effects. Apparently, salt has a different impact on water molecules close to the surface than on water molecules in the bulk.
Results and discussion
The top panel in Fig. 1 depicts V-SFG spectra of the silica/water interface within the C–H-/O–H-stretch frequency window for three different NaCl concentrations. The spectra show the typical double peak O–H feature between ∼2900 and 3500 cm−1, as discussed in earlier studies of water in contact with silica surfaces.7–10 Due to the absence of any C–H vibrational signatures, there is no indication of surface contamination with organic impurities. However, we caution that the preparation of consistent silica surfaces itself is challenging since charged surfaces might adsorb unwanted moieties. Compared to pure water and the 1 M NaCl solution, which show similar intensity, the signal from the 5 × 10−4 molar solution is significantly enhanced. The presented spectra in Fig. 1 are raw data, not normalized to the spectrum of the IR pulse as we are only interested in relative changes of the O–H-band. The normalized spectra can be found in the ESI† (Fig. S1). For a dilution series of 20 different NaCl concentrations, we integrate the corresponding spectra between 2800 and 3600 cm−1, and the resulting integrated signals are plotted as a function of the ion concentration in the bottom panel of Fig. 1.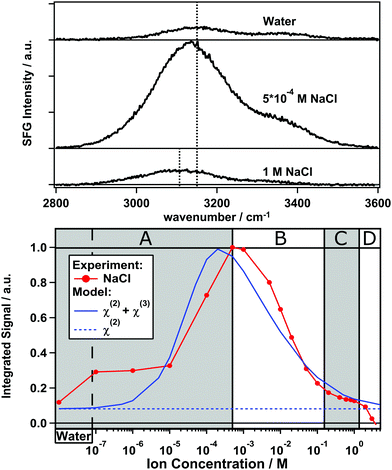 | ||
| Fig. 1 Top panel: Non-normalized O–H-stretch V-SFG signal from the silica/water interface for pure water, 5 × 10−4 M and 1 M NaCl solutions. The black dashed lines mark the frequency at peak maximum for pure water and the 1 M NaCl solution. Bottom panel: Integrated V-SFG signal (red) as a function of NaCl concentration and the predicted intensity (blue solid) by invoking modulation by charge screening and interference (eqn (4)).15 The blue dashed line represents the considered field-independent, true second order contribution to the V-SFG response. | ||
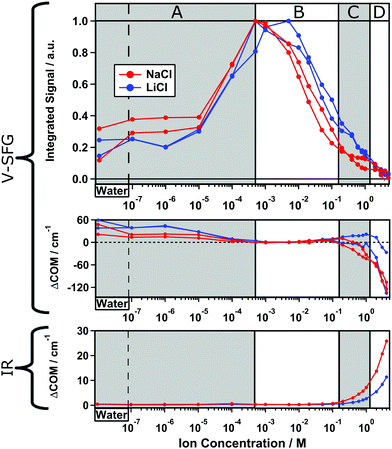
As illustrated in Fig. 1, the V-SFG intensity of the O–H-stretching band dramatically depends on the bulk ion concentration. Overall, we observe an order of magnitude variation in the V-SFG signal upon the addition of NaCl to pure water. At both low and high concentration, the signal is small, while a maximum in the V-SFG intensity appears at ∼5 × 10−4 M NaCl. SFG experiments with SPS polarization reveal a very similar trend, so that the dependence of the SFG intensity on electrolyte concentration cannot be accounted for by concentration-dependent orientation of interfacial water molecules. This decrease of the V-SFG intensity for NaCl concentrations exceeding 5 × 10−4 M has been observed by Jena et al.10 In that study, four different regimes of ion concentration have been distinguished (A–D). In a similar fashion, we will now discuss our results and provide new insight into the concentration regime below 5 × 10−4 M (A). For the high concentration regimes (B–D), our results agree with the above mentioned observations10 which we only summarize here.
Regime B: for [NaCl] > 5 × 10−4 M, the V-SFG signal decreases with increasing ion concentration due to increased screening.
Regime C: for high ionic strengths of around 1 M, the intensity is almost constant which indicates that the number of probed molecules and their orientation do not change substantially within this regime. It has been argued before that the signal in this region corresponds mostly to the intrinsic χ(2) response, providing insight into the Stern layer of the silica/water interface.10
Regime D: for concentrations higher than 2 M, the intensity drops more rapidly which suggests either randomization of Stern layer water molecules or replacement by ions directly adsorbing on the silica surface.
Regime A: in contrast to Jena et al.,10 we find that in this regime where [NaCl] < 5 × 10−4 M, the V-SFG intensity decreases with further decreasing salt concentration. For neat water, we observe a very low V-SFG signal. To avoid contamination due to dissolution of silica which is known to affect the V-SFG signal,24 we flushed the cell with sample solution before starting each measurement. This finding can be rationalized, according to the model in ref. 15, by considering the Debye screening length of pure water to be larger than the coherence length of the V-SFG process in the given experimental geometry (∼40 nm) which gives rise to destructive interference and cancellation of the χ(3) contribution. As the penetration depth of the DC field decreases upon adding salt, phase matching is increasingly fulfilled by approaching the coherence length, which results in a higher V-SFG intensity.
For understanding our data on a quantitative level, we employed the model for predicting the non-linear response as proposed in ref. 15 which uses a Gouy–Chapman description of the EDL and phase matching condition of the non-linear process as given by:
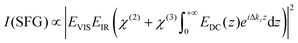 | (3) |
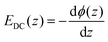 and by considering an exponentially decaying potential ϕ(z) = ϕ0(c) × exp(−κ(c)z) along the z-direction (perpendicular to the silica/water interface), the V-SFG intensity dependence on ionic strength can be formulated as follows:
and by considering an exponentially decaying potential ϕ(z) = ϕ0(c) × exp(−κ(c)z) along the z-direction (perpendicular to the silica/water interface), the V-SFG intensity dependence on ionic strength can be formulated as follows: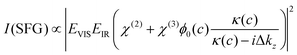 | (4) |
Besides the intensity of the involved optical beams and the non-linear susceptibilities of water, the resulting V-SFG intensity is determined by the ionic strength-dependent Debye length, κ(c), and surface potential, ϕ0(c), (as described by the Grahame equation) as well as the phase mismatch along the probing depth, Δkz, whose explicit definitions are given in the ESI† (eqn (S1)–(S3)). As can be seen in eqn (S1)–(S3) (ESI†), the surface potential is also directly dependent on the surface charge density, σ0, and the relative permittivity of the aqueous medium, εr. For the V-SFG intensity vs. concentration curve generated in Fig. 1, we have used σ0 = −0.05 C m−2 and εr = 78 as suggested in ref. 15. Through comparison with our experimental data, we infer a χ(3)/χ(2) ratio of −17.5 V−1. Within the range of reported surface charge densities for fused silica around neutral pH, −0.06 C m−2 < σ0 < −0.02 C m−2,2,4,14,26,27 we find that comparable intensity curves can be obtained for −22.25 V−1 < χ(3)/χ(2) < −16.50 V−1 as reported in the ESI† (Fig. S2). These values for the χ(3)/χ(2) ratio seem reasonable compared with previous studies of water at charged surfaces.20,23 Please note that for simplicity we assume that the charge density is constant for all salt concentrations. Small variation with concentration cannot be excluded as the surface charge density of silica (−0.06 C m−2 < σ0 < −0.02 C m−2)2,4,14,26,27 is typically around the critical surface charge density (σ0,crit) above which counterion condensation occurs.28
We observe that the shape of the V-SFG intensity vs. ion concentration curve generated by the model agrees remarkably well with our experimental data. As predicted, pure water shows similar intensity as NaCl solutions within regime C (Fig. 1) while the intensity is enhanced for an intermediate concentration regime with its maximum around [NaCl] = 5 × 10−4 M. Based on the employed theoretical framework,15 this indicates that the χ(2)-contribution (blue dashed line in Fig. 1) dominates the pure water response and interfacial layer sensitivity is obtained not only at short but also at very large screening lengths. In contrast, the probing depth amounts to a few tens of nanometers for the maximum at 5 × 10−4 M NaCl. In its current form, the model seems to overestimate the screening contribution of NaCl, reducing the V-SFG intensity in the B and C regime and shifting the maximum to lower concentration than what is observed in the experiment.
While eqn (4) discriminates between ions species with different valence, the effect of different ionic radii is ignored. However, ion size not only determines the Stern-layer thickness,5 but might also be relevant for the screening ability since the ion mobility changes with the hydrated radius. For a negatively charged surface, the properties of the cations are especially important.13,29 Therefore, we compare two not-too-different alkali ions, Na+ and Li+, where however Li+ shows a lower ion mobility due to a smaller ionic but larger hydrated radius. In the same fashion as presented in Fig. 1, we will now discuss the results of two measurement series for both NaCl and LiCl solutions which are shown in Fig. 2. Again, the integrated signal is plotted as a function of ion concentration and the curves are each normalized to their maximum.
Overall, the intensity curve shape for LiCl is very similar to that already discussed for NaCl solutions in Fig. 1. However, the curves for LiCl are shifted to slightly higher concentrations than those for NaCl. Again, in regime B–D, the intensity decreases with increasing ion concentration while regime A shows inverted concentration dependence. By comparing the two measurement series for NaCl, we find a slightly varying ratio between the maximum intensity and the plateau in regime A and C indicating a small variability of the surface charge on silica, which can likely be traced to slight, unintentional differences in the preparation of the surface.
Besides the shift of the curve toward higher concentration for LiCl compared to NaCl, we observe a steeper intensity increase within regime B–C which suggests that for generating the same screening length, a higher LiCl concentration is required than for NaCl. In other words, Na+ ions seem to shield surface charges more effectively than Li+ ions but both are still less efficient than predicted by eqn (4) as shown in Fig. 1. Additionally, the intensity plateau within regime C is less pronounced for LiCl than for NaCl. This indicates that the bonded interfacial layer of water gets perturbed and/or replaced more easily by Li+ than Na+ ions. In summary, we observe an impact of the ionic radius on the V-SFG intensity curves which seems to be a consequence of a higher screening efficiency for larger cations with equal valence. One explanation may be that alkali ions with larger ionic radii are less hydrated providing higher ion mobility in aqueous media. Consequently, an external field may attract the highly mobile Na+ ions more easily than Li+ ions. However, at short distance to the surface, Na+ seems to show a lower surface propensity than Li+, as reflected by the O–H-stretch V-SFG intensity plateau at high NaCl concentration. Both findings are in line with recent atomic force microscopy studies and molecular dynamics simulations.3,30
Second harmonic generation (SHG) spectroscopy has been widely employed for studying the silica/water interface.6,11–14,16,17 In contrast to V-SFG, SHG probes a non-linear signal that is not resonantly enhanced and therefore not sensitive to a particular molecule or moiety but may result from any molecular and atomic species present which is in particular relevant for high salt concentrations. Generally speaking, any added substance could cause an unintentional increase of the SHG response. Azam et al. have shown that, within regime C, opposed to our V-SFG results, the SHG intensity has inverted concentration dependence for LiCl as compared to NaCl. This observation has been attributed to ion specific effects on the surface charge.13 Boamah et al. have demonstrated that for NaCl, the SHG intensity does not drop to zero at high ionic strength and this has been rationalized by assuming either dramatic changes in the surface charge density of silica or in the relative permittivity of water in the diffuse layer.17 Our data do not show this effect. These comparisons seem to indicate that a direct probe of interfacial molecules or functional groups, as provided with V-SFG, is helpful for understanding the decaying surface potential at charged surfaces in contact with an aqueous solution.
As discussed above, V-SFG seems to provide interfacial layer sensitivity at the silica/water interface for pure water and ∼1 M ion concentration. As V-SFG is a resonant probe of vibrational states, here the O–H stretching of interfacial water, the V-SFG spectrum can provide insights into the interfacial interactions through comparison of band frequencies. From the upper panel of Fig. 1 it is evident that the O–H stretching band is shifting upon changing the salt concentration. For a quantitative analysis, we calculated the spectral first moment (‘center of mass’, COM) for the corresponding spectra and compared changes relative to the largest signal (5 × 10−4 and 5 × 10−3 M for NaCl and LiCl, respectively) as depicted in the middle panel of Fig. 2.
For all measurement series, we consistently observe an overall red-shifting O–H-stretch V-SFG band upon increasing ion concentration – Fig. 2, middle panel. In contrast, corresponding bulk spectra show a blue-shifting O–H-stretch band as illustrated in the lower panel of Fig. 2 for IR measurements and reported in ref. 31 for Raman. Therefore, the ion-induced red-shift of the SFG band seems to be a purely surface-related effect. In between these two ionic concentrations at which we measure an SFG response originating purely from the outermost interfacial layer, i.e. pure water and ∼1 M electrolyte, we observe a red-shift of about 60 cm−1 which suggests that interfacial water in presence of salt has substantially stronger hydrogen bonds.
Conclusion
To the best of our knowledge, this work is the first experimental evidence that interference limits the extent to which SFG probes the interface of water in contact with a charged surface such as silica. The maximum SFG signal is generated around millimolar ionic strength which for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte corresponds to a Debye length of tens of nanometers. As a consequence of interference, not only short, but also large Debye lengths, as present for pure water, provide nearly monolayer insight into the interfacial region. The proposed model for the ionic-strength dependent non-linear response from a charged surface, using previously reported surface charge densities for silica and an exponentially decaying surface potential, can be used for describing our SFG data. However, the decay length of the surface potential seems to depend not only on the ion valence: In fact, our data suggest that ions with smaller hydration radii screen surface charges more efficiently, while the Stern layer water is perturbed more easily by ions with larger hydration radii. Irrespective of the ion identity, the O–H stretch SFG band undergoes a redshift with increasing bulk ionic strength as opposed to a blueshift observed for bulk water which indicates that the intermolecular structure of interfacial water at the silica surface changes differently in presence of salt than what observed in bulk. We interpret the observed red-shift as a strengthening of the interfacial H-bonding structure.
1 electrolyte corresponds to a Debye length of tens of nanometers. As a consequence of interference, not only short, but also large Debye lengths, as present for pure water, provide nearly monolayer insight into the interfacial region. The proposed model for the ionic-strength dependent non-linear response from a charged surface, using previously reported surface charge densities for silica and an exponentially decaying surface potential, can be used for describing our SFG data. However, the decay length of the surface potential seems to depend not only on the ion valence: In fact, our data suggest that ions with smaller hydration radii screen surface charges more efficiently, while the Stern layer water is perturbed more easily by ions with larger hydration radii. Irrespective of the ion identity, the O–H stretch SFG band undergoes a redshift with increasing bulk ionic strength as opposed to a blueshift observed for bulk water which indicates that the intermolecular structure of interfacial water at the silica surface changes differently in presence of salt than what observed in bulk. We interpret the observed red-shift as a strengthening of the interfacial H-bonding structure.
Experimental methods
Spectroscopy
The SFG spectra presented in this work are recorded with an experimental setup that uses a Ti:sapphire regenerative amplifier (Solstice® Ace™, Spectra Physics) which generates 800 nm pulses with ∼40 fs duration and 1 kHz repetition rate. For producing broadband (∼450 cm−1) infrared pulses with 5 μJ, a commercial optical parametric amplifier (TOPAS Prime, Spectra Physics) is used together with a non-collinear difference frequency generation (NDFG) scheme. By guiding the visible upconverting pulse through a Fabry–Perot etalon (SLS Optics Ltd), it is spectrally narrowed to a FWHM of ∼20 cm−1 with ∼20 μJ. The SFG signal is spectrally resolved using a spectrograph (Acton Spectro Pro® SP-2300, Princeton Instruments) and detected with an electron-multiplied charge couple device (emCCD) camera (ProEM 1600, Roper Scientific). All spectra are recorded in ssp polarization combination (s-polarized SFG, s-polarized visible and p-polarized IR) and at incident angles θVis ≈ 37° and θIR ≈ 33°. Each spectrum results from 10 minute accumulation. For normalization, the frequency dependent IR field is measured on an equally prepared silica window, coated with 100 nm chromium-free gold.The IR data presented in the lower panel of Fig. 2 result from ATR measurements accomplished with a Bruker Tensor II (Platinum ATR) and are corrected for the penetration depth in pure water by using the refractive index as reported in ref. 32.
Sample preparation
Lithium chloride and sodium chloride, purchased from Sigma Aldrich (≥99.5%, CAS 7647-14-5) and Roth (≥99.5%, CAS 7447-41-8), respectively, are dissolved in demineralized H2O, filtered with a Millipore unit (resistivity = 18 MΩ cm). For removing organic residues, sodium chloride is baked at 650 °C for 6 hours. Before each experiment, the (parallel faced) fused silica window (Korth Kristalle GmbH Infrasil® 302, s/d: 60/40) is treated by UV-Ozone cleaning for 30 min. All sample solutions are measured at least one hour after preparation to ensure CO2-equilibration. Before each measurement, the cell (as detailed in ref. 24) is flushed with the sample solution (Vtotal = 100 mL) for 5 minutes (500 mL min−1).Acknowledgements
We thank Dan Lis for initiating this project. This work was funded by an ERC Starting Grant (Grant No. 336679). Open Access funding provided by the Max Planck Society.References
- P. M. Dove and C. M. Craven, Surface Charge Density on Silica in Alkali and Alkaline Earth Chloride Electrolyte Solutions, Geochim. Cosmochim. Acta, 2005, 69, 4963–4970 CrossRef CAS.
- M. Karlsson, C. Craven, P. M. Dove and W. H. Casey, Surface Charge Concentrations on Silica in Different 1.0 M Metal-Chloride Background Electrolytes and Implications for Dissolution Rates, Aquat. Geochem., 2001, 7, 13–32 CrossRef CAS.
- J. Morag, M. Dishon and U. Sivan, The Governing Role of Surface Hydration in Ion Specific Adsorption to Silica: An AFM-Based Account of the Hofmeister Universality and Its Reversal, Langmuir, 2013, 29, 6317–6322 CrossRef CAS PubMed.
- M. A. Brown, A. Goel and Z. Abbas, Effect of Electrolyte Concentration on the Stern Layer Thickness at a Charged Interface, Angew. Chem., Int. Ed., 2016, 55, 3790–3794 CrossRef CAS PubMed.
- M. A. Brown, Z. Abbas, A. Kleibert, R. G. Green, A. Goel, S. May and T. M. Squires, Determination of Surface Potential and Electrical Double-Layer Structure at the Aqueous Electrolyte-Nanoparticle Interface, Phys. Rev. X, 2016, 6, 011007 Search PubMed.
- S. Ong, X. Zhao and K. B. Eisenthal, Polarization of Water Molecules at a Charged Interface: Second Harmonic Studies of the Silica/Water Interface, Chem. Phys. Lett., 1992, 191, 327–335 CrossRef CAS.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, Vibrational Spectra of Water at Water/α-Quartz (0001) Interface, Chem. Phys. Lett., 2004, 386, 144–148 CrossRef CAS.
- V. Ostroverkhov, G. A. Waychunas and Y. R. Shen, New Information on Water Interfacial Structure Revealed by Phase-Sensitive Surface Spectroscopy, Phys. Rev. Lett., 2005, 94, 046102 CrossRef PubMed.
- K. C. Jena and D. K. Hore, Variation of Ionic Strength Reveals the Interfacial Water Structure at a Charged Mineral Surface, J. Phys. Chem. C, 2009, 113, 15364–15372 CAS.
- K. C. Jena, P. A. Covert and D. K. Hore, The Effect of Salt on the Water Structure at a Charged Solid Surface: Differentiating Second- and Third-Order Nonlinear Contributions, J. Phys. Chem. Lett., 2011, 2, 1056–1061 CrossRef CAS.
- M. S. Azam, C. N. Weeraman and J. M. Gibbs-Davis, Specific Cation Effects on the Bimodal Acid–Base Behavior of the Silica/Water Interface, J. Phys. Chem. Lett., 2012, 3, 1269–1274 CrossRef CAS PubMed.
- M. S. Azam, C. N. Weeraman and J. M. Gibbs-Davis, Halide-Induced Cooperative Acid–Base Behavior at a Negatively Charged Interface, J. Phys. Chem. C, 2013, 117, 8840–8850 CAS.
- M. S. Azam, A. Darlington and J. M. Gibbs-Davis, The Influence of Concentration on Specific Ion Effects at the Silica/Water Interface, J. Phys.: Condens. Matter, 2014, 26, 244107 CrossRef PubMed.
- A. M. Darlington and J. M. Gibbs-Davis, Bimodal or Trimodal? The Influence of Starting pH on Site Identity and Distribution at the Low Salt Aqueous/Silica Interface, J. Phys. Chem. C, 2015, 119, 16560–16567 CAS.
- G. Gonella, C. Lütgebaucks, A. G. de Beer and S. Roke, Second Harmonic and Sum-Frequency Generation from Aqueous Interfaces Is Modulated by Interference, J. Phys. Chem. C, 2016, 120, 9165–9173 CAS.
- P. E. Ohno, S. A. Saslow, H.-F. Wang, F. M. Geiger and K. B. Eisenthal, Phase-Referenced Nonlinear Spectroscopy of the α-Quartz/Water Interface, Nat. Commun., 2016, 7, 13587–13591 CrossRef CAS PubMed.
- M. D. Boamah, P. E. Ohno, F. M. Geiger and K. B. Eisenthal, Relative Permittivity in the Electrical Double Layer from Nonlinear Optics, 2017, arXiv:1702.02496v1.
- L. Dalstein, E. Potapova and E. Tyrode, The Elusive Silica/Water Interface: Isolated Silanols under Water as Revealed by Vibrational Sum Frequency Spectroscopy, Phys. Chem. Chem. Phys., 2017, 19, 10343–10349 RSC.
- D. E. Gragson and G. L. Richmond, Investigations of the Structure and Hydrogen Bonding of Water Molecules at Liquid Surfaces by Vibrational Sum Frequency Spectroscopy, J. Phys. Chem. B, 1998, 102, 3847–3861 CrossRef CAS.
- Y.-C. Wen, S. Zha, X. Liu, S. Yang, P. Guo, G. Shi, H. Fang, Y. R. Shen and C. Tian, Unveiling Microscopic Structures of Charged Water Interfaces by Surface-Specific Vibrational Spectroscopy, Phys. Rev. Lett., 2016, 116, 016101 CrossRef PubMed.
- A. Eftekhari-Bafrooei and E. Borguet, Effect of Surface Charge on the Vibrational Dynamics of Interfacial Water, J. Am. Chem. Soc., 2009, 131, 12034–12035 CrossRef CAS PubMed.
- B. Levine and C. G. Bethea, Second and Third Order Hyperpolarizabilities of Organic Molecules, J. Chem. Phys., 1975, 63, 2666–2682 CrossRef CAS.
- C. Lütgebaucks, G. Gonella and S. Roke, Optical Label-Free and Model-Free Probe of the Surface Potential of Nanoscale and Microscopic Objects in Aqueous Solution, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 195410 CrossRef.
- D. Lis, E. H. G. Backus, J. Hunger, S. H. Parekh and M. Bonn, Liquid Flow Along a Solid Surface Reversibly Alters Interfacial Chemistry, Science, 2014, 344, 1138–1142 CrossRef CAS PubMed.
- P. A. Covert, K. C. Jena and D. K. Hore, Throwing Salt into the Mix: Altering Interfacial Water Structure by Electrolyte Addition, J. Phys. Chem. Lett., 2013, 5, 143–148 CrossRef PubMed.
- S. H. Behrens and D. G. Grier, The Charge of Glass and Silica Surfaces, J. Chem. Phys., 2001, 115, 6716–6721 CrossRef CAS.
- M. Wang and A. Revil, Electrochemical Charge of Silica Surfaces at High Ionic Strength in Narrow Channels, J. Colloid Interface Sci., 2010, 343, 381–386 CrossRef CAS PubMed.
- G. Manning, Counterion Condensation Theory of Attraction between Like Charges in the Absence of Multivalent Counterions, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1–18 CrossRef CAS PubMed.
- T. A. Gmür, A. Goel and M. A. Brown, Quantifying Specific Ion Effects on the Surface Potential and Charge Density at Silica Nanoparticle–Aqueous Electrolyte Interfaces, J. Phys. Chem. C, 2016, 120, 16617–16625 Search PubMed.
- S. Hocine, R. Hartkamp, B. Siboulet, M. Duvail, B. Coasne, P. Turq and J.-F. Dufrêche, How Ion Condensation Occurs at a Charged Surface: A Molecular Dynamics Investigation of the Stern Layer for Water–Silica Interfaces, J. Phys. Chem. C, 2016, 120, 963–973 CAS.
- X. Wu, W. Lu, W. Ou, M. C. Caumon and J. Dubessy, Temperature and Salinity Effects on the Raman Scattering Cross Section of the Water OH-Stretching Vibration Band in NaCl Aqueous Solutions from 0 to 300 °C, J. Raman Spectrosc., 2016, 48, 314–322 CrossRef.
- J. E. Bertie and Z. Lan, Infrared Intensities of Liquids XX: The Intensity of the OH Stretching Band of Liquid Water Revisited, and the Best Current Values of the Optical Constants of H2O (l) at 25 °C between 15
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 1 cm−1, Appl. Spectrosc., 1996, 50, 1047–1057 CrossRef CAS.
000 and 1 cm−1, Appl. Spectrosc., 1996, 50, 1047–1057 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02251d |
| This journal is © the Owner Societies 2017 |