Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Concomitant polymorphism and the martensitic-like transformation of an organic crystal†
Michael T.
Ruggiero
 ab,
J.
Axel Zeitler
ab,
J.
Axel Zeitler
 b and
Timothy M.
Korter
b and
Timothy M.
Korter
 *a
*a
aDepartment of Chemistry, Syracuse University, 1-014 Center for Science and Technology, Syracuse, NY 13244-4100, USA. E-mail: tmkorter@syr.edu
bDepartment of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, Cambridge, CB3 0AS, UK
First published on 18th October 2017
Abstract
Crystalline polymorphism is a phenomenon that occurs in many molecular solids, resulting in a diverse range of possible bulk structures. Temperature and pressure can often be used to thermodynamically control which crystal form is preferred, and the associated transitions between polymorphic phases are often discontinuous and complete. N-Methyl-4-carboxypyridinium chloride is a solid that undergoes an apparent continuous temperature-dependent phase transition from an orthorhombic to a monoclinic polymorph. However, a hybrid characterization approach using single-crystal X-ray diffraction, terahertz time-domain spectroscopy, and solid-state density functional theory reveals the transformation to be actually a slowly changing ratio of the two discrete polymorphic forms. The potential energy surface of this process can be directly accessed using terahertz radiation, and the data show that a very low barrier (43.3 J mol−1) exists along the polymorph transformation coordinate.
With the three-dimensional structures of molecular crystals becoming increasingly important in wide-ranging applications (e.g. electronics, energy storage, and pharmaceutics)1,2 the understanding of the atomistic origins of their bulk properties is paramount for effective utilization. One of the most critical aspects to consider when working with molecular solids is their rich polymorphism, and their propensity for forming numerous crystalline phases of the same molecule at or near ambient conditions.3 In particular, it is the phase transitions between forms, both intended and unexpected, that make it challenging to successfully utilize such materials. Polymorphism leads to the potential for a single solid to have significant differences in its bulk properties depending on which polymorph it assumes. These physical properties include solubility and melting point,4 which have traditionally been of great importance for the pharmaceutical industry5 but are equally essential in many other fields.6,7 One such example is the steel industry, where work-hardened steel is the result of a diffusionless displacive (Martensitic) transformation from one form to another, leading to desirable mechanical properties.8
Polymorph transitions in molecular solids are typically viewed as discontinuous,9,10 exhibiting clear and immediate transformations between forms, yet continuous transformations have also been reported.11 A possible explanation for an apparent continuous phase transformation involves the ability of two (or more) polymorphs to exist simultaneously (concomitant polymorphism), which could manifest itself experimentally as a continuous redistribution of the relative populations of the two polymorphs involved. While single-crystal X-ray diffraction (SCXRD) is the most common method for determining solid-state structures, it is difficult to characterize the packing energies or thermodynamic stabilities of materials with it. An alternative technique, terahertz time-domain spectroscopy (THz-TDS), can be used in this sense, since the low-frequency (100 cm−1) radiation excites large-amplitude vibrational motions of entire molecules within a material, meaning that intermolecular potential energy surface can be readily probed, and that any subtle changes in the molecular interactions will result in significant spectral differences.12,13 Combining THz-TDS data with SCXRD and highly-accurate quantum mechanical simulations enables a complete description of the intermolecular forces and the thermodynamic parameters of the two polymorphs to be extracted.14 By comparing the Gibbs free energy curves of the two materials, an indication of the transition temperature and relative stabilities of the two forms can be deduced.
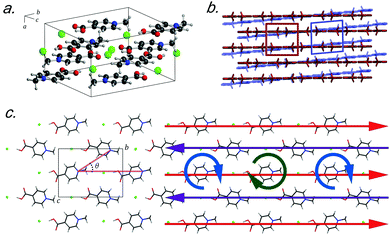
Recently, crystals of N-methyl-4-carboxypyridinium chloride (Me4CP·Cl) were found to have a low-temperature (90 K) polymorph that only differed slightly from the published room-temperature structure.15 At ambient conditions, crystals of Me4CP·Cl (Fig. 1) are orthorhombic, exhibiting Pnma space group symmetry with lattice parameters of a = 6.670 Å, b = 12.937 Å, c = 9.519 Å, and β = 90° (high-temperature, HT-form), transforming at low temperatures to a monoclinic P21/n cell with lattice parameters of a = 6.530 Å, b = 12.865 Å, c = 9.501 Å, and β = 94.207° (low-temperature, LT-form). The pyridinium rings form infinite sheets with the individual molecules arranged in a herringbone pattern within each sheet, and the transformation primarily involves the slipping of one plane relative to the other (i.e. shearing). The overall structural pattern remains intact between the two crystalline forms, and closer examination reveals very little change between the two polymorphs, both in the internal and external arrangements of the atoms. With respect to the individual molecular structures there is very little deviation between the non-hydrogen containing bond lengths and angles, with root-mean squared deviations (RMSDs) of 0.008 Å and 0.356° between the two experimental polymorph structures. However, the symmetry breaking results in a change in the planarity of the pyridinium ring, with the most obvious change occurring in the rotation of the carboxylate group, which deviates from co-planarity in the HT-form to 3.28° out-of-plane in the LT-form.
Externally, there are only two significant deviations between the two forms that ultimately help shed light on the lattice parameter changes. The first is that the herringbone angle (θ, defined in Fig. 1 as the angle between three nitrogen atoms within a single sheet) decreases from 50.34° in the HT-form to 49.80° in the LT-form, an effect that when considered in the context of the entire unit cell (and thus throughout the entire solid) contributes to the change in the bulk β-angle. The related second change occurs in the linearity of the nitrogen–chloride bond, which decreases to 166.15° (from 168.21° in the LT-form). Such modifications lead to the changes in the lattice parameters, where the sliding of the molecular sheets past one another results in the Martensitic-like transition.
To study the thermal transformation, a single-crystal of the sample was used to determine the unit cell parameters as a function of temperature. Me4CP·Cl was purchased from Sigma-Aldrich (>98%) and was used as-received. A single crystal was mounted on a Bruker KAPPA APEX II X-ray diffractometer, and the temperature was reduced in 5 K intervals, allowing 15 minutes in between measurements for equilibration. The results of unit-cell indexing (β-angle plotted in Fig. 2, full set of lattice parameters available in the ESI†) show that the polymorphic transition occurs between 165 and 170 K, with a first initial jump to 90.61° in the cell β-angle followed by a linear change until it plateaus at approximately 105 K. The process was shown to be reversible, and there was no evidence that longer equilibration times resulted in any significant difference to the lattice parameters, indicating that the crystal was in thermal equilibrium at each temperature. Finally, it is important to note that multiple experiments performed on different days, and on different single crystals from the bulk sample, all yielded equivalent results confirming the validity of the presented data.
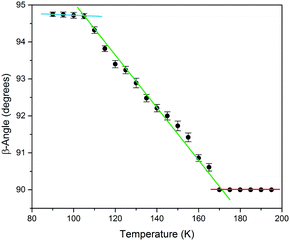 | ||
| Fig. 2 The experimental SCXRD unit cell β-angle of Me4CP·Cl crystals over the 90 to 195 K temperature range. Linear fits of the three regions have been added as guides. | ||
THz-TDS is useful for characterizing crystalline polymorphs because it is sensitive to changes in the packing arrangement of molecules within the solid, and can provide complementary information to SCXRD data.14,16 The terahertz spectra of Me4CP·Cl between 300 K and 100 K are shown in Fig. 3.
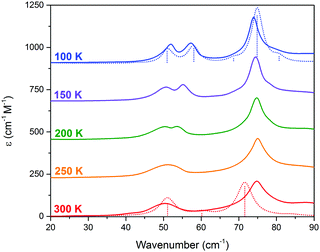 | ||
| Fig. 3 THz-TDS spectra of Me4CP·Cl from 100 to 300 K (offset for clarity). The simulated spectra for the HT and LT forms are plotted as dotted red and blue lines, respectively. | ||
Similar to the SCXRD data, the vibrational spectra appear to change continuously over the temperature range of the experiment. The room-temperature spectrum, performed on a powdered crystalline sample mixed with polytetrafluoroethylene using previously described techniques15,16 with each presented spectrum representing 32 time-domain waveforms, averaged and Fourier transformed, and repeated four times for each temperature, contains two clear absorptions at 50.0 and 74.7 cm−1. Upon cooling, two features are increasingly resolved from the 300 K single absorption at 50.0 cm−1, with the coldest 100 K spectrum containing absorptions at 51.5, 58.2, 73.9, and 78.7 cm−1. The spectral features exhibit an obvious frequency shift upon cooling; however the magnitude of the shifts are relatively atypical of organic molecules.17 While the 50.0 cm−1 feature seemingly splits into a doublet and moves to higher frequencies, there is a rather significant shift between the single absorption at 300 K and the second peak in the 100 K spectrum. Specifically, the largest changes occur after 200 K, with the second peak exhibiting its largest shifts between 200 K and 150 K (2.4 cm−1), and 150 K and 100 K (2.1 cm−1), while the rest of the spectrum undergoes relative minor changes (e.g. the first peak shifts by a total of 1.5 cm−1 between 300 K and 100 K). It is important to note that as with the SC-XRD experiments, the THz-TDS response was also shown to be reversible and reproducible.
At first consideration, the THz-TDS data seem to agree with the SCXRD results that suggest a continuous phase transition involving a multitude of intermediate states is occurring. However, given the rather significant changes in the 50 cm−1 vibrational feature there is an implication that a more in-depth description might be possible, especially when considering that polymorphic systems usually involve only two possible states with no intermediates. Yet, experimentally distinguishing between the possibility of a continuous versus discontinuous phase transition is difficult, and thus theoretical methods must be employed to further understand such a process.
To explore the energetics of the two polymorphs and explain the observed experimental results, analyses of the vibrational and corresponding thermodynamic properties of the two polymorphs of Me4CP·Cl were performed using solid-state DFT calculations. A developmental version of the CRYSTAL14 ab initio code, which incorporates periodic boundary conditions, was used for all simulations.18 The Grimme D3 dispersion corrected19,20 generalized gradient approximation Perdew–Burke–Ernzerhof (PBE)21 functional was coupled with the Ahlrichs TZVP basis set.22 The experimental atomic positions were used to initialize the geometry optimizations, which were performed without any constraints other than the space group symmetry of the solids, with all structural parameters allowed to relax (atomic positions and lattice vectors). Vibrational normal mode eigenvectors and eigenvalues were calculated from the optimized structures and infrared intensities determined using the Berry phase method.23,24 Energy convergence criteria were set to ΔE < 10−8 and 10−11 Hartree for the geometry and vibrational calculations, respectively.
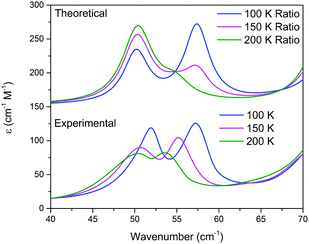
The results of the vibrational simulations (Fig. 3) are in good agreement with the respective experimental spectra, indicating that both the potential energy surfaces and atomic charges were well modelled to a high level of accuracy (sub-100 cm−1 transitions are below the current state-of-the-art standard of 1 kcal mol−1 for theoretical energy simulations). Additionally, the simulated Gibbs free energy curves (which are dependent on the accurate treatment of the phonons) predict the correct ordering of the two polymorphs, with the LT-form being the energetically favored polymorph at lower-temperatures and a predicted crossing occurring at 167.5 K. This temperature also corresponds to the onset of the phase transition as determined from SCXRD (Fig. 2), further indicating that the solid-state DFT simulations are accurate.
The vibrational simulations enable an in-depth understanding of the transformation mechanism that occurs in this system to be obtained. Investigation of the normal modes indicates that the 58.2 cm−1 transition in the LT-form (calculated at 57.9 cm−1) directly corresponds to the coordinate responsible for the phase transition. This is an antisymmetric translation of the individual rows and a corresponding antisymmetric rotation of the individual molecules with respect to one another (see Fig. 1(c)), overall indicating that the transition pathway contains a relatively low energy barrier. However, comparison with the experimental spectra suggests that the second peak is present before the transition is occurring, which implies that the HT-form has an additional feature. Inspection of the simulated phonons of the HT-form shows that the predicted mode at 60.1 cm−1 is similar to the mode in the LT-form, although with no motion of the carboxylate group due to symmetry restrictions. It can be assumed that this feature becomes much softer as a function of increasing temperature, and by performing a vibrational simulation at an expanded volume (2% expansion, analogous to thermal expansion to ambient conditions), the effective dependence of this mode on temperature can be obtained. The results show that while most of the predicted features only slightly red-shift (by ∼2–4 cm−1), this particular mode drastically decreases in frequency by 14 cm−1. This further indicates that this mode is fundamentally linked to the phase-change phenomena, and provides clear mechanistic insight into the processes.
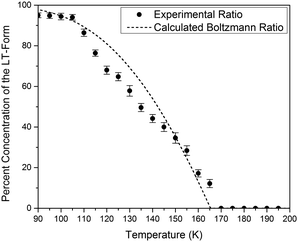
The simulated vibrational dynamics and Gibbs curves, while indicating that a phase transition between the two polymorphs is predicted to occur, provides no insight into the apparent continuous phase change that is observed experimentally. However, given the similar energies of the two solids it is reasonable to consider that rather than an instantaneous complete transformation of every unit cell in the solid (the commonly encountered phenomenon), the two polymorphic forms may simultaneously coexist (hence concomitant polymorphs) in a Boltzmann distributed population ratio between the two states,
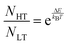 | (1) |
This analysis can be extended to the terahertz vibrational spectra by considering the data to be a linear combination of the individual polymorph spectra. This is illustrated in Fig. 5, where the experimental spectra were compared to a linear combination of the simulated spectra. The comparison with experiment is achieved by weighting the two spectra by their predicted thermal populations from Fig. 4. Fig. 5 shows that the observed “continuous” shifting can actually be modeled as a linear combination because the positions and intensities of the spectral features appear to form a continuous transition, but in fact they can arise out of just a simple mixture of two samples. It is important to note that in addition to the inherent frequency positions of the two polymorphs, there still exists a degree of intermolecular anharmonicity that manifests itself as contraction of the unit cells with reduced temperature and leads to an inherent blue shifting that is not explicitly included in this type of analysis. This concept is important for making a distinction between the two experimental techniques utilised, as the THz-TDS measurements are highly sensitive to intermolecular force strength, anharmonic coupling and vibrational relaxation (i.e. temperature-dependent intensities), and related phenomena, while the SC-XRD is based solely on the static structural component. Thus, it is not surprising that neither technique is fully capable of capturing this process in its entirety, but through the combination the overall features can be extracted. Nonetheless, it is clear that such a characterization results in both good quantitative and qualitative agreement with the experimental observations.
The discovery of a low-frequency infrared-active vibrational mode that corresponds to the transformation coordinate between the two polymorphs provides valuable insight into the origins of the observed effects by yielding a measure of both the transformation mechanism and energy barriers. Combining THz-TDS with additional supporting data from quantum-mechanical simulations and experimental single-crystal X-ray diffraction experiments offers compelling evidence for the chemical origins of the phase transition. The fact that the transition corresponds directly to an infrared-active phonon has implications for the use of high-field terahertz pulses for exerting control over the solid-state polymorphism, as previously suggested for other systems.25,26 The Me4CP·Cl crystal presents an excellent target system for demonstrating the experimental ability of terahertz radiation to initiate polymorphic phase transitions at arbitrary temperatures. If successful, this concept should be transferrable to other complex solids (e.g. pharmaceuticals), where selective growth of metastable polymorphs is of high value.
M. T. R. and T. M. K. acknowledge the support of a grant from the National Science Foundation (CHE-1301068). M. T. R. and J. A. Z. acknowledge support from the UK Engineering and Physical Science Research Council (EP/N022769/1). Additional data related to this publication are available at the University of Cambridge data repository (https://doi.org/10.17863/CAM.13417).
Conflicts of interest
There are no conflicts to declare.References
- V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Chem. Rev., 2007, 107, 926–952 CrossRef CAS PubMed.
- P. Vishweshwar, J. A. McMahon, J. A. Bis and M. J. Zaworotko, J. Pharm. Sci., 2006, 95, 499–516 CrossRef CAS PubMed.
- G. J. O. Beran, Chem. Rev., 2016, 116, 5567–5613 CrossRef CAS PubMed.
- R. Censi and P. Di Martino, Molecules, 2015, 20, 18759–18776 CrossRef CAS PubMed.
- S. P. Delaney, T. M. Smith, D. Pan, S. X. Yin and T. M. Korter, Cryst. Growth Des., 2014, 14, 5004 CAS.
- C. C. Mattheus, A. B. Dros, J. Baas, A. Meetsma, J. L. de Boer and T. T. M. Palstra, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2001, 57, 939 CAS.
- S. Schiefer, M. Huth, A. Dobrinevski and B. Nickel, J. Am. Chem. Soc., 2007, 129, 10316–10317 CrossRef CAS PubMed.
- A. Gilbert and W. S. Owen, Acta Metall., 1962, 10, 45–54 CrossRef CAS.
- K. Kawakami, J. Pharm. Sci., 2007, 96, 982–989 CrossRef CAS PubMed.
- E. Gunn, I. A. Guzei, T. Cai and L. Yu, Cryst. Growth Des., 2012, 12, 2037 CAS.
- G. S. Nichol and W. Clegg, Acta Crystallogr., Sect. B: Struct. Sci., 2005, 61, 464–472 Search PubMed.
- E. P. J. Parrott and J. A. Zeitler, Appl. Spectrosc., 2015, 69, 1–25 CrossRef CAS PubMed.
- F. Zhang, H.-W. Wang, K. Tominaga, M. Hayashi, T. Hasunuma and A. Kondo, Chem. – Asian J., 2016, 12, 324–331 CrossRef PubMed.
- M. T. Ruggiero, J. Sibik, J. A. Zeitler and T. M. Korter, J. Phys. Chem. A, 2016, 120, 7490 CrossRef CAS PubMed.
- M. T. Ruggiero, J. Gooch, J. Zubieta and T. M. Korter, J. Phys. Chem. A, 2016, 120, 939–947 CrossRef CAS PubMed.
- M. T. Ruggiero, J. Sibik, R. Orlando, J. A. Zeitler and T. M. Korter, Angew. Chem., Int. Ed., 2016, 55, 6877–6881 CrossRef CAS PubMed.
- Y. C. Shen, P. C. Upadhya, E. H. Linfield and A. G. Davies, Appl. Phys. Lett., 2003, 82, 2350 CrossRef CAS.
- R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D’Arco, Y. Noël, M. Causà, M. Rérat and B. Kirtman, J. Quantum Chem., 2014, 114, 1287 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef.
- F. Pascale, C. M. Zicovich-Wilson, F. L. Gejo, B. Civalleri, R. Orlando and R. Dovesi, J. Quantum Chem., 2004, 25, 888–897 CAS.
- Y. Noël, C. M. Zicovich-Wilson, B. Civalleri, Ph. D’Arco and R. Dovesi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 014111 CrossRef.
- H. Hoshina, H. Suzuki, C. Otani, M. Nagai, K. Kawase, A. Irizawa and G. Isoyama, Sci. Rep., 2016, 6, 27180 CrossRef PubMed.
- M. González-Jiménez, G. Ramakrishnan, T. Harwood, A. J. Lapthorn, S. M. Kelly, E. M. Ellis and K. Wynne, Nat. Commun., 2016, 7, 11799 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp04666a |
| This journal is © the Owner Societies 2017 |