Kinetics study of the Ru/C-catalysed hydrogenolysis of polyols – insight into the interactions with the metal surface

Abstract

The aqueous Ru/C-catalysed hydrogenolysis of xylitol and sorbitol was studied in a temperature range between 393–443 K under 6 MPa H₂. For the three main reactions, stereoisomerisation, decarbonylation and deoxygenation, kinetic models were formulated and fitted to the experimental data. The obtained rate constants were used to determine apparent activation enthalpies via the Eyring method. The data reveals a clear dependence of the type and position of the reacting hydroxyl group as well as the length of the polyol on the activation energies. It is proposed that these differences are the result of increased stabilisation due to polydentate interactions with the metal surface.

---

Introduction

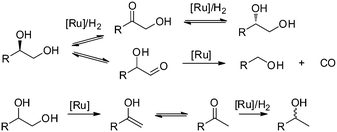
The utilisation of renewable feedstocks such as lignocellulose for fuel and chemical production is a promising way to reduce CO₂ emission and decrease the dependence on fossil resources.¹ By using a combination of acid-catalysed hydrolysis and metal-catalysed hydrogenation reactions, a wide variety of products are obtainable from (hemi-)cellulose.² Performing these reactions in a one-pot fashion directly yields sugar alcohols such as sorbitol and xylitol. In turn, they can be further converted to various other polyols (e.g. sorbitan, isosorbide, ethylene glycol, propanediol, glycerol, etc.) or light alkanes. Particularly, diols such as ethylene glycol and propanediol are important bulk chemicals that, if prepared from cellulose, would constitute a massive reduction in CO₂ emission. As a consequence, the hydrolytic hydrogenation and/or hydrogenolysis of cellulosic biomass has been studied intensively.³

The employed catalyst systems can roughly be divided into noble metal-based (e.g. Pt,⁴ Ru^5,6) and non-noble metal-based (Ni,⁷ Cu⁸). In the presence of homogeneous acidic co-catalysts, noble metals are preferred due to increased stability. Ru-based catalysts are particularly attractive due to their good activity and comparatively low price. However, in addition to the desired hydrogenation reaction, Ru also catalyses side reactions leading to decreased yields of hexitols in the hydrolytic hydrogenation of cellulose.⁹ Recently, we have presented a detailed study on the product mixture and reaction network observed for the Ru/C-catalysed hydrogenolysis of biomass-based polyols under neutral and acidic conditions.¹⁰ The data revealed the formation of a complex product mixture due to the occurrence of (de)hydrogenation, stereoisomerisation, decarbonylation and deoxygenation reactions (Scheme 1).

Scheme 1 Proposed elementary transformations for the Ru/C-catalysed hydrogenolysis of polyols.

This demonstrates that Ru exhibits a rich surface chemistry with polyols, which is still not adequately understood. Valuable insights into reaction pathways of volatile oxygenates on clean Ru surfaces (e.g. acids, alcohols, carbonyls) have been obtained through UHV techniques (e.g. HREELS) and TPD experiments.¹¹ However, the multifunctional nature of higher polyols and the harsh reaction conditions (i.e. water, high temperature, high pressure) used in hydrogenolysis hinder the application of these methods. Therefore, the development of alternative concepts especially applicable to (hemi-)cellulose-based C₅- and C₆-polyols is essential. Fortunately, the complex substrate structure and broad product distributions of higher polyols can provide insight into the reactions occurring on the metal surface. Previously, we proposed simplified reaction mechanisms, though a detailed understanding of the interactions of polyols with the metal surface is still lacking. Here, we tackle this problem using a comprehensive kinetic analysis of the stereoisomerisation, decarbonylation and deoxygenation of sorbitol and xylitol. To this end, kinetic models were proposed and kinetic parameters were estimated. The obtained rate constants and equilibrium compositions were used to assess thermodynamic quantities such as apparent activation enthalpies and isomer energies. In addition, a description of the reactions of higher polyols with the Ru surface is proposed based on the obtained parameters.

Results and discussion

Stereoisomerisation

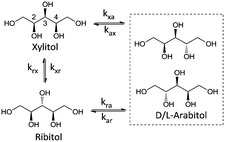
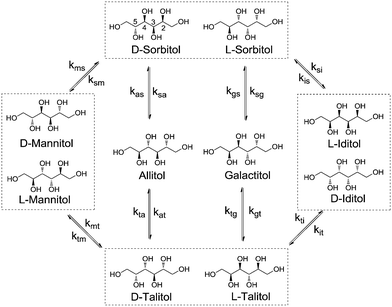
Stereoisomerisation is commonly observed in the hydrogenation/hydrogenolysis of sugars and sugar alcohols. Depending on the employed reaction conditions (i.e. alkaline or Lewis acidic), aldose and ketose sugars can be interconverted through the Lobry de Bruyn–Alberda van Ekenstein (LBE) reaction. Racemisation is caused by either reversible enol–keto tautomerisation or Lewis acid-catalysed 1,2-hydride shifts.¹² Hydrogenation of the ketoses formed in these reactions also leads to a racemic mixture. For the hydrogenolysis of sugar alcohols, initial dehydrogenation to aldose and ketose sugars is required to enable cleavage reactions. If a formed ketose desorbs and re-adsorbs, then epimerisation can proceed via reversible (de)hydrogenation alone. For Ru catalysts under neutral conditions, it is proposed that stereoisomerisation proceeds via this mechanism.¹³ A systematic treatise of all possible epimerisation reactions of pentitols and hexitols leads to reaction networks where enantiomers may be treated separately (e.g. epimerisation of D-sorbitol at the 5-position leads to L-iditol, whereas that of L-sorbitol leads to D-iditol). However, since chiral separation was not performed, no distinction was made between enantiomers. Scheme 2 shows the reaction network of pentitol isomerisation (i.e., xylitol (XYL), D-/L-arabitol (ARA) and ribitol (RIB)). First-order kinetics are assumed for the formulation of rate equations (see eqn (2)–(4) in the ESI†).

Scheme 2 Reaction network of the epimerisation of pentitols.

Rate constant k_xa corresponds to the epimerisation of xylitol at the 2- or 4-positions yielding ARA and k_xr corresponds to epimerisation at the 3-position yielding RIB. For the hexitols (i.e., D-/L-sorbitol (SOR), D-/L-mannitol (MAN), allitol (ALL), galactitol (GAL), D-/L-iditol (IDI) and D-/L-talitol (TAL)), the same approach was applied (Scheme 3, see eqn (5)–(10) in the ESI†).

Scheme 3 Reaction network for the epimerisation of hexitols.

Here, k_sm, k_sa, k_sg and k_si correspond to the rate constants for the epimerisation of SOR at the 2-position yielding MAN, 3-position yielding ALL, 4-position yielding GAL and 5-position yielding IDI, respectively.

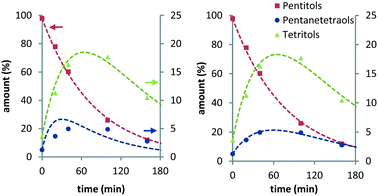
From previous studies, it is known that Ru/C exhibits an induction period in these reactions.¹⁰ To avoid artefacts, time zero of the fitted curves was chosen 20–30 min after the reaction temperature had been reached. Fig. 1 shows the experimental data and curve fitting for the evolution of the various pentitols and hexitols relative to their total amount (see Fig. S1 and S2 in the ESI†).

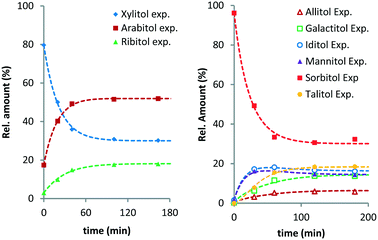Fig. 1 Ru/C-catalysed stereoisomerisation of xylitol (left) and sorbitol (right) (conditions: 2 g substrate, 20 ml H₂O, 0.4 g Ru/C (5 wt%), 433 K, 6 MPa H₂).

XYL isomerises to ARA and RIB, with ARA as the major product. At temperatures above 423 K, the composition equilibrates within the monitored timeframe. In all cases, a final composition with on average 51.5% ARA, 30.5% XYL and 18.0% RIB is observed (Table 1). This is well in line with isomer distributions observed previously for the Ru/C-catalysed hydrogenation and isomerisation of xylose syrup by Beck et al.¹⁴ From the isomer distribution, it follows that XYL and RIB are respectively 1.9 and 3.8 kJ mol⁻¹ higher in Gibbs energy than ARA.

Table 1 Equilibrium compositions and relative energies of pentitols and hexitols

Isomer	Equilibrium composition (%)	ΔG^423K (kJ mol^−1)
Pentitols	Lit.^14	This work
Arabitol	50	51.5	0
Xylitol	29	30.5	1.9
Ribitol	21	18.0	3.8

---

Hexitols	Lit.^15
Sorbitol	41.4	31.4	0
Talitol	—	18.4	1.9
Iditol	26.5	16.3	2.4
Mannitol	31.5	14.5	2.8
Galactitol	—	13.7	3.0
Allitol	—	5.8	6.1

---

A similar behaviour was observed for the isomerisation of SOR. SOR converts to all other isomers and at 433 K an apparent equilibrium is reached after 3 h. The final composition contains 31.4% SOR, 18.4% TAL, 16.3% IDI, 14.5% MAN, 13.7% GAL and 5.8% ALL. It follows that ALL is 6.1 kJ mol⁻¹ higher in energy than SOR, whereas TAL, IDI, MAN and GAL are between 1.9–3.0 kJ mol⁻¹ higher. To the best of our knowledge, data concerning the equilibrium composition of hexitols from Ru/C-catalysed isomerisation has not been reported before. A report by Wright et al. describes the isomerisation of hexitols catalysed by Ni/kieselguhr under alkaline conditions.¹⁵ The authors proposed that the isomerisation proceeds via aldose formation and enediol intermediates.

This proposal is supported by the absence of TAL, GAL and ALL, which are only available by isomerisation at the 3-/4-positions. Our data differs significantly and shows that the isomerisation occurs on all positions of the polyol.

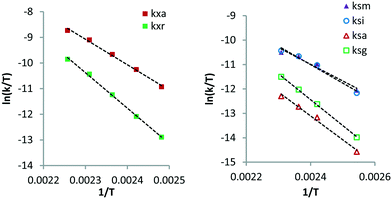
The rate constants obtained from curve fitting at different reaction temperatures were used to calculate apparent activation energies via the Eyring method (Table 2). The Eyring plots all show a clear linear trend within the temperature range of 403–443 K. The data for XYL reveals that the apparent activation enthalpy of k_xa (2-/4-pos., 82.5 kJ mol⁻¹) is 32.3 kJ mol⁻¹ lower than that of k_xr (3-pos., 114.8 kJ mol⁻¹). Thus, isomerisation at the 3-position is significantly more difficult than that at the 2-/4-positions. A similar behaviour is observed for SOR where the activation enthalpies of k_sm (2-pos., 56.7) and k_si (5-pos., 62.7) are roughly 25 kJ mol⁻¹ lower than those of k_sa (3-pos., 81.2) and k_sg (4-pos., 88.1). These data suggest that large differences exist between the reactivity of the different hydroxyl positions on the Ru surface. This is rather puzzling since these hydroxyl groups are chemically and sterically equivalent.

Table 2 Summary of the Eyring–Polanyi regression and thermodynamic data of the stereoisomerisation of hexitols and pentitols

Rate constant	Epimerisation position	Δ^‡Happ (kJ mol^−1)	R ^2
Xylitol
k xa	2-/4-	82.5	0.99
k xr	3-	114.8	0.99
Sorbitol
k sm	2-	56.7	0.96
k sa	3-	81.2	0.99
k sg	4-	88.1	0.99
k si	5-	62.7	0.98

---

To further verify the validity of the model, additional reactions were performed with MAN and GAL (Fig. 2). As expected, MAN converts to the other isomers with SOR as the main product. The composition after 160 min resembles the equilibrium composition observed for SOR. Interestingly, for GAL, this is not the case. Here, the main product of the reaction is TAL. This again shows that isomerisation at the 2-/5-position (GAL to TAL) is significantly faster than that at the 3-/4-position (GAL to SOR). Leaving the reaction for a longer period was not possible due to conversion of hexitols via decarbonylation and deoxygenation reactions. Even though the equilibrium was not reached in this case, these data confirm the general observations for the XYL and SOR reactions.

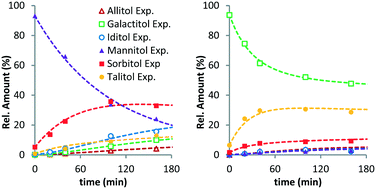Fig. 2 Ru/C-catalysed stereoisomerisation of mannitol (left) and galactitol (right) (conditions: 2 g substrate, 20 ml H₂O, 0.4 g Ru/C (5 wt%), 433 K, 6 MPa H₂).

Decarbonylation and deoxygenation

In our previous study, we showed that Ru/C catalyses decarbonylation and deoxygenation reactions which occur simultaneously on the substrate and all of the subsequent products. The consecutive nature of these reactions is clearly reflected in the evolution of the product mixture that confirms a stepwise loss of CH(OH) units or OH groups and leads to a pyramidal reaction network. Kinetic modelling of the whole network is not feasible because of inseparable contributions to the accumulation of compounds that are formed and consumed by both reactions. Still, kinetic modelling can be performed using two approaches. The first option is to consider only the top of the pyramid, i.e. hexitols to pentitols and hexanepentaols or pentitols to tetritols (k_pt) and pentanetetraols (k₅₄) (Scheme 4).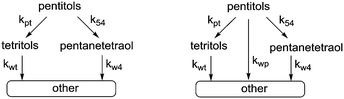

Scheme 4 Kinetic models for simultaneous decarbonylation and deoxygenation (left: only decarbonylation and deoxygenation (model 1); right: with an additional reaction path (model 2)).

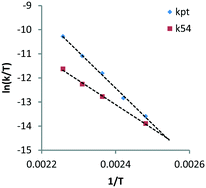
Here, decarbonylation and deoxygenation are treated as irreversible reactions. Kinetic modelling of XYL at 423 K (Fig. 3, left) using model 1 shows a good fit for decarbonylation, whereas for deoxygenation, the fit shows a systematic error indicating a problem with the model. When a third reaction path (k_wp) is included (model 2), the fit for deoxygenation improves significantly (Fig. 3, right). This suggests that another decomposition reaction may be involved in the hydrogenolysis reaction. However, GC and LC analysis of the reaction mixture did not reveal any other products. A possible explanation for this is that adsorbed species can react multiple times without intermediate dissociation, i.e. the first model assumes that the fragments formed from cleavage reactions are completely hydrogenated and desorbed before further reaction. However, if adsorption of the polyol is strong, a second cleavage reaction may ensue without desorption. Given the improved fits, the latter model was used for the Eyring analysis of the rate constants k_pt and k₅₄ (Table 3, see eqn (11)–(13) and Fig. S3 in the ESI†). The data shows that the apparent activation enthalpy for deoxygenation (83.1 kJ mol⁻¹) is significantly lower than that for decarbonylation (124.3 kJ mol⁻¹). Interestingly, deoxygenation is considerably slower than decarbonylation. This suggests that there are fewer sites catalysing deoxygenation.

Fig. 3 Experimental data of the Ru/C-catalysed hydrogenolysis of xylitol and curves fitted using simultaneous decarbonylation and deoxygenation (left: model 1; right: model 2) models (conditions: 2 g substrate, 20 ml H₂O, 0.4 g Ru/C (5 wt%), 423 K, 6 MPa H₂).

Table 3 Summary of the Eyring–Polanyi regression and thermodynamic data of the simultaneous deoxygenation and decarbonylation of xylitol

Reaction	Rate constant	Δ^‡Happ (kJ mol^−1)	R ^2
Decarbonylation	k pt	124.3	0.99
Deoxygenation	K 54	83.1	0.99

---

The second approach to model the hydrogenolysis kinetics is to consider consecutive decarbonylation or consecutive deoxygenation. Unfortunately, consecutive deoxygenation could not be determined with sufficient accuracy (i.e. low amounts, overlapping peaks in GC). Scheme 5 shows the reaction sequence for the consecutive decarbonylation of hexitols down to ethylene glycol.

Scheme 5 Reaction network for the consecutive decarbonylation of polyols.

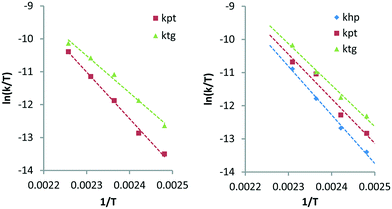
Here, k_hp represents the rate constant for the decarbonylation of hexitols to pentitols and k_wh indicates the rate constant corresponding to the loss of hexitols to side reactions. All stereoisomers of a polyol were treated as equally reactive and grouped. As with stereoisomerisation, first-order kinetics was assumed for the formulation of the rate equations (see eqn (14)–(18) and Fig. S4 and S5 in the ESI†). Fig. 4 shows the experimental data and curve fitting of sorbitol and xylitol at 433 K. As expected, the model exhibits excellent agreement with the experimental data. The maximum accumulation of pentitols, tetritols and glycerol decreases with decreasing chain length. In view of accuracy, only the first few follow-up reactions were considered for Eyring analysis. Table 4 shows the Eyring plots of the rate constants k_hp, k_pt and k_tg obtained for the SOR and XYL reactions in the temperature range of 403–443 K.

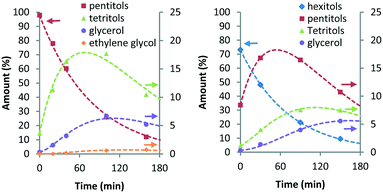Fig. 4 Ru/C-catalysed decarbonylation of pentitols (left) and hexitols (right) (conditions: 2 g substrate, 20 ml H₂O, 0.4 g Ru/C (5 wt%), 433 K, 6 MPa H₂).

Table 4 Summary of the Eyring–Polanyi regression and thermodynamic data of the consecutive decarbonylation of pentitols (left) and hexitols (right)

Rate constant	Δ^‡Happ (kJ mol^−1)	R ^2
Xylitol
k pt	117.8	0.99
k tg	93.8	0.99
Sorbitol
k hp	121.9	0.99
k pt	111.7	0.96
k tg	104.0	0.99

---

The plots show a clear linear trend and the calculated apparent activation enthalpies are clustered between 94–122 kJ mol⁻¹. Comparison of the same transformations e.g. decarbonylation of pentitols (k_pt) and tetritols (k_tg) observed for the SOR and XYL reactions shows that they are comparable and have differences between 6.1–10.2 kJ mol⁻¹. Interestingly in both cases, the activation energy slightly decreases with each subsequent step. This suggests that the length of the polyol has an influence on the activation energy. The activation enthalpy of k_pt obtained from the XYL dataset using the simultaneous deoxygenation and decarbonylation model (Scheme 4, Table 3, 124.3 kJ mol⁻¹) is approximately 13 kJ mol⁻¹ higher than that for the consecutive decarbonylation model (Scheme 5, Table 4, 111.7 kJ mol⁻¹). This shows that both models provide comparable results. However, further studies are required to determine these activation energies with greater accuracy.

Surface mechanism

Adsorption. The data presented above provides interesting hints concerning the interactions of polyols with the Ru catalyst. Moreover, the data suggests that the reactivity of hydroxyl groups depends not only on the type and position but also on the length of the polyol. In order to rationalize these differences, it is first necessary to describe the state of the metal surface and the polyol adsorption process. As mentioned above, in all cases, an induction period was observed. Since the commercial Ru/C catalyst was used as is, it is proposed that the induction period is the result of the in situ reduction of an oxidic phase to metallic Ru. Various in-depth studies on the wetting of Ru(0001) surfaces have provided convincing evidence that water fully covers the surface and that at higher temperatures adsorption is also accompanied by dissociation.¹⁶ It is reasonable to assume that, under the reaction conditions, the Ru surface is saturated with adsorbates such as water, hydroxyl and hydrogen in various proportions (Scheme 6).

Scheme 6 Schematic representation of adsorption and dissociation of water and hydrogen on Ru.

When taking this situation as a reference state, polyol adsorption cannot proceed without prior desorption of adsorbates (e.g. water). A recent study by Murzin et al. revealed that the adsorption energy of the primary hydroxyl group of C_n (n = 1–4) polyols on clean Ru surfaces increases from −0.65 (n = 1) to −0.93 eV (n = 3, 4).¹⁷ Compared to the adsorption energy of water (−0.47 to −0.54 eV), this confirms that for higher polyols there is still a significant net adsorption energy. The results of Miller et al. on the adsorption of glycerol on Ru-sponge also suggest stronger adsorption for higher polyols.¹⁸ In addition, polydentate polyol adsorption will be entropically favoured due to the successive release of adsorbates (Scheme 7). For this adsorption process, many permutations exist which differ in the order of hydroxyl attachment and polyol geometries on the surface. Even if full polydentate adsorption is not possible (e.g. due to steric constraints), it is expected that hydrogen-bonding interactions will lead to additional stabilisation of the polyol on the surface.

Scheme 7 Schematic representation of stepwise hydroxyl adsorption on Ru with adsorbate displacement.

(De)hydrogenation and epimerisation

As discussed above, dehydrogenation can occur on each position of the polyol chain. In the overall reaction, one hydroxyl adsorbate is converted to one ketone/aldehyde and two hydrogen ligands. As before, it is reasonable to assume that each dissociation reaction is accompanied by desorption reactions. Because of the exceptional hydrogenation activity of Ru in aqueous medium, the mechanism of (de)hydrogenation on Ru has been studied on several accounts.¹⁹ Presently, two different mechanisms are discussed which differ in the order of hydrogen addition/abstraction (i.e. an alkoxide path and a hydroxide path). In our previous study, we observed that Ru/C-catalysed H/D exchange only occurs on hydroxylated positions and does not affect ethers/acetals.¹⁰ This leads us to believe that under the applied reaction conditions, dehydrogenation preferentially proceeds through the alkoxide path (Scheme 8). It is proposed that epimerisation proceeds via either a η(O)-carbonyl intermediate (C*) or complete desorption of the ketone (C).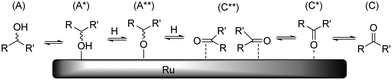

Scheme 8 Schematic representation of Ru-catalysed epimerisation reaction (hydrogen, water and other adsorbates not shown for clarity).

The H/D-exchange data also revealed that exchange occurs readily with retention of configuration at temperatures around 373 K.¹⁰ This indicates that the formation of species A*, A** and C** is reversible and fast and that conversion of C** to C* or C is rate determining for epimerisation. Based on this, we propose that the activation enthalpies of stereoisomerisation (Table 2) are related to desorption of the ketone. As a reference, we have calculated the reaction energy between species A and C + H₂ for the dehydrogenation of xylitol at the 1-/5-, 2-/4- and 3-positions in aqueous solvent. The results are summarized in Table 5.

Table 5 DFT data of the overall dehydrogenation of xylitol at 1-/5-, 2-/4-, and 3-positions at 298 K (NWChem software package, M11-L/6-311++G**/COSMO-SMD)²⁰

	ΔH298K (kJ mol^−1)	ΔG298K (kJ mol^−1)	ΔS (J mol^−1 K^−1)
1-/5-position	105.3	138.6	−111.8
2-/4-position	91.7	123.2	−105.8
3-position	85.4	117.4	−107.1

---

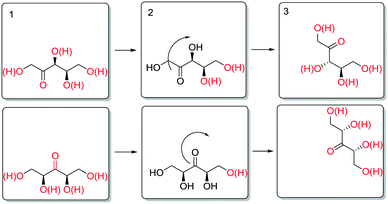
The enthalpy for aldose formation (105.3 kJ mol⁻¹) is 13–20 kJ mol⁻¹ higher than those for ketose formation (85.4–91.7 kJ mol⁻¹). Interestingly, the enthalpy for 3-ketose formation is 6.3 kJ mol⁻¹ lower than that for 2-,4-ketose formation. In contrast, the apparent activation enthalpies of the epimerisation at the different hydroxyl groups of SOR and XYL (Table 2) revealed that the enthalpies for the innermost positions (3-,4- or 3-) are approximately 25–30 kJ mol⁻¹ higher than those for the outer positions (2-,5- or 2,4-). Structurally, these positions differ only in the nature of neighbouring carbon atoms (i.e. 1° or 2°) and the number of neighbouring hydroxyl groups. The increases in activation energy can originate either from increased stabilisation of the reactant state or from destabilisation of the transition state. Although subtle differences in stability are to be expected for positional isomers and stereoisomers, on average their stabilisation at the surface is expectedly comparable. Also, the data for the 3- and 4-positions of SOR show that the stereochemical configuration of the neighboring positions has a relatively small influence on the activation energy. It appears therefore that the increased activation energy results from destabilisation of the transition state. A possible way to account for this is to consider desorption of the carbonyl, which is necessary for stereoinversion. Scheme 9 shows a schematic representation of the proposed desorption of 2-/4- and 3-ketose intermediates.

Scheme 9 Schematic representation of partial ketose desorption and re-adsorption (top: 2-/4-ketose, bottom: 3-ketose. Red color denotes interaction with the surface (viewed from above) via either adsorption or hydrogen bonding. Other adsorbates not shown for clarity).

In the initial state (1), the hydroxyl groups and the carbonyl are color coded red to signify interaction with the surface (e.g. as adsorbed or via hydrogen bonding). To invert the stereotopic plane of the carbonyl on the metal, desorption of the carbonyl and neighbouring hydroxyl groups is necessary (2). For the 2-ketose, this entails desorption of at least the 1-OH, 2-CO and most likely also 3-OH groups, to allow for free rotation of the carbonyl. For the 3-ketose, the required desorption is even more extensive (i.e. 1-OH, 2-OH, 3-CO and 4-OH). Thus, it is proposed that the higher apparent activation enthalpy for epimerisation of the inner positions is due to more difficult desorption of the carbonyl groups as a result of polydentate interactions of the neighbouring hydroxyl groups.

Decarbonylation

Earlier reports on the Ru/C-catalyzed hydrogenolysis of polyols have proposed both retro-aldol condensation²¹ and decarbonylation²² as possible C–C cleavage mechanisms. Recent studies by our group¹⁰ and Bitter et al.²³ provide clear evidence that under neutral conditions decarbonylation is the prevailing mechanism. Although it is well known in homogeneous catalysis²⁴ and for other metal catalysts,²⁵ only a few studies have been published on the heterogeneous Ru-catalyzed decarbonylation reaction.²⁶ The mechanism of decarbonylation involves a series of steps which include dehydrogenation of a primary hydroxyl group (A) to yield an aldose adsorbate (C**), further dehydrogenation to yield an acyl species (Ac*) and a C–C cleavage reaction yielding CO and R adsorbates (Scheme 10).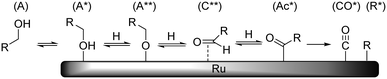

Scheme 10 Schematic representation of Ru-catalysed decarbonylation reaction (hydrogen and other adsorbates not shown for clarity).

Previous H/D exchange experiments on SOR showed that the C–H groups at the 1-/6-positions are rapidly and completely exchanged at 373 K without the occurrence of decarbonylation.¹⁰ This indicates that the reaction path between A and C** is fast and reversible. It is proposed that the observed activation energy is related to the formation of either Ac* or CO* + R*. The data in Table 4 show that the apparent activation enthalpy decreases with decreasing polyol chain length. Also here, the chemical nature of the reacting group is identical and the change in activation energy may be attributed to polydentate interactions of neighbouring hydroxyl groups. However, contrary to epimerisation where the reaction can be traced to desorption and rotation of a single carbonyl fragment, it is not obvious how the increasing polydentate binding leads to higher reaction barriers in this case. One possible way to account for this is to consider that the reacting group must go through several geometrical changes and bonding modes. Since the rest of the polyol chain is also attached to the reacting group, it must also accommodate these changes by reorganisation on the surface. This reorganisation again depends on desorption of the polyol, which will be increasingly more difficult with increasing chain length.

Conclusions

In conclusion, a comprehensive kinetic analysis was performed for the aqueous Ru/C-catalysed hydrogenolysis of xylitol and sorbitol under neutral conditions in a temperature range of 393–443 K. Kinetic models were proposed for the main reactions, stereoisomerisation, decarbonylation and deoxygenation. Curve fitting gave good fits in all cases and the obtained rate constants were used to assess activation enthalpies via the Eyring method. The results reveal that the activation energies for epimerisation at the innermost positions of the polyols are 20–30 kJ mol⁻¹ higher than those at the outer positions. The activation energies for decarbonylation increase with increasing chain length. For pentitols, the activation energy for decarbonylation is 40 kJ mol⁻¹ higher than that for deoxygenation although deoxygenation is considerably slower, suggesting the presence of multiple active sites catalysing different reactions. Thus, the data reveal a clear dependence of the type and position of the reacting hydroxyl group as well as the length of the polyol on the activation energies. These results are rationalized by considering the adsorption and desorption processes of polyols on ruthenium and it is proposed that these differences are the result of increased stabilisation due to polydentate interactions with the metal surface.

Acknowledgements

The authors kindly thank Heike Fickers-Boltz, Elke Biener, and Hannelore Eschemann for the GC analyses, Noah Avraham for HPLC analyses, and Ines Bachmann for NMR analyses. This work was supported by the Robert Bosch Foundation within the Robert Bosch Junior Professorship for the efficient utilisation of renewable resources. This work was performed as part of the Cluster of Excellence “Tailor-Made Fuels from Biomass” funded by the Excellence Initiative by the German federal and state governments to promote science and research at German universities.

Notes and references

1. (a) M. J. Climent, A. Corma and S. Iborra, Green Chem., 2014, 16, 516–547; (b) C. Li, X. Zhao, A. Wang, G. W. Huber and T. Zhang, Chem. Rev., 2015, 115, 11559; (c) F. H. Isikgor and C. Remzi Becer, Polym. Chem., 2015, 6, 4497; (d) I. Delidovich, P. J. C. Hausoul, L. Deng, R. Pfuetzenreuter, M. Rose and R. Palkovits, Chem. Rev., 2016, 116, 1540; (e) B. R. Caes, R. E. Teixeira, K. G. Knapp and R. T. Raines, ACS Sustainable Chem. Eng., 2015, 3, 2591.
2. (a) M. Besson, P. Gallezot and C. Pinel, Chem. Rev., 2014, 114, 1827; (b) R. J. van Putten, J. C. van der Waal, E. de Jong, C. B. Rasrendra, H. J. Heeres and J. G. de Vries, Chem. Rev., 2013, 113, 1499.
3. (a) A. M. Ruppert, K. Weinberg and R. Palkovits, Angew. Chem., Int. Ed., 2012, 51, 2564; (b) X. Liu, X. Wang, S. Yao, Y. Jiang, J. Guan and X. Mu, RSC Adv., 2014, 4, 49501; (c) H. Kobayashi, T. Komanoya, S. K. Guha, K. Hara and A. Fukuoka, Appl. Catal., A, 2011, 409–410, 13; Y. Li, Y. Liao, X. Cao, T. Wang, L. Ma, J. Long, Q. Liu and Y. Xua, Biomass Bioenergy, 2015, 74, 148.
4. (a) A. Yamaguchi, O. Sato, N. Mimura, Y. Hirosaki, H. Kobayashi, A. Fukuoka and M. Shirai, Catal. Commun., 2014, 54, 22; (b) H. Hirokazu, Y. Yamakoshi, Y. Hosaka, M. Yabushita and A. Fukuoka, Catal. Today, 2014, 226, 204; (c) D. Wang, W. Niu, M. Tan, M. Wu, X. Zheng, Y. Li and N. Tsubaki, ChemSusChem, 2014, 7, 1398; A. Yamaguchi, O. Sato, N. Mimura and M. Shirai, Catal. Commun., 2015, 67, 59; L. Yang, X. Yan, Q. Wang, Q. Wang and H. Xia, Carbohydr. Res., 2015, 404, 87; E. Girard, D. Delcroix and A. Cabiac, Catal. Sci. Technol., 2016, 6, 5534.
5. (a) Y. Liao, Q. Liu, T. Wang, J. Long, Q. Zhang, L. Ma, Y. Liu and Y. Li, Energy Fuels, 2014, 28, 5778; (b) W. Zhu, H. Yang, J. Chen, C. Chen, L. Guo, H. Gan, X. Zhao and Z. Hou, Green Chem., 2014, 16, 1534; (c) Y. Liao, Q. Liu, T. Wang, J. Long, L. Ma and Q. Zhang, Green Chem., 2014, 16, 3305; (d) Q.-Y. Liu, Y.-H. Liao, T.-J. Wang, C.-L. Cai, Q. Zhang and N. Tsubaki, Ind. Eng. Chem. Res., 2014, 53, 12655; (e) W. Deng, E. Zhu, M. Liu, Q. Zhang and Y. Wang, RSC Adv., 2014, 4, 43131; (f) Y. Liu, L. Chen, T. Wang, Y. Xu, Q. Zhang, L. Ma, Y. Liao and N. Shi, RSC Adv., 2014, 4, 52402; (g) T. Ennaert, J. Geboers, E. Gobachiya, C. M. Courtin, M. Kurttepeli, K. Houthoofd, C. E. A. Kirschhock, P. C. M. M. Magusin, S. Bals, P. A. Jacobs and B. F. Sels, ACS Catal., 2015, 5, 754; (h) L. S. Ribeiro, J. J. M. Órfão and M. F. R. Pereira, Green Chem., 2015, 17, 2973; (i) J. M. A. R. Almeida, L. Da Vià, P. Demma Carà, Y. Carvalho, P. N. Romano, J. A. O. Peña, L. Smith, E. F. Sousa-Aguiar and J. A. Lopez-Sanchez, Catal. Today, 2017, 279, 178.
6. (a) J. Xi, D. Ding, Y. Shao, X. Liu, G. Lu and Y. Wang, ACS Sustainable Chem. Eng., 2014, 2, 2355; (b) O. V. Manaenkov, V. G. Matveeva, E. M. Sulman, A. E. Filatova, O. Y. Makeeva, O. V. Kislitza, A. I. Sidorov, V. Y. Doluda and M. G. Sulman, Top. Catal., 2014, 57, 1476; (c) G. Xu, A. Wang, J. Pang, M. Zheng and J. Yin, Appl. Catal., A, 2015, 502, 65; (d) Y. Liu and H. Liu, Catal. Today, 2015, 269, 74; (e) Fabičovicová, M. Lucas and P. Claus, Green Chem., 2015, 17, 3075; (f) H. Wang, Y. Guo, D. Zheng and J. Han, J. Porous Mater., 2015, 22, 919; (g) L. S. Ribeiro, J. J. Delgado, J. J. de Melo Órfão and M. F. R. Pereira, Catal. Today, 2017, 279, 244; (h) T. Ennaert, B. Op de Beeck, J. Vanneste, A. T. Smit, W. J. J. Huijgen, A. Vanhulsel, P. A. Jacobs and B. F. Sels, Green Chem., 2016, 18, 2095; (i) A. Romero, E. Alonso, A. Sastre and A. Nieto-Márquez, Microporous Mesoporous Mater., 2016, 244, 1.
7. (a) C. van der Wijst, X. Duan, I. Skeie Liland, J. C. Walmsley, J. Zhu, A. Wang, T. Zhang and D. Chen, ChemCatChem, 2015, 7, 2991; (b) B. Zhang, X. Li, Q. Wu, C. Zhang, Y. Yu, M. Lan, X. Wei, Z. Ying, T. Liu, G. Liang and F. Zhao, Green Chem., 2016, 18, 3315; (c) G. Liang, L. He, H. Cheng, C. Zhang, X. Li, S.-I. Fujita, B. Zhang, M. Arai and F. Zhao, J. Catal., 2015, 325, 79; (d) Y. Yang, W. Zhang, F. Yang, D. E. Brown, Y. Ren, S. Lee, D. Zeng, Q. Gao and X. Zhang, Green Chem., 2016, 18, 3949; (e) H. Liu, L. Qin, X. Wang, C. Du, D. Sun and X. Meng, Catal. Commun., 2016, 77, 47.
8. (a) Z. Xiao, S. Jin, M. Pang and C. Liang, Green Chem., 2013, 15, 891; (b) D. Liang, C. Liu, S. Deng, Y. Zhu and C. Lv, Catal. Commun., 2014, 54, 108; (c) X. Jin, J. Shen, W. Yan, M. Zhao, P. S. Thapa, B. Subramaniam and R. V. Chaudari, ACS Catal., 2015, 5, 6545; (d) B. A. Dar, S. Khalid, T. A. Wani, M. A. Mir and M. Farooqui, Green Sustainable Chem., 2015, 5, 15; (e) S. Zhu, X. Gao, Y. Zhu and Y. Li, Green Chem., 2016, 18, 782.
9. T. Komanoya, H. Kobayashi, K. Hara, W.-J. Chun and A. Fukuoka, ChemCatChem, 2014, 6, 230.
10. P. J. C. Hausoul, L. Negahdar, K. Schute and R. Palkovits, ChemSusChem, 2015, 8, 3323.
11. (a) M. Mavrikakis and M. A. Barteau, J. Mol. Catal. A: Chem., 1998, 131, 135; (b) A. B. Anton, J. E. Parmeter and W. H. Weinberg, J. Am. Chem. Soc., 1985, 107, 5558; (c) A. B. Anton, N. R. Avery, B. H. Toby and W. H. Weinberg, J. Am. Chem. Soc., 1986, 108, 684; (d) A. B. Anton, J. E. Parmeter and W. H. Weinberg, J. Am. Chem. Soc., 1986, 108, 1823; (e) M. A. Anderson, Y. Zhou and J. M. White, J. Am. Chem. Soc., 1989, 111, 1185.
12. I. Delidovich, K. Leonhard and R. Palkovits, Energy Environ. Sci., 2014, 7, 2803.
13. (a) S. Wuyts, D. E. de Vos, F. Verpoort, D. Depla, R. De Gryse and P. A. Jacobs, J. Catal., 2003, 219, 417; (b) A. Zsigmond, A. Keeskeméti, K. Bogár, F. Notheisz and E. Mernyák, Catal. Commun., 2005, 6, 520.
14. R. H. F. Beck, M. Elseviers and S. M. J. Coomans, US Pat., 5714602A, 1998.
15. L. Wright and L. Hartmann, J. Org. Chem., 1961, 26, 1588.
16. (a) D. Menzel, Science, 2002, 295, 58; (b) P. J. Feibelman, Science, 2002, 295, 99; (c) A. Michaelides, A. Alavi and D. A. King, J. Am. Chem. Soc., 2003, 125, 2746; (d) K. Andersson, A. Nikitin, L. G. M. Pettersson, A. Nilsson and H. Ogasawara, Phys. Rev. Lett., 2004, 93, 196101; (e) G.-C. Wang, S.-X. Tao and X.-H. Bu, J. Catal., 2006, 244, 10; (f) C. Michel, F. Göltl and P. Sautet, Phys. Chem. Chem. Phys., 2012, 14, 15286.
17. R. Cortese, R. Schimmenti, N. Armata, F. Ferrante, A. Prestianni, D. Duca and D. Y. Murzin, J. Phys. Chem. C, 2015, 119, 17182.
18. L. Peereboom, J. E. Jackson and D. J. Miller, Green Chem., 2009, 11, 1979.
19. (a) B. S. Akpa, C. D'Agostino, L. F. Gladden, K. Hindle, H. Manyar, J. McGregor, R. Li, M. Neurock, N. Sinha, E. H. Stitt, D. Weber, J. A. Zeitler and D. W. Rooney, J. Catal., 2012, 289, 30; (b) N. K. Sinha and M. Neurock, J. Catal., 2012, 295, 31; (c) H. Wan, A. Vitter, R. V. Chaudhari and B. Subramaniam, J. Catal., 2014, 309, 174; (d) C. Michel, J. Zaffran, A. M. Ruppert, J. Matras-Michalska, M. Jędrzejczyk, J. Grams and P. Sautet, Chem. Commun., 2014, 50, 12450; (e) C. Michel and P. Gallezot, ACS Catal., 2015, 5, 4130; (f) J. Zaffran, C. Michel, F. Delbecq and P. Sautet, Catal. Sci. Technol., 2016, 6, 6615.
20. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477.
21. (a) D. K. Sohounloue, C. Montassier and J. Barbier, React. Kinet. Catal. Lett., 1983, 22, 391; (b) C. Montassier, J. C. Menezo, L. C. Hoang, C. Renaud and J. Barbier, J. Mol. Catal., 1991, 70, 99.
22. K. L. Deutsch, D. G. Lahr and B. H. Shanks, Green Chem., 2012, 14, 1635.
23. F. van der Klis, L. Gootjes, J. van Haveren, D. S. van Es and J. H. Bitter, Green Chem., 2015, 17, 3900.
24. N. Sieffert, R. Reocreux, P. Lorusso, D. J. Cole-Hamilton and M. Bühl, Chem. – Eur. J., 2014, 20, 4141.
25. (a) L. Vilcocq, A. Cabiac, C. Especel, S. Lacombe and D. Duprez, J. Catal., 2014, 320, 16; (b) B. Liu and J. Greeley, Phys. Chem. Chem. Phys., 2013, 15, 6475.
26. (a) F. Aiouache, L. McAleer, Q. Gan, A. H. Al-Muhtaseb and M. N. Ahmad, Appl. Catal., A, 2013, 466, 240; (b) S. Rangarajan, R. R. O. Brydon, A. Bhan and P. Daoutidis, Green Chem., 2014, 16, 813; (c) J. Lu, M. Faheem, S. Behtash and A. Heyden, J. Catal., 2015, 324, 14; (d) E. I. Gürbüz, D. D. Hibbitts and E. Iglesia, J. Am. Chem. Soc., 2015, 137, 11984.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cy02104b

---