Ethene hydrogenation vs. dimerization over a faujasite-supported [Rh(C2H4)2] complex. A computational study of mechanism†‡
Agalya
Govindasamy§
a,
Velina K.
Markova§
a,
Alexander
Genest
a and
Notker
Rösch
*ab
aInstitute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, #16-16 Connexis, Singapore 138632, Singapore. E-mail: roesch@mytum.de
bDepartment Chemie and Catalysis Research Center, Technische Universität München, 85747 Garching, Germany
First published on 28th November 2016
Abstract
Single-site catalysts offer great chances for unraveling the mechanism and the selectivity of catalytic mechanism, in particular when the system is experimentally well characterized. A particular interesting system of this type is the hydrogenation and the dimerization of ethene by the faujasite-supported complex [Rh(C2H4)2]+. We have examined this system computationally, treating periodic models with a density functional method. The complex [Rh(C2H4)2]+ binds in a bidentate fashion, as previously suggested, inside the faujasite supercage at the oxygen atoms of a 12-member ring. The calculations on this model complex showed ethene hydrogenation to be preferred over dimerization. The highest free energy barrier for forming a C–H bond was calculated at 33 kJ mol−1 at room temperature. This value is significantly lower than the lowest activation free energy, 97 kJ mol−1, calculated for C–C bond formation. The results of this mechanistic study allow one to rationalize the experimental observation that the faujasite-supported [Rh(C2H4)2]+ complex in the presence of H2 is active for hydrogenation, producing ethane as the main product.
Introduction
Numerous metal complexes are known to catalyze hydrogenation and C–C coupling reactions that are widely applied for alkene hydrogenation and polymerization reactions.1–5 Rhodium complexes catalyze a broad range of reactions of alkenes, e.g., oligomerization, hydrogenation, isomerization, hydroformylation, hydroboration, and hydrosilation.6,7 For routine application of such Rh complexes it is beneficial to anchor them on a support, without changing their functionality.8 An example, well characterized by EXAFS, IR, and NMR experiments and density functional theory (DFT) calculations, is the site-isolated complex [Rh(C2H4)2]+, supported on highly dealuminated zeolite HY.9,10 These studies confirmed the structure of the complex, anchored at a zeolite wall, and revealed that, in the presence of hydrogen, an ethyl moiety is formed from one ethene.10 Acidic zeolites catalyze C–C bond formation11 or incorporate transition metal complexes as well as particles tuning their catalytic activity12 or acting as a well-defined support.Experiments showed that at room temperature this anchored Rh complex catalyzes both the hydrogenation and the dimerization of ethene, with selectivities to ethane of ∼20% and to butenes of ∼75%.13 The selectivity varies at most by 5% with the C2H4/H2 ratio of the feed.13 The Rh-diethene catalyst with exposure to a H2 stream mainly forms ethane, as expected.9,10 Rh3 and Rh4 clusters were observed when the catalyst was pre-treated with H2; such supported clusters are very active in ethene hydrogenation at low C2H4/H2 ratios, with an ethane selectivity of 89%.13–16
DFT studies explored the catalytic activity of this zeolite-supported Rh complex, namely the trimerization of acetylene17 as well as the hydrogenation18 and the dimerization of ethene.18 Complexes of zeolite-supported Rh clusters at various hydrogen loadings, with ethene and ethene-derived moieties, have recently been examined computationally.19,20 In passing, we mention that the dimerization of ethene has also been studied computationally for acidic zeolites that do not contain any metal species.21,22
The present computational study focuses on the faujasite-supported [Rh(C2H4)2]+ complex and its role as catalyst as derived from the experiments,14 probing both observed transformations, hydrogenation to ethane and dimerization to butene. We address mechanistic pathways directly at the metal center, taking the support into account as poly-dentate ligand of the metal center.23 In this way, we intend to elucidate the role of the metal functionality in this experimentally particularly well-characterized catalyst system. Finally, in a broader perspective, this work aims to contribute from the theoretical side to the understanding of the reactivity of well-defined catalytic sites in heterogeneous catalysis.24
Results and discussion
Thus far, in most DFT investigations of reactions occurring inside zeolite cages that contain catalytically active extra-framework metal species, cluster models were employed to represent the zeolite.10,17,18,21,22,25,26 These cluster models were treated either directly by a method of quantum mechanics (QM)10,17,18,25,26 or by a QM/MM (molecular mechanics) embedding approach.18,21,22 As alternative to these cluster model strategies, one may describe the zeolite structure and the enclosed active sites by an extended model, periodic in three dimensions. A recent study18 compared results of periodic models plane-wave DFT calculations to results of cluster models that were embedded in an environment described by the force field UFF.27 Both modeling approaches used the same QM level of theory, namely the generalized gradient approximation (GGA)28 as suggested by Perdew, Burke and Ernzerhof (PBE),29,30 augmented by the empirical D2 correction31 for dispersion interactions that had been shown to impact significantly calculated structure of zeolites and the chemistry in zeolite cavities.32–34 In that study, it was found that corresponding results for selected C–H and C–C bond formation barriers deviated at most by 10 kJ mol−1.18 For the present study we decided to apply this PBE-D2 method to periodic models.Faujasite model
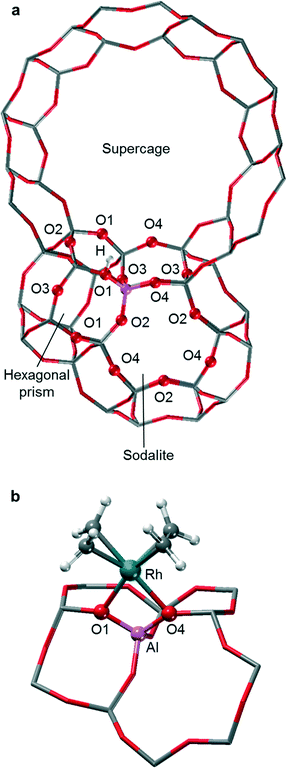
Faujasite is an aluminosilicate zeolite with a highly symmetric cubic structure that belongs to the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and contains three types of building units: supercages, sodalite cages (SOD), and hexagonal prisms (D6R); see Fig. S1 of the ESI.‡35 The unit cell of faujasite comprises 192 T atoms, with a single distinct T site and four types of oxygen atoms, referred to as O1, O2, O3, and O4 (Fig. 1). The crystal structure of silicalite faujasite was taken from the IZA website. Small cluster models of zeolites are unable to reflect in full the distinct catalytic activity and confinement effects exhibited by structurally diverse zeolites.36–39 Therefore, we employed in this study a periodic model of faujasite, but for computational economy, we used an often invoked, slightly simplified structure with a reduced triclinic unit cell that contains 48 T atoms (Fig. S2 of the ESI‡).40,41
m and contains three types of building units: supercages, sodalite cages (SOD), and hexagonal prisms (D6R); see Fig. S1 of the ESI.‡35 The unit cell of faujasite comprises 192 T atoms, with a single distinct T site and four types of oxygen atoms, referred to as O1, O2, O3, and O4 (Fig. 1). The crystal structure of silicalite faujasite was taken from the IZA website. Small cluster models of zeolites are unable to reflect in full the distinct catalytic activity and confinement effects exhibited by structurally diverse zeolites.36–39 Therefore, we employed in this study a periodic model of faujasite, but for computational economy, we used an often invoked, slightly simplified structure with a reduced triclinic unit cell that contains 48 T atoms (Fig. S2 of the ESI‡).40,41
Calculated results obtained with a GGA functional in general tend to overestimate lattice constants.42–45 To elucidate the impact of the dispersion interaction on the lattice parameters, we optimized the silicalite triclinic unit cell at the PBE level, both without and with the D2 corrections, Table S1 of the ESI.‡ The results for lattice parameters and the cell volume, calculated at the PBE level, compare better with the experimental values46 when the D2 correction is applied. Therefore, we selected the PBE-D2 method for the present study.
To mimic highly de-aluminated faujasite, one of the T atoms in the primitive cell of the model silicalite was substituted by an Al atom, representing a framework with a ratio Si/Al = 47 (exp. Si/Al = 30).13 The resulting net negative charge of the lattice was compensated by a proton. All four types of oxygen atoms were considered for the binding of the proton; see section S1 of the ESI.‡ The calculated relative stability of the different proton sites are O3–H ≃ O1–H > O2–H > O4–H, which agrees with the results of a previous QM/MM cluster study of faujasite.47
Adsorption of the complex Rh(C2H4)2 on faujasite
Identifying the most stable adsorption site for the metal complex is crucial before starting the mechanistic study. When synthesizing metal complexes supported on zeolites, complexes with acetylacetonate (acac) ligands often are used as precursors.9,13,48 For the complex [Rh(L)n(acac)], IR spectroscopic studies suggested that, during the adsorption process, the acac ligand dissociates from the rhodium species by abstracting an acidic proton of the zeolite and discharges as acetylacetone. The [Rh(L)n]+ fragment left behind is anchored at framework oxygen centers.9 In view of this experimental procedure, we examined the adsorption sites of the complex using the model reaction| [Rh(L)n(acac)] + Hzeo → zeo[Rh(L)n] + Hacac | (1) |
Here, zeo, L, acac, and Hacac represent the zeolite, the ligands (ethene), acetylacetonate, and acetylacetone, respectively. The preferred adsorption complex is characterized by the most favorable reaction free energy Gr for L = C2H4.
EXAFS studies revealed that the Rh center of the moiety [Rh(C2H4)2]+ binds on average to two oxygen atoms of the support.9,13 Therefore, we explored the stability of adsorption complexes where the zeolite lattice formally acts as bidentate ligand (Fig. S3 of the ESI‡). The various sites are discussed in more detail in section S1 of the ESI.‡ The reaction free energies calculated according to eqn (1) (Table S2 of the ESI‡) reveal that the cationic species [Rh(C2H4)2]+ prefers to bind at site O1O4, where the calculated binding energy is −61.4 kJ mol−1. The two oxygen centers of site O1O4 are directly bonded to the Al T-site. This bidentate binding site is located on the 12-member ring (MR) of the supercage.
Using the GGA-type functional BP86 (see below the section “Computational”), an early computational study on the adsorption of [Rh(CO)2]+ at Al substituted 4-MR and 6-MR cluster models of faujasite predicted two oxygen atoms of a 4-MR as the preferred binding site. Recall that the 6-MR of faujasite exhibits an O2O4 binding site, while the 4-MR of faujasite features the sites O1O2, O1O3, and O3O4 (Fig. 1b). However, that early work did not include sites of 12-MR that were determined as preferred in the present study. Also using the BP86 functional, a more recent QM/MM study on the adsorption of [Rh(CO)2]+ in faujasite demonstrated that the cage environment needs to be included in the model to obtain an adequate description of the adsorption site. This latter work showed that adsorption of [Rh(CO)2]+ at the sites O1O2 and O2O4 is less favorable (by 47 kJ mol−1 and 16 kJ mol−1, respectively) than adsorption at site O1O4 of 12-MR, just as found in the present study for the complex [Rh(C2H4)2]+.49
Ethene hydrogenation in the supported complex Rh(C2H4)2(H2)
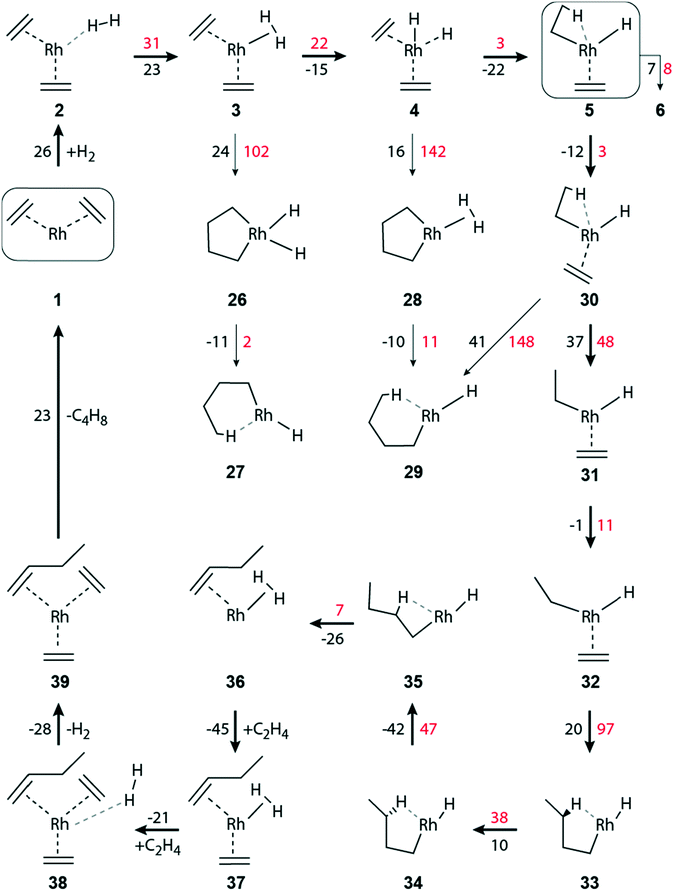
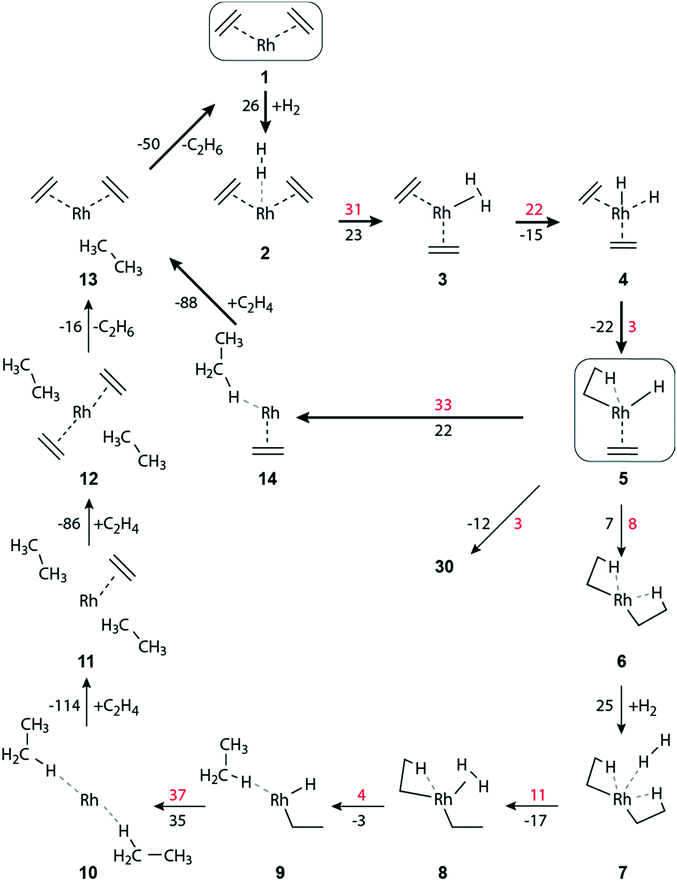 | ||
| Fig. 2 Schematic representation of the hydrogenation of ethene to ethane on a zeolite-supported [Rh(C2H4)2]+ complex. Reaction free energies and activation free energies (in kJ mol−1) of individual steps are given as black and red values, respectively. Bold arrows indicate the preferred pathway. The zeolite framework, including the two zeolite oxygen centers at the adsorption site of the Rh complex, are omitted for clarity. The main dimerization pathway in the presence of hydrogen starts with step 5 → 30; see Fig. 3. | ||
When the distance between H2 and the Rh center decreases significantly, complex 3 is formed, exhibiting an η2-H2 ligand in axial position (Table S4 of the ESI‡). Structure 3 is by 23 kJ mol−1 less stable than complex 2 (Fig. 2). In 3, one of the ethene ligands is displaced from its equatorial position. Due to this distortion, 3 exhibits a pseudo trigonal bipyramidal geometry. The activation free energy of the transformation 2 → 3 is 31 kJ mol−1, Fig. 2. The product 3 is ∼8 kJ mol−1 lower in energy than the transition state (TS) 2–3, Table S4 of the ESI.‡
H2 activation by transition metal complexes via formation of a short-lived η2-H2σ complex, such as 3, is well known.51–53 Intermediate 3 undergoes oxidative addition of H2, forming the cis-dihydride complex 4; ΔGa(3 → 4) = 22 kJ mol−1, ΔGr(3 → 4) = −15 kJ mol−1 (Fig. 2). In the structure TS 3–4, the distance H1–H2 = 98 pm is elongated by 15 pm compared to 3, and correspondingly the distances Rh–H1/H2 are shortened by 16 pm to 169/164 pm, Table S4 of the ESI.‡
The formation, 5 → 6, of the di-ethyl complex requires a reaction free energy of 7 kJ mol−1 and the final state 6 is accessed after overcoming an activation barrier of ΔGa(5 → 6) = 8 kJ mol−1, Fig. 2. The resulting di-ethyl complex 6 also exhibits a pseudo octahedral structure, just as complex 5. Both ethyl ligands of 6 undergo an agostic interaction with the Rh center (Table S4 of the ESI‡). Due to the trans effect, the agostic interaction of the β-H occupying the equatorial position trans to the zeolite oxygen binds tighter (Rh–H2 = 167 pm, C4–H2 = 130 pm; Table S4 of the ESI‡) than the β-H in axial position (Rh–H1 = 205 pm, C1–H1 = 115 pm).
The barriers of ethene hydrogenation, 4 → 5 and 5 → 6, are calculated very low, 3 kJ mol−1 and 8 kJ mol−1. Therefore, one expects the intermediates 4 and 5, with H ligands bound to the metal center, to be very short-lived, forming the di-ethyl complex 6 essentially instantaneously via a second migratory insertion of ethene into the remaining Rh–H bond.
Intermediate 5 plays a key role in the overall reaction network because, formally, the reaction path branches here in a three-way fashion, Fig. 2 and 3. Besides forming the di-ethyl complex 6 as just discussed, either the reductive elimination 5 → 14 of ethane may occur, or the transformation 5 → 30 that initiates the pathway to C–C coupling (Fig. 3). Next, we will discuss the reductive elimination 5 → 14, then the elimination of ethane via the di-ethyl intermediate 6, before we will address C–C coupling further below.
The initial complex 1 can be regenerated from 14, by introducing one molecule of ethene, ΔGr(14 → 13) = −88 kJ mol−1, followed by the somewhat less exergonic elimination of ethane, ΔGr(13 → 1) = −50 kJ mol−1, Fig. 2.
The oxidative addition of the η2-H2 ligand of 8 to form a cis-dihydride species [Rh(H)2(C2H5)2]+ is highly improbable, as it would result in an octahedral 16-electron Rh(V) complex, of which only very few have been found.54 Moreover, attempts of optimizing such a cis-dihydride structure always resulted in 9, i.e., the direct hydrogenation of an ethyl ligand.
In the reductive elimination 9 → 10, a second ethane molecule is formed, with ΔGr(9 → 10) = 35 kJ mol−1 (Fig. 2). The calculated barrier, ΔGa(9 → 10) = 37 kJ mol−1, of this elimination is similar to that obtained for reaction 5 → 14, 33 kJ mol−1, where ethene is an additional ligand on the metal center. However, in absolute terms ΔGa(9 → 10) is higher by 15 kJ mol−1 than the competing barrier ΔGa(5 → 14), Fig. 2 and Table S3 of ESI.‡ Ethane formation via8 → 9 is thermodynamically more favorable than the analogous steps 5 → 14 and 9 → 10, Fig. 2. Note that the latter two processes represent reductive elimination steps Rh(III) → Rh(I), but in 8 → 9 the metal center remains in the oxidation state III, due to the presence of an ethyl and a hydride ligand.
The initial [Rh(C2H4)2]+ complex 1 can be regenerated from 10 in two stages, where two incoming ethene molecules are exchanged for the leaving ethane units. The consecutive attachment steps 10 → 11 and 11 → 12 of an ethene each are both calculated to be quite exergonic, −114 kJ mol−1 and −86 kJ mol−1, respectively (Fig. 2). The reaction energy of the second addition is very similar to the value calculated for the analogous ethene attachment step 14 → 13. On the other hand, the consecutive adsorption reactions of two ethene molecules on a bare Rh+ attached to the zeolite framework are calculated notably more exergonic, −157 kJ mol−1 and −178 kJ mol−1, respectively.
Finally, the catalyst complex 1 is regenerated after subsequent elimination steps via ΔGr(12 → 13) = −16 kJ mol−1, and ΔGr(13 → 1) = −50 kJ mol−1 (Fig. 2).
In the absence of ethene in the feed, after the elimination of the hydrogenation product ethane, the bare Rh+ cation will remain anchored at zeolite oxygen centers. Such bare Rh+ species might diffuse in the zeolite pores and agglomerate to form Rh metal clusters.14–16
Ethene dimerization in the supported complex Rh(C2H4)2
Next, we explored the dimerization of ethene in the faujasite-supported complex [Rh(C2H4)2]+1 to understand pertinent experimental findings.13,14 In fact, the dimerization product n-butene was not observed for exclusive H2 feed, but it appeared as major product when the feed contained the mixture C2H4 + H2. We refrained from modeling reaction steps involving directly the zeolite wall, e.g. via a second acidic center.14,55 Before addressing the particulars of the dimerization steps after adsorption of H2, we first briefly discuss dimerization pathways in the absence of additional hydrogen.The oxidative C–C coupling of the two ethene ligands, π-bonded to the Rh(I) center, to form the metallo-cyclopentane species 15 (Fig. 4) is extremely endergonic, ΔGr(1 → 15) = 127 kJ mol−1, with a rather high activation barrier ΔGa(1 → 15) = 150 kJ mol−1. Complex 15 may undergo H abstraction by the metal to produce complex 22, Fig. 4. We were not able to locate a transition state for this step; even a displacement of 20 pm away from 15 lead to the much more stable species 22; see section S2 of the ESI.‡ We expect the barrier to be negligible and very much like structure 15. Below, we will discuss the elimination of the product via formation of complex 22.
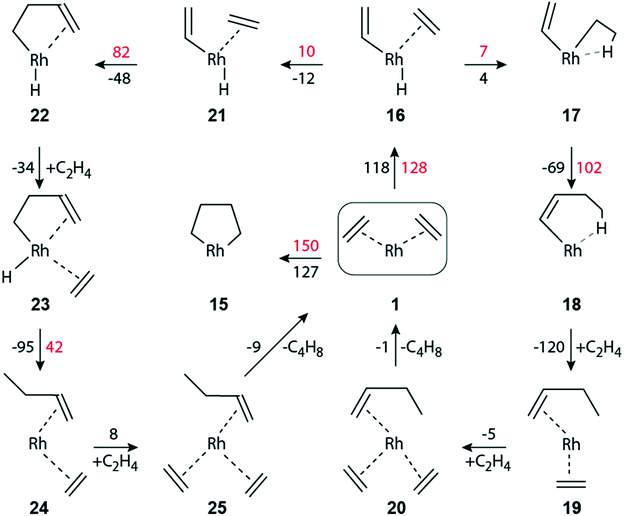 | ||
| Fig. 4 Schematic representation of the dimerization of ethene to 1-butene on a zeolite-supported [Rh(C2H4)2]+ complex in the absence of hydrogen. Same lay-out as Fig. 2. | ||
Ethene dimerization over a Ga+-ZSM-5 zeolite was calculated26 to be highly exothermic, Er = −93 kJ mol−1 for the C–C coupling step, if the reaction proceeds via a direct proton transfer from one π-adsorbed ethene on Ga+ to the other ethene, resulting in a complex with vinyl and ethyl ligands. That step occurs via an activation energy Ea of 141 kJ mol−1. For the subsequent C–C coupling between vinyl and the other adsorbed ethene, an even higher activation energy has to be overcome, Ea = 170 kJ mol−1.26 We were unable to locate a similar proton transfer that would lead to a [Rh(C2H5)(C2H3)]+ complex, i.e., with ethyl and vinyl ligands.
A Rh(III) complex with ethyl and vinyl can be formed by prior H abstraction 1 → 16 by Rh from one ethene, forming the hydride–vinyl complex [Rh(C2H4)(H)(C2H3)]+16, and subsequent addition 16 → 17 of the H ligand to the other ethene (Fig. 4). Step 1 → 16 is highly endergonic, ΔGr(1 → 16) = 118 kJ mol−1, ΔGa(1 → 16) = 128 kJ mol−1 (Fig. 4). For the subsequent addition 16 → 17 of the H ligand we calculated ΔGr(16 → 17) = 4 kJ mol−1 and ΔGa(16 → 17) = 7 kJ mol−1. The C–C coupling of vinyl and ethyl to form a butene ligand is exergonic, ΔGr(17 → 18) = −69 kJ mol−1 with a notable barrier, ΔGa(17 → 18) = 102 kJ mol−1.
Like on the path to the hydrogenation of ethene, the initial [Rh(C2H4)2]+ complex can be regenerated by introducing two molecules of ethene, 18 → 19 and 19 → 20 (Fig. 4). The adsorption steps were calculated exergonic, −120 kJ mol−1 and −5 kJ mol−1, respectively. The catalytic cycle is closed via a thermoneutral product elimination, ΔGr(20 → 1) = −1 kJ mol−1 (Fig. 4).
Another path for C–C coupling without participation of H2 also starts from the high-lying intermediate 16, producing complex 21via an easy rotation of ethene (Fig. 4). The C–C coupling 21 → 22 between vinyl and ethene, forming a butylene moiety, is by 21 kJ mol−1 less exergonic than the C–C coupling 17 → 18. Yet, the corresponding barrier, ΔGa(21 → 22) = 82 kJ mol−1, is by 20 kJ mol−1 lower than ΔGa(17 → 18) (Fig. 4). The product butene is finally eliminated, ΔGr(25 → 1) = −9 kJ mol−1, after facile ethene adsorption and ligand rearrangement steps, 22 → 23 → 24 → 25. Details of these dimerization pathways without H2 feed are given in the ESI.‡
The activation of H2 and the oxidative C–C coupling occur synchronously in reaction 3 → 26. The reaction is endergonic, ΔGr(3 → 26) = 24 kJ mol−1, and requires overcoming a moderately high activation barrier, ΔGa(3 → 26) = 102 kJ mol−1 (Fig. 3). The concurrent C–C bond formation and the H–H bond activation in TS 3–26 are confirmed by the reduced C–C separation between the two C2H4 ligands, from 299 pm to 206 pm, and the elongation of H–H from 83 pm to 90 pm, Table S4 of the ESI.‡ Subsequently, butyl forms instantaneously as this exergonic conversion, ΔGr(26 → 27) = −11 kJ mol−1, is essentially without barrier, ΔGa(26 → 27) = 2 kJ mol−1 (Fig. 3).
Besides forming ethyl 4 → 5 (described above), the metal-dihydride species 4 can undergo oxidative C–C coupling, 4 → 28. This step is slightly endergonic, by 16 kJ mol−1. However, the activation barrier of concurrent C–C and H–H bond formation is rather high, ΔGa(4 → 28) = 142 kJ mol−1 (Fig. 3). The subsequent formation of butyl, 28 → 29, through concurrent hydrogen activation and ring opening is induced by a hydride shift from the metal to the metallacyclopentane moiety. Similar as in step 26 → 27, it occurs rather easily: ΔGr(28 → 29) = −10 kJ mol−1, ΔGa(28 → 29) = 11 kJ mol−1 (Fig. 3).
A high barrier encountered early on a pathway can be taken to indicate that this branch will not contribute to the reaction network as a whole. In such a case, we refrained from tracing such dimerization branches until the release of the product butene. As example, we mention the branches with the calculated high barriers of the rate-limiting C–C coupling steps 3 → 26 and 4 → 28. We will discuss the comparative overall energetics below in the final section.
Complex 29 can also be reached by C–C coupling in 30via ethene insertion into the Rh–C(ethyl) bond. Complex 30 is a slightly more stable isomer of 5, ΔGr(5 → 30) = −12 kJ mol−1, that is very easily reached, ΔGa(5 → 30) = 3 kJ mol−1 (Fig. 3). After a rotation of the ethene ligand in 5, the C2–C3 distance in 30 between the carbon atoms of the ethyl and the ethene ligands is reduced, from 309 pm to 275 pm (Table S4 of the ESI‡). The C–C coupling step to form 29 is endergonic, ΔGr(30 → 29) = 41 kJ mol−1, via a substantial barrier, ΔGa(30 → 29) = 148 kJ mol−1.
Another change in the ligand conformation, namely a rotation of the ethyl moiety, leads from 30 to its rotamer 31. While 30 shows a pseudo octahedral geometry, 31 features a square-pyramidal structure. In 30, the ethyl moiety displays a β-agostic interaction (Rh–H1 = 190 pm, C1–H1 = 117 pm, Rh–C1 = 236 pm, Rh–C2–C1 = 82°) whereas ethyl in 31 is turned away from the metal center (Rh–C1 = 312 pm, Rh–C2–C1 = 124°, Table S4 of the ESI‡). The rotation of the ethyl ligand is endergonic, ΔGr(30 → 31) = 37 kJ mol−1, and has to overcome a moderate barrier, ΔGa(30 → 31) = 48 kJ mol−1 (Fig. 3). A further isomer, 32, is hardly more stable, by 1 kJ mol−1, and reachable via a small rotational barrier, ΔGa(31 → 32) = 11 kJ mol−1. From there, C–C coupling occurs via ethene insertion into a Rh–C(ethyl) bond. That step is slightly endergonic, ΔGr(32 → 33) = 20 kJ mol−1, but has a notable activation barrier, ΔGa(32 → 33) = 97 kJ mol−1 (Fig. 3).
The butyl complexes 29 and 33 are also rotational isomers, both showing a square-pyramidal structure with an agostic interaction in equatorial position. In 29, it is through δ-H of the butyl ligand (Rh–C1 = 238 pm, Rh-δ-H1 = 172 pm, C1-δ-H1 = 120 pm, Table S4 of the ESI‡), whereas the agostic interaction in 33 occurs via γ-H (Rh–C2 = 235 pm, Rh-γ-H3 = 173 pm, C2-γ-H3 = 120 pm, Table S4 of the ESI‡). The barrier of C–C coupling in the step 32 → 33 is calculated by 51 kJ mol−1 lower than in the step 30 → 29 (Fig. 3). The structural constraints imposed in TS 30–29 by the agostic interaction could be the reason for this kinetic disadvantage.
The path to the product butene continues from 33via two rotamer intermediates. The first one, complex 34, is by 10 kJ mol−1 less stable than complex 33; it is formed after overcoming a barrier of 38 kJ mol−1, by a rotation of the C3–C4 bond within the trans-butyl ligand. In 34 the interacting γ-H center of the CH2 fragment is changed. In this way, the distance Rh-γ-H4 is reduced from 266 pm to 174 pm while simultaneously the distance Rh-γ-H3 has increased from 173 pm to 281 pm (Table S4 of the ESI‡). In the next step 34 → 35, the rotation occurs around the C2–C3 bond. After overcoming a rotation barrier of 47 kJ mol−1, intermediate 35 is reached, with ΔGr(34 → 35) = −42 kJ mol−1 (Fig. 3).
The crucial step, β-H abstraction 35 → 36 by the metal, results in a Rh(η2-H2)(C4H8) complex where the C–C double bond of the product butene is π-coordinated at the Rh center. A rather low activation barrier, ΔGa(35 → 36) = 7 kJ mol−1, was calculated for this slightly exergonic reaction, ΔGr(35 → 36) = −26 kJ mol−1.
The initial complex 1 can be regenerated from 36 by introducing two units of ethene, followed by the elimination of a hydrogen molecule and a butene molecule. For attaching the first ethene ligand one calculates ΔGr(36 → 37) = −45 kJ mol−1 (Fig. 3). In a slightly exergonic step, ΔGr(37 → 38) = −21 kJ mol−1, a second ethene molecule binds at the Rh center and H2 remains only loosely bound. The elimination of the H2 moiety is also exergonic, ΔGr(38 → 39) = −28 kJ mol−1. Ultimately, the elimination of butene is moderately endergonic, ΔGr(39 → 1) = 23 kJ mol−1, and one regains the initial Rh(I) di-ethene complex 1 (Fig. 3).
Discussion and conclusions
Table 1 collects the highest barriers of the various hydrogenation and dimerization pathways studied. For each of these two sets of pathways, Fig. 5 compares the free energy profiles with the lowest overall activation energy relative to the zeolite-supported [Rh(C2H4)2]+ complex 1. Alternative free energy profiles for the dimerization of ethene, both without and with preceding hydrogenation, are summarized in Fig. S4 and S5 of the ESI,‡ respectively. At the end of the catalytic cycles, one arrives at the reaction free energies for the overall transformations studied, Fig. 5, the hydrogenation and the dimerization of ethene in the gas phase. Both reactions are calculated to be exergonic, with overall reaction free energies ΔGr = −105 kJ mol−1 and ΔGr = −73 kJ mol−1, respectively. These values are somewhat lower than those experimentally determined, 136 kJ mol−1 for the formation of ethane56 and 105 kJ mol−1 for the formation of 1-butene.57| Reaction path | TSb | ΔGab | ||
|---|---|---|---|---|
| a Difference of the energies of the highest lying TS structure along the reaction path considered and the initial complex; from data of Table S3 of the ESI. b Transition state structure with the highest free energy along the path considered and the corresponding ΔG value relative to complex 1. c See Fig. 2. d Transition state structure of the highest free energy along the sub-path considered and the corresponding ΔG value relative to complex 5. e See Fig. 3. f See Fig. 4. g Only an approximate structure of TS 15–22 is available, but that structure clearly is the one with the highest free energy value on this pathway. | ||||
| Hydrogenationc | 1–5–6–13 | 3–4 | 71.1 | |
| 5–6–13 | 9–10 | 48.2 | ||
| 1–5–14–13 | 3–4 | 71.1 | ||
| 5–14–13 | 5–14 | 33.2 | ||
| Dimerization | H2 presente | 1–3–26–27 | 3–26 | 151.8 |
| 1–4–28–29 | 4–28 | 176.5 | ||
| 1–5–30–39 | 32–33 | 133.3 | ||
| H2 absentf | 1–15 | 1–15 | 150.1 | |
| 1–16–17–20 | 17–18 | 224.0 | ||
| 1–16–21–25 | 21–22 | 187.5 | ||
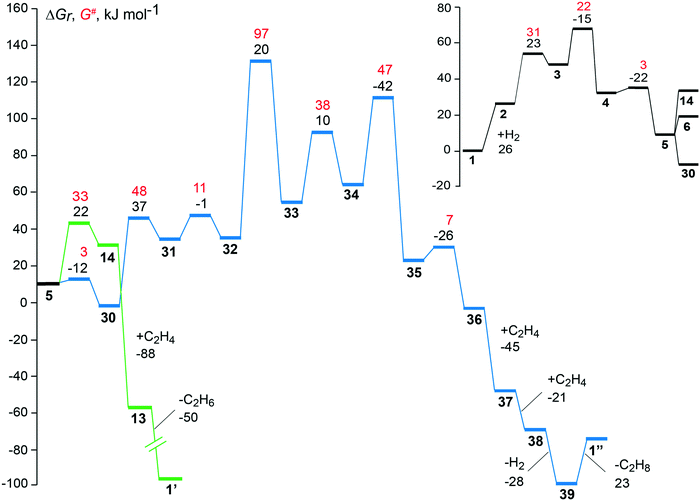 | ||
| Fig. 5 Free energy profiles of the preferred pathways to the hydrogenation (green) and the dimerization (blue) of ethene over the faujasite-supported complex [Rh(C2H4)2]+. Reaction free energies and activation free energies of individual steps are given as black and red values, respectively. The inset in the upper right-hand corner provides the common part of the two reaction pathways, from the initial state 1 to intermediate 5; see Fig. 2 and 3. The regeneration of the catalyst complexes 1′ and 1′′, after desorption of the products 1-butene and one ethane molecule from the intermediates 39 and 13, is associated with overall free energy changes of −72 kJ mol−1 and −104 kJ mol−1, respectively. | ||
Two hydrogenation pathways were found plausible on the supported [Rh(C2H4)2]+ complex. The product of hydrogenation, ethane, may be obtained directly from the monoethyl species 5 through reductive elimination or via the di-ethyl complex 6. Fig. S6 of the ESI‡ compares the energy profiles of these two pathways. The absolute activation energy of hydrogenation is calculated at 71 kJ mol−1 where the highest point of the profile is the transition state 3–4 for the oxidative addition of a hydrogen molecule to the metal center. Both hydrogenation pathways are identical until the key complex 5 with one ethene and one ethyl ligand that exhibits an agostic interaction with the metal. After that intermediate, the highest point of the di-ethyl path 1–5–6–13 is the transition state of the step 9 → 10, the reductive elimination of the second ethane molecule. The analogous overall barrier of the monoethyl path 1–5–14–13, i.e. TS 5–14, is by 15 kJ mol−1 lower (Fig. S6 of the ESI‡).
The dimerization of ethene was studied with and without prior hydrogenation. Dimerization pathways in the absence of H2 were calculated to have higher absolute activation energies than the lowest-lying C–C coupling path with H2, via32–33 where one finds the absolute barrier at 133 kJ mol−1 (Table 1). The lowest absolute free energy barrier for the dimerization without H2, 150 kJ mol−1 was calculated for the oxidative addition of the two ethene ligands, 1 → 15, to form a metallacycle (Fig. S4 of the ESI‡). The highest calculated absolute barrier, 224 kJ mol−1, is on the path involving C–C coupling through insertion of ethene into a Rh–C(ethyl) bond 17 → 18 in the absence of hydrogen. The high absolute barrier is related to the strongly endergonic H abstraction step that precedes the C–C formation (Fig. S4 of the ESI‡). The two alternative pathways on the hydrogenated Rh complex involving intermediates 27 and 29 have absolute free energy barriers that are higher by 18 kJ mol−1 and 43 kJ mol−1, compared to the dimerization path in the presence of hydrogen with lowest absolute activation barrier 1–5–30–39 (Table 1).
It is worthwhile to compare the present results with known C–C formation mechanisms of other catalysts. The dimerization of ethene to butene is a well-studied topic where various catalysts have been used, e.g. complexes of Ti, Ni, Al, Ta, W, Pd, Ru, V, Mn, Fe, Co, and Cr.3,58 For Rh the complex RhCl3 was discussed early on as catalyst, which leads to an insertion of ethene into a Rh–C bond, similarly as determined in this work.3 In solution protons have been discussed3 as source for transforming one ethene ligand at the complex to ethyl, which is subsequently regenerated by β-hydrogen elimination of butyl to form the final product butene. The present results regarding ethene dimerization also show some similarity to those of recent DFT studies on the mechanism of ethylene oligomerization over a Ni metal center anchored in a H-SSZ-24 type zeolite framework.59 Using periodic models, the mechanism that includes the formation of metallacycle was shown to be the least favorable one, with a high activation energy, 115 kJ mol−1, for the oxidative C–C coupling.59 In contrast, the insertion of ethene into the Ni–C(alkyl) bond has the lowest activation energy, 68 kJ mol−1, and is the preferred path to C–C bond formation.59 In the present work, we also find the dimerization via pathways with oxidative addition 1–15, 1–3–26–27, and 1–4–28–29via a metallacycle to be disfavored by at least 17 kJ mol−1 in the absolute activation energy, as compared to the insertion pathway 1–5–30–39, see below.
The dimerization path with lowest calculated absolute free activation barrier (Table 1) on the zeolite-supported [Rh(C2H4)2]+ complex starts with the addition of a hydrogen molecule and follows the same intermediates for the first five steps as the hydrogenation path until the key intermediate 5, Fig. 5. The highest absolute barrier is calculated for the transition state of the C–C formation step, ΔGa(32 → 33) = 97 kJ mol−1, which is by 62 kJ mol−1 higher in free energy than the highest point on the lowest-lying hydrogenation path. The large energy separation of the two reaction pathways (Fig. 5) clearly shows that on the experimentally suggested supported [Rh(C2H4)2]+ complex the hydrogenation to ethane will be preferred over the dimerization to butene. This result is in good agreement with EXAFS data which show the formation of ethyl species on the supported Rh catalyst when a mixture of ethene and H2 was flowing.9,14 Earlier studies also reported that Rh(I) and Rh(III) species, supported in Y zeolite, catalyze predominantly the hydrogenation of ethene.60
In this study we focused on the catalyst as suggested from experiment,9 faujasite and [Rh(C2H4)2]+, to probe the reactivity of the single-site anchored catalyst particle present in the zeolite. The favorable adsorption site of a [Rh(C2H4)2]+ species on a faujasite zeolite is the 12-member ring window of the supercage where the complex binds in a bidentate fashion. The absolute activation free energy determined for the C–H bond formation, 71 kJ mol−1, on this adsorption complex is just about half as much as the lowest absolute activation free energy calculated for the C–C bond formation (Table 1). Therefore, such a complex will promote the hydrogenation of ethene when hydrogen is present in the feed. The results of this study agree with the experimental observation that a faujasite-supported [Rh(C2H4)2]+ complex, when treated with H2, catalyzes the hydrogenation of ethene to ethane as the predominant product.9
The present computational study, starting from a well characterized zeolite-supported single-site Rh catalyst, demonstrated the overall complexity of the underlying mechanism. Yet, further studies are needed to understand the factors that favor the C–C bond formation observed in the experiment for certain reaction conditions.
Computational
For the plane-wave electronic structure calculations, we employed the Vienna Ab Initio Simulation Package (VASP 5.2.12).61,62 The electron–ion interactions were described using the projector augmented wave (PAW) formalism.63,64 We applied the generalized gradient approximation (GGA)28 as suggested by Perdew, Burke and Ernzerhof (PBE).29,30Structures were optimized with the conjugate-gradient algorithm; in a few cases, we accelerated the convergence with the help of the quasi-Newton algorithm.52 An optimization was considered converged when the force acting on each atom was below 0.01 eV Å−1. The convergence criterion for the self-consistent field (SCF) procedure was set to 10−7 eV. The cut-off energy of the plane-wave basis set was chosen to be 800 eV for the optimization of the unit cell34 and 400 eV for structure relaxations for a fixed unit cell. The unit cell optimization was repeated until the energy of the system was converged. The Brillouin zone was sampled at the Γ point only. We invoked a Gaussian level broadening (0.01 eV) and extrapolated the energies to zero broadening.65
For determining approximate transition state structures, we applied the nudged elastic band method.66 The resulting structures were refined by the dimer method.67 For all stationary points we carried out a normal-mode analysis on the metal complex, anchored on a 5 T cluster model of the zeolite wall (Fig. S7 of the ESI‡), as used in a previous QM/MM study.18 The Hessian of this reduced model was constructed by displacing all atoms by 0.002 Å in each Cartesian direction. The remainder of the zeolite framework was kept fixed. All but four TS structures showed a single imaginary frequency. Those four TS structures 8–9, 33–34, 34–35, 35–36 exhibit in addition a small imaginary frequency of at most 50i cm−1, due to a hindered translational movement of the supported complex. Modes with such a small imaginary frequency, corresponding to a hindered translation of the metal complex, were also obtained for five intermediate structures. Even with tightened convergence criteria (10−8 eV for SCF, 0.005 eV Å−1 for forces on each atom), these small imaginary frequencies persisted while there was hardly any change in the geometries and the energetics, <1 kJ mol−1. For the free energy calculations, we replaced these small imaginary frequencies by 50 cm−1.68 When applied to hydrocarbons physisorbed and chemisorbed in H-FAU, this procedure was reported to give more consistent results than the strategy where the imaginary modes are neglected.68
The reported Gibbs free energies were calculated in standard fashion.69 The entropy values of the zeolite-supported Rh complexes and the various transition states were calculated in the harmonic approximation. The Gibbs free energy of the molecules in the gas phase was derived using the ideal gas approximation including rotational and translation contributions to the entropy term. All values are obtained for 303 K and 1 atm to represent the experimental conditions.13
Overall the present study on periodic models of 157–173 atoms per unit cell required the determination of 66 stationary structures, 27 of which represented transition states.
Acknowledgements
We acknowledge generous computing resources provided by the A*STAR Computational Resource Centre (A*CRC).References
- B. R. James, Adv. Organomet. Chem., 1979, 17, 319–405 CrossRef CAS.
- T. Dwars and G. Oehme, Adv. Synth. Catal., 2002, 344, 239–260 CrossRef CAS.
- S. M. Pillai, M. Ravindranathan and S. Sivaram, Chem. Rev., 1986, 86, 353–399 CrossRef CAS.
- V. Ritleng, C. Sirlin and M. Pfeffer, Chem. Rev., 2002, 102, 1731–1770 CrossRef CAS PubMed.
- S. Mecking, Angew. Chem., Int. Ed., 2001, 40, 534–540 CrossRef CAS.
- K. Fagnou and M. Lautens, Chem. Rev., 2003, 103, 169–196 CrossRef CAS PubMed.
- P. A. Evans, Modern rhodium-catalyzed organic reactions, Wiley-VCH Verlag, Weinheim, 2005 Search PubMed.
- J. Guzman and B. C. Gates, Dalton Trans., 2003, 3303–3318 RSC.
- A. J. Liang, V. A. Bhirud, J. O. Ehresmann, P. W. Kletnieks, J. F. Haw and B. C. Gates, J. Phys. Chem. B, 2005, 109, 24236–24243 CrossRef CAS PubMed.
- A. J. Liang, R. Craciun, M. Chen, T. G. Kelly, P. W. Kletnieks, J. F. Haw, D. A. Dixon and B. C. Gates, J. Am. Chem. Soc., 2009, 131, 8460–8473 CrossRef CAS PubMed.
- D. E. Resasco, B. Wang and S. Crossley, Catal. Sci. Technol., 2016, 6, 2543–2559 CAS.
- S. Abate, K. Barbera, G. Centi, P. Lanzafame and S. Perathoner, Catal. Sci. Technol., 2016, 6, 2485–2501 CAS.
- P. Serna and B. C. Gates, J. Am. Chem. Soc., 2011, 133, 4714–4717 CrossRef CAS PubMed.
- P. Serna and B. C. Gates, Angew. Chem., 2011, 123, 5642–5645 CrossRef.
- A. J. Liang and B. C. Gates, J. Phys. Chem. C, 2008, 112, 18039–18049 CAS.
- P. Serna and B. C. Gates, J. Catal., 2013, 308, 201–212 CrossRef CAS.
- P. W. Kletnieks, A. J. Liang, R. Craciun, J. O. Ehresmann, D. M. Marcus, V. A. Bhirud, M. M. Klaric, M. J. Hayman, D. R. Guenther, O. P. Bagatchenko, D. A. Dixon, B. C. Gates and J. F. Haw, Chem. – Eur. J., 2007, 13, 7294–7304 CrossRef CAS PubMed.
- S. Dinda, A. Govindasamy, A. Genest and N. Rösch, J. Phys. Chem. C, 2014, 118, 25077–25088 CAS.
- V. K. Markova, G. N. Vayssilov and N. Rösch, J. Phys. Chem. C, 2015, 119, 1121–1129 CAS.
- V. K. Markova, G. N. Vayssilov, A. Genest and N. Rösch, Catal. Sci. Technol., 2015, 6, 1726–1736 Search PubMed.
- S. Namuangruk, P. Pantu and J. Limtrakul, ChemPhysChem, 2005, 6, 1333–1339 CrossRef CAS PubMed.
- Y. Chu, B. Han, A. Zheng and F. Deng, J. Phys. Chem. C, 2012, 116, 12687–12695 CAS.
- A. Hu, K. M. Neyman, M. Staufer, T. Belling, B. C. Gates and N. Rösch, J. Am. Chem. Soc., 1999, 121, 4522–4523 CrossRef CAS.
- J. M. Thomas, Design and Applications of the Single-Site Heterogeneous Catalysts. Contributions to Green Chemistry, Clean Technology and Sustainability, World Scientific Press, Singapore, 2012 Search PubMed.
- T. Maihom, P. Khongpracha, J. Sirijaraensre and J. Limtrakul, ChemPhysChem, 2013, 14, 101–107 CrossRef CAS PubMed.
- E. A. Pidko, E. J. Hensen and R. A. van Santen, J. Phys. Chem. C, 2008, 112, 19604–19611 CAS.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891–891 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- C. M. Nguyen, M. F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2010, 12, 9481–9493 RSC.
- J. Van der Mynsbrugge, K. Hemelsoet, M. Vandichel, M. Waroquier and V. Van Speybroeck, J. Phys. Chem. C, 2012, 116, 5499–5508 CAS.
- C.-c. Chiu, G. N. Vayssilov, A. Genest, A. Borgna and N. Rösch, J. Comput. Chem., 2014, 35, 809–819 CrossRef CAS PubMed.
- D. Olson and E. Dempsey, J. Catal., 1969, 13, 221–231 CrossRef CAS.
- N. Y. Chen, W. E. Garwood and F. G. Dwyer, Shape selective catalysis in industrial applications, Marcel Dekker, Inc., New York, 1996 Search PubMed.
- M. Boronat, C. M. Zicovich-Wilson, A. Corma and P. Viruela, Phys. Chem. Chem. Phys., 1999, 1, 537–543 RSC.
- C. Otero Arean, D. Nachtigallova, P. Nachtigall, E. Garrone and M. Rodriguez Delgado, Phys. Chem. Chem. Phys., 2007, 9, 1421–1437 RSC.
- D. Lesthaeghe, B. De Sterck, V. Van Speybroeck, G. B. Marin and M. Waroquier, Angew. Chem., Int. Ed., 2007, 46, 1311–1314 CrossRef CAS PubMed.
- G. J. Kramer and R. Van Santen, J. Am. Chem. Soc., 1993, 115, 2887–2897 CrossRef CAS.
- G. Sastre, N. Katada, K. Suzuki and M. Niwa, J. Phys. Chem. C, 2008, 112, 19293–19301 CAS.
- C. Stampfl, W. Mannstadt, R. Asahi and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 155106 CrossRef.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104 CrossRef.
- L. Schimka, R. Gaudoin, J. Klimeš, M. Marsman and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214102 CrossRef.
- P. Ugliengo, B. Civalleri, C. M. Zicovich-Wilson and R. Dovesi, Chem. Phys. Lett., 2000, 318, 247–255 CrossRef CAS.
- C. Baerlocher, L. B. McCusker and D. H. Olson, Atlas of zeolite framework types, Elsevier, 2007, http://www.iza-structure.org/databases Search PubMed.
- A. H. de Vries, P. Sherwood, S. J. Collins, A. M. Rigby, M. Rigutto and G. J. Kramer, J. Phys. Chem. B, 1999, 103, 6133–6141 CrossRef CAS.
- I. Ogino and B. C. Gates, Chem. – Eur. J., 2009, 15, 6827–6837 CrossRef CAS PubMed.
- S. S. Laletina, A. M. Shora, E. A. Shor, V. A. Nasluzov and A. I. Rubaylo, Journal of Siberian Federal University "Chemistry", 2008, vol. 1, pp. 190–199 Search PubMed.
- R. H. Crabtree, The organometallic chemistry of the transition metals, John Wiley & Sons, Hoboken, New Jersey, 2009 Search PubMed.
- J. Y. Saillard and R. Hoffmann, J. Am. Chem. Soc., 1984, 106, 2006–2026 CrossRef CAS.
- G. J. Kubas, J. Organomet. Chem., 2001, 635, 37–68 CrossRef CAS.
- X. Yuan, S. Bi, Y. Ding, L. Liu and M. Sun, J. Organomet. Chem., 2010, 695, 1576–1582 CrossRef CAS.
- P. W. Atkins, T. Overton, J. P. Rourke, M. Weller and F. A. Armstrong, Shriver & Atkins' inorganic chemistry, Oxford University Press, Oxford, 2010 Search PubMed.
- S. Dinda, A. Genest and N. Rösch, unpublished results. Using embedded cluster models, C–C bond formation barriers of steps involving ethene molecules at the zeolite wall or a second acidic center were calculated at least by 30 kJ mol−1 higher than the lowest barriers reported here.
- F. D. Rossini, J. Res. Natl. Bur. Stand., 1963, 17, 629–638 CrossRef.
- E. J. Prosen, F. W. Maron and F. D. Rossini, J. Res. Natl. Bur. Stand., 1951, 46, 106–112 CrossRef CAS.
- A. M. Al-Jarallah, J. A. Anabtawi, M. A. B. Siddiqui, A. M. Aitani and A. W. Al-Sa'doun, Catal. Today, 1992, 14, 1–121 CrossRef.
- R. Y. Brogaard and U. Olsbye, ACS Catal., 2016, 6, 1205–1214 CrossRef CAS.
- Y. Okamoto, N. Ishida, T. Imanaka and S. Teranishi, J. Catal., 1979, 58, 82–94 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- C. L. Fu and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 5480–5486 CrossRef CAS.
- H. Jonsson, G. Mills and K. W. Jacobsen, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. J. Berne, G. Ciccotti and D. F. Coker, World Scientific, Lerici, Italy, 1998 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- B. A. De Moor, M.-F. Reyniers and G. B. Marin, Phys. Chem. Chem. Phys., 2009, 11, 2939–2958 RSC.
- D. A. McQuarrie and J. D. Simon, Molecular thermodynamics, University Science Books, Sausalito, California, 1999 Search PubMed.
Footnotes |
| † To Bruce C. Gates, University of California at Davis, for delivering insight into single-site catalysts via detailed structural and kinetic studies which lead him to formulating mechanistic hypotheses that, time and again, challenged computational research. |
| ‡ Electronic supplementary information (ESI) available: Information on the location of the di-ethlylene Rh(I) complex in the faujasite framework, alternative pathways for the dimerization of ethene in the [Rh(C2H4)2]+ complex; free energy profiles of alternative pathways for ethene hydrogenation over a di-ethene Rh(I) complex; total energies, relative energies and free energies of reactants, transition structures, and products; calculated structural parameters of reactants, transition states and products; representation of the 5 T cluster model used for the normal-mode analysis. Cartesian coordinates of pertinent stationary structures. See DOI: 10.1039/c6cy02147f |
| § Both authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2017 |