CO oxidation on Rh-doped hexadecagold clusters†
Jin-Xun
Liu‡
a,
Zhiling
Liu‡
b,
Ivo A. W.
Filot
a,
Yaqiong
Su
a,
Ionut
Tranca
a and
Emiel J. M.
Hensen
*a
aInorganic Materials Chemistry, Department of Chemistry and Chemical Engineering, Eindhoven University of Technology, Eindhoven, 5600 MB, Netherlands. E-mail: e.j.m.hensen@tue.nl
bSchool of Chemistry & Material Science, Shanxi Normal University, Linfen, 041004, P. R. China
First published on 29th November 2016
Abstract
Exploring the unique catalytic properties of gold clusters associated with specific nano-architectures is essential for designing improved catalysts with a high mass-specific activity. We investigate the geometric and electronic structure of hexadecagold clusters in which Rh was doped. Density functional theory calculations demonstrate that the resulting neutral and negatively charged Rh-doped Au16 clusters are stable and bind CO and O2 stronger than Au16. Consequently, activation barriers for CO oxidation are lowered. Microkinetics simulations predict especially negatively charged Rh-doped Au16 clusters to exhibit very high CO oxidation activity, already at sub-ambient temperature. Our findings highlight the promise of alloying gold clusters with more reactive transition metals and the importance of charge transfer from the support in heterogeneous gold systems in catalyzing CO oxidation.
Introduction
Gold has been at the center of the attention of the catalysis community, since early reports of Haruta and Hutchings demonstrated the outstanding catalytic properties of nanoscale gold.1–4 An important corollary from the extensive follow-up work on heterogeneous gold systems is that size, morphology and oxidation state all profoundly affect gold's unique catalytic properties.5–13 Identification of the exact morphology of Au particles remains a considerable challenge, especially when their size is smaller than 1 nm.14 In the past two decades, many studies have dealt with the structure of small gold clusters in the gas phase,14–29 which are model systems for supported gold nanoparticles.30 A cluster that has caught significant attention is the hollow hexadecagold cage with tetrahedral (Td) point symmetry.19,22,23In heterogeneous systems, charge transfer between gold and the support plays an important role in, for instance, CO oxidation.8 Due to gold's high electronegativity, small clusters can easily take up electrons from the support. Charging of gas-phase clusters, which is experimentally readily achieved, serves as a very simple model to study influence of charging. A change in the oxidation state of gold clusters is known to affect the binding of molecules and, henceforth, the catalytic properties.31–37 Also doped Au clusters have received increasing attention, because doping presents a way to tune the electronic and catalytic properties.38–40 Relevant to the fullerene-type Au16 cluster is its endohedral doping by other atoms.41–44 It has been experimentally demonstrated that endohedrally doped M–Au16− clusters (M = Fe, Co, Ni) are stable compounds, despite significant structural distortion induced by the foreign metal atom.42 Among these, Cu doping does not affect the structure of the cluster.21 Important to catalysis, doping can result in the activation of molecules such as O2, as for instance observed when Si is inserted into the Au16 cluster.41 Although most Au–metal combinations are not expected to give rise to stable alloys in nanoparticles,45 doped clusters may be considered models for near-surface alloys, a topic which is also of growing relevance to heterogeneous catalysis.46 Indeed, synergistic effects have been reported for heterogeneous Au catalysts containing small amounts of Rh, amongst others in CO oxidation.47,48 How such doping influences the (electronic) structure and catalytic behavior remains an open question. In this work, we use density functional theory (DFT) calculations to investigate the structure of neutral and anionic Rh-doped Au16 clusters and explore how Rh-doping affects the rate of CO oxidation on such clusters.
We here use a genetic search algorithm based on DFT calculations to compute the energy of candidate structures to predict stable Au16 and neutral and anionic Rh-doped Au16 clusters. The algorithm correctly identifies the Td cage as the most stable structure for Au16. These calculations also demonstrate the possibility of endohedral doping by Rh and, in this way, we show that neutral and anionic Rh–Au16 clusters (Rh@Au16). As Rh is preferentially located in the Au16 cage, the clusters expose only Au atoms at their surface. First-principles microkinetics simulations highlight the exceptionally high potential of the bimetallic clusters in catalyzing CO oxidation: Rh-doped Au16 clusters are much more active in CO oxidation than the Au16 cluster. The improved activity is due to increased electron density around the Fermi level in the presence of Rh, which results in stronger adsorption of CO and O2 and lower activation barriers for the surface CO oxidation step. This work provides inspiration to the design of transition metal doped Au cluster and nanoparticle catalysts to significantly speed up heterogeneous reactions.
Methods
All spin-polarized density functional theory (DFT) calculations were performed by using projector augmented wave (PAW)49 potentials and the Perdew–Burke–Ernzerhof (PBE) functional50 implemented in the Vienna ab initio simulation package (VASP)51,52 code. The global minimum structures of Au16, Rh@Au16 and Rh@Au16− clusters were obtained by employing a genetic algorithm (GA) code to generate structures, whose geometries were optimized by first-principles DFT calculations. The clusters were placed in a 15 Å × 15 Å × 15 Å cubic supercell for geometry optimization. Brillouin zone sampling was restricted to the Γ point. All the atoms in the clusters were allowed to relax. The energy cutoff for the plane wave basis set was set to 270 eV for these structures optimizations, and forces on each atom below 0.05 eV Å−1 was used as convergence criterion. For computing the adsorption energies of the intermediates, the cutoff energy was set to 400 eV and the force convergence criterion was 0.02 eV Å−1. The improved force reversed method was used to determine the transition states for CO oxidation53 and the force tolerance of 0.05 eV Å−1 was used. It was verified that this approach led to similar TSs as the climbing-image nudged elastic band (CI-NEB) method.54,55 All the energies were zero-point energy corrected, for which a frequency analysis was performed.Infrared (IR) spectra of the Au16 and the two Rh@Au16 clusters were simulated using the Gaussian package employing a PBE0/LANL2DZ basis set.56 The same program was used to simulate the photoelectron spectrum of the anionic Rh@Au16 cluster. Theoretical predicted IR spectra were obtained by applying Lorentzian functions with the theoretical harmonic vibrational frequencies scaled by a 2 cm−1 full width at half-maximum. The photoelectron simulation was done by fitting the distribution of the calculated vertical detachment energies (VDEs) with unit-area Gaussian functions of 0.06 eV half-width. The first VDE of the anionic Rh@Au16− cluster was calculated as the difference between the energies of the neutral and anionic global minimums clusters. The higher VDEs were approximated by the addition of the binding energies of the deeper occupied orbitals of the anionic cluster (i.e., the density of states) to the first VDE. In our work, a vibration analysis (Table S1†) has been done to make sure that the obtained structures are local minima on the potential energy surfaces without imaginary frequency.
Structure of gold clusters
The GA code employed to identify the global minimum structure of gold clusters is based on the principle of natural evolution and includes random generation of an initial population of clusters, geometric optimization of the candidate structures, assigning fitness to these structures based on their electronic energy, and generating a new population by crossover operations, as introduced by Deaven and Ho,57,58 as well as random mutations by moving of atoms.59 Typically, an initial population of ten random structures was generated and optimized at DFT-PAW-PBE level. Electronic energies calculated by DFT calculations were used to determine the fitness, structures with lower energy having higher probably of being retained in the population.60 The two relatively most stable structures were kept in the next population. Energies and bond distances were used to reject multiple occurrences of structures in the population. Typically, around 700 structures were optimized to find the global minimum structures of Au16 or RhAu16 clusters.Microkinetic simulations
The activation barriers are used to calculate the forward and backward rate constant for CO oxidation. For surface reactions, the rate constants for the forward and backward elementary reaction were determined by the Eyring equation: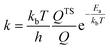 | (1) |
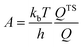 is set to 1013 s−1 for all the elementary reactions.
is set to 1013 s−1 for all the elementary reactions.
For non-activated molecular adsorption, the rate of adsorption is determined by the rate of surface impingement of gas-phase molecules. The flux of incident molecules is given by Hertz–Knudsen equation:61
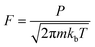 | (2) |
Hence, the molecular adsorption rate constant can be expressed as:
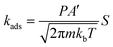 | (3) |
For the desorption process, it is assumed that there are three rotational degrees of freedom and two translational degrees of freedom in the transition state. Accordingly, the rate of desorption is given by
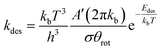 | (4) |
The approach to microkinetic simulations has been presented in detail elsewhere.63,64 Differential equations for all the surface reaction intermediates were constructed using the rate constants and the set of elementary reaction steps. For each of the M components in the kinetic network, a single differential equation in the form
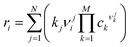 | (5) |
The CO oxidation rate is calculated by the in-house developed MKMCXX program.63–65 Steady-state coverages were found by integrating the ordinary differential equations in time until the changes in the surface coverages were very small. Because chemical systems typically give rise to stiff sets of ODEs, we have used the backward differentiation formula method for the time integration. The rates of the individual elementary reaction steps can be obtained based on the calculated steady-state surface coverages. In our simulations, the gas phase contained a mixture of CO and O2 in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio at a total pressure of 0.05 atm.
3 molar ratio at a total pressure of 0.05 atm.
The rate limiting step can be determined via the “degree of rate control (DRC)” method as introduced by Campbell et al.66–68 For elementary step i, the degree of rate control XRC,i can be defined as
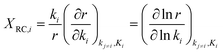 | (6) |
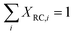 | (7) |
Results and discussion
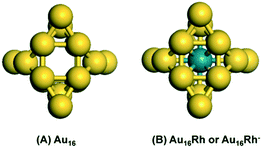
The global minimum structures of Au16 and two Rh-doped Au16 clusters, i.e., one neutral (Au@Rh16) and one anionic (Rh@Au16−) clusters were identified by our GA-DFT approach. These structures are shown in Fig. 1 (other low-energy structures for these three systems are collected in Fig. S1†). The most stable structure for Au16 is a tetrahedral cage with Td symmetry (Fig. 1A) and is similar to the optimal structure reported by Chen et al.,22 leading considerable credence to our algorithm. This tetrahedral Au16 cluster has slightly lower energy compared with other isomers (Fig. S1†). In our calculations, this lowest lying Au16 cluster structure is more stable by 0.09 eV and 0.61 eV than other proposed stable structures with C2v and Td symmetry,19,23 respectively. The diameter of the empty cage is approximately 5.5 Å, which is sufficient to allow doping by other metals. The GA algorithm predicts the endohedral insertion of Rh in the Au16 cage to be the most stable structure (Fig. 1B) for both the anionic and neutral Rh-doped gold clusters. The ground state of anionic Rh@Au16− adopts a Td symmetry with a valence electron configuration of (12a1)2(13e)4(25t2)6(14e)0. However, removal of an electron from the degenerate 25t2 molecular orbital will induce symmetry degradation due to the Jahn–Teller effect,69 this results in a slightly distorted tetrahedral structure with a lower D2d symmetry for the neutral Rh@Au16 cluster with a degenerated ground state. This slight distortion allows lowering of the energy of Rh@Au16 cluster through the removal of some of the degeneracy present in the more symmetric Rh@Au16− structure. The Au16 cluster host maintains the tetrahedral structure during the insertion of Rh atom; the tetrahedral cage is slightly enlarged by 0.1 Å for the neutral and anionic Rh@Au16 clusters. Such Rh@Au160/− cluster is significantly more stable than other structures. Similar to Au16, these clusters have six square faces and eight triangular faces, capped with four more gold atoms on the non-nearest neighbour triangles. They only expose Au atoms with coordination numbers of three and five.The geometric and electronic structure of Au16 clusters has only been scarcely investigated. Synthesis of Aun− clusters is possible by means of laser vaporization of a pure gold target.15 Infrared absorption spectroscopy (IR) can yield information about the structure and symmetry of neutral and charged clusters.70 The calculated IR spectra for neutral Au16 and neutral and anionic Rh@Au16 clusters are shown in Fig. 2. The IR spectrum of neutral Au16 cluster contains a dominant vibrational mode at 150 cm−1. The spectrum of Rh@Au16− contains similar features that of Au16, except of the red shift of main band to 130 cm−1. The IR spectrum of neutral Rh@Au16 is much more complex and comprises a larger number of active vibrational modes due to the lower symmetry of the cluster (D2d point group). These three gold clusters can be distinguished by measuring their IR spectra. Photoelectron spectroscopy (PES) can be employed to investigate the structure of anionic clusters.15,19,71,72 The calculated PES spectra for the ionic Rh@Au16 cluster is presented in Fig. S2† which is extremely helpful to clarify its structure in experiment.
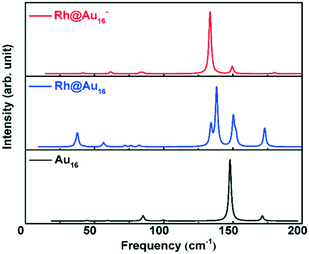 | ||
| Fig. 2 Simulated infrared absorption spectroscopy of Au16, neutral and negatively charged Rh@Au16 clusters. | ||
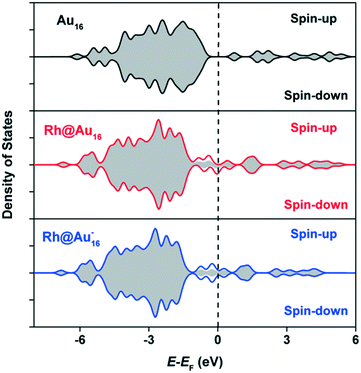
In order to gain more insight into the effect of Rh doping on neutral and anionic clusters, we analyze the electronic structure of the three gold clusters. The total density of states (DOS) is depicted in Fig. 3. Upon Rh doping, the broad band below the Fermi level, predominantly comprised of d-orbitals, shifts to lower energies. Apparent is also the non-metallic and anti-ferromagnetic character of the Au16 cluster. The increased DOS around the Fermi-level highlights the more pronounced metallic character of the Rh-doped clusters. The difference plots in Fig. 3 show that part of the increased electron density around the Fermi level is due to the introduction of Rh. The neutral Rh@Au16 cluster contains an unpaired electron. Thus, Rh modification of Au16 leads to substantial changes in the electronic structure, which we may expect to strongly affect catalytic performance.
To probe the catalytic potential of the novel Rh-doped gold clusters, we investigate the mechanism of CO oxidation for the three gold clusters by DFT calculations. Using computed adsorption energies and reaction barriers, microkinetics simulations are then performed to determine CO conversion rates and identify possible rate-controlling steps. As the surface will be predominantly covered by CO, an Eley–Rideal mechanism – involving gaseous O2 – is not reasonable in this case. Accordingly, we considered the well-accepted Langmuir-Hinshelwood mechanism73 involving reaction between molecularly adsorbed CO and O2, i.e., CO* + O2* → OCOO** (N.B.: * points to surface vacancies). The OCOO** intermediate, which occupies two adjacent sites, will decompose to produce CO2 and an adsorbed O atom (OCOO** → CO2 + O* + *), followed by CO adsorption and reaction of CO* with O* to produce CO2 and regeneration of the surface vacancies (CO* + O* → CO2 + 2*). The computed potential energy diagrams for CO oxidation on the three clusters are depicted in Fig. 5. For the Au16 cluster, CO and O2 adsorb on the corner Au atoms (Fig. S3†) with adsorption energies of −0.70 eV and −0.14 eV, respectively (Table S2†). The relatively weak binding of O2 is consistent with previous results for gold.23,74–77 Rh doping affects the adsorption of CO and O2 substantially. On the neutral Rh@Au16 cluster, the adsorption energies of CO and O2 are −0.86 eV and −0.27 eV, respectively. The O–O stretch frequency, which is computed to be 1563 cm−1 in the gas phase, decreases to 1366 cm−1 upon adsorption on Au16 and 1284 cm−1 upon adsorption to Rh@Au16. The stronger perturbation of the O–O frequency is in line with the Blyholder model,78 that is to say, the O–O bond is weakened by donation of electron density from the metal into the anti-bonding 2π* orbital of the O2 molecule. On the negatively charged Rh@Au16− cluster, CO adsorbs with similar adsorption energy (−0.85 eV) as on the neutral Rh@Au16 cluster, while O2 adsorbs strongest (−0.34 eV) among the three investigated clusters. Relatively speaking, doping the Au16 cluster with Rh affects more significantly the binding energy of O2 than that of CO.
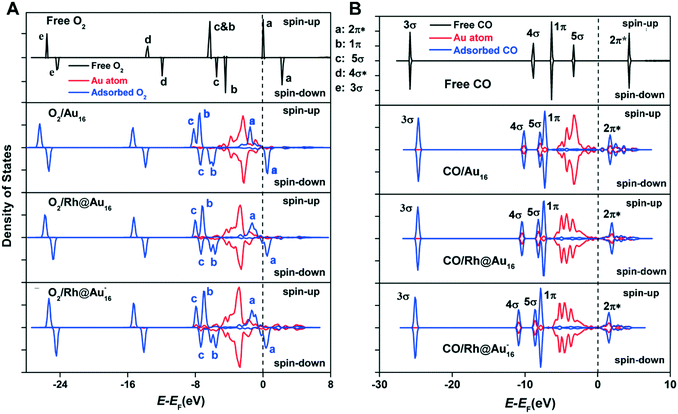
To understand the origin of the stronger adsorption of CO and O2 on the Rh-doped Au16 clusters, Bader charge and local density of states (LDOS) analysis were conducted. For the three clusters considered, O2 adsorbs in a similar configuration (Fig. S3†), with one of its O atom binding to the corner atom of the cluster, which is the most reactive one with a coordination number of three. Whilst this corner atom has only a small negative charge (−0.09e) for Au16, doping with Rh leads to values of −0.13e and −0.23e for the neutral and anionic Rh-doped clusters, respectively. The DFT calculations therefore demonstrate that a higher electron density of Au leads to stronger adsorption of O2, in line with previous investigations.79
Fig. 4A depicts the LDOS for free and adsorbed O2 on Au16, Rh@Au16 and Rh@Au16−. On Au16, the spin-down state of the O2 2π* orbital is unoccupied due to its relatively high energy. For both Rh-doped Au16 clusters, there are more states near the Fermi-level (Fig. 3), which can hybridize with the orbitals of O2. This enhances the adsorption of O2. Fig. 4A shows that doping of Au16 leads to electron transfer from the Au d-band to the spin-down component of the 2π* orbital of O2. This back-donation is more pronounced for the bimetallic clusters due to the lower-lying energy of the spin-down component of the 2π* orbital. These effects are most pronounced for the anionic Rh@Au16− cluster, explaining the highest O2 binding energy for this case. Whilst coordination of O2 is similar for all three clusters, Rh-doping changes the coordination mode of CO. CO prefers to bind at a corner Au atom on Au16, while it is located on the Au atom directly interacting with Rh on the doped clusters. The main reason for the stronger adsorption of CO as compared with O2 is the slightly stronger interaction of CO's 4σ and 5σ orbitals with the Au d-bands. As the 2π* orbital of CO is not occupied, the variation in binding energy is smaller as compared with O2.
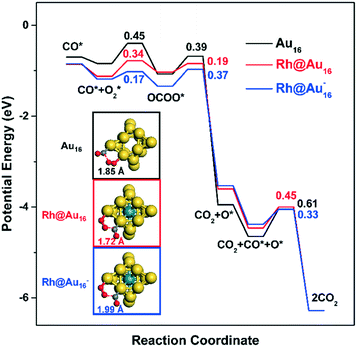
Stabilization of CO and O2 adsorption strongly affects reaction energetics and kinetics for CO oxidation (Fig. 5). Nørskov and co-workers showed that stronger CO and O2 adsorption lead to the stabilization of the transition states for CO2-forming surface reactions.80,81 Consistent with this, we find that the activation barriers for the CO* + O2* → OCOO** reaction, 0.45 eV for Au16, 0.34 eV for Rh@Au16 and 0.17 eV for Rh@Au16−, are decreased when CO and O2 bind stronger (Fig. 5, Table S3†). In this respect, it is important to mention that the transition state for this reaction on Au16 is different from the ones on the Rh-doped clusters (see the Fig. S4†). This is due to the different preferred adsorption modes of CO and O2. In the former case, O2 migrates to the less stable adsorption site (neighboring the corner atom) and the cluster is significantly distorted in the transition state, increasing the activation barrier. On the other hand, for the bimetallic clusters, CO and O2 remain at their favorable adsorption sites in the transition state with much less distortion of the cluster itself. This is certainly due to the presence of Rh inside the cage. Comparison of the two Rh-doped clusters shows that the lowest barrier of anionic Rh@Au16− cluster is associated with the most favorable reaction energy, consistent with Brønsted–Evans–Polanyi (BEP) considerations.82
Decomposition of the OCOO surface intermediate to CO2 and an O adatom is strongly exothermic in all cases. Computed activation barriers for the OCOO* → CO2 + O* reaction are 0.39 eV, 0.19 eV and 0.37 eV for the Au16, Rh@Au16 and Rh@Au16− clusters, respectively. OCOO** decomposition has similar transition state configurations on Au16 and Rh@Au16 clusters (Fig. S4†). We found that the O atom remaining on the surface binds stronger to Rh@Au16 by 0.45 eV in the transition state, which explains the lower activation barrier for CO2 formation. This is consistent with the projected DOS of the O atom in the transition state given in Fig. S5.† The higher electron density on the Au atoms with coordination number 5 in anionic Rh@Au16− cluster displaces the O atom to top adsorption instead of bridge adsorption. This small difference is unfavorable and increases slightly the barrier for OCOO** decomposition on this cluster. Summarizing, OCOO** decomposition is more facile than its formation for Au16 and neutral Rh@Au16, and the reverse holds for the anionic Rh@Au16− cluster.
The catalytic cycle is closed by removal of the O adatom by another CO molecule. O preferably adsorbs in the cluster's three-fold sites with energies of −0.81 eV, −0.46 eV, and −0.39 eV, respectively, for Au16, Rh@Au16, and Rh@Au16−. The nature of the transition states for the CO* + O* → CO2 + 2* reactions are nearly the same for all three clusters (Fig. S4†) and the corresponding activation energies for Au16 (0.61 eV), Rh@Au16 (0.45 eV) and Rh@Au16− (0.33 eV) obey the Brønsted–Evans–Polanyi relation. These differences in reaction energetics point out the significant effect of Rh-doping and the extra electron on the cluster's reactivity.
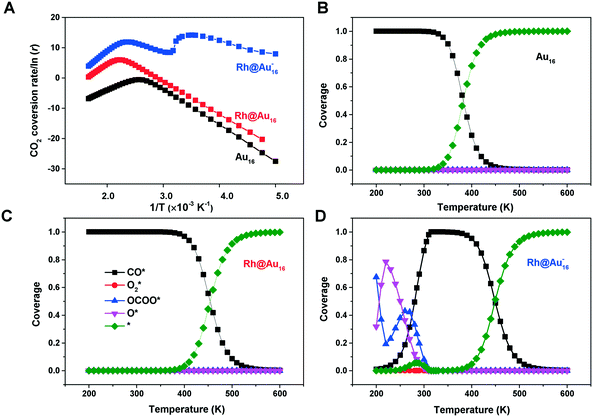
We then used microkinetics simulations to predict the CO conversion rate based on the computed kinetic parameters.65 Arrhenius plots in Fig. 6 highlight the increased CO oxidation activity upon doping of the cluster by Rh. The anionic Rh@Au16− cluster exhibits the highest activity and displays already outstanding performance at sub-ambient conditions. At room temperature, its activity is much higher than that of the neutral bimetallic cluster. The Au16 presents the lowest activity. The lower optimum reaction temperature for the Rh-doped clusters relates to the stronger binding of CO and O2. At high temperature, the reaction rates for all clusters decrease due to lowered CO and O2 coverages (Fig. 6B–D). The very high activity of the anionic Rh@Au16− cluster relates to the low barrier for the CO* + O2* → OCOO** reaction. A degree of rate control (DRC)66–68 analysis (Fig. S6†) shows that, for this cluster, the removal of O from the surface is controlling the overall rate at low temperature, whereas for the other two clusters the oxidation of CO with O2 is the most difficult step (CO* + O2* → OCOO**). The higher activity of the Rh@Au16 compared with Au16 is due to the lower barriers for all three reactions. There is a strong competition between CO and O2 adsorption on Au16 and Rh@Au16 clusters. As is shown in Fig. 6B and C, CO is almost fully covered these two clusters and O2 coverage is significantly low due to its lower adsorption energy. The peculiar temperature dependence of the anionic cluster's rate and consequently the strong changes in DRC values (Fig. S6†) are due to the competition for surface sites of O atoms with OCOO below room temperature and with CO at higher temperature.
The other two clusters show more conventional behavior: CO poisons the surface at low temperature. Table 1 also highlights that at room temperature the higher rate of Rh@Au16 than Au16 is not due to increased O2 surface coverage. Instead, the difference can be entirely explained by the lower barrier for the CO* + O2* surface reaction. Maximum reaction rates for Au16, Rh@Au16 and Rh@Au16− clusters occur at 390 K, 450 K and 280 K with values of 5.5 × 10−1 mol s−1 site−1, 3.8 × 102 mol s−1 site−1 and 1.3 × 106 mol s−1 site−1, respectively. This difference emphasizes the promise of doping of gold clusters by Rh and the importance of the negatively charge state of the cluster. There is no explicit experimental evidence yet for the benefit of Rh doping in Au clusters for CO oxidation. CO and O2 adsorption strengths are increased when the gold cluster hosts a Rh atom, especially when the cluster is negatively charged. Au–Rh nanoparticles have been shown to be more active in CO oxidation than Au nanoparticles.48 Charge transfer from the support to Au clusters has been well demonstrated in heterogeneous systems.83–85 Obviously, the here discussed clusters will change their shape upon interaction with a solid oxide support. Our work provides a hint at a novel strategy to improve the performance of gold catalysts by doping with more reactive transition metals and tuning the charge state of the active phase.
| Cluster | Θ CO | θ O2 | Θ OCOO | Θ O | Θ * | r (mol s−1) |
|---|---|---|---|---|---|---|
| Au16 | ∼1.0 × 100 | 7 × 10−10 | 1 × 10−10 | 5 × 10−7 | 1 × 10−3 | 5 × 10−4 |
| Rh@Au16 | ∼1.0 × 100 | 2 × 10−10 | 5 × 10−13 | 2 × 10−8 | 3 × 10−6 | 8 × 10−3 |
| Rh@Au16− | 9 × 10−1 | 4 × 10−5 | 8 × 10−2 | 2 × 10−2 | 4 × 10−2 | 9 × 105 |
Conclusions
The stable structures of Au16 and neutral and anionic Rh@Au16 clusters were identified by a DFT-based genetic search algorithm. All clusters form a Au16 cage-like structure with Td or D2d symmetry with Rh being located inside the cage in the doped clusters. Doping results in significant changes in the gold clusters' electronic properties, profoundly affecting the binding energies of CO and O2. These changes are more pronounced when an electron is added to the Rh@Au16 cluster. Stronger adsorption and activation of O2 are due to increased electron density of the cluster just below the Fermi level, which overlaps with the O2 2π* orbital. The further consequence is that the activation barrier for the reaction of adsorbed CO with adsorbed O2 is decreased. Similarly, the barriers for decomposition of the OCOO surface intermediate and the reaction of CO with the remaining O adatom are more favorable for the doped clusters. Kinetically, the negatively charged Rh@Au16 cluster presents very high activity in CO oxidation, as the barrier for the initial CO oxidation step is so low that CO and O compete for the free sites. The other clusters display conventional CO-poisoning kinetic behavior. These data show the promise of doping and charging of gold clusters for CO oxidation, providing a hint at a novel strategy for enhancing the performance of supported gold systems.Acknowledgements
EJMH, IAWF, YS, IT and JXL acknowledge financial support by NWO-VICI and NWO-TOP grants. ZL acknowledges the start-up fund from Shanxi Normal University for support (Grant No. 02070388).Notes and references
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16(2), 405–408 CrossRef.
- A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936 CrossRef PubMed.
- J. Guzman, S. Carrettin and A. Corma, J. Am. Chem. Soc., 2005, 127, 3286–3287 CrossRef CAS PubMed.
- A. A. Herzing, C. J. Kiely, A. F. Carley, P. Landon and G. J. Hutchings, Science, 2008, 321, 1331–1335 CrossRef CAS PubMed.
- M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650 CrossRef CAS PubMed.
- M. Comotti, W.-C. Li, B. Spliethoff and F. Schüth, J. Am. Chem. Soc., 2006, 128, 917–924 CrossRef CAS PubMed.
- O. Lopez-Acevedo, K. A. Kacprzak, J. Akola and H. Häkkinen, Nat. Chem., 2010, 2, 329–334 CrossRef CAS PubMed.
- Y.-G. Wang, Y. Yoon, V.-A. Glezakou, J. Li and R. Rousseau, J. Am. Chem. Soc., 2013, 135, 10673–10683 CrossRef CAS PubMed.
- J. Guzman and B. C. Gates, J. Am. Chem. Soc., 2004, 126, 2672–2673 CrossRef CAS PubMed.
- Z.-Y. Li, Z. Yuan, X.-N. Li, Y.-X. Zhao and S.-G. He, J. Am. Chem. Soc., 2014, 136, 14307–14313 CrossRef CAS PubMed.
- X.-N. Li, Z. Yuan and S.-G. He, J. Am. Chem. Soc., 2014, 136, 3617–3623 CrossRef CAS PubMed.
- X. N. Li, Z. Y. Li, H. F. Li and S. G. He, Chem. – Eur. J., 2016, 22, 9024 CrossRef CAS PubMed.
- N. Li, H. M. Zhang, Z. Yuan and S. G. He, Nat. Commun., 2016, 7, 11404 CrossRef PubMed.
- J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035418 CrossRef.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867 CrossRef CAS PubMed.
- X. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165423 CrossRef.
- G. Mills, M. S. Gordon and H. Metiu, Chem. Phys. Lett., 2002, 359, 493–499 CrossRef CAS.
- H. Häkkinen, B. Yoon, U. Landman, X. Li, H.-J. Zhai and L.-S. Wang, J. Phys. Chem. A, 2003, 107, 6168–6175 CrossRef.
- S. Bulusu, X. Li, L.-S. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326–8330 CrossRef CAS PubMed.
- H.-J. Zhai, J. Li and L.-S. Wang, J. Chem. Phys., 2004, 121, 8369–8374 CrossRef CAS PubMed.
- L. M. Wang, S. Bulusu, H. J. Zhai, X. C. Zeng and L. S. Wang, Angew. Chem., Int. Ed., 2007, 46, 2915–2918 CrossRef CAS PubMed.
- G. Chen, Q. Wang, Q. Sun, Y. Kawazoe and P. Jena, J. Chem. Phys., 2010, 132, 194306 CrossRef PubMed.
- Y. Gao, N. Shao, Y. Pei, Z. Chen and X. C. Zeng, ACS Nano, 2011, 5, 7818–7829 CrossRef CAS PubMed.
- Y. Gao, N. Shao and X. C. Zeng, ACS Nano, 2008, 2, 1497–1503 CrossRef CAS PubMed.
- W. Huang, S. Bulusu, R. Pal, X. C. Zeng and L.-S. Wang, ACS Nano, 2009, 3, 1225–1230 CrossRef CAS PubMed.
- Y. Pei, N. Shao, Y. Gao and X. C. Zeng, ACS Nano, 2010, 4, 2009–2020 CrossRef CAS PubMed.
- Y. Pei, N. Shao, H. Li, D.-E. Jiang and X. C. Zeng, ACS Nano, 2011, 5, 1441–1449 CrossRef CAS PubMed.
- B. Schaefer, R. Pal, N. S. Khetrapal, M. Amsler, A. Sadeghi, V. Blum, X. C. Zeng, S. Goedecker and L.-S. Wang, ACS Nano, 2014, 8, 7413–7422 CrossRef CAS PubMed.
- R. Zhou, X. Wei, K. He, J. E. Shield, D. J. Sellmyer and X. C. Zeng, ACS Nano, 2011, 5, 9966–9976 CrossRef CAS PubMed.
- S. M. Lang and T. M. Bernhardt, Phys. Chem. Chem. Phys., 2012, 14, 9255–9269 RSC.
- J.-H. Liu, A.-Q. Wang, Y.-S. Chi, H.-P. Lin and C.-Y. Mou, J. Phys. Chem. B, 2005, 109, 40–43 CrossRef CAS PubMed.
- J. Xu, T. White, P. Li, C. He, J. Yu, W. Yuan and Y.-F. Han, J. Am. Chem. Soc., 2010, 132, 10398–10406 CrossRef CAS PubMed.
- X. Liu, A. Wang, X. Wang, C.-Y. Mou and T. Zhang, Chem. Commun., 2008, 3187–3189 RSC.
- S. Zhou, G. S. Jackson and B. Eichhorn, Adv. Funct. Mater., 2007, 17, 3099–3104 CrossRef CAS.
- C. L. Hill, J. Mol. Catal. A: Chem., 2007, 262, 2–6 CrossRef CAS.
- W. T. Wallace and R. L. Whetten, J. Am. Chem. Soc., 2002, 124, 7499–7505 CrossRef CAS PubMed.
- J. Hagen, L. D. Socaciu, M. Elijazyfer, U. Heiz, T. M. Bernhardt and L. Wöste, Phys. Chem. Chem. Phys., 2002, 4, 1707–1709 RSC.
- J.-Y. Luo, M. Meng, X. Li, X.-G. Li, Y.-Q. Zha, T.-D. Hu, Y.-N. Xie and J. Zhang, J. Catal., 2008, 254, 310–324 CrossRef CAS.
- D. I. Enache, J. K. Edwards, P. Landon, B. Solsona-Espriu, A. F. Carley, A. A. Herzing, M. Watanabe, C. J. Kiely, D. W. Knight and G. J. Hutchings, Science, 2006, 311, 362–365 CrossRef CAS PubMed.
- J. K. Norskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef CAS PubMed.
- M. Walter and H. Häkkinen, Phys. Chem. Chem. Phys., 2006, 8, 5407–5411 RSC.
- L.-M. Wang, J. Bai, A. Lechtken, W. Huang, D. Schooss, M. M. Kappes, X. C. Zeng and L.-S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 033413 CrossRef.
- H.-F. Li and H.-Q. Wang, Phys. Chem. Chem. Phys., 2014, 16, 244–254 RSC.
- Y. Gao, N. Shao, S. Bulusu and X. C. Zeng, J. Phys. Chem. C, 2008, 112, 8234–8238 CAS.
- G. H. Jóhannesson, T. Bligaard, A. V. Ruban, H. L. Skriver, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. Lett., 2002, 88, 255506 CrossRef PubMed.
- J. Greeley and M. Mavrikakis, Nat. Mater., 2004, 3, 810–815 CrossRef CAS PubMed.
- M. Conte, A. F. Carley, G. Attard, A. A. Herzing, C. J. Kiely and G. J. Hutchings, J. Catal., 2008, 257, 190–198 CrossRef CAS.
- V. Abdelsayed, A. Aljarash, M. S. El-Shall, Z. A. Al Othman and A. H. Alghamdi, Chem. Mater., 2009, 21, 2825–2834 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- K. Sun, Y. Zhao, H. Y. Su and W. X. Li, Theor. Chem. Acc., 2012, 131, 1–10 CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, et al., Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- D. Deaven and K. Ho, Phys. Rev. Lett., 1995, 75, 288 CrossRef CAS PubMed.
- D. Daven, N. Tit, J. Morris and K. Ho, Chem. Phys. Lett., 1996, 256, 195–200 CrossRef.
- X.-L. Ding, Z.-Y. Li, J.-H. Meng, Y.-X. Zhao and S.-G. He, J. Chem. Phys., 2012, 137, 214311 CrossRef PubMed.
- L. Cheng, W. Cai and X. Shao, Chem. Phys. Lett., 2004, 389, 309–314 CrossRef CAS.
- P. Nitoń, A. Żywociński, M. Fiałkowski and R. Hołyst, Nanoscale, 2013, 5, 9732–9738 RSC.
- A. P. J. Jansen, An introduction to kinetic Monte Carlo simulations of surface reactions, Springer, 2012 Search PubMed.
- I. A. W. Filot, R. A. van Santen and E. J. M. Hensen, Angew. Chem., 2014, 126, 12960–12964 CrossRef.
- I. A. Filot, R. J. Broos, J. P. van Rijn, G. J. van Heugten, R. A. van Santen and E. J. Hensen, ACS Catal., 2015, 5, 5453–5467 CrossRef CAS.
- http://www.mkmcxx.nl/ .
- C. T. Campbell, Top. Catal., 1994, 1, 353–366 CrossRef CAS.
- C. T. Campbell, J. Catal., 2001, 204, 520–524 CrossRef CAS.
- C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 8077–8082 CrossRef CAS PubMed.
- R. Englman, The Jahn-Teller effect in molecules and crystals, Wiley-Interscience, New York, 1972 Search PubMed.
- P. Gruene, D. M. Rayner, B. Redlich, A. F. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674–676 CrossRef CAS PubMed.
- M. Ji, X. Gu, X. Li, X. Gong, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2005, 44, 7119–7123 CrossRef CAS PubMed.
- W. Huang and L.-S. Wang, Phys. Rev. Lett., 2009, 102, 153401 CrossRef PubMed.
- Z.-P. Liu, P. Hu and A. Alavi, J. Am. Chem. Soc., 2002, 124, 14770–14779 CrossRef CAS PubMed.
- P. Legare, L. Hilaire, M. Sotto and G. Maire, Surf. Sci., 1980, 91, 175–186 CrossRef CAS.
- J. Pireaux, M. Chtaib, J. Delrue, P. Thiry, M. Liehr and R. Caudano, Surf. Sci., 1984, 141, 211–220 CrossRef CAS.
- M. Bartram and B. Koel, Surf. Sci., 1989, 213, 137–156 CrossRef CAS.
- X. L. Ding, Z. Y. Li, J. L. Yang, J. G. Hou and Q. S. Zhu, J. Chem. Phys., 2004, 120, 9594 CrossRef CAS PubMed.
- G. Blyholder, J. Phys. Chem., 1964, 68, 2772–2777 CrossRef CAS.
- R. Coquet, K. L. Howard and D. J. Willock, Chem. Soc. Rev., 2008, 37, 2046–2076 RSC.
- I. N. Remediakis, N. Lopez and J. K. Nørskov, Appl. Catal., A, 2005, 291, 13–20 CrossRef CAS.
- I. N. Remediakis, N. Lopez and J. K. Nørskov, Angew. Chem., 2005, 117, 1858–1860 CrossRef.
- M. A. Barteau, Catal. Lett., 1991, 8, 175–183 CrossRef CAS.
- A. Sanchez, S. Abbet, U. Heiz, W.-D. Schneider, H. Häkkinen, R. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578 CrossRef CAS.
- L. M. Molina and B. Hammer, Phys. Rev. Lett., 2003, 90, 206102 CrossRef CAS PubMed.
- L. B. Vilhelmsen and B. Hammer, Phys. Rev. Lett., 2012, 108, 126101 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cy02277d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2017 |