Requirements for reversible extra-capacity in Li-rich layered oxides for Li-ion batteries†
Y.
Xie‡
a,
M.
Saubanère
 ab and
M.-L.
Doublet
ab and
M.-L.
Doublet
 *ab
*ab
aInstitut Charles Gerhardt – CNRS and Université Montpellier, Place Eugène Bataillon – 34095 Montpellier, France. E-mail: Marie-Liesse.Doublet@umontpellier.fr
bRéseau Français sur le Stockage Electrochimique de l'Energie – RS2E FR3459, Amiens, France
First published on 28th November 2016
Abstract
The structural stability and the redox mechanism of Li-rich layered oxides (LLOs) are two very important aspects for high energy density. The former is related to the irreversible loss of lattice oxygen and capacity fading during cycling, while the latter determines the overall capacity of the materials. This paper aims at clarifying the factors governing the structural stability, the extra capacity and the redox mechanism of LLOs upon Li-removal. The results show that the structural stability against oxygen vacancy formation is improved with increasing M–O covalency, while it decreases with increasing d-shell electron number and with electrochemical extraction of lithium from the lattice. The redox mechanism of Li2−xMO3 electrodes formed by 3d metals or by heavier metals with a d0 electronic configuration is related to the electron depletion from the oxygen lone-pairs (localized non-bonding O(2p) states) leading to an irreversible anionic redox ending with the reductive elimination of O2 upon cycling. For these phases, long-term cycling is predicted to be very unlikely due to the irreversible loss of lattice oxygen upon charging. For the electrodes formed by 4d and 5d metals with intermediate dn electronic configurations, reversible cationic and anionic redox activities are predicted, therefore enabling reversible extra-capacities. The very different redox mechanisms exhibited by Li2−xMO3 electrodes are then linked to the delicate balance between the Coulomb repulsions (U term) and the M–O bond covalency (Δ term) through the general description of charge-transfer vs. Mott–Hubbard insulators. The present findings will provide a uniform guideline for tuning the band structures of Li2MO3 phases and thus activating desired redox mechanisms, being beneficial for the design of high-energy density electrode materials for Li-ion battery applications.
Broader contextIncreasing the energy density of electrode materials for Li-ion batteries is a central goal to the ongoing research in energy storage. One strategy is to increase the number of electronic states available for extra-electrons (extra-Li), without penalizing the structural integrity of the material. This is achieved with Li-rich layered transition metal oxides Li2MO3 (LLOs) for which the larger O/M ratio compared to classical LiMO2 oxides leads to one extra-band in the electronic structure of the materials that can serve as a reservoir for extra-capacity. This extra-band arises from the oxygen 2p-lone pairs (|O2p) that are not involved in the M–O bonds and allows cumulating cationic and anionic redox activity in LLOs to improve the energy density of LLOs up to 300 mA h g−1. Nevertheless, for this anionic redox to be reversible, the O− oxidized species that are generated by Li-extraction from the |O2p–band must be stabilized in the structure to prevent O2 release. This work shows that the M–O covalency is an absolute condition for this stabilization to be efficient, which is achieved through the (partial) substitution of M(3d) for heavier M(4d,5d) metals. Our finding provides a uniform guideline for the design of stable high energy density cathode materials in the near future. |
I. Introduction
Lithium-ion batteries (LIBs) have been considered as an indispensable energy storage technology in the modern society. Despite their extremely successful applications in portable electric devices, the energy density of current LIBs is still far below the requirements of the electrical vehicle (EV) industry.1 It is well known that the bottleneck of this problem lies in the capacity of the cathode materials.2 Being one important category of cathode materials, layered transition metal (TM) oxides were first proposed by Goodenough3 in 1980, with the Li1−xCoO2 electrode delivering a practical capacity of 145 mA h g−1.4 Doping the LiCoO2 material with cheaper and more environmentally benign elements such as Ni and Mn led in the early 2000 to the Li[Ni/Mn/Co]O2 phases, coined as NMC and offering improved reversible capacities, but still less than 200 mA h g−1.5,6 Lithium-rich layered oxides (LLOs) were then proposed to achieve significantly higher capacities (>250 mA h g−1) and higher voltages, leading to attractive energy densities.7,8 However, lithium extraction from these electrodes causes severe structural changes, resulting in huge irreversibility during the first cycle,7 continuous capacity degradation upon cycling,9 and irreversible loss of lattice oxygen.10–14 Such irreversibilities were partially suppressed with the use of heavier M(4d) and M(5d) metals,15–18 among which the model Ru- and Ir-based electrodes can deliver reversible capacities as high as ∼260–270 mA h g−1 with negligible capacity fading and O2 release upon cycling.15 A cumulative cationic (M4+/M5+) and anionic (O2−/(O2)n−) redox activity was demonstrated for these electrodes, further confirmed by electron paramagnetic resonance (EPR) measurements19 and high-resolution TEM microscopy.20 Apart from these experimental studies, theoretical investigations of various LLOs led to the same conclusion that pure oxygen O(2p) states are required at the Fermi level to reach extra-capacities,21,22 and that the relative energy of the transition metal band with respect to these pure oxygen states is a crucial parameter that dictates the redox activity of the materials vs. Li+/Li0 among three possible mechanisms: a reversible cationic redox, a reversible anionic redox and an irreversible O2 anionic redox leading to gas release.21In this article, the oxygen evolution problem and the redox mechanism of the Li2MO3 (M = 3d, 4d, 5d) family of compounds are systematically evaluated as a function of the lithium content and the transition metal. Our findings provide a uniform guideline for the design of stable high energy density cathode materials in the near future.
II. General methodology
At high charging potentials, the Li2−xMO3 electrodes exhibit various irreversible phenomena, i.e. oxygen evolution,10,12 TM migrations,17,23 phase transitions,24 and surface and side reactions.25–27 To reduce, and hopefully suppress these irreversibilities, information regarding the structural stabilities of relevant oxides against oxygen release is of great importance. To evaluate this problem, the following reaction was considered: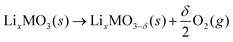 | (1) |
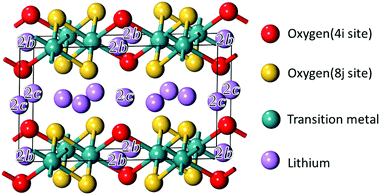
The structural model of Li2MO3 is shown in Fig. 1. The compounds have a monoclinic cell with a C2/m symmetry. For the sake of comparison, structures with only one transition metal (TM) layer were considered with transition metals orderly spread in the honeycomb layer. The validity of this layered-type model was checked with respect to the Material Project (MP) database (see the ESI,† Table S1).29,30 It was found that 76% of the Li2MO3 layered phases considered in this study have a formation energy below the convex hull of the T = 0 K phase diagrams available today in the MP database and are therefore stable polymorphs. The other phases based on M′ = V, Cr, Nb, Hf, Ta were found to be above the convex hull by a few tens of meV per atom. Because chemical substitutions can be used to stabilize Li2M(1−y)M′yO3 layered-type structures, these metastable phases were kept in the study. Following the Wyckoff positions of the C2/m symmetry, different distributions of lithium- and oxygen-vacancies were then considered in the calculations for the Li2−xMO3−δ phases (see the ESI,† Fig. S2).
III. Results
Fig. 2a shows the stability of the metal oxides as a function of the lithium content, the metal row and the number of electrons in the TM d-shell. For the Li2MO3 phases, the oxygen extraction reactions are found to be endothermic, suggesting that the removal of oxygen from the lattice is difficult and that the metal oxide networks formed by 3d, 4d, and 5d metals are all stable. Relying on first-principles calculations, several groups have evaluated independently the structural stabilities and oxygen vacancy formation energies for Li2MnO3,11,31,32 Li1.25Ni0.25Mn0.58O2,12 and Li2RuO3.33 Although the obtained values are different, to a certain extent, to our numerical data depending on the models applied, the oxygen vacancy ratio and the numerical corrections to the O2 enthalpy, they all confirm the stability of the Li2MO3 phases.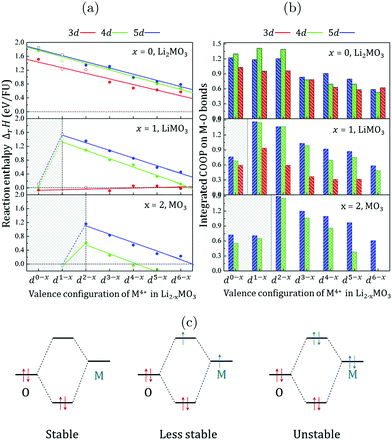 | ||
| Fig. 2 (a) Reaction enthalpies (ΔrH in eV FU−1) computed for Li2−xMO3 with a δ fraction of the oxygen vacancy of 1/12 and plotted as a function of the dn valence configuration of the transition metal for the whole series of 3d (red), 4d (green) and 5d (blue) metals. Filled (empty) circles refer to materials for which the Li2MO3 layered structure is stable (unstable) with respect to the MP database (see the ESI,† Table S1). Calculations have been performed within the DFT+U formalism with Ueff = 3 eV for each transition metal. As shown in the ESI,† Fig. S1, the Ueff parameter has a limited impact on ΔrH due to the small change in the TM oxidation state. (b) Integrated Crystal Orbital Overlap Populations (COOP) for each computed systems showing the variation trend for the M–O bond-order as a function of the dn-shell electron number and moving down from 3d to 4d and 5d TM elements. (c) Qualitative illustration of the 2 centers-n electrons interactions following the variation trend of the M–O COOPs when moving along one row of the periodic table from early (low dn) to late (high dn) transition metals. | ||
When moving down from one row to another in the periodic table, the lines representing the Li2MO3 phases formed by 3d, 4d and 5d metals are almost parallel to each other and the formation of oxygen vacancies becomes more difficult. From 5d to 4d systems, ΔrH decreases in average by about 0.05 eV per formula unit (FU) while it drops by 0.22 eV FU−1 from 4d to 3d systems (see the ESI,† Table S2). Now, when moving along one given row of the periodic table from early (low dn) to late (high dn) transition metals, ΔrH decreases showing that the extraction of oxygen from the lattice becomes easier or equivalently that the TM-oxide network becomes gradually less stable. Because the changes in the reaction energies are related to the M(d)–O(2p) orbital interactions, it is interesting to perform a Crystal Orbital Overlap Population (COOP)34 analysis to visualize this effect. This tool is a powerful bonding descriptor constructed by generating an overlap population-weighted density of states on the different bonds occurring in a crystal structure. The integration of the COOPs up to the Fermi level gives a reasonable estimate of the M–O bond-order and is shown in Fig. 2b. Except for the d6−x systems, the M(4d)–O and M(5d)–O bonds are found to be stronger than the M(3d)–O ones at each given d-electron filling, indicating that increasing the M–O covalency improves the structural stability of the Li2MO3 layered phases at any given d-electron filling. In contrast, when increasing the d-electron number by moving along one given row of the periodic table, the M–O bond-orders decrease concomitantly with the decrease of ΔrH. Hence, while the M(d)–O(2p) overlap is generally expected to increase from early to late TM (in particular for 3d-metals), the M–O bond-order and therefore the thermodynamic stability of the TM-oxides appear to be primarily dictated by the number of d-electrons to fill the antibonding (MO*) states. This phenomenon can be qualitatively explained by the 2 centres-n electrons picture shown in Fig. 2c. When the TM d-orbitals interact by symmetry with the oxygen 2p-orbitals, the interaction is as more stabilizing for the system as the number of electrons in the two interacting orbitals is 2. For higher electron counts, the antibonding levels start to be filled and the interaction is less and less stabilizing for the system.
1. From Li2MO3 to LiMO3
When one lithium is deintercalated from Li2MO3, the reaction enthalpies (ΔrH) decrease for all considered systems (Fig. 2a), suggesting that the LiMO3 phases are less stable than the Li2MO3 phases. For the d0−x phases for which no electrons occur in the d-band, ΔrH are very close to zero or even negative meaning that the LiMO3 phases are prone to release oxygen. For all other dn−x systems (n > 0), the reaction enthalpies for the LiMO3 phases formed by 4d and 5d metals are reduced by about 0.38 and 0.18 eV, respectively, in comparison to the Li2MO3 phases, but the phases are still stable (see the ESI,† Table S2). The LiMO3 phases formed by 3d metals show a different behavior with reaction enthalpies being insensitive to the d-shell electron number and almost zero, suggesting that the LiM(3d)O3 phases are highly unstable with respect to O2 release. According to our calculations, most of the LiM(3d)O3 phases show a strong tendency to form short O–O dimers inside the TM layer, accompanied by a significant decrease of the M(3d)–O bond orders (see Fig. 2b). For LiNiO3, O4i ions even de-coordinate from the lattice, leading to the formation of free O2 molecules in the structure with O–O distances at 1.236 Å. This phase is thus clearly unstable with respect to O2 release, as confirmed by phonon calculations (see the ESI,† Fig. S3). This result is consistent with the recent report of Bruce and co-workers who used operando mass spectrometry to investigate the electrochemical properties of Li1.2[Ni0.13Co0.13Mn0.54]O2 during the first charge. Their investigations unambiguously showed that O is extracted from the lattice at and above 4.5 Volt with part of it reacting with the electrolyte to form CO2 gas.14 Moreover, recent theoretical investigations have already confirmed that the oxygen vacancy formation energies for the LiMnO3 phase is very close to zero or negative (0.05 eV,11 ±0.05,32 and −0.23 eV31), and that LixMnO3 exhibits a thermodynamic instability towards oxygen release for x < 1,11,13,32,35 well consistent with our results. Because of the presence of oxygen vacancies, it was reported that the migration barriers for Ni and Mn ions in the Li[Li1/6Ni1/6Co1/6Mn1/2]O2 compound are significantly lowered,12 making the layered to spinel phase transformation possible.24,27 Recently, this behavior has been nicely confirmed by Ab Initio Molecular Dynamics (AIMD) calculations,13,35 showing that the generation of oxygen vacancies in the highly-charged Li2−xMnO3 electrode enables Mn ion migration in the structure which becomes a precursor to the voltage fade occurring during subsequent cycling. To clarify the origin of these instabilities, further discussion on the electronic structures of these phases is needed and will be presented later.2 From LiMO3 to MO3
When half or one more lithium is extracted from the lattice to form the fully delithiated MO3 state, the formation energies ΔrH keep decreasing (see Fig. 2a and ESI,† Table S2, Fig. S1b). The values for d1−x systems in MO3 phases now become negative, indicating that the formation of O-vacancies is spontaneous. Except for the d1−x systems, the MO3 phases formed by 3d metals are also highly unstable with respect to O2 release, leading to a transformation from layered to condensed structures (see the ESI,† Fig. S4) which stabilizes the structures by 0.96–1.81 eV FU−1. In the condensed structures, two adjacent TM layers slip along the a-axis with the decrease of the c-axis, and short O–O interlayer bonds with bond lengths about 1.5 Å are formed. Based on the O K-edge XAS, Oishi and co-workers have investigated the electrochemical properties of pure Li2MnO3, and their results suggest that O2−Mn4+O− or O−Mn4+O−states are more stable than the O2− Mn5+/6+ O2− states when lithium is extracted, leading to the combination of neighboring radical anions O−˙ to form the peroxide ion (O2)2−.36The layered MO3 phases formed by 4d and 5d metals remain stable from d2 to d4 and from d2 to d6, respectively. In comparison, the relative weaker M(4d)–O covalency with respect to M(5d)–O (see Fig. 2b) results in two unstable MO3 phases, namely RhO3 and PdO3. Although our calculated formation energy for RuO3 (−0.04 eV FU−1) is slightly smaller than the reported value (0.12 eV FU−1),33 it can be identified clearly from Fig. 2b that due to the increasing M–O covalency from M(3d) to M(4d) and M(5d), the formation of oxygen vacancies will be suppressed or postponed, confirming an increasing thermodynamic stability for Li-rich layered TM-oxides when moving down in the periodic table. Given that oxygen vacancies are much more difficult to occur in Li2RuO3 than in Li2MnO3, it can be expected that partial mixing of Ru and Mn in Li2Ru1−yMnyO3 phases or in classical LiMO2 compounds is helpful to improve the structural stability of the systems and to reduce the loss of lattice oxygen, which is confirmed by experiments.15,16
IV. Discussion
An anionic redox has been proposed15–17,20,21,31,36,37 to explain the (first cycles) extra capacities observed in Li-rich transition metal oxides. From an experimental point of view, this process is often regarded as reversible, because oxygen redox activity related to the extra capacity of the cathode materials is observed for a few cycles, despite a continuous loss of the lattice oxygen. However, from a theoretical viewpoint, once O2 is released (even in small quantity), there is no way for the system to recover the pristine fully charged materials, which makes this electrochemical reaction irreversible.21 While the reversibility of this anionic redox is still under debate, it seems uniformly accepted that the origin of the extra-capacity is linked to the occurrence of pure oxygen electronic levels in the electronic structure of the LLO materials.14,21,22 The occurrence of these pure O(2p) states in fact arises from symmetry and increases with the O/M ratio in TM-oxides: moving from LiMO2 to Li-rich Li2MO3 systems, the increase of the O/M ratio decreases the number of M(d)-orbitals that can interact with the O(2p)-orbitals to form M–O bonds. This inevitably leaves lone-pairs on the oxygens that are characterized in the electronic band structure of the materials by non-bonding localized O(2p) states lying between the antibonding (MO*) states of the d-band and the bonding (MO) states of the p-band (see the ESI,† Fig. S5). Because these localized O(2p) states do not overlap with the transition metal d-orbitals, their chemical potential primarily depends on the electrostatic field exerted by the other ions in the crystal which in turns, depends on the charge distribution in the materials, i.e. on the M–O bond covalency.21 Hence, although these pure O(2p) states arise from symmetry, their relative energy in the electronic band structure of Li-rich layered TM-oxides is influenced by the degree of the M–O covalency and by the Li-content through the O2−–Li+ stabilizing interactions.21,22 The energy of the O(2p) states with respect to the d-band is therefore an important question, as it determines whether or not they can participate to the electrochemical reactions.To evidence the participation of these localized O(2p) states in the redox activity of LLOs, it is useful to focus on the d0−x case in Li2MO3 structures (M = Ti, Zr, Hf). For these structures, the nominal oxidation state of the transition metal is 4+, leading to an electronic structure characterized by one fully occupied low-lying band (generally labelled as the p-band) and one fully empty high-lying band (generally labelled as the d-band), both separated by a band gap. This is confirmed by the Density of States (DOS) of Li2MO3 (M = Ti, Zr, and Hf) showing large band gaps of 3.1, 4.4, and 4.9 eV, respectively (see Fig. 3 and ESI,† Fig. S6). This suggests that these materials will exhibit poor electronic conductivity and poor electrochemical activities. Nevertheless, if an electrochemical activity could be achieved for these d0−x materials, our DOS results show that holes should be created on pure O(2p) states lying just below the Fermi level, leading to a partially-filled O(2p)-band that might split to stabilize the total energy of the system. As shown in Fig. 3b, the splitting of the pure O(2p)-band is achieved through the formation of peroxo-groups (O2)2− between the O4i ions inside the TM layer, with an O–O distance of ∼1.5 Å. The total energies of the systems then decrease by about 0.64, 1.01, and 0.91 eV per formula unit for LiTiO3, LiZrO3 and LiHfO3 phases, respectively. In response to the geometry variations, the electronic structures of LiMO3 (M = Ti, Zr, and Hf) show that the 2p states of the O8j ions only shift slightly, while the 2p states of the O4i ions split into the characteristic peaks of (O–O) dimers: the σ and π bonding states shift to significantly lower energies, while the corresponding σ* antibonding states are depleted and push above the Fermi level, which is now reset on the top of the π* antibonding states of the peroxo groups. Furthermore, as the O4i ions are oxidized from −2 to −1 (Fig. 3c), the electric neutrality of the LiMO3 (M = Ti, Zr, and Hf) phases is maintained (Li+M4+(O8j)24− [(O4i)22−]1/2). Although the formation of the peroxo groups between O4i ions is helpful to reduce the total energy of the system, the enhanced O4i–O4i interactions also result in much longer and weaker M–O4i bonds. According to our estimations, the COOP integration of the M–O bonds decreases by about 42%, 47%, and 35% for LiTiO3, LiZrO3, and LiHfO3 systems, respectively, as depicted in Fig. 2b. Therefore, the peroxo groups de-coordinate from the metal oxide network, and the oxygen oxidation should be irreversible. It should be noted here that similar electronic structures are obtained for d1−x metals at x = 1 and for d2−x metals at x = 2. Hence, if an electrochemical activity could be achieved in such poorly conductive d0-based LLOs, an irreversible anionic activity would occur ending by a reductive elimination of O2 and by a LixMO3 to LixMO2 or MO2 phase decomposition that would most likely start at the surface of the particles. This is consistent with the report of Thackeray et al. on Li2TiO3 and Li2ZrO3 showing either no electrochemical reaction or high irreversibility,38 and with the Material Project database showing that either LiMO2 or MO2 polymorphs exist for all d0 metals, irrespectively of their structure-type. This is also consistent with a recent study on Li1.3−xNb0.3Mn0.4O2 showing that niobium ions (Nb5+, 4d0) are electrochemically inactive, and that charge compensation in this compound is achieved by the redox of oxygen anions coupled with the redox of manganese.18 Clearly, the combination of Nb5+(4d) and Mn3+(3d) here allows stabilizing the oxygen network by increasing the M–O covalency (compared to the pure Mn-based system) and decreasing the band gap with a lighter and partially-filled 3d metal (compared to the pure Nb-based system). Nevertheless, this Nb/Mn-based material also shows capacity fade upon cycling, in full agreement with our expectation of irreversible anionic activity in M(3d)-based LLOs at a high charging rate.18
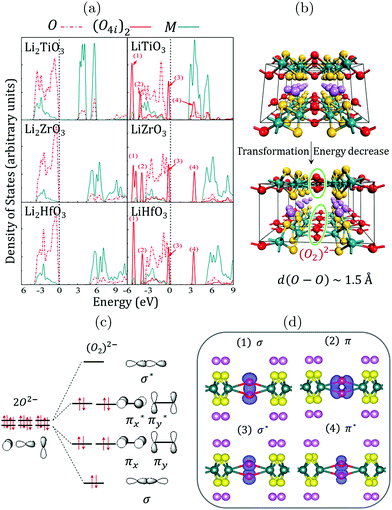 | ||
| Fig. 3 (a) Atom-projected Density of States (DOS) computed for the d0 Li2MO3 (left) and LiMO3 (right) phases (M = Ti, Zr, Hf) within the DFT+U framework using Ueff = 3 eV for the transition metals. The global shape of the DOS is preserved whatever is the functional used in the calculations (see the ESI,† Fig. S6). (b) Structural transformation occurring when removing one Li from the lattice showing the formation of short O–O bonds with d(O–O) ∼ 1.5 Å within the TM layer. (c) Local reorganization of the TM coordination sphere and qualitative representation of the (O2)2− molecular orbitals. (d) Visualization of the crystal orbitals identified in the DOS and labelled from (1) to (4). | ||
For 4dn and 5dn (n ≥ 2) metal configurations in Li2MO3, the electronic band structures of the materials show significant d/p-band overlap and the relative energy of the localized O(2p) states with respect to the Fermi level is now very sensitive to the subtle interplay between the M–O covalency, d-electron correlation and d-band filling (and therefore very sensitive to the functional used in the calculations). Recent experimental investigations of the Li2−xMO3 (M = Mo, Ru, Ir) electrode15,20,39 have suggested a cumulative cationic (M4+/M6+) and anionic (O2−/(O2)n−) redox activity upon delithiation from Li2MO3 to MO3. This result is consistent with our structural relaxations showing that some O–O bonds are formed upon delithiation, with however rather long distances from 2.3–2.5 Å (see the ESI,† Table S3). In contrast to Li-rich TM-oxides based on 3d metals, these weak dimers do not de-coordinate from the lattice and are systematically found for 4d metals with a d2 to d4 filling and 5d metals with a d2 to d6 filling. The crystal structures pertaining to these long O–O dimers are very similar to the one recently reported for the Ru-based Li2−xRuO3 electrode,21 in which a reductive coupling mechanism (RCM) has been proposed to rationalize the structural and electronic transformation occurring during the second anionic process. This mechanism results from the pinning of both the (MO*) antibonding states of the d-band and the pure O(2p) localized states of the p-band at the Fermi level, which induces an electronic instability (degenerated ground-state) that can be removed through a reorganisation of the O-network, similar to a Jahn–Teller distortion.21 This allows for stabilizing the (O–O) peroxo-like species in the delithiated structures thanks to significant M(d)–O2(σ) covalent bonding. It should be noted here that if the (MO) bonding states of the p-band were involved in the oxidation process, it will inevitably lead to structural instability as these states are the fundaments of the crystal structure integrity. The fact that pure O(2p) states, with no interaction with the metal d-orbitals, (non-bonding states) are present in the electronic structure of Li-rich TM-oxides clearly avoids M–O bond destabilization when they are involved in the oxidation process (see Fig. 2b). Such a feature of the electronic structure was already reported in the high-capacity LixMP4 electrodes40–42 for which the large P/M ratio induces a large number of pure non-bonding P(3p) states at the Fermi level responsible for the impressive extra-capacity of these materials with limited structural degradation upon cycling. The “Li-poor” LiMO2 TM-oxides by having a lower O/M ratio do not present such pure O(2p) states in their electronic band structure (see the ESI,† Fig. S5), therefore avoiding a reductive coupling mechanism to occur to stabilize the O-network upon delithiation. In the same line, Li-extra-rich Li3MO4 are expected to exhibit more oxygen lone-pairs, i.e. more O(2p) states in their electronic structure, which could be an advantage for reaching higher anionic extra-capacities than Li2−xMO3 electrodes.
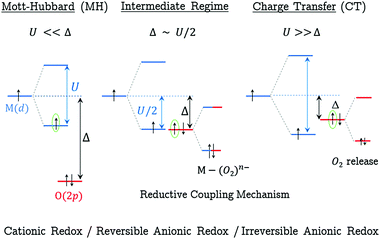
In order to give a global picture of the different redox mechanisms discussed above, it is helpful to use the qualitative Zaanen–Sawatsy–Allen picture of Mott–Hubbard vs. charge-transfer insulators.43 In this representation, the electronic band structure of a given material can be inferred from the U/Δ ratio where U and Δ stand for the on-site (TM) Coulomb repulsion and the charge-transfer parameter, respectively. As shown in Fig. 4, a Mott–Hubbard regime (MH) is predicted when U ≪ Δ. In this case, the d-band built on (MO*) antibonding states lies at the Fermi level, suggesting a cationic redox when Li is extracted from the material. In contrast, a charge-transfer regime (CT) is predicted when U ≫ Δ. In this case, the O(2p) states of the p-band lie at the Fermi level, suggesting an anionic redox. As demonstrated above and in previous theoretical21 and experimental14 works, such anionic redox is likely irreversible due to the generation of highly unstable holes on localized states, leading to highly reactive O−˙ radicals. As discussed above, this situation leads to the formation of peroxo species with small O–O distances lower than 1.5 Å which de-coordinate from the metallic network, leading to progressive material decomposition over the electrochemical cycles.21 An interesting scenario arises from the intermediate regime when U/2 ∼ Δ. In that case, both the (MO*) states and the O(2p) states lie at the Fermi level and the removal of Li leads to a partially-filled degenerated electronic state which is unstable with respect to a collective distortion (CD) such as a Jahn–Teller-type distortion. By lowering the local symmetry, the distortion enables the (MO*) and O(2p) states to interact, leading to the formation of M(d)–O2(σ) covalent bonds and charge reorganization between M and O.21 Because it affects both the (MO*) and the O(2p) states, this redox mechanism should be described as a mixed anionic and cationic redox. Nevertheless, as shown experimentally, both the structural and electronic modifications coming along with this redox process are mainly visible on the O-network, the reason why this mechanism is here seen as a reversible anionic redox in opposition with the irreversible anionic redox predicted when U ≫ Δ.
Using the general picture of Fig. 4 to classify the various Li2−xMO3 materials in each specific scenario is tempting but still hazardous at this stage as the relative energy of the d- vs. p-band (i.e. the U/Δ ratio) is known to be strongly functional-dependent.44 General trends can however be outlined from our study. In the following discussion, only the M-based LLOs being stable in the fully lithiated composition Li2MO3 (see the ESI,† Table S1) are considered. Given that 3d metals exhibit a larger U and weaker M–O bond covalency than 4d and 5d metals, a CT regime is expected for all M(3d)-based LLOs (M = Ti, Mn, Fe, Co Ni), as well as for the poorly conductive M(4d)-based LLOs with a d0 electronic configuration (M = Zr). This is consistent with the high structural instability of these electrodes with respect to O2 release when Li is removed from the Li2MO3 layered phases. For 4d and 5d metals where U is reduced compared to 3d, a crossover from the MH to the CD regime is expected when going from early (low d2) to late M (high d6) transition metals, consistent with the higher structural stability of these systems upon the first oxidation process from Li2MO3 to LiMO3. At higher charging, a MH to CD or a CD to CT crossover is expected for these 4d-and 5d-based systems due to the depletion of electrons from the metallic d-band and the concomittant U increase.
In a more prospective approach, the general picture of Fig. 4 can also be used to infer the behavior of other transition metal oxides. Following the basic concepts of electronic band structure theory, the variation of the U/Δ ratio can be deduced from the change in the crystal structure and/or Li–M–O stoichiometry. (i) For a given stoichiometry, i.e. one given oxidation state for the transition metal, the Δ parameter depends only weakly on the crystal structure and can be considered as constant. (ii) In contrast, the U parameter strongly depends on the Li–M–O stoichiometry through the bandwidth, i.e. the ability of the electron to delocalize over the system. When the O/M ratio is varied, the topology of interactions in the structure is strongly affected through the variation of the MOn polyhedral interconnections. Hence, the more compact the structure, the larger the bandwidth and the lower the U parameter. All transition metal oxides having the same Li–M–O stoichiometry (one given transition metal in one given oxidation state) are thus expected to belong to the same regime (MH, CT or CD), irrespectively of their structure-type. In contrast, a change in Li–M–O stoichiometry will favor a change of the regime for each given Mn+ ion. As an example, going from LiMO3 to Li3MO4 is expected to increase the U parameter and therefore promote a CD or CT regime over MH. Finally, for transition metal oxides having the appropriate U/Δ ratio to favor a CD intermediate state, an important requirement to achieve a reversible anionic redox is the occurrence of O(2p) lone-pairs. Such lone-pairs arise from the system symmetry and indirectly from the O/M ratio. It is therefore irrelevant to seek for a CD regime in systems having no oxygen lone-pairs as it would result in the removal of electrons from the bonding MO states and inevitably alter the material structure stability.
V. Conclusion
Relying on first-principles calculations, the structural stabilities and redox mechanisms of the Li-rich layered Li2−xMO3 phases (LLOs) were investigated for the series of 3d, 4d and 5d metals. The propensity of these systems to release lattice oxygen is shown to be gradually more favorable when increasing the d-shell electron number, decreasing the TM–O covalency and decreasing the lithium content in the lattice. Due to the larger O/M ratio occurring in the Li-rich Li2MO3 phases compared to LiMO2, some of the O(2p)-orbitals have not the right symmetry to interact with the metal d-orbitals which leaves pure O(2p) states corresponding to oxygen lone-pairs at the top portion of the p-band. The relative energy of these O(2p) lone-pairs with respect to the antibonding (MO*) states of the d-band indirectly depends on the M–O covalency through the system electrostatics and is then a crucial parameter that determines which states are involved in the electrochemical activity of the LLOs.The redox mechanisms of the LLOs were then deduced from the subtle balance between the TM(nd)–O(2p) covalency and the electronic coulombic repulsions in the d-shell (i.e. U/Δ ratio) and from the dn electronic configuration of the transition metal in the Li2−xMO3 electrodes. This allowed us to link the well-known classification of charge-transfer vs. Mott–Hubbard insulators of Zaanen–Zawatzky–Allen to the redox mechanisms susceptible to occur in LLOs as a function of the transition metal row and dn electronic configuration. An irreversible anionic redox leading to oxygen loss upon charge is predicted in the charge transfer regime, i.e. for all M(3d)-based LLOs and for heavier M(4d/5d)-based LLOs with a metallic d0 electronic configuration (empty d-band) due to the occurrence of the O(2p) lone-pair states at the Fermi level. No matter if the radical anions O−˙ generated by Li-removal directly react with the electrolyte or form peroxo (O2)2− species no longer coordinated to the metallic network, O-loss seems inevitable for these electrodes at high charging. Reversible extra capacities and long-term cycling are then very unlikely for 3d- and d0-based LLOs. A reversible cationic redox is predicted for 4d and 5d-based LLOs exhibiting low dn electronic configurations when the Fermi level leaves the (MO*) states of the d-band far above the O(2p) states of the p-band. Finally, a reversible anionic redox (or a mixed cationic and anionic redox) is predicted for 4d and 5d-based LLOs exhibiting higher dn electron configurations (or low Li-content) when both the (MO*) states and the O(2p) states lie at the Fermi level. This regime, previously denoted as a “reductive coupling mechanism” in a more local picture, postpones or even prevents oxygen release from the lattice. Although cationic migration phenomena were also observed in these materials upon high charging, it is clear that the high structural stability provided by the use of heavier 4d and 5d metals is the key for a reversible extra-capacity to be achieved in these Li2−xMO3 electrodes.
Author contributions
All authors contributed equally to this work.Competing financial interest
The authors declare no competing financial interest.Acknowledgements
Y. X. thanks the National Natural Science Foundation of China for funding his stay in Institut Charles Gerhardt through the grant no. 21301052. MS and MLD thank the Agence National pour la Recherche and the National Center of Resources (CINES) for supporting the research on Li-rich transition metal oxides through the grant ANR-14-CE05-0020-05 and the project number cmm6691.References
- S. Hy, H. Liu, M. Zhang, D. Qian, B.-J. Hwang and Y. S. Meng, Performance and design considerations for lithium excess layered oxide positive electrode materials for lithium ion batteries, Energy Environ. Sci., 2016, 9, 1931–1954 CAS.
- M. S. Whittingham, Lithium Batteries and Cathode Materials, Chem. Rev., 2004, 104, 4271–4302 CrossRef CAS PubMed.
- K. Mizushima, P. C. Jones, P. J. Wiseman and J. B. Goodenough, LixCoO2 (0 < x < 1): A new cathode material for batteries of high energy density, Mater. Res. Bull., 1980, 15, 783–789 CrossRef CAS.
- J. N. Reimers and J. R. Dahn, Electrochemical and In Situ X-Ray Diffraction Studies of Lithium Intercalation in LixCoO2, J. Electrochem. Soc., 1992, 139(8), 2091–2097 CrossRef CAS.
- T. Ohzuku and Y. Makimura, Layered lithium insertion material of LiCo1/3Ni1/3Mn1/3O2 for lithium-ion batteries, Chem. Lett., 2001, 642–643 CrossRef CAS.
- Z. Lu, D. D. MacNeil and J. R. Dahn, Layered Li[NixCo12xMnx]O2 Cathode Materials for Lithium-Ion Batteries, Electrochem. Solid-State Lett., 2001, 4, A200–A203 CrossRef CAS.
- M. M. Thackeray, C. S. Johnson, J. T. Vaughey, N. Li and S. A. Hackney, Advances in manganese-oxide composite™ electrodes for lithium-ion batteries, J. Mater. Chem., 2005, 15, 2257–2267 RSC.
- T. Ohzuku, M. Nagayama, K. Tsuji and K. Ariyoshi, High-capacity lithium insertion materials of lithium nickel manganese oxides for advanced lithium-ion batteries: toward rechargeable capacity more than 300 mA h g−1, J. Mater. Chem., 2011, 21, 10179–10188 RSC.
- A. Ito, D. Li, Y. Sato, M. Arao, M. Watanabe, M. Hatano, H. Horie and Y. Ohsawa, Cyclic deterioration and its improvement for Li-rich layered cathode material Li[Ni0.17Li0.2Co0.07Mn0.56]O2, J. Power Sources, 2010, 195, 567–573 CrossRef CAS.
- A. R. Armstrong, M. Holzapfel, P. Novk, C. S. Johnson, S.-H. Kang, M. M. Thackeray and P. G. Bruce, Demonstrating Oxygen Loss and Associated Structural Reorganization in the Lithium Battery Cathode Li[Ni0.2Li0.2Mn0.6]O2, J. Am. Chem. Soc., 2006, 128, 8694–8698 CrossRef CAS PubMed.
- E. Lee and K. A. Persson, Structural and Chemical Evolution of the Layered Li-Excess LixMnO3 as a Function of Li Content from First-Principles Calculations, Adv. Energy Mater., 2014, 4, 1400498 CrossRef.
- D. Qian, B. Xu, M. Chi and Y. S. Meng, Uncovering the roles of oxygen vacancies in cation migration in lithium excess layered oxides, Phys. Chem. Chem. Phys., 2014, 16, 14665–14668 RSC.
- J. R. Croy, H. Iddir, K. Gallagher, C. S. Johnson, R. Benedek and M. Balasubramanian, First-charge instabilities of layered-layered lithium-ion-battery materials, Phys. Chem. Chem. Phys., 2015, 17, 24382–24391 RSC.
- K. Luo, M. R. Roberts, R. Hao, N. Guerrini, D. M. Pickup, Y.-S. Liu, K. Edstrm, J. Guo, A. V. Chadwick, L. C. Duda and P. G. Bruce, Charge-compensation in 3d-transition-metal-oxide intercalation cathodes through the generation of localized electron holes on oxygen, Nat. Chem., 2016, 8, 684–691 CrossRef CAS PubMed.
- M. Sathiya, G. Rousse, K. Ramesha, C. P. Laisa, H. Vezin, M.-T. Sougrati, M.-L. Doublet, D. Foix, D. Gonbeau, W. Walker, A. S. Prakash, M. Ben Hassine, L. Dupont and J.-M. Tarascon, Reversible anionic redox chemistry in high-capacity layered-oxide electrodes, Nat. Mater., 2013, 12, 827–835 CrossRef CAS PubMed.
- M. Sathiya, K. Ramesha, G. Rousse, D. Foix, D. Gonbeau, A. S. Prakash, M. L. Doublet, K. Hemalatha and J. M. Tarascon, High Performance Li2Ru1yMnyO3 (0.2 y 0.8) Cathode Materials for Rechargeable Lithium-Ion Batteries: Their Understanding, Chem. Mater., 2013, 25, 1121–1131 CrossRef CAS.
- M. Sathiya, A. M. Abakumov, D. Foix, G. Rousse, K. Ramesha, H. Vezin, C. P. Laisa, A. Prakash, D. Gonbeau, M. Saubanre, M.-L. Doublet, G. VanTendeloo and J.-M. Tarascon, Origin of voltage decay in high-capacity layered oxide electrodes, Nat. Mater., 2015, 14, 230–238 CrossRef CAS PubMed.
- N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, High-capacity electrode materials for rechargeable lithium batteries: Li3NbO4-based system with cation-disordered rocksalt structure, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650–7655 CrossRef CAS PubMed.
- M. Sathiya, J.-B. Leriche, E. Salager, D. Gourier, J.-M. Tarascon and H. Vezin, Electron paramagnetic resonance imaging for real-time monitoring of Li-ion batteries, Nat. Commun., 2015, 6, 6276 CrossRef CAS PubMed.
- E. McCalla, A. M. Abakumov, M. Saubanere, D. Foix, E. J. Berg, G. Rousse, M.-L. Doublet, D. Gonbeau, P. Novak, G. Van Tendeloo, R. Dominko and J.-M. Tarascon, Visualization and impact of O–O peroxo-like dimers in high capacity layered oxides for Li-ion batteries, Science, 2015, 350, 1516–1521 CrossRef CAS PubMed.
- M. Saubanere, E. McCalla, J. M. Tarascon and M. L. Doublet, The Intriguiging Question of Anionic Redox in High-Energy Density Cathodes for Li-ion Batteries, Energy Environ. Sci., 2016, 9, 984–991 CAS.
- D.-H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials, Nat. Chem, 2016, 8, 692–697 CrossRef CAS PubMed.
- Y. Koyama, I. Tanaka, M. Nagao and R. Kanno, First-principles study on lithium removal from Li2MnO3, J. Power Sources, 2009, 189, 798–801 CrossRef CAS.
- M. Gu, I. Belharouak, J. Zheng, H. Wu, J. Xiao, A. Genc, K. Amine, S. Thevuthasan, D. R. Baer, J.-G. Zhang, N. D. Browning, J. Liu and C. Wang, Formation of the spinel phase in the layered composite cathode used in Li-ion batteries, ACS Nano, 2013, 7, 760–767 CrossRef CAS PubMed.
- N. Yabuuchi, K. Yoshii, S.-T. Myung, I. Nakai and S. Komaba, Detailed Studies of a High-Capacity Electrode Material for Rechargeable Batteries, Li2MnO3-LiCo1/3Ni1/3Mn1/3O2, J. Am. Chem. Soc., 2011, 133, 4404–4419 CrossRef CAS PubMed.
- J. Hong, H.-D. Lim, M. Lee, S.-W. Kim, H. Kim, S.-T. Oh, G.-C. Chung and K. Kang, Critical Role of Oxygen Evolved from Layered LiExcess Metal Oxides in Lithium Rechargeable Batteries, Chem. Mater., 2012, 24, 2692–2697 CrossRef CAS.
- S. Hy, F. Felix, J. Rick, W.-N. Su and B. J. Hwang, Direct In situ Observation of Li2O Evolution on Li-Rich High-Capacity Cathode Material, Li[NixLi(12x)/3Mn(2x)/3]O2 (0 < x < 0.5), J. Am. Chem. Soc., 2014, 136, 999–1007 CrossRef CAS PubMed.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- S. P. Ong, L. Wang, B. Kang and G. Ceder, Li–Fe–P–O2, Phase Diagram from First Principles Calculations, Chem. Mater., 2008, 20(5), 1798–1807 CrossRef CAS.
- A. Jain, G. Hautier, S. P. Ong, C. Moore, C. Fischer, K. Persson and G. Ceder, Formation enthalpies by mixing GGA and GGA+U calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(4), 045115 CrossRef.
- R. Xiao, H. Li and L. Chen, Density Functional Investigation on Li2MnO3, Chem. Mater., 2012, 24, 4242–4251 CrossRef CAS.
- J.-M. Lim, D. Kim, Y.-G. Lim, M.-S. Park, Y.-J. Kim, M. Cho and K. Cho, Mechanism of oxygen vacancy on impeded phase transformation and electrochemical activation in inactive Li2MnO3, ChemElectroChem, 2016, 3, 943–949 CrossRef CAS.
- B. Li, R. Shao, H. Yan, L. An, B. Zhang, H. Wei, J. Ma, D. Xia and X. Han, Understanding the Stability for Li-Rich Layered Oxide Li2RuO3 Cathode, Adv. Funct. Mater., 2016, 26, 1330–1337 CrossRef CAS.
- R. Dronskowski and P. E. Blchl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97, 8617–8624 CrossRef CAS.
- H. Iddir, J. Bareno and R. Benedek, Stability of Li- and Mn-Rich Layered-Oxide Cathodes within the First-Charge Voltage Plateau, J. Electrochem. Soc., 2016, 163, A1784–A1789 CrossRef CAS.
- M. Oishi, K. Yamanaka, I. Watanabe, K. Shimoda, T. Matsunaga, H. Arai, Y. Ukyo, Y. Uchimoto, Z. Ogumi and T. Ohta, Direct observation of reversible charge compensation by oxygen ion in Li-rich manganese layered oxide positive electrode material, Li1.16Ni0.15Co0.19Mn0.50O2, J. Mater. Chem. A, 2016, 4, 9293–9302 CAS.
- H. Koga, L. Croguennec, M. Mntrier, P. Mannessiez, F. Weill and C. Delmas, Reversible Oxygen Participation to the Redox Processes Revealed for Li1.20Mn0.54Co0.13Ni0.13O2, J. Power Sources, 2013, 236, 250–258 CrossRef CAS.
- J. T. Vaughey, A. M. Geyer, N. Fackler, C. S. Johnson, K. Edstrom, H. Bryngelsson, R. Benedek and M. M. Thackeray, Studies of layered lithium metal oxide anodes in lithium cells, J. Power Sources, 2007, 174, 1052–1056 CrossRef CAS.
- J. Ma, Y.-N. Zhou, Y. Gao, X. Yu, Q. Kong, L. Gu, Z. Wang, X.-Q. Yang and L. Chen, Feasibility of Using Li2MoO3 in Constructing Li-Rich High Energy Density Cathode Materials, Chem. Mater., 2014, 26, 3256–3262 CrossRef CAS.
- M.-L. Doublet, F. Lemoigno, F. Gillot and L. Monconduit, The LixVPn4 Ternary Phases (Pn = P, As): Rigid Networks for Lithium Intercalation/Deintercalation, Chem. Mater., 2002, 14, 4126–4133 CrossRef CAS.
- D. C. S. Souza, V. Pralong, A. J. Jacobson and L. F. Nazar, A reversible solid-state crystalline transformation in a metal phosphide induced by redox chemistry, Science, 2002, 296(5575), 2012–2015 CrossRef CAS PubMed.
- M.-P. Bichat, F. Gillot, L. Monconduit, F. Favier, M. Morcrette, F. Lemoigno and M.-L. Doublet, Redox Induced Structural Change in Anode Materials Based on (MPn4)x− Transition Metal Pnictides, Chem. Mater., 2004, 16, 1002–1013 CrossRef CAS.
- J. Zaanen, G. A. Sawatzky and J. W. Allen, Band gaps and electronic structure of transition-metal compounds, Phys. Rev. Lett., 1985, 55, 418–421 CrossRef CAS PubMed.
- D. W. Seo, A. Urban and G. Ceder, Calibrating transition-metal energy levels and oxygen bands in first-principles calculations: Accurate prediction of redox potentials and charge transfer in lithium transition-metal oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115118 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ee02328b |
| ‡ Permanent address: Key Laboratory of Functional Inorganic Material Chemistry, Ministry of Education – School of Chemistry and Materials Science, Heilongjiang University – Harbin 150080, P. R. China. |
| This journal is © The Royal Society of Chemistry 2017 |