Atmospheric implication of the hydrogen bonding interaction in hydrated clusters of HONO and dimethylamine in the nighttime†
Hailiang
Zhao
and
Lin
Du
 *
*
Environment Research Institute, Shandong University, Shanda South Road 27, 250100 Shandong, China. E-mail: lindu@sdu.edu.cn; Fax: +86 531 8836 6072; Tel: +86 531 8836 6072
First published on 1st December 2016
Abstract
In this study, the stability of clusters formed by the trans- and cis-isomers of nitrous acid (HONO) with dimethylamine (DMA) and water has been characterized by density functional theory. The large red shifts of the OH-stretching transitions of both HONO isomers in the clusters indicate the formation of strong hydrogen bonds. At standard temperature and pressure, H2O (acceptor) binds to HONO (donor) with binding energies of −25.0 to −24.6 kJ mol−1, less stable than those of DMA (acceptor) with HONO (donor) (−50.5 to −45.3 kJ mol−1). Our findings indicate that hydration enhances proton transfer from HONO to DMA, and consequently increases the interaction strength (binding energies = −67.8 to −78.6 kJ mol−1). The topological and generalized Kohn–Sham energy decomposition confirms strong hydrogen bond interactions. The clustering of HONO with DMA in the atmosphere is negligible as compared to the important H2SO4–DMA clusters.
Environmental impactHONO as an important atmospheric species starts to accumulate at nighttime. The chemistry of HONO has aroused research interest, but studies on clustering interactions from a molecular perspective are limited. In this paper, we provide an overview of the hydrogen bonding interactions between HONO and dimethylamine (DMA), and then demonstrate that hydration promotes proton transfer from HONO to DMA. |
Introduction
Amines have been confirmed as potential stabilizers for atmospheric nucleation, enhancing new particle formation and growth.1–4 About 150 amines have been identified in the atmosphere. The total emission of amines, including monomethylamine (MMA), dimethylamine (DMA) and trimethylamine (TMA), is estimated to be ∼300 Gg N a−1 globally.5 Their atmospheric sources include anthropogenic sources (animal husbandry, industries and combustion, etc.) and natural sources (ocean organisms, biomass burning, vegetation, geologic sources, etc.).5 Amines can modify the acid/base nature of aerosols.6Nitrous acid (HONO) is a source of the most important daytime radical, the OH radical, and its photolysis during the daytime may account for 30–60% of the OH production.7,8 HONO could be formed by the heterogeneous conversion of NO2 on wet surfaces:9
| 2NO2 + H2O → HONO + HNO3 | (1) |
The heterogeneous conversion of NO2 on adsorbed hydrocarbons (HC) is also of importance:10,11
| NO2 + HCred → HONO + HCox | (2) |
The following two heterogeneous reactions have been suggested to explain the observed nighttime reactions:12
| NO + NO2 (or N2O3) + H2O → 2HONO | (3) |
| HNO3(ads) + NO(g) → HONO + NO2 | (4) |
In addition, the photo-induced heterogeneous reactions have been suggested to be potential sources of daytime HONO, for example, the photosensitized reduction of NO2 on an organic surface.13 On the other hand, the homogeneous formation pathways of HONO could also play an important role. HONO is formed by the reaction of NO with OH radicals:14,15
| OH + NO (+M) → HONO (+M) | (5) |
The reaction of electronically excited NO2 with H2O vapor could also be an important homogeneous source of HONO:16
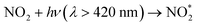 | (6) |
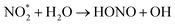 | (7) |
Furthermore, soil bacteria have been suggested as a significant source of the atmospheric HONO, which may account for up to 50% of the reactive nitrogen released from soil.17
Direct emissions are another source of HONO: combustion processes,18 diesel engines,19 gas space heaters and stoves,20etc. The photolytic life time of HONO is only about 10 minutes at midday during summer time, due to the rapid production of OH and NO by absorbing sunlight at wavelengths shorter than 390 nm during the daytime.21 At nighttime, the photolytic loss mechanism stops. As a result, HONO starts to accumulate with concentrations of 0.1–10 ppbv and decreases rapidly after sunrise.22–24 The concentration of HONO was observed to be 1.4 and 0.4–0.5 ppbv in the morning and in the afternoon, respectively, for the urban atmosphere of New York City.25 In contrast, the concentrations of sulfuric acid (H2SO4) in the atmospheric boundary layers are about 0.04–1.2 pptv, which are much less than those of HONO.26
HONO can form hydrogen bonded complexes with other compounds. The complexes formed between HONO and ethene,27 diethyl ether,28 and acetone28 have been studied in argon matrices. The red shifts of the OH-stretching vibrational transitions were found to be 136, 376 and 413 cm−1 for ethene,27 diethyl ether28 and acetone28 with respect to the trans-HONO monomer, respectively. The investigation of the structural, energetic, and spectroscopic parameters of the hydrogen bonded complexes formed by HONO with many atmospheric species could help to understand its contribution to atmospheric clustering.
Hydrogen bonding interactions have been commonly suggested as the driving forces for the formation of atmospheric molecular complexes, and the corresponding hydrogen bonding strength reveals the thermodynamic stability of these complexes.4,29–31 H2SO4 has been well accepted as one of the crucial nucleating species.32–34 Besides H2SO4, other nucleating precursors, such as ammonia, amines, and organic compounds, have been suggested to be involved in the formation of the critical nucleus by serving as stabilizing components.4 For example, DMA can promote H2SO4–water nucleation in the atmosphere.3,26 The experiments in the CLOUD (Cosmics Leaving OUtdoor Droplets) chamber at CERN show that amines can enhance particle formation rates more than 1000 times as compared with NH3.26 The lifetime of DMA against OH in the atmosphere is 4.3 h.35 Since the concentration of OH decreases dramatically at nighttime and the lifetime of DMA becomes much longer, it is an interesting and essential topic to study the initial clustering steps involving amines.
In the present work, we report the hydrogen bonding interactions of HONO with atmospheric species (DMA, water) at nighttime. The most stable structures of the hydrogen bonded complexes and the changes in the structural and vibrational characteristics of the monomers upon complexation are predicted. Atoms in molecules (AIM) analysis was carried out to investigate the electronic densities and the inter-molecular hydrogen bonding interactions in the complexes.36,37 Generalized Kohn–Sham energy decomposition analysis (GKS-EDA) was performed to study the contribution of different components to the total interaction energy.38
Computational methods
All the structures were optimized using the B3LYP-D3 functional and the aug-cc-pVTZ basis set with the Gaussian 09 (Revision E.01) program.39 There is no imaginary frequency for the optimized structures and the zero-point vibrational energy (ZPVE) was evaluated using thermodynamic corrections at the B3LYP-D3/aug-cc-pVTZ level of theory. The choice of the B3LYP-D3 computational method is based on its good performance on atmospheric relevant clusters, including the prediction of Gibbs free energies, infrared frequencies and structural characteristics.40–44 In order to obtain explicit estimates of thermodynamic constants, two additional options, an extremely tight optimization convergence criteria (opt = verytight) and a very high accuracy grid integration (integral = ultrafine), were used in all DFT calculations.45,46Bader's theory of atoms in molecules (AIM) has been widely applied to understand and characterize both covalent and non-covalent molecular interactions.36,37 The topological properties of electron density ρ(r) at the bond critical point (BCP) have been widely used to get deep insight into the nature of the hydrogen bonding.47 The wavefunctions obtained at the B3LYP-D3/aug-cc-pVTZ level were used to evaluate the electron density ρ(r) and laplacian ∇2ρ(r) at the bond critical points and the atomic charge q(H) in the atomic basin of hydrogen. The topological analysis was carried out by utilizing the AIM2000 program (version 2) package for the monomers and complexes.
Hydrogen bonding interactions were investigated using a new energy decomposition analysis scheme (GKS-EDA) based on the generalized Kohn–Sham (GKS) and the localized molecular orbital energy decomposition analysis (LMO-EDA) scheme, which is implemented in the GAMESS (US) program.48 The total interaction energy (EINT) is divided into electrostatic energy (EES), exchange energy (EEX), repulsion energy (EREP), polarization energy (EPOL), Grimme's dispersion energy (EDISP) and correlation energy (ECORR).38
Results and discussion
Structure and stability
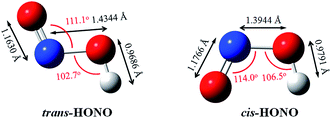
The gas phase nitrous acid (HONO) molecule is one of the smallest molecules that can adopt both a cis- and a trans-form (Fig. 1), and exhibits a cis–trans conformational equilibrium. In an early study, the isotopic IR spectra of HONO were obtained in the vapor and solid phases. The energy difference between trans-HONO and cis-HONO was 1.6 ± 4.2 kJ mol−1 with the trans-HONO being more stable, which was deducted from the temperature dependence of fundamentals of the two isomers and the isotopic frequencies of the torsion fundamentals.49 However, the barrier of inter-conversion obtained was as much as 40 kJ mol−1 through identifying all the observed fundamentals of both forms and fit into the barrier potential energy.49 The energy difference between the trans- and cis-form was calculated to be 2.7 kJ mol−1 (B3LYP-D3/aug-cc-pVTZ, with ZPVE correction), with the former being more stable. The structures of both forms were accurately determined on the basis of the inertial defects of microwave spectra.50 The key parameters rN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, rN–O, rO–H, θONO and θNOH for trans-HONO were found to be 1.170 Å, 1.432 Å, 0.958 Å, 110.7° and 102.1°, respectively. For cis-HONO, these parameters were determined to be 1.185 Å, 1.392 Å, 0.982 Å, 113.6° and 104.0°, respectively. Our calculated structures obtained at the B3LYP-D3/aug-cc-pVTZ level (Fig. 1) are consistent with these experimental values. The structural parameters of DMA have been experimentally determined based on the rotational constants in the microwave spectra,51 which are also in good agreement with our calculated values.
O, rN–O, rO–H, θONO and θNOH for trans-HONO were found to be 1.170 Å, 1.432 Å, 0.958 Å, 110.7° and 102.1°, respectively. For cis-HONO, these parameters were determined to be 1.185 Å, 1.392 Å, 0.982 Å, 113.6° and 104.0°, respectively. Our calculated structures obtained at the B3LYP-D3/aug-cc-pVTZ level (Fig. 1) are consistent with these experimental values. The structural parameters of DMA have been experimentally determined based on the rotational constants in the microwave spectra,51 which are also in good agreement with our calculated values.
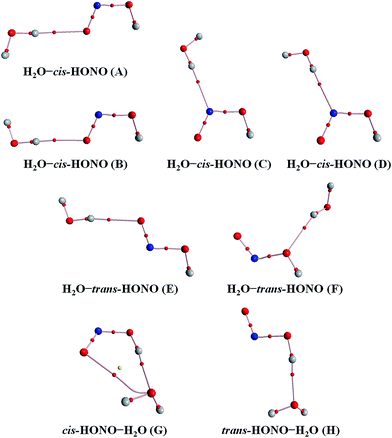
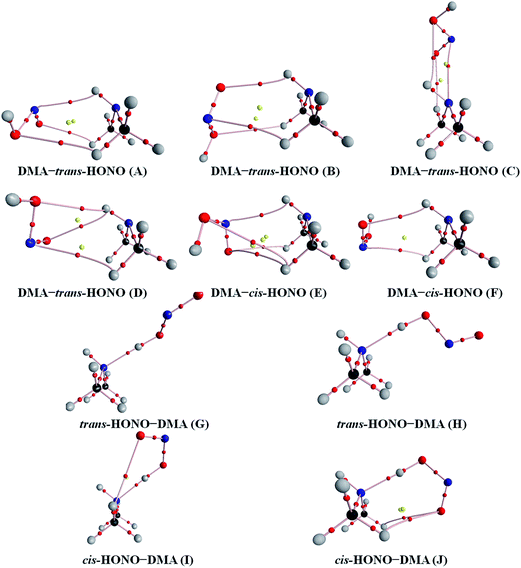
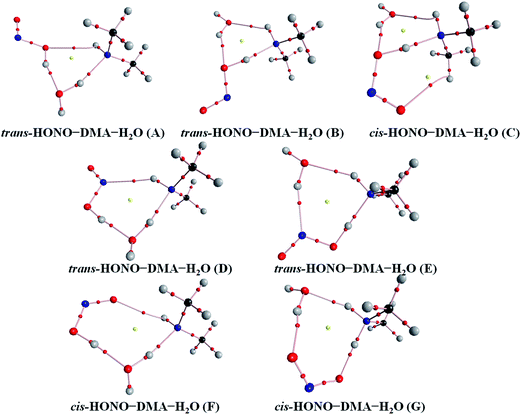
Quantum chemical calculations for the heterodimers (HONO–H2O, HONO–DMA, H2O–HONO, DMA–HONO) and the hydrated heterotrimer clusters (HONO–DMA–H2O) were performed to search for stable structures. In these heterodimers and heterotrimers, HONO can be a hydrogen bond donor or an acceptor. The optimized structures of the most stable clusters at the B3LYP-D3/aug-cc-pVTZ level are shown in Fig. 2–4. For the HONO–DMA–H2O heterotrimer, only cyclic ring structures were considered in this study.
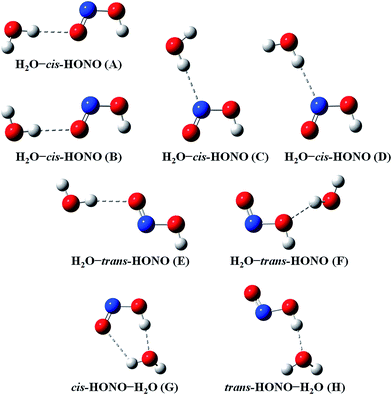 | ||
| Fig. 2 The stable structures of the heterodimer clusters consisting of one water and one HONO calculated at the B3LYP-D3/aug-cc-pVTZ level. | ||
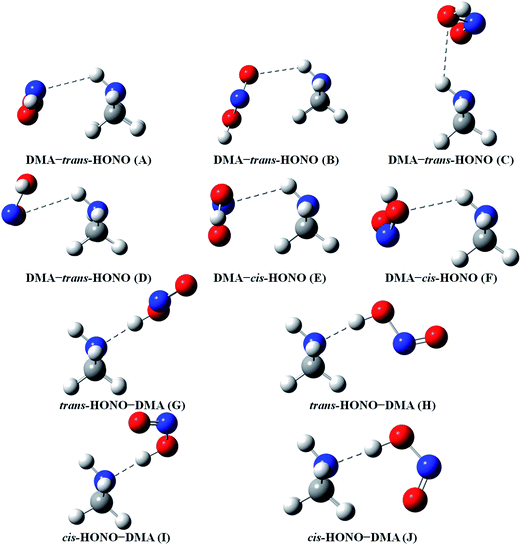 | ||
| Fig. 3 The stable structures of the heterodimer clusters consisting of one DMA and one HONO calculated at the B3LYP-D3/aug-cc-pVTZ level. | ||
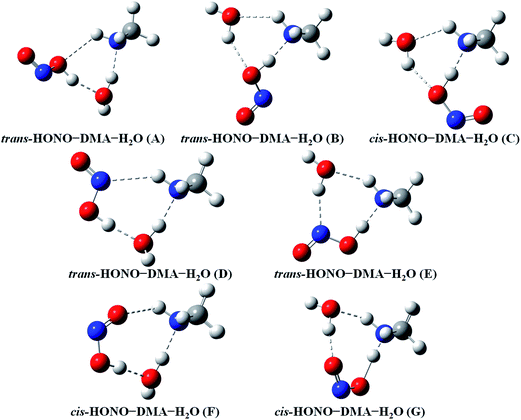 | ||
| Fig. 4 The stable structures of the heterotrimer clusters consisting of one water, one DMA and one HONO calculated at the B3LYP-D3/aug-cc-pVTZ level. | ||
In the HONO–DMA (G–J) and HONO–H2O (G–H) heterodimers, HONO acts as the hydrogen bond donor approaching DMA or H2O. Upon complexation, the changes in the OH bond length of the HONO–H2O (G–H) complexes vary from 0.0147 to 0.0167 Å, and the corresponding O–H⋯O hydrogen bond angles deviate within 10° from the ideal linear orientation. The changes in the OH bond length of the HONO–DMA (G–J) complexes are much larger (0.0448 to 0.0550 Å), and the corresponding O–H⋯N hydrogen bond angles (173.5–178.2°) are much closer to the linear orientation. The O–H⋯N hydrogen bonds between DMA and HONO are much stronger than the O–H⋯O hydrogen bonds between H2O and HONO. This is similar with the results for the trans-HONO–NH3 complex, where the hydrogen bond angle was calculated to be 175.8° (MP2/aug-cc-pVTZ).52 As compared with the HONO–acetone complex, the trans- and cis-HONO isomers deviate from a linear hydrogen bond of acetone: 170.3° for trans-HONO and 162.2° for cis-HONO (B3LYP/6-311++G**).53 In the nitric acid (HONO2)–H2O complex, the hydrogen bond angle (HONO2 as the hydrogen bond donor) was calculated to be 170.0° (B3LYP/6-31G**).54 When proton transfer occurs in the formation of the heterodimer clusters, the DMA molecule obtains the proton from HONO to form an N–H bond. On the other hand, others such as water and acetone form weak hydrogen bonds. In the DMA–HONO (A–F) and H2O–HONO (A–F) heterodimer clusters, HONO acts as the hydrogen bond acceptor. The changes in the OH bond length are small, 0.0021 to 0.0031 Å for H2O–HONO (A–F). In contrast, the changes in the NH bond length are −0.0006 to 0.0004 Å for DMA–HONO (A–F). The elongated hydrogen bonded XH length is a typical feature of the traditional hydrogen bonding. However, there is another type of hydrogen bonds known as improper hydrogen bonds, which shows a decrease of the bonded XH length upon complex formation.55,56
The HONO–DMA–H2O heterotrimers form six- to eight-membered ring structures. In the HONO–DMA–H2O (A, D, F) complexes, HONO binds with H2O to form an O–H⋯O hydrogen bond. Similar to the HONO–H2O (G–H) heterodimer complexes, the changes in the OH bond length of HONO are much larger in the HONO–DMA–H2O (B, C, E, G) complexes. However, the changes of the OH bond length as HONO binds with DMA are much larger, ranging from 0.0667 to 0.5182 Å, in the HONO–DMA–H2O (B, C, E, G) complexes than the HONO–DMA (G–J) complexes. We can clearly see the proton transfer from HONO to DMA. It may indicate that hydration enhances proton transfer (Table 1).
| Type | O–H⋯O/N (HONO) | N–H⋯O/N (DMA) | O–H⋯O/N (H2O) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Δra | r | θ | Δra | r | θ | Δra | r | θ | ||
| a Δr = rdimer − rmonomer, is the change in the OH bond length upon complexation. b Inter-molecular hydrogen bond distance. c Inter-molecular hydrogen bond angle. | ||||||||||
| H2O–HONO | (A) | — | — | — | — | — | — | 0.0021 | 2.1721 | 176.8 |
| (B) | — | — | — | — | — | — | 0.0020 | 2.1713 | 177.0 | |
| (C) | — | — | — | — | — | — | 0.0026 | 2.2181 | 177.0 | |
| (D) | — | — | — | — | — | — | 0.0027 | 2.2212 | 178.7 | |
| (E) | — | — | — | — | — | — | 0.0021 | 2.1708 | 171.0 | |
| (F) | — | — | — | — | — | — | 0.0031 | 2.0853 | 156.2 | |
| HONO–H2O | (G) | 0.0167 | 1.7846 | 170.9 | — | — | — | 0.0034 | 2.4363 | 113.5 |
| (H) | 0.0147 | 1.8076 | 170.6 | — | — | — | — | — | — | |
| DMA–HONO | (A) | — | — | — | −0.0003 | 2.5000 | 122.7 | — | — | — |
| (B) | — | — | — | −0.0004 | 2.4272 | 127.1 | — | — | — | |
| (C) | — | — | — | 0.0003 | 2.5436 | 123.9 | — | — | — | |
| (D) | — | — | — | −0.0002 | 2.6475 | 119.2 | — | — | — | |
| (E) | — | — | — | −0.0006 | 2.4775 | 119.3 | — | — | — | |
| (F) | — | — | — | −0.0003 | 2.4220 | 125.7 | — | — | — | |
| HONO–DMA | (G) | 0.0448 | 1.7083 | 176.7 | — | — | — | — | — | — |
| (H) | 0.0449 | 1.7079 | 173.5 | — | — | — | — | — | — | |
| (I) | 0.0537 | 1.6766 | 177.4 | — | — | — | — | — | — | |
| (J) | 0.0550 | 1.6740 | 178.2 | — | — | — | — | — | — | |
| HONO–DMA–H2O | (A) | 0.0260 | 1.7014 | 171.9 | 0.0031 | 2.6303 | 121.2 | 0.0360 | 1.6033 | 172.4 |
| (B) | 0.0667 | 1.7794 | 170.2 | 0.0037 | 2.8073 | 114.2 | 0.0056 | 1.5220 | 175.3 | |
| (C) | 0.0946 | 1.8573 | 168.6 | 0.0026 | 2.9844 | 107.2 | 0.0052 | 1.4407 | 178.2 | |
| (D) | 0.0322 | 1.6709 | 173.1 | 0.0037 | 2.4394 | 141.7 | 0.0411 | 1.7432 | 165.7 | |
| (E) | 0.0791 | 1.5885 | 179.7 | 0.0053 | 2.0562 | 144.0 | 0.0113 | 2.0072 | 158.2 | |
| (F) | 0.0339 | 1.6603 | 175.2 | 0.0018 | 2.4387 | 122.4 | 0.0418 | 1.7353 | 168.6 | |
| (G) | 0.5182 | 1.1067 | 175.9 | 0.0202 | 1.8162 | 146.6 | 0.0261 | 1.7408 | 168.0 | |
The calculated binding energy (BE), zero-point vibrational energy (ZPVE), enthalpy of formation (ΔHθ298K), and Gibbs free energy of formation (ΔGθ298K) at 298.15 K and 1 atm for the HONO heterodimer and heterotrimer complexes at the B3LYP-D3/aug-cc-pVTZ level are presented in Table 2. For the heterodimer complexes formed with the acid as the acceptor and DMA as the donor, the BEs show that the DMA–HONO (A–F) complexes are less stable (−8.7 to −6.0 kJ mol−1) than their corresponding analogues (−50.5 to −45.3 kJ mol−1) where the acid is the donor and DMA is the acceptor. The HONO–DMA complexes are slightly more stable than the trans-HONO–NH3 and cis-HONO–NH3 complexes (BEs = −40.1 and −36.4 kJ mol−1 (MP2/6-311+G(2d,2p)), respectively).57 For the HONO–H2O complexes, the BEs are −9.0 to −4.7 kJ mol−1 for the complexes with the acid as the acceptor and −25.0 to −24.6 kJ mol−1 for the complexes with the acid as the donor. In a previous study, the BEs of the trans-HONO–(CH3)2CO and cis-HONO–(CH3)2CO complexes were calculated to be −29.6 and −27.6 kJ mol−1 (MP2/6-311++G**), respectively.53 This may imply that (CH3)2CO is similar to H2O as a hydrogen bond acceptor. The BEs of the dimer clusters containing sulfuric acid and various amines (CH3NH2, (CH3)2NH, (CH3)3N, CH3CH2NH2, (CH3CH2)2NH, (CH3CH2)3N, and CH3CH2NHCH3) were calculated to be from −138.4 to −91.6 kJ mol−1 (RI-MP2/aug-cc-pV(D+d)Z).3 This reveals that H2SO4 is a stronger hydrogen bond donor than HONO.
| Type | BEb | ZPVE | ΔHθ298K | ΔGθ298K | |
|---|---|---|---|---|---|
| a Energies are in kJ mol−1. b BEs are corrected with ZPVE. | |||||
| H2O–HONO | (A) | −4.7 | 4.6 | −5.9 | 24.2 |
| (B) | −4.9 | 4.8 | −3.8 | 19.2 | |
| (C) | −4.8 | 5.1 | −4.0 | 20.2 | |
| (D) | −4.5 | 5.2 | −3.6 | 20.2 | |
| (E) | −5.1 | 5.0 | −4.1 | 20.3 | |
| (F) | −9.0 | 4.8 | −8.3 | 15.1 | |
| HONO–H2O | (G) | −25.0 | 8.9 | −27.0 | 9.9 |
| (H) | −24.6 | 7.8 | −25.3 | 6.1 | |
| DMA–HONO | (A) | −6.9 | 3.6 | −5.1 | 29.5 |
| (B) | −6.7 | 2.8 | −4.2 | 25.0 | |
| (C) | −8.3 | 2.9 | −5.7 | 24.4 | |
| (D) | −8.2 | 3.0 | −5.8 | 26.2 | |
| (E) | −8.7 | 3.6 | −7.1 | 29.1 | |
| (F) | −6.0 | 3.0 | −3.7 | 26.2 | |
| HONO–DMA | (G) | −50.5 | 7.0 | −49.8 | −13.1 |
| (H) | −48.2 | 7.1 | −48.0 | −9.3 | |
| (I) | −45.3 | 5.7 | −45.3 | −5.9 | |
| (J) | −46.9 | 6.4 | −47.4 | −4.5 | |
| HONO–DMA–H2O | (A) | −67.8 | 15.5 | −69.4 | 1.0 |
| (B) | −72.6 | 12.4 | −72.8 | −1.6 | |
| (C) | −73.9 | 10.8 | −74.5 | 0.5 | |
| (D) | −74.5 | 16.5 | −76.9 | −0.2 | |
| (E) | −79.3 | 14.2 | −80.8 | −4.8 | |
| (F) | −74.0 | 15.7 | −76.4 | 2.4 | |
| (G) | −78.6 | 18.1 | −81.8 | 1.8 | |
For the heterotrimer complexes, the BEs of −79.3 to −67.8 kJ mol−1 indicate that these complexes are very stable. The heterotrimer complexes are more stable than the heterodimer complexes because these heterotrimer complexes are formed via three hydrogen bonds, and the heterodimer complexes contain only one hydrogen bond. Moreover, the seven- and eight-membered heterotrimer complexes are slightly more stable than the six-membered heterotrimer complexes.
Calculated NH- and OH-stretching transitions
The vibrational frequency shifts to lower wavenumbers and the infrared intensities of the stretching vibrational transitions of the monomer increase upon complexation. The red shift (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) is the wavenumber difference between the free and hydrogen bonded NH-/OH-stretching vibrational transitions (Δ
) is the wavenumber difference between the free and hydrogen bonded NH-/OH-stretching vibrational transitions (Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) =
= ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) monomer −
monomer − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) dimer). The calculated NH- and OH-stretching fundamental transition wavenumbers and the red shifts upon complexation of the HONO heterodimer and heterotrimer complexes at the B3LYP-D3/aug-cc-pVTZ level are summarized in Table 3.
dimer). The calculated NH- and OH-stretching fundamental transition wavenumbers and the red shifts upon complexation of the HONO heterodimer and heterotrimer complexes at the B3LYP-D3/aug-cc-pVTZ level are summarized in Table 3.
| Type | O–H⋯O/N (HONO) | N–H⋯O/N (DMA) | O–H⋯O/N (H2O) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) b b |
f D/fMc |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) b b |
f D/fMc |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)
|
Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) b b |
f D/fMc | ||
a The values in the parentheses are the parameters for the anti-symmetric OH-stretching transition of H2O.
b Δ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) = = ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) monomer − monomer − ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) dimer.
c
f
D/fM represents the increase of intensity upon complexation. dimer.
c
f
D/fM represents the increase of intensity upon complexation.
|
||||||||||
| H2O–HONO | (A) | — | — | — | — | — | — | 3773 (3883) | 23 (16) | 25.0 (2.4) |
| (B) | — | — | — | — | — | — | 3774 (3883) | 22 (17) | 24.6 (2.2) | |
| (C) | — | — | — | — | — | — | 3762 (3878) | 34 (21) | 29.5 (2.1) | |
| (D) | — | — | — | — | — | — | 3761 (3878) | 35 (21) | 29.7 (2.1) | |
| (E) | — | — | — | — | — | — | 3773 (3883) | 23 (16) | 22.9 (2.4) | |
| (F) | — | — | — | — | — | — | 3756 (3879) | 40 (20) | 31.2 (2.0) | |
| HONO–H2O | (G) | 3260 | 317 | 25.0 | — | — | — | 3763 (3875) | 33 (24) | 5.1 (1.6) |
| (H) | 3459 | 290 | 10.9 | — | — | — | — | — | — | |
| DMA–HONO | (A) | — | — | — | 3531 | −6 | 6.2 | — | — | — |
| (B) | — | — | — | 3539 | −13 | 5.6 | — | — | — | |
| (C) | — | — | — | 3526 | 0 | 5.2 | — | — | — | |
| (D) | — | — | — | 3539 | −13 | 10.4 | — | — | — | |
| (E) | — | — | — | 3539 | −13 | 8.9 | — | — | — | |
| (F) | — | — | — | 3534 | −9 | 4.7 | — | — | — | |
| HONO–DMA | (G) | 2868 | 880 | 30.2 | — | — | — | — | — | — |
| (H) | 2865 | 883 | 27.6 | — | — | — | — | — | — | |
| (I) | 2582 | 995 | 82.4 | — | — | — | — | — | — | |
| (J) | 2564 | 1013 | 74.7 | — | — | — | — | — | — | |
| HONO–DMA–H2O | (A) | 3267 | 482 | 15.2 | 3495 | 30 | 36.6 | 3107 | 792 | 11.4 |
| (B) | 2507 | 1242 | 35.0 | 3492 | 34 | 80.3 | 3720 | 179 | 2.7 | |
| (C) | 2000 | 1576 | 79.3 | 3509 | 17 | 41.0 | 3728 | 171 | 2.3 | |
| (D) | 3163 | 585 | 17.3 | 3485 | 41 | 127.6 | 3009 | 890 | 12.1 | |
| (E) | 2310 | 1438 | 38.4 | 3462 | 64 | 219.4 | 3605 | 294 | 7.2 | |
| (F) | 2912 | 665 | 63.5 | 3517 | 9 | 30.4 | 3060 | 839 | 6.1 | |
| (G) | 2090 | 1487 | 82.8 | 3225 | 301 | 599.6 | 3347 | 552 | 15.5 | |
The OH-stretching transition of the trans-HONO monomer was calculated to be 3749 cm−1 (B3LYP-D3/aug-cc-pVTZ). However, the OH-stretching transition of the cis-HONO monomer was computed to be red shifted by 172 cm−1 and the intensity was reduced to 0.3 as compared with the value of the trans-HONO monomer. This may be due to the inter-molecular hydrogen bonding interaction. When HONO as a hydrogen bond donor approaches H2O (HONO–H2O (G–H)), the OH-stretching transitions in HONO were red shifted by 290–317 cm−1. In contrast, the OH-stretching transitions were much red shifted by 880–1013 cm−1 in the HONO–DMA (G–J) complexes. The OH-stretching transitions in the trans-HONO–NH3 and cis-HONO–NH3 complexes were calculated to be red shifted by 614–620 cm−1 (MP2/6-31+G**) with respect to their corresponding monomer, and the experimental observations showed a red shift of 831 cm−1 in an argon matrix.57 In the same study, the observed 3323 cm−1 band was assigned to the HONO–H2O complex with a red shift of 249 cm−1 in an argon matrix as compared to the trans-HONO monomer.57 This is close to the calculated red shift of the OH-stretching transition (290 cm−1) of the trans-HONO–H2O (H) complex. The OH-stretching vibrational transitions of the bimolecular complexes formed between trans-HONO and acetone or diethyl ether were 413, 376 cm−1 red shifted in an argon matrix with respect to the trans-HONO monomer, respectively.28 Moreover, HONO could form stable 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 hydrogen bonded complexes with H2C
1 hydrogen bonded complexes with H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 in an argon matrix, where the OH group of HONO interacts with the π-electron system of H2C
CH2 in an argon matrix, where the OH group of HONO interacts with the π-electron system of H2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2. The corresponding red shifts of the OH-stretching transitions in the O–H⋯π complexes were much smaller (136 cm−1 for the trans-complex and 103 cm−1 for the cis-complex) as compared with the former red shifts in the O–H⋯O complexes.27 For the DMA–HONO (A–F) complexes, the NH-stretching vibrational transitions of DMA were blue shifted by less than 13 cm−1 with respect to the DMA monomer. For the H2O–HONO (A–F) complexes where H2O acts as the hydrogen bond donor, H2O shows small red shifts of the symmetric (22–40 cm−1) and anti-symmetric (16–21 cm−1) OH-stretching vibrational transitions as compared with the H2O monomer. As seen in Fig. 4, HONO binds with H2O to form an O–H⋯O hydrogen bond in the HONO–DMA–H2O (A, D, F) complexes. The OH-stretching transitions of HONO were calculated to be red shifted by 482–665 cm−1 upon complexation. However, the same OH-stretching transitions in the HONO–H2O (G–F) complexes were only red shifted by 290–317 cm−1 with respect to the HONO monomer. Similarly, HONO binds with DMA to form O–H⋯N hydrogen bonds in the HONO–DMA–H2O (B, C, E, G) complexes. The OH-stretching vibrational transitions of HONO were calculated to be red shifted by 1242–1576 cm−1 upon complexation. Again, the same OH-stretching transitions in the HONO–DMA (G–J) have smaller red shifts (880–1013 cm−1) with respect to the HONO monomer. These indicate that the O–H⋯O/N (HONO) hydrogen bonds in the heterotrimers are much stronger than the same type of bonds in the heterodimer complexes. It further proves that the heterotrimer complexes are much more stable than the heterodimer complexes.
CH2. The corresponding red shifts of the OH-stretching transitions in the O–H⋯π complexes were much smaller (136 cm−1 for the trans-complex and 103 cm−1 for the cis-complex) as compared with the former red shifts in the O–H⋯O complexes.27 For the DMA–HONO (A–F) complexes, the NH-stretching vibrational transitions of DMA were blue shifted by less than 13 cm−1 with respect to the DMA monomer. For the H2O–HONO (A–F) complexes where H2O acts as the hydrogen bond donor, H2O shows small red shifts of the symmetric (22–40 cm−1) and anti-symmetric (16–21 cm−1) OH-stretching vibrational transitions as compared with the H2O monomer. As seen in Fig. 4, HONO binds with H2O to form an O–H⋯O hydrogen bond in the HONO–DMA–H2O (A, D, F) complexes. The OH-stretching transitions of HONO were calculated to be red shifted by 482–665 cm−1 upon complexation. However, the same OH-stretching transitions in the HONO–H2O (G–F) complexes were only red shifted by 290–317 cm−1 with respect to the HONO monomer. Similarly, HONO binds with DMA to form O–H⋯N hydrogen bonds in the HONO–DMA–H2O (B, C, E, G) complexes. The OH-stretching vibrational transitions of HONO were calculated to be red shifted by 1242–1576 cm−1 upon complexation. Again, the same OH-stretching transitions in the HONO–DMA (G–J) have smaller red shifts (880–1013 cm−1) with respect to the HONO monomer. These indicate that the O–H⋯O/N (HONO) hydrogen bonds in the heterotrimers are much stronger than the same type of bonds in the heterodimer complexes. It further proves that the heterotrimer complexes are much more stable than the heterodimer complexes.
Topological and GKS-EDA analysis
AIM analysis helps to understand the type of interactions using electron density and its topological information, and the analysis was performed using the wavefunctions computed at the B3LYP-D3/aug-cc-pVTZ level. The AIM plots of the HONO complexes with bond critical points (BCPs), ring critical points (RCPs) and electron density paths are shown in Fig. 5–7. The BCPs and RCPs are presented by the red and yellow balls, respectively. In addition, the C–H⋯O and C–H⋯N hydrogen bonds were obtained in the DMA–HONO (A–F) complexes as seen in Fig. 6. They are known as cooperative hydrogen bonding interactions, which play an important role in determining the structure and properties of materials.58,59 Due to the weakness of these interactions, they are out of the scope of this study. The topological parameters, including electron density ρ(r) and laplacian ∇2ρ(r) at the BCPs and change in atomic charge Δq(H) at the H atom at the B3LYP-D3/aug-cc-pVTZ level, are listed in Table 4.| Type | O–H⋯O/N (HONO) | N–H⋯O/N (DMA) | O–H⋯O/N (H2O) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Δq(H) | ρ(BCP) | ∇2ρ(BCP) | Δq(H) | ρ(BCP) | ∇2ρ(BCP) | Δq(H) | ρ(BCP) | ∇2ρ(BCP) | ||
| H2O–HONO | (A) | — | — | — | — | — | — | 0.033 | 0.0123 | 0.0635 |
| (B) | — | — | — | — | — | — | 0.032 | 0.0123 | 0.0621 | |
| (C) | — | — | — | — | — | — | 0.034 | 0.0122 | 0.0654 | |
| (D) | — | — | — | — | — | — | 0.035 | 0.0122 | 0.0649 | |
| (E) | — | — | — | — | — | — | 0.030 | 0.0123 | 0.0623 | |
| (F) | — | — | — | — | — | — | 0.036 | 0.0153 | 0.0760 | |
| HONO–H2O | (G) | 0.094 | 0.0264 | 0.1579 | — | — | — | 0.033 | 0.0097 | 0.0464 |
| (H) | 0.094 | 0.0259 | 0.1434 | — | — | — | — | — | — | |
| DMA–HONO | (A) | — | — | — | −0.022 | 0.0079 | 0.0389 | — | — | — |
| (B) | — | — | — | −0.017 | 0.0076 | 0.0386 | — | — | — | |
| (C) | — | — | — | −0.026 | 0.0078 | 0.0303 | — | — | — | |
| (D) | — | — | — | −0.019 | 0.0068 | 0.0291 | — | — | — | |
| (E) | — | — | — | −0.016 | 0.0082 | 0.0405 | — | — | — | |
| (F) | — | — | — | −0.024 | 0.0081 | 0.0398 | — | — | — | |
| HONO–DMA | (G) | 0.125 | 0.0346 | 0.2318 | — | — | — | — | — | — |
| (H) | 0.127 | 0.0346 | 0.2323 | — | — | — | — | — | — | |
| (I) | 0.133 | 0.0360 | 0.2486 | — | — | — | — | — | — | |
| (J) | 0.139 | 0.0360 | 0.2484 | — | — | — | — | — | — | |
| HONO–DMA–H2O | (A) | 0.115 | 0.0293 | 0.1915 | 0.026 | 0.0064 | 0.0285 | 0.127 | 0.0314 | 0.1846 |
| (B) | 0.156 | 0.0394 | 0.2824 | 0.050 | 0.0119 | 0.0566 | 0.038 | 0.0150 | 0.0791 | |
| (C) | 0.184 | 0.0449 | 0.3271 | 0.044 | 0.0099 | 0.0445 | 0.040 | 0.0146 | 0.0791 | |
| (D) | 0.129 | 0.0319 | 0.2131 | 0.044 | 0.0087 | 0.0450 | 0.145 | 0.0330 | 0.2002 | |
| (E) | 0.171 | 0.0412 | 0.3040 | 0.078 | 0.0177 | 0.0943 | 0.067 | 0.0184 | 0.1133 | |
| (F) | 0.131 | 0.0320 | 0.2207 | 0.030 | 0.0080 | 0.0384 | 0.145 | 0.0332 | 0.2024 | |
| (G) | 0.048 | 0.0454 | 0.3700 | 0.153 | 0.0273 | 0.1764 | 0.106 | 0.0263 | 0.1872 | |
According to the criteria proposed by Popelier, the electron density at the BCPs ρ(BCP) is in the range of 0.002–0.040 a.u. for a hydrogen bond.60,61 The electron densities at the BCPs are in the ranges of 0.0123–0.0332, 0.0068–0.0273 and 0.0259–0.0454 a.u. for the O–H⋯O/N (H2O), O–H⋯O/N (DMA) and O–H⋯O/N (HONO) hydrogen bonds, respectively. Similarly, the laplacian of charge densities ∇2ρ(BCP) of the complexes are in the ranges of 0.0464–0.2024, 0.0285–0.1764 and 0.1434–0.3700 a.u. for the O–H⋯O/N (H2O), O–H⋯O/N (DMA) and O–H⋯O/N (HONO) hydrogen bonds, respectively. These values are higher than the upper value of the laplacian criteria (0.014–0.139 a.u.) for a hydrogen bond.60,61 In particular, the ∇2ρ(BCP) values of the O–H⋯O/N (HONO) hydrogen bond are much higher than the upper value of the laplacian criteria. This is due to the strong acid–base interactions between HONO and DMA, thus leading to proton transfer from HONO to DMA.
Upon complexation, charge transfer (CT) from the hydrogen bond acceptor to the donor is usually observed; thus the charge of the hydrogen atom involved in the hydrogen bond will decrease.62 AIM atomic charge difference on the H atoms (Δq(H)) upon complexation is summarized in Table 4. The atomic charges at the H atoms (Δq(H)) for the O–H⋯O/N (H2O) hydrogen bonds are changed by 0.033–0.145 a.u., while 0.094–0.184 a.u. are obtained for the O–H⋯O/N (HONO) hydrogen bonds. For the O–H⋯O/N (DMA) hydrogen bond, the atomic charges at the H atoms are negative (−0.026 to −0.016 a.u.) in the DMA–HONO (A–F) complexes. For the remaining O–H⋯O/N (DMA) hydrogen bonds, the atomic charges at the H atoms are changed by 0.026–0.153 a.u. In general, the larger the Δq(H), the greater the red shifts of the NH-/OH-stretching transitions, which is a similar observation to that in our previous study on the hydrogen bonding in the carboxylic acid–sulfuric acid complexes.43
The distance between a BCP and an RCP has been applied as an indicator to determine the structural stability of a hydrogen bond.63 The distances between BCPs and RCPs are listed in Table 5. In the HONO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMA
DMA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (1
H2O (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) heterotrimer complexes, the distances between the BCP of the O–H⋯O/N (H2O) hydrogen bond and the RCP in the HONO–DMA–H2O (A) complexes are much larger than the distances for the other two hydrogen bonds. The O–H⋯O/N (H2O) hydrogen bonds in the HONO–DMA–H2O (A) are relatively more stable than the other two hydrogen bonds. In the case of the HONO–DMA–H2O (E) complex, the N–H⋯O/N (DMA) hydrogen bonds are the strongest hydrogen bonds. In the remaining HONO–DMA–H2O complexes, the O–H⋯O/N (HONO) hydrogen bonds are the strongest.
1) heterotrimer complexes, the distances between the BCP of the O–H⋯O/N (H2O) hydrogen bond and the RCP in the HONO–DMA–H2O (A) complexes are much larger than the distances for the other two hydrogen bonds. The O–H⋯O/N (H2O) hydrogen bonds in the HONO–DMA–H2O (A) are relatively more stable than the other two hydrogen bonds. In the case of the HONO–DMA–H2O (E) complex, the N–H⋯O/N (DMA) hydrogen bonds are the strongest hydrogen bonds. In the remaining HONO–DMA–H2O complexes, the O–H⋯O/N (HONO) hydrogen bonds are the strongest.
| Conformer | O–H⋯O/N (HONO) | N–H⋯O/N (DMA) | O–H⋯O/N (H2O) |
|---|---|---|---|
| (A) | 2.2754 | 1.1251 | 2.3071 |
| (B) | 2.1451 | 1.8267 | 1.8313 |
| (C) | 2.1319 | 1.6718 | 1.8456 |
| (D) | 2.5685 | 1.8442 | 2.5510 |
| (E) | 2.4093 | 2.4265 | 2.1018 |
| (F) | 2.8998 | 1.8346 | 2.3551 |
| (G) | 2.6994 | 2.3176 | 2.0399 |
The energy decomposition analysis (EDA) is a powerful tool for a quantitative interpretation of non-covalent interactions in terms of various components. In this study, we have utilized Su's generalized Kohn–Sham energy decomposition analysis (GKS-EDA) for energy decomposition analysis.64 This method has been used to analyze the weak inter-molecular (phenylenediamine dimer clusters)65 and intra-molecular (malonaldehyde, methallyl carbinol, etc.)66 non-covalent interactions. The total interaction energy along with the individual components obtained at the B3LYP-D3/aug-cc-pVTZ level is listed in Table 6. The GKS-EDA shows that the EES and EEX terms are the main driving forces for the formation of the complexes while the EREP term is not favorable for the formation of complexes. The EREP term is positive, which is about ∼75–87% of the total attractive energies. The terms EES and EEX are the dominating contributors about ∼13–34% and ∼44–53% to the total attractive energies, respectively. For the HONO (acceptor) heterodimer complexes, the EPOL contribution is about −5% to 14% to the total attractive energies, and the ECORR (∼6–22% to the total attractive energies) and EDISP (∼4–22% to the total attractive energies) contributions are close to each other. However, for the remaining heterodimer and heterotrimer complexes, these three contributions are quite different from those of the HONO (acceptor) heterodimer complexes, where the EPOL contribution is about ∼15–21% to the total attractive energies, ∼3–4% for ECORR and ∼3–5% for EDISP.
| Type | ΔEES | ΔEEX | ΔEREP | ΔEPOL | ΔEDISP | ΔECORR | ΔEINT | |
|---|---|---|---|---|---|---|---|---|
| a NP = the proton transfer from HONO to DMA is very large (0.5182 Å) in the HONO–DMA–H2O (G) complex; thus it was not possible to perform GKS-EDA analysis. | ||||||||
| H2O–HONO | (A) | −11.7 | −18.1 | 30.9 | −4.2 | −3.1 | −3.1 | −9.2 |
| (B) | −12.3 | −18.2 | 31.1 | −3.9 | −3.1 | −3.3 | −9.7 | |
| (C) | −13.8 | −22.7 | 39.2 | −2.9 | −3.1 | −6.4 | −9.7 | |
| (D) | −13.5 | −22.5 | 38.9 | −2.8 | −3.1 | −6.5 | −9.5 | |
| (E) | −12.4 | −17.9 | 30.8 | −4.5 | −3.1 | −2.9 | −10.1 | |
| (F) | −19.0 | −26.2 | 45.5 | −8.1 | −3.7 | −2.3 | −13.8 | |
| HONO–H2O | (G) | −65.6 | −96.0 | 171.8 | −30.7 | −5.9 | −8.4 | −35.0 |
| (H) | −52.7 | −67.5 | 120.9 | −22.7 | −4.1 | −7.6 | −33.6 | |
| DMA–HONO | (A) | −9.3 | −38.3 | 62.9 | 3.6 | −13.0 | −15.7 | −9.8 |
| (B) | −7.6 | −26.4 | 43.5 | 1.3 | −10.7 | −8.9 | −8.9 | |
| (C) | −13.6 | −30.4 | 50.7 | −3.7 | −9.7 | −3.8 | −10.6 | |
| (D) | −9.5 | −28.5 | 46.0 | −1.3 | −12.5 | −4.7 | −10.5 | |
| (E) | −11.1 | −41.9 | 69.0 | 3.7 | −14.2 | −17.2 | −11.8 | |
| (F) | −6.8 | −26.9 | 44.5 | 2.0 | −10.8 | −10.5 | −8.4 | |
| HONO–DMA | (G) | −98.8 | −145.7 | 267.0 | −59.3 | −10.0 | −14.2 | −61.0 |
| (H) | −99.2 | −147.9 | 270.5 | −60.5 | −11.2 | −14.8 | −62.9 | |
| (I) | −112.7 | −183.4 | 335.1 | −76.7 | −12.0 | −12.0 | −61.7 | |
| (J) | −114.2 | −189.6 | 344.3 | −78.1 | −14.1 | −13.0 | −64.7 | |
| HONO–DMA–H2O | (A) | −148.0 | −225.1 | 406.6 | −81.8 | −16.2 | −24.3 | −88.8 |
| (B) | −150.7 | −232.2 | 423.5 | −96.9 | −18.5 | −21.2 | −95.9 | |
| (C) | −177.1 | −302.6 | 554.0 | −137.3 | −22.5 | −18.0 | −103.5 | |
| (D) | −165.9 | −256.8 | 464.9 | −95.7 | −16.5 | −31.4 | −101.3 | |
| (E) | −179.2 | −283.0 | 518.7 | −118.1 | −18.7 | −33.6 | −114.0 | |
| (F) | −168.8 | −272.8 | 492.2 | −106.0 | −18.9 | −25.3 | −99.1 | |
| (G) | NP | NP | NP | NP | NP | NP | NP | |
Atmospheric implications
The strong primary hydrogen bond in the HONO–DMA system is formed with the acid as the donor and the amine as the acceptor. The Gibbs free energies of formation were calculated in the range of −13.1 to −4.5 kJ mol−1. The Gibbs free energies computed for the dimer containing sulfuric acid and various amine formation reactions at 298 K and 1 atm were much greater at −72.3 to −41.6 kJ mol−1 (RI-CC2/aug-cc-pV(T+d)Z).3 The acidity of H2SO4 is much stronger than that of HONO. However, the hydration energies of the HONO–DMA complexes increased from −4.8 to 1.0 kJ mol−1. The Gibbs free energy of H2SO4–DMA was −47.6 kJ mol−1 (PW91PW91/6-311++G(3df)), and after hydration, it changed to −65.0 kJ mol−1.67 It shows that hydration is unlikely to promote (thermodynamically unfavorable reaction) clustering of the HONO–DMA clusters. The hydration of H2SO4 was computed to be thermodynamically stable (ΔGθ298K = −9.5 kJ mol−1, PW91PW91/6-311++G(3df,3pd)).68 However, the hydration free energies of HONO in the present study were much higher, 6 to 10 kJ mol−1.The atmospheric relevance of the calculated results has been assessed with the law of mass balance. The mixing ratio of the cluster, e.g. HONO–DMA, can be computed as following:
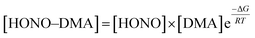 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppmv.70 Consequently, the upper limits of the concentrations for each species (10 ppbv for HONO, 100 pptv for DMA, 50
000 ppmv.70 Consequently, the upper limits of the concentrations for each species (10 ppbv for HONO, 100 pptv for DMA, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppmv for H2O) were used in the assessments. Using eqn (8) together with the calculated Gibbs free energies for complexation at 298 K and 1 atm (Table 2), we have computed the concentrations of the most stable conformers of the heterodimer clusters: HONO–H2O (H) and HONO–DMA (G). The predicted cluster concentrations of HONO–H2O (H) and HONO–DMA (G) are 1.0 × 109 and 4.9 × 103 molecule cm−3, respectively. In contrast, the Gibbs free energy of formation of H2SO4–DMA and H2SO4–H2O was calculated to be −69.1 (298 K, RI-CC2/aug-cc-pV(T+d)Z//RI-MP2/aug-cc-pV(D+d)Z),3 and −9.5 kJ mol−1 (298 K, PW91PW91/6-311++G(3df,3pd)),68 respectively. The atmospheric concentration of H2SO4 is about 0.04–1.2 pptv.26 Based on eqn (8), the concentrations of H2SO4–DMA and H2SO4–H2O are estimated to be 1.3 × 108–3.8 × 109 and 2.3 × 106–6.8 × 107 molecule cm−3, respectively. Therefore, HONO could form more hydrated clusters in the atmosphere than H2SO4 due to the high concentration of HONO; however, the clustering of HONO with DMA is negligible as compared to the important H2SO4–DMA clusters. Consequently, the role of HONO in new particle formation in the atmosphere is very limited. In the troposphere, the temperature decreases about 6.49 K for every 1 km increase in height.71,72 The temperature effects on the thermodynamic properties of clusters have been demonstrated to be important for understanding the atmospheric clustering mechanism.43 However, it is not possible to obtain a reasonable estimate of the changes of DMA or HONO concentrations as a function of altitude due to the different sources and sinks of DMA and HONO. Thus, their corresponding atmospheric relevance as a function of altitude could not be obtained. Nevertheless, these calculations were only simplified models and the real situation in the atmosphere is very complicated.
000 ppmv for H2O) were used in the assessments. Using eqn (8) together with the calculated Gibbs free energies for complexation at 298 K and 1 atm (Table 2), we have computed the concentrations of the most stable conformers of the heterodimer clusters: HONO–H2O (H) and HONO–DMA (G). The predicted cluster concentrations of HONO–H2O (H) and HONO–DMA (G) are 1.0 × 109 and 4.9 × 103 molecule cm−3, respectively. In contrast, the Gibbs free energy of formation of H2SO4–DMA and H2SO4–H2O was calculated to be −69.1 (298 K, RI-CC2/aug-cc-pV(T+d)Z//RI-MP2/aug-cc-pV(D+d)Z),3 and −9.5 kJ mol−1 (298 K, PW91PW91/6-311++G(3df,3pd)),68 respectively. The atmospheric concentration of H2SO4 is about 0.04–1.2 pptv.26 Based on eqn (8), the concentrations of H2SO4–DMA and H2SO4–H2O are estimated to be 1.3 × 108–3.8 × 109 and 2.3 × 106–6.8 × 107 molecule cm−3, respectively. Therefore, HONO could form more hydrated clusters in the atmosphere than H2SO4 due to the high concentration of HONO; however, the clustering of HONO with DMA is negligible as compared to the important H2SO4–DMA clusters. Consequently, the role of HONO in new particle formation in the atmosphere is very limited. In the troposphere, the temperature decreases about 6.49 K for every 1 km increase in height.71,72 The temperature effects on the thermodynamic properties of clusters have been demonstrated to be important for understanding the atmospheric clustering mechanism.43 However, it is not possible to obtain a reasonable estimate of the changes of DMA or HONO concentrations as a function of altitude due to the different sources and sinks of DMA and HONO. Thus, their corresponding atmospheric relevance as a function of altitude could not be obtained. Nevertheless, these calculations were only simplified models and the real situation in the atmosphere is very complicated.
Conclusions
Hydrated HONO and dimethylamine (DMA) clusters have been investigated to illustrate hydrogen bonding interactions with a theoretical approach. The presence of water enhances proton transfer from HONO to DMA, but reduces the Gibbs free energies of formation. The red shifts of the OH-stretching vibrational transition of HONO are very large upon complexation. Topological analysis confirms that the interactions between HONO (donor) and amine or H2O exceed the upper range of hydrogen bond criteria. GKS-EDA demonstrates that the electrostatic and exchange interactions play a major role in stabilizing the heterodimer and heterotrimer complexes. HONO has higher concentration in the troposphere, and it is much less important in new particle formation than H2SO4 due to its relatively weaker bonding with the nucleation species.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21407095 and 21577080), Shandong Provincial Natural Science Foundation, China (ZR2014BQ013 and ZR2016BB36) and High Performance Computing Center of Shandong University. We thank Prof. Peifeng Su of Xiamen University for providing the generalized Kohn–Sham energy decomposition analysis (GKS-EDA) software package.References
- R. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2012, 112, 1957–2011 CrossRef CAS PubMed.
- R. Zhang, Science, 2010, 328, 1366–1367 CrossRef CAS PubMed.
- T. Kurtén, V. Loukonen, H. Vehkamaki and M. Kulmala, Atmos. Chem. Phys., 2008, 8, 4095–4103 Search PubMed.
- M. Kulmala, J. Kontkanen, H. Junninen, K. Lehtipalo, H. E. Manninen, T. Nieminen, T. Petaja, M. Sipila, S. Schobesberger, P. Rantala, A. Franchin, T. Jokinen, E. Jarvinen, M. Aijala, J. Kangasluoma, J. Hakala, P. P. Aalto, P. Paasonen, J. Mikkila, J. Vanhanen, J. Aalto, H. Hakola, U. Makkonen, T. Ruuskanen, R. L. Mauldin III, J. Duplissy, H. Vehkamaki, J. Back, A. Kortelainen, I. Riipinen, T. Kurten, M. V. Johnston, J. N. Smith, M. Ehn, T. F. Mentel, K. E. J. Lehtinen, A. Laaksonen, V.-M. Kerminen and D. R. Worsnop, Science, 2013, 339, 943–946 CrossRef CAS PubMed.
- X. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
- D. Lee and A. S. Wexler, Atmos. Environ., 2013, 71, 95–103 CrossRef CAS.
- X. Ren, H. Harder, M. Martinez, R. L. Lesher, A. Oliger, J. B. Simpas, W. H. Brune, J. J. Schwab, K. L. Demerjian, Y. He, X. Zhou and H. Gao, Atmos. Environ., 2003, 37, 3639–3651 CrossRef CAS.
- H. Su, Y. F. Cheng, M. Shao, D. F. Gao, Z. Y. Yu, L. M. Zeng, J. Slanina, Y. H. Zhang and A. Wiedensohler, J. Geophys. Res., 2008, 113, 762–770 Search PubMed.
- B. J. Finlayson-Pitts, L. M. Wingen, A. L. Sumner, D. Syomin and K. A. Ramazan, Phys. Chem. Chem. Phys., 2003, 5, 223–242 RSC.
- L. Gutzwiller, F. Arens, U. Baltensperger, H. W. Gäggeler and M. Ammann, Environ. Sci. Technol., 2002, 36, 677–682 CrossRef CAS PubMed.
- M. Ammann, E. Rossler, R. Strekowski and C. George, Phys. Chem. Chem. Phys., 2005, 7, 2513–2518 RSC.
- N. A. Saliba, M. Mochida and B. J. Finlayson-Pitts, Geophys. Res. Lett., 2000, 27, 3229–3232 CrossRef CAS.
- K. Stemmler, M. Ammann, C. Donders, J. Kleffmann and C. George, Nature, 2006, 440, 195–198 CrossRef CAS PubMed.
- B. Alicke, U. Platt and J. Stutz, J. Geophys. Res.: Atmos., 2002, 107, 8196 CrossRef.
- P. Pagsberg, E. Bjergbakke, E. Ratajczak and A. Sillesen, Chem. Phys. Lett., 1997, 272, 383–390 CrossRef CAS.
- S. P. Li, J. Matthews and A. Sinha, Science, 2008, 319, 1657–1660 CrossRef CAS PubMed.
- R. Oswald, T. Behrendt, M. Ermel, D. Wu, H. Su, Y. Cheng, C. Breuninger, A. Moravek, E. Mougin, C. Delon, B. Loubet, A. Pommerening-Röser, M. Sörgel, U. Pöschl, T. Hoffmann, M. O. Andreae, F. X. Meixner and I. Trebs, Science, 2013, 341, 1233–1235 CrossRef CAS PubMed.
- A. Rondon and E. Sanhueza, Tellus, Ser. B, 2010, 41, 474–477 Search PubMed.
- J. N. Pitts, H. W. Biermann, A. M. Winer and E. C. Tuazon, Atmos. Environ., 1984, 18, 847–854 CrossRef CAS.
- A. Febo, C. Perrino, M. Gherardi and R. Sparapani, Environ. Sci. Technol., 1995, 29, 2390–2395 CrossRef CAS PubMed.
- R. M. Harrison, J. D. Peak and G. M. Collins, J. Geophys. Res., 1996, 101, 14429–14439 CrossRef CAS.
- C. J. Young, R. A. Washenfelder, J. M. Roberts, L. H. Mielke, H. D. Osthoff, C. Tsai, O. Pikelnaya, J. Stutz, P. R. Veres, A. K. Cochran, T. C. Vandenboer, J. Flynn, N. Grossberg, C. L. Haman, B. Lefer, H. Stark, M. Graus, J. De Gouw, J. B. Gilman, W. C. Kuster and S. S. Brown, Environ. Sci. Technol., 2012, 46, 10965–10973 CrossRef CAS PubMed.
- H. Su, Y. F. Cheng, P. Cheng, Y. H. Zhang, S. Dong, L. M. Zeng, X. Wang, J. Slanina, M. Shao and A. Wiedensohler, Atmos. Environ., 2008, 42, 6219–6232 CrossRef CAS.
- J. Kleffmann, R. Kurtenbach, J. Lörzer, P. Wiesen, N. Kalthoff, B. Vogel and H. Vogel, Atmos. Environ., 2003, 37, 2949–2955 CrossRef CAS.
- X. R. Ren, H. Harder, M. Martinez, R. L. Lesher, A. Oliger, J. B. Simpas, W. H. Brune, J. J. Schwab, K. L. Demerjian, Y. He, X. L. Zhou and H. G. Gao, Atmos. Environ., 2003, 37, 3639–3651 CrossRef CAS.
- J. Almeida, S. Schobesberger, A. Kurten, I. K. Ortega, O. Kupiainen-Maatta, A. P. Praplan, A. Adamov, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, N. M. Donahue, A. Downard, E. Dunne, J. Duplissy, S. Ehrhart, R. C. Flagan, A. Franchin, R. Guida, J. Hakala, A. Hansel, M. Heinritzi, H. Henschel, T. Jokinen, H. Junninen, M. Kajos, J. Kangasluoma, H. Keskinen, A. Kupc, T. Kurten, A. N. Kvashin, A. Laaksonen, K. Lehtipalo, M. Leiminger, J. Leppa, V. Loukonen, V. Makhmutov, S. Mathot, M. J. McGrath, T. Nieminen, T. Olenius, A. Onnela, T. Petaja, F. Riccobono, I. Riipinen, M. Rissanen, L. Rondo, T. Ruuskanen, F. D. Santos, N. Sarnela, S. Schallhart, R. Schnitzhofer, J. H. Seinfeld, M. Simon, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Trostl, G. Tsagkogeorgas, P. Vaattovaara, Y. Viisanen, A. Virtanen, A. Vrtala, P. E. Wagner, E. Weingartner, H. Wex, C. Williamson, D. Wimmer, P. Ye, T. Yli-Juuti, K. S. Carslaw, M. Kulmala, J. Curtius, U. Baltensperger, D. R. Worsnop, H. Vehkamaki and J. Kirkby, Nature, 2013, 502, 359–363 CrossRef CAS PubMed.
- M. Krajewska, Z. Mielke and K. G. Tokhadze, J. Mol. Struct., 1997, 404, 47–53 CrossRef CAS.
- Z. Mielke, M. Wierzejewska, A. Olbert, M. Krajewska and K. G. Tokhadze, J. Mol. Struct., 1997, 436, 339–347 CrossRef.
- V. Vaida, J. Chem. Phys., 2011, 135, 020901 CrossRef PubMed.
- H. G. Kjaergaard, T. W. Robinson, D. L. Howard, J. S. Daniel, J. E. Headrick and V. Vaida, J. Phys. Chem. A, 2003, 107, 10680–10686 CrossRef CAS.
- J. Kirkby, J. Curtius, J. Almeida, E. Dunne, J. Duplissy, S. Ehrhart, A. Franchin, S. Gagne, L. Ickes, A. Kuerten, A. Kupc, A. Metzger, F. Riccobono, L. Rondo, S. Schobesberger, G. Tsagkogeorgas, D. Wimmer, A. Amorim, F. Bianchi, M. Breitenlechner, A. David, J. Dommen, A. Downard, M. Ehn, R. C. Flagan, S. Haider, A. Hansel, D. Hauser, W. Jud, H. Junninen, F. Kreissl, A. Kvashin, A. Laaksonen, K. Lehtipalo, J. Lima, E. R. Lovejoy, V. Makhmutov, S. Mathot, J. Mikkila, P. Minginette, S. Mogo, T. Nieminen, A. Onnela, P. Pereira, T. Petaja, R. Schnitzhofer, J. H. Seinfeld, M. Sipila, Y. Stozhkov, F. Stratmann, A. Tome, J. Vanhanen, Y. Viisanen, A. Vrtala, P. E. Wagner, H. Walther, E. Weingartner, H. Wex, P. M. Winkler, K. S. Carslaw, D. R. Worsnop, U. Baltensperger and M. Kulmala, Nature, 2011, 476, 429–433 CrossRef CAS PubMed.
- W. Klemperer and V. Vaida, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10584–10588 CrossRef CAS PubMed.
- S. Schobesberger, H. Junninen, F. Bianchi, G. Lonn, M. Ehn, K. Lehtipalo, J. Dommen, S. Ehrhart, I. K. Ortega, A. Franchin, T. Nieminen, F. Riccobono, M. Hutterli, J. Duplissy, J. Almeida, A. Amorim, M. Breitenlechner, A. J. Downard, E. M. Dunne, R. C. Flagan, M. Kajos, H. Keskinen, J. Kirkby, A. Kupc, A. Kuerten, T. Kurten, A. Laaksonen, S. Mathot, A. Onnela, A. P. Praplan, L. Rondo, F. D. Santos, S. Schallhart, R. Schnitzhofer, M. Sipila, A. Tome, G. Tsagkogeorgas, H. Vehkamaki, D. Wimmer, U. Baltensperger, K. S. Carslaw, J. Curtius, A. Hansel, T. Petaja, M. Kulmala, N. M. Donahue and D. R. Worsnop, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17223–17228 CrossRef CAS PubMed.
- L. L. Van Loon, H. C. Allen and B. E. Wyslouzil, J. Phys. Chem. A, 2008, 112, 10758–10763 CrossRef CAS PubMed.
- S. A. Carl and J. N. Crowley, J. Phys. Chem. A, 1998, 102, 8131–8141 CrossRef CAS.
- J. R. Lane, J. Contreras-Garcia, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS PubMed.
- R. Parthasarathi, V. Subramanian and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 3349–3351 CrossRef CAS PubMed.
- P. F. Su, Z. Jiang, Z. C. Chen and W. Wu, J. Phys. Chem. A, 2014, 118, 2531–2542 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, USA, 2013 Search PubMed.
- Q. Zhang and L. Du, Comput. Theor. Chem., 2016, 1078, 123–128 CrossRef CAS.
- H. Zhao, J. Chang and L. Du, Comput. Theor. Chem., 2016, 1084, 126–132 CrossRef CAS.
- H. Zhao, S. Tang, S. Li, L. Ding and L. Du, Struct. Chem., 2016, 27, 1241–1253 CrossRef CAS.
- H. Zhao, Q. Zhang and L. Du, RSC Adv., 2016, 6, 71733–71743 RSC.
- S. Tang, H. Zhao and L. Du, RSC Adv., 2016, 6, 91233–91242 RSC.
- A. S. Hansen, L. Du and H. G. Kjaergaard, Phys. Chem. Chem. Phys., 2014, 16, 22882–22891 RSC.
- A. S. Hansen, L. Du and H. G. Kjaergaard, J. Phys. Chem. Lett., 2014, 5, 4225–4231 CrossRef CAS PubMed.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- G. E. McGraw, D. L. Bernitt and I. C. Hisatsune, J. Chem. Phys., 1966, 45, 1392–1399 CrossRef CAS PubMed.
- A. P. Cox, A. H. Brittain and D. J. Finnigan, Trans. Faraday Soc., 1971, 67, 2179–2194 RSC.
- J. E. Wollrab and V. W. Laurie, J. Chem. Phys., 1968, 48, 5058–5066 CrossRef CAS.
- V. P. Bulychev, M. V. Buturlimova and K. G. Tokhadze, J. Phys. Chem. A, 2013, 117, 9093–9098 CrossRef CAS PubMed.
- Y. Dimitrova, Spectrosc. Lett., 2010, 43, 282–289 CrossRef CAS.
- Y. Dimitrova, Spectrochim. Acta, Part A, 2004, 60, 1–8 CrossRef.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1636 CAS.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641 CAS.
- Z. Mielke, K. G. Tokhadze, Z. Latajka and E. Ratajczak, J. Phys. Chem., 1996, 100, 539–545 CrossRef CAS.
- S. Blanco, P. Pinacho and J. C. López, Angew. Chem., Int. Ed., 2016, 55, 1–6 CrossRef PubMed.
- A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS PubMed.
- U. Koch and P. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- I. S. Bushmarinov, K. A. Lyssenko and M. Y. Antipin, Russ. Chem. Rev., 2009, 78, 283–302 CrossRef CAS.
- P. Popelier, J. Phys. Chem. A, 1998, 102, 1873–1878 CrossRef CAS.
- P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102 CrossRef PubMed.
- C. Yuan, H. Wu, M. Jia, P. Su, Z. Luo and J. Yao, Phys. Chem. Chem. Phys., 2016, 18, 29249–29257 RSC.
- P. F. Su, Z. C. Chen and W. Wu, Chem. Phys. Lett., 2015, 635, 250–256 CrossRef CAS.
- A. B. Nadykto, J. Herb, F. Yu and Y. Xu, Chem. Phys. Lett., 2014, 609, 42–49 CrossRef CAS.
- A. B. Nadykto and F. Yu, Chem. Phys. Lett., 2007, 435, 14–18 CrossRef CAS.
- A.-J. Kieloaho, H. Hellén, H. Hakola, H. E. Manninen, T. Nieminen, M. Kulmala and M. Pihlatie, Atmos. Environ., 2013, 80, 369–377 CrossRef CAS.
- J. M. Wallace and P. V. Hobbs, Atmospheric Science: An Introductory Survey, Academic Press, New York, 2nd edn, 2006 Search PubMed.
- J. Gonzalez, J. M. Anglada, R. J. Buszek and J. S. Francisco, J. Am. Chem. Soc., 2011, 133, 3345–3353 CrossRef CAS PubMed.
- Y. M. Ji, H. H. Wang, Y. P. Gao, G. Y. Li and T. C. An, Atmos. Chem. Phys., 2013, 13, 11277–11286 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6em00598e |
| This journal is © The Royal Society of Chemistry 2017 |