Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intermolecular interactions in molecular crystals: what’s in a name?
Alison J.
Edwards
 a,
Campbell F.
Mackenzie
a,
Campbell F.
Mackenzie
 b,
Peter R.
Spackman
b,
Peter R.
Spackman
 b,
Dylan
Jayatilaka
b,
Dylan
Jayatilaka
 b and
Mark A.
Spackman
b and
Mark A.
Spackman
 *b
*b
aAustralian Centre for Neutron Scattering, Australian Nuclear Science and Technology Organization, Lucas Heights, NSW, Australia
bSchool of Molecular Sciences, University of Western Australia, Perth, WA, Australia. E-mail: mark.spackman@uwa.edu.au
First published on 8th March 2017
Abstract
Structure–property relationships are the key to modern crystal engineering, and for molecular crystals this requires both a thorough understanding of intermolecular interactions, and the subsequent use of this to create solids with desired properties. There has been a rapid increase in publications aimed at furthering this understanding, especially the importance of non-canonical interactions such as halogen, chalcogen, pnicogen, and tetrel bonds. Here we show how all of these interactions – and hydrogen bonds – can be readily understood through their common origin in the redistribution of electron density that results from chemical bonding. This redistribution is directly linked to the molecular electrostatic potential, to qualitative concepts such as electrostatic complementarity, and to the calculation of quantitative intermolecular interaction energies. Visualization of these energies, along with their electrostatic and dispersion components, sheds light on the architecture of molecular crystals, in turn providing a link to actual crystal properties.
“In many cases, with the exception of hydrogen bonding, molecular pairings responsible for the largest part of the interaction energy in a crystal show no particular atom–atom feature, no easily identifiable “bond”, not even aromatic stacks, or the like; they stick together by compatibility of minor and diffuse features in the electrostatic potential, that defy recognition and, a fortiori, classification. Only a quantitative calculation of cohesion energies can reveal true crystal structure determinants”. A. Gavezzotti, CrystEngComm, 2013, 15, 4027.
Introduction
The detailed analysis of the interactions between molecules and ions in crystals plays an increasingly important role in modern solid state chemistry, and in particular crystal engineering, where the derivation of predictive structure–property relationships is key to a genuine “engineering” of crystals. This, of course, was articulated some time ago by Desiraju who described the crystal engineering of molecular solids as the “understanding of intermolecular interactions in the context of crystal packing and the utilization of such understanding in the design of new solids with desired physical and chemical properties”.1 Utilization and design require understanding as an essential precursor, and the context of crystal packing in this statement is especially important. Recent years have seen an explosion of publications focusing on the description, characteristics and relative importance of different non-canonical interactions such as lithium,2 beryllium,3 triel,4–6 tetrel/carbon,7–10 pnicogen/pnictogen,11–14 chalcogen,15–19 halogen20–28 and aerogen29,30 “bonds”. (The list of “bonds” or “interactions” is not exhaustive, and the cited literature is only representative). These interactions have also been collected under the more general terms of “σ-hole” and “π-hole”,31 referring to localised patches of positive electrostatic potential (ESP) in otherwise negative regions of ESP mapped on a molecular surface.32But it is arguable whether this activity has enhanced our understanding of the relationship between the structure of molecules (geometric and electronic), the crystal structures they form, and their consequent chemical and physical properties. Are we getting closer to the requisite intimate, and ultimately useful, understanding of why molecules and ions are arranged in crystals as observed, or are we merely cataloguing more and more examples of intermolecular “bonds” or “interactions” while losing sight of their common origins? In many instances where there is a focus on specific interactions, stronger – and frequently more important – interactions are being completely overlooked.
Our approach to understanding crystal packing combines colour mapping on molecular surfaces of properties derived from molecular wavefunctions and the efficient calculation of remarkably reliable intermolecular interaction energies33,34 along with a graphical representation of their magnitude.35 Considerable insight can be obtained via the anisotropy of the network of pairwise intermolecular interaction energies. This whole-of-molecule approach, which is blind to specific atom⋯atom contacts and/or interactions that may be deemed to be important, complements and challenges some current atom–atom approaches.36–38
In this paper we highlight how these non-canonical interactions can be understood – in the same way as hydrogen bond interactions – through their common origin in the redistribution of electron density that results from chemical bonding. This redistribution is directly linked to the molecular ESP, commonly used to rationalise “σ-hole” and “π-hole” interactions,22,23,32,39 and hence to qualitative concepts such as electrostatic complementarity (alluded to by Gavezzotti in the epigraph above) and the calculation of meaningful intermolecular interaction energies. Finally, we show how visualization of the relative importance of electrostatic and dispersion contributions to intermolecular energies can reveal information about the architecture of molecular crystals, and possible links to their physical properties.
Visualizing the redistribution of electrons upon bonding aids in understanding the electrostatic potential
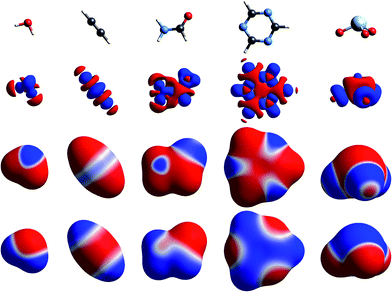
The simplest way to understand the nature of the ESP of a molecule is through the electron distribution, and in particular the redistribution that occurs on chemical bonding. The crystallographer’s model for the electron density of a molecule in a crystal – the independent atom model – comprises spherically averaged electron densities located at the nuclear positions. It is not commonly recognised (but see, for example, the discussion in ref. 22) that the ESP of a spherical atom is necessarily positive everywhere, decaying to zero at infinity, as a result of the incomplete shielding of the nuclear charge by the electron distribution at any finite distance. So regions of negative ESP for a neutral molecule arise from a local increase of electron density, and this necessarily results in a concomitant decrease of electron density elsewhere in the molecule, and a more positive ESP in that region.Fig. 1 to 4 show how, for a small number of molecules, this relationship can be visualized in several ways. These figures display positive (blue) and negative (red) isosurfaces of the deformation electron density, Δρ, which correspond to local increases and decreases, respectively, of electron density relative to the sum of spherical atoms. An isosurface of the promolecule electron density, a molecular surface that closely resembles a van der Waals surface,40 is used to map Δρ as well as the molecular ESP. All calculations in this paper are based on B3LYP/6-31G(d,p) electron densities (B3LYP/DGDZVP where Br, I or Xe are involved) using molecular geometries from known crystal structures, with X–H bond lengths normalized to standard neutron diffraction values. Interaction energies are all based on the CE-B3LYP model33,34 embodied in CrystalExplorer17.41 Isosurfaces of Δρ in these figures illustrate a number of recurring features for atoms in common bonding environments, and by mapping the same property on a molecular surface these facilitate a better appreciation of the origin of features in the maps of the ESP.
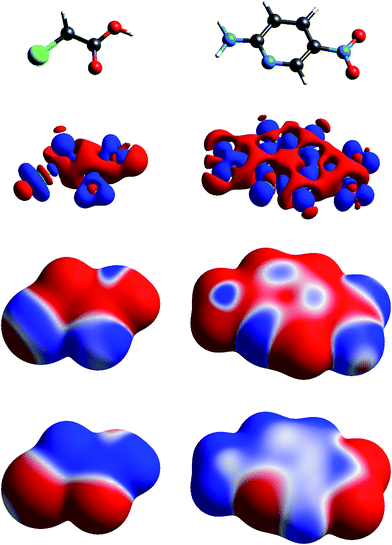 | ||
| Fig. 2 Molecular diagrams, deformation electron density and ESP of (left to right) chloroacetic acid and 2-amino-5-nitropyridine. See Fig. 1 for details. | ||
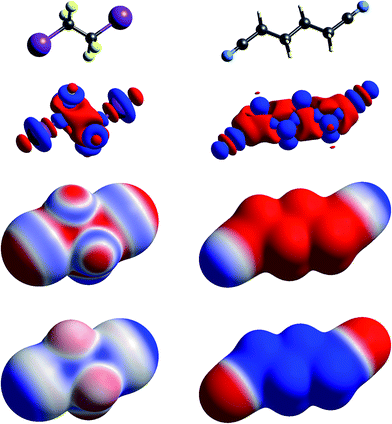 | ||
| Fig. 3 Molecular diagrams, deformation electron density and ESP of (left to right) 1,2-diiodo-1,1,2,2-tetrafluoroethane and 1,4-dicyanobutane. See Fig. 1 for details. | ||
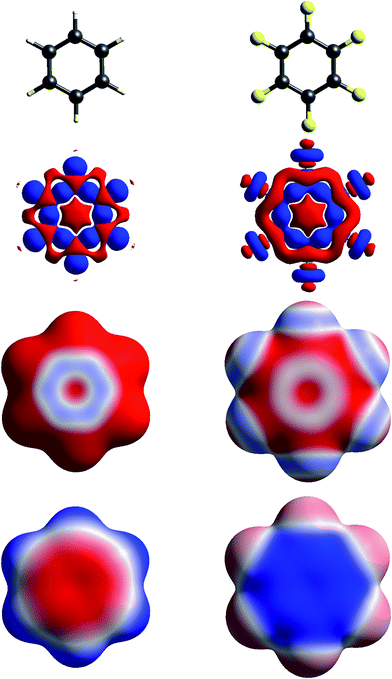 | ||
| Fig. 4 Molecular diagrams, deformation electron density and ESP of (left to right) benzene and hexafluorobenzene. See Fig. 1 for details. | ||
The build up of “lone pair” electron density above and behind the oxygen atom in water (Fig. 1) is clearly directly related to the broad region of negative ESP surrounding the oxygen atom. Similar “lone pair” Δρ features are evident for the ring N atoms in s-triazine and 2-amino-5-nitropyridine (Fig. 2), all resulting in prominent electronegative regions in the ESP. The build up of electron density in the C–C bond in acetylene results in a band of negative ESP around the waist of the molecule, and a concomitant positive ESP around the hydrogen atoms. In formamide we see characteristic Δρ features around the carbonyl O atom, which are repeated in chloroacetic acid and 2-amino-5-nitropyridine (Fig. 2). Also evident in the Δρ maps for formamide and 2-amino-5-nitropyridine are small deficits of electron density beyond the N atoms (and between the H atoms) in the planar amino groups, which have been labelled “σ-holes” and discussed in the context of the pnicogen bond.42 However, the Δρ maps for those two molecules clearly show that the positive ESP characteristic of the –NH2 group results from a broad band of negative Δρ that is largely due to the electron density deficits beyond the H atoms.
We include maps of Δρ and ESP for XeO3 in Fig. 1 as that molecule has been claimed to display a “σ-hole” feature at the Xe atom, leading to what the authors proposed as “aerogen bonding”.29 But the Δρ map actually shows a small build up above the Xe atom in Fig. 1; the Δρ feature that results in a broad electropositive ESP region around the Xe atom comes largely from substantial withdrawal of electron density from the Xe–O bonds and their vicinity. We believe that the term “σ-hole” – if it is meant to convey a localised region of positive ESP associated with a σ-bonded atom – is certainly not appropriate in this case. Here the region of positive ESP encompasses a large part of the molecular surface.
The term “σ-hole” most commonly occurs in discussions of halogen bonding, where it refers to the localised positive ESP associated with a deficit of electron density in the region beyond terminally bonded halogen atoms. This feature is very clearly seen in Δρ isosurface maps for chlorine in chloroacetic acid (Fig. 2), iodine in 1,2-diiodo-1,1,2,2-tetrafluoroethane (Fig. 3) and fluorine in hexafluorobenzene (Fig. 4). But it should also be obvious that this deficit does not occur in isolation – it is part of a roughly quadrupolar feature directed along the C–X bond in all cases, and is always accompanied by a torus of electron density deficit around the C–X bond. In combination these Δρ features lead to localised positive ESP features along the extension of the C–X bond, with negative ESP regions surrounding the bond. As is well known, these features are strongest for iodine, less obvious for chlorine, and barely evident in the ESP map for fluorine.
Fig. 4 contrasts Δρ and ESP maps for benzene and hexafluorobenzene. It shows how the positive Δρ isosurface features around the H atoms and in the C–C bonds in benzene are not evident in the mapping of Δρ on the molecular surface, which is dominated by the electron density deficit features. This in turn results in an ESP map that shows electropositive H atoms and broad electronegative regions above and below the ring. Although the benzene skeleton is largely unchanged in hexafluorobenzene, the Δρ features associated with the fluorine atoms, in particular the torus of positive Δρ discussed above, result in moderate electronegative ESP around the F atoms, and broad electropositive regions above and below the ring. The complementary nature of the ESP maps for these two molecules is reflected in their quadrupole moments, which are opposite in sign and very similar in magnitude,43 an important consideration in rationalizing the packing of molecules in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal, discussed further in the next section.
1 co-crystal, discussed further in the next section.
In Fig. 1 to 4 we have deliberately mapped the ESP over an identical range for all molecules, namely ±0.025 a.u. (±65.6 kJ mol−1 per unit charge). Thus, dark red regions are where the ESP on the molecular surface is more negative than −0.025 a.u., and dark blue regions more positive than +0.025 a.u.; white regions depict near-zero potential. In this manner it is quite straightforward to broadly compare the electrostatic nature of various molecules on the basis of the ESP maps in these figures. For example, in Fig. 3 we see that 1,2-diiodo-1,1,2,2-tetrafluoroethane displays relatively neutral ESP features across the surface except for the electropositive regions at the extensions of the C–I bonds. In contrast, the ESP for 1,4-dicyanobutane shows strong electronegative regions around the cyano groups, with the butane framework strongly electropositive.
Pictures of electrostatic complementarity correlate with electrostatic interaction energies
Some time ago we showed that mapping molecular ESPs onto Hirshfeld surfaces, in the context of a crystal packing diagram, considerably enhances the discussion of close molecular contacts in the crystal, using the concept of “electrostatic complementarity” between touching surface patches in adjacent molecules.44 Here we elaborate further on this, with Fig. 5 to 9 showing small clusters of molecules extracted from a number of crystals, with the molecular ESP mapped on Hirshfeld surfaces, along with values of the electrostatic interaction energy computed directly from the two molecular charge (electron + nuclear) distributions.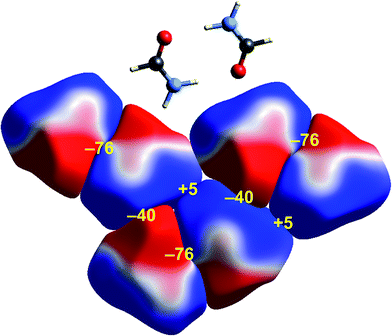 | ||
| Fig. 5 Formamide (FORMAM02): ESP mapped on Hirshfeld surfaces for three hydrogen-bonded pairs in the crystal. Colour mapping and range for ESP as for Fig. 1, and the electrostatic interaction energies (kJ mol−1) for nearest neighbour pairs of molecules are indicated in yellow. | ||
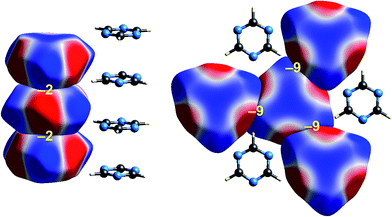 | ||
| Fig. 6 s-Triazine (TRIZIN): ESP mapped on Hirshfeld surfaces. Left: columnar arrangement in the crystal; right: arrangement of molecules in the perpendicular direction. Colour mapping and range for ESP as for Fig. 1, and the electrostatic interaction energies (kJ mol−1) for nearest neighbour pairs of molecules are indicated in yellow. | ||
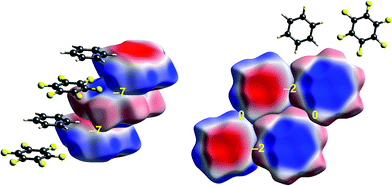 | ||
| Fig. 7 Benzene:hexafluorobenzene co-crystal (BICVUE01): ESP mapped on Hirshfeld surfaces. Left: offset stacking arrangement in the crystal; right: arrangement of molecules in the perpendicular direction. Colour mapping and range for ESP as for Fig. 1, and the electrostatic interaction energies (kJ mol−1) for nearest neighbour pairs of molecules are indicated in yellow. | ||
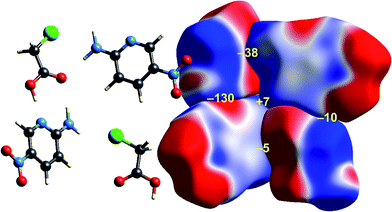 | ||
| Fig. 8 2-Amino-5-pyridine:chloroacetic acid co-crystal (TETXUL01): ESP mapped on Hirshfeld surfaces for a cluster of molecules in the crystal. Colour mapping and range for ESP as for Fig. 1, and the electrostatic interaction energies (kJ mol−1) for nearest neighbour pairs of molecules are indicated in yellow. | ||
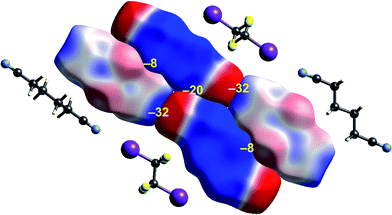 | ||
| Fig. 9 1,4-Dicyanobutane:1,2-diiodo-1,1,2,2-tetrafluoroethane co-crystal (EBIHIH): ESP mapped on Hirshfeld surfaces for a cluster of molecules in the crystal. Colour mapping and range for ESP as for Fig. 1, and the electrostatic interaction energies (kJ mol−1) for nearest neighbour pairs of molecules are indicated in yellow. | ||
Formamide
A cluster of three centrosymmetric hydrogen-bonded formamide dimers (Fig. 5) illustrates the sort of insight that can be gained through this approach. There is an obvious complementarity between ESP maps for the molecules involved in these pairs, with an almost perfect matching of zero potential (the white lines), and electronegative (red) patches paired with electropositive (blue) patches in adjacent molecules. The computed electrostatic energy for this pair, −76 kJ mol−1, reflects the strong complementarity in this case. Another hydrogen bond interaction shows a similar red-blue complementarity, but over a smaller area, and this correlates with a smaller electrostatic energy of −50 kJ mol−1. An electrostatic energy of +5 kJ mol−1 results where electropositive regions of adjacent molecules are in contact.s-Triazine
Intermolecular interactions for s-triazine are much weaker (Fig. 6). The stacking interaction shown on the left of the figure is stabilizing but electrostatically very weak at only −2 kJ mol−1. But even here there is an exquisite complementarity between the ESP maps for adjacent molecules in this arrangement; each molecule is rotated 60° with respect to those above and below in order to maximise overlap between positive and negative regions. In the perpendicular direction, adjacent molecules also clearly pack in an arrangement that maximises this red-blue complementarity, and here the stabilizing electrostatic energy between adjacent molecules is somewhat greater but still much smaller than seen for formamide.Benzene:hexafluorobenzene co-crystal
The interactions between adjacent molecules in the co-crystal of benzene and hexafluorobenzene are depicted in Fig. 7. In this case the stacking arrangement is offset, presumably to obtain a lower electrostatic energy (−7 kJ mol−1, compared with only −2 kJ mol−1 for s-triazine). In the perpendicular direction, the electrostatic interactions are weak to negligible, as expected from the much lighter colours of the ESP for these two molecules. Although these electrostatic energies are quite small, negative values coincide with red-blue complementarity in all cases, and values near zero with contacts that are either blue–blue (for benzene–benzene) or red–red (for hexafluorobenzene).Chloroacetic acid:2-amino-5-nitropyridine co-crystal
As observed for formamide, the complementary nature of contacts between chloroacetic acid and 2-amino-5-nitropyridine in the co-crystal (Fig. 8) is obvious, and coincides with two stabilizing electrostatic energies of −130 and −38 kJ mol−1. Very small positive electrostatic energies arise for close contacts between like molecules, where there is no evidence of complementarity. The arrangement of the molecular pair at top left in this figure is that discussed by Sarkar et al.42 as providing experimental validation of pnicogen bonding based on their experimental charge density analysis. The present analysis based on electrostatics suggests that it is difficult to impossible to separate a specific N⋯Cl interaction from the molecule⋯molecule picture in Fig. 8. The two molecules at the left of Fig. 8 are linked by a cyclic pair of O–H⋯N and N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds, and a very large stabilizing electrostatic energy, much larger than for the putative “pnicogen bonded” pair.
C hydrogen bonds, and a very large stabilizing electrostatic energy, much larger than for the putative “pnicogen bonded” pair.
1,2-Diiodo-1,1,2,2-tetrafluoroethane:1,4-dicyanobutane co-crystal
The final example in this section (Fig. 9) illustrates the strong electrostatic complementarity between molecules in the linear arrangement of 1,2-diiodo-1,1,2,2-tetrafluoroethane and 1,4-dicyanobutane in their 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal, attributed to N⋯I halogen bonding.45 The electrostatic energy associated with this molecular pair is considerable at −32 kJ mol−1, and in line with the expectation from the strong red-blue complementarity at the ends of these two molecules. But this is not the only strong interaction evident in this 2D arrangement in the figure. There is also a very obvious electrostatic complementarity between cyanobutane molecules in adjacent 1D “chains”, and once more we see almost perfect matching of zero potential for these two molecules. The electrostatic energy of −20 kJ mol−1 associated with this pairing is also substantial. A still weaker interaction is also evident between iodoperfluoroethane and cyanobutane molecules in adjacent 1D “chains”.
1 co-crystal, attributed to N⋯I halogen bonding.45 The electrostatic energy associated with this molecular pair is considerable at −32 kJ mol−1, and in line with the expectation from the strong red-blue complementarity at the ends of these two molecules. But this is not the only strong interaction evident in this 2D arrangement in the figure. There is also a very obvious electrostatic complementarity between cyanobutane molecules in adjacent 1D “chains”, and once more we see almost perfect matching of zero potential for these two molecules. The electrostatic energy of −20 kJ mol−1 associated with this pairing is also substantial. A still weaker interaction is also evident between iodoperfluoroethane and cyanobutane molecules in adjacent 1D “chains”.
Energy frameworks reveal the architecture of molecular crystals
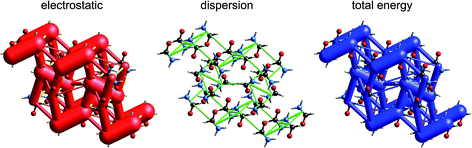
Although our original report and introduction of energy frameworks focused on their application to mechanical properties, we noted then that the accurate and efficient computation of interaction energies, coupled with their visualization in the form of an energy framework, represents a powerful tool for quantitatively exploring interaction energies in molecular crystals.35 Here we apply this visualization tool to the same molecular crystals for which electrostatic interactions were analysed in the previous section. Fig. 10 to 14 show the same three frameworks for each crystal, and the energy scale used – the width of the cylinders linking nearest neighbour molecules – is the same in all figures, enabling direct comparison of the relative importance of electrostatic (red) and dispersion (green) contributions to the total intermolecular energies (blue). This also facilitates comparison between molecular crystals, shedding light on which interactions are important, and how this differs between crystals.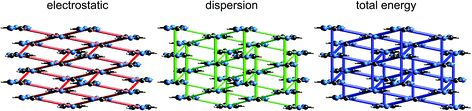 | ||
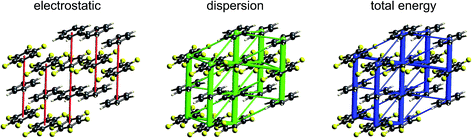
| Fig. 11 s-Triazine (TRIZIN): energy frameworks for separate electrostatic (red) and dispersion (green) contributions to the total nearest neighbour pairwise interaction energies (blue). See Fig. 10 for details. | ||
 | ||
| Fig. 12 Benzene:hexafluorobenzene co-crystal (BICVUE01): energy frameworks for separate electrostatic (red) and dispersion (green) contributions to the total nearest neighbour pairwise interaction energies (blue). See Fig. 10 for details. | ||
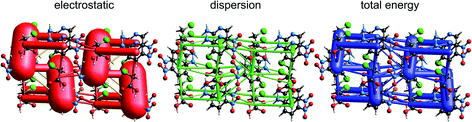 | ||
| Fig. 13 2-Amino-5-pyridine:chloroacetic acid co-crystal (TETXUL01): energy frameworks for separate electrostatic (red) and dispersion (green) contributions to the total nearest neighbour pairwise interaction energies (blue). See Fig. 10 for details. | ||
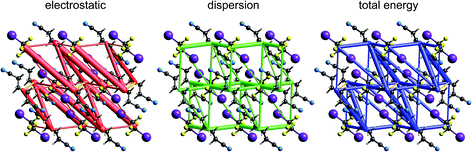 | ||
| Fig. 14 1,4-Dicyanobutane:1,2-diiodo-1,1,2,2-tetrafluoroethane co-crystal (EBIHIH): energy frameworks for separate electrostatic (red) and dispersion (green) contributions to the total nearest neighbour pairwise interaction energies (blue). See Fig. 10 for details. | ||
Formamide
Energy frameworks for formamide (Fig. 10) show immediately that the total interaction energies for molecular pairs are largely due to electrostatics, as the total energy framework closely mirrors that for the electrostatic contribution; the repulsion energy essentially cancels the sum of smaller polarization and dispersion terms, as well as part of the electrostatic. The cyclic pair of molecules involving two N–H⋯O hydrogen bonds is evident in the electrostatic and total energy pictures (total CE-B3LYP energy = −64 kJ mol−1), and these pairs are linked by single N–H⋯O hydrogen bonds (−31 kJ mol−1) to adjacent molecules. The interaction depicted in Fig. 5 with a positive electrostatic energy of +5 kJ mol−1 results in a total energy of +3 kJ mol−1. It is important to emphasize that although polarization and dispersion terms are relatively small in this case, they are nevertheless essential for the computation of accurate energies. The accuracy and reliability of these CE-B3LYP energies can be assessed by their summation to estimate a lattice energy; the resulting value of −83 kJ mol−1 compares well with the reference lattice energy of −78.7 kJ mol−1 reported by Otero de la Roza and Johnson.46s-Triazine
The energy frameworks for s-triazine (Fig. 11) differ greatly from those for formamide. For the two interactions depicted in Fig. 6, where the electrostatic energies are −2 and −9 kJ mol−1, for stacking and in-plane nearest neighbours, the ordering of dispersion energies is the reverse, at −16 and −8 kJ mol−1, respectively. As a result, the two interactions are very close in energy and just over −12 kJ mol−1. The electrostatic and dispersion frameworks show quite different architectures, most notably for the stacking interaction, and we conclude that the crystal structure of s-triazine represents a subtle balance between electrostatic and dispersion contributions of similar magnitude and importance. The computed CE-B3LYP lattice energy of −55 kJ mol−1 is also close to the reference value of −60.5 kJ mol−1.46Benzene:hexafluorobenzene co-crystal
As seen in Fig. 7, stacking interactions are also important for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 co-crystal of benzene and hexafluorobenzene, and here the electrostatic energy is largest for the stacking motif, and much less for in-plane nearest neighbours. The corresponding energy frameworks (Fig. 12) show clearly the more dominant role of dispersion in this crystal. The CE-B3LYP energy for the stacking interaction is −22 kJ mol−1 (with electrostatic and dispersion terms of −7 and −28 kJ mol−1, respectively), almost twice that for the most stabilizing in-plane interaction, that between benzene and hexafluorobenzene, of −12 kJ mol−1 (with electrostatic and dispersion terms of −3 and −15 kJ mol−1, respectively). The total energies for the other various in-plane interactions are all in the narrow range of −4 to −6 kJ mol−1, with the exception of the benzene–benzene closest pair depicted in Fig. 7, which has a total energy of only −1 kJ mol−1.
1 co-crystal of benzene and hexafluorobenzene, and here the electrostatic energy is largest for the stacking motif, and much less for in-plane nearest neighbours. The corresponding energy frameworks (Fig. 12) show clearly the more dominant role of dispersion in this crystal. The CE-B3LYP energy for the stacking interaction is −22 kJ mol−1 (with electrostatic and dispersion terms of −7 and −28 kJ mol−1, respectively), almost twice that for the most stabilizing in-plane interaction, that between benzene and hexafluorobenzene, of −12 kJ mol−1 (with electrostatic and dispersion terms of −3 and −15 kJ mol−1, respectively). The total energies for the other various in-plane interactions are all in the narrow range of −4 to −6 kJ mol−1, with the exception of the benzene–benzene closest pair depicted in Fig. 7, which has a total energy of only −1 kJ mol−1.
Chloroacetic acid:2-amino-5-nitropyridine co-crystal
In their charge density study of the co-crystal between chloroacetic acid and 2-amino-5-nitropyridine, Sarkar et al. focused their attention on the –NH2⋯Cl close contact, and the possibility of either a pnicogen bond between N and Cl, or the “less probable” bifurcated N–H⋯Cl hydrogen bonds.42 But, and importantly, they also commented: “However, it should be noted that the crystal structure… is stabilized by typical N–H⋯O, O–H⋯N hydrogen bonding along with π–π stacks”. Based on the maps of Δρ and ESP we have already noted that the interaction involving the –NH2⋯Cl close contact is clearly stabilizing, with an electrostatic energy of −38 kJ mol−1, but dissecting this into pnicogen vs. bifurcated hydrogen bonds is next to impossible. The total CE-B3LYP energy for this interaction is −33 kJ mol−1. The much stronger interaction anticipated by Sarkar et al. is that involving a cyclic pair of N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and O–H⋯N hydrogen bonds. The electrostatic energy of −130 kJ mol−1 for this pair dominates the electrostatic energy framework in Fig. 13. Polarization and repulsion energies are also large, and the total energy of −69 kJ mol−1 makes this interaction the strongest in this crystal, and this is shown clearly in the total energy framework in Fig. 13. The interaction with the largest dispersion contribution, namely that coming directly out of the page in Fig. 13, is the stacking interaction between two 2-amino-5-nitropyridine molecules, with an electrostatic energy of +1 kJ mol−1 and a dispersion energy of −26 kJ mol−1, resulting in a total energy of −11 kJ mol−1.
C and O–H⋯N hydrogen bonds. The electrostatic energy of −130 kJ mol−1 for this pair dominates the electrostatic energy framework in Fig. 13. Polarization and repulsion energies are also large, and the total energy of −69 kJ mol−1 makes this interaction the strongest in this crystal, and this is shown clearly in the total energy framework in Fig. 13. The interaction with the largest dispersion contribution, namely that coming directly out of the page in Fig. 13, is the stacking interaction between two 2-amino-5-nitropyridine molecules, with an electrostatic energy of +1 kJ mol−1 and a dispersion energy of −26 kJ mol−1, resulting in a total energy of −11 kJ mol−1.
1,2-Diiodo-1,1,2,2-tetrafluoroethane:1,4-dicyanobutane co-crystal
Energy framework pictures for this co-crystal (Fig. 14) show that although the N⋯I halogen bond has the most negative electrostatic energy (Fig. 9), it is far from the strongest – or most important – intermolecular interaction in this crystal. The strongest is that between cyanobutane molecules in adjacent “chains”, with an energy of −25 kJ mol−1, much greater than for the halogen bonded pair, −14 kJ mol−1. The mix of electrostatic and dispersion contributions is responsible for this, as is the large repulsion energy associated with the close N⋯I contact. There are also two other notable molecular pairs, with total CE-B3LYP energies of −14 and −18 kJ mol−1, both between tetrafluoroethane and cyanobutane molecules in adjacent “chains”, and for which the dispersion contribution exceeds −20 kJ mol−1 in both cases. These results clearly contradict the observation in ref. 45 that the halogen bonds “are the only strong interactions present” in this co-crystal, and they indicate that the original description of the crystal in terms of 1D “chains” is clearly inaccurate. This linear arrangement of alternating tetrafluoroethane and cyanobutane molecules is observable in the total energy framework in Fig. 14, but other interactions between these molecules are at least as strong (and important), and the cyanobutane–cyanobutane interaction is by far the strongest.Putting it all together: hexachlorobenzene and hexabromobenzene
The crystal structures of hexachlorobenzene (HCB) and hexabromobenzene (HBB) have been discussed in the context of the nature of halogen⋯halogen interactions and their mechanical properties, in particular bending and nanoindentation.47,48 HCB has since been subjected to detailed analysis of the experimental charge density at 100 K in order to characterize the nature of Cl⋯Cl interactions in the crystal, especially the so-called halogen trimer (X3 or Hal3) synthon.49,50 Most recently, plastic bending in HCB has also been examined in considerable detail by micro-IR and micro-X-ray diffraction.51 HBB is isostructural with HCB but, unlike HCB, it only exhibits bending at elevated temperatures (∼400 K).48 These studies acknowledge the strongly anisotropic intermolecular interactions that are responsible for the mechanical behaviour of HCB, and although this anisotropy has been quantified for HCB using counterpoise-corrected BLYP-D/def2-TZVP energies for molecular pairs,52 no comparison has been made with HBB. Here we use CE-B3LYP model energies, and the separate electrostatic and dispersion contributions, to investigate the interaction anisotropy in HCB and HBB using energy framework diagrams (Fig. 15) and a detailed analysis of the various interactions between a molecule and the 14 nearest neighbours in its first coordination sphere (Table 1 and Fig. 16). We use the original 100 K structures reported by Reddy et al.48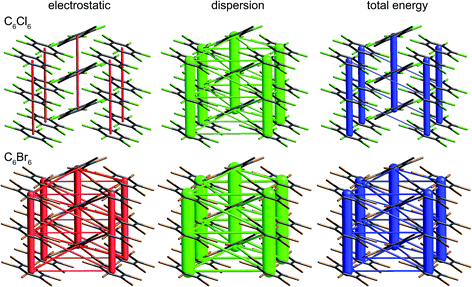 | ||
| Fig. 15 Hexachlorobenzene (HCLBNZ12) and hexabromobenzene (HBRBEN02): energy frameworks for separate electrostatic (red) and dispersion (green) contributions to the total nearest neighbour pairwise interaction energies (blue). All energies with a magnitude less than 5 kJ mol−1 have been omitted from the frameworks. See Fig. 10 for further details. | ||
| E ele | E pol | E dis | E rep | E tot | N | Pair | Close X⋯X contacts | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Although all close contacts between symmetry-related atoms (e.g., Cln⋯Cln, n = 1–3, etc.) in these stacking interactions are identical, an additional close contact results from the offset stacking arrangement. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HCB | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stackinga | −11.9 | −0.7 | −53.1 | 31.0 | −34.7 | 2 | All Cln⋯Cln 3.761 Å, Cl1⋯Cl3 (3.813 Å, twice) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −2.9 | −0.1 | −7.6 | 5.5 | −5.1 | 2 | A⋯B | Cl2⋯Cl3 (3.666 Å, twice), Cl3⋯Cl3 (3.634 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −3.1 | −0.1 | −6.9 | 5.4 | −4.5 | 4 | A⋯C | Cl1⋯Cl2 (3.444 Å), Cl2⋯Cl2 (3.816 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −3.1 | −0.1 | −6.7 | 6.1 | −3.7 | 4 | B⋯C | Cl1⋯Cl3 (3.470 Å), Cl1⋯Cl1 (3.624 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Other | −1.6 | 0.0 | −8.3 | 5.6 | −4.3 | 2 | Cl2⋯Cl3 (3.902 Å, twice), Cl3⋯Cl3 (3.653 Å) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| HBB | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Stackinga | −36.8 | −0.4 | −69.1 | 52.7 | −53.5 | 2 | All Brn⋯Brn 3.949 Å, Br2⋯Br3 (3.931 Å, twice) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −9.1 | −0.1 | −12.7 | 12.5 | −9.5 | 2 | A⋯B | Br1⋯Br3 (3.787 Å, twice), Br3⋯Br3 (3.747 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −9.6 | −0.2 | −11.1 | 12.5 | −8.3 | 4 | A⋯C | Br1⋯Br2 (3.550 Å), Br1⋯Br1 (3.946 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hal3 | −9.7 | −0.2 | −10.6 | 13.7 | −6.9 | 4 | B⋯C | Br2⋯Br2 (3.756 Å), Br2⋯Br3 (3.563 Å) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Other | −6.3 | −0.1 | −12.6 | 10.6 | −8.5 | 2 | Br1⋯Br3 (4.132 Å, twice), Br3⋯Br3 (3.831 Å) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
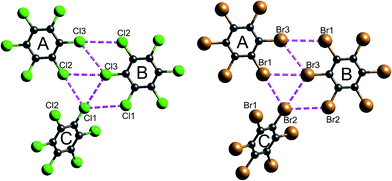 | ||
| Fig. 16 Closest Cl⋯Cl and Br⋯Br contacts (magenta dashed lines) between adjacent molecules in hexachlorobenzene (HCLBNZ12) and hexabromobenzene (HBRBEN02). The atom labelling is the same as that in the original CIF files. See Table 1 for interaction energies between molecules A, B and C, as well as those involved in the stacking motif. | ||
The energy framework diagrams (Fig. 15) provide immediate insight into the columnar architecture of these two crystal structures, and especially the differences between them. Electrostatic interactions between adjacent molecules are small for HCB (and only there between molecules arranged in a stacking fashion), but much more significant for HBB. In both crystals dispersion plays a very important role, again more so for HBB. The total energy frameworks (blue) suggest that HCB is best described in terms of columns involving relatively strong interactions between adjacent molecules (−35 kJ mol−1; Table 1), with much smaller interaction energies between molecules in adjacent columns (between −4 and −5 kJ mol−1). All interactions are stronger in HBB: stacked pairs at −54 kJ mol−1, and intercolumn pairs between −7 and −10 kJ mol−1. The essential difference between HCB and HBB is revealed to be the stronger interaction between molecules in adjacent columns in the latter, resulting in a failure to bend at room temperature. Presumably the observed bending at ∼400 K is facilitated by expansion of the unit cell, reducing the interaction energies as molecules become further apart.
It is tempting to compare the results in Table 1 with energies reported by Brezgunova et al.,49 based on bond critical point (bcp) properties derived from topological analysis of electron distributions. There are many assumptions involved in such an analysis, as well as substantial experimental errors – including model dependence – when derived from a charge density experiment, and one of us has recently demonstrated that results of that kind are unreliable.53 But, if we assume that it is somehow possible to derive reliable interaction energies from the electron density and its Laplacian at bcps for intermolecular interactions, we are faced with the dilemma highlighted in Fig. 16 (see also data for Cl⋯Cl contacts in Table 1). In their analysis of the halogen trimer synthon, Brezgunova et al.49 summed energy estimates based on just the three bcps that are identified immediately with the triangle of short contacts, namely Cl1⋯Cl2, Cl2⋯Cl3 and Cl1⋯Cl3 in Fig. 16 (the atom labelling is not the same as that used by those authors). But it should be obvious that the interaction between molecules A and B involves three of those short Cl⋯Cl contacts, and hence three such bcps if they exist. Taken together, the halogen trimer energy, would require summing over all six Cl⋯Cl bcps identified in the earlier study by Bui et al.50 (see Table 1 in that work).
The present CE-B3LYP energies in Table 1 simplify this inquiry considerably. The energy associated with the halogen trimer synthon in these crystals is the sum of the three intermolecular energies for pairs depicted in Fig. 16, and given in Table 1: −13 kJ mol−1 for HCB and −25 kJ mol−1 for HBB, suggesting this synthon is nearly twice as strong in HBB than in HCB, in contrast to a difference of only 17% estimated by Brezgunova et al.49 But once more, we question the focus on this particular structural motif, as it ignores another intercolumn interaction with similar energy to those for the other molecular pairs, namely −4 kJ mol−1 for HCB and −9 kJ mol−1 for HBB (Table 1). As we have done for formamide and s-triazine, we can estimate the reliability of the CE-B3LYP energies for HCB and HBB by comparing computed lattice energies with experimental sublimation enthalpies. The CE-B3LYP estimated lattice energies are −69 (HCB) and −115 (HBB) kJ mol−1, compared with sublimation enthalpies of 88 ± 12 kJ mol−1 (from 12 measurements) for HCB, and a single value of 118 kJ mol−1 for HBB.54 (We note that the interaction energies reported in ref. 52 for HCB are all ∼25% greater than the present CE-B3LYP results, but we cannot identify the origin of this difference).
Conclusions
The question asked in the title of this paper has appeared in the title of recent discussions relating to the nomenclature and definition of polymorphs, salts and co-crystals,55 pseudopolymorphism,56 and in the context of what is – and is not – a halogen bond according to its definition.57,58 Nomenclature, and being precise about what we mean by the terms we use, is of course enormously important in science. For that reason both the hydrogen bond59 and halogen bond24 have been the subjects of recent IUPAC recommendations regarding their use and definition (see also the proposal to systematically name noncovalent interactions by the group of the periodic table to which the electrophilic atom belongs60). But it is not at all obvious to us how those recommendations help in the “understanding of intermolecular interactions in the context of crystal packing”. We have identified in this work instances where paying attention to particular interactions, because they are expected to be important, or because they have been given a special name, can result in ignoring significantly more important interactions.To best understand the nature of intermolecular interactions in the context of crystal packing we believe a more balanced approach is needed – one that avoids any bias towards a focus on specific atom⋯atom interactions, or what appear to be novel interactions. We have presented one such way of achieving this, using the graphical and computational tools embodied in our research toolbox CrystalExplorer, but it is certainly not the only one. The broad details of non-covalent interactions, including hydrogen bonds, can be largely understood through their common origin in the redistribution of electron density that results from bonding. This redistribution is directly linked to the molecular electrostatic potential, to qualitative concepts such as electrostatic complementarity, and to the efficient calculation of reliable intermolecular interaction energies. Visualization of these energies, along with their electrostatic and dispersion components, sheds light on the architecture of molecular crystals, in turn providing a link to actual crystal properties.
Acknowledgements
This work has been supported by the Australian Research Council (DP130103304) and the Danish National Research Foundation (Center for Materials Crystallography, DNRF-93).Notes and references
- Crystal Engineering: The Design of Organic Solids, ed. G. R. Desiraju, Elsevier, Amsterdam, 1989 Search PubMed.
- P. Lipkowski and S. J. Grabowski, Chem. Phys. Lett., 2014, 591, 113–118 CrossRef CAS.
- M. Yanez, P. Sanz, O. Mo, I. Alkorta and J. Elguero, J. Chem. Theory Comput., 2009, 5, 2763–2771 CrossRef CAS PubMed.
- A. Bauza and A. Frontera, ChemPhysChem, 2016, 17, 3181–3186 CrossRef CAS PubMed.
- S. J. Grabowski, Molecules, 2015, 20, 11297–11316 CrossRef CAS PubMed.
- S. J. Grabowski, ChemPhysChem, 2014, 15, 2985–2993 CrossRef CAS PubMed.
- A. Bauza, T. J. Mooibroek and A. Frontera, Chem. Rec., 2016, 16, 473–487 CrossRef CAS PubMed.
- E. C. Escudero-Adan, A. Bauza, A. Frontera and P. Ballester, ChemPhysChem, 2015, 16, 2530–2533 CrossRef CAS PubMed.
- S. P. Thomas, M. S. Pavan and T. N. G. Row, Chem. Commun., 2014, 50, 49–51 RSC.
- A. Bauza, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef CAS PubMed.
- A. Bauza, D. Quinonero, P. M. Deya and A. Frontera, CrystEngComm, 2013, 15, 3137–3144 RSC.
- S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288 CrossRef CAS PubMed.
- S. Scheiner, Int. J. Quantum Chem., 2013, 113, 1609–1620 CrossRef CAS.
- S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem.–Eur. J., 2011, 17, 6034–6038 CrossRef CAS PubMed.
- S. P. Thomas, K. Satheeshkumar, G. Miugesh and T. N. Guru Row, Chem.–Eur. J., 2015, 21, 1–9 CrossRef.
- M. Pyziak, J. Pyziak, M. Hoffmann and M. Kubicki, Cryst. Growth Des., 2015, 15, 5223–5232 CAS.
- L. M. Azofra and S. Scheiner, J. Phys. Chem. A, 2014, 118, 3835–3845 CrossRef CAS PubMed.
- M. E. Brezgunova, J. Lieffrig, E. Aubert, S. Dahaoui, P. Fertey, S. Lebegue, J. G. Angyan, M. Fourmigue and E. Espinosa, Cryst. Growth Des., 2013, 13, 3283–3289 CAS.
- W. Z. Wang, B. M. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135 CrossRef CAS PubMed.
- G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478–2601 CrossRef CAS PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278–294 CrossRef CAS PubMed.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- P. Metrangolo, G. Resnati, T. Pilati and S. Biella, Struct. Bonding, 2008, 126, 105–136 CrossRef CAS.
- P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127 CrossRef CAS PubMed.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS PubMed.
- P. Metrangolo and G. Resnati, Chem.–Eur. J., 2001, 7, 2511–2519 CrossRef CAS.
- A. Bauza and A. Frontera, Angew. Chem., Int. Ed., 2015, 54, 7340–7343 CrossRef CAS PubMed.
- A. Bauza and A. Frontera, Phys. Chem. Chem. Phys., 2015, 17, 24748–24753 RSC.
- A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef CAS PubMed.
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- C. F. Mackenzie, P. R. Spackman, D. Jayatilaka and M. A. Spackman, IUCrJ, 2017, 4 DOI:10.1107/S205225251700848X.
- M. J. Turner, S. Grabowsky, D. Jayatilaka and M. A. Spackman, J. Phys. Chem. Lett., 2014, 5, 4249–4255 CrossRef CAS PubMed.
- M. J. Turner, S. P. Thomas, M. W. Shi, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2015, 51, 3735–3738 RSC.
- J. D. Dunitz, IUCrJ, 2015, 2, 157–158 CrossRef CAS PubMed.
- C. Lecomte, E. Espinosa and C. F. Matta, IUCrJ, 2015, 2, 161–163 CrossRef CAS PubMed.
- T. S. Thakur, R. Dubey and G. R. Desiraju, IUCrJ, 2015, 2, 159–160 CrossRef CAS PubMed.
- J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038 CrossRef CAS PubMed.
- A. S. Mitchell and M. A. Spackman, J. Comput. Chem., 2000, 21, 933–942 CrossRef CAS.
- M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer17, University of Western Australia, 2017, http://hirshfeldsurface.net Search PubMed.
- S. Sarkar, M. S. Pavan and T. N. G. Row, Phys. Chem. Chem. Phys., 2015, 17, 2330–2334 RSC.
- G. L. D. Ritchie and J. N. Watson, Chem. Phys. Lett., 2000, 322, 143–148 CrossRef CAS.
- M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377–388 CAS.
- P. Metrangolo, T. Pilati, G. Resnati and A. Stevenazzi, Chem. Commun., 2004, 1492–1493 RSC.
- A. Otero de la Roza and E. J. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS PubMed.
- C. M. Reddy, R. C. Gundakaram, S. Basavoju, M. T. Kirchner, K. A. Padmanabhan and G. R. Desiraju, Chem. Commun., 2005, 3945–3947 RSC.
- C. M. Reddy, M. T. Kirchner, R. C. Gundakaram, K. A. Padmanabhan and G. R. Desiraju, Chem.–Eur. J., 2006, 12, 2222–2234 CrossRef CAS PubMed.
- M. E. Brezgunova, E. Aubert, S. Dahaoui, P. Fertey, S. Lebegue, C. Jelsch, J. G. Angyan and E. Espinosa, Cryst. Growth Des., 2012, 12, 5373–5386 CAS.
- T. T. T. Bui, S. Dahaoui, C. Lecomte, G. R. Desiraju and E. Espinosa, Angew. Chem., Int. Ed., 2009, 48, 3838–3841 CrossRef CAS PubMed.
- M. K. Panda, S. Ghosh, N. Yasuda, T. Moriwaki, G. D. Mukherjee, C. M. Reddy and P. Naumov, Nat. Chem., 2015, 7, 65–72 CrossRef CAS PubMed.
- O. V. Shishkin, V. V. Medvediev and R. I. Zubatyuk, CrystEngComm, 2013, 15, 160–167 RSC.
- M. A. Spackman, Cryst. Growth Des., 2015, 15, 5624–5628 CAS.
- W. Acree and J. S. Chickos, J. Phys. Chem. Ref. Data, 2016, 45, 033101 CrossRef.
- S. Aitipamula, R. Banerjee, A. K. Bansal, K. Biradha, M. L. Cheney, A. R. Choudhury, G. R. Desiraju, A. G. Dikundwar, R. Dubey, N. Duggirala, P. P. Ghogale, S. Ghosh, P. K. Goswami, N. R. Goud, R. R. K. R. Jetti, P. Karpinski, P. Kaushik, D. Kumar, V. Kumar, B. Moulton, A. Mukherjee, G. Mukherjee, A. S. Myerson, V. Puri, A. Ramanan, T. Rajamannar, C. M. Reddy, N. Rodriguez-Hornedo, R. D. Rogers, T. N. G. Row, P. Sanphui, N. Shan, G. Shete, A. Singh, C. C. Sun, J. A. Swift, R. Thaimattam, T. S. Thakur, R. Kumar Thaper, S. P. Thomas, S. Tothadi, V. R. Vangala, N. Variankaval, P. Vishweshwar, D. R. Weyna and M. J. Zaworotko, Cryst. Growth Des., 2012, 12, 2147–2152 CAS.
- G. R. Desiraju, Cryst. Growth Des., 2004, 4, 1089–1090 CAS.
- R. Glaser and R. F. Murphy, CrystEngComm, 2006, 8, 948–951 RSC.
- P. Metrangolo, T. Pilati and G. Resnati, CrystEngComm, 2006, 8, 946–947 RSC.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641 CAS.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati and G. Terraneo, Cryst. Growth Des., 2014, 14, 2697–2702 CAS.
| This journal is © The Royal Society of Chemistry 2017 |