Open Access Article
Open Access ArticleMulti-functional scaling methodology for translational pharmacokinetic and pharmacodynamic applications using integrated microphysiological systems (MPS)†
Christian
Maass
 a,
Cynthia L.
Stokes
b,
Linda G.
Griffith
a and
Murat
Cirit
*a
a,
Cynthia L.
Stokes
b,
Linda G.
Griffith
a and
Murat
Cirit
*a
aDepartment of Biological Engineering, Massachusetts Institute of Technology, Cambridge, USA. E-mail: mcirit@mit.edu
bStokes Consulting, Redwood City, USA
First published on 1st March 2017
Abstract
Microphysiological systems (MPS) provide relevant physiological environments in vitro for studies of pharmacokinetics, pharmacodynamics and biological mechanisms for translational research. Designing multi-MPS platforms is essential to study multi-organ systems. Typical design approaches, including direct and allometric scaling, scale each MPS individually and are based on relative sizes not function. This study's aim was to develop a new multi-functional scaling approach for integrated multi-MPS platform design for specific applications. We developed an optimization approach using mechanistic modeling and specification of an objective that considered multiple MPS functions, e.g., drug absorption and metabolism, simultaneously to identify system design parameters. This approach informed the design of two hypothetical multi-MPS platforms consisting of gut and liver (multi-MPS platform I) and gut, liver and kidney (multi-MPS platform II) to recapitulate in vivo drug exposures in vitro. This allows establishment of clinically relevant drug exposure–response relationships, a prerequisite for efficacy and toxicology assessment. Design parameters resulting from multi-functional scaling were compared to designs based on direct and allometric scaling. Human plasma time–concentration profiles of eight drugs were used to inform the designs, and profiles of an additional five drugs were calculated to test the designed platforms on an independent set. Multi-functional scaling yielded exposure times in good agreement with in vivo data, while direct and allometric scaling approaches resulted in short exposure durations. Multi-functional scaling allows appropriate scaling from in vivo to in vitro of multi-MPS platforms, and in the cases studied provides designs that better mimic in vivo exposures than standard MPS scaling methods.
Insight, innovation, integrationMicrophysiological systems provide relevant physiological environments in vitro for studies of pharmacokinetics, pharmacodynamics and biological mechanisms for translational research. Designing multi-MPS platforms is essential to study multi-organ systems. There is an immediate need for a mechanistic approach to design multi-MPS platforms. Common approaches for MPS scaling (sizes, volumes and flow rates) are direct miniaturization and allometric scaling. These empirical approaches consider each MPS individually and are based on physical size. Subsequently, integrated multi-MPS platforms are built by simply connecting individually developed MPSs together. In this work, a novel multi-functional scaling approach is introduced to design integrated multi-MPS platforms, which is adaptable to various research interests, e.g. different MPS types or arrangements and study objectives (pharmacokinetics, pharmacodynamics, disease models). |
1. Introduction
Over the last decade, development of microphysiological systems (MPS) aiming to represent relevant human physiology and organ-specific functions in vitro has accelerated, in part driven by federal funding agency initiatives in the United States and internationally.1–3 Numerous individual MPSs have been developed to represent specific organs or sub-organ systems, including liver, kidney, lung, muscle, cardiac and skin,4–10 and multi-MPS platforms with interconnected MPSs are also being developed to capture multi-organ physiology.11–14The vision is for MPS technologies to provide improved in vitro tools and increased translational success for pharmacokinetic, pharmacodynamic, toxicology and biomarker discovery applications.15–18 Results from current in vitro models as well as animal models frequently differ from early clinical trial results, and appropriately designed MPSs will most likely represent in vivo tissue and organ biology more adequately. This in turn should provide improved preclinical tools to guide decision-making with regards to drug efficacy and patient safety in clinical trials, as well as potentially informing early disease modeling for complex or systemic diseases.
Within an MPS device, the cell types included, micro-architecture for cell culture, fluid flow rates, and culture protocol work synergistically together to mimic desirable features of the 3D structure, mechanical strain and flow shear stress5 found in vivo. For interconnected MPSs, design parameters (e.g. tissue sizes, medium volumes) and operational strategies (e.g., flow partitioning, flow rates) need to be specified to reproduce desired biological functions within practical constraints, and in consideration of the applications (i.e., the systems-level biological phenomena of interest). The most appropriate design approach for MPSs interacting on a fluidic platform at a systems level continues to be debated. The specific applications of a single or multi-MPS platform (e.g. drug pharmacokinetics, specific pharmacodynamics, toxicology or biomarker discovery) will likely drive design, since it is unlikely that a single design will be appropriate for all applications.
Common scaling approaches to date include direct miniaturization and allometric scaling of a variety of in vivo physical characteristics such as organ/tissue mass, blood flowrates, volumes and residence times.1,11,19,20 The focus of these approaches is to preserve the relative biomass scales of each organ (e.g. blood volume to flow rate, or volume to mass ratios). These methodologies result in one design for single- or multi-MPS platforms, which is independent of the study application. Therefore, it is widely acknowledged that more function-based scaling is desirable.19,21–23
Functional scaling aims at recapitulating selected in vivo physiological processes or functions in the in vitro environment (e.g. an MPS). The idea is to determine design parameters for single MPSs or multi-MPS platforms by considering functions of MPSs relevant to the application or study objective of interest. These designs would be based upon recapitulating the functions rather than relative masses, flow rates, and similar, the typical considerations in direct or allometric scaling approaches.
Examples of biological functions to be considered in functional scaling might be drug metabolism and excretion (for pharmacokinetic and pharmacodynamic applications), insulin production, and glucose metabolism rates (for diabetes studies), or cytokine production rates and concentrations (for inflammation studies).
A mechanistic modeling approach would provide an appropriate framework as it allows consideration of each MPS function and characteristics of an integrated multi-MPS platform simultaneously. Further, as any individual MPS seldom replicates every feature of the organ in vivo, application-driven design of MPS components to capture essential features for the application is crucial to create a relevant physiological and pharmacological environment.1,2,19,21,24
Several multi-MPS platforms11,19 have been developed by interconnecting existing single-MPSs. While the MPSs in such systems are typically on the same approximate physical scale as each other, each has usually been developed independently and the interconnections were limited by practical considerations (e.g., ease of handling, pumping constraints, etc.). A recent theoretical study introduced a quantitative approach to multi-MPS design and data analysis. The authors investigated sensitivity and impact of design parameters (e.g. medium volumes or flow rates) in an integrated four-MPS system on pharmacologically relevant metrics for drug concentration and distribution.13 However, a method to simultaneously consider multiple MPS functions as the basis for specifying MPS design and guiding multi-MPS operations is still needed. Such an approach requires consideration of functions from each MPS as well as integrated MPS function simultaneously.
The aim of this work is to develop and demonstrate feasibility and applicability of a multi-functional scaling approach to inform the design of study-specific, integrated, multi-MPS platforms. A novel multi-functional scaling framework was developed based on mechanistic modeling of the biological mechanisms, specification of an objective function, and identification of design parameters (those, which would be specified in order to optimize the objective function). As use cases, two multi-MPS platforms (gut–liver and gut–liver–kidney) were investigated computationally, focusing on pharmacological applications using available preclinical and clinical data. To evaluate our approach, we test how well our designed multi-MPS platforms recapitulate drug exposure of additional drugs not used in the initial multi-MPS platform design by comparing predicted exposures in the theoretical in vitro platform to known in vivo exposures. Recapitulating relevant exposures in vitro is important to establish exposure–response relationships, which describe a response or an effect in the body or an organ of interest due to the drug over time.25 These relationships provide a foundation for further studies of efficacy and toxicology in a more clinically-relevant manner, as well as a means to identify potentially safe and hazardous dosing regimens for drugs.
In addition, we compare our scaling approach to results from designing the two multi-MPS platforms using the traditional methods of allometric scaling and direct scaling. We find that our multi-functional scaling methodology can provide system designs that should recapitulate relevant in vivo drug exposures in vitro.
2. Materials and methods
The goal of the application-specific design for a hypothetically integrated multi-MPS system was to recapitulate human drug exposures in vitro. Two different multi-MPS platforms – gut–liver MPS platform (multi-MPS platform I) and a gut–liver–kidney MPS platform (multi-MPS platform II) – were investigated. Three different scaling approaches to design multi-MPS platforms were applied: (i) multi-functional scaling, (ii) direct scaling, and (iii) allometric scaling.In general, the multi-functional scaling algorithm consists of (1) mathematical models of the biological mechanisms of each MPS and integrated multi-MPS platform, (2) specification of known or desired model parameters (both biological and operational), (3) specification of an objective function that embodies the critical MPS platform biological functions of interest and the selection of related, available experimental data to be used in the optimization process, (4) selection of design parameters – operational parameters to be estimated by minimizing the objective function, (5) specification of constraints for design parameters, and (6) assessment of design outcome by evaluating a metric related to the objective function and biological functions of the platform.
The details of the scaling approaches and mathematical equations are included in our descriptions of the two multi-MPS platform test cases below as well as in Supplement S1 (ESI†).
All simulations and parameter estimations were performed in Matlab (R2016a, The MathWorks, Inc., Natick, Massachusetts, United States).
In contrast, the general workflow for direct and allometric scaling to determine design parameters consists of steps (1) and (2) as described above, (3) calculation of design parameters by applying a scaling factor or a power-law equation, and (4) evaluation of design outcome by the same metric.
Computational investigation of multi-MPS designs
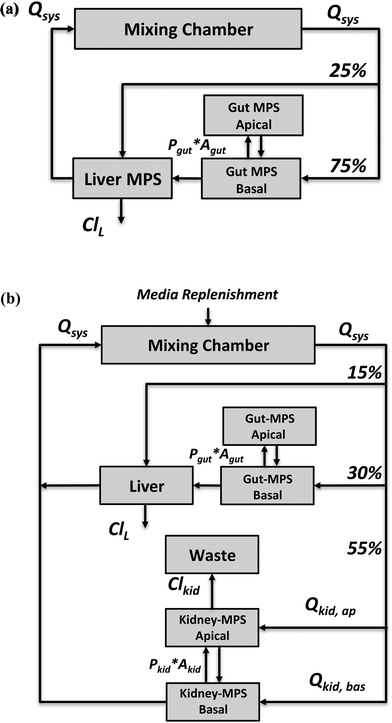
The application focus of the two multi-MPS platforms we investigated is pharmacokinetics following oral administration of drugs. Both platforms were mathematically described by a set of ordinary differential equations.The first multi-MPS platform investigated comprises gut and liver MPSs plus a mixing chamber (Fig. 1(a)), to capture the basic processes of drug absorption, metabolism and distribution in a closed-loop system. The systemic circulation flow rate (Qsys) distributes cell culture medium and drugs between the mixing chamber and the MPSs. Flow partitioning to each MPS was based on physiological partitioning of cardiac output for liver (hepatic artery) and gut (portal vein).26,27 Drugs can be administered either to the mixing chamber (representing intravenous (IV) administration) or the apical site of the gut MPS (representing oral administration). For the latter, permeability constants (Pgut) of various drugs for transport through CaCo-2 cell monolayers, a typical gut epithelium model, were obtained from the literature and are used in the model. Drug is assumed to be metabolized in the liver MPS by hepatocytes only. Both parent drug and metabolites are distributed by flow among the mixing chamber, gut and liver. Intrinsic clearance rates (ClL) for parent drugs by hepatocytes in vitro were obtained from literature reports for suspension hepatocyte cultures.
The second multi-MPS platform investigated is a semi-closed system comprising gut, liver, kidney MPSs and a mixing chamber (Fig. 1(b)) to additionally include excretion and reabsorption processes via the kidney MPS. The features of the gut and liver MPSs are the same as in multi-MPS platform I. The flowrate to the kidney MPS (Qkid) is estimated relative to the physiological flows in vivo to gut and liver.27 This flow is divided between the renal lumen (Qkid,ap) and the interstitium (Qkid,bas). Reabsorption rates from lumen to interstitium as well as secretion rates from interstitium to lumen were obtained from in vitro permeability studies using renal proximal epithelial cells (MDR1-MDCK). To recapitulate excretion of parent drug from the kidney MPS, a constant flow to a waste container (Qwaste) was introduced and set equal to the renal luminal flow (Qkid,ap). As no active filtration between medium and drug occurs, medium was replenished at the same rate as the excretion rate (Qwaste) to the mixing chamber (media replenishment).
Mechanistic models using ordinary differential equations were implemented for each of the platforms to describe absorption, distribution, metabolism and excretion of a compound and their effects on that compound's time–concentration profile in the integrated MPS platform in silico (see Supplement S1, ESI†).
MPS scaling using three approaches
Training sets of eight drugs for each platform (Tables 1 and 2) were used to identify design parameters. In the algorithm, the objective function is a weighted squared difference between a model outcome and corresponding measurements:
 | (1) |
| Drug | BDDCS class | Hepatic clearance in vitro (ml min−1 kg−1) | Hepatic clearance in vivoa (ml min−1 kg−1) | Apparent permeability of CaCo-2 cells (10−6 cm s−1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Intrinsic clearance values in vivo based on a well-stirred model from Hallifax et al. (2010).56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Training set | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Diazepam | 1 | 6.6 | 15.3 | 36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Diclofenac | 1 | 86.8 | 418 | 18 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Fenoprofen | 1 | 27.5 | 34.3 | 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ibuprofen | 2 | 32.6 | 59.1 | 26 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Lidocaine | 1 | 15.3 | 82.1 | 44 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Phenacetin | 2 | 36.2 | 615 | 20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Propranolol | 1 | 29.2 | 267 | 29 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Warfarin | 2 | 1.2 | 4.5 | 23 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Test set | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Acetaminophen | 1 | 2.5 | 6.3 | 37 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Clozapine | 2 | 20.8 | 160 | 31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Imipramine | 1 | 42.8 | 318 | 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Oxazepam | 2 | 6.9 | 38.5 | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sildenafil | 1 | 24.4 | 89.8 | 31 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Drug | BDDCS class | Fraction excreted unchanged parent drug (%) | Apparent permeability of CaCo-2 cells (10−6 cm s−1) | Apparent permeability of MDR1-MDCK cells (10−6 cm s−1) | Hepatic clearance in vitro (ml min−1 kg−1) | Hepatic clearance in vivoc (ml min−1 kg−1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Reported values are derived using CaCo-2 cells (see section ‘Pharmacokinetic data’ for more detail). b AB: apical to basal; BA: basal to apical. c Intrinsic clearance values in vivo based on a well-stirred model from Hallifax et al. (2010)56 and from Paixao et al. (2010)57 for linezolid. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Training set | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Betaxolol | 1 | 15 | 12 | 20a | 7.4 | 8.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Linezolid | 1 | 30 | 36 | 10a | 2.1 | 1.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pindolol | 3 | 54 | 20 | 60 | 7.8 | 9.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Prednisolone | 1 | 16 | 19 | 20a | 30.0 | 27.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Quinidine | 1 | 19 | 12 |
AB: 2b
BA: 7 |
18 | 34.2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ranitidine | 3 | 30 | 3 | 0.4 | 3.0 | 4.38 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Theophylline | 1 | 18 | 63 | 65a | 2.6 | 2.6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Timolol | 1 | 15 | 12 | 18 | 4.4 | 49.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Test set | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Acebutolol | 1 | 27 | 2 | 2 | 5.1 | 5.3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Alprazolam | 1 | 20 | 3 |
AB: 37
BA: 33 |
2.1 | 2.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Indomethacin | 2 | 15 | 13 |
AB: 16
BA: 21 |
27.1 | 126 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ketoprofen | 2 | 50 | 33 | 20 | 11.0 | 77.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Nadolol | 3 | 73 | 1 | 1 | 7.7 | 3.5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
More specifically, in multi-MPS platform I, the study objective was to recapitulate clinically observed plasma concentration profiles (observation) of each drug from the training set in the mixing chamber (prediction) using model calculations of the drug concentration profile in the mixing chamber. In multi-MPS platform II, the study objective included two elements, recapitulating the plasma concentration profiles as done in multi-MPS platform I and to recapitulate the fraction excreted parent drug in humans (observation) in the waste container (prediction, Fig. 1(b)) of the platform. For each platform, the information was simultaneously modeled to yield a single set of design parameters based on all eight drugs.
To account for the dose and bioavailability differences of drugs in vivo, the in vivo time–concentration profiles were normalized as follows:
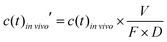 | (2) |
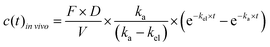 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vivo is the measured time-dependent drug plasma concentration, c(t)in
vivo is the measured time-dependent drug plasma concentration, c(t)in![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vivo′ is the normalized drug concentration, F is bioavailability, D is administered dose, V is the volume of distribution, ka is the absorption rate constant, kel is the elimination rate constant, and t is time. Eqn (3) is based on the standard ordinary differential equation for the time-dependent plasma concentration profile in vivo in a one-compartmental model with first-order oral absorption and metabolism after a single dose.
vivo′ is the normalized drug concentration, F is bioavailability, D is administered dose, V is the volume of distribution, ka is the absorption rate constant, kel is the elimination rate constant, and t is time. Eqn (3) is based on the standard ordinary differential equation for the time-dependent plasma concentration profile in vivo in a one-compartmental model with first-order oral absorption and metabolism after a single dose.
To compare the in vitro platform response to the normalized in vivo time–concentration profiles, the same conceptual normalization was performed for the model concentration:
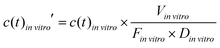 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vitro is the total media volume of the platform, Din
vitro is the total media volume of the platform, Din![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vitro the administered dose to the apical site of the gut-MPS (‘oral dose’) and Fin
vitro the administered dose to the apical site of the gut-MPS (‘oral dose’) and Fin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vitro is the fraction of drug in the systemic circulation. In this work, Fin
vitro is the fraction of drug in the systemic circulation. In this work, Fin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vitro was determined based on the following equation:
vitro was determined based on the following equation: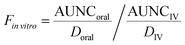 | (5) |
For the computational simulations, a unit concentration of drug was administered to the platform (1 μg ml−1), which is equivalent to an administered dose of 10 μg for an apical volume of the gut MPS of 0.1 ml.
This normalization method for both the in vivo and in vitro time–concentration profiles allows direct comparison since the normalized profiles represent the response after a unit concentration in a unit distribution volume in terms of absorption and elimination rate constants (representing hepatic and renal elimination).
The following design parameters were investigated (i.e. fitted): medium volumes for gut, liver and mixing chamber (multi-MPS platform I) or gut, liver and kidney medium volumes and the luminal flow to the kidney (Qkid,lum, multi-MPS platform II). To reduce the number of fitting parameters in platform II, the mixing chamber volume was fixed based on the results in platform I. Standard errors for these parameters were estimated based on a Jacobian matrix28 provided by the Matlab built-in function lsqnonlin.
Prior to estimation, certain limits on the range of design parameters to be fitted were imposed based on experimental feasibility and practicality. For medium volumes in each MPS and the mixing chamber the allowable range was 0.1–2 ml, and for the filtered flow to the kidney the allowable range was 1–10 ml per day. Remaining model parameters were fixed as given in Tables 3 and 4 for platforms I and II, respectively.
| Parameter | Human values | Direct scaling | Allometric scalingc | Multi-functional scaling | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (70 kg) | Milli-human (70 mg) | Micro-human (70 μg) | Micro-human (70 mg) | Nano-human (70 μg) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Human volumes refer to whole organ volumes and total blood volume (Vmix); for all scaling approaches volumes refer to MPS media volumes. References for human values:a Brown et al. (1989).26b Valentin et al. (2002).73c Wikswo et al. (2013).19d Martin et al. (1985).74e Estimated using multi-functional scaling. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q sys (ml per day) | 9.4 × 106 | 9.4 | 9.4 × 10−3 | 259 | 1.0 | 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q gut (ml per day) | 0.10 × Qsys | 0.75 × Qsys | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q liv (ml per day) | 0.05 × Qsys | 0.25 × Qsys | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A gut (cm2) | 30 × 104 | 30 × 10−2 | 30 × 10−5 | 1.4 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
7.7 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
4.67 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V gut,ap (ml) | 510 | 0.5 × 10−3 | 0.5 × 10−6 | 4.6 × 10−3 | 0.7 × 10−5 | 0.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V gut,bas (ml) | 510 | 0.5 × 10−3 | 0.5 × 10−6 | 4.6 × 10−3 | 0.7 × 10−5 | 0.6 ± 0.03e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V liv (ml) | 1800 | 1.8 × 10−3 | 1.8 × 10−6 | 3.9 × 10−3 | 1.1 × 10−5 | 0.3 ± 0.01e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V mix (ml) | 5300 | 5.3 × 10−3 | 5.3 × 10−6 | 5.3 × 10−3 | 5.3 × 10−6 | 0.4 ± 0.02e | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hepatocytesc (number) | 3 × 1011 | 3 × 105 | 3 × 102 | 8 × 105 | 2 × 103 | 5 × 105 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Parameter | Human values | Direct scaling | Allometric scalingc | Multi-functional scaling | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (70 kg) | Micro-human (70 mg) | Nano-human (70 μg) | Micro-human (70 mg) | Nano-human (70 μg) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Human volumes refer to whole organ volumes and total blood volume (Vmix); for all scaling approaches volumes refer to MPS media volumes. References for human values:a Brown et al. (1989).26b Valentin et al. (2002).73c Wikswo et al. (2013).19d Scotcher et al. (2016).61e Scaled using number of nephrons.f Martin et al. (1985).74g Estimated using multi-functional scaling. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q sys (ml per day) | 9.4 × 106 | 9.4 | 9.4 × 10−3 | 259 | 1.0 | 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q gut (ml per day) | 0.10 × Qsys | 0.30 × Qsys | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q liv (ml per day) | 0.05 × Qsys | 0.15 × Qsys | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q kid (ml per day) | 0.19 × Qsys | 0.55 × Qsys | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Q K,lum (ml per day) | 18 × 104 | 0.18 | 1.8 × 10−4 | 7.8 | 5.4 × 10−2 | 3.0 ± 0.04![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) g g |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A gut (cm2) | 30 × 104 | 30 × 10−2 | 30 × 10−5 | 1.4 × 10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
7.7 × 10−4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
4.67 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A kid (cm2) | 6.1 × 104 | 6.1 × 10−2 | 6.1 × 10−6 | 11.6e | 0.16e | 4.67 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V gut,ap (ml) | 510 | 0.5 × 10−3 | 0.5 × 10−6 | 4.6 × 10−3 | 0.7 × 10−5 | 0.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V gut,bas (ml) | 510 | 0.5 × 10−3 | 0.5 × 10−6 | 4.6 × 10−3 | 0.7 × 10−5 | 0.3 ± 0.02g | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V liv (ml) | 1800 | 1.8 × 10−3 | 1.8 × 10−6 | 3.9 × 10−3 | 1.1 × 10−5 | 0.2 ± 0.03g | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V mix (ml) | 5300 | 5.3 × 10−3 | 5.3 × 10−6 | 5.3 × 10−3 | 5.3 × 10−6 | 0.4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V kid,ap (ml) | 155 | 1.6 × 10−4 | 1.6 × 10−7 | 1.1 × 10−3 | 3.1 × 10−6 | 0.1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| V kid,bas (ml) | 155 | 1.6 × 10−4 | 1.6 × 10−7 | 1.1 × 10−3 | 3.1 × 10−6 | 0.8 ± 0.3g | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Waste (ml) | Q K,lum × t | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Hepatocytesc (number) | 3 × 1011 | 3 × 105 | 3 × 102 | 8 × 105 | 2 × 103 | 5 × 105 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
To apply this approach to MPS design, the design parameter values (i.e., all model parameters) were determined by scaling the corresponding in vivo parameters as follows:
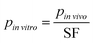 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vitro is the design parameter, pin
vitro is the design parameter, pin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) vivo is the corresponding in vivo parameter and SF is a scaling factor. Using the concept of micro- and nano-humans being 10−6 or 10−9 the size of a human,15 we designed both micro- and nano-human scale in vitro platforms by using the scaling factors of 106 and 109, respectively. All cell numbers, organ volumes and flows were scaled this way. Using the resulting parameterized platform models, in vitro time–concentration profiles were calculated using the mechanistic models for platforms I and II. For comparison to in vivo concentration profiles, the in vitro time–concentration profiles were normalized according to eqn (4). Total media volume for the platforms was calculated based on the individual MPS volumes and the administered dose to the apical site of the gut was calculated from an initial concentration of c0 = 1 μg ml−1. Normalization was applied to the resulting in vitro time–concentration profiles as was described for the multi-functional approach.
vivo is the corresponding in vivo parameter and SF is a scaling factor. Using the concept of micro- and nano-humans being 10−6 or 10−9 the size of a human,15 we designed both micro- and nano-human scale in vitro platforms by using the scaling factors of 106 and 109, respectively. All cell numbers, organ volumes and flows were scaled this way. Using the resulting parameterized platform models, in vitro time–concentration profiles were calculated using the mechanistic models for platforms I and II. For comparison to in vivo concentration profiles, the in vitro time–concentration profiles were normalized according to eqn (4). Total media volume for the platforms was calculated based on the individual MPS volumes and the administered dose to the apical site of the gut was calculated from an initial concentration of c0 = 1 μg ml−1. Normalization was applied to the resulting in vitro time–concentration profiles as was described for the multi-functional approach.
For the micro- and nano-human, the required design parameters were calculated (Tables 3 and 4) according to the following equation:
| Y = a × Mb | (7) |
Quantitative evaluation of exposure times
To quantitatively evaluate the performance of all three scaling approaches to produce clinically relevant exposure times, the area under the normalized time–concentration curve (AUNC) was calculated from the time of administration (t = 0) to the last measurement point (tf) of the drug specific time–concentration profile by integration: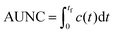 | (8) |
Additionally, for multi-MPS platform II, the model outcome of fraction unchanged excreted parent drug was estimated and compared to the reported clinical values for each drug.
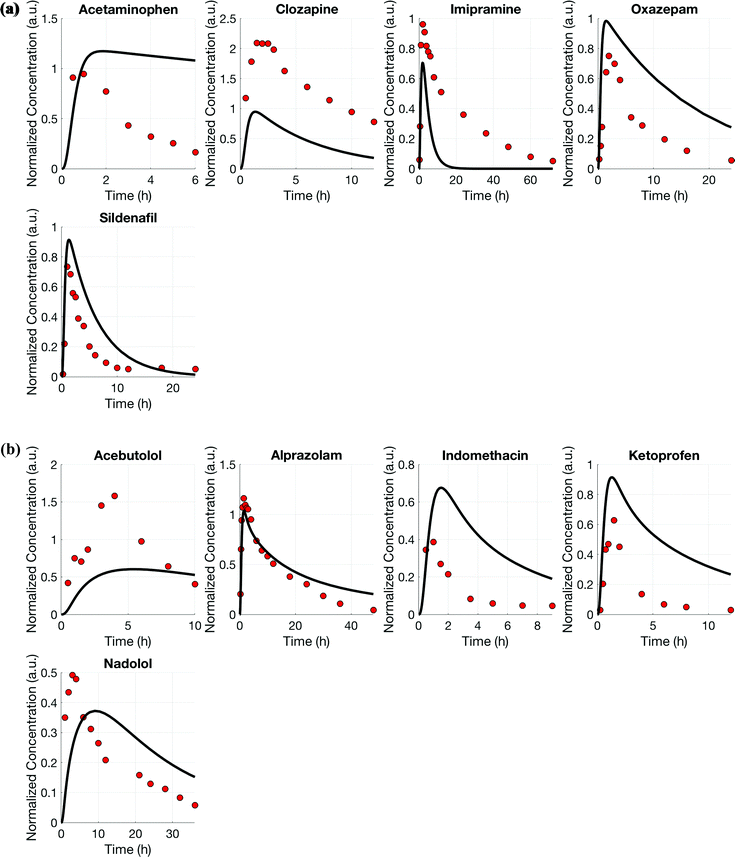
Using the multi-functional scaling approach, the distribution of five additional drugs was simulated for each platform (Tables 1 and 2, test set) to validate the estimated design parameters. Subsequently, AUNCs were determined to evaluate the estimated design parameter values and model performance for this test set of drugs that had not been included in the design process.
Pharmacokinetic data
Drugs in the training set for multi-MPS platform I were selected based on intrinsic in vitro clearance values covering a wide range (1.2–86.6 ml min−1 kg−1). Similarly, for multi-MPS platform II, including drugs with a wide range of clearance by the liver (2.1–30.0 ml min−1 kg−1) as well as the fraction excreted unchanged drug (0.15–0.54) guided selection of the drugs. Drugs in the test set were chosen to fall within the training ranges of clearance and excreted fraction.The training set of eight drugs for multi-MPS platform I included: diazepam,29 diclofenac,30 fenoprofen,31 ibuprofen,32 lidocaine,33 phenacetin,34 propranolol,35 warfarin.36 For multi-MPS platform II they were: betaxolol,37 linezolid,38 pindolol,39 prednisolone,40 quinidine,41 ranitidine,42 theophylline43 and timolol.44
The test set of five drugs used in the multi-functional scaling approach to evaluate the resulting design parameters for multi-MPS platform I included: acetaminophen,45 clozapine,46 imipramine,47 oxazepam48 and sildenafil;49 for multi-MPS platform II: acebutolol,50 alprazolam,51 indomethacin,52 ketoprofen53 and nadolol.54 References indicate source of time–concentration profiles and administered dose. Volumes of distribution and oral bioavailability were derived from literature.55 Data were digitized in graphical format (Plot Digitizer v2.6.8, http://https://sourceforge.net/projects/plotdigitizer/). More detailed information of the investigated drugs for both platforms is presented in Tables 1 and 2.
Intrinsic in vitro clearance values by hepatocytes for all drugs were taken from ref. 56, except for linezolid.57 Clearance values reported (in ml min−1 kg−1 bodyweight) were scaled to a reference human with a bodyweight of 70 kg (ref. 26) and normalized to a hepatocyte count of 3 × 1011 (clearance/hepatocyte; Tables 1 and 2).19 Subsequently, this value was scaled linearly to clearance in the liver MPS using 5 × 105 hepatocytes.
Permeability values for CaCo-2 cells were taken from ref. 58, except for fenoprofen,59 phenacetin,60 and linezolid and prednisolone.61 Permeability values of MDR1-MDCK cells for pindolol and timolol were derived from ref. 62 and for quinidine from ref. 63. For betaxolol, linezolid, prednisolone and theophylline corresponding CaCo-2 cell permeability values were used61 (recent work indicates that there is a linear relationship between estimated permeability values from CaCo-2 and MDR1-MDCK cells64–66). Fraction excreted unchanged drug as well as drug classes were derived from ref. 67.
3. Results and discussion
The aim of this work was to develop a function-based scaling methodology for designing multi-MPS platforms. This methodology bases design on multiple MPS functions simultaneously and explicitly considers the application of interest, e.g., pharmacokinetics or other pharmacological applications of small molecule drugs.The devised multi-functional scaling approach specifies an objective that represents the desired pharmacological or biological mechanisms the integrated multi-MPS platform should reproduce, and estimates parameter values for platform design and operation that best satisfy the objective function.
This novel approach was tested with two platforms relevant to the study and prediction of drug exposure. Multi-MPS platform I, including gut and liver MPSs, provides a biological representation of absorption through gut epithelium, metabolism by the liver, and distribution between these and a non-biological mixing chamber that approximates the collection of blood by venous circulation before it is recirculated by the heart in human. Multi-MPS platform II adds a kidney MPS to include additional elimination of a drug, which is a critical modulator of drug exposure and PK for numerous compounds. Active development and testing of gut, liver and kidney MPSs related to those described in this study's models are underway in several laboratories,11,12 so while the study is theoretical, its applicability to actual MPS technologies is relevant today.
Multi-functional scaling
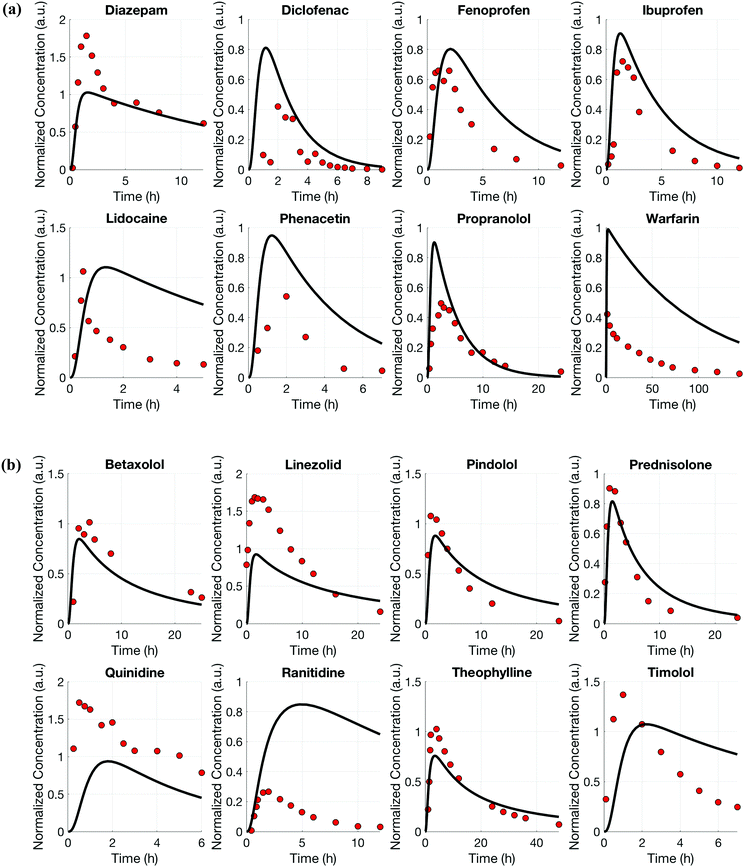
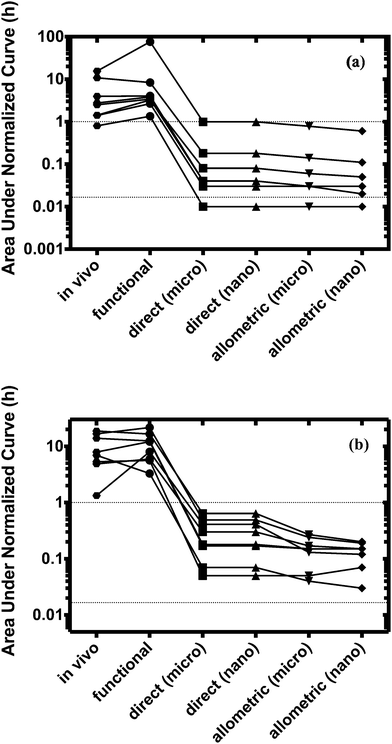
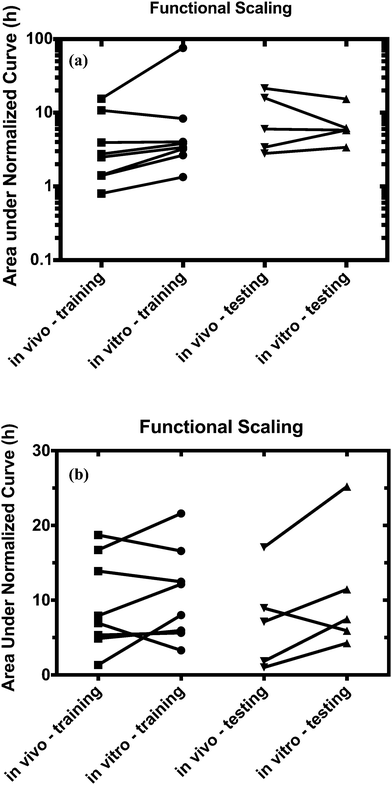
For both platforms I and II, the model output for time–concentration profiles based on design parameters (Tables 3 and 4) identified by the optimization algorithm agrees well with reported clinical data (Fig. 2) for a majority of the drugs, although not all were equally well captured. In platform I, the model description for diazepam captured the elimination phase while the observed maximum concentration is about 2-fold less. The description for lidocaine was systematically off. Warfarin showed a 2.5-fold higher concentration than the reported data, but a similar decline after the end of the absorption phase can be seen. These are possibly due to differences between in vitro and in vivo clearance values of these drugs by hepatocytes (Table 1). In platform II, the model profile for ranitidine showed a 3-fold higher maximum concentration compared to the clinical data, but a similar elimination phase. For quinidine, the clearance from the system appears to be faster than reported in vivo, suggesting differences between in vitro and in vivo hepatic clearance values.Quantitative evaluation of these drug profiles was performed by assessing area under the normalized time–concentration curve for both platforms. Clinically observed drug exposures were well recapitulated in the theoretical in vitro platforms. On average, the ratio of in vivo to in vitro drug exposures was (mean and standard deviation): 0.7 ± 0.3 and 1.0 ± 0.6 for platforms I and II, respectively (Fig. 3). Various methods are presently used for in vitro–in vivo extrapolation of PK, where human PK characteristics are extrapolated from measurements made in animals, hepatocyte cultures or hepatocyte microsomes. It is informative to compare those to the results of our theoretical gut–liver and gut–liver–kidney MPS platforms designed using multi-functional scaling. A common measure of acceptance is whether extrapolated values are within 2× or 3× of the (eventually) measured in vivo human PK parameter value.56,68–70 By that measure, results from our platforms I and II designed by multi-functional scaling easily fall within the accepted extrapolative capabilities of these other approaches, showing promise for using our multi-functional MPS design approach for pharmacokinetic/pharmacodynamic (PK/PD) applications.
Fraction excreted parent drug from the system in platform II was on average (3.0 ± 1.4)-fold higher than found in vivo (range: 15–54%; Table 2 and Fig. S1, ESI†). Possibly, permeability through the MDR1-MDCK-monolayer is considerably lower in vitro resulting in less reabsorption of the parent drug than observed in vivo. This in turn leads to an increased excreted amount of drug, which is then not available for hepatic clearance.
Estimated design parameter values are reported in Tables 3 and 4. In platform I, the combination of simulated hepatocyte number (5 × 105), the surface area of the gut MPS (4.67 cm2) and the resulting total media volume on the order of milliliters is likely to supply sufficient nutrients, e.g. oxygen and glucose, to the cell cultures based upon standard laboratory cell culture protocols. Introducing boundaries (lower and upper limit) for medium volumes allowed the multi-functional scaling approach to identify an optimal combination of design parameter values to satisfy the specific study purpose as well as these practical constraints. This is in contrast to direct scaling and allometric scaling approaches, in which the scaling is applied without considering the application of interest and interaction between MPSs.
Similarly, in platform II, the total media volume is in the order of milliliters, the same number of hepatocytes were simulated and surface areas for kidney and gut MPSs are in accordance with commonly used transwells and inserts (Table 4). Moreover, the semi-closed architecture of this platform allows a continuous medium supply and required nutrients.
Using the test set of five drugs, quantitative evaluation of the profiles (Fig. 4) showed on average a (1.3 ± 0.8)-fold higher and (0.7 ± 0.5)-fold lower drug exposure than in vivo for multi-MPS platforms I and II, respectively (Fig. 5).
Direct and allometric scaling
The design of multi-MPS platforms I and II was also performed using direct and allometric scaling. Feasibility of each of these scaling approaches was assessed by estimating drug exposures for the same training set (eight drugs per platform) and subsequent comparison to in vivo results. The estimated design parameters were also compared to those from the multi-functional scaling approach. The test set of five drugs was not evaluated using direct and allometric scaling.Scaling of the relevant model parameters for multi-MPS platforms I and II to simulate a theoretical micro-human (70 mg) or nano-human (70 μg, Tables 3 and 4) lead to highly impractical design parameter values. Due to the relative high number of cells and small medium volumes, these systems would most likely be nutrient limited (e.g. oxygen or glucose) and would require more frequent medium changes. However, choosing a different scaling factor or estimating these parameters based on a milli-human (70 g), would increase the absolute parameter values, but not changing the estimation of the area under the normalized curve (due to linear kinetics).
The model profiles underpredicted the actual human plasma drug time–concentration profiles for all drugs as can be seen in Fig. 3.
Direct scaling in platform I was able to capture the concentration maximum. However, both platforms and approaches showed extremely fast clearance (within minutes) compared to in vivo (Fig. S2, ESI†). On average, 50–300-fold lower drug exposure times were estimated for both platforms.
Three major differences in the multi-functional scaling approach compared to direct or allometric scaling are as follows: (1) this approach optimizes a design by accounting for multiple biological functions of each MPS simultaneously, (2) it works to optimize the design for multiple MPSs simultaneously rather than independently, and (3) it explicitly accounts for planned research applications of a (multi-)MPS platform during design. In comparison, direct and allometric scaling approaches focus on reproducing single characteristics independently of one another, and these are typically size-related (mass, volume, area, etc.). As demonstrated in the comparisons made among approaches, the multi-functional scaling approach provided a better representation of in vivo drug exposure than did either of the others. Points 1 and 2 are clearly desirable to best inform designs that represent simultaneously all functions related to all MPS. The critical importance of point 3 becomes evident when looking at the design parameter values: the multi-functional scaling resulted in medium volumes substantially larger than the other two methods because this was required to recapitulate in vivo drug exposures in the multi-MPS platforms studied. This demonstrates that hewing closely to in vivo tissue characteristics, while intuitively appealing, will not automatically result in MPS designs that reproduce desired functions – direct and allometric scaling failed to recapitulate the relevant pharmacology properties, in this case drug exposures.
A thought experiment further demonstrates that different planned applications may require different MPS designs. If the desire had been to reproduce concentration profiles for cell-produced mediators such as cytokines or growth factors, then using the multi-functional scaling algorithm might result in much smaller volume-to-tissue ratios for design parameters than it did for drug exposure. This is because the volumes would need to be small (comparable to extracellular volumes in vivo) to result in mediator concentrations similar to in vivo for a given cell number within an MPS, whereas larger volumes would cause excess dilution.
Normalized exposure times were calculated and used to quantitatively evaluate the performance of all the scaling approaches. Only the multi-functional scaling methodology captured exposure times similar to in vivo, whereas direct and allometric scaling resulted in exposure times that were orders of magnitude smaller.
Based on our experience culturing these cells, the operation of MPS scaled with the latter approaches will be severely limited by nutrient depletion due to the small medium-to-tissue ratios in closed- and semi-closed loop platforms described. Alternatives to alleviate these limitations would be to change medium much more frequently than is typical for closed-loop systems (every 2–3 days) or go to continuous fresh medium feed in an open-loop system. These are valid operational approaches, but bring different limitations by limiting exposure time to drug and thereby drug metabolism, as well as frequently or continuously removing cell-produced mediators that might be of interest for study of MPS–MPS interactions.
An obvious challenge in utilizing this new multi-functional scaling approach is the need for appropriate data (both in vitro and in vivo) to inform the objective function as well as to parameterize the necessary system models. The demonstration cases herein, focused on pharmacokinetics, benefited from the large body of available data on in vivo drug pharmacokinetics and in vitro cell biological data.
Although this work primarily focused on the drug profiles in the plasma, a potential improvement would be to include drug concentrations in each organ of interest in the objective function along with plasma drug profiles. This would help the final designed multi-MPS platforms achieve pharmacologically relevant drug concentrations in each MPS and better enable studying drug interactions with uptake transporters or metabolizing enzymes as well as pharmacodynamic effects. However, a limitation to doing so would be the availability of data at the organ level.
Improving the cell to media ratio will also likely affect the volume of distribution. For instance, the multi-functional scaling resulted in considerably smaller media volumes for both multi-MPS platforms I and II than those currently used in typical transwell-based MPSs.13 The reduction in volume-to-tissue ratio will affect cellular uptake rates and, hence, drug clearance. For larger media volumes (compared to the cell volumes), this effect may become negligible and would therefore lead to a non-physiological response, which will subsequently affect the translation to in vivo. Recent work demonstrated the need for improved cell to media ratios: secreted factors by dendritic cells stimulated CD4+ primary human T cells only, when a physiologically relevant cell to media volume ratio was provided22 (media volumes ∼ microliters). On the contrary, smaller media volumes for commonly used cell cultures may be detrimental as limited nutrients are provided.
Accurate recapitulation of physiological processes is essential for a successful translation to clinical outcomes. The investigated theoretical kidney MPS covers the functions of reabsorption, secretion, filtration and excretion. In the modeled kidney MPS, the filtration and excretion processes are dictated by hardware (i.e. practical constraints), whereas reabsorption, and secretion occur through proximal tubular epithelial tissue. This may lead to a systematically different concentration gradient between the lumen and interstitial space of the kidney MPS resulting in an over-prediction of excreted unchanged drug. Mimicking the 3D microarchitecture of the human kidneys in vitro would potentially improve the description of filtration and excretion.
It is likely that the larger the set of relevant functional considerations included when applying the multi-functional scaling methodology described herein, the better the resulting platform design. For example, the case studies herein focused on recapitulating clinically relevant drug exposures may be further improved with the inclusion of additional a priori knowledge about physicochemical properties of drugs (molecular weight, charge, lipophilicity), the volume of distribution, bioavailability and the fraction of unbound drug. Similarly, inclusion of donor-to-donor variability for the simulated liver or kidney MPSs could be considered in the multi-functional scaling methodology for multi-MPS platforms. Moreover, a larger set of drugs and drugs with different classifications (BDDCS67) could be used as training and test sets to further verify the methodology's applicability. Additionally, multi-MPS platforms could be used to study time–concentration profiles of metabolites and metabolite formation, since these can be important for both efficacy and adverse effects,71 depending on the drug.
Considering the biology of MPSs, data obtained from more advanced MPS technologies will also further improve multi-MPS design strategies. For example, metabolism by the gut contributes considerably to PK in vivo and bioavailability of drugs. Therefore, the use of human primary cells instead of cell lines are likely to further improve the predictability of such systems.
While our case studies have necessarily used data from existing drugs, the desire to design MPS platforms to predict exposure for new investigational entities raises the question of which platform to use in the absence of clinical data. A decision can be based on physicochemical properties to assess if the compound would be mainly metabolized by the liver or excreted via kidneys.72
The methodology described herein can be applied and readily adapted to other study objectives such as normal and disease biology, pharmacodynamics, toxicity or optimization of media compositions. For instance, studying diabetes would require a carefully designed multi-MPS platform to recapitulate relevant glucose and glucose-induced insulin levels. Potentially, a fat–muscle–liver–pancreas–gut platform would serve this purpose and chronic exposures of increased glucose levels and the effect on insulin production by the pancreas MPS may be more adequately investigated.
While MPSs are a promising technology for improving translation of preclinical results to clinical outcomes, the promise will be limited if the design is not able to capture the essence of in vivo physiology appropriately to enable in vitro–in vivo translation. Thus, the multi-functional scaling approach presents a novel framework to tailor integrated multi-MPS platforms to a specific and intended study objective across multiple areas of interest.
4. Conclusion
The novel multi-functional scaling approach described here allowed the design of integrated multi-MPS platforms for relevant pharmacological applications. In the applications demonstrated here, the resulting design parameter values are practical and can be easily implemented. The approach can be readily adapted to various multi-MPS platforms for a variety of study purposes. Current scaling approaches (direct and allometric scaling) were not able to meet the study objective in this work. Recapitulation of in vivo drug exposure times in vitro allows to establish exposure–response relationships and thus for more relevant studies of pharmacodynamics and toxicity.Acknowledgements
Financial support for this project was provided by the DARPA Microphysiological Systems Program (W911NF-12-2-0039) and the NIH Microphysiological Systems Program (4-UH3-TR000496-03).References
- H. E. Abaci and M. L. Shuler, Integr. Biol., 2015, 7, 383–391 RSC.
- C. Moraes, J. M. Labuz, B. M. Leung, M. Inoue, T. H. Chun and S. Takayama, Integr. Biol., 2013, 5, 1149–1161 RSC.
- U. Marx, T. B. Andersson, A. Bahinski, M. Beilmann, S. Beken, F. R. Cassee, M. Cirit, M. Daneshian, S. Fitzpatrick, O. Frey, C. Gaertner, C. Giese, L. Griffith, T. Hartung, M. B. Heringa, J. Hoeng, W. H. de Jong, H. Kojima, J. Kuehnl, M. Leist, A. Luch, I. Maschmeyer, D. Sakharov, A. J. Sips, T. Steger-Hartmann, D. A. Tagle, A. Tonevitsky, T. Tralau, S. Tsyb, A. van de Stolpe, R. Vandebriel, P. Vulto, J. Wang, J. Wiest, M. Rodenburg and A. Roth, ALTEX, 2016, 33, 272–321 Search PubMed.
- S. Y. Chang, E. J. Weber, K. P. Van Ness, D. L. Eaton and E. J. Kelly, Clin. Pharmacol. Ther., 2016, 100, 464–478 CrossRef CAS PubMed.
- D. D. Huh, Ann. Am. Thorac. Soc., 2015, 12(suppl 1), S42–S44 CrossRef PubMed.
- B. Atac, I. Wagner, R. Horland, R. Lauster, U. Marx, A. G. Tonevitsky, R. P. Azar and G. Lindner, Lab Chip, 2013, 13, 3555–3561 RSC.
- A. Grosberg, A. P. Nesmith, J. A. Goss, M. D. Brigham, M. L. McCain and K. K. Parker, J. Pharmacol. Toxicol. Methods, 2012, 65, 126–135 CrossRef CAS PubMed.
- M. M. Laronda, J. E. Burdette, J. J. Kim and T. K. Woodruff, Stem Cell Res. Ther., 2013, 4, 1–5 CrossRef PubMed.
- A. Marsano, C. Conficconi, M. Lemme, P. Occhetta, E. Gaudiello, E. Votta, G. Cerino, A. Redaelli and M. Rasponi, Lab Chip, 2016, 16, 599–610 RSC.
- K. Domansky, W. Inman, J. Serdy, A. Dash, M. H. Lim and L. G. Griffith, Lab Chip, 2010, 10, 51–58 RSC.
- I. Maschmeyer, A. K. Lorenz, K. Schimek, T. Hasenberg, A. P. Ramme, J. Hubner, M. Lindner, C. Drewell, S. Bauer, A. Thomas, N. S. Sambo, F. Sonntag, R. Lauster and U. Marx, Lab Chip, 2015, 15, 2688–2699 RSC.
- C. Oleaga, C. Bernabini, A. S. Smith, B. Srinivasan, M. Jackson, W. McLamb, V. Platt, R. Bridges, Y. Cai, N. Santhanam, B. Berry, S. Najjar, N. Akanda, X. Guo, C. Martin, G. Ekman, M. B. Esch, J. Langer, G. Ouedraogo, J. Cotovio, L. Breton, M. L. Shuler and J. J. Hickman, Sci. Rep., 2016, 6, 20030 CrossRef CAS PubMed.
- J. Yu, N. A. Cilfone, E. M. Large, U. Sarkar, J. S. Wishnok, S. R. Tannenbaum, D. J. Hughes, D. A. Lauffenburger, L. G. Griffith, C. L. Stokes and M. Cirit, CPT: Pharmacometrics Syst. Pharmacol., 2015, 4, 585–594 CrossRef CAS PubMed.
- Z. Xu, E. Li, Z. Guo, R. Yu, H. Hao, Y. Xu, Z. Sun, X. Li, J. Lyu and Q. Wang, ACS Appl. Mater. Interfaces, 2016, 8, 25840–25847 CAS.
- J. H. Sung, C. Kam and M. L. Shuler, Lab Chip, 2010, 10, 446–455 RSC.
- E. W. Esch, A. Bahinski and D. Huh, Nat. Rev. Drug Discovery, 2015, 14, 248–260 CrossRef CAS PubMed.
- E. L. LeCluyse, R. P. Witek, M. E. Andersen and M. J. Powers, Crit. Rev. Toxicol., 2012, 42, 501–548 CrossRef CAS PubMed.
- R. Baudoin, J. M. Prot, G. Nicolas, J. Brocheton, C. Brochot, C. Laegallais, H. Benech and E. Leclerc, Xenobiotica, 2013, 43, 140–152 CrossRef CAS PubMed.
- J. P. Wikswo, E. L. Curtis, Z. E. Eagleton, B. C. Evans, A. Kole, L. H. Hofmeister and W. J. Matloff, Lab Chip, 2013, 13, 3496–3511 RSC.
- N. Ucciferri, T. Sbrana and A. Ahluwalia, Front. Bioeng. Biotechnol., 2014, 2, 74 Search PubMed.
- C. L. Stokes, M. Cirit and D. A. Lauffenburger, CPT: Pharmacometrics Syst. Pharmacol., 2015, 4, 559–562 CrossRef CAS PubMed.
- J. P. Wikswo, Exp. Biol. Med., 2014, 239, 1061–1072 CrossRef PubMed.
- L. Vernetti, A. Gough, N. Baetz, S. Blutt, J. R. Broughman, J. A. Brown, J. Foulke-Abel, N. Hasan, J. In, E. Kelly, O. Kovbasnjuk, J. Repper, N. Senutovitch, J. Stabb, C. Yeung, N. C. Zachos, M. Donowitz, M. Estes, J. Himmelfarb, G. Truskey, J. P. Wikswo and D. L. Taylor, Sci. Rep., 2017, 7, 42296 CrossRef CAS PubMed.
- V. Sharma and J. H. McNeill, Br. J. Pharmacol., 2009, 157, 907–921 CrossRef CAS PubMed.
- R. V. Overgaard, S. H. Ingwersen and C. W. Tornoe, CPT: Pharmacometrics Syst. Pharmacol., 2015, 4, 565–575 CrossRef CAS PubMed.
- R. P. Brown, M. D. Delp, S. L. Lindstedt, L. R. Rhomberg and R. P. Beliles, Toxicol. Ind. Health, 1997, 13, 407–484 CrossRef CAS PubMed.
- ICRP, Ann. ICRP, 2002, 32, 5–265 CrossRef.
- P. H. Richter, TDA Prog. Rep., 1995, 42, 107–137 Search PubMed.
- H. Friedman, D. J. Greenblatt, G. R. Peters, C. M. Metzler, M. D. Charlton, J. S. Harmatz, E. J. Antal, E. C. Sanborn and S. F. Francom, Clin. Pharmacol. Ther., 1992, 52, 139–150 CrossRef CAS PubMed.
- J. V. Willis, M. J. Kendall, R. M. Flinn, D. P. Thornhill and P. G. Welling, Eur. J. Clin. Pharmacol., 1979, 16, 405–410 CrossRef CAS PubMed.
- J. F. Nash, L. D. Bechtol, R. J. Bopp, K. Z. Farid, C. T. Spradlin and C. A. Bunde, J. Pharm. Sci., 1979, 68, 1087–1090 CrossRef CAS PubMed.
- D. R. Abernethy and D. J. Greenblatt, Arthritis Rheum., 1985, 28, 1117–1121 CrossRef CAS PubMed.
- P. N. Bennett, L. J. Aarons, M. R. Bending, J. A. Steiner and M. Rowland, J. Pharmacokinet. Biopharm., 1982, 10, 265–281 CrossRef CAS PubMed.
- Z. Q. Qu, X. D. Li, H. L. Liu, P. He, X. Zhang and M. C. Wu, Int. J. Clin. Pharmacol. Ther., 2007, 45, 55–62 CrossRef CAS PubMed.
- L. Borgstroem, C. Johansson, H. Larsson and R. Lenander, J. Pharmacokinet. Biopharm., 1981, 9, 419–429 CrossRef CAS.
- J. Dingemanse and P. Hoever, Drugs R&D, 2013, 13, 145–151 Search PubMed.
- J. F. Giudicelli, M. Chauvin, C. Thuillez, C. Richer, G. Bianchetti, R. Gomeni and P. L. Morselli, Br. J. Clin. Pharmacol., 1980, 10, 41–49 CrossRef CAS PubMed.
- M. S. Dryden, J. Antimicrob. Chemother., 2011, 66(suppl 4), iv7–iv15 CAS.
- R. Gugler, W. Herold and H. J. Dengler, Eur. J. Clin. Pharmacol., 1974, 7, 17–24 CrossRef CAS PubMed.
- M. E. Pickup, Clin. Pharmacokinet., 1979, 4, 111–128 CrossRef CAS PubMed.
- R. A. Wooding-Scott, J. Smalley, J. Visco and R. L. Slaughter, Br. J. Clin. Pharmacol., 1988, 26, 415–421 CrossRef CAS PubMed.
- M. L. McFayden, P. I. Folb, R. Miller, I. N. Marks and M. G. Moshal, Eur. J. Clin. Pharmacol., 1983, 24, 441–447 CrossRef.
- V. Rovei, F. Chanoine and M. Strolin Benedetti, Br. J. Clin. Pharmacol., 1982, 14, 769–778 CrossRef CAS PubMed.
- A. Bobik, G. L. Jennings, P. Ashley and P. I. Korner, Eur. J. Clin. Pharmacol., 1979, 16, 243–249 CrossRef CAS.
- M. D. Rawlins, D. B. Henderson and A. R. Hijab, Eur. J. Clin. Pharmacol., 1977, 11, 283–286 CrossRef CAS PubMed.
- W. Tassaneeyakul, K. Kittiwattanagul, S. Vannaprasaht, J. Kampan, A. Tawalee, P. Puapairoj, S. Tiamkao, S. Juthagridsada, V. Kukongviriyapan and W. Tassaneeyakul, J. Pharm. Pharm. Sci., 2005, 8, 47–53 CAS.
- D. A. Ciraulo, J. G. Barnhill and J. H. Jaffe, Clin. Pharmacol. Ther., 1988, 43, 509–518 CrossRef CAS PubMed.
- J. Sonne, S. Loft, M. Døssing, A. Vollmer-Larsen, K. L. Olesen, M. Victor, F. Andreasen and P. B. Andreasen, Eur. J. Clin. Pharmacol., 1988, 35, 385–389 CrossRef CAS PubMed.
- D. J. Nichols, G. J. Muirhead and J. A. Harness, Br. J. Clin. Pharmacol., 2002, 53, 5S–12S CrossRef CAS PubMed.
- C. M. Kaye, C. R. Kumana, M. Leighton, J. Hamer and P. Turner, Clin. Pharmacol. Ther., 1976, 19, 416–420 CrossRef CAS PubMed.
- D. J. Greenblatt and C. E. Wright, Clin. Pharmacokinet., 1993, 24, 453–471 CrossRef CAS PubMed.
- H. W. Emori, G. D. Champion, R. Bluestone and H. E. Paulus, Ann. Rheum. Dis., 1973, 32, 433 CrossRef CAS PubMed.
- F. Jamali and D. R. Brocks, Clin. Pharmacokinet., 1990, 19, 197–217 CrossRef CAS PubMed.
- M. Korting-Schäfer, N. Bach, H. Knauf and E. Mutschler, Eur. J. Clin. Pharmacol., 1984, 26, 125–127 CrossRef.
- M. V. Varma, R. S. Obach, C. Rotter, H. R. Miller, G. Chang, S. J. Steyn, A. El-Kattan and M. D. Troutman, J. Med. Chem., 2010, 53, 1098–1108 CrossRef CAS PubMed.
- D. Hallifax, J. A. Foster and J. B. Houston, Pharm. Res., 2010, 27, 2150–2161 CrossRef CAS PubMed.
- P. Paixao, L. F. Gouveia and J. A. Morais, Eur. J. Pharm. Sci., 2010, 39, 310–321 CrossRef CAS PubMed.
- P. Paixao, L. F. Gouveia and J. A. Morais, Eur. J. Pharm. Sci., 2010, 41, 107–117 CrossRef CAS PubMed.
- R. Gozalbes, M. Jacewicz, R. Annand, K. Tsaioun and A. Pineda-Lucena, Bioorg. Med. Chem., 2011, 19, 2615–2624 CrossRef CAS PubMed.
- S. Khan, H. Batchelor, P. Hanson, Y. Perrie and A. R. Mohammed, J. Pharm. Sci., 2011, 100, 4281–4294 CrossRef CAS PubMed.
- D. Scotcher, C. Jones, A. Rostami-Hodjegan and A. Galetin, Eur. J. Pharm. Sci., 2016, 94, 59–71 CrossRef CAS PubMed.
- J. D. Irvine, L. Takahashi, K. Lockhart, J. Cheong, J. W. Tolan, H. E. Selick and J. R. Grove, J. Pharm. Sci., 1999, 88, 28–33 CrossRef CAS PubMed.
- M. Patel, N. K. Mandava, D. Pal and A. K. Mitra, Int. J. Pharm., 2014, 464, 196–204 CrossRef CAS PubMed.
- X. Jin, T. L. Luong, N. Reese, H. Gaona, V. Collazo-Velez, C. Vuong, B. Potter, J. C. Sousa, R. Olmeda, Q. Li, L. Xie, J. Zhang, P. Zhang, G. Reichard, V. Melendez, S. R. Marcsisin and B. S. Pybus, J. Pharmacol. Toxicol. Methods, 2014, 70, 188–194 CrossRef CAS PubMed.
- A. Avdeef and K. Y. Tam, J. Med. Chem., 2010, 53, 3566–3584 CrossRef CAS PubMed.
- A. Braun, S. Hämmerle, K. Suda, B. Rothen-Rutishauser, M. Günthert, S. D. Krämer and H. Wunderli-Allenspach, Eur. J. Pharm. Sci., 2000, 11, S51–S60 CrossRef CAS PubMed.
- L. Z. Benet, F. Broccatelli and T. I. Oprea, AAPS J., 2011, 13, 519–547 CrossRef CAS PubMed.
- G. W. Caldwell, J. A. Masucci, Z. Yan and W. Hageman, Eur. J. Drug Metab. Pharmacokinet., 2004, 29, 133–143 CrossRef CAS PubMed.
- R. S. Obach, Drug Metab. Dispos., 1997, 25, 1359–1369 CAS.
- N. Tsamandouras, T. Kostrzewski, C. L. Stokes, L. G. Griffith, D. J. Hughes and M. Cirit, J. Pharmacol. Exp. Ther., 2016, 360, 95–105 CrossRef PubMed.
- M. Pirmohamed, N. R. Kitteringham and B. K. Park, Drug Saf., 1994, 11, 114–144 CrossRef CAS PubMed.
- L. Di, B. Feng, T. C. Goosen, Y. Lai, S. J. Steyn, M. V. Varma and R. S. Obach, Drug Metab. Dispos., 2013, 41, 1975–1993 CrossRef CAS PubMed.
- J. Valentin, Ann. ICRP, 2002, 32, 5–265 CrossRef.
- R. D. Martin, D. J. Chivers, A. M. MacLarnon and C. M. Hladik, in Size and Scaling in Primate Biology, ed. W. L. Jungers, Springer US, Boston, MA, 1985, pp. 61–89 DOI:10.1007/978-1-4899-3647-9_5.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ib00243a |
| This journal is © The Royal Society of Chemistry 2017 |