Computational design of biological circuits: putting parts into context

Abstract

The rational design of synthetic gene circuits has led to many successful applications over the past decade. However, increasingly complex constructs also revealed that analogies to electronics design such as modularity and ‘plug-and-play’ composition are of limited use: biology is less well characterized, more context-dependent, and overall less predictable. Here, we summarize the main conceptual challenges of synthetic circuit design to highlight recent progress towards more tailored, context-aware computational design methods for synthetic biology. Emerging methods to guide the rational design of synthetic circuits that robustly perform desired tasks might reduce the number of experimental trial and error cycles.

---

Eleni Karamasioti

Eleni Karamasioti obtained her BSc in Computer Science from the Department of Informatics and Telecommunications of University of Athens and her MSc in Bioinformatics by the same University in 2013. She has since been a PhD candidate at the Department of Biosystems Science and Engineering of ETH Zurich. Her research, under the supervision of Prof. Joerg Stelling, entails predicting how features of DNA sequences affect different biological processes, and using this predictive power for the optimal in silico design of DNA sequences, necessary for synthetic biology applications.

Claude Lormeau

Claude Lormeau graduated with a MSc in Biomedical Engineering from ETH Zurich and a MSc in Engineering from Ecole CentraleSupelec in 2015. She is currently a PhD candidate in the department of Biosystems Science and Engineering at ETH Zurich under the supervision of Professor Joerg Stelling. Her research areas focus on the model-based design of robust synthetic biological circuits.

Jörg Stelling

Jörg Stelling is a Professor of Computational Systems Biology at the Department of Biosystems Science and Engineering of ETH Zurich. He obtained a MSc degree in Biotechnology (Technical University of Braunschweig) and received his PhD from the Department of Mechanical Engineering, University of Stuttgart. His group's current research interests are focused on the analysis and synthesis of biological networks using – and further developing – methods from systems theory, computer science, and experimental biology.

---

Design, System, Application

This review focuses on the computational design of synthetic gene circuits based on mathematical models of different types, such as statistical, thermodynamic, and dynamic systems descriptions, and their (possible) integration. Desired systems functionalities are predictability under uncertainty and biological variability; a primary corresponding design constraint is circuit robustness to effects of biological context. The immediate application potential of emerging methods to guide the rational design of synthetic circuits that robustly perform desired tasks is to reduce the number of experimental trial and error cycles. In perspective, the methods can enable rational design for therapeutic applications through rational re-wiring of natural systems.

Introduction

Synthetic biology aims to enable the rational engineering or re-engineering of biology to endow biological systems with functions not seen in nature. At its core lies the transfer of traditional engineering concepts and workflows to biology, for example, to implement novel synthetic gene circuits. Ideally, automated (computational) workflows for circuit design translate quantitative performance specifications into one or a few alternatives for circuit implementation and testing in order to replace the extensive experimental cycles of trial and error in ‘traditional’ biotechnology.¹ In particular, analogies between synthetic biological circuits and digital electrical circuits have been powerful driving concepts for the field: they suggest a plug-and-play approach where independent building blocks, if carefully selected and smartly plugged together, are sufficient to make a circuit behave as desired.^2,3 Recent progress in areas such as the design of gene circuits that perform complex logical functions continues to demonstrate the usefulness of this electrical engineering paradigm.⁴

Electrical circuit analogies are potentially useful in abstracting from complicated biological phenomena, but they are not necessarily correct statements about biological reality. Synthetic gene circuits operate as (bio)chemical reaction networks in which, in principle, the network context matters for a specific part's (protein's or gene's) function. Unlike electric circuits, they do not have physically and functionally separated parts and dedicated ‘wires’ for targeted communication between them. Especially progress in synthetic biology towards more complex circuits now revealed important limitations of the plug-and-play approach inspired by electrical engineering. A reliable design of gene circuits needs to account for the following: (i) parts may behave differently when other synthetic parts are acting upstream or downstream of them; (ii) large synthetic circuits may impose a substantial load on the cell's resources, (iii) synthetic circuits may cross-talk with endogenous pathways; and (iv) for functional assembly into complicated circuits, biological parts behaviors may be too variable, either because parts are insufficiently characterized or because of intrinsic biological variability due to molecular noise.^1,2,5–7 These are unintended design challenges imposed by context dependence and uncertainty. In addition, the use of synthetic circuits for the analysis and control of natural biological systems, for example, in therapeutic applications requires an intentional integration of synthetic and natural circuits.⁸ Note that, although cell-free systems seem to circumvent many of these uncertainties, they do not offer the same range of applications as in vivo systems and they face their own challenges such as costly resources and difficult scale-up.⁹

Computational methods for circuit design based on mathematical models have been integral to synthetic biology from its start, and with the increasing challenges of context dependence and uncertainty, their relevance is bound to increase. For example, while one could rely on trial and error to figure out a part configuration for simple synthetic circuits, the rational design of more sophisticated circuits has proven nearly impossible without the help of computational methods. Consequently, a plethora of computational design methods for synthetic gene circuits exists (see ref. 10–14 for detailed reviews). However, only recently approaches are emerging that systematically account for context dependence and uncertainty in the design process. Starting from methods for the simple assembly of well-characterized parts into (theoretically) functional circuits, we here review current methods that tackle at least one of the issues related to context and uncertainty. To reach overall a better predictability and robustness of synthetic gene circuit design, we then argue that concepts from neighboring disciplines such as systems biology and control engineering provide inspirations for next-generation computational methods. For complementary experimental resources and sources of quantitative data, we refer to recent reviews.^15,16

2 The ‘plug-and-play’ approach

2.1 Parts with predictable behavior: control of gene expression

Akin to electrical circuit design, the plug-and-play approach for the development of synthetic circuits relies on (the assumption of) composable genetic parts that have predictable behaviors. The characterization of parts is therefore critical for the successful design and implementation of synthetic circuits. To focus on one area of parts design, predictive power on, and fine control over protein expression is important for the implementation of synthetic circuits in this paradigm. With the wealth of accumulated biological knowledge on how gene sequences affect protein expression through transcriptional and translational control, a logical question is whether one can accurately estimate functional parameters of gene expression just by examining the DNA sequence.

The promoter, located directly upstream of the transcription initiation site, is one of the elements of a gene's sequence that controls transcription initiation and thus gene expression. Most computational models that predict gene expression from promoter sequence are statistical in nature, derived from in vivo gene expression data in one or a few experimental conditions, using machine learning methods such as Gaussian mixture models¹⁷ and support vector machines.¹⁸ In a slightly different approach, Rhodius et al. developed a computational model describing the strength of full-length constitutive promoters in E. coli; again it is a statistical model based on RNA polymerase binding motifs, but it accounts for effects of polymerase concentration on gene expression.¹⁹ Another model for inducible promoters in E. coli²⁰ is conceptually different: it uses thermodynamic principles to predict the probability of RNA polymerase binding to the promoter. By assuming that the rate of gene expression is proportional to polymerase binding, the model could predict promoter efficiency in a different regulatory context, at least for simple repression of gene expression.²⁰

Computational models for translation cover the second major tuning knob for gene expression. Early methods focused on qualitative ways to maximize the efficiency of translation by minimizing factors known to reduce its efficiency. Such factors include the presence of secondary structures in the mRNA²¹ as well as a codon usage that is not adapted to the host.²² For example, Gaspar et al. showed that one can redesign mRNA sequences with less stable secondary structures by maximizing an mRNA molecule's minimum free energy.²³ Second-generation methods seek more quantitative control of translation in order to achieve a specific protein expression level, primarily by assuming translation initiation as the rate limiting step.²⁴ The ribosome-binding site (RBS) sequence in bacteria has been a main target for the development of models with increasing predictive power. While some models are purely data-driven with uncertain generalizability,²⁵ others incorporate thermodynamic/biophysical principles such as binding energy contributions to interactions between mRNA and ribosome.^26–28 A similar biophysical model allows for the rational design of riboswitches that regulate the expression of the corresponding gene at the translation level.²⁹ In a complementary effort, Welch et al. studied the effect of codon bias on protein expression in E. coli and showed that a (bilinear regression) model could predict protein expression for designed genes.³⁰

Compared to protein production processes, however, computationally designed control of protein expression by degradation processes has received little attention. For example, synthetic post-translational control of protein abundances through targeted degradation is achievable by modifying the degradation tag in a protein's C-terminus.³¹ Recently, Cameron et al. built an inducible degradation system for E. coli proteins based on components of an orthogonal bacterial transfer-messenger RNA system, which allowed them to regulate protein degradation by controlling inducer molecule concentration,³² but quantitative experimental data were not yet used to establish predictive computational models.

Hence, there appears to be no shortage of computational methods for the design of genetic parts in general. However, as noted earlier,¹³ most (and an apparently increasing fraction) of the models are statistical, inferred from natural or engineered gene variants. Learning models that generalize beyond the immediate scope of a specific study faces the problem of combinatorial explosion, for example, to characterize the space of possible sequence variants for long sequences, or the space of (relevant) interactions with other genetic elements. Increasing experimental capabilities as well as possible design principles to be uncovered may help reduce this problem. For example, promoter activity in bacteria in complex environmental conditions appears to be well-described by the linear superposition of expression dynamics in simple conditions.³³ However, we argue that biophysical models that relate sequence features to functional parameters such as binding affinities hold more promise because they integrate more easily into modeling frameworks for biochemical reaction networks to reflect context effects. For example, a recent large-scale analysis of gene expression determinants in E. coli revealed substantial competition between translation elongation and mRNA degradation processes, thereby relating codon usage effects and global cellular physiology.³⁴ Such multi-dimensional dependencies are hard to cover in a purely data-driven fashion; conversely, for more mechanistic approaches, defining the relevant connections is critical.

2.2 Design by (optimal) selection of parts

Well-characterized and predictable parts could be connected to each other to form synthetic circuits performing desired tasks. Depending on the task, however, it is not always intuitive to find a circuit structure that is functional given the properties of individual parts. Basic computational tools assist in this task by visualizing and modeling potential design architectures, as well as by predicting a predefined network's behavior via simulation. However, they support neither the definition of the biological parts' parameters (such as detailed kinetic parameters or phenomenological efficiencies), nor the specification of the wiring of parts, that is, the circuit topology.^10,12

Optimization-based methods fill this gap by searching for a potential circuits' architecture and for parametrizations in the corresponding model's parameter space to provide functional solutions. They typically focus on the optimal selection of circuit components from libraries of characterized parts with the objective of designing a circuit that best fits the desired behavior. Examples include a framework for optimal parts' selection for a predefined circuit topology,³⁵ and a more advanced framework that identifies an optimal circuit topology as well.³⁶ A single design criterion such as optimal dynamics may not be sufficient in practice, which is why multi-objective optimization methods for system design were recently developed. They yield a set of optimal solutions, the Pareto front, where none of the objectives can be improved without degrading one of the other objectives. This can reveal trade-offs between different design criteria such as precision and sensitivity, thus allowing the designer to choose the solution that best fits each problem.^37–40

Especially for gene circuits that implement digital logic operations, automated design in the plug-and-play mode has demonstrated successes in theory⁴¹ and in practice.⁴ However, it is important to note that uncertainties and mis-specifications at the parts level will propagate to the circuit level, which limits reliable design at larger scale. Promising approaches to this problem combine either phenomenological characterizations of parts⁴² or biophysical models of parts⁴³ with dynamic mechanistic models for their interactions, but they are limited, for example, to circuits without feedback. In general, analyzing circuit behaviors experimentally and systematically incorporating this data into iterative cycles of computational design remains a key challenge.²

2.3 Context dependence and limitations of the ‘plug-and-play’ approach

Uncertainty propagation in circuit design is a general problem, but additional causes of potential design failures in the plug-and-play approach relate to context dependence. These causes usually lie in three areas (Fig. 1; see ref. 7 for a detailed review of different types of context dependences): the compositional context (other synthetic parts acting upstream or downstream of a building block), the host context (the type of organism hosting a circuit and the host's physiological state), or the environmental context (for example, temperature).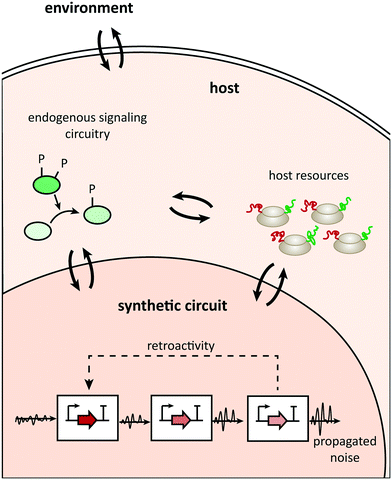

Fig. 1 Communication channels between the parts constituting a synthetic network, the host, and its environment.

First, the general assumption of parts' modularity (their theoretical ability to connect to each other at will and not to allow their internal functions to affect other parts) rarely applies in the strict sense posited. For example, unwanted communication between individual components in a gene circuit can occur because of retroactivity, the emergence of undesired interconnections between connected components.⁴⁴ In addition, stochastic fluctuations in gene expression might propagate towards downstream components of a gene network, thus causing significant changes in a circuit's programmed behavior.⁴⁵

Second, an in vivo synthetic circuit is integrated into some host and thus part of a bigger picture. This entails several (unexpected) channels of communication between the circuit and the host, which could cause side effects. Such effects could emerge from potential unpredicted cross talk between components of the circuit and endogenous components.⁴⁶ In addition, a synthetic circuit relies on the limited, potentially changeable, host's resources such as energy supply and gene expression machinery, which could affect not only the circuit itself but also the host's endogenous operation.^47,48

Finally, considering a synthetic circuit as part of a host, one cannot ignore environmental stimuli such as temperature and pH that could directly affect the circuit's performance.^49–51 Indirect effects of environmental factors mediated by the host are also relevant; any factor that alters the host's physiology could affect the circuit behavior. For example, changes in the available carbon sources modulate the growth rate in bacteria, which in turn affects the host's gene expression machinery and the growth-mediated dilution of intracellular components.⁵²

3 Ensuring robustness to specific uncertainties

The sources of failure described in the previous section represent uncertainties on the parts towards which a circuit should be robust. Computational methods exist that explicitly take into account at least one of these uncertainties to design robust circuits.

3.1 Robustness to sources of non-modularity

Very commonly, although the information flow in a system appears unidirectional when connecting parts in a modular way, downstream elements affect upstream elements by imposing a load on their operation, a phenomenon called retroactivity (Fig. 2A). For example, Jiang et al. showed both theoretically and experimentally that the addition of downstream elements leads to unexpected alterations in the dynamic behavior of a signaling system (such as the response time and bandwidth of a signaling network), for example, by sequestering regulatory upstream elements via binding reactions.⁵³ Hence, there is active research in understanding, modeling, and predicting retroactivity to design more robust synthetic circuits. Inspired by electrical engineering, Del Vecchio et al. proposed to attenuate retroactivity by using insulation devices between components; they showed mathematically that appropriate insulators in biological circuits could be realized based on transcriptional activation or on protein phosphorylation.⁴⁴ In theory, retroactivity can be attenuated arbitrarily when the operating time scale of a subsystem is substantially faster than that of its upstream subsystem.⁵⁴ This principle of timescale separation underlies an experimentally validated genetic device called ‘load driver’ that moderates the effect of retroactivity on the behavior of synthetic circuits.⁵⁵ This intermediate module is a phosphorylation cascade with highly abundant regulators and fast dynamics, which helps buffering the effect of sequestering downstream elements. The concept also allows to estimate the effect of load imposed by the system's downstream elements and to define a quantitative metric for the robustness of a module's behavior when connected to other modules.⁵⁶ However, it is unclear to what extent the insulator approach scales because of the additional devices' demands on cellular energy supply and gene expression capacity.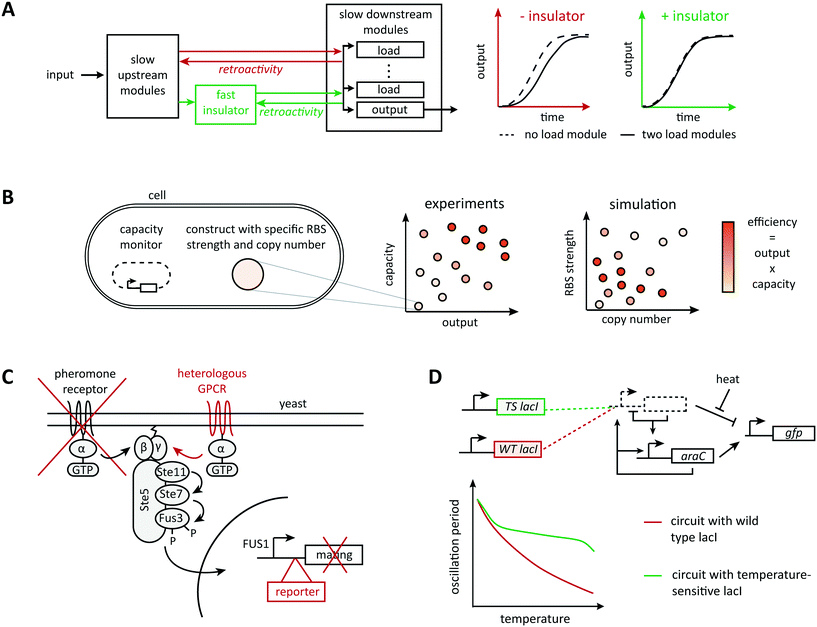

Fig. 2 Mechanisms of context dependence. Any collection of well characterized components will be part of a bigger system, which it will affect and be affected by. (A) Taking advantage of the time-scale separation principle, Mishra et al., designed a load driver operating on fast time scales able to attenuate retroactivity effects between components operating on slower time scales.⁷³ (B) Excess usage of the host resources would result in a huge burden imposed on the host leading to circuit failure. With the aid of a computational model of translation illustrating the resource usage, Ceroni et al. evaluated different circuit designs with respect to their output capacity and ribosome usage.^69,70 (C) Rewiring circuits to natural pathways can provide interesting dynamic behaviors with very few parts. The yeast mating pathway has been rewired to a heterologous G-protein coupled receptor (GPCR), the mating genes have been replaced by a reporter, and the natural receptor has been knocked out.¹⁰⁹ (D) Environmental factors are known to affect the physiology of model organisms and could consequently perturb any subsystem. Hussain et al. used computational modeling to understand the effect of temperature perturbations on their system of interest and counteracted it by substituting the wild type LacI repressor with a temperature sensitive mutant.⁸²

Propagation of intrinsic noise, namely of stochastic fluctuations of molecular components internal to the circuit and independent of the circuit's context, is another important source of non-modularity. Broad experimental and theoretical evidence suggests that intrinsic noise can cause miscommunication between components, loss of modularity, and partial or complete collapse of the circuit's functionality.^3,57 Many methods have been developed to account for and to control noise and its propagation in biological circuits, but examples for successful translations to improved circuit design are still rare.⁵⁸ However, the potential is demonstrated by an application of stochastic principles that has recently led to modifications on the famous bacterial repressilator circuit,⁵⁹ reducing noise propagation and thereby resulting in drastically more robust oscillatory behavior.⁶⁰ For future design improvements, several recent theoretical concepts appear relevant. Adaptations of the concept of signal to noise ratio from electronics and its application to libraries of biological parts or whole circuits could help characterize their efficacy.⁶¹ One can decompose the noise propagated from an input signal to the output into a dynamical error (encoding how well dynamics of the input are tracked) and a mechanistic error (encoding the deviation of the signal magnitude) to find network motifs that influence signal fidelity and to evaluate trade-offs between the two types of errors.⁶² Finally, Oyarzun et al., focusing on a negative autoregulation system (one of the first motifs shown to attenuate stochastic fluctuations), studied the effect of repression parameters on the noise of the circuit's output, and expressed this noise as a function of the design parameters (promoter strength, promoter sensitivity, and repression strength). Such formalisms can enable the definition of conditions on the parameters with the objective of reducing noise.⁶³

3.2 Robustness to host effects

Ideally, a cell functions as a neutral ‘chassis’ ready to accept and assist any heterologous circuit. However, synthetic gene circuits rely on and affect the host's resources in a two-way communication, which can result in host-mediated alterations of synthetic circuit behavior.^64,65 The underlying issue of (metabolic) burden and competition for cellular resources (Fig. 2B) is well-known in biotechnology and the need for computational models to reflect it has been recognized.^66,67 A main open question, however, is which cellular resources to represent at which level of detail.

Specifically geared towards communication via the gene expression machinery, early work suggested minimizing the use of ribosomal resources by constructing orthogonal ribosomes specific for heterologous mRNA; rational computational design of orthogonal ribosomes aimed to minimize interference with the native translation machinery.⁶⁸ Representing only the natural context, Algar et al. developed a model of gene expression accounting for ribosome resources to assist in the selection of candidate designs with minimal load,⁶⁹ and model predictions were also validated experimentally.⁷⁰ Similarly, models with explicit representation of RNA polymerase were instrumental in designing precisely controllable transcription factors.⁷¹ Qian et al. also recently proposed a more phenomenological model based on conservation laws to predict unexpected effective interactions between genes.⁷² These ideas extend to whole-cell models of resource sharing. Notably, Weiße et al. accounted for energy equivalents, free ribosomes, and proteins in a coarse-grained representation of yeast; by incorporating a synthetic circuit in this model, they were able to predict its dynamic behavior in communication with the host.⁷³ Even more detailed whole cell computational models were proposed to design synthetic circuits that account for host dependences and study their effect on the host,^74,75 but it is hard, if not impossible, to validate such detailed models. To deal with metabolic burden, alternative strategies that rely on closed-loop control are also emerging. For example, for metabolic engineering applications that aim to divert a natural pathway towards a synthetic product, Oyarzun et al. designed a synthetic controller capable of dampening perturbations in the host flux distribution while increasing the production of the synthetic product, and also identified trade-offs in the design of promoter and RBS strength.⁷⁶

Interference with host signaling has received considerably less attention, despite its importance, for example, in potential therapeutic applications. The design of orthogonal signaling components de novo, or by exploiting unnatural mechanisms for the design, is one possible avenue to reduce interference. For example, Green et al. designed transcriptional riboregulators that rely on linear-linear RNA interactions engineered in vitro using thermodynamic models, which are absent from natural systems.⁷⁷ Yet, especially to interface natural and synthetic signaling, it seems safer to rewire already well-characterized endogenous signaling pathways (Fig. 2C). This approach is strongly encouraged by pioneering work on the mating pathway in yeast: the pathway can be rewired to non-natural inputs and outputs⁷⁸ and pathway dynamics can be reshaped by engineering scaffolds for host endogenous kinases.⁷⁹ Rewiring natural pathways also led to first, striking therapeutic and diagnostics applications in mammalian systems.^80,81 However, the signaling area does not yet take all the advantage it could from widely used computational approaches for the analysis of natural signaling pathways. Further developing these methods for the design of synthetic controllers or the prediction of optimal rewiring designs could provide substantial advances.

3.3 Robustness to environmental perturbations

Even hypothetical, fully orthogonal synthetic systems will always be subject to environmental perturbations, either directly through changes in conditions such as temperature and pH, or indirectly through changes that the host experiences. For example, these changes can translate to changes in growth rate, which in turn affect the behavior of the synthetic circuit. While host-mediated approaches discussed above capture host-mediated effects in principle, direct effects warrant a different treatment.

For example, temperature dependencies of chemical reactions as represented in the Arrhenius law are expected to translate to different behaviors of synthetic circuits under different temperatures, which requires more detailed computational models. For example, Hussain et al. engineered a synthetic gene oscillator that shows robustness with respect to temperature alterations (Fig. 2D) by first incorporating temperature effects on the reaction parameters into a computational model and predicting the expected changes in the circuit's dynamic behavior due to temperature changes. They then identified and implemented a modification in the circuit with the opposite dependency on temperature to balance temperature effects on reaction rates.⁸² A similar approach was used to study temperature effects on a feed-forward circuit.⁸³ This work identified inherent circuit properties associated with robustness to changes in temperature, such as similar temperature dependencies of production rates or similar degradation rates for different states, and proposed circuit modifications such as negative feedbacks to enhance temperature robustness. Here, an internal model of temperature dependences helped designing appropriate feedback loops for compensation of these dependences. This is an instance of the internal model principle from control theory. Adaptations of the principle to biology are rare,⁸⁴ but they constitute an interesting research direction for the design of synthetic circuits that are able to compensate for environmental perturbations.

Environmental perturbations (as well as intrinsic biological variability) also induce extrinsic noise, defined as fluctuations of circuit parameters that depend on the context of the circuit or the host cell in which it is integrated. Considering unknown external stimuli as potential sources of extrinsic noise, Zechner et al. developed a method for the estimation of dynamically changing noise, which, following principles of noise cancellation in electrical circuits, could be a prerequisite for counteracting it.⁸⁵ In addition, first methods are available to decompose variation in biochemical circuits into potential sources of variation, such as intrinsic noise and specific properties of the intra- or extracellular environment.⁸⁶ Noise decomposition approaches so far may suggest which reporters to add to the system to predict the magnitudes of different variation components, but they do not yet provide guidelines on ways to make circuits more robust to specific environmental perturbations. Overall, hence, going from parts to host to environment, computational methods for predictable design are becoming increasingly rare, indicating clear needs for future developments.

4 Generalizing robust circuit design

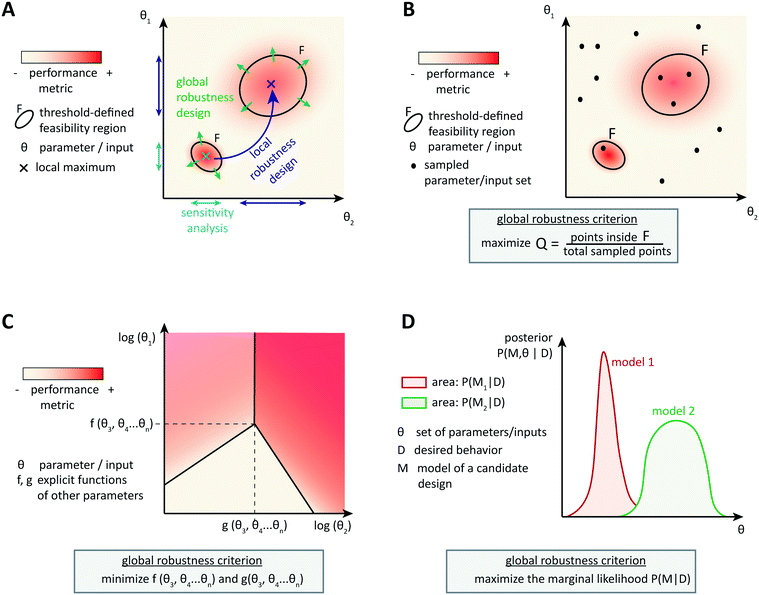
Optimization-based computational methods assist in the design of circuits able to achieve a particular behavior that is encoded by a performance metric, given well-characterized parts. Involving models of context-dependences or other sources of variability in the design process can result in more reliable synthetic circuit designs. However, as it is impossible to account for all context-dependences and because of the inherent uncertainty of biological parts and systems, it is important to design circuits able to achieve a good performance over a broad range of (model) parameters. Robust circuit design aims at building circuits that tolerate many unpredictable variations of the parameters while maintaining the target performance.

4.1 Local robustness: analysis and design

An intuitive approach is to design a circuit according to optimization methods described so far and then to assess the circuit performance when parameters vary locally around the candidate, optimal parameter set (Fig. 3A). Steady state robustness can be assessed by differential sensitivity analysis.⁸⁷ Assuming an input x (a parameter, species concentration, or reaction rate) and an output y (a concentration or reaction rate), relative sensitivity is defined as the logarithmic gain ∂ ln (y)/ ∂ ln (x) evaluated at the steady state. For example, Rodrigo et al. analyzed the sensitivity of different feed-forward loop architectures to the input and to parameters around the optimal parameter set selected for each architecture, and thereby selected the most locally robust architecture able to perform fold-change detection.⁸⁸

Fig. 3 Generalized strategies for robust design. (A) Principles of sensitivity analysis, local robustness design, and global robustness design strategies for the example of a single performance metric. (B–D) Global robustness design strategies: sampling and Q-value estimation (B), design space construction (C), and Bayesian posterior estimation (D).

One cannot directly assess robustness of a dynamic behavior to perturbations by differential sensitivity analysis. Several approaches for dynamic analysis have been proposed, but they are not widely used yet. For example, one can define a linear temporal logic property to translate the target dynamic behavior into a Boolean property. The size of the largest region of parameters around the optimal parameter set, for which the property is still valid, then indicates robustness of the system.⁸⁹ Dynamic performance criteria in the time domain can also be formulated as approximate formal control-like specifications in the frequency domain. Then the structured singular value, a tool for robustness analysis in control engineering, evaluates the largest perturbations that the system can withstand while keeping the target behavior, for example, in signaling to protein kinase cascades.⁹⁰ Iadevaia et al. give an example of local robustness analysis of a dynamic behavior towards topology perturbations, namely of mutations of up to four network nodes.⁹¹ Robustness is measured by the ability of a network to achieve the desired dynamic behavior for at least one parameter set, which is still local because it is assessed around the initial topology. Thus, local robustness analysis can help identifying which parameters might cause a loss of performance, and analyzing post-hoc the circuit robustness to small perturbations in parameters, inputs, or topology.

More advanced methods account for the system's tolerance to local perturbations during the design optimization (Fig. 3B). One possibility is to augment the objective function with a term corresponding to the average or the variance of the performance over an uncertainty region around the currently assessed parameter set. For example, Rodrigo et al. defined a scaled cost function ϕ* = (1 − λ)ϕ + λ〈ϕ〉, where ϕ is the metric function (accounting for the distance between the simulated and the target dynamic behavior) and 〈ϕ〉 is the average of this function over pre-defined variations in all parameter values. The user specifies the robustness weight λ, which biases the optimization towards best performance or towards highest robustness.^92,93 In local robustness design, a trade-off between the best fit of the circuit's behavior to the target behavior and the best local robustness is a general feature. The structured singular value approach could be extended to compute this precise trade-off using skewed μ, which gives the worst-case performance for a given parameter uncertainty.⁹⁰ So-called μ-synthesis algorithms, which enable to adjust robustness and performance weights until the best trade-off is found, are common in engineering,⁹⁴ but not yet transferred to gene circuit design.

4.2 Design for global robustness

Designing local robustness enables one to ensure tolerance to perturbations around the optimal parameter set found during circuit design. However, unpredicted context-dependences can shift the real optimal parameter set far from the designed one, and thereby make the designed system non-functional. Global approaches to robust design anticipate that because of uncertainties, actual parameters may occupy any region of the parameter space (Fig. 3A). Therefore, they aim to extend the feasible region(s), defined as region(s) in the parameter space that exhibit(s) the target behavior with a performance value above a certain threshold, as much as possible to increase the probability of obtaining a functional system.

The most straight-forward and commonly used approach to analyze the global robustness of a biological system consists of sampling parameter sets in the whole parameter space and checking for each set whether it is located within the feasible region or not (Fig. 3B). The ratio of samples in the feasible region over the total number of samples, often called the Q-value, approximates the relative area of the feasible region. For a given performance threshold, the extent of the feasible region, and thus the Q-value, is a property of the system's topology, which allows to evaluate and compare the global robustness of network topologies. This method was originally used for studying the evolution of robustness in natural systems such as circadian oscillators.^95,96 More recently, the method has been used to derive design principles for biochemical circuits able to achieve adaptation to varying, but time-constant stimuli.⁹⁷ Another example of application of the Q-value for circuit design was given by Chau et al.: they identified combinations of network motifs that can achieve robust cell polarization and cells with implemented circuits predicted to be more robust indeed showed a higher frequency of robust polarization (65% vs. 5% for topologies expected to be less robust).⁹⁸

Specifically for steady-state global robustness towards parameter variations, it is possible to use an analytical method to construct a so-called design space (Fig. 3C). Ordinary differential equations used for modeling biochemical systems at steady state can be reduced to an S-system (a set of first-order ordinary differential equations that are all a difference of products of power-law functions) by introducing new variables and neglecting non-dominant terms.⁹⁹ This representation enables the dimensional compression of the parameter landscape, in a design space that can be constructed and analyzed automatically.^100,101 The design space is a two-dimensional log-space defined by two of the system's parameters, where the model's equations determine the bounds of phenotypic regions. The phenotypic regions enable a simple discrimination of circuit behaviors according to some local robustness criteria, such as robustness of a certain flux to parameter variations. Importantly, region boundaries of the design space incorporate the influence of the whole parameter landscape on the circuit's steady states, not only the dependency of a certain performance on two parameters.^102,103 Analytical expressions involving steady state concentrations and kinetic rates describe the regions' boundaries, and therefore the extension of regions satisfying a certain robustness criterion, and thus global robustness design, is straightforward. It is also possible to analyze the circuit's global robustness towards the fluctuation of a particular parameter. Since performance criteria can also be plotted on the phenotypic regions, this method is very convenient for identifying trade-offs between local performance and robustness. Again, the approach was primarily developed to infer design principles of natural systems, but first design-oriented applications have been presented, for example, for the construction of synthetic oscillators.¹⁰⁴

Finally, the Bayesian computation framework, used originally for parameter inference, offers the possibility to directly estimate the global robustness of a circuit (Fig. 3D).^105,106 Bayesian inference is a probabilistic method based on Bayes' theorem. In the systems biology context, it enables the inference of a model topology and of parameters (specifically: of posterior distributions of parameter values) that caused a certain observed behavior as defined by data D. For circuit design, a similar method can find the optimal circuit topology and corresponding parameters by simply replacing the observed behavior by the target behavior. The marginalization of the posterior probabilities of a topology (or model) M with parameters θ, given the target behavior D, over all possible parameters, 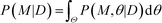, is a measure for the global robustness of one model. For the simple case of two parameters, this marginalization corresponds to determining the volume below the surface of the posterior probability (Fig. 3D). In performing optimization over circuit (model) topologies with this criterion, the method naturally converges towards a flatter and, thus, more robust solution. However, approximate Bayesian computation incurs high computational costs for sampling and simulation, which currently prevents a systematic enumeration of topologies with more than four nodes. Mathematical or computational complexity of all of the methods for global robust design discussed in this section has so far prevented wide-spread adoption for synthetic circuit design (and, to our knowledge, no experimentally demonstrated proofs of principle), but these are clearly promising approaches for the field.

5 Conclusions

The design of synthetic circuits has evolved from a largely part-centric, ‘plug-and-play’ paradigm towards approaches that account more for biological context and uncertainty – within circuits, in interactions with the host, and due to environmental variability. Current computational design methods, however, only consider subsets of these aspects, making the resulting designs only robust to the aspects covered. Critical open questions for rational circuit design are how to integrate approaches within the field, and how to borrow concepts from neighboring areas such as systems biology (to capture intended or unavoidable interfaces between natural and synthetic systems) and control engineering (drawing on methodologies for robust design, but also to exploit feedback for inherently robust circuit operation).

First steps in the direction of methods integration have been taken, for example, with the Cello design environment for the automated design of synthetic Boolean circuits, which not only accounts for the burden imposed by the circuit on the host, but also aims to insulate designed components from their context.⁴ More integrated approaches will need to handle at least two kinds of trade-offs. First, trade-offs between circuit complexity and context dependence will manifest themselves. For example, while insulator devices can reduce retroactivity, they consume gene expression capacity and cellular energy, and their strategic placement will therefore be essential. Second, there are inherent trade-offs between complexity (computational complexity as well as requirement on experimental data for calibration) and accuracy of the mathematical models underlying the design methods. We need models that encompass the parts' details (sequence as well as function), the parts' main interfaces with the host (e.g., polymerase, ribosome, and energy requirements), and sufficiently abstract representations of the host. We argue that neither purely statistical models on the parts' end (because of limited generalization), nor detailed whole-cell models for the host (because of virtually impossible validation) hold particular promise. Rather, biophysically motivated, more mechanistic models for parts could be combined with ‘resource-oriented’, systems biology models of the host⁷³ of manageable complexity.

For robust design in general, it will be important to leverage concepts from both systems biology and from ‘traditional’ engineering disciplines beyond electrical circuit design (analogies). We highlighted concepts from control engineering such as the internal model principle and the structured singular value, that tailored design methods for synthetic biology could be based on.⁵⁸ For example, control concepts could help establish feedback via previously proposed dynamic load sensors.^66,67 In principle, global robustness methods from systems biology can provide guidelines on the type of topology to use for circuit design, without any prior knowledge on parameter values. In addition to addressing computational complexity and usability, we think that it will be crucial to augment existing methods with practical considerations such as whether a predicted, robust circuit (parametrization) can be implemented experimentally, and what the associated effort is.

Finally, three specific areas and concepts appear particularly promising for future developments. Systematic computational methods are virtually absent for design that accounts for stochastic effects, for example, in gene expression, and for the (re)-wiring of cell signaling using synthetic components. Recent developments on feedback controllers that ensure robust adaptation also with gene expression noise,¹⁰⁷ and first therapeutic applications of re-wired signaling pathways for diabetes treatment,^81,108 respectively attest to the potential of these two areas. In addition, most of the current rational design methods operate in open-loop – predicted designs are tested experimentally, but without systematic feedback of data to models for design improvements. As noted earlier,¹ closed-loop, iterative design is a major challenge. First approaches in this direction are restricted to circuits without (explicit) feedback.⁴² We suggest that Bayesian methods are particularly suitable for data assimilation, and eventual design and testing in closed-loop. This could increase robustness of synthetic circuits in the face of biological uncertainties, and substantially reduce experimental efforts associated with either (intuitive) trial-and-error, or with screening of design alternatives (only) predicted to work as synthetic systems.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We acknowledge financial support by the National Centre of Competence in Research (NCCR) Molecular Systems Engineering funded by the Swiss National Science Foundation (SNSF).

References

1. J. C. Way, J. J. Collins, J. D. Keasling and P. A. Silver, Cell, 2014, 157, 151–161.
2. D. E. Cameron, C. J. Bashor and J. J. Collins, Nat. Rev. Microbiol., 2014, 12, 381–390.
3. P. E. Purnick and R. Weiss, Nat. Rev. Mol. Cell Biol., 2009, 10, 410–422.
4. A. A. Nielsen, B. S. Der, J. Shin, P. Vaidyanathan, V. Paralanov, E. A. Strychalski, D. Ross, D. Densmore and C. A. Voigt, Science, 2016, 352, aac7341.
5. J. A. N. Brophy and C. A. Voigt, Nat. Methods, 2014, 11, 508–520.
6. O. S. Venturelli, R. G. Egbert and A. P. Arkin, J. Mol. Biol., 2016, 428, 928–944.
7. S. Cardinale and A. P. Arkin, Biotechnol. J., 2012, 7, 856–866.
8. N. Nandagopal and M. B. Elowitz, Science, 2011, 333, 1244–1248.
9. C. E. Hodgman and M. C. Jewett, Metab. Eng., 2012, 14, 261–269.
10. P. Carbonell and J. Y. Trosset, Methods Mol. Biol., 2015, 1244, 3–21.
11. M. A. Marchisio and J. Stelling, Curr. Opin. Biotechnol., 2009, 20, 479–485.
12. E. Appleton, C. Madsen, N. Roehner and D. Densmore, Cold Spring Harbor Perspect. Biol., 2017, 9, a023978.
13. K. Wu and C. V. Rao, Curr. Opin. Chem. Biol., 2012, 16, 318–322.
14. M. H. Medema, R. van Raaphorst, E. Takano and R. Breitling, Nat. Rev. Microbiol., 2012, 10, 191–202.
15. L. Huynh and I. Tagkopoulos, ACS Synth. Biol., 2016, 5, 1412–1420.
16. R. W. Bradley, M. Buck and B. Wang, J. Mol. Biol., 2016, 428, 862–888.
17. J. K. Cheng and H. S. Alper, ACS Synth. Biol., 2016, 5, 1455–1465.
18. H. Meng, Y. Ma, G. Mai, Y. Wang and C. Liu, Quant. Biol., 2017, 5, 90–98.
19. V. A. Rhodius, V. K. Mutalik and C. A. Gross, Nucleic Acids Res., 2012, 40, 2907–2924.
20. R. C. Brewster, D. L. Jones and R. Phillips, PLoS Comput. Biol., 2012, 8, e1002811.
21. M. Kozak, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 2850–2854.
22. T. E. Quax, N. J. Claassens, D. Soll and J. van der Oost, Mol. Cell, 2015, 59, 149–161.
23. P. Gaspar, G. Moura, M. A. Santos and J. L. Oliveira, Nucleic Acids Res., 2013, 41, e73.
24. N. Jacques and M. Dreyfus, Mol. Microbiol., 1990, 4, 1063–1067.
25. M. T. Bonde, M. Pedersen, M. S. Klausen, S. I. Jensen, T. Wulff, S. Harrison, A. T. Nielsen, M. J. Herrgard and M. O. Sommer, Nat. Methods, 2016, 13, 233–236.
26. H. M. Salis, E. A. Mirsky and C. A. Voigt, Nat. Biotechnol., 2009, 27, 946–950.
27. D. Na, S. Lee and D. Lee, BMC Syst. Biol., 2010, 4, 71.
28. S. W. Seo, Metab. Eng., 2013, 15, 67–74.
29. A. Espah Borujeni, D. M. Mishler, J. Wang, W. Huso and H. M. Salis, Nucleic Acids Res., 2016, 44, 1–13.
30. M. Welch, S. Govindarajan, J. E. Ness, A. Villalobos, A. Gurney, J. Minshull and C. Gustafsson, PLoS One, 2009, 4, e7002.
31. K. E. McGinness, T. A. Baker and R. T. Sauer, Mol. Cell, 2006, 22, 701–707.
32. D. E. Cameron and J. J. Collins, Nat. Biotechnol., 2014, 32, 1276–1281.
33. D. Rothschild, E. Dekel, J. Hausser, A. Bren, G. Aidelberg, P. Szekely and U. Alon, PLoS Comput. Biol., 2014, 10, e1003602.
34. G. Boel, R. Letso, H. Neely, W. N. Price, K. H. Wong, M. Su, J. D. Luff, M. Valecha, J. K. Everett, T. B. Acton, R. Xiao, G. T. Montelione, D. P. Aalberts and J. F. Hunt, Nature, 2016, 529, 358–363.
35. L. Huynh, J. Kececioglu, M. Köppe and I. Tagkopoulos, PLoS One, 2012, 7, e35529.
36. M. S. Dasika and C. D. Maranas, BMC Syst. Biol., 2008, 2, 24.
37. I. Otero-Muras and J. R. Banga, BMC Syst. Biol., 2014, 8, 113.
38. I. Otero-Muras, D. Henriques and J. R. Banga, Bioinformatics, 2016, 32, 3360–3362.
39. Y. Boada, G. Reynoso-Meza, J. Pico and A. Vignoni, BMC Syst. Biol., 2016, 10, 27.
40. N. Roehner, E. M. Young, C. A. Voigt, D. B. Gordon and D. Densmore, ACS Synth. Biol., 2016, 5, 507–517.
41. M. A. Marchisio and J. Stelling, PLoS Comput. Biol., 2011, 7, e1001083.
42. N. Davidsohn, J. Beal, S. Kiani, A. Adler, F. Yaman, Y. Li, Z. Xie and R. Weiss, ACS Synth. Biol., 2015, 4, 673–681.
43. I. Farasat, M. Kushwaha, J. Collens, M. Easterbrook, M. Guido and H. M. Salis, Mol. Syst. Biol., 2014, 10, 731.
44. D. Del Vecchio, A. J. Ninfa and E. D. Sontag, Mol. Syst. Biol., 2008, 4, 161.
45. J. M. Pedraza and A. van Oudenaarden, Science, 2005, 307, 1965–1969.
46. C. G. Kalodimos, N. Biris, A. M. Bonvin, M. M. Levandoski, M. Guennuegues, R. Boelens and R. Kaptein, Science, 2004, 305, 386–389.
47. J. Vind, M. A. Sorensen, M. D. Rasmussen and S. Pedersen, J. Mol. Biol., 1993, 231, 678–688.
48. N. A. Cookson, W. H. Mather, T. Danino, O. Mondragon-Palomino, R. J. Williams, L. S. Tsimring and J. Hasty, Mol. Syst. Biol., 2011, 7, 561.
49. H. Giladi, D. Goldenberg, S. Koby and A. B. Oppenheim, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 2184–2188.
50. C. Madrid, J. M. Nieto, S. Paytubi, M. Falconi, C. O. Gualerzi and A. Juarez, J. Bacteriol., 2002, 184, 5058–5066.
51. L. You, R. S. Cox, 3rd, R. Weiss and F. H. Arnold, Nature, 2004, 428, 868–871.
52. S. Klumpp, Z. Zhang and T. Hwa, Cell, 2009, 139, 1366–1375.
53. P. Jiang, A. C. Ventura, E. D. Sontag, S. D. Merajver, A. J. Ninfa and D. Del Vecchio, Sci. Signaling, 2011, 4, ra67.
54. S. Jayanthi and D. Del Vecchio, IEEE Trans. Autom. Control, 2011, 56, 748–761.
55. D. Mishra, P. M. Rivera, A. Lin, D. Del Vecchio and R. Weiss, Nat. Biotechnol., 2014, 32, 1268–1275.
56. A. Gyorgy and D. Del Vecchio, PLoS Comput. Biol., 2014, 10, e1003486.
57. A. Raj and A. van Oudenaarden, Cell, 2008, 135, 216–226.
58. D. Del Vecchio, A. J. Dy and Y. Qian, J. R. Soc., Interface, 2016, 13, 20160380.
59. M. B. Elowitz and S. Leibler, Nature, 2000, 403, 335–338.
60. L. Potvin-Trottier, N. D. Lord, G. Vinnicombe and J. Paulsson, Nature, 2016, 538, 514–517.
61. J. Beal, Front. Bioeng. Biotechnol., 2015, 3, 93.
62. C. G. Bowsher, M. Voliotis and P. S. Swain, PLoS Comput. Biol., 2013, 9, e1002965.
63. D. A. Oyarzun, J. B. Lugagne and G. B. Stan, ACS Synth. Biol., 2015, 4, 116–125.
64. C. Tan, P. Marguet and L. You, Nat. Chem. Biol., 2009, 5, 842–848.
65. S. Cardinale, M. P. Joachimiak and A. P. Arkin, Cell Rep., 2013, 4, 231–237.
66. O. Borkowski, F. Ceroni, G. B. Stan and T. Ellis, Curr. Opin. Microbiol., 2016, 33, 123–130.
67. G. Wu, Q. Yan, J. A. Jones, Y. J. Tang, S. S. Fong and M. A. Koffas, Trends Biotechnol., 2016, 34, 652–664.
68. L. M. Chubiz and C. V. Rao, Nucleic Acids Res., 2008, 36, 4038–4046.
69. R. J. R. Algar, T. Ellis and G.-B. Stan, presented in part at the 53rd IEEE Conference on Decision and Control, Los Angeles, California, USA, 2014.
70. F. Ceroni, R. Algar, G. B. Stan and T. Ellis, Nat. Methods, 2015, 12, 415–418.
71. D. S. Ottoz, F. Rudolf and J. Stelling, Nucleic Acids Res., 2014, 42, e130.
72. Y. Qian, H. H. Huang, J. I. Jimenez and D. Del Vecchio, ACS Synth. Biol., 2017, 6, 1263–1272.
73. A. Y. Weiße, D. A. Oyarzun, V. Danos and P. S. Swain, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E1038–1047.
74. J. R. Karr, J. C. Sanghvi, D. N. Macklin, M. V. Gutschow, J. M. Jacobs, B. Bolival Jr., N. Assad-Garcia, J. I. Glass and M. W. Covert, Cell, 2012, 150, 389–401.
75. O. Purcell, B. Jain, J. R. Karr, M. W. Covert and T. K. Lu, Chaos, 2013, 23, 025112.
76. D. A. Oyarzun and G. B. Stan, J. R. Soc., Interface, 2013, 10, 20120671.
77. A. A. Green, P. A. Silver, J. J. Collins and P. Yin, Cell, 2014, 159, 925–939.
78. A. J. Brown, S. L. Dyos, M. S. Whiteway, J. H. White, M. A. Watson, M. Marzioch, J. J. Clare, D. J. Cousens, C. Paddon, C. Plumpton, M. A. Romanos and S. J. Dowell, Yeast, 2000, 16, 11–22.
79. C. J. Bashor, N. C. Helman, S. Yan and W. A. Lim, Science, 2008, 319, 1539–1543.
80. K. Rossger, G. Charpin-El Hamri and M. Fussenegger, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18150–18155.
81. D. Auslander, S. Auslander, G. Charpin-El Hamri, F. Sedlmayer, M. Muller, O. Frey, A. Hierlemann, J. Stelling and M. Fussenegger, Mol. Cell, 2014, 55, 397–408.
82. F. Hussain, C. Gupta, A. J. Hirning, W. Ott, K. S. Matthews, K. Josic and M. R. Bennett, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 972–977.
83. S. Sen, J. Kim and R. M. Murray, presented in part at the 53rd IEEE Conference on Decision and Control, Los Angeles, California, USA, 2014.
84. B. W. Andrews, E. D. Sontag and P. A. Iglesias, IFAC Proceedings Volumes, 2008, vol. 41, pp. 15873–15878.
85. C. Zechner, G. Seelig, M. Rullan and M. Khammash, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 4729–4734.
86. C. G. Bowsher and P. S. Swain, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E1320–1328.
87. Z. Zi, IET Syst. Biol., 2011, 5, 336.
88. G. Rodrigo and S. F. Elena, PLoS One, 2011, 6, e16904.
89. G. Batt, B. Yordanov, R. Weiss and C. Belta, Bioinformatics, 2007, 23, 2415–2422.
90. F. J. Doyle and J. Stelling, IFAC Proceedings Volumes, 2005, vol. 38, pp. 31–36.
91. S. Iadevaia, L. K. Nakhleh, R. Azencott and P. T. Ram, PLoS One, 2014, 9, e91743.
92. G. Rodrigo, J. Carrera and A. Jaramillo, Nucleic Acids Res., 2011, 39, e138.
93. G. Rodrigo and A. Jaramillo, ACS Synth. Biol., 2013, 2, 230–236.
94. S. Skogestad, Multivariable Feedback Control: Analysis and Design, Wiley-Blackwell, 2005.
95. M. Hafner, H. Koeppl, M. Hasler and A. Wagner, PLoS Comput. Biol., 2009, 5, e1000534.
96. A. Wagner, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11775–11780.
97. W. Ma, A. Trusina, H. El-Samad, W. A. Lim and C. Tang, Cell, 2009, 138, 760–773.
98. A. H. Chau, J. M. Walter, J. Gerardin, C. Tang and W. A. Lim, Cell, 2012, 151, 320–332.
99. M. A. Savageau, P. M. Coelho, R. A. Fasani, D. A. Tolla and A. Salvador, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6435–6440.
100. R. A. Fasani and M. A. Savageau, Bioinformatics, 2010, 26, 2601–2609.
101. J. G. Lomnitz and M. A. Savageau, Front. Genet., 2016, 7, 118.
102. J. Stricker, S. Cookson, M. R. Bennett, W. H. Mather, L. S. Tsimring and J. Hasty, Nature, 2008, 456, 516–519.
103. J. Sardanyes, A. Bonforti, N. Conde, R. Sole and J. Macia, Front. Physiol., 2015, 6, 281.
104. J. G. Lomnitz and M. A. Savageau, ACS Synth. Biol., 2014, 3, 686–701.
105. C. P. Barnes, D. Silk and M. P. Stumpf, Interface Focus, 2011, 1, 895–908.
106. C. P. Barnes, D. Silk, X. Sheng and M. P. Stumpf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 15190–15195.
107. C. Briat, A. Gupta and M. Khammash, Cell Syst., 2016, 2, 15–26.
108. M. Xie, H. Ye, H. Wang, G. Charpin-El Hamri, C. Lormeau, P. Saxena, J. Stelling and M. Fussenegger, Science, 2016, 354, 1296–1301.
109. T. Gunde and A. Barberis, BioTechniques, 2005, 39, 541–549.

---

Footnote

† These authors contributed equally.

---