A substrate-dependent mechanism for the reactions of a hydrido(hydrosilylene)ruthenium complex with carbonyl compounds: insights from quantum chemical calculations

Abstract

The detailed mechanisms for the reactions of a neutral silylene ruthenium complex with ketones and aldehydes have been investigated with the aid of density functional theory calculations. Through the investigation, the difference in reactivity between ketones and aldehydes towards the ruthenium silylene hydride complex has been explained and discussed. The calculations showed that the reaction mechanisms are dependent on the substituents of the carbonyl substrates. The present calculations are consistent with the experimental observations.

---

Introduction

Transition-metal silylene complexes have been proposed as influential intermediates for various transformation reactions of organosilicon compounds in most of their stoichiometric and catalytic processes.¹ In the past few decades, many experimental studies have manifested that silylene complexes can react not only with simple organic substrates but also with more unsaturated carbonyl compounds.^2,3

Recently, Tobita et al. investigated the reaction of the neutral base-free silylene tungsten complex [Cp*(CO)₂(H)W=Si(H)][C(SiMe₃)₃] with RCN (R = Me, ^tBu).² They proposed the mechanisms involving H-migration and coordination of the lone pair of the N atom to the tungsten center for the MeCN reactant and 1,2-H migration from the Si atom to the W atom for the Me^tBu reactant, respectively. While this silylene tungsten complex reacts with acetone, the presumable key step is that the tungsten center abstracts an α-hydrogen of acetone through a six-membered transition state to give [(Cp*)(CO)₂(H)W=Si(OiPr){C(SiMe₃)₃}].^3a Subsequently, a [2_σ+2_π] addition between the Si–H bond of the silylene ligand instead and the carbonyl of acetone was observed.^3b A theoretical study by Wu et al. provided evidence to support this formation, and the DFT calculation results showed that both electronic and steric factors favored the hydride migration mechanism for the reaction of acetone.⁴ Interestingly, the reaction with α,β-unsaturated acetone underwent a [2+4] cycloaddition via a six-membered transition state, accompanied by the Si–H reductive elimination and rearrangement to form an anti-η³-siloxyallyl complex.⁵ This mechanism was afterwards supported by theoretical investigations.⁶

Similar to the silylene tungsten complex, the significant cycloaddition reaction of silylene ruthenium complexes was developed. The cationic silylene complex [Cp*(PMe₃)₂Ru=SiR₂][B(C₆F₅)₄] (R = Me, Ph) was reported to undergo reactions with a formal [2+2] cycloaddition and an insertion into an Si–H bond with isocyanates.⁷ The mechanism involving a [2_σ+2_π] addition between the Si–H bond of the silylene complexes and an olefin C=C double bond, related to the regioselective anti-Markovnikov hydrosilylation of a double bond, was supported by theoretical studies.^8,9 Moreover, the direct addition of an Si–H bond on the silylene ligand to alkenes was developed by Tilley et al. on the stoichiometric and catalytic hydrosilylations of alkenes¹⁰ and carbonyl¹¹ compounds using silylene iridium and ruthenium complexes. Besides, it was believed that the reaction of Cp*(CO)(H)Ru=Si(H){C(SiMe₃)₃} with ArNCO is related to the coordination of the oxygen atom to the Si atom, inducing hydride migration from the Ru atom to the carbon atom and subsequent rotation along the C–O bond to give five-membered ring products. In terms of ArNCS, it was considered to proceed with a [2+2] cycloaddition between the Ru=Si and C=S bonds followed by reductive elimination of the Si–H bond. The alternative route involved the coordination of ArNCS to the ruthenium atom of the unsaturated silyl complex produced by 1,2-H migration from the Ru atom to the Si atom, followed by the silyl migration to the sulfur atom to form C–S bond-cleavaged products.¹² DFT calculations were performed to investigate the reaction between the cationic silylene complex [Cp(PH₃)Ru(H)₂(SiH₂)]⁺ and ethylene. The results provided theoretical evidence for a new mechanism of the catalytic hydrosilylation cycle involving the ethylene insertion into a remote Si–H bond of this complex, which was 8 kcal mol⁻¹ more favourable than the Chalk–Harrod and modified Chalk–Harrod mechanisms.¹³

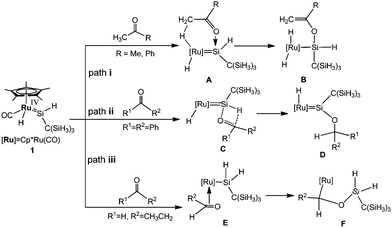
More recently, Tobita et al. carried out the reactions of the ruthenium analogue Cp*(CO)(H)Ru=Si(H)[C(SiMe₃)₃] (1) with some unsaturated organic substrates at room temperature.¹⁴ They proposed possible mechanisms for the reactions of 1 with several carbonyl compounds (Scheme 1) to account for the formation of α-hydrogen abstraction, hydrosilylation, and [2_σ+2_π] cycloaddition products with different substrates.¹⁵ Although much progress has been achieved from experiments, the reaction mechanism is still elusive. In this paper, continuing our interest in the reactions of small molecules with metal cyclopentadienyl complexes,¹⁶ our theoretical calculations using density functional theory aim at further exploring the possible mechanisms.

Scheme 1 The reactions of a hydrido(hydrosilylene)ruthenium complex with carbonyl compounds.

Computational methods

Molecular geometries of the reactants, intermediates, transition states and products were fully optimized by density functional theory (DFT) calculations using the M06 method.¹⁷ The 6-31G(d,p) basis set¹⁸ was used for the C, H and O atoms, while the effective core potentials (ECPs) of Hay and Wadt with a double-ζ basis set (LanL2DZ)¹⁹ were utilized to describe the Ru and Si atoms. Frequency analyses were also performed at the same level to obtain zero-point energies (ZPE) and to identify all stationary points as minima (zero imaginary frequency) or transition states (one imaginary frequency). We also employed intrinsic reaction coordinate (IRC)²⁰ calculations for the transition states to ascertain that such structures indeed connect two relevant minima. Meanwhile, the Tris(trimethylsilyl)methyl [C(SiMe₃)₃] group was replaced by the Tris(silyl)methyl [C(SiH₃)₃] group for cost-efficient calculations. All calculations were implemented with the Gaussian03 software package.²¹

With regard to a solvent effect, the conductor-like polarizable continuum model (CPCM)²² was applied to calculate the single-point energy of all optimized species. Therefore, in this paper, hexane was selected as solvent according to the experiments and solvation-corrected relative free energies were provided in order to achieve more accurate results.

In order to reduce the computational cost, the Tris(trimethylsilyl)methyl [C(SiMe₃)₃] group was replaced by a small Tris(silyl)methyl [C(SiH₃)₃] group. This simplification was tested for the rate-determining transition states of three different pathways for the reaction of acetone with the hydrido(hydrosilylene)ruthenium complex (Scheme 1). In the case of a small model group, TS_23a, TS_56b and TS_24a are 13.5, 17.5 and 25.2 kcal mol⁻¹ with respect to the energy reference point respectively. In the case of the real Tris(trimethylsilyl)methyl [C(SiMe₃)₃] group, TS_23O, TS_56O and TS_89O are 16.7, 20.1 and 28.1 kcal mol⁻¹ with respect to the energy reference point respectively. It is noted that the barriers calculated using the full Tris(trimethylsilyl)methyl group are much higher by ca. 3 kcal mol⁻¹ than those calculated using the small model group. The changes in relative barriers are the most important numbers in our discussion, while the effect of the changes in relative barriers on the free energy profiles is almost negligible by using different-sized model groups, and have little effect on the conclusions we have obtained in the following discussion.

Results and discussion

Preliminary experimental results allowed Tobita and coworkers to propose a mechanism (Scheme 1) for the reactions of a hydrido(hydrosilylene)ruthenium complex with carbonyl compounds. Herein, we have performed DFT calculations to explore the mechanism in detail, and the effect of different substrates on the reaction mechanism has also been demonstrated.

As mentioned in the Introduction, our main objective is to understand the reactivity difference of carbonyl compounds (ketones and aldehydes) towards the hydrido(hydrosilylene)ruthenium complex. As shown in Scheme 1, in the proposed pathways for the reaction of carbonyl compounds with the hydrido(hydrosilylene)ruthenium complex, the reaction mechanisms depend on the substituents of the substrates. For the reaction of acetone and acetophenone, an a-H abstraction reaction takes place to yield Cp*(CO)(H)₂–Ru[Si(H){OC(=CH₂)R}C(SiH₃)₃] (R = Me, Ph). For the reaction of benzophenone with no a-H atom, the hydrosilylation of the carbonyl group takes place. For the reaction of propylaldehyde, it undergoes a [2_σ+2_π] cycloaddition reaction.

Mechanism for the reaction of acetone and acetophenone

We first examined the mechanism for the reaction of acetone with the hydrido(hydrosilylene)ruthenium complex 1 (Scheme 1). Fig. 1 shows the free energy profiles calculated, and the optimized structures are described in Fig. 2.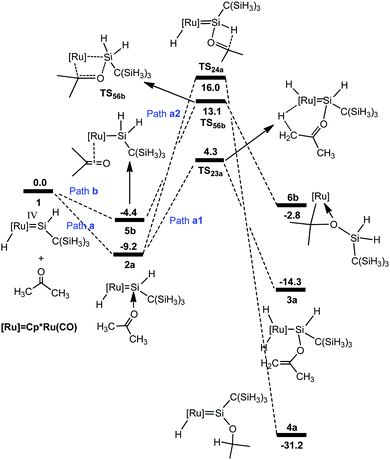

Fig. 1 Free energy profiles calculated for the reaction of a ruthenium–silylene complex with acetone. The relative free energies in solvent are given in kcal mol⁻¹.

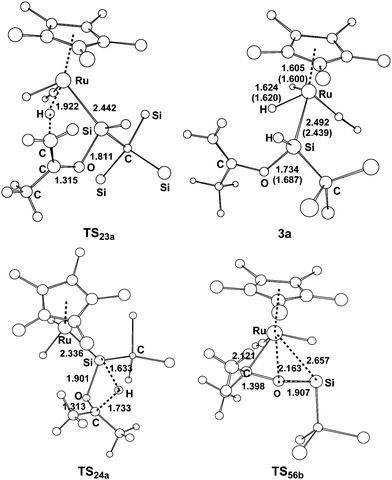Fig. 2 Optimized structures with selected bond lengths (Å) for the species shown in Fig. 1.

From complex 1, the first step involves the coordination of the acetone oxygen atom to the silylene Si center to form an acid–base adduct 2a, and this step is exergonic by 9.2 kcal mol⁻¹. From adduct 2a, two possible pathways are proposed. Path a1 involves the a-H abstraction mechanism, and path a2 is related to the carbonyl hydrosilylation mechanism. On the basis of the calculations, path a1 is kinetically more favorable. In path a1, a hydride migration from the C atom to the Ru atom occurs, yielding the experimentally observed product 3a. This hydride migration step is facile and needs to overcome a free energy barrier of only 13.5 kcal mol⁻¹ from 2a to TS_23a. The calculations clearly support the proposed mechanism by Tobita et al., as shown in Scheme 1 for the reaction of acetone.¹⁴ According to the calculations, the calculated structural parameters of product 3a are in good agreement with the experimentally measured parameters shown in parentheses in Fig. 2,¹⁴ suggesting that the theoretical method used in the present calculations is reasonable.

As mentioned in the Introduction, the reaction of aldehyde yields a product in which the [2_σ+2_π] cycloaddition takes place. Therefore, for the reaction of acetone, we also calculated the possible pathway to examine the energetic aspect related to the experimentally not-observed products; the free energy profiles are shown in Fig. 1 (path b). From complex 1, the hydride migrates to the silylene Si center accompanying an η² coordination of acetone through the C=O unit to give the silyl intermediate 5b. Then a [2_σ+2_π] cycloaddition gives 6b. The free energy barrier for this step is calculated to be 17.5 kcal mol⁻¹ from 5b to TS_56b, which is much higher than that in path a1 and makes this pathway inaccessible.

A similar mechanism was also found for the reaction of the hydrido(hydrosilylene)ruthenium complex with acetophenone (Fig. 3), and the optimized structures are displayed in Fig. 4. The calculations showed that the pathway involving an a-H abstraction (14.5 kcal mol⁻¹ from 2c to TS_23c) is more favorable than that of the [2_σ+2_π] cycloaddition (17.5 kcal mol⁻¹ from 5d to TS_56d) and hydrosilylation of the carbonyl group (27.7 kcal mol⁻¹ from 2c to TS_24c).

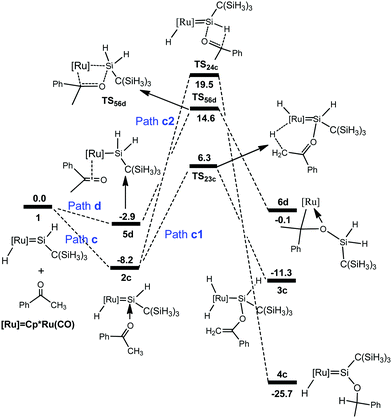Fig. 3 Free energy profiles calculated for the reaction of a ruthenium–silylene complex with acetophenone. The relative free energies in solvent are given in kcal mol⁻¹.

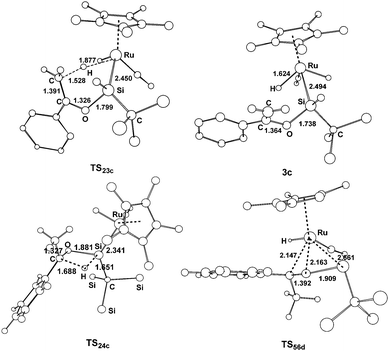Fig. 4 Optimized structures with selected bond lengths (Å) for the species shown in Fig. 3.

Mechanism for the reaction of benzophenone

To understand the different reactivity of benzophenone from acetone, we calculated the above-discussed three pathways for the reaction of benzophenone with the hydrido(hydrosilylene)ruthenium complex 1. However, the a-H abstraction mechanism is impossible due to the absence of the a-H atom. Thus [2_σ+2_π] cycloaddition and carbonyl hydrosilylation mechanisms are considered in the present calculations. Fig. 5 shows the calculated free energy profiles and the corresponding geometries are presented in Fig. 6.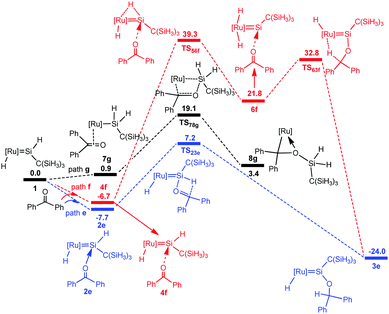

Fig. 5 Free energy profiles calculated for the reaction of a ruthenium–silylene complex with benzophenone. The relative free energies in solvent are given in kcal mol⁻¹.

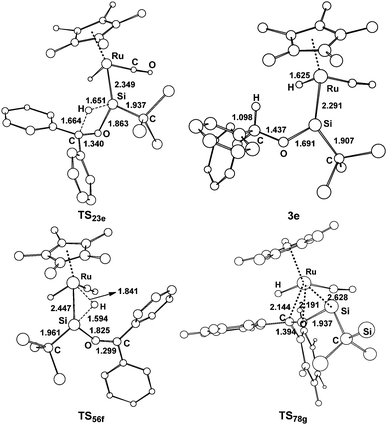Fig. 6 Optimized structures with selected bond lengths (Å) for the species shown in Fig. 5.

From complex 1, three possible pathways are proposed according to the different coordination modes of benzophenone. We first consider the coordination of the carbonyl oxygen atom of benzophenone to the electron-deficient silylene silicon atom via two different directions. One (path e) is the same as the hydride ligand and the other (path f) is opposite to the hydride ligand. Our calculations suggest that the former is energetically more favorable.

The benzophenone oxygen atom is initially coordinated to the electron-deficient silylene silicon atom to afford the base-stabilized adduct 2e, and this step is exergonic by 7.7 kcal mol⁻¹. From 2e, the hydrosilylation of the carbonyl occurs to form product 3evia the transition state TS_23e. This step is facile and needs to overcome a free energy barrier of 14.9 kcal mol⁻¹. The [2_σ+2_π] cycloaddition mechanism (path g) is also considered for this reaction; however, product 8g is unstable due to the steric repulsion between the phenyl groups and the C(SiH₃)₃ group, which is in agreement with the experiments that this product is not observed.¹⁴

Mechanism for the reaction of propylaldehyde

To understand the different reactivities of carbonyl compounds, we also calculated the above-discussed three pathways for the reaction of propylaldehyde with hydrido(hydrosilylene)ruthenium complex 1. The free-energy profiles for the reaction are described in Fig. 7. The corresponding optimized structures are shown in Fig. 8.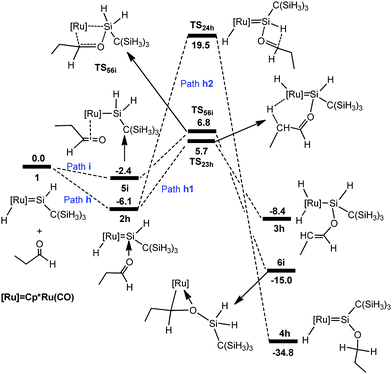

Fig. 7 Free energy profiles calculated for the reaction of a ruthenium–silylene complex with propylaldehyde. The relative free energies in solvent are given in kcal mol⁻¹.

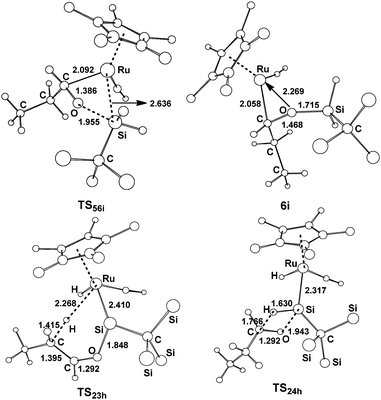Fig. 8 Free optimized structures with selected bond lengths (Å) for the selected species shown in Fig. 7.

From complex 1, the hydride migrates to the silylene Si center accompanying an η² coordination of aldehyde through the C=O unit to give the silyl intermediate 5i. Then a [2_σ+2_π] addition gives 6ivia the transition state TS_56i; an overall free energy barrier of 12.9 kcal mol⁻¹ from 2h to TS_56i is required for this step. From 2h, the path h1 involving the a-H abstraction is reversible at room temperature, because the forward and reverse barriers are only 11.8 kcal mol⁻¹ and 14.1 kcal mol⁻¹, respectively. Thus the formation of 6i is energetically more favorable. In addition, path h2 involving the hydrosilylation of the carbonyl group (25.6 kcal mol⁻¹ from 2h to TS_24h) has a much higher barrier.

We then explain why TS_24a is less stable than TS_56b (Fig. 1), and why TS_78g is less stable than TS_23e. TS_24a and TS_23e are involved in the Glaser–Tilley [2_σ+2_π] reaction mechanism. Previous research studies^8,11,13 showed that a cationic ruthenium–silylene complex catalyzes the hydrosilylation of alkenes via the Glaser–Tilley [2_σ+2_π] mechanism. A recent experimental and theoretical study of osmium-silylene-mediated ethylene hydrosilylation showed that a large positive charge on Si of the silylene ligand promoted the Glaser–Tilley mechanism.^4,8 According to the NBO analysis,²³ the silylene silicon atoms in 2a and TS_24a have the charges of 0.86e and 1.41e, respectively, while the silylene silicon atoms in 2e and TS_23e have the charges of 0.95e and 1.52e, respectively. The larger positive charge on the Si atom of the silylene ligand in 2e and TS_23e may explain why TS_24a is less stable than TS_56b (Fig. 1), and why TS_78g is less stable than TS_23e (Fig. 1).

We also investigate why TS_56i is more stable compared to TS_78g and TS_56b. First, we consider the charge distribution of the three transition states, and no obvious rule was found. Then we determine the steric repulsions of the three transition states. It was found that the steric repulsion in TS_56i, which originates from the interaction between the substrate and the Cp* ring, is much smaller than those of TS_78g and TS_56b.

Conclusions

On the basis of the DFT calculations, the difference in reactivity between ketones and aldehydes towards the ruthenium silylene hydride complex has been studied. The calculations showed that the mechanisms are dependent on the substituents of the substrates. In the reaction of acetone and acetophenone, an a-H abstraction reaction takes place to yield Cp*(CO)(H)₂–Ru[Si(H){OC(=CH₂)R}C(SiH₃)₃] (R = Me, Ph). In the reaction of benzophenone with no a-H atom, the hydrosilylation of the carbonyl group takes place. For the reaction of propylaldehyde, it undergoes a [2_σ+2_π] cycloaddition reaction. The calculations showed that TS_24a is less stable than TS_56b and TS_78g is less stable than TS_23e, which is ascribed to the large positive charge on Si of the silylene ligand that promotes the [2_σ+2_π] Glaser–Tilley mechanism. The calculations also indicated that TS_56i is more stable compared to TS_78g and TS_56b, which originates from the smaller steric repulsion in TS_56i between the substrate and the Cp* ring compared to that in TS_56b and TS_78g.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (21203166 and 21473157), the Natural Science Foundation of Zhejiang Province (LY16B030001), the Food Science and Engineering the Most Important Discipline of Zhejiang Province (JYTsp2014111), and excellent food talent science and technology training project (20151210). We thank the State Key Laboratory of Physical Chemistry of Solid Surfaces (Xiamen University) for providing computational resources.

Notes and references

1. (a) T. D. Tilley, Inorg. Chem., 1990, 10, 37; (b) D. C. Pestana, T. S. Koloski and D. H. Berry, Organometallics, 1994, 13, 4173; (c) H. K. Sharma and K. H. Pannell, Chem. Rev., 1995, 95, 1351; (d) S. R. Klei, T. D. Tilley and R. G. Bergman, Organometallics, 2002, 21, 4648; (e) M. Okazaki, H. Tobita and H. Ogino, J. Chem. Soc., Dalton Trans., 2003, 493; (f) R. Waterman, P. G. Hayes and T. D. Tilley, Acc. Chem. Res., 2007, 40, 712.
2. T. Watanabe, H. Hashimoto and H. Tobita, J. Am. Chem. Soc., 2006, 128, 2176.
3. (a) T. Watanabe, H. Hashimoto and H. Tobita, Angew. Chem., Int. Ed., 2004, 43, 218; (b) T. Watanabe, H. Hashimoto and H. Tobita, Chem. – Asian J., 2012, 7, 1408.
4. X. H. Zhang, L. W. Chung, Z. Y. Lin and Y. D. Wu, J. Org. Chem., 2008, 73, 820.
5. T. Watanabe, H. Hashimoto and H. Tobita, J. Am. Chem. Soc., 2007, 129, 11338.
6. S. W. Bi, Y. X. Liu, G. Chen, L. S. Zhang, M. Sun and P. Li, J. Org. Chem., 2009, 694, 3456.
7. G. P. Mitchell and T. D. Tilley, J. Am. Chem. Soc., 1997, 119, 11236.
8. (a) U. Böhme, J. Org. Chem., 2006, 691, 4400; (b) P. G. Hayes, C. Beddie, M. B. Hall, R. Waterman and T. D. Tilley, J. Am. Chem. Soc., 2006, 128, 428; (c) C. Beddie and M. B. Hall, J. Phys. Chem. A, 2006, 110, 1416.
9. L. W. Chung, PhD thesis, The Hong Kong University of Science and Technology, (HK), 2006.
10. S. R. Klei, T. D. Tilley and R. G. Bergman, Organometallics, 2002, 21, 4648.
11. P. B. Glaser and T. D. Tilley, J. Am. Chem. Soc., 2003, 125, 13640.
12. M. Ochiai, H. Hashimoto and H. Tobita, Organometallics, 2012, 31, 527.
13. C. Beddie and M. B. Hall, J. Am. Chem. Soc., 2004, 126, 13564.
14. M. Ochiai, H. Hashimoto and H. Tobita, Angew. Chem., Int. Ed., 2007, 46, 8192.
15. M. Ochiai, H. Hashimoto and H. Tobita, Dalton Trans., 2009, 1812.
16. (a) H. J. Xie and Z. Y. Lin, Organometallics, 2014, 33, 892; (b) H. J. Xie, L. Yang, X. C. Ye and Z. X. Cao, Organometallics, 2014, 33, 1553; (c) X. C. Ye, L. Yang, Y. Li, J. Y. Huang, L. Zhou, Q. F. Lei, W. J. Fang and H. J. Xie, Eur. J. Inorg. Chem., 2014, 1502; (d) H. J. Xie, C. C. Liu, Y. Yuan, T. Zhou, T. Fan, Q. F. Lei and W. J. Fang, Dalton Trans., 2016, 45, 1152.
17. (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215; (b) Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 5121; (c) Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 13126.
18. (a) M. S. Gordon, Chem. Phys. Lett., 1980, 76, 163; (b) R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206.
19. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
20. (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009.
22. (a) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995; (b) M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669.
23. (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735; (b) A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736; (c) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized structures used in the theoretical calculations. See DOI: 10.1039/c6nj02361d

---