Growth of centimeter-sized [(CH3)2NH2][Mn(HCOO)3] hybrid formate perovskite single crystals and Raman evidence of pressure-induced phase transitions†
Lipeng
Xin
 *a,
Zhen
Fan
bg,
Guanghui
Li
c,
Ming
Zhang
d,
Yonghao
Han
c,
John
Wang
b,
Khuong P.
Ong
e,
Lei
Qin
f,
Yanzhen
Zheng
*a,
Zhen
Fan
bg,
Guanghui
Li
c,
Ming
Zhang
d,
Yonghao
Han
c,
John
Wang
b,
Khuong P.
Ong
e,
Lei
Qin
f,
Yanzhen
Zheng
 f and
Xiaojie
Lou
*a
f and
Xiaojie
Lou
*a
aMulti-disciplinary Materials Research Center (MMRC), Frontier Institute of Science and Technology (FIST), and State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710049, P. R. China. E-mail: ybsyh3@163.com; xlou03@mail.xjtu.edu.cn; Fax: +86-29-83395131; Tel: +86-29-83395141
bDepartment of Materials Science and Engineering, National University of Singapore, 7 Engineering Drive 1, 117574 Singapore, Singapore
cState Key Laboratory of Superhard Materials, Institute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China
dInstitute of Materials, China Academy of Engineering Physics, Chengdu 621907, China
eMaterials Science & Engineering Department, Institute of High Performance Computing, 1 Fusionopolis Way, 138632 Singapore, Singapore
fCentre for Applied Chemical Research (CACR), Frontier Institute of Science and Technology (FIST), Xi'an Jiaotong University, Xi'an 710049, P. R. China
gInstitute for Advanced Materials and Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, South China Normal University, Guangzhou 510006, P. R. China
First published on 15th November 2016
Abstract
[(CH3)2NH2][Mn(HCOO)3], an organic–inorganic perovskite-like hybrid multiferroic, shows promising aspirations for the next generation magnetic storage devices, light-weight chips, optical devices, etc. However, the growth of centimeter-sized large single crystals of [(CH3)2NH2][Mn(HCOO)3] remains a big challenge. Herein, we report a facile, environmentally friendly approach to grow [(CH3)2NH2][Mn(HCOO)3] single crystals whose size could be up to 10 × 9.61 × 3.6 mm, the biggest one ever reported to date. In addition, high-pressure Raman spectra of the material exhibited the existence of three high-pressure polymorphs at 2.1, 4.1, and 6.7 GPa. The high-pressure phase transitions are associated with highly distorted frameworks, and the phase under a pressure larger than 6.7 GPa induces large structural changes in the hydrogen bond-related interactions, which is different from the highly ordered low-temperature monoclinic ferroelectric phase (Cc) observed at ambient pressure. Our studies may shed light on the phase transition mechanisms of the multiferroic metal–organic framework [(CH3)2NH2][Mn(HCOO)3] under high pressures.
1. Introduction
Materials with a perovskite structure are appealing for the scientists and engineers due to their fascinating properties and their potential applications in electronic, optical, and energy storage devices.1–3 Especially, the novel inorganic–organic hybrid perovskite analogues, which possess excellent photovoltaic,4 photoelectronic,5 and ferroelectric/multiferroic properties,6–9 have been proposed as promising substitutes to the traditional all-inorganic perovskite oxides (AIPOs) for advanced next generation applications.10 Inorganic–organic hybrid perovskites with the general formula AMX3, where A = protonated amine, M = divalent metal ion, and X = monovalent anion (halide, formate, etc.), could be divided into hybrid halide perovskites (HHPs) and metal formate frameworks (MFFs) depending on the type of the linker group (X−). Inspired by the pioneering works reported by Wang11 and P. Jain,12,13 MFFs compounds have recently attracted significant interest due to their intriguing properties, such as quasi-one-dimensional antiferromagnetic properties,14 negative linear compressibility (NLC),15 negative thermal expansion (NTE),16,17 and ferroelectric/multiferroic properties,13,18,19 which originate from their enormous crystallography and chemical variety.20As is known to all, the Goldschmidt Tolerance Factor (TF) is a powerful semi-empirical equation21 to guide the study of classical AIPOs (by modulating the effective ionic radii (reff) of A, B, and X components). Accordingly, similar strategies can also be expanded to inorganic–organic hybrid perovskites.22,23 In this case, the structure topology of the MFFs can be changed by varying the size of the protonated amine. The use of mid-sized alkylammonium (rA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eff = 216–280 pm, CH3NH3+, CH3CH2NH3+, NH2NH3+, (CH3)2NH2+, (NH2)2CH+, C3N2H5+, C(NH2)3+, etc.) templates will induce a 412 × 63 topology, where the divalent metal ion (B site) has six adjoining atoms to form an octahedron.24–28 However, a relatively small organic cation, such as NH4+ (rA
eff = 216–280 pm, CH3NH3+, CH3CH2NH3+, NH2NH3+, (CH3)2NH2+, (NH2)2CH+, C3N2H5+, C(NH2)3+, etc.) templates will induce a 412 × 63 topology, where the divalent metal ion (B site) has six adjoining atoms to form an octahedron.24–28 However, a relatively small organic cation, such as NH4+ (rA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eff = 146 pm), leads to a unique chiral hexagonal structure with a 49 × 69 topology.29 Moreover, the divalent metal ions (M2+) that construct the metal-formate frameworks with formate linkers (HCOO−) play an important role in the paraelectric to ferroelectric phase transition temperature (Tt). For instance, the Tt of [(CH3)2NH2][M(HCOO)3] (DMMF) family, a representative inorganic–organic hybrid perovskite, falls in the range from 160 to 185 K (ref. 13) with the transition metal series (M2+ = Zn2+, Mn2+, Fe2+, Co2+, and Ni2+). Tt could drastically increase up to 270 K (near room temperature) by using s-block metal cation (Mg2+),30 which release the low-temperature constraints during device applications. Note that doping with trivalent metal ions in the B site, or A site by using mixed-ammonium, would be another effective approach to tune the properties of the MFFs. Recently, Mączka et al.31 reported that a decrease in the ferroelectric phase transition temperature (Tc) occurs in Cr3+-doped DMMnF small single crystals. Moreover, the intrinsic and strongly first-order feature in pure crystals changes to a partially diffuse one. The Gao group32 found that a decrease in the formate framework distortion with A-site modification can change the para-ferroelectric phase transitions to a more diffused one in [(NH2NH3)x(CH3NH3)1−x][Mn(HCOO)3] (x = 1.00–0.67) solid solutions.
eff = 146 pm), leads to a unique chiral hexagonal structure with a 49 × 69 topology.29 Moreover, the divalent metal ions (M2+) that construct the metal-formate frameworks with formate linkers (HCOO−) play an important role in the paraelectric to ferroelectric phase transition temperature (Tt). For instance, the Tt of [(CH3)2NH2][M(HCOO)3] (DMMF) family, a representative inorganic–organic hybrid perovskite, falls in the range from 160 to 185 K (ref. 13) with the transition metal series (M2+ = Zn2+, Mn2+, Fe2+, Co2+, and Ni2+). Tt could drastically increase up to 270 K (near room temperature) by using s-block metal cation (Mg2+),30 which release the low-temperature constraints during device applications. Note that doping with trivalent metal ions in the B site, or A site by using mixed-ammonium, would be another effective approach to tune the properties of the MFFs. Recently, Mączka et al.31 reported that a decrease in the ferroelectric phase transition temperature (Tc) occurs in Cr3+-doped DMMnF small single crystals. Moreover, the intrinsic and strongly first-order feature in pure crystals changes to a partially diffuse one. The Gao group32 found that a decrease in the formate framework distortion with A-site modification can change the para-ferroelectric phase transitions to a more diffused one in [(NH2NH3)x(CH3NH3)1−x][Mn(HCOO)3] (x = 1.00–0.67) solid solutions.
Note that most of the above mentioned studies focus on the structural or property modification of MFFs. However, large single crystals of MFFs in the centimeter-size, which are crucial for device applications, have never been obtained to date. Moreover, among all these diversified properties, the multiferroic behavior (with M2+ = Mn2+, Fe2+, Co2+, and Ni2+), triggered by the combination of hydrogen-bond ordering and magnetic ordering, would be the most promising aspiration for the new generations magnetic storage devices, light-weight spintronic devices, hybrid four-state logic devices, and magnetoelectric random access memories (MERAMs) devices, etc.33,34 As we all know, electrical measurements are sensitive to the structural imperfections of the samples,35,36 such as inclusions in micro-crystals, grain boundaries in polycrystalline pellets, and defects. These drawbacks of the micro-sized single crystal samples reported in the literature can lead to artifacts and/or accidental results, affecting the discovery of the intrinsic properties of MFFs. However, large-sized single crystals (in centimeter or even larger sizes) are more suitable for the fabrication of practical electronic devices and studying their intrinsic physical properties (such as phase transition). Unfortunately, although considerable attention has been emphasized on the bulk large single crystals of HHPs for the clarification of their intrinsic properties and device applications,37 such as charge carrier lifetimes,38 photoluminescence,39 ferroelectricity,40 photodetectors,41 and solar cells,42 the controllable synthesis of the large-sized (centimeter-scale) single crystals have never been reported in MFFs or their analogues to date.
DMMnF is the first of prototypical multiferroic MFFs that have been discovered.13,43 It exhibits an order–disorder ferroelectric transition (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c to Cc) below 185 K and weak ferromagnetism (T < 8.5 K). Moreover, DMMnF shows the most negative enthalpy of formation (−47.95 ± 1.12 kJ mol−1) in the DMMF multiferroic isostructures, where M2+ = Fe2+, Co2+, Ni2+, and Mn2+.44 Therefore, DMMnF is suggested to be thermodynamically more stable than the others, making it a promising candidate for device applications. In addition, pressure is another important dynamic variable for functional materials.45–47 However, the effect of pressure on the structure modification of multiferroic DMMnF remains unclear. Most recently, Ghosh et al.48 showed that the ferroelectric polarization could be enhanced up to more than three times by applying a compressive strain to the multiferroic frameworks (C(NH2)3Cr(HCOO)3 and (CH3CH2NH3)Mn(HCOO)3) using first-principles density-functional theory (DFT). However, there is no report of the experimentally pressure-induced phase transition of these multiferroic MFFs. Understanding the response of the multiferroic MFFs under an external pressure will provide us profound insights on the structural diversity and spin–phonon coupling mechanisms in these materials.
c to Cc) below 185 K and weak ferromagnetism (T < 8.5 K). Moreover, DMMnF shows the most negative enthalpy of formation (−47.95 ± 1.12 kJ mol−1) in the DMMF multiferroic isostructures, where M2+ = Fe2+, Co2+, Ni2+, and Mn2+.44 Therefore, DMMnF is suggested to be thermodynamically more stable than the others, making it a promising candidate for device applications. In addition, pressure is another important dynamic variable for functional materials.45–47 However, the effect of pressure on the structure modification of multiferroic DMMnF remains unclear. Most recently, Ghosh et al.48 showed that the ferroelectric polarization could be enhanced up to more than three times by applying a compressive strain to the multiferroic frameworks (C(NH2)3Cr(HCOO)3 and (CH3CH2NH3)Mn(HCOO)3) using first-principles density-functional theory (DFT). However, there is no report of the experimentally pressure-induced phase transition of these multiferroic MFFs. Understanding the response of the multiferroic MFFs under an external pressure will provide us profound insights on the structural diversity and spin–phonon coupling mechanisms in these materials.
In this work, by using an innovative slow evaporation method, we have successfully achieved the controllable synthesis of DMMnF from micro-crystals to centimeter-sized large single crystals. We found that the growth of large single crystals is highly restricted during the nucleation stage. The high-pressure Raman scattering technique was used to study the effects of applying an external pressure on the phase transition properties of the DMMnF samples. A non-monoclinic phase transition has been observed and the possible mechanisms behind this are discussed.
2. Experimental
2.1 Sample synthesis
All the starting reagents used in this work were commercially available (Sinopharm Chemical Reagent Co. Ltd, analytical grade) and used without further purification. The whole procedure for the synthesis of DMMnF crystals could be described as follows. First, the precursor solution for crystallization was fabricated by a solvothermal reaction. In a typical synthetic approach, 15 mL of dimethylformamide was added to 15 mL of deionized water with vigorous stirring. Then, 2.5 mmol pale pink MnCl2·4H2O was added into the mixture, providing a transparent solution. After vigorous stirring for 30 min, the solution was subsequently sealed in a Teflon-lined autoclave with a capacity of 50 mL. The hydrolysis reaction was carried out in a Teflon-lined autoclave at 140 °C for 3 days. As the reaction was finished, the temperature-falling program was carried out at a rate of 1 °C min−1 to room temperature to prevent the crystallization of the solute. After the autoclave was removed from the furnace, the supernatant was extracted into a filter flask to subtract any residual impurities.Micro-scale and large-scale single crystals were grown from the precursor solutions by a modified slow evaporation method. The transparent solution was poured into a beaker (50 mL) at ambient temperature. The growth cell (beaker) was covered with a perforated parafilm and kept undisturbed under constant ambient conditions (298 K, 23% RH). After 2 days, transparent micro-crystals with cuboidal shapes were found at the bottom or along the walls of the beaker. The colorless transparent crystals of DMMnF were collected from the mother liquid and quickly rinsed by ethanol, avoiding the formation of Mn(HCOO)2·2H2O. Finally, the fresh micro-crystals were dried under vacuum at 45 °C for 30 min. To grow DMMnF in larger sizes, the plastic vessel (50 mL) was used to conduct a slow evaporation process. The plastic vessel was sealed with a perforated cap and left to crystallize, yielding large single crystals after 11 days in a dark box at 298 K, 23% RH.
2.2 Characterization
The single-crystal X-ray diffraction data of the micro-crystals were obtained by a Bruker Apex II DUO diffractometer equipped with graphite monochromated Mo Kα radiation (λ = 0.71073 Å) at room temperature. The crystal structure was solved by a full-matrix least-squares refinement using the SHELXL-97 software.49 The crystal phase of the products was investigated by powder X-ray diffraction (Smartlab, Rigaku, Japan) using Cu Kα radiation (λ = 1.5418 Å). Optical microscopic images of the single crystal were obtained using an Olympus optical microscope.2.3 Ambient and high-pressure Raman scattering
Room-temperature Raman spectra of a DMMnF single crystal were obtained using a HR LabRam micro-Raman spectrometer (Jobin-Yvon-Horiba, Germany) in backscattering mode with 514![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm excitation.
nm excitation.
High-pressure Raman measurements were carried out in a backscattering geometry with a Princeton Acton SP2500 spectrograph (0.5 m imaging triple grating monochromator, 532 nm solid state laser excitation source). A T301 stainless-steel gasket, pre-indented to 80 μm thickness with a 100 μm hole drilled in the indentation, served as the sample cavity. The powdered DMMnF obtained from grinding was loaded in a diamond-anvil cell (DAC) with chips of ruby. No pressure transmitting medium (PTM) was utilized in the high-pressure experiments because the samples were very sensitive to hydrous or organic PTM due to their solubility. A similar method is commonly used in organic molecule or inorganic–organic hybrid samples due to their softness.50–53 The quasi-hydrostatic conditions were confirmed by a sharp ruby R1 peak, which was used to monitor the experimental pressure.54 All the Raman spectra were obtained at room temperature (298 K, 20% RH) and the integration time for each point was 60 s. Several minutes were allowed for equilibrium to rule out any kinetic factors after the elevation of pressure. The as-obtained scattering spectra were analyzed using Labspec 5 software.
2.4 Density functional calculations
We performed the first-principles calculations with generalized gradient approximation of Perdew, Burke and Ernzerhof (PBE-GGA)55 as implemented in the Vienna ab initio simulation package (VASP), which employs the projected-augmented wave (PAW) method. We used a 2 × 3 × 3 Monkhorst–Pack k-mesh and an energy cutoff of 400 eV for the plane wave expansion. The initial structure of the ferroelectric Cc phase of DMMnF was constructed according to the experimental data.43 We had set a G-type antiferromagnetic ordering for Mn, which was previously demonstrated to be reasonable in an analogous system.56 All the atoms in the structure were relaxed towards equilibrium until the Hellmann–Feynman forces were less than 0.02 eV Å−1. The ferroelectric polarization was estimated by the point charge model.3. Results and discussion
3.1 Crystal growth and characterization
To date, all the reported MFFs crystals were mainly synthesized using solvothermal-slow evaporation,13 a modified one-step solvothermal approach57,58 or a slow-diffusion method.11,59 The size of the as-synthesized crystals in our synthesis ranges from about 100 micrometers to 3 millimeters, as shown in Fig. 1(a). Generally, crystal growth from the solution consists of two essential steps: the nucleation process and the crystal growth process.60 The size of the obtained crystals can be affected by various experimental parameters, among which the number of nucleation sites is the most important parameter. The fewer the number of nucleation sites formed on the substrate (in vessel), the larger the size of the crystals obtained. We performed a multitude of trials to optimize the growth conditions of DMMnF crystals by using a solvothermal-slow evaporation strategy. Note that DMMnF easily crystallizes in a glass vessel, such as a beaker, test tube, or culture dish. Therefore, we selected a plastic vessel as the growth cell to prohibit rapid nucleation. As expected, a pale pink DMMnF single crystal up to 10 × 9.61 × 3.6 mm in size was obtained (see Fig. 1c). The formation of a large single crystal may be attributed to the lower affinity between the solute molecules and the surfaces of the crystallization vessel (plastic). | ||
| Fig. 1 Images of the as-grown DMMnF micro-crystals (a) and the large single crystal (c). Optical images of the micro-crystals (b) and large single crystal (d) on the crystalline {012} surface. | ||
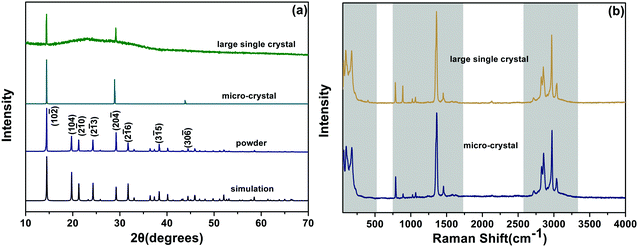
The as-grown DMMnF micro-crystal powder (obtained from grinding), micro-crystal, and large single crystal were characterized by X-ray diffraction (XRD). As shown in Fig. 2(a), the clear sharp peaks of the powder sample could be attributed to the diffraction of (10![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ), (104), (2
), (104), (2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), (2
0), (2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 3), (20
3), (20![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) ), (2
), (2![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 6), (3
6), (3![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 5), and (30
5), and (30![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) ) crystal planes of the trigonal phase DMMnF at room temperature. Moreover, the experimental results are in good agreement with our single crystal simulation patterns, confirming the phase purity of the sample. Comparing the powder XRD observations, a highly preferred {012} orientation of the micro-crystal and large single crystal suggest that DMMnF has an invariable crystallization habit. Fig. 2(b) shows the Raman spectra of the as-grown DMMnF. All of the observed frequencies for the large single crystal are in accordance with those for the micro-crystal, implying high quality of the large single crystal.
) crystal planes of the trigonal phase DMMnF at room temperature. Moreover, the experimental results are in good agreement with our single crystal simulation patterns, confirming the phase purity of the sample. Comparing the powder XRD observations, a highly preferred {012} orientation of the micro-crystal and large single crystal suggest that DMMnF has an invariable crystallization habit. Fig. 2(b) shows the Raman spectra of the as-grown DMMnF. All of the observed frequencies for the large single crystal are in accordance with those for the micro-crystal, implying high quality of the large single crystal.
The growth mechanism of the crystal was strongly reflected by its surface morphology. The slight fluctuation in the supersaturation would result in diverse micro-patterns of the crystal surface. The observed step layers of the grown micro-crystals (Fig. 1a and b) indicate the existence of two dimensional (2D) nucleation mechanisms.62 To create a 2D crystal nucleus, the growth units (DMA+, (HCOO)−, Mn2+) would diffuse to the surface. However, continuous growth is hindered unless substantial kinks are produced, as is depicted by the arrows in Fig. 1(a and b). However, due to the rapid nucleation during the initial stage in the beaker, local supersaturation must be seriously influenced. Accordingly, irregular growth layers are frequently observed on the {012} surfaces of the micro-crystals. However, slower nucleation would induce uniform growth steps in case of plastic growth vessel, as shown in Fig. 1(d).
3.2 DFT calculations of ferroelectric polarization
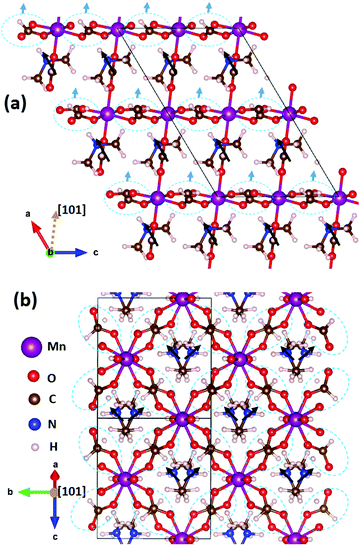
DMMnF undergoes a ferroelectric transition, which has been reported in the previous studies, that is determined by the dielectric property measurements and temperature-dependent vibrational spectroscopy.13,63 The origin of ferroelectricity is due to the ordering of the [(CH3)2NH2]+ cations.64 However, the exact nature of the ferroelectric polarization remains unclear.We have first identified three possible sources of polarization, including the off-center motion of Mn within MnO6 octahedra and the dipole moments of (CH3NH2CH3)+ and (HCOO)−. The off-center motion of Mn is quite weak, in the order of only ∼0.01 Å; therefore, the polarization contribution from the displacement of Mn could be neglected. All the (CH3NH2CH3)+ dipoles are oriented towards the +a-axis (Fig. 3a), whereas those of (CH3NH2CH3)+ dipoles cancel each other along the b-axis (Fig. 3b). The resulting polarization is thus pointing towards the +a-axis and there are no projections along the other directions. The polarization contribution of (CH3NH2CH3)+ was quantified to be (5.08, 0, 0) μC cm−2 (note that the monoclinic coordinate system is used here). The (HCOO)− groups can be further divided into two classes: the first class contains those staying in the apical positions of the MnO6 octahedra along the [101] direction, and the second class contains those staying within the planes perpendicular to the [101] direction, i.e., the equatorial positions of the MnO6 octahedra. The sum of all apical (HCOO)− dipole moments is zero, as it has no projections within the aoc plane (Fig. 3a) nor along the b-axis (the image is not shown here). However, the overall polarization contribution from the equatorial (HCOO)− dipoles is along the [101] direction (Fig. 3a), as all the equatorial (HCOO)− dipole moments cancel each other within the plane perpendicular to the [101] direction. The overall polarization of (HCOO)− can thus be estimated to be (1.30, 0, 0.79) μC cm−2 (the vector is along [101] direction). Therefore, the total polarization, taking into account all three contributions, is summed up to be (6.38, 0, 0.79) μC cm−2.
In this study, the Berry phase method was not used for three reasons. (i) The calculated system was not insulating and did not meet the criteria for using the Berry phase method. The not-insulating-issue was caused by the band gap underestimation of the PBE functional for the systems having strong correlated d-electrons. (ii) Finding a reference centric structure is mandatory for the Berry phase method; however, in this particular system, the A-site cation has three components of CH3, NH2, and CH3, which can show many degrees of freedom and thus, makes it difficult to determine the centric structure. The selection of the centric structure would have been quite arbitrary.56 (iii) The point charge model can considerably give accurate estimations of the polarization values, as reported by Fan et al.65 Therefore, it may not be necessary to use the Berry phase method in this study. During the process of submission of this paper, the polarization component of the A-site cations by the Berry phase method (7.3 μC cm−2) was calculated by a recent work.61 The value is indeed quite close to that reported by us, i.e., (5.08, 0, 0) μC cm−2 for A-site cations, which provides a good support for the results obtained in this study.
3.3 High-pressure Raman scattering of DMMnF
The Raman spectra of DMMnF at high-pressures are shown in Fig. 4. Band positions (in wavenumbers) as a function of pressure are also revealed using the linear equation ω(P) = ω0 + αP to fit the experimental data (see Fig. 5). The detailed parameters, such as the wavenumber intercepts (ω0), pressure coefficients (α), and assignment of the Raman-active modes, are listed in Table S1 (ESI†).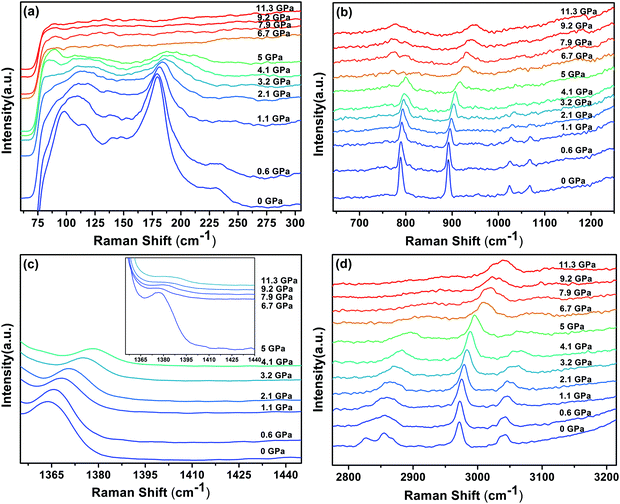 | ||
| Fig. 4 Raman spectra of the DMMnF sample under different pressures, and the inset in (c) is the enlarged spectra (5–11.3 GPa) corresponding to the spectral range 1350–1440 cm−1. | ||
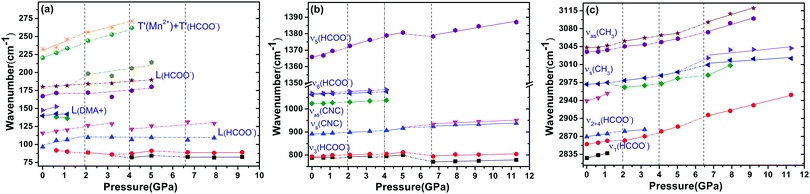 | ||
| Fig. 5 The pressure dependencies of the Raman band positions in DMMnF. Dashed lines serve as visual aids. | ||
When DMMnF was compressed to 1.1 GPa, its Raman spectra was similar to that obtained under ambient pressure, with regular pressure-induced blue shifts in the Raman bands (Fig. 4). However, the band near 105 cm−1 began to weaken at 0.6 GPa, and another weak band appeared at 92 cm−1. When the pressure reached 2.1 GPa, the spectral changes can be summarized as follows: (i) disappearance of the L (DMA+) bands (136 cm−1, 142 cm−1) and weakening of the ν1(HCOO−) band, (ii) a splitting of the 184 cm−1 bands corresponding to the L (HCOO−) vibrational modes, and (iii) a splitting of the νs(CH3) band (Fig. 4 and 5). The observed changes suggest that the phase transition at 2.1 GPa gives rise to a deformed formate framework. In this case, the librational modes of the formate anions were drastically influenced during the compression process; however, the distortion or ordering of the DMA+ skeletons (C–N–C) wasn't observed. The pressure-dependent strong lattice modes indicate that the internal vibrations (HCOO−) are less sensitive to the external compression pressure at 2.1 GPa. In the previous studies, Sánchez-Andújar et al. proposed a large pressure dependence of Tc in DMMnF with ∼46 K GPa−1,66 namely, the pressure-induced ferroelectric transition would be observed at ∼2.4 GPa. As observed in the DFT results, the ferroelectric polarization was mainly attributed to the DMA+ cations pointing towards the +a-axis and the (HCOO)− dipoles along the [101] direction. Thus, the synergistic coordination of DMA+ and the formate frameworks, as well as an increase in the H-bond strength, would result in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c to Cc transitions. As reported in the previous studies,63 the temperature-dependent vibrational spectroscopy revealed that the significant characteristics of the paraelectric to ferroelectric phase transformation (R
c to Cc transitions. As reported in the previous studies,63 the temperature-dependent vibrational spectroscopy revealed that the significant characteristics of the paraelectric to ferroelectric phase transformation (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c to Cc) of DMMnF are obvious splitting of many Raman bands related to the (HCOO)− and DMA+ groups. Therefore, the structure of the high-pressure phase at 2.1 GPa is distinct from the low-temperature ferroelectric phase (Cc). The seemingly conflicting phenomenon may be ascribed to the deformation orientation, hydrogen-bonding energy, and energy barriers.
c to Cc) of DMMnF are obvious splitting of many Raman bands related to the (HCOO)− and DMA+ groups. Therefore, the structure of the high-pressure phase at 2.1 GPa is distinct from the low-temperature ferroelectric phase (Cc). The seemingly conflicting phenomenon may be ascribed to the deformation orientation, hydrogen-bonding energy, and energy barriers.
When the pressure was further increased to 4.1 GPa, clear changes in the Raman spectra could be observed (Fig. 4). First, a weak band at 86 cm−1 splits into doublets with increase in the intensity. Pronounced changes in the librational modes reveal that significant structure modification takes place in DMMnF. A representative broadening in the Raman band occurs at 170–200 cm−1, as shown in Fig. 4(a), indicating the possible multi-phonon coupling in the crystal lattice. The obvious broadening in the Raman librational modes reflects the large instantaneous local instability of the formate frameworks. Second, the bands corresponding to ν6(HCOO−) and νas(CNC) disappear at 4.1 GPa, indicating that such pressure strongly affects the C–H out-of-plane bending and C–N–C antisymmetric stretching. It directly shows that this transition further induces a distortion in the formate frameworks, whereas the DMA+ cations are not largely influenced.
Distinct changes in the high-pressure Raman spectra were found at 6.7 GPa (Fig. 4 and 5). There were several characteristic variations in the pressure coefficient (see Table S1, ESI†), such as the splitting of vibrational modes (νs(CNC), νs(CH3)), the increase in the full width at half maximum (FWHM), and the decrease in the band intensity. The observed pronounced softening of the ν5(HCOO−) and ν3(HCOO−) bands suggest the abrupt lengthening of the C–H and C–O bonds, respectively. Moreover, the obvious weakening in the vibrational modes of the formate ions under high-pressure compression (above 6.7 GPa) may presumably influence the medium-strength N–H⋯O hydrogen bonds between the DMA+ cations and the formate frameworks (increasing the band length of C–H and C–O). As is known, the Raman spectrum is sensitive to changes in the chemical bonding. Splitting of the Raman active modes into multiples (νs(CNC), νs(CH3)) indicates the presence of different crystallographic components in the high-pressure phase. Accordingly, the bands at 3010 cm−1 and 900 cm−1, related to the DMA+ modes, become asymmetric at 6.7 GPa, and all these behaviors indicate the appearance of a high-pressure phase III with distorted hydrogen bonding networks in the cavities. Moreover, the pressure-dependent Raman spectra above 6.7 GPa indicates the disappearance of some bands and the pronounced softening of the ν5(HCOO−) and ν3(HCOO−) bands, which is also different from the temperature-induced monoclinic ferroelectric phase observed at ambient pressure.63 Whether the high pressure phase is also another novel ferroelectric polar-phase will depend on other techniques to clarify, such as synchrotron X-ray powder diffraction or high-pressure SHG measurements.
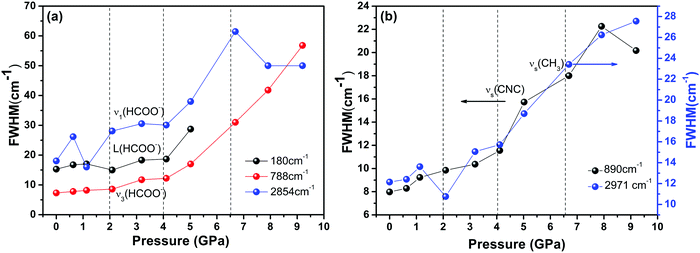
Finally, we found severe changes in the FWHM of some unique internal Raman modes. As shown in Fig. 6, the large variations in the Raman band width under pressures above 4 GPa, along with change in the peak intensity, illustrate that the whole DMMnF framework undergoes a strong tortuosity or distortion. Note that the high-pressure distorted structure remains stable up to 11.3 GPa. In addition, the high-pressure phase could be recovered after releasing the pressure. The mechanism of the reversible transition may be due to the organic cations ((CH3)2NH2+) in the dense frameworks, which will act as rigid centers for the reversible transition.67
4. Conclusions
In summary, we report a modified solvothermal-slow evaporation approach to grow large single crystals of DMMnF (up to 10 × 9.61 × 3.6 mm in size). Herein, the growth substrate is an important factor for the synthesis of large-single crystals of the metal-formate multiferroic frameworks. A similar approach could also be applied for the growth of MFFs films on different substrates. Our findings provide an efficient way for the fabrication of MFFs materials and their analogues.The high-pressure Raman data show that DMMnF undergoes three high-pressure structure transitions near 2.1, 4.1, and 6.7 GPa, respectively. The pressure is expected to induce distortion in the metal-formate anions frameworks, and the phase transition at 6.7 GPa is accompanied with a significant change in the hydrogen-bonding along with a large structural modification in the whole crystal structure. In combination with our DFT calculations, we would suggest that the temperature-induced ferroelectric transition in these materials is mainly triggered by the changes in the synergistic coordination of DMA+ and the formate frameworks. Under high-pressure compression, DMMnF tends to be highly distorted, with complicated subtle structures, which are different from those of the highly ordered low-temperature monoclinic ferroelectric phase.
Acknowledgements
This work are supported by the National Nature Science Foundation of the People's Republic of China (No. 51372195, 41372055), the CSS project (Grant No. YK2015-0602006), the Ministry of Science and Technology of China through a 973-Project (No. 2012CB619401), and the Fundamental Research Funds for the Central Universities (2013JDGZ03). X. J. Lou would like to thank the “One Thousand Youth Talents” program for support.References
- W. Wang, M. O. Tade and Z. P. Shao, Chem. Soc. Rev., 2015, 44, 5371–5408 RSC.
- Z. B. Shen, X. H. Wang, B. C. Luo and L. T. Li, J. Mater. Chem. A, 2015, 3, 18146–18153 RSC.
- I. Grinberg, D. V. West, M. Torres, G. Y. Gou, D. M. Stein, L. Y. Wu, G. N. Chen, E. M. Gallo, A. R. Akbashev, P. K. Davies, J. E. Spanier and A. M. Rappe, Nature, 2013, 503, 509–512 CrossRef CAS PubMed.
- G. C. Xing, N. Mathews, S. Y. Sun, S. S. Lim, Y. M. Lam, M. Gratzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347 CrossRef CAS PubMed.
- J. J. Xie, Y. Liu, J. J. Liu, L. Lei, Q. Q. Gao, J. Q. Li and S. W. Yang, J. Power Sources, 2015, 285, 349–353 CrossRef CAS.
- A. Stroppa, P. Barone, P. Jain, J. M. Perez-Mato and S. Picozzi, Adv. Mater., 2013, 25, 2284–2290 CrossRef CAS PubMed.
- A. O. Polyakov, A. H. Arkenbout, J. Baas, G. R. Blake, A. Meetsma, A. Caretta, P. H. M. van Loosdrecht and T. T. M. Palstra, Chem. Mater., 2012, 24, 133–139 CrossRef CAS.
- H. Y. Ye, Y. Zhang, D. W. Fu and R. G. Xiong, Angew. Chem., Int. Ed., 2014, 53, 11242–11247 CrossRef CAS PubMed.
- W. Q. Liao, Y. Zhang, C. L. Hu, J. G. Mao, H. Y. Ye, P. F. Li, S. P. D. Huang and R. G. Xiong, Nat. Commun., 2015, 6 Search PubMed.
- C. N. R. Rao, A. K. Cheetham and A. Thirumurugan, J. Phys.: Condens. Matter, 2008, 20, 083202 CrossRef.
- Z. M. Wang, B. Zhang, T. Otsuka, K. Inoue, H. Kobayashi and M. Kurmoo, Dalton Trans., 2004, 2209–2216 RSC.
- P. Jain, N. S. Dalal, B. H. Toby, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2008, 130, 10450–10451 CrossRef CAS PubMed.
- P. Jain, V. Ramachandran, R. J. Clark, H. D. Zhou, B. H. Toby, N. S. Dalal, H. W. Kroto and A. K. Cheetham, J. Am. Chem. Soc., 2009, 131, 13625–13627 CrossRef CAS PubMed.
- Z. X. Wang, P. Jain, K. Y. Choi, J. van Tol, A. K. Cheetham, H. W. Kroto, H. J. Koo, H. Zhou, J. M. Hwang, E. S. Choi, M. H. Whangbo and N. S. Dalal, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224406 CrossRef.
- W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. K. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943 CrossRef CAS PubMed.
- R. Shang, G. C. Xu, Z. M. Wang and S. Gao, Chem. – Eur. J., 2014, 20, 1146–1158 CrossRef CAS PubMed.
- S. Chen, R. Shang, K. L. Hu, Z. M. Wang and S. Gao, Inorg. Chem. Front., 2014, 1, 83–98 RSC.
- G. C. Xu, X. M. Ma, L. Zhang, Z. M. Wang and S. Gao, J. Am. Chem. Soc., 2010, 132, 9588–9590 CrossRef CAS PubMed.
- N. Abhyankar, S. Bertaina and N. S. Dalal, J. Phys. Chem. C, 2015, 119, 28143–28147 CrossRef CAS.
- W. Zhang and R. G. Xiong, Chem. Rev., 2012, 112, 1163–1195 CrossRef CAS PubMed.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- G. Kieslich, S. J. Sun and A. K. Cheetham, Chem. Sci., 2014, 5, 4712–4715 RSC.
- G. Kieslich, S. J. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- R. Shang, X. Sun, Z. M. Wang and S. Gao, Chem. – Asian J., 2012, 7, 1697–1707 CrossRef CAS PubMed.
- R. Shang, S. Chen, B. W. Wang, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2016, 55, 2097–2100 CrossRef CAS PubMed.
- M. Mączka, A. Ciupa, A. Gągor, A. Sieradzki, A. Pikul, B. Macalik and M. Drozd, Inorg. Chem., 2014, 53, 5260–5268 CrossRef PubMed.
- F. F. Wang, C. Chen, Y. Zhang, H. Y. Ye, Q. Ye and D. W. Fu, J. Mater. Chem. C, 2015, 3, 6350–6358 RSC.
- K. L. Hu, M. Kurmoo, Z. M. Wang and S. Gao, Chem. – Eur. J., 2009, 15, 12050–12064 CrossRef CAS PubMed.
- Z. M. Wang, B. Zhang, K. Inoue, H. Fujiwara, T. Otsuka, H. Kobayashi and M. Kurmoo, Inorg. Chem., 2007, 46, 437–445 CrossRef CAS PubMed.
- B. Pato-Doldán, M. Sánchez-Andújar, L. C. Gómez-Aguirre, S. Yáñez-Vilar, J. López-Beceiro, C. Gracia-Fernández, A. A. Haghighirad, F. Ritter, S. Castro-García and M. A. Señarís-Rodríguez, Phys. Chem. Chem. Phys., 2012, 14, 8498–8501 RSC.
- M. Mączka, A. Sieradzki, B. Bondzior, P. Dereń, J. Hanuza and K. Hermanowicza, J. Mater. Chem. C, 2015, 3, 9337–9345 RSC.
- S. Chen, R. Shang, B. W. Wang, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2015, 54, 11093–11096 CrossRef CAS PubMed.
- C. M. Chang, B. K. Mani, S. Lisenkov and I. Ponomareva, Phys. Rev. Lett., 2015, 114, 177205 CrossRef PubMed.
- A. K. Cheetham and C. N. R. Rao, Science, 2007, 318, 58–59 CrossRef CAS PubMed.
- D. Lebeugle, D. Colson, A. Forget and M. Viret, Appl. Phys. Lett., 2007, 91, 022907 CrossRef.
- H. Fukumura, S. Matsui, H. Harima, T. Takahashi, T. Itoh, K. Kisoda, M. Tamada, Y. Noguchi and M. Miyayama, J. Phys.: Condens. Matter, 2007, 19, 365224 CrossRef CAS PubMed.
- Y. Y. Dang, D. X. Ju, L. Wang and X. T. Tao, Crystengcomm, 2016, 18, 4476–4484 RSC.
- Y. Bi, E. M. Hutter, Y. J. Fang, Q. F. Dong, J. S. Huang and T. J. Savenije, J. Phys. Chem. Lett., 2016, 7, 923–928 CrossRef CAS PubMed.
- Q. F. Dong, Y. J. Fang, Y. C. Shao, P. Mulligan, J. Qiu, L. Cao and J. S. Huang, Science, 2015, 347, 967–970 CrossRef CAS PubMed.
- P. J. Zhao, J. B. Xu, X. Y. Dong, L. Wang, W. Ren, L. Bian and A. M. Chang, J. Phys. Chem. Lett., 2015, 6, 2622–2628 CrossRef CAS PubMed.
- G. Maculan, A. D. Sheikh, A. L. Abdelhady, M. I. Saidaminov, M. A. Hague, B. Murali, E. Alarousu, O. F. Mohammed, T. Wu and O. M. Bakr, J. Phys. Chem. Lett., 2015, 6, 3781–3786 CrossRef CAS PubMed.
- D. Shi, V. Adinolfi, R. Comin, M. J. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522 CrossRef CAS PubMed.
- M. Sánchez-Andújar, S. Presedo, S. Yáñez-Vilar, S. Castro-García, J. Shamir and M. A. Señarís-Rodríguez, Inorg. Chem., 2010, 49, 1510–1516 CrossRef PubMed.
- G. P. Nagabhushana, R. Shivaramaiah and A. Navrotsky, J. Am. Chem. Soc., 2015, 137, 10351–10356 CrossRef CAS PubMed.
- M. Mączka, T. A. da Silva, W. Paraguassu, M. Ptak and K. Hermanowicz, Inorg. Chem., 2014, 53, 12650–12657 CrossRef PubMed.
- M. Mączka, P. Kadłubański, P. T. C. Freire, B. Macalik, W. Paraguassu, K. Hermanowicz and J. Hanuza, Inorg. Chem., 2014, 53, 9615–9624 CrossRef PubMed.
- L. C. Gómez-Aguirre, B. Pato-Doldán, A. Stroppa, S. Yanez-Vilar, L. Bayarjargal, B. Winkler, S. Castro-García, J. Mira, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, Inorg. Chem., 2015, 54, 2109–2116 CrossRef PubMed.
- S. Ghosh, D. Di Sante and A. Stroppa, J. Phys. Chem. Lett., 2015, 6, 4553–4559 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- S. R. Li, K. Wang, M. Zhou, Q. Li, B. B. Liu, G. T. Zou and B. Zou, J. Phys. Chem. B, 2011, 115, 8981–8988 CrossRef CAS PubMed.
- R. Rao, T. Sakuntala, A. K. Arora and S. K. Deb, J. Chem. Phys., 2004, 121, 7320–7325 CrossRef CAS PubMed.
- L. Kang, K. Wang, X. D. Li and B. Zou, J. Phys. Chem. C, 2016, 120, 14758–14766 CrossRef CAS.
- Y. H. Wang, X. J. Lu, W. G. Yang, T. Wen, L. X. Yang, X. T. Ren, L. Wang, Z. S. Lin and Y. S. Zhao, J. Am. Chem. Soc., 2015, 137, 11144–11149 CrossRef CAS PubMed.
- H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res.: Solid Earth, 1986, 91, 4673–4676 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Di Sante, A. Stroppa, P. Jain and S. Picozzi, J. Am. Chem. Soc., 2013, 135, 18126–18130 CrossRef CAS PubMed.
- T. Asaji and K. Ashitomi, J. Phys. Chem. C, 2013, 117, 10185–10190 CrossRef CAS.
- J. López-Beceiro, C. Gracia-Fernández, S. Gomez-Barreiro, S. Castro-García, M. Sánchez-Andújar and R. Artiaga, J. Phys. Chem. C, 2012, 116, 1219–1224 CrossRef.
- M. Simenas, A. Ciupa, M. Maczka, A. Poppl and J. Banys, J. Phys. Chem. C, 2015, 119, 24522–24528 CrossRef CAS.
- I. Weissbuch, R. Popovitzbiro, M. Lahav and L. Leiserowitz, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 115–148 CrossRef.
- P. Jain, A. Stroppa, D. Nabok, A. Marino, A. Rubano, D. Paparo, M. Matsubara, H. Nakotte, M. Fiebig and S. Picozzi, npj Quantum Materials, 2016, 1, 16012 CrossRef.
- R. Boistelle and J. P. Astier, J. Cryst. Growth, 1988, 90, 14–30 CrossRef CAS.
- M. Mączka, A. Gągor, B. Macalik, A. Pikul, M. Ptak and J. Hanuza, Inorg. Chem., 2014, 53, 457–467 CrossRef PubMed.
- D. W. Fu, W. Zhang, H. L. Cai, Y. Zhang, J. Z. Ge, R. G. Xiong, S. D. Huang and T. Nakamura, Angew. Chem., Int. Ed., 2011, 50, 11947–11951 CrossRef CAS PubMed.
- Z. Fan, J. X. Xiao, K. Sun, L. Chen, Y. T. Hu, J. Y. Ouyang, K. P. Ong, K. Y. Zeng and J. Wang, J. Phys. Chem. Lett., 2015, 6, 1155–1161 CrossRef CAS PubMed.
- M. Sánchez-Andújar, L. C. Gómez-Aguirre, B. P. Doldán, S. Yáñez-Vilar, R. Artiaga, A. L. Llamas-Saiz, R. S. Manna, F. Schnelle, M. Lang, F. Ritter, A. A. Haghighirad and M. A. Señarís-Rodríguez, Crystengcomm, 2014, 16, 3558–3566 RSC.
- J. S. Tse, D. D. Klug, J. A. Ripmeester, S. Desgreniers and K. Lagarec, Nature, 1994, 369, 724–727 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1. The wavenumber intercepts at zero pressure (ω0) and pressure coefficients (α) obtained from the linear fitting of the Raman data. See DOI: 10.1039/c6nj02798a |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2017 |