Macroscopic and tunable nanoparticle superlattices†
Honghu
Zhang
a,
Wenjie
Wang
b,
Surya
Mallapragada
c,
Alex
Travesset
d and
David
Vaknin
*d
aAmes Laboratory and Department of Materials Science and Engineering, Iowa State University, Ames, Iowa 50011, USA
bDivision of Materials Sciences and Engineering, Ames Laboratory, U.S. DOE, Ames, Iowa 50011, USA
cAmes Laboratory and Department of Chemical and Biological Engineering, Iowa State University, Ames, Iowa 50011, USA
dAmes Laboratory and Department of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA. E-mail: vaknin@ameslab; Tel: +(515) 294-6023
First published on 24th October 2016
Abstract
We describe a robust method to assemble nanoparticles into highly ordered superlattices by inducing aqueous phase separation of neutral capping polymers. Here we demonstrate the approach with thiolated polyethylene-glycol-functionalized gold nanoparticles (PEG-AuNPs) in the presence of salts (for example, K2CO3) in solutions that spontaneously migrate to the liquid–vapor interface to form a Gibbs monolayer. We show that by increasing salt concentration, PEG-AuNP monolayers transform from two-dimensional (2D) gas-like to liquid-like phase and eventually, beyond a threshold concentration, to a highly ordered hexagonal structure, as characterized by surface sensitive synchrotron X-ray reflectivity and grazing incidence X-ray diffraction. Furthermore, the method allows control of the inplane packing in the crystalline phase by varying the K2CO3 and PEG-AuNPs concentrations and the length of PEG. Using polymer-brush theory, we argue that the assembly and crystallization is driven by the need to reduce surface tension between PEG and the salt solution. Our approach of taking advantage of the phase separation of PEG in salt solutions is general (i.e., can be used with any nanoparticles) leads to high-quality macroscopic and tunable crystals. Finally, we discuss how the method can also be applied to the design of orderly 3D structures.
1. Introduction
Self-assembly of nanoparticles and molecular-scale building blocks into hierarchically designed ordered structures provides a promising route for the production of metamaterials and nanodevices through bottom-up approaches.1–6 Particularly, chemically stable gold nanoparticles (AuNPs) that seem to possess desirable optical and electrical properties have been assembled into three-dimensional (3D) ordered structures by use of complementary single-stranded DNA or DNA origami with unique programmable features.4–8 Concomitantly, two-dimensional (2D) self-assembly of AuNPs at solid– or vapor–liquid interfaces have also been developed,9–11 providing valuable understanding of general mechanisms involved in self-assembly that can be readily applied in other dimensions. Employing a self- and guided-assembly approach, it has been shown that capped AuNPs, AgNPs, or magnetite with various surfactants (including thiolated-acyl chains, -PEG, and others) can be manipulated in a Langmuir trough to form ordered 2D domains, which can be transferred to solid support by the Langmuir–Blodgett technique for further applications.12–21 Recently, it has been shown that unpaired thiolated ssDNA functionalized AuNPs (ssDNA-AuNPs) self-assemble and crystallize at gas–solution interfaces spontaneously simply by tuning various salts concentrations.22–24 These studies established that the complexed ssDNA-AuNP is amphiphilic in character by virtue of the polyelectrolytic nature of DNA that competes with the hydrophobicity that is inadvertently introduced in the thiolating process of DNA.24 Another approach to 2D assembly exploits electrostatic interactions between a positively charged template formed by a Langmuir monolayer and the negatively charged ssDNA-AuNPs or even unfunctionalized (bare) AuNPs.25–27 These studies point to the possibility that the functionalizing DNA can be replaced by macromolecules that display intrinsic amphiphilic character. Thus, inspired by our findings,24 we have embarked on a robust approach to explore the interfacial and 3D self-assembly of gold nanoparticles by functionalizing them with polyelectrolytes and amphiphilic polymers. Here, we report on the properties and self-assembly of polyethylene-glycol (PEG)-functionalized AuNPs (PEG-AuNPs). PEG is a remarkable linear polymer that resides on the hydrophobic/hydrophilic edge where one or the other (hydrophobic or hydrophilic) can be readily tweaked by varying salts concentrations, pH, and temperature.28,29 These properties of PEG mixed with dextran or salts have been widely used in the separation and extraction of macromolecules and organelles of cells by the so-called aqueous biphasic systems technique (ABS).30–32 Owing to PEG's biocompatibility and the low cytotoxicity of Au, studies of PEG-AuNPs have been focused towards nanomedicine applications.33–35 In this study, grazing incidence small-angle X-ray scattering (GISAXS) and X-ray reflectivity (XRR) are used to determine the in-plane structure and surface-normal density profile, respectively, of self-assembled PEG-AuNPs at the vapor–liquid interface by manipulating the concentration of a specific salt, K2CO3 that has been efficiently used in ABS.30,31 The evolution of 2D PEG-AuNP superlattice formation is systematically studied with two kinds of PEG (molecular weight of 6000 and 800 Da) by manipulating K2CO3 and PEG-AuNP concentrations.2. Experimental
2.1. Reagents and materials
Poly(ethylene glycol) methyl ether thiol (PEG-SH; Sigma-Aldrich) with average molecular weight of 800 and 6000 g mol−1 (the number of monomers Nr = 18 and 136, respectively; Kuhn length b = 7.24 Å; see the ESI†) was dissolved in degassed Millipore water with slight sonication. The freshly-prepared PEG-SH solution was added to aqueous suspension of citrate-stabilized gold nanoparticles (AuNPs, with nominal size of 10 nm; Ted Pella) in large excess (molar ratio of PEG-SH/AuNP ≈ 6000) under vigorous stirring. The mixture of PEG-SH and AuNPs was gently stirred at room temperature for one day to allow for maximum PEG loading after ligand exchange. The as-prepared PEG-AuNPs were concentrated via centrifugation (at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g × 1 h). The supernatant was discarded and the precipitate was collected and redispersed in Millipore water. This washing process with centrifugation and redispersion was done at least twice prior to further measurements. The concentration of PEG-AuNPs was determined by UV-Visible absorption measurements. Aqueous solution of potassium carbonate (anhydrous, K2CO3; Fisher Scientific) was prepared and mixed with PEG-AuNPs suspensions at desired concentrations of K2CO3 (0.05–1000 mM) and PEG-AuNPs (0.05–10 nM) prior to X-ray measurements. We note that PEG-AuNPs form visible precipitates at 1 M K2CO3 after overnight incubation, while they are stable as suspension for months at low K2CO3 concentrations.
000g × 1 h). The supernatant was discarded and the precipitate was collected and redispersed in Millipore water. This washing process with centrifugation and redispersion was done at least twice prior to further measurements. The concentration of PEG-AuNPs was determined by UV-Visible absorption measurements. Aqueous solution of potassium carbonate (anhydrous, K2CO3; Fisher Scientific) was prepared and mixed with PEG-AuNPs suspensions at desired concentrations of K2CO3 (0.05–1000 mM) and PEG-AuNPs (0.05–10 nM) prior to X-ray measurements. We note that PEG-AuNPs form visible precipitates at 1 M K2CO3 after overnight incubation, while they are stable as suspension for months at low K2CO3 concentrations.
2.2. Experimental setup
Specular X-ray reflectivity (XRR) and grazing incidence small-angle X-ray scattering (GISAXS) measurements were conducted on the liquid surface spectrometer (LSS) at beamline 9ID-B, Advanced Photon Source (APS), Argonne National Laboratory. The aqueous solution of the PEG-AuNPs in absence and presence of K2CO3 was contained in a shallow trough (surface area 6 × 6 cm2 and enclosed in gas tight canister) where the aqueous surface was illuminated with a highly collimated and monochromatic X-ray beam (photon energy E = 8.0 keV and wavelength λ = 1.5497 Å). For an XRR measurement, a point detector (Bicron) that moves within the scattering plane, was used to collect the X-ray reflection from the surface at the exit angle (with respect to the surface) αf in such way that αf = αi, αi being the X-ray incident angle with respect to the surface. The reflectivity, R, is measured as a function of Qz that equals (4π/λ) sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αi and is the z-component (along the surface normal) of the moment transfer Q. The trough was allowed to move laterally to provide fresh portions of the surface in the course of the reflectivity measurement. For a GISAXS measurement, a digital, two-dimensional Pilatus 100K detector (487 × 195 pixels, 172 × 172 μm per pixel) was placed downstream from the sample and was calibrated with the standard calibrating material, i.e., silver behenate powder. The GISAXS intensity was obtained as a function of the three orthogonal components denoted as (Qx, Qy, Qz), where Qz component is along the surface normal, while Qx and Qy components are parallel to the liquid surface. In this study, Qy is defined as parallel to the detector surface while Qx ≈ 0. Thus, the magnitude of the in-plane scattering vector, Qxy, defined as
αi and is the z-component (along the surface normal) of the moment transfer Q. The trough was allowed to move laterally to provide fresh portions of the surface in the course of the reflectivity measurement. For a GISAXS measurement, a digital, two-dimensional Pilatus 100K detector (487 × 195 pixels, 172 × 172 μm per pixel) was placed downstream from the sample and was calibrated with the standard calibrating material, i.e., silver behenate powder. The GISAXS intensity was obtained as a function of the three orthogonal components denoted as (Qx, Qy, Qz), where Qz component is along the surface normal, while Qx and Qy components are parallel to the liquid surface. In this study, Qy is defined as parallel to the detector surface while Qx ≈ 0. Thus, the magnitude of the in-plane scattering vector, Qxy, defined as 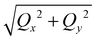 , is practically equivalent to Qy. In the small angle regime, Qy ≈ (4π/λ)θ, 2θ being the in-plane scattering angle. The X-ray exposure time and incident beam attenuation are carefully chosen in such way that each GISAXS frame has a good signal to noise ratio and sample radiation damage is minimal. The trough was sealed in a canister that has Kapton windows for X-ray passage. It was purged with water-saturated helium in the course of the X-ray measurements to minimize the background scattering and radiation damage. More experimental details can be found elsewhere.36 Solution small-angle X-ray scattering (SAXS) experiments for determining the size of the nanoparticles in suspension were performed at beamline 12ID-B at APS with similar setups employed for biomolecules before.27,37
, is practically equivalent to Qy. In the small angle regime, Qy ≈ (4π/λ)θ, 2θ being the in-plane scattering angle. The X-ray exposure time and incident beam attenuation are carefully chosen in such way that each GISAXS frame has a good signal to noise ratio and sample radiation damage is minimal. The trough was sealed in a canister that has Kapton windows for X-ray passage. It was purged with water-saturated helium in the course of the X-ray measurements to minimize the background scattering and radiation damage. More experimental details can be found elsewhere.36 Solution small-angle X-ray scattering (SAXS) experiments for determining the size of the nanoparticles in suspension were performed at beamline 12ID-B at APS with similar setups employed for biomolecules before.27,37
3. Results and discussion
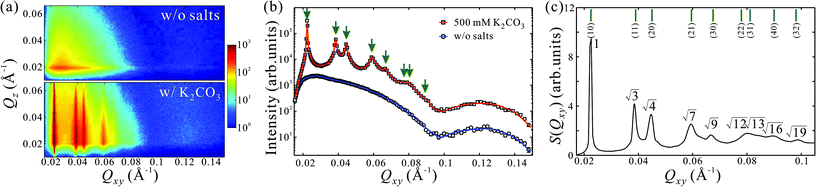
GISAXS patterns as functions of Qxy and Qz for aqueous solutions of PEG6k-AuNPs without salts and with 500 mM K2CO3 are shown in Fig. 1a. In the absence of salts, sector-shaped and broad circular features at low and high Qxy ranges originate from the form factor of PEG6k-AuNPs, which is dominated by the bare form factor of AuNPs (see ESI†).24,27 This indicates that PEG6k-AuNPs spontaneously accumulate at the interface without any salts in solutions albeit dispersed at low coverage. As shown in Fig. S1,† the corresponding GISAXS pattern of unfunctionalized (bare) AuNPs without PEG does not show any features associated with the form factor. Although GISAXS patterns from aqueous solutions of pure PEG6k without or with salts do not show any features different from water surface in the current Qxy window (Fig. S1†), PEG itself has been reported to form Gibbs monolayers at the air–water interface.28,29,38–40 Clearly, PEG drives the functionalized PEG6k-AuNPs to the gas–water interface. However, as the GISAXS pattern shows, the particles are not correlated. By contrast, in the presence of 500 mM K2CO3, up to 5 sharp Bragg rods become apparent, evidencing the formation of a long-range ordered crystalline layer of PEG6k-AuNPs at the interface. Fig. 1b shows horizontal linecut profiles along Qxy direction (at Qz = 0.020 Å−1) from the GISAXS patterns in Fig. 1a. The linecut profile from PEG6k-AuNPs mixed with 500 mM K2CO3 represents a combination of both form factor (see SAXS data from bulk solution in Fig. S2†) and structure factor.24,27 The extracted structure factor at the low Qxy range (0.02–0.1 Å−1) is plotted in Fig. 1c. The diffraction peak-positions ratios with respect to the fundamental peak (Q1 = 0.0225 Å−1) satisfy Qi/Q1 ≈ 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √3
√3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √4
√4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √7
√7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) √9… (i = 1–9) revealing the formation of a long-range ordered 2D hexagonal superlattice of AuNPs with an inter-particle distance of aL = 4π/(√3Q1) = 322 Å, where the corresponding diffraction peaks are indexed as (10), (11), (20), (21), (30) and higher-order Bragg reflections. This demonstrates that K2CO3 plays a crucial role in promoting interfacial self-assembly and crystallization of PEG6k-AuNPs. Recently, single-stranded DNA functionalized AuNPs (ssDNA-AuNPs) have been found to form a Gibbs monolayer and crystallize as hexagonal superlattices at the vapor–liquid interface.22–24 Here, the PEG6k-AuNP/K2CO3 exhibits much higher crystalline quality exemplified by nine Bragg reflections. Below, we describe the evolution of PEG6k-AuNP superlattices systematically by regulating K2CO3 or PEG-AuNP concentrations.
√9… (i = 1–9) revealing the formation of a long-range ordered 2D hexagonal superlattice of AuNPs with an inter-particle distance of aL = 4π/(√3Q1) = 322 Å, where the corresponding diffraction peaks are indexed as (10), (11), (20), (21), (30) and higher-order Bragg reflections. This demonstrates that K2CO3 plays a crucial role in promoting interfacial self-assembly and crystallization of PEG6k-AuNPs. Recently, single-stranded DNA functionalized AuNPs (ssDNA-AuNPs) have been found to form a Gibbs monolayer and crystallize as hexagonal superlattices at the vapor–liquid interface.22–24 Here, the PEG6k-AuNP/K2CO3 exhibits much higher crystalline quality exemplified by nine Bragg reflections. Below, we describe the evolution of PEG6k-AuNP superlattices systematically by regulating K2CO3 or PEG-AuNP concentrations.
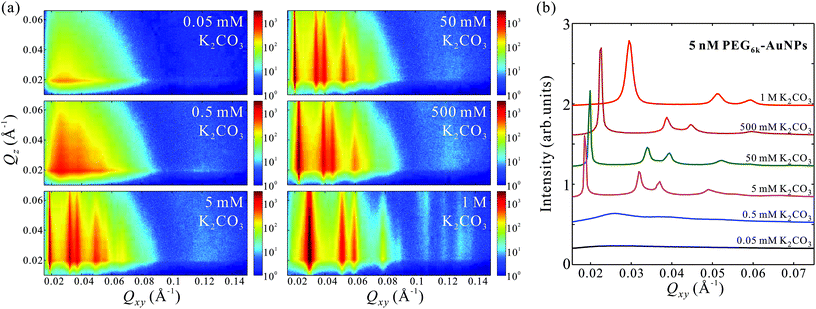
The GISAXS patterns in Fig. 2a for aqueous solutions of 5 nM PEG6k-AuNPs mixed in varying amounts of K2CO3 in the range of 0.05 mM–1 M indicate an in-plane structural transformations from uncorrelated to short-range ordering, and eventually to long-range hexagonal order at threshold concentration of about 5 mM K2CO3. Furthermore, the linecut profiles in Fig. 2b show that the hexagonal inter-particle distance decreases with the increase of salt concentration, as evidenced by gradual peaks-positions shift to higher Qxy values. This demonstrates that K2CO3 is capable of tuning the 2D hexagonal superlattice at the vapor–liquid interface such that the lattice constant aL takes values in the range aL = 245–388 Å under the current tested conditions (see more details in Table 1). For concentrations 5–500 mM K2CO3, the diffraction peaks are extremely sharp with a peak full width at half maximum (FWHM) of the (10) reflection (FWHM(10) ≈ 0.0003–0.0006 Å−1) that is comparable to the instrumental resolution (≈0.0003 Å−1), suggesting that the estimated crystalline size is on the micrometer scale, significantly larger than that found in 2D superlattices formed by ssDNA-AuNPs.22,24 At the highest K2CO3 concentration (1 M) the FWHM(10) ≈ 0.0019 Å−1 with a 2D crystalline size on the order of 3.4 × 103 Å, which is still superior than that found in ssDNA-AuNPs superlattices.22,24 This trend suggests that higher K2CO3 concentrations, while promoting the formation of denser packing of AuNPs, induce defects in the superlattices and tend to decrease the crystalline size (Table 1).
| [PEG6k-AuNPs] (nM) | [K2CO3] (mM) | Q 1 (Å−1) | Lattice constant, aL (Å) | FWHM (Å−1) | Estimated crystalline size (Å) |
|---|---|---|---|---|---|
| 5 | 5 | 0.0187 | 388 ± 4 | ∼0.0003 | 2.1 × 104 |
| 5 | 50 | 0.0198 | 366 ± 5 | ∼0.0004 | 1.5 × 104 |
| 5 | 500 | 0.0225 | 322 ± 3 | ∼0.0006 | 1.0 × 104 |
| 5 | 1000 | 0.0296 | 245 ± 2 | ∼0.0019 | 3.4 × 103 |
| 2.5 | 500 | 0.0215 | 338 ± 4 | ∼0.0007 | 8.4 × 103 |
| 5 | 500 | 0.0225 | 322 ± 3 | ∼0.0006 | 1.0 × 104 |
| 10 | 500 | 0.0235 | 309 ± 3 | ∼0.0004 | 1.7 × 104 |
In addition to its dependence on K2CO3 concentration, the self-assembly depends on the PEG6k-AuNP concentration, as shown in Fig. S3† at a fixed K2CO3 500 mM at various concentrations of PEG6k-AuNPs (0.05–10 nM). The GISAXS patterns as well as the corresponding linecut profiles in Fig. S3b† show that short-range hexagonal order emerges at 0.25–0.5 nM PEG6k-AuNPs, and at higher concentrations long-range order of micrometer size 2D crystallines sets in with aL = 338 ± 4 Å and aL = 309 ± 3 Å at 2.5 and 10 nM, respectively (see Table 1). Qualitatively, the effect of nanoparticle concentration on monolayer density and compressibility can be understood via generalized Gibbs adsorption. Increasing the nanoparticle concentration in the bulk leads to an increase of nanoparticle surface density and the corresponding increase of surface pressure, originating from the entropy and inter-particle interaction, similar to the soft crystallization of ssDNA-AuNPs.8
AuNPs functionalized with a shorter chain PEG (MW = 800 Da) show similar 2D superlattices under similar conditions to those used for PEG6k-AuNPs discussed above. GISAXS patterns in Fig. S4† show the evolution of the self-assembly and crystallization of a fixed concentration PEG800-AuNPs and varying the amount of K2CO3 in solution, and Fig. S5† shows the development at a fixed 500 mM K2CO3 for various PEG800-AuNPs concentrations. Compared to PEG6k-AuNPs, the diffractions peaks of PEG800-AuNPs shift to larger Qxy values, evidence for closer packing as expected for a shorter and smaller hydrodynamic radius of PEG800-AuNPs (see Fig. S7†). We note that crystallization of PEG800-AuNPs is observed only for high concentrations of K2CO3 and PEG-AuNPs, i.e., aL = 149 ± 1 Å at 1 M K2CO3 and 5 nM PEG800-AuNPs, and aL = 158 ± 3 Å at 500 mM K2CO3 and 10 nM PEG800-AuNPs.
To determine the density profile of the crystalline film across the interface we employ X-ray reflectivity, which provides the electron density (ED) profile, ρ, as function of depth (along z-axis, i.e., the surface normal) by refining a model that fits the reflectivity data through the Prarratt's recursive method.36,41,42
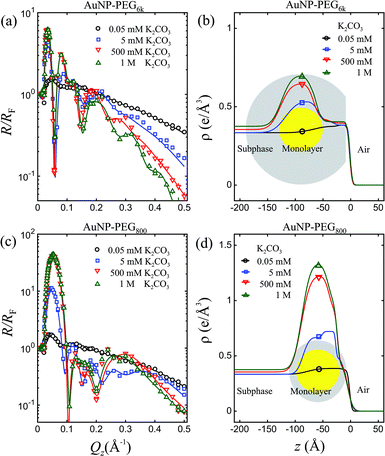
Fig. 3 shows X-ray reflectivity normalized to that of ideally flat water, R/RF, for PEG6k-AuNPs and PEG800-AuNPs at 5 nM in the presence of different amounts of K2CO3 in the aqueous subphase as indicated (these are the same samples on which the GISAXS described above have been performed). The dramatic increase of the first maximum in R/RF with the concentration of K2CO3, as shown in both (a) and (c) signals a huge accumulation of capped-AuNPs at the interface. Quantitative analysis of the R/RF, based on the effective-density model,43 yields the corresponding ED profiles shown in (b) and (d) with an enhancement region over that of the solution on a ∼100 Å length scale, very close to the diameter of AuNPs (D = 88 ± 9 Å, see Fig. S2†). The ED of densely packed PEG as well as water-saturated-PEG is very close to that of the water subphase, therefore yielding only a small increase in the ED of the submerged polymer tails, whereas at the air/particle interface, a ∼50 Å strata can be associated with densely-packed PEG, as depicted in Fig. 4. This practically indicates that the films that are formed at the surface consist of a mono-particle layer, and combination of the GISAXS and R/RF results allows determination of surface coverage and conformation of the particles as discussed below. We note that the maximum R/RF for PEG800-AuNPs film are much higher than PEG6k-AuNPs under otherwise identical conditions (i.e., concentrations of AuNPs and K2CO3). This higher surface density compared to PEG6k-AuNPs is consistent with the corresponding difference in lattice parameters of the two capped-AuNPs. Based on the measured lattice parameters obtained by GISAXS, the ED of a thin slab of 2D crystalline and using a simple space filling model (see details in ESI†), we estimate the surface coverage of pure 2D hexagonal superlattice is nearly 100%. The observation of limited lattice constant tunability for the shorter PEG indicates that the relatively more rigid PEG800-AuNPs remain in the liquid state (short range order) over a wider range of salt concentrations compared to the softer PEG6k-AuNPs.
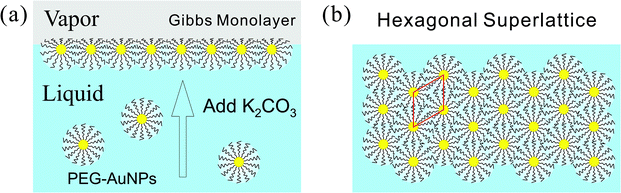 | ||
| Fig. 4 A schematic of 2D self-assembly and crystallization of PEG-AuNPs at liquid–vapor interface induced by K2CO3 (a) side view and (b) top view. | ||
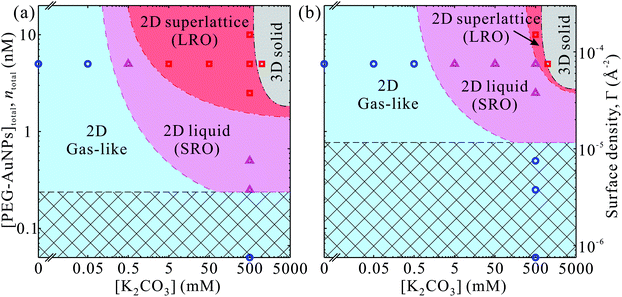
Our main results are summarized in phase-diagrams of PEG-AuNPs versus K2CO3 concentrations as shown in Fig. 5 for both polymers. At low K2CO3 and PEG-AuNPs concentrations, the accumulated particles at the interface lack any order forming a gas-like phase. In the intermediate concentrations of K2CO3 and PEG-AuNPs, more PEG-AuNPs adsorb at the interface and promote formation of liquid-like state of short-range hexagonal order. At threshold concentrations of K2CO3 and PEG-AuNPs, a long-range order phase of 2D hexagonal superlattices is established with total surface coverage (nearly 100%). At concentrations ≥1 M K2CO3 the PEG-AuNPs precipitate most likely in simple 3D structure (fcc, for instance). The phase diagram of PEG6k-AuNPs shows that the lattice constant can be tuned by both K2CO3 and PEG-AuNP concentrations without loss of materials due to precipitation. By contrast, in the phase diagram of PEG800-AuNPs, the phase boundaries between the three 2D phases shift to higher K2CO3 and PEG-AuNP concentrations, and thus the superlattice region without precipitation is suppressed. This indicates that the tunability in lattice constant PEG6k-AuNPs is due to the compressibility of the corona from the longer chain PEG as shown schematically in Fig. 4. We argue that the tunability of the lattice constant of the PEG6k-AuNP supercrystals is different from that in ssDNA-AuNP superlattices.23,24 The ssDNA chains behave as polyelectrolytes such that the added salts screen charges of phosphate groups on the ssDNA backbones and cause the shrinkage of ssDNA chains as have been observed in X-ray scattering and dynamic lighting scattering (DLS) measurements accounting for lattice constant changes as a function of salt concentrations.24 By contrast, while PEG-AuNPs show K2CO3 induced tunability of lattice parameters, the ED profiles extracted from the XRR do not show clear changes on overall monolayer thickness (including Au cores and PEG shells) along the surface-normal direction (Fig. 3), and furthermore, the DLS measurements of PEG-AuNPs dispersed in the bulk solution with and without salts do not exhibit any differences of hydrodynamic size (Fig. S7†). This indicates that during formation of PEG-AuNP superlattices at the vapor–liquid interface the PEG shells bear in-plane isotropic forces leading to the hexagonal packing. Below, we provide brief general properties of the PEG used in this study based on literature44 and theoretical characterization of the PEG-AuNPs in terms of brush-polymer on spherical surfaces, and rationalize the accumulation and crystallization at the solution interface (more details are provided in the ESI†).
Based on the reported phase diagrams of PEG–salt solutions,31,32 there are a single- and a two-phase regions, the latter, consisting of a high salt and a low salt plus PEG phases. Even in the region of the single component phase, our results show finite interfacial accumulation suggesting that there is a depletion of ions within the spherical brush, which induces an osmotic pressure gradient. Nevertheless, we find that the effect of salt (0 to 0.5 M) on the hydrodynamic radius of PEG-AuNPs is negligible (see ESI†). This observation can be explained by a blob size ξ that is smaller than the thermal correlation length ξT, thus leading to chains that are ideal and a solvent (water + salt) inside the brush that is at the θ-point.45,46 Still, the overall surface tension of the entire brush with the poor solvent (high salt concentration) is very significant (of order 60–250 kBT per PEG6k-AuNPs), so the PEG-AuNPs readily migrate to the interface, where such surface tension can be drastically reduced. Under this picture, the effective (hydrodynamic) spherical radius of a given PEG-AuNP (Rh) with Au-core radius R is given by45,46
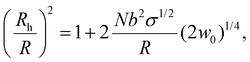 | (1) |
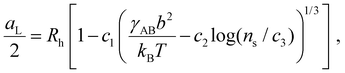 | (2) |
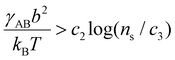 , which sets a threshold on the lowest PEG-AuNP concentration where crystallization occurs. To apply eqn (2) (or the more rigorous eqn (S23)†) a dependence of γAB on ionic strength is needed, which is expected to vary as
, which sets a threshold on the lowest PEG-AuNP concentration where crystallization occurs. To apply eqn (2) (or the more rigorous eqn (S23)†) a dependence of γAB on ionic strength is needed, which is expected to vary as 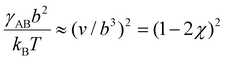 , where v is the excluded volume and χ > 1/2 is the Flory parameter for PEG in the poor solvent high salt solution. Although attempts to determine χ
, where v is the excluded volume and χ > 1/2 is the Flory parameter for PEG in the poor solvent high salt solution. Although attempts to determine χ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50,51 have not been very successful, see ref. 30 and 31, χ is an increasing function of ionic strength. We have fitted eqn (2) to a simple logarithmic dependence,
50,51 have not been very successful, see ref. 30 and 31, χ is an increasing function of ionic strength. We have fitted eqn (2) to a simple logarithmic dependence, 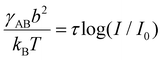 (where τ and I0 are constants and I is the K2CO3 concentration; see ESI†), which captures qualitatively well the dependence of the lattice constant at moderate salt concentrations, is not too high, assuming solvent quality between 0.51 < χ < 0.65. This is consistent with the assumption that the blob size is less than the thermal correlation length. Perhaps the most important result of our analysis is that the dependence of the surface tension on ionic strength is considerably stronger than a simple logarithm at high ionic strengths, which may lead to the assembly of PEG-AuNPs via colloidal destabilization into 3D supercrystals.
(where τ and I0 are constants and I is the K2CO3 concentration; see ESI†), which captures qualitatively well the dependence of the lattice constant at moderate salt concentrations, is not too high, assuming solvent quality between 0.51 < χ < 0.65. This is consistent with the assumption that the blob size is less than the thermal correlation length. Perhaps the most important result of our analysis is that the dependence of the surface tension on ionic strength is considerably stronger than a simple logarithm at high ionic strengths, which may lead to the assembly of PEG-AuNPs via colloidal destabilization into 3D supercrystals.
4. Conclusion
Using synchrotron X-ray diffraction at small angles (GISAXS) and X-ray reflectivity (XRR) we demonstrate that functionalized complexed PEG-AuNPs in aqueous solutions can spontaneously accumulate at the vapor-solution interface by manipulating salt concentrations in the bulk (K2CO3, in this case). At very low salt concentrations, the XRR indicates the formation of a mono-particle layer and the GISAXS patterns show features of a form factor characteristic of individually uncorrelated spherical particles. As the salt concentration increases, short-range 2D hexagonal order develops and above a threshold concentration, the complexes exhibit highly ordered hexagonal crystallinity. Furthermore, the size of the hexagonal unit cell formed by the long chain PEG6k-AuNPs can be varied appreciably by increasing salt concentration, such that the incipient lattice parameter aL can be varied from 39 to 25 nm for 0.005 to 1 M K2CO3, respectively. Similar unit cell shrinkage can also be achieved by manipulating the PEG6k-AuNP concentration at a moderate 0.5 M K2CO3. For the shorter chain PEG800-AuNPs, the threshold salt concentration for crystallinity is significantly higher than that of the longer PEG6k and the range of varying the unit cell size is much narrower, aL ∼ 15 ± 1 nm. Our detailed analysis reveals a nearly perfect surface coverage (close to 100%) of densely packed macroscopic crystalline domains (average domain size larger than micro-meter). These results show that the surface density (i.e., unit-cell size) scales with the chain-length but more importantly they also reflect on the conformation of the corona formed by tethered PEG brushes on curved surfaces. In a salt free solution, the long chain PEG6k corona is consistent with an infinitely long brush in θ-solvent. However, we find that the hydrodynamic radius of the PEG-AuNPs is practically independent of salt concentration (up to 0.5 M). Heuristically, this can be explained in terms of an effective semipermeable membrane surrounding the corona that maintains a constant salt concentration up to the θ-point. Effectively, the PEG-AuNPs reside in a low salt concentration (liquid A) that is separated at the boundaries of the corona from high concentration salt (liquid B) with an effective surface tension γAB between the two liquids. Even though the surface tension energy per polymer is low (less than kBT), thus preventing the polymer from shrinking, the overall surface tension for the entire PEG-AuNP is very large (of order of 100 kBT or more for the PEG6k-AuNPs) and drives the self-assembly and, through optimization of the packing of PEG chains, to crystallization. The tunability of the 2D hexagonal superlattice structure can be achieved over a very wide range by manipulating salt or PEG-AuNPs concentrations and also by the choice of polymer length. Here, we also provide a method to engineer 3D crystals, since sufficiently high salt or PEG-AuNP concentrations induce the formation of 3D precipitates (see Fig. 5), which will be further explored and optimized in the future.Acknowledgements
We thank Ivan Kuzmenko at beamline 9ID-B, APS, Argonne National Laboratory for technical support with the liquid surface scattering measurements. We acknowledge Xiaobin Zuo at beamline 12ID-B, APS, Argonne National Laboratory for technical support in measuring bulk SAXS. H. Z. thanks Prof. Mufit Akinc (Ames Laboratory and Iowa State University) for useful discussions on the phase diagram. Research was supported by the U.S. Department of Energy (U.S. DOE), Office of Basic Energy Sciences, Division of Materials Sciences and Engineering. Ames Laboratory is operated for the U.S. DOE by Iowa State University under Contract No. DE-AC02-07CH11358. Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. DOE Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357.References
- E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Nature, 2006, 439, 55–59 CrossRef CAS PubMed.
- Y. Zhang, F. Lu, K. G. Yager, D. van der Lelie and O. Gang, Nat. Nanotechnol., 2013, 8, 865–872 CrossRef CAS PubMed.
- K. L. Young, M. B. Ross, M. G. Blaber, M. Rycenga, M. R. Jones, C. Zhang, A. J. Senesi, B. Lee, G. C. Schatz and C. A. Mirkin, Adv. Mater., 2014, 26, 653–659 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, Nature, 2008, 451, 549–552 CrossRef CAS PubMed.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, Nature, 2008, 451, 553–556 CrossRef CAS PubMed.
- R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Science, 2011, 334, 204–208 CrossRef CAS PubMed.
- W. Liu, M. Tagawa, H. L. Xin, T. Wang, H. Emamy, H. Li, K. G. Yager, F. W. Starr, A. V. Tkachenko and O. Gang, Science, 2016, 351, 582–586 CrossRef CAS PubMed.
- W. Cheng, M. R. Hartman, D.-M. Smilgies, R. Long, M. J. Campolongo, R. Li, K. Sekar, C.-Y. Hui and D. Luo, Angew. Chem., Int. Ed., 2010, 49, 380–384 CrossRef CAS PubMed.
- S. Narayanan, J. Wang and X.-M. Lin, Phys. Rev. Lett., 2004, 93, 135503 CrossRef PubMed.
- T. P. Bigioni, X.-M. Lin, T. T. Nguyen, E. I. Corwin, T. A. Witten and H. M. Jaeger, Nat. Mater., 2006, 5, 265–270 CrossRef CAS PubMed.
- D. G. Schultz, X.-M. Lin, D. Li, J. Gebhardt, M. Meron, J. Viccaro and B. Lin, J. Phys. Chem. B, 2006, 110, 24522–24529 CrossRef CAS PubMed.
- A. Tao, P. Sinsermsuksakul and P. Yang, Nat. Nanotechnol., 2007, 2, 435–440 CrossRef CAS PubMed.
- V. Aleksandrovic, D. Greshnykh, I. Randjelovic, A. Frömsdorf, A. Kornowski, S. V. Roth, C. Klinke and H. Weller, ACS Nano, 2008, 2, 1123–1130 CrossRef CAS PubMed.
- P. Siffalovic, L. Chitu, E. Majkova, K. Vegso, M. Jergel, S. Luby, I. Capek, A. Satka, G. A. Maier, J. Keckes, A. Timmann and S. V. Roth, Langmuir, 2010, 26, 5451–5455 CrossRef CAS PubMed.
- A. T. Heitsch, R. N. Patel, B. W. Goodfellow, D.-M. Smilgies and B. A. Korgel, J. Phys. Chem. C, 2010, 114, 14427–14432 CAS.
- C. Stefaniu, M. Chanana, D. Wang, D. V. Novikov, G. Brezesinski and H. Möhwald, ChemPhysChem, 2010, 11, 3585–3588 CrossRef CAS PubMed.
- C. Stefaniu, M. Chanana, D. Wang, D. V. Novikov, G. Brezesinski and H. Möhwald, Langmuir, 2011, 27, 1192–1199 CrossRef CAS PubMed.
- C. Stefaniu, M. Chanana, D. Wang, G. Brezesinski and H. Möhwald, J. Phys. Chem. C, 2011, 115, 5478–5484 CAS.
- C. Stefaniu, M. Chanana, H. Ahrens, D. Wang, G. Brezesinski and H. Möhwald, Soft Matter, 2011, 7, 4267–4275 RSC.
- M. A. Mahmoud, D. O'Neil and M. A. El-Sayed, Chem. Mater., 2014, 26, 44–58 CrossRef CAS.
- M. A. Mahmoud, J. Phys. Chem. C, 2015, 119, 305–314 CAS.
- M. J. Campolongo, S. J. Tan, D.-M. Smilgies, M. Zhao, Y. Chen, I. Xhangolli, W. Cheng and D. Luo, ACS Nano, 2011, 5, 7978–7985 CrossRef CAS PubMed.
- S. J. Tan, J. S. Kahn, T. L. Derrien, M. J. Campolongo, M. Zhao, D.-M. Smilgies and D. Luo, Angew. Chem., Int. Ed., 2014, 53, 1316–1319 CrossRef CAS PubMed.
- H. Zhang, W. Wang, N. Hagen, I. Kuzmenko, M. Akinc, A. Travesset, S. Mallapragada and D. Vaknin, Adv. Mater. Interfaces, 2016, 3, 1600180 CrossRef.
- S. Srivastava, D. Nykypanchuk, M. Fukuto and O. Gang, ACS Nano, 2014, 8, 9857–9866 CrossRef CAS PubMed.
- S. Srivastava, D. Nykypanchuk, M. Fukuto, J. D. Halverson, A. V. Tkachenko, K. G. Yager and O. Gang, J. Am. Chem. Soc., 2014, 136, 8323–8332 CrossRef CAS PubMed.
- W. Wang, H. Zhang, I. Kuzmenko, S. Mallapragada and D. Vaknin, Sci. Rep., 2016, 6, 26462 CrossRef CAS PubMed.
- J. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 8378–8379 CrossRef CAS.
- J. Zhou, F. Ke, Y.-Y. Tong, Z.-C. Li and D. Liang, Soft Matter, 2011, 7, 9956–9961 RSC.
- H. D. Willauer, J. G. Huddleston and R. D. Rogers, Ind. Eng. Chem. Res., 2002, 41, 1892–1904 CrossRef CAS.
- J. G. Huddleston, H. D. Willauer and R. D. Rogers, J. Chem. Eng. Data, 2003, 48, 1230–1236 CrossRef CAS.
- H. Walter, Partitioning in Aqueous Two-Phase System: Theory, Methods, Uses, and Applications to Biotechnology, Elsevier Science, 2012 Search PubMed.
- C. H. J. Choi, J. E. Zuckerman, P. Webster and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6656–6661 CrossRef CAS PubMed.
- X.-D. Zhang, D. Wu, X. Shen, J. Chen, Y.-M. Sun, P.-X. Liu and X.-J. Liang, Biomaterials, 2012, 33, 6408–6419 CrossRef CAS PubMed.
- K. Rahme, L. Chen, R. G. Hobbs, M. A. Morris, C. O'Driscoll and J. D. Holmes, RSC Adv., 2013, 3, 6085–6094 RSC.
- D. Vaknin, X-Ray Diffraction Techniques for Liquid Surfaces and Monomolecular Layers, in Characterization of Materials, John Wiley & Sons, New York, 2012, vol. 2, pp. 1393–1423 Search PubMed.
- H. Zhang, X. Liu, S. Feng, W. Wang, K. Schmidt-Rohr, M. Akinc, M. Nilsen-Hamilton, D. Vaknin and S. Mallapragada, Langmuir, 2015, 31, 2818–2825 CrossRef CAS PubMed.
- M. Winterhalter, H. Bürner, S. Marzinka, R. Benz and J. J. Kasianowicz, Biophys. J., 1995, 69, 1372–1381 CrossRef CAS PubMed.
- K. Prasitnok and M. R. Wilson, Phys. Chem. Chem. Phys., 2013, 15, 17093–17104 RSC.
- C. Fuchs, H. Hussain, E. Amado, K. Busse and J. Kressler, Macromol. Rapid Commun., 2015, 36, 211–218 CrossRef CAS PubMed.
- J. Als-Nielsen and D. McMorrow, Elements of Modern X-ray Physics, John Wiley & Sons, 2011 Search PubMed.
- P. S. Pershan and M. L. Schlossman, Liquid Surface and Interfaces: Synchrotron X-ray Methods, Cambridge University Press, 2012 Search PubMed.
- M. Tolan, X-Ray Scattering from Soft-Matter Thin Films: Materials Science and Basic Research, Springer-Verlag, 1999 Search PubMed.
- J. E. Mark and P. J. Flory, J. Am. Chem. Soc., 1963, 87, 1415–1423 CrossRef.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CAS.
- C. M. Wijmans and E. B. Zhulina, Macromolecules, 1993, 26, 7214–7224 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- K. Binder and A. Milchev, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 1515–1555 CrossRef CAS.
- A. Travesset, J. Chem. Phys., 2014, 141, 164501 CrossRef PubMed.
- T. Hino and J. M. Prausnitz, J. Appl. Polym. Sci., 1998, 68, 2007–2017 CrossRef CAS.
- P. U. Kenkare and C. K. Hall, AIChE J., 1996, 42, 3508–3522 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr07136h |
| This journal is © The Royal Society of Chemistry 2017 |