Elemental steps of the thermodynamics of dihydropyrimidine: a new class of organic hydride donors

Abstract

25 Dihydropyrimidine derivatives, a new class of organo-hydrides, were designed and synthesized by the Biginelli reaction. For the first time, the thermodynamic driving forces of the six elemental steps to obtain a hydride in acetonitrile were determined by isothermal titration and electrochemical methods, respectively. The effects of molecular structures and substituents on these thermodynamic parameters were examined, uncovering some interesting structure–reactivity relationships. Both the thermodynamic and kinetic studies show that the hydride transfer from dihydropyrimidines to 9-phenylxanthylium (PhXn⁺ClO₄⁻) prefers a concerted mechanism.

---

Introduction

Inspired by the functions of organic hydride cofactors in vivo such as coenzyme NAD(P)H^1–6 and F420,^7–11 organo-hydrides have received significant attention from the fields of chemistry, biology, pharmaceuticals and energy science, etc. In recent years, biomimetic organo-hydrides, represented by N-benzyl-1,4-dihydronicotinamide (BNAH),^12–16 Hantzsch esters (HEH)^17–23 and dihydrobenzoimidazole (ImH₂)^24–28 (Scheme 1) have been extensively applied in the hydrogenation of C=C, C=O, C=N double bonds to afford versatile building blocks, owing to their advantages of excellent reactivity, mild experimental conditions, good functional group tolerance, ready availability and environmentally-friendly nature. The redox potentials of organic-hydrides and bond dissociation energies to release a hydride or a hydrogen atom are vital to measure their hydrogenation abilities and judge the hydrogenation mechanisms in both organic synthesis and living metabolism. Consequently, these basic parameters and reaction mechanisms related to organo-hydrides were extensively studied by thermodynamic and kinetic methods during the past half century. T. C. Bruice,^29–33 L. L. Miller,^34–37 S. Fukuzumi,^38–42 J. M. Mayer,^43–46 H. Mayr,^47,48 Y. Lu^49–51 and other groups^52–58 have figured out the detailed hydride transfer mechanisms from NADH models to various substrates using integrated approaches, including intermediate capture, spectrum detection and kinetic analysis. J.-M. Savéant and others^59–63 have devoted a lot of effort to mechanistic studies of multi-step oxidation of NADH models in acetonitrile through electrochemical kinetics. The structure–reactivity relationships of NADH and ImH₂ models were extensively investigated by M. M. Kreevoy and I. S. H. Lee^64–69via investigation of the location of the substitution and the tightness of the transition state as well as the resemblance of the transition state to reactants and products. Combined with the thermodynamic cycles from Hess's law, our group have systematically determined the thermodynamic parameters in each elemental step for various organic hydride donors and corresponding intermediates by experimental techniques, and further established a thermodynamic driving-force database for hundreds of biomimetic organic hydrides in acetonitrile solution.^70–74 Through our thermodynamic analytic platform, the most likely pathway of the hydride transfer from NADH analogues to olefin, imine, carbonyl compounds and some carbocations can be well diagnosed.^75–78 Besides, a classical but new kinetic equation was established to estimate the rate constants of hydride transfer reactions in acetonitrile by two available parameters related to bond energies.⁷⁹

Scheme 1 Conventional organic hydride donors widely employed in synthesis.

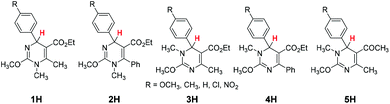
Although great advances have been achieved in mechanistic studies and synthetic applications, almost all the existing organo-hydrides have been limited to the dihydropyridine skeleton, complemented by a few benzimidazole derivatives (Scheme 1). The paucity of the species diversity has seriously restricted further development of organic hydride chemistry. Therefore, the design and synthesis of a new class of organo-hydrides, and determination of their reducing capacity are challenging and urgently needed to respond to the booming development of organic hydride chemistry. Similar to the structure of pyridine, pyrimidine is another ubiquitous heterocyclic moiety as a privileged structure in various drugs and natural products.^80–84 Naturally, we wonder whether dihydropyrimidine can act as a good hydride donor. Is the hydride-donating ability influenced by incorporation of two N atoms into the benzene ring? What's the difference between the reduction ability of 1,2- and 1,4-dihydropyrimidine? Fortunately, we found that the Biginelli reaction,^85–89 a generally accepted method to synthesize various dihydropyrimidines, supplied us a good opportunity to design and synthesize some dihydropyrimidine-type organo-hydrides with a novel skeleton. In the present work, we have synthesized 25 dihydropyrimidine derivatives (Scheme 2) and determined their thermodynamic parameters for hydride-donating abilities (defined as the enthalpy changes to release a hydride). Considering that the electron-donating ability is also one of the basic parameters to measure the reducing capacity, and hydride transfer is often initiated by electron transfer, the redox potential was also determined. Through thermodynamic cycles, the thermodynamic driving forces of the six elemental steps to release a hydride in acetonitrile were obtained. The mechanism of hydride transfer from dihydropyrimidine to 9-phenylxanthylium (PhXn⁺ClO₄⁻) was diagnosed through both thermodynamic and kinetic experiments.

Scheme 2 Structures of dihydropyrimidine derivatives (XH) examined in this work.

Results

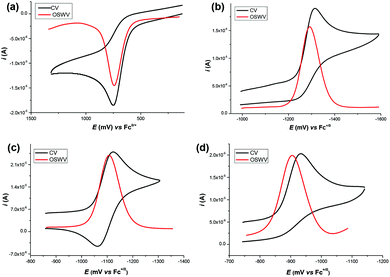
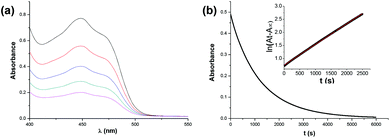
The target dihydropyrimidine derivatives were synthesized through the Biginelli reaction^90–96 and identified by H NMR.^79,97–104 Oxidation potentials of the 25 dihydropyrimidines (XH) and reduction potentials of their corresponding cations (X⁺) were determined using BAS-100B electrochemical workstations by cyclic voltammetry (CV) and Osteryoung square wave voltammetry (OSWV) methods in acetonitrile at 298 K. All the potential values are calibrated to Fc^+/0 (Fig. 1). The results are summarized in Table 1. The kinetics of the hydride transfer from 1H(R = OCH₃) (4.8 × 10⁻³ mol L⁻¹) to PhXn⁺ClO₄⁻ (cal. 2 × 10⁻⁴ mol L⁻¹) in acetonitrile at 298 K were determined from the UV spectrum under pseudo-first-order conditions (for details see the Experimental section) (Fig. 2).

Fig. 1 CV and OSWV for the oxidation of 1H(R = H) (a), the reduction of 1⁺(R = H) (b), 2⁺(R = Cl) (c) and 2⁺(R = NO₂) (d) (about 1 mol L⁻¹) in deaerated acetonitrile containing 0.1 M n-Bu₄NPF₆ as supporting electrolyte (sweep rate = 0.1 V s⁻¹), respectively.

Fig. 2 (a) Profiles of the hydride transfer from 1H(R = OCH₃) to PhXn⁺ClO₄⁻ in acetonitrile at 298 K. (b) Decrease of the absorbance at 450 nm during the reaction of PhXn⁺ClO₄⁻ (cal. 2 × 10⁻⁴ mol L⁻¹) with 1H(R = OCH₃) (4.8 × 10⁻³ mol L⁻¹); insert: fit to a single exponential decay function.

Table 1 Reaction enthalpy changes of XH with PhXn⁺ as well as the redox potentials of relative species in acetonitrile at 298 K

XH	R	ΔHr ^a	E(XH^+/0)^b		E(X^+^/0)^b
			CV	OSWV	CV	OSWV
a ΔHr was obtained from the reaction heats of eqn (3) by ITC in acetonitrile at 298 K. The data, given in kcal mol^−1, were average values of at least three independent runs, each of which was an average value of more than ten consecutive titrations. The reproducibility is ±0.05 kcal mol^−1. b Measured by CV and OSWV methods in acetonitrile at 298 K, the unit is V vs. Fc^+/0 and reproducible to 5 mV or better.
1H	OCH3	−21.8	0.736	0.719	−1.373	−1.358
	CH3	−21.7	0.743	0.730	−1.342	−1.318
	H	−21.4	0.763	0.745	−1.267	−1.249
	Cl	−21.1	0.792	0.766	−1.204	−1.170
	NO2	−20.3	0.843	0.818	−0.973	−0.950
2H	OCH3	−21.0	0.772	0.756	−1.298	−1.278
	CH3	−20.8	0.786	0.768	−1.254	−1.240
	H	−20.6	0.805	0.788	−1.213	−1.190
	Cl	−20.2	0.820	0.800	−1.138	−1.115
	NO2	−19.4	0.872	0.844	−0.933	−0.908
3H	OCH3	−20.1	0.626	0.606	−1.453	−1.438
	CH3	−20.0	0.634	0.612	−1.424	−1.408
	H	−19.9	0.656	0.630	−1.386	−1.360
	Cl	−19.8	0.670	0.648	−1.307	−1.285
	NO2	−19.4	0.713	0.692	−1.098	−1.080
4H	OCH3	−18.8	0.627	0.608	−1.270	−1.248
	CH3	−18.7	0.642	0.620	−1.248	−1.228
	H	−18.5	0.650	0.632	−1.217	−1.199
	Cl	−18.4	0.674	0.652	−1.172	−1.150
	NO2	−17.8	0.725	0.700	−1.046	−1.028
5H	OCH3	−19.9	0.604	0.585	−1.440	−1.422
	CH3	−19.9	0.619	0.596	−1.409	−1.388
	H	−19.7	0.632	0.612	−1.341	−1.324
	Cl	−19.5	0.652	0.636	1.253	−1.236
	NO2	−19.1	0.727	0.694	−1.074	−1.052

---

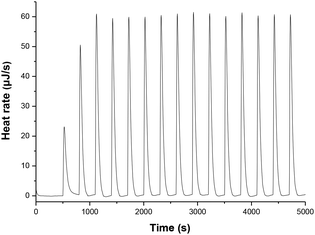
The thermodynamic driving forces in this work were defined as the enthalpy changes (ΔH_H-D(XH)) of XH to release a hydride anion in acetonitrile (eqn (1) and (2)), which can be obtained from the reaction enthalpy changes (ΔH_r) of hydride transfers from XH to 9-phenylxanthylium perchlorate (PhXn⁺ClO₄⁻) in acetonitrile (eqn (3) and (4)). In eqn (4), ΔH_r is the enthalpy change of the reaction of eqn (3) in acetonitrile, which can be determined using isothermal titration calorimetry (ITC); ΔH_H-A(PhXn⁺) is the hydride affinity of PhXn⁺ in acetonitrile, which is available from our previous work (−96.8 kcal mol⁻¹).¹⁰⁵ The molar enthalpy changes (ΔH_r) of the hydride transfer from dihydropyrimidine derivatives XH to PhXn⁺ClO₄⁻ (eqn (3)) were measured using titration calorimetry in acetonitrile (Fig. 3 and ESI†). The detailed enthalpy changes and thermodynamic driving force of 25 XH to release hydride anion in acetonitrile are summarized in Table 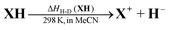1.

ΔH_H-D(XH) = ΔH_f(X⁺) + ΔH_f(H⁻) − ΔH_f(XH) (2)

ΔH_H-D(XH) = ΔH_r − ΔH_H-A(PhXn⁺) (4)

Fig. 3 Isothermal titration calorimetry (ITC) for the reaction heat of 1H(R = OCH₃) with 9-phenylxanthylium perchlorate (PhXn⁺ClO4⁻) in acetonitrile at 298 K. Titration was conducted by adding 10 µL of 1H(R = OCH₃) (3.03 mM) every 300 s into the acetonitrile containing PhXn⁺ClO4⁻ (ca. 30 mM).

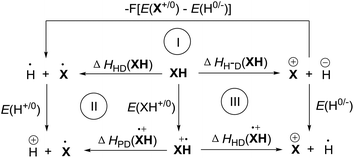
ΔH_HD(XH) is the enthalpy change of XH to release hydrogen atoms. ΔH_DP(XH˙⁺) and ΔH_HD(XH˙⁺) are the enthalpy changes of the intermediate XH˙⁺ to release protons and hydrogen atoms, respectively. Evidently, it is difficult to directly determine the enthalpy changes of XH to release a hydrogen and that of XH˙⁺ to release protons or hydrogen atoms in acetonitrile, experimentally. In order to obtain their enthalpy changes in acetonitrile, three thermodynamic cycles were constructed according to the chemical process of XH to release hydride anion (Scheme 3).²⁴

Scheme 3 Thermodynamic cycles of XH constructed on the basis of Hess's law.

From three thermodynamic cycles, eqn (5)–(7) were derived according to Hess's law. In eqn (5)–(7), E(X^+/0), E(XH^+/0), E(H^0/−), and E(H^+/0) are the standard redox potentials of X⁺, XH, H⁺ and H⁻ in acetonitrile, respectively. Obviously, ΔH_HD(XH), ΔH_PD(XH˙⁺) and ΔH_HD(XH˙⁺) are easy to obtain if ΔH_H-D(XH), E(X^+/0), E(XH^+/0), E(H^0/−) and E(H^+/0) are available. In fact, ΔH_H-D(XH), E(X^+/0) and E(XH^+/0) are available from the above work (Table 1). E(H^0/−) and E(H^+/0) can also be obtained from the literature.¹⁰⁶ The detailed values of ΔH_HD(XH), ΔH_PD(XH˙⁺) and ΔH_HD(XH˙⁺) of 25 dihydropyrimidine derivatives (XH) in acetonitrile are summarized in Table 2.

ΔH_HD(XH) = ΔH_H-D(XH) − F[E(X^+/0) − E(H^0/−)] (5)

ΔH_PD(XH˙⁺) = ΔH_HD(XH) − F[E(XH^+/0) − E(H^+/0)] (6)

ΔH_HD(XH˙⁺) = ΔH_H-D(XH) − F[E(XH^+/0) − E(H^0/−)] (7)

Table 2 Enthalpy changes of XH to release hydride anion and hydrogen atoms as well as those of XH˙⁺ to release protons and hydrogen atoms in acetonitrile at 298 K (in kcal mol⁻¹)

XH	R	ΔHH-D(XH)^a	ΔHHD(XH)^b	ΔHPD(XH˙^+)^b	ΔHHD(XH˙^+)^b
a ΔHH-D(XH) were derived from eqn (4), taking ΔHH-A(PhXn^+) = −96.8 kcal mol^−1 in acetonitrile, the uncertainties are all smaller than 1 kcal mol^−1. b ΔHHD(XH), ΔHPD(XH˙^+) and ΔHHD(XH˙^+) were estimated from eqn (5)–(7), respectively, taking E(H^+/0) = −2.307 V, E(H^0/−) = −1.137 V, which were derived from Parker's work adjusted to versus Fc^+/0 by adding −0.357 V.^106 Relative uncertainties were estimated to be smaller than or close to 1 kcal mol^−1 in each case. The standard oxidation potential values of XH and X˙ in acetonitrile were all derived from the experimental results using OSWV method, because OSWV has been verified to be a more exact electrochemical method for evaluating the standard one-electron redox potentials of analyte with irreversible electrochemical processes than CV.
1H	OCH3	75.0	80.1	10.3	32.2
	CH3	75.1	79.3	9.3	32.1
	H	75.4	77.9	7.6	31.9
	Cl	75.7	76.4	5.6	31.8
	NO2	76.5	72.2	0.1	31.4
2H	OCH3	75.8	79.0	8.41	32.1
	CH3	76.0	78.4	7.46	32.1
	H	76.2	77.5	6.15	31.8
	Cl	76.6	76.1	4.41	31.9
	NO2	77.4	72.1	−0.55	31.7
3H	OCH3	76.7	83.6	16.5	36.5
	CH3	76.8	83.0	15.7	36.4
	H	76.9	82.0	14.3	36.1
	Cl	77.0	80.4	12.3	35.9
	NO2	77.4	76.1	7.0	35.2
4H	OCH3	78.0	80.6	13.4	37.8
	CH3	78.1	80.2	12.7	37.6
	H	78.3	79.7	11.9	37.5
	Cl	78.4	78.8	10.5	37.2
	NO2	79.0	76.5	7.1	36.6
5H	OCH3	76.9	83.9	17.2	37.2
	CH3	76.9	82.7	15.8	37.0
	H	77.1	81.4	14.1	36.8
	Cl	77.3	79.6	11.7	36.4
	NO2	77.8	75.8	6.6	35.5

---

Discussion

Thermodynamic driving forces of dihydropyrimidine derivatives (XH) and related intermediates (XH˙⁺) in acetonitrile

The enthalpy change (ΔH_H-D(XH)) is a very important thermodynamic parameter of XH to scale the ability of XH to donate a hydride anion. Overall, the enthalpy changes of the 25 XH range from 75.0 kcal mol⁻¹ for 1H (R = OCH₃) to 79.0 kcal mol⁻¹ for 4H (R = NO₂). The relatively small span (about 4 kcal mol⁻¹) indicates an insensitivity of the hydride-donating ability to remote substituent effects and structural variants. That is, a substituent at the para position of the benzene ring plays a small role in the hydride-donating ability of the dihydropyrimidine derivatives. Electron-donating groups at the para position of the benzene ring, such as methyl and methoxyl groups, can slightly increase the hydride-donating ability; while electron-withdrawing groups, such as chlorine atom and –NO₂, decrease it.

The elaborate variants of core structures allowed a close investigation of the structure–reactivity relationship for the process of dihydropyrimidine derivatives to release hydrides. A relative energy scale is established in Fig. 4, with 1H (R = H) as a reference. Intriguingly, the hydride donor abilities of the 1,2-isomers are undoubtedly 1.5 kcal mol⁻¹ weaker than those of the 1,4-ones, which completely depart from previous observations in all dihydropyridine-type hydrides, such as BNAH, HEH, AcrH₂. The contradiction can probably be attributed to the electron-withdrawing abilities of the two incorporated nitrogen atoms compared with carbon atoms, as well as the resonance of the methoxyl group ortho to two nitrogen atoms. The resonance should be more significant for the conjugated dienes in the 1,2-isomers than the separated dienes in the 1,4-isomers and naturally, stabilized the former better. Replacement of the methyl by a phenyl group resulted in a 0.8 kcal mol⁻¹ decrease of hydride-donating abilities. It's not unexpected since the electron density on the dihydropyrimidine skeleton could delocalize to the benzene ring better. Additionally, changing the –CO₂Et group on the 1,2-isomer into –COCH₃ increases the enthalpy changes slightly (about 0.2 kcal mol⁻¹), because of the slightly stronger electron-withdrawing ability of –COCH₃ than –CO₂Et. The quantitative analysis of the dependence of the hydride-donating abilities on the structural variants could supply us with a theoretical guidance and a practical tool to rationally modify and design new hydride donors.

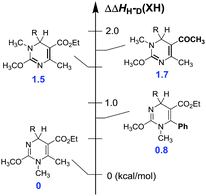Fig. 4 Effects of structural variants on the hydride-donating abilities of dihydropyrimidine derivatives in acetonitrile (1H(R = H) as a reference).

In order to intuitively compare the hydride-donating abilities of dihydropyrimidine derivatives (XH) with some other conventional hydride donors, a thermodynamic scale was established according to their enthalpy changes to release hydride anions in acetonitrile (Fig. 5). From Fig. 5, it is clear that the enthalpy changes of the 25 XH lie in the middle of the scale, indicating their moderate hydride-donating abilities. In other words, their corresponding cations generated by released hydride anion, can also be moderate hydride acceptors. The enthalpy changes are larger than some typically strong hydrides which are widely employed as hydride reductants, such as LiAlH₄ (48 kcal mol⁻¹),^107,108 NaBH₄ (55 kcal mol⁻¹),^107,108 BNAH (64.2 kcal mol⁻¹), Hantzsch (69.3 kcal mol⁻¹) and so on; but smaller than 9-phenyl-9H-xanthene (96.8 kcal mol⁻¹), TEMPOH (105.6 kcal mol⁻¹), toluene (118.0 kcal mol⁻¹), whose corresponding cations are always used as the hydride acceptors in organic synthesis. Actually, their values are close to 9,10-dihydro-10-methylacridine (AcrH₂ 81.1 kcal mol⁻¹). Therefore, the moderate hydride-donating abilities of dihydropyrimidine derivatives provide a good balance of stabilities and reactivities as hydride donors, and make them potentially useful as ideal reductants and in some case, their corresponding cations as good oxidants.

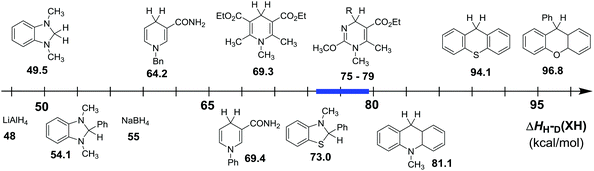Fig. 5 Comparison of hydride dissociation energies of some typical organic hydrides (XH) in acetonitrile.

The hydrogen-donating ability of the dihydropyrimidine derivatives (XH) is defined by the enthalpy change (ΔH_HD(XH)) of XH to release a hydrogen atom. From Table 2, it shows that ΔH_HD(XH) spans a range of about 12 kcal mol⁻¹, from the strongest hydrogen donor 2H(R = NO₂) 72.1 kcal mol⁻¹ to the weakest one 5H(R = OCH₃) 83.9 kcal mol⁻¹. These values are comparable to common antioxidants¹⁰⁹ (CH₃)₃SnH 68.8 kcal mol⁻¹, PhSH 78.6 kcal mol⁻¹, i-C₃H₇OOH 80.3 kcal mol⁻¹, PhOH, 81.7 kcal mol⁻¹, HOOH 83.4 kcal mol⁻¹, indicating it's a good alternative to be used in the antioxidant process. The higher hydrogen-donating abilities of XH with electron-withdrawing groups than those with electron-donating groups implies that the electron-donating group can improve the stability of the resulting carbon radical (X˙) better, which further hints that those radicals have some positive charge densities on the radical carbon atom and tend to be electron-deficient. Similar to the tendency observed for the hydride-donating ability, the enthalpy changes of 1,2-isomers to release hydrogen atoms are on average 2 kcal mol⁻¹ larger than those of 1,4-isomers. That's to say, the separated dienes in the 1,4-isomers can delocalize the single electron in the resulting carbon radicals more effectively than the conjugated dienes in the 1,2-isomers and therefore, lead to a better stability for the radicals of 1,4-isomers.

The radical cation is one of the most important reactive intermediates in both academic research and industrial production. Due to their high reactivities, their thermodynamic parameters are generally unavailable and thus, invaluable. Through our thermodynamic cycles, the enthalpy changes of XH˙⁺ to release protons ΔH_PD(XH˙⁺) and hydrogen atoms ΔH_HD(XH˙⁺) could be derived, which are two vital parameters to measure the stabilities of the corresponding radical cations. These parameters range from −0.6 kcal mol⁻¹2H(R = NO₂) to 17.2 kcal mol⁻¹5H(R = OCH₃) for ΔH_PD(XH˙⁺), and from 31.4 kcal mol⁻¹1H(R = NO₂) to 37.8 kcal mol⁻¹4H(R = OCH₃) for ΔH_HD(XH˙⁺), respectively. The relatively small ΔH_PD(XH˙⁺) values show that the resulting radical cations should be extremely strong organic acids, compared with PhCO₂H 32.5 kcal mol⁻¹ (ref. 110) and CF₃CO₂H 22.4 kcal mol⁻¹ (ref. 111) in acetonitrile. If there are basic substrates in a reaction system or even in a neutral system, the degradation of radical cations (XH˙⁺) through the acid–base neutralization could proceed, preferentially and smoothly. Considering the larger values of ΔH_HD(XH˙⁺), their degradation mechanisms through the hydrogen transfer pathway seem inhibited, unless there is a strong hydrogen acceptor in the reaction system or under acidic reaction conditions. Therefore, the high instabilities of XH˙⁺ mainly originate from their strong proton-donating abilities, in other terminology “their stronger acidities”, which can be further verified by the irreversibility of the electrochemical measurements in following sections.

Electrochemical behavior for the redox reaction of dihydropyrimidine (XH) and related X⁺ in acetonitrile

The redox potential is a basic thermodynamic parameter to measure the single-electron redox capacity of organic compounds. In the present work, the oxidation potentials of dihydropyrimidine derivatives and the reduction potentials of their corresponding cations (X⁺) were determined by cyclic voltammetry (CV) and Osteryoung square wave voltammetry (OSWV) methods in acetonitrile at 298 K. All the hydride donors exhibit an irreversible oxidation peak with a range of 0.604 V vs. Fc^+/0 for 5H(R = OCH₃) to 0.872 V for 2H(R = NO₂) as shown in Fig. 1 and ESI.† The irreversibility of the electrochemical oxidation process is ascribed to the rapid degradation of the resulting radical cations (XH˙⁺), mainly through a deprotonation process to the solution or another substrate, to generate neutral radicals (X˙), as described above.¹¹² The effect of bases or acids on the deprotonation process of the radical cations (XH˙⁺), produced in situ by electrochemical oxidation, have been analyzed in detail in some previous work.^59–62,97 These oxidation potentials are remarkably larger than conventional dihydropyridine hydride donors,⁷⁰ 0.219 V for BNAH, 0.460 V for AcrH₂ and 0.479 V for HEH, corresponding to their very weak single-electron reductants. It is noteworthy that the radicals (X˙), generated through the deprotonation of XH˙⁺, should be very strong single-electron reducing agents, which were immediately oxidized at the oxidation potential of parent XH. Hence, the CV peaks of the parent XH likely correspond to a two-electron transfer process.

Because of the inaccessibility of the highly reactive radicals X˙ in our experimental conditions, their oxidation potentials are determined by the reduction process of X⁺, instead. The reduction potentials of related cations X⁺ distribute between −1.440 for 5H(R = OCH₃) and −0.933 for 2H(R = NO₂), implying they are very weak oxidants. Conversely, their corresponding neutral radicals X˙ are extremely strong single-electron reduction reagents. Additionally, cyclic voltammetry (CV) technology can be employed to test the relative stabilities of the resulting radicals according to the reversibility of the CV peaks. For series 1H, 3H and 5H, which have a methyl group at the 6 position of the pyrimidine, the reduction of X⁺ is an irreversible process, indicating that the resulting X˙ is too reactive to be captured under the present electrochemical conditions. However, when the methyl at the 6 position of the benzene was replaced by a phenyl, the CV behave nearly reversible for series 2H and 4H, except for those with a strong withdrawing group NO₂ (Fig. 1c and d). It is directly indicated that the produced radicals 2˙ and 4˙ are more stable than 1˙, 3˙ and 5˙. The different reversibility between the reduction of series 1⁺ and 2⁺ shows that a phenyl at the 6 position of the pyrimidine stabilizes the X˙ better than a methyl group, through its delocalization. Additionally, for 2H and 4H, the radicals X˙ with R = OCH₃, CH₃, H, and Cl are more stable than R = NO₂, from which we can safely speculate that the radicals X˙ are somewhat electron deficient and an electron-donating substituent can significantly stabilize the reactive X˙.

Interestingly, as a hydride reductant, the 1,4-isomer (75.35 kcal mol⁻¹ for 1H(R = H)) is stronger than the 1,2-isomer (76.88 kcal mol⁻¹ for 3H(R = H)). While when used as an electron reductant, it is just the opposite, 0.656 V for 3H(R = H) vs. 0.763 V for 1H(R = H). Such a rare discrepancy offered an alternative mechanistic probe to diagnose whether dihydropyrimidine derivatives are oxidized through a concerted hydride transfer or electron transfer initiated multi-step pathway, if a suitable reaction system could be well-designed.

From Tables 1 and 2, it is clear that all the enthalpy changes of XH and their intermediates XH˙⁺ depend on the nature of the substituent at the para position of the phenyl ring, as well as the redox potentials of XH and X⁺. To elucidate the relationship of substituents with these parameters, the effects of remote substituents are examined, respectively.^113,114 The results in Fig. s40 and s41 (ESI†) show that all these values are linearly dependent on Hammett substituent parameters σ_p with good correlation coefficients, implying that the linear free energy relationship holds well in these chemical and electrochemical processes. With the slopes and the intercepts of these linear correlations, mathematical formulae are derived [Fig. s40 and s41 in ESI†]. Evidently, for any para or meta position of the phenyl, it is easy to estimate the enthalpy changes and redox potentials, as long as the corresponding σ value is available. Hence, these formulae might quantitatively guide us to modify dihydropyrimidine analogues with suitable substituents for a special use.

Diagnoses of mechanistic possibilities for the hydride transfer from dihydropyrimidines XH to PhXn⁺

Possible reactions between XH and hydride acceptors should include hydride transfer, hydrogen transfer, and electron transfer, which could be assigned to the possible elemental steps of hydride transfer reactions (Scheme 4). Since thermodynamics could offer intrinsic criteria for diagnosing the possibilities of reactions, it might be efficient and comprehensive to elucidate the possibilities of all the elemental steps of hydride transfer. With all the six thermodynamic parameters, the thermodynamic analytic platform for the hydride donor XH can be constructed. The same goes for the hydride acceptor PhXn⁺, whose parameters were available from our previous work⁷⁶ (Scheme 4). According to Hess's law, it is easy to access the thermodynamic driving forces of all possible elemental steps of the hydride transfer from XH to PhXn⁺, as shown in Scheme 4. Herein, the reaction of 1H(R = OCH₃) with PhXn⁺ was taken as an example to diagnose the detailed mechanisms of hydride transfers according to the thermodynamic analytic platform.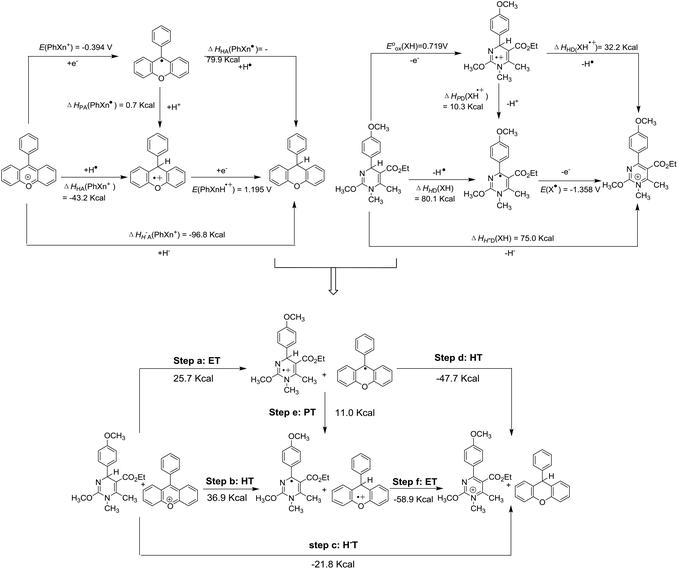

Scheme 4 Thermodynamic diagnosis of possible hydride transfer mechanisms between 1H(R = OCH₃) and PhXn⁺ in acetonitrile.

From Scheme 4, it is obvious that among the three initial steps (steps a, b and c) of the four possible pathways, hydride transfer (step c) from XH to PhXn⁺ should be spontaneous, since it's thermodynamically favorable by 21.8 kcal mol⁻¹. While the electron transfer (step a) and hydrogen atom transfer (step b) are thermodynamically forbidden by more than 25.7 kcal mol⁻¹. Even if the electron transfer or hydrogen transfer is triggered, the generated transient ion pairs of XH˙⁺ and PhXn˙, or X˙ and PhXnH˙⁺ would immediately react with each other through the possible stepwise routes (steps b–f, a–e, or a–f), until they give the same pair of stable products of X⁺ and PhXnH as produced by the concerted hydride transfer (step c). Therefore, it might be concluded that the hydride transfer reaction tends to proceed through a concerted manner, rather than the stepwise hydrogen or electron transfer patterns.

In order to further verify the reaction mechanism of 1H(R = OCH₃) with PhXn⁺ClO₄⁻, the kinetics of the reaction was examined (Fig. 2) in acetonitrile at 298 K under a pseudo-first-order condition. The reaction rates k₂ were 0.16 L (mol s)⁻¹ (for details see the Experimental section). The activation parameter was obtained from the Eyring equation (18.5 kcal mol⁻¹), which is much smaller than the enthalpy changes of the initial electron transfer (step a, 25.7 kcal mol⁻¹) and hydrogen transfer (step b, 36.89 kcal mol⁻¹). On the basis of a general reaction law¹¹⁵ that the activation energy change is always larger than or at least equal to the corresponding standard state energy change for any elemental reaction, it is evident that both the initial steps a and b could be ruled out. Therefore, from the kinetic analysis, the hydride transfer from XH to PhXn⁺ClO₄⁻ is also concerted.

Conclusions

In the present work, we have developed a series of readily available dihydropyrimidine organo-hydrides. The thermodynamic driving forces of each elemental step for hydride donors in acetonitrile were obtained for the first time through thermodynamic cycles, as well as those for the corresponding reactive intermediates, which allow us to evaluate their reducing capacity quantitatively and elucidate the most accessible hydride transfer mechanism. Thermodynamic parameters indicated that they are moderate reducing reagents in both the hydride and electron redox process, lying between conventional biomimetic hydride donors BNAH and AcrH₂. The 1,4-isomers are stronger hydride donors than the 1,2-isomers, different from any reported dihydropyridine derivatives. The opposite tendency between the electron and hydride reducing ability supplies a potential probe for mechanistic research. The linear free energy relationships between these thermodynamic parameters and substituent constants are exactly held. The mechanism of hydride transfer from the dihydropyrimidine XH to PhXn⁺ is most probably through a concerted pathway according to both the thermodynamic and kinetic analysis. These thermodynamic and mechanistic studies are critical to understanding the reducing properties of dihydropyrimidine derivatives, offering a practical guide for the rational design of new organic-hydrides and opening an avenue for the wide application of dihydropyrimidine derivatives in various hydrogenation processes.

Experimental section

Materials

All reagents were of commercial quality from freshly opened containers or were purified before use. Reagent grade acetonitrile was refluxed over KMnO₄ and K₂CO₃ for several hours and was doubly distilled over P₂O₅ under argon before use. The commercial tetrabutylammonium hexafluorophosphate (n-Bu₄NPF₆, Aldrich) was recrystallized from CH₂Cl₂ and dried at 110 °C overnight before preparation of the supporting electrolyte solution. 9-Phenylxanthium perchlorate (PhXn⁺ClO₄⁻)⁷⁰ and dihydropyrimidines (XH)^90–96 were obtained according to literature methods, and the final products were identified by ¹H NMR.

Isothermal titration calorimetry (ITC)

The titration experiments were performed on a CSC4200 isothermal titration calorimeter in acetonitrile at 298 K as described previously. The performance of the calorimeter was checked by measuring the standard heat of neutralization of an aqueous solution of sodium hydroxide with standard aqueous HCl solution. The heat of reaction was determined following 10 automatic injections from a 250 µL injection syringe containing standard solution (3 mM) into the reaction cell (1.30 mL) containing 1mL concentrated 9-phenylxanthium perchlorate (PhXn⁺ClO₄⁻). Injection volumes (10 µL) were delivered at 0.5 s time intervals with 300–350 s between every two injections. The reaction heat was obtained by integration of each peak except the first.

Measurement of redox potentials

The electrochemical experiments were carried out by cyclic voltammetry (CV) and Osteryoung square wave voltammetry (OSWV) using a BAS100B electrochemical apparatus in deaerated acetonitrile under argon atmosphere at 298 K as described previously.^{70,71,76,77,105}n-Bu₄NPF₆ (0.1 M) in acetonitrile was employed as the supporting electrolyte. A standard three-electrode cell consists of a glassy carbon disk as work electrode, a platinum wire as counter electrode, and 0.1 M AgNO₃/Ag (in 0.1 M n-Bu₄NPF₆-acetonitrile) as reference electrode. The ferrocenium/ferrocene redox couple (Fc^+/0) was taken as internal standard. The reproducibilities of the potentials were usually ≤5 mV for ionic species and ≤10 mV for neutral species.

Kinetic measurements

Kinetic measurements were carried out in acetonitrile by a UV/vis spectrophotometer connected to a super thermostat circulating bath to regulate the temperature of cell compartments. The oxidation rate of XH by PhXn⁺ClO₄⁻ was measured at 298 K by monitoring the changes of absorption of PhXn⁺ClO₄⁻ (cal. 2 × 10⁻⁴ mol L⁻¹) at 450 nm under pseudo-first-order conditions (1H(R = OCH₃) 4.8 × 10⁻³ mol L⁻¹, over 20-fold excess). The pseudo-first-order rate constant was obtained k_obs = 7.91 × 10⁻³ s⁻¹ from the slope of the work plot, and then converted to k₂. The activation parameters were derived from the Eyring equation.

Acknowledgements

Financial support from the National Natural Science Foundation of China (Grant No. 21472099, 21390400 and 21102074) and the 111 Project (B06005) is gratefully acknowledged.

Notes and references

1. M. Ushio-Fukai, A. M. Zafari, T. Fukui, N. Ishizaka and K. K. Griendling, J. Biol. Chem., 1996, 271, 23317–23321.
2. S. Rajagopalan, S. Kurz, T. Münzel, M. Tarpey, B. A. Freeman, K. K. Griendling and D. G. Harrison, J. Clin. Invest., 1996, 97, 1916–1923.
3. K. K. Griendling, C. A. Minieri, J. D. Ollerenshaw and R. W. Alexander, Circ. Res., 1994, 74, 1141–1148.
4. W. Ying, Antioxid. Redox Signaling, 2007, 10, 179–206.
5. R. H. Houtkooper, C. Cantó, R. J. Wanders and J. Auwerx, Endocr. Rev., 2010, 31, 194–223.
6. H. Lin, Org. Biomol. Chem., 2007, 5, 2541–2554.
7. B. W. J. te Brömmelstroet, W. J. Geerts, J. T. Keltjens, C. v. d. Drift and G. D. Vogels, BBA, Biochim. Biophys. Acta, Protein Struct. Mol., 1991, 1079, 293–302.
8. U. Deppenmeier, Cell. Mol. Life Sci., 2002, 59, 1513–1533.
9. J. A. Fox, D. J. Livingston, W. H. Orme-Johnson and C. T. Walsh, Biochemistry, 1987, 26, 4219–4227.
10. T. C. Bruice, Acc. Chem. Res., 1980, 13, 256–262.
11. C. H. Hagemeier, S. Shima, R. K. Thauer, G. Bourenkov, H. D. Bartunik and U. Ermler, J. Mol. Biol., 2003, 332, 1047–1057.
12. F. Hollmann, I. W. C. E. Arends and K. Buehler, ChemCatChem, 2010, 2, 762–782.
13. J. C. Moore, D. J. Pollard, B. Kosjek and P. N. Devine, Acc. Chem. Res., 2007, 40, 1412–1419.
14. A. Berenguer-Murcia and R. Fernandez-Lafuente, Curr. Org. Chem., 2010, 14, 1000–1021.
15. B. Procuranti and S. J. Connon, Chem. Commun., 2007, 1421–1423.
16. T. Matsuda, R. Yamanaka and K. Nakamura, Tetrahedron: Asymmetry, 2009, 20, 513–557.
17. Q. Kang, Z.-A. Zhao and S.-L. You, Adv. Synth. Catal., 2007, 349, 1657–1660.
18. T. B. Nguyen, H. Bousserouel, Q. Wang and F. Guéritte, Adv. Synth. Catal., 2011, 353, 257–262.
19. S. G. Ouellet, A. M. Walji and D. W. C. Macmillan, Acc. Chem. Res., 2007, 40, 1327–1339.
20. J. B. Tuttle, S. G. Ouellet and D. W. C. MacMillan, J. Am. Chem. Soc., 2006, 128, 12662–12663.
21. N. J. A. Martin, X. Cheng and B. List, J. Am. Chem. Soc., 2008, 130, 13862–13863.
22. M. Rueping and T. Theissmann, Chem. Sci., 2010, 1, 473–476.
23. M. Rueping, J. Dufour and F. R. Schoepke, Green Chem., 2011, 13, 1084–1105.
24. E. Hasegawa and S. Takizawa, Aust. J. Chem., 2015, 68, 1640–1647.
25. E. Hasegawa, T. Ohta, S. Tsuji, K. Mori, K. Uchida, T. Miura, T. Ikoma, E. Tayama, H. Iwamoto, S. Takizawa and S. Murata, Tetrahedron, 2015, 71, 5494–5505.
26. H. H. E. Hasegawa, K. Sasaki, S. Takizawa, T. Seida and N. Chiba, Heterocycles, 2009, 77, 1147–1161.
27. E. Hasegawa, M. Tateyama, T. Hoshi, T. Ohta, E. Tayama, H. Iwamoto, S. Takizawa and S. Murata, Tetrahedron, 2014, 70, 2776–2783.
28. E. Hasegawa, K. Mori, S. Tsuji, K. Nemoto, T. Ohta and H. Iwamoto, Aust. J. Chem., 2015, 68, 1648–1652.
29. M. F. Powell, J. C. Wu and T. C. Bruice, J. Am. Chem. Soc., 1984, 106, 3850–3856.
30. M. F. Powell and T. C. Bruice, J. Am. Chem. Soc., 1982, 104, 5834–5836.
31. M. Bruestlein and T. C. Bruice, J. Am. Chem. Soc., 1972, 94, 6548–6549.
32. G. X. He, A. Blasko and T. C. Bruice, Bioorg. Chem., 1993, 21, 423–430.
33. M. F. Powell and T. C. Bruice, Prog. Clin. Biol. Res., 1988, 274, 369–385.
34. B. W. Carlson and L. L. Miller, J. Am. Chem. Soc., 1985, 107, 479–485.
35. B. W. Carlson, L. L. Miller, P. Neta and J. Grodkowski, J. Am. Chem. Soc., 1984, 106, 7233–7239.
36. B. W. Carlson and L. L. Miller, J. Am. Chem. Soc., 1983, 105, 7453–7454.
37. A. Kitani, Y. H. So and L. L. Miller, J. Am. Chem. Soc., 1981, 103, 7636–7641.
38. S. Fukuzumi, Y. Fujii and T. Suenobu, J. Am. Chem. Soc., 2001, 123, 10191–10199.
39. S. Fukuzumi, H. Kotani, Y.-M. Lee and W. Nam, J. Am. Chem. Soc., 2008, 130, 15134–15142.
40. S. Fukuzumi, N. Nishizawa and T. Tanaka, J. Org. Chem., 1984, 49, 3571–3578.
41. H. G. Korth, R. Sustmann, C. Thater, A. R. Butler and K. U. Ingold, J. Biol. Chem., 1994, 269, 17776–17779.
42. S. Fukuzumi, Phys. Chem. Chem. Phys., 2008, 10, 2283–2297.
43. J. M. Mayer, Acc. Chem. Res., 1998, 31, 441–450.
44. J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46.
45. T. Matsuo and J. M. Mayer, Inorg. Chem., 2005, 44, 2150–2158.
46. J. P. Roth, J. C. Yoder, T.-J. Won and J. M. Mayer, Science, 2001, 294, 2524–2526.
47. D. Richter, Y. Tan, A. Antipova, X.-Q. Zhu and H. Mayr, Chem – Asian J., 2009, 4, 1824–1829.
48. D. Richter and H. Mayr, Angew. Chem., Int. Ed., 2009, 48, 1958–1961.
49. B. Hammann, M. Razzaghi, S. Kashefolgheta and Y. Lu, Chem. Commun., 2012, 48, 11337–11339.
50. Y. Lu, F. Qu, Y. Zhao, A. M. J. Small, J. Bradshaw and B. Moore, J. Org. Chem., 2009, 74, 6503–6510.
51. Y. Lu, F. Qu, B. Moore, D. Endicott and W. Kuester, J. Org. Chem., 2008, 73, 4763–4770.
52. T. Iyanagi and I. Yamazaki, Biochim. Biophys. Acta, Bioenerg., 1970, 216, 282–294.
53. B. Keita, K. Essaadi, L. Nadjo, R. Contant and Y. Justum, J. Electroanal. Chem., 1996, 404, 271–279.
54. P. J. Elving, W. T. Bresnahan, J. Moiroux and Z. Samec, Bioelectrochem. Bioenerg., 1982, 9, 365–378.
55. E. V. Bakhmutova-Albert, D. W. Margerum, J. G. Auer and B. M. Applegate, Inorg. Chem., 2008, 47, 2205–2211.
56. N. Song, M.-T. Zhang, R. A. Binstead, Z. Fang and T. J. Meyer, Inorg. Chem., 2014, 53, 4100–4105.
57. Y. Lu, Y. Zhao, K. L. Handoo and V. D. Parker, Org. Biomol. Chem., 2003, 1, 173–181.
58. B. Maharjan, M. Raghibi Boroujeni, J. Lefton, O. R. White, M. Razzaghi, B. A. Hammann, M. Derakhshani-Molayousefi, J. E. Eilers and Y. Lu, J. Am. Chem. Soc., 2015, 137, 6653–6661.
59. P. Hapiot, J. Moiroux and J. M. Saveant, J. Am. Chem. Soc., 1990, 112, 1337–1343.
60. A. Anne, P. Hapiot, J. Moiroux, P. Neta and J. M. Saveant, J. Am. Chem. Soc., 1992, 114, 4694–4701.
61. A. Anne, J. Moiroux and J. M. Saveant, J. Am. Chem. Soc., 1993, 115, 10224–10230.
62. A. Anne, S. Fraoua, V. Grass, J. Moiroux and J.-M. Savéant, J. Am. Chem. Soc., 1998, 120, 2951–2958.
63. H. Jaegfeldt, J. Electroanal. Chem. Interfacial Electrochem., 1980, 110, 295–302.
64. R. M. G. Roberts, D. Ostovic and M. M. Kreevoy, Faraday Discuss. Chem. Soc., 1982, 74, 257–265.
65. M. M. Kreevoy, D. Ostovic, D. G. Truhlar and B. C. Garrett, J. Phys. Chem., 1986, 90, 3766–3774.
66. I.-S. H. Lee, E. H. Jeoung and M. M. Kreevoy, J. Am. Chem. Soc., 1997, 119, 2722–2728.
67. Y. Kim, D. G. Truhlar and M. M. Kreevoy, J. Am. Chem. Soc., 1991, 113, 7837–7847.
68. M. M. Kreevoy and I. S. H. Lee, J. Am. Chem. Soc., 1984, 106, 2550–2553.
69. D. Ostovic, R. M. G. Roberts and M. M. Kreevoy, J. Am. Chem. Soc., 1983, 105, 7629–7631.
70. X.-Q. Zhu, Y. Tan and C.-T. Cao, J. Phys. Chem. B, 2010, 114, 2058–2075.
71. X.-Q. Zhu, M.-T. Zhang, A. Yu, C.-H. Wang and J.-P. Cheng, J. Am. Chem. Soc., 2008, 130, 2501–2516.
72. X.-Q. Zhu, Y. Yang, M. Zhang and J.-P. Cheng, J. Am. Chem. Soc., 2003, 125, 15298–15299.
73. X.-Q. Zhu, H.-R. Li, Q. Li, T. Ai, J.-Y. Lu, Y. Yang and J.-P. Cheng, Chem – Eur. J., 2003, 9, 871–880.
74. X.-Q. Zhu, L. Cao, Y. Liu, Y. Yang, J.-Y. Lu, J.-S. Wang and J.-P. Cheng, Chem – Eur. J., 2003, 9, 3937–3945.
75. X.-Q. Zhu, X. Chen and L.-R. Mei, Org. Lett., 2011, 13, 2456–2459.
76. X.-Q. Zhu, Y.-Y. Mu and X.-T. Li, J. Phys. Chem. B, 2011, 115, 14794–14811.
77. X.-Q. Zhu, Q.-Y. Liu, Q. Chen and L.-R. Mei, J. Org. Chem., 2010, 75, 789–808.
78. X.-Q. Zhu, M. Zhang, Q.-Y. Liu, X.-X. Wang, J.-Y. Zhang and J.-P. Cheng, Angew. Chem., Int. Ed., 2006, 45, 3954–3957.
79. X.-Q. Zhu, F.-H. Deng, J.-D. Yang, X.-T. Li, Q. Chen, N.-P. Lei, F.-K. Meng, X.-P. Zhao, S.-H. Han, E.-J. Hao and Y.-Y. Mu, Org. Biomol. Chem., 2013, 11, 6071–6089.
80. G. R. Wyatt, Biochem. J., 1951, 48, 584–590.
81. M. W. Powner, B. Gerland and J. D. Sutherland, Nature, 2009, 459, 239–242.
82. C. Shih, V. J. Chen, L. S. Gossett, S. B. Gates, W. C. MacKellar, L. L. Habeck, K. A. Shackelford, L. G. Mendelsohn, D. J. Soose, V. F. Patel, S. L. Andis, J. R. Bewley, E. A. Rayl, B. A. Moroson, G. P. Beardsley, W. Kohler, M. Ratnam and R. M. Schultz, Cancer Res., 1997, 57, 1116–1123.
83. G. B. Elion, E. Burgi and G. H. Hitchings, J. Am. Chem. Soc., 1952, 74, 411–414.
84. R. W. Klecker, J. M. Collins, R. Yarchoan, R. Thomas, J. F. Jenkins, S. Broder and C. E. Myers, Clin. Pharmacol. Ther., 1987, 41, 407–412.
85. C. Oliver Kappe, Tetrahedron, 1993, 49, 6937–6963.
86. F. Bigi, S. Carloni, B. Frullanti, R. Maggi and G. Sartori, Tetrahedron Lett., 1999, 40, 3465–3468.
87. J. Peng and Y. Deng, Tetrahedron Lett., 2001, 42, 5917–5919.
88. B. C. Ranu, A. Hajra and U. Jana, J. Org. Chem., 2000, 65, 6270–6272.
89. C. O. Kappe, Acc. Chem. Res., 2000, 33, 879–888.
90. M. Nizam Mohideen, A. Rasheeth and C. A. M. A. Huq, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, o1812.
91. W. C. Wong, W. Sun, B. Lagu, D. Tian, M. R. Marzabadi, F. Zhang, D. Nagarathnam, S. W. Miao, J. M. Wetzel, J. Peng, C. Forray, R. S. L. Chang, T. B. Chen, R. Ransom, S. O'Malley, T. P. Broten, P. Kling, K. P. Vyas, K. Zhang and C. Gluchowski, J. Med. Chem., 1999, 42, 4804–4813.
92. G. C. Rovnyak, S. D. Kimball, B. Beyer, G. Cucinotta, J. D. DiMarco, J. Gougoutas, A. Hedberg, M. Malley and J. P. McCarthy, J. Med. Chem., 1995, 38, 119–129.
93. G. C. Rovnyak, K. S. Atwal, A. Hedberg, S. D. Kimball, S. Moreland, J. Z. Gougoutas, B. C. O'Reilly, J. Schwartz and M. F. Malley, J. Med. Chem., 1992, 35, 3254–3263.
94. K. S. Atwal, B. N. Swanson, S. E. Unger, D. M. Floyd, S. Moreland, A. Hedberg and B. C. O'Reilly, J. Med. Chem., 1991, 34, 806–811.
95. K. S. Atwal, G. C. Rovnyak, S. D. Kimball, D. M. Floyd, S. Moreland, B. N. Swanson, J. Z. Gougoutas, J. Schwartz, K. M. Smillie and M. F. Malley, J. Med. Chem., 1990, 33, 2629–2635.
96. K. S. Atwal, G. C. Rovnyak, J. Schwartz, S. Moreland, A. Hedberg, J. Z. Gougoutas, M. F. Malley and D. M. Floyd, J. Med. Chem., 1990, 33, 1510–1515.
97. E. Kolvari, N. Koukabi and O. Armandpour, Tetrahedron, 2014, 70, 1383–1386.
98. S. Maddila and S. B. Jonnalagadda, Arch. Pharm., 2012, 345, 163–168.
99. B. Piqani and W. Zhang, Beilstein J. Org. Chem., 2011, 7, 1294–1298.
100. Suresh, A. Saini, D. Kumar and J. S. Sandhu, Green Chem. Lett. Rev., 2009, 2, 29–33.
101. G. A. Gross, H. Wurziger and A. Schober, J. Comb. Chem., 2006, 8, 153–155.
102. A. Lengar and C. O. Kappe, Org. Lett., 2004, 6, 771–774.
103. J. Lu, Y. Bai, Z. Wang, B. Yang and H. Ma, Tetrahedron Lett., 2000, 41, 9075–9078.
104. C. O. Kappe and P. Roschger, J. Heterocycl. Chem., 1989, 26, 55–64.
105. X.-Q. Zhu, H. Liang, Y. Zhu and J.-P. Cheng, J. Org. Chem., 2008, 73, 8403–8410.
106. D. D. M. Wayner and V. D. Parker, Acc. Chem. Res., 1993, 26, 287–294.
107. Z. M. Heiden and A. P. Lathem, Organometallics, 2015, 34, 1818–1827; X.-Q. Zhu, J. Zhou, C.-H. Wang, X.-T. Li and S. Jing, J. Phys. Chem. B, 2011, 115, 3588–3603.
108. E. S. Wiedner, M. B. Chambers, C. L. Pitman, R. M. Bullock, A. J. M. Miller and A. M. Appel, Chem. Rev., 2016, 116, 8655–8692.
109. Y.-R. Luo, Handbook of Bond Dissociation Energies in Organic Compounds, 3rd edn, Science Press, 2002.
110. I. M. Kolthoff and M. K. Chantooni, J. Phys. Chem., 1966, 70, 856–866.
111. Y. Hayakawa, T. Iwase, E. J. Nurminen, M. Tsukamoto and M. Kataoka, Tetrahedron, 2005, 61, 2203–2209.
112. O. B. Ryan, M. Tilset and V. D. Parker, J. Am. Chem. Soc., 1990, 112, 2618–2626.
113. L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103.
114. C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195.
115. N. S. Isaacs, Longman Scientific & Technical, Wiley & Sons, 1995, ch. 2.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed NMR, CV, OSWV and ITC spectra of dihydropyrimidine derivatives; the plots of thermodynamic parameters against the Hammett substituent parameter. See DOI: 10.1039/c6ob02195f

---