Role of Lewis acid additives in a palladium catalyzed directed C–H functionalization reaction of benzohydroxamic acid to isoxazolone†
C.
Athira
and
Raghavan B.
Sunoj
*
Department of Chemistry, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India. E-mail: sunoj@chem.iitb.ac.in
First published on 23rd November 2016
Abstract
Metallic salts as well as protic additives are widely employed in transition metal catalyzed C–H bond functionalization reactions to improve the efficiency of catalytic protocols. In one such example, ZnCl2 and pivalic acid are used as additives in a palladium catalyzed synthesis of isoxazolone from a readily available benzohydroxamic acid under one pot conditions. In this article, we present some important mechanistic insights into the role of ZnCl2 and pivalic acid, gained by using density functional theory (M06) computations. Two interesting modes of action of ZnCl2 are identified in various catalytic steps involved in the formation of isoxazolone. The conventional Lewis acid coordination wherein zinc chloride (ZnCl2·(DMA)) binds to the carbonyl group is found to be more favored in the C–H activation step. However, the participation of a hetero-bimetallic Pd–Zn species is preferred in reductive elimination leading to Caryl–N bond formation. Pivalic acid helps in relay proton transfer in C–H bond activation through a cyclometallation deprotonation (CMD) process. The explicit inclusion of ZnCl2 and solvent N,N-dimethyl acetamide (DMA) stabilizes the transition state and also helps reduce the activation barrier for the C–H bond activation step. The electronic communication between the two metal species is playing a crucial role in stabilizing the Caryl–N bond formation transition state through a Pd–Zn hetero-bimetallic interaction.
Introduction
Transition metal catalyzed aromatic C–H bond functionalization has evolved as an effective tool in organic synthesis.1 In spite of its impressive progress, selective C–H bond activation continues to present certain challenges.2 The desired selectivity can be achieved either by using a Directing Group (DG) on the substrate3 or by suitable ligand combinations on the transition metal.4 For instance, ortho aryl C–H bond activations are typically accomplished by using various DGs.5 Different kinds of DGs are used in C–H bond activation reactions.6 In a typical scenario, the transition metal binds to the DG and enables the formation of a metallacyclic intermediate.7 These directing groups can be electron donating or electron withdrawing in nature.8 Among these directing groups, the –CONHR group has gained considerably more attention because of its versatility and due to its ability to serve as a precursor to C–N bond formation through additional synthetic manipulation.9 The selectivity can also be altered due to the nature of the R group on the amide moiety.10 The molecular understanding of chemo-selectivity and reactivity offered by the DGs has formed the basis of a number of experimental as well as computational studies.6,11The reactivity and selectivity in directed aryl C–H bond activation are sometimes improved by using a protic species or a metallic salt as additives.12 The most recent practices indicate an increasing usage of Lewis acids (LA) and silver salt (oxidants) additives. Metallic salt additives, such as that of copper and silver, are not only known to act as oxidants in the regeneration of the catalyst but they can also help in other steps of the catalytic cycle.13 Such metal salts are proposed to interact with the substrate or with the native catalyst. However, the molecular understanding of the role of additives in a catalytic cycle remains only in its infancy at this time.
Although amides are important DGs in C–H functionalization, other variants such as hydroxamic acid have also been employed in the synthesis of interesting natural products.14 In a recent example, benzisoxazolones,15 an important biologically active compound was synthesized from benzohydroxamic acids via C–H bond activation by using palladium catalysis in the presence of zinc chloride (ZnCl2) and pivalic acid under one-pot conditions (Scheme 1).16 A few important features of this C–H functionalization reaction are (a) the use of a relatively less common ZnCl2 as the Lewis acid additive,17 (b) it offers a method for Caryl–N bond formation, which is mechanistically less understood than the analogous Caryl–C bond forming reactions.18 In arene functionalization, zinc salts are generally regarded as transmetalating agents that provide an intermediate organo zinc compound. Alternative modes of participation of zinc salts in transition metal catalysis are not widely reported. Hence, it is of inherent interest to examine the potential role of ZnCl2 in the mechanism of formation of benzisoxazolones.
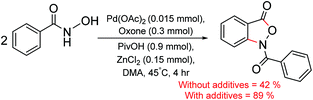 | ||
| Scheme 1 Palladium catalyzed isoxazolone synthesis from benzohydroxamic acid (ref. 16). | ||
It is important to note that the reactivity and efficiency in palladium-catalyzed isoxazolone synthesis, as shown in Scheme 1, have been reported to be better with ZnCl2.16 To establish the role of these additives, we first envisaged two different modes of action of ZnCl2 in the catalytic cycle. In the Lewis acid mode of action, ZnCl2 is bound to the directing group (carbonyl oxygen of the hydroxamic moiety) without any direct interaction with the palladium centre. In another mode, the involvement of a Pd–Zn hetero-bimetallic interaction is considered in various steps of the catalytic cycle. In the following sections, interesting energetic and geometric features of the catalytic cycle is presented.
Computational methods
All the stationary points on the potential energy surface such as reactants, intermediates, transition states and products were optimized in the gas phase at the M06/LANL2DZ basis set (Pd and Zn) with the corresponding Hay–Wadt effective core potential for Pd and Zn, 6-31G**(C, H, O, N, Cl) level of theory by using the Gaussian09 suite of quantum chemical programs.19,20 Fully optimized geometries of all the stationary points were characterized by frequency calculations at the M06/LANL2DZ(Pd,Zn),6-31G** level of theory in order to verify that the transition states (TSs) have one and only one imaginary frequency for the desired reaction coordinate and all minima have no imaginary frequencies. Intrinsic Reaction Coordinate (IRC) calculations were also performed at the same level of theory to further verify that the TS on the potential energy surface connects to the desired minima on either side of the first order saddle point.21 The final geometries obtained from the IRC calculations on both sides of the first order saddle point were subsequently subjected to further geometry optimization by using ‘OPT = CALCFC’ option. The effect of solvation was carried out by using N,N-dimethyl acetamide as the continuum dielectric (ε = 37.781) using the SMD solvation model.22 Single point energies were calculated in the condensed phase at the SMD(DMA)/M06/SDD(Pd,Zn),6-31G** and also at the SMD(DMA)/M06/LANL2DZ(Pd,Zn),6-31G** levels of theory using the gas phase geometries.23 Thermal and entropic corrections were then applied to the single point energies to obtain the Gibbs energies of various stationary points. The default electronic energies, which refer to an ideal gas (p = 1 atm) standard state, were corrected so as to convert the same to the standard state corresponding to a species in solution with a standard concentration of 1 mol L−1. A uniform standard state correction of RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.5) was added to the electronic energies of the reactants, intermediates and transition states computed at the SMD(DMA)/M06/SDD(Pd,Zn),6-311+G** level of theory to obtain the Gibbs free energies using eqn (1) given below, where ‘°’ and ‘°′’ are the standard states respectively at 1 atm pressure and 1 mol L−1, in the gas phase.24 The temperature of the reaction under investigation is 45 °C and hence T is set equal to 318 K in eqn (1).16 Numerical value for the correction factor for the above equation is 2.0 kcal mol−1. The discussions are presented on the basis of the Gibbs free energies at the SMD(DMA)/M06/SDD(Pd,Zn),6-311+G**//M06/LANL2DZ(Pd,Zn),6-31G** level of theory. The single point energies in the condensed phase at the SMD(DMA)/M06/LANL2DZ(Pd,Zn),6-31G**//M06/LANL2DZ(Pd,Zn),6-31G** level of theory are provided in the ESI.† Natural Bonding and Orbital (NBO) analysis was carried out for some of the important Caryl–N bond formation transition states involving a Pd–Zn heterobimetallic species.25
ln(24.5) was added to the electronic energies of the reactants, intermediates and transition states computed at the SMD(DMA)/M06/SDD(Pd,Zn),6-311+G** level of theory to obtain the Gibbs free energies using eqn (1) given below, where ‘°’ and ‘°′’ are the standard states respectively at 1 atm pressure and 1 mol L−1, in the gas phase.24 The temperature of the reaction under investigation is 45 °C and hence T is set equal to 318 K in eqn (1).16 Numerical value for the correction factor for the above equation is 2.0 kcal mol−1. The discussions are presented on the basis of the Gibbs free energies at the SMD(DMA)/M06/SDD(Pd,Zn),6-311+G**//M06/LANL2DZ(Pd,Zn),6-31G** level of theory. The single point energies in the condensed phase at the SMD(DMA)/M06/LANL2DZ(Pd,Zn),6-31G**//M06/LANL2DZ(Pd,Zn),6-31G** level of theory are provided in the ESI.† Natural Bonding and Orbital (NBO) analysis was carried out for some of the important Caryl–N bond formation transition states involving a Pd–Zn heterobimetallic species.25ΔG°′ = ΔG + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Q°′|Q°) ln(Q°′|Q°) | (1) |
The relative energies of all the stationary points are calculated with respect to the infinitely separated reactants. The catalyst used in the reaction under investigation is palladium acetate in N,N-dimethyl acetamide (DMA) solvent. Palladium acetate is known to exist as a trimer in the gas phase and in solvents of low polarity.26 In highly polar solvents, the palladium acetate trimer dissociates to form a monomer.27 Since DMA is a polar solvent (ε = 37.781), the palladium acetate trimer is considered as a monomer in the present investigation. The structure of ZnCl2 is linear in the gas phase.28 In the solvent phase, ZnCl2 generally adopts a tetrahedral geometry by coordinating with two solvent molecules or with other available ligands.29 In the present reaction, DMA can coordinate with zinc either via the nitrogen of the amide group or via the oxygen of the carbonyl group. On the basis of this literature precedence and chemical intuition, we have taken ZnCl2 bound to two molecules of DMA through the carbonyl oxygen as the reference. The use of ZnCl2(DMA)2 ensures that the central metal ion is maintained in its preferred tetra-coordinate environment. Binding of DMA to ZnCl2 through the carbonyl oxygen is found to be relatively more preferred (∼11.5 kcal mol−1) than that to the nitrogen. Benzohydroxamic acid exists mainly as a Z-amide wherein it is stabilized by intramolecular hydrogen bonding.30 It has been suggested that in polar aprotic solvents, benzohydroxamic acid exists as an N-acid whereas in polar protic solvents it acts as an O-acid.29b Thus, the Z-amide structure of benzohydroxamic acid in its N-acid form is considered as the reference for our calculation of the relative free energies. In addition, in the reaction mixture, both acetate and pivalate ions are present and both these ligands can bind to the palladium centre. Thus, we have also investigated each step in the catalytic cycle, with either acetate or pivalate as ligands.
Results and discussion
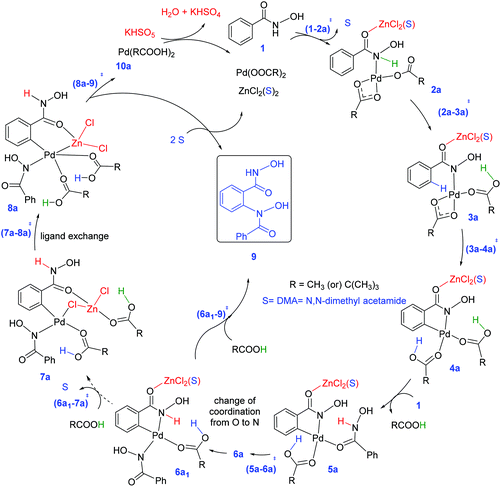
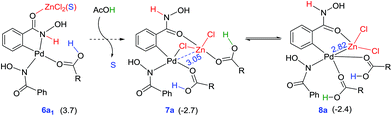
The mechanism of formation of isoxazolone in the presence of zinc chloride is shown in Scheme 2. One of the key objectives of this study is to examine whether the incorporation of ZnCl2 has any notable effect on the energetic course of the reaction. To this end, each elementary step of the catalytic cycle is considered with and without the participation of ZnCl2. Since pivalic acid is used as a protic additive, it could displace the palladium-bound acetate(s), leading to additional possibilities.31 In the beginning of the catalytic cycle, the formation of a catalyst–substrate complex is considered wherein the nitrogen atom of the directing group coordinates to Pd(II) through (1–2a)‡ to give intermediate 2a.32 The next step involves N–H deprotonation via(2a–3a)‡ to give intermediate 3a. In 3a, Pd(II) comes in close proximity to the ortho C–H bond of benzohydroxamic acid, and helps in ortho C–H bond activation. The ensuing cyclometallation deprotonation (CMD) through (3a–4a)‡ leads to a five-membered palladacycle intermediate (4a). As a result of these steps, two of the carboxylate ligands on palladium become neutral carboxylic acids which are labile, rendering a conducive situation for ligand exchange. Thus in the next step, a second molecule of the substrate (1) enters the catalytic cycle by displacing one of the carboxylic acid molecules from the inner-sphere of 4a. An intramolecular proton transfer in the resulting intermediate 5avia(5a–6a)‡ leads to 6a.33 The intermediate 6a undergoes a change of coordination of hydroxamic acid from oxygen to nitrogen to give intermediate 6a1. The intermediate 6a1 can undergo a direct reductive elimination to give product 9via(6a1–9)‡.An alternative possibility is to consider the participation of the neutral acetic acid, generated in the earlier steps of the catalytic cycle. As it can be noticed the coordination environment of zinc is satisfied by one DMA and the other by the substrate in 6a1. It can be envisaged that one such solvent molecule on the zinc atom can be substituted by an acetic acid. We noticed that the displacement of DMA by acetic acid leads to an interesting chloro bridged cyclopalladated intermediate 7a. In intermediate 7a, when the acetic acid migrates from zinc to the palladium centre, another intermediate (8a) with a hetero-bimetallic Pd–Zn interaction is identified. The reductive elimination from the bimetallic intermediate 8avia(8a–9)‡ generates the desired product 9. The intermediate 9 formed through reductive elimination can now undergo nucleophilic addition–elimination to furnish the desired isoxazolone as the final product.34 The Pd(0) intermediate 10a can then be oxidized by KHSO5 to regenerate the native catalyst such that the catalytic cycle continues with the uptake of a new molecule of the substrates.
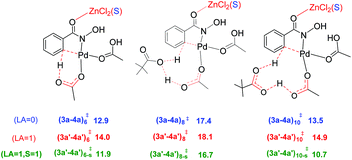
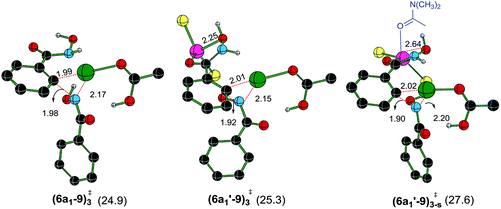
The N–H deprotonation of the hydroxamic acid moiety is found to be a barrierless process.33,35 The effect of the Lewis acid, if any, is therefore expected to be more pronounced in the other steps such as the C–H activation and/or the reductive elimination (Caryl–N bond formation). Fig. 1 provides a succinct comparison of different likely CMD transition states with and without the participation of (i) the protic additive (pivalic acid), and (ii) Lewis acid (ZnCl2 and ZnCl2 bound to an explicit solvent, denoted using ′).36 It can be noted that the most preferred CMD transition state is (3a′–4a′)10-s‡ (where subscripts 10 and s respectively denote the number of atoms involved in the CMD process and solvent molecules coordinated to the zinc atom). Here, an explicit molecule of pivalic acid assists in the transfer of the Caryl–H proton to the Pd-bound acetate while ZnCl2·(DMA) is bound to the carbonyl oxygen of the directing group. A comparison of (3a′–4a′)10-s‡ and (3a′–4a′)6-s‡ suggests that ZnCl2·(DMA) and pivalic acid can lead to a lower energy CMD pathway. In (3a′–4a′)10-s‡, the carboxylic acid additive (pivalic acid) acts in a bifunctional mode in the C–H activation. Such kind of proton relay facilitated by protic additives (Brønsted acids, water or other protic solvents) is reported to lower the activation energy as well as relative energies of the proton transfer transition state.37 We note that zinc tends to form a strained higher energy chelated structure with the OH group of the hydroxamic moiety in the absence of an explicit DMA on it. DMA coordination provides additional stabilization by relieving the strain in the chelated binding mode. The coordination of Lewis acid (ZnCl2·DMA) as well as the H-bonding ability of the carboxylic acid additive can act together toward lowering the transition state energy of the C–H activation step.38
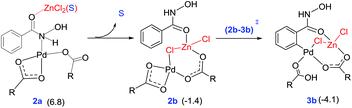
An increasing number of reports have emerged in the recent times on hetero-bimetallic interactions and its role in catalysis.39 Potential involvement of hetero-bimetallic complexes under homogeneous catalytic conditions is now being discussed in the current literature. Most of such reports are on the use of bimetallic catalysts by design. In other words, the catalysts were prepared prior to the use in a reaction. Herein, we ask a different question as to whether such bimetallic interactions could exist when a transition metal catalyst is used in conjunction with another metal salt additive. The possibility of such intermetallic interactions should be regarded as higher when one aims to understand the role of metallic additives, such as in the present reaction, wherein the actual role of ZnCl2 remained rather vague. Recently, we as well as other groups have reported that the presence of a Pd–Ag heterobimetallic interaction could exhibit notable energetic advantage over a conventional monometallic alternative in an aryl amination reaction in the C–H activation step of the reaction.13 A likely scenario involving a Pd–Zn hetero-bimetallic interaction is examined in this study.40 First, a number of different bridged Pd–Zn species (e.g., acetate–acetate and chloro-acetate) were examined to find that a chloro-carboxylate mixed bridging arrangement is the most preferred one.41 The catalyst–substrate complex 2a (6.8 kcal mol−1) can rearrange to another intermediate 2b that exhibits a Pd–Zn hetero-bimetallic interaction (−1.4 kcal mol−1). This can be achieved by the displacement of the solvent molecule from the zinc centre by the Pd-bound acetate ligand, as shown in Fig. 2. This intermediate 2b with a chloro-acetate intermetallic bridge can then undergo C–H activation via(2b–3b)‡ resulting in a carbopalladated intermediate 3b (−4.1 kcal mol−1).42
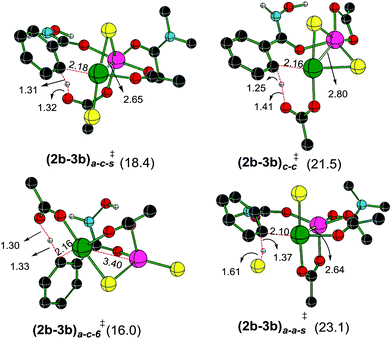
A representative set of bridging ligand combinations and the corresponding transition states are provided in Fig. 3. The subscripts a and c respectively denote an acetate and a chloro bridge, leading to a bis-acetate (a–a), bis-chloro (c–c), and mixed (a–c) bridges between Pd and Zn (subscript s denotes the binding of solvent DMA to zinc).43 Owing to the oxophilicity of zinc, substrate coordination through the carbonyl oxygen is found to be more preferred. It can be noted that the Pd–Zn distances exhibit significant variations depending on the nature of the bridging ligand. For instance, the Pd–Zn distance in the case of an a–c mixed bridge is short (2.65 Å), which is comparable to the experimentally known Pd–Zn distance of 2.58 Å.40 Geometric comparison between (2b–3b)a–c-s‡ and (2b–3b)a–c-6‡ conveys that the coordination of the solvent DMA molecule on zinc results in a decrease in the Pd–Zn distance. A shorter distance facilitates an enhanced interaction between the two metals and is found to destabilize the CMD transition state. The a–c bridged (2b–3b)a–c-6‡ is the lowest energy CMD transition state with a Pd–Zn distance of 3.46 Å, suggesting that the enhanced interaction between the two metals is not rendering much stabilization to the CMD transition state. A similar trend is observed in the case of (2b–3b)a–a-s‡ having a bis-acetate bridge with a Pd–Zn distance of 2.64 Å, which is about 7.1 kcal mol−1 higher than (2b–3b)a–c-6‡. The nature of the ligand that is involved in the deprotonation is also important in influencing the energies of the Pd–Zn hetero-bimetallic transition states. For example, in (2b–3b)a–c-s‡ and (2b–3b)a–a-s‡, both having a Pd–Zn distance of ∼2.65 Å, (2b–3b)a–c-s‡ lower by about 4.7 kcal mol−1 than (2b–3b)a–a-s‡. The nature of the ligands on (i) the metals, (ii) intermetallic bridges and (iii) that involved in the CMD process can all influence the energetics of these transition states. The comparison of two different modes of action of Lewis acid on the CMD transition states suggests that the transition state with a Pd–Zn interaction is less favored ((2b–3b)a–c-6‡, 16.0 kcal mol−1, Fig. 3) over that devoid of the Pd–Zn contact ((3a′–4a′)10-s‡, 10.7 kcal mol−1, Fig. 1). Even though the formation of Pd–Zn hetero-bimetallic species is favorable in the initial stages of the reaction (Fig. 2) via ligand displacement, the corresponding C–H bond activation from 2b is energetically less favorable.43
The next most important step in the catalytic cycle is the Caryl–N bond formation through a reductive elimination in intermediate 6a1. The effect of ZnCl2 on reductive elimination is analyzed by comparing two scenarios, with and without the binding of ZnCl2 on the directing group. As presented earlier, after the N–H deprotonation from the second hydroxamic acid, intermediate 6a1 is formed. Now, the Caryl–N bond formation can occur via a three-membered reductive elimination transition state (6a1–9)3‡ as shown in Fig. 4.44 Contrary to that in the CMD step, the Gibbs free energy of (6a1′–9)3-s‡, wherein ZnCl2·(DMA) is bound to the substrate, is found to be energetically less preferred over a chelated binding mode of ZnCl2 without any DMA coordination ((6a1′–9)3‡) and that without any ZnCl2 as in (6a1–9)3‡. The relative Gibbs free energies of the reductive elimination transition states for the formation of the Caryl–N bond, with (only ZnCl2) and without the Lewis acid, are of comparable energy (25.3 and 24.9 kcal mol−1via(6a1′–9)3‡ and (6a1–9)3‡ respectively). This indicates that the solvent dissociation is likely to occur prior to the reductive elimination step.
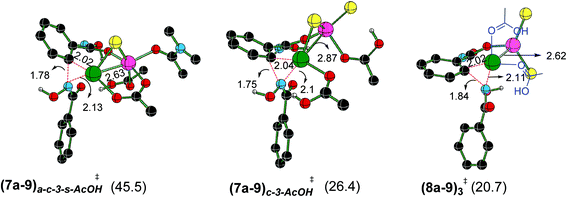
Similar to that in the previous step, the intermediate 6a1′s can also undergo ligand exchange to generate intermediate 7a where the zinc comes in close contact with the palladium center as shown in Fig. 5. The palladacycle intermediate 6a1′s with a Pd–N coordination is found to be capable of a facile amide bond rotation to furnish another intermediate 7a with a chloro bridge between Zn and Pd.45 What is more important in 7a is that it exhibits a Pd–Zn hetero-bimetallic interaction facilitated by an intermetallic chloro bridge.46 The intermediate 7a, in turn, can undergo further rearrangement wherein the carboxylic acid migrates from Zn to Pd. A more direct Pd–Zn interaction is noted in the resulting intermediate 8a (−2.4 kcal mol−1) without the chloro bridge.47 The intermediate 7a or 8a with Pd–Zn hetero-bimetallic interaction can now undergo reductive elimination to generate the product precursor 9.
The optimized geometries of important Caryl–N bond formation transition states in the Pd–Zn hetero-bimetallic mode of activation are provided Fig. 6.48 The closer intermetallic contact in (8a–9)3‡ is likely to help in tuning the electronic feature of palladium center that promotes a single-site reductive elimination. Alternative possibilities for Caryl–N bond formation, involving hetero-bimetallic a–c bridged ((7a–9)a–c-3-s-AcOH‡) and chloride bridged ((7a–9)c-3-AcOH‡) transition states are found to be of higher energy (here, the subscripts immediately following the transition state notations denote the bridging ligands and the later ones are for the solvent coordination to the zinc atom). The coordination of neutral ligands (DMA, AcOH or both) on zinc does not offer any notable advantage in the Caryl–N bond formation ((7a–9)a–c-3-s-AcOH‡ and (7a–9)c-3-AcOH‡). The natural bond orbital analysis revealed vital electron delocalizations from Pd to Zn in these transition states,49 that helps lower the electron density on palladium and thus favors the reductive elimination. Zinc is found to act as a better acceptor in the lower energy transition state (8a–9)3‡ as compared to (7a–9)a–c-3-s-AcOH‡ and (7a–9)c-3-AcOH‡. In two of the latter cases, zinc accepts electrons from the coordinated AcOH and DMA.
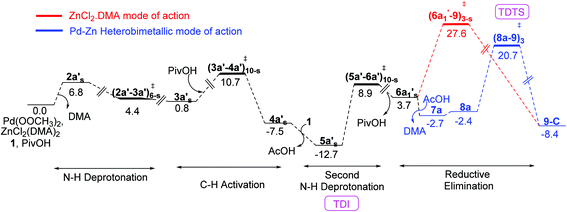
The Gibbs free energy profile for the catalytic cycle, leading to the formation of the product precursor 9, is provided in Fig. 7. Some interesting features of this reaction can be gathered through the inspection of the energetics. The elementary step barrier for the CMD process, when ZnCl2·DMA coordinated to the carbonyl oxygen of the directing group, computed as the difference in energy between (3a′–4a′)10-s‡ and the preceding intermediate 3a′s, is found to be 9.9 kcal mol−1. The corresponding activation energy for the CMD process without ZnCl2·DMA participation is of much higher energy (14.0 kcal mol−1).35b After the second hydroxamic acid N–H deprotonation, the intermediate 6a1′s rearranges to a lower energy Pd–Zn hetero-bimetallic species 7avia ligand exchange. The Gibbs free energy of the transition states for the Caryl–N bond formation with a shorter Pd–Zn contact, is about 4–7 kcal mol−1 lower than that when the conventional monometallic palladium acetate is considered as the active catalyst (Fig. 6). For instance, the Gibbs free energy of (8a–9)3‡ exhibiting a direct Pd–Zn interaction is 6.9 kcal mol−1 lower than (6a1′–9)3-s‡ in a conventional monometallic mechanism wherein ZnCl2·DMA is bound only to the carbonyl oxygen of the directing group. Similarly, the hetero-bimetallic transition state (8a–9)3‡ is 4.2 kcal mol−1 lower than (6a1–9)3‡ in the absence of ZnCl2·DMA (Fig. 4 and 6). The corresponding activation barrier without Lewis acid participation is found to be 34.8 kcal mol−1.50 The activation barrier for the Caryl–N bond formation through (8a–9)3‡, calculated with respect to the preceding exoergic intermediate 7a (23.4 kcal mol−1) and the relative energy with respect to the separated reactants (20.7 kcal mol−1) are lower than the corresponding conventional monometallic reductive elimination transition state (6a1′–9)3-s‡. In fact, the activation barrier for the conventional monometallic route is as high as 40.2 kcal mol−1 with respect to the preceding exoergic intermediate (5a′s).35b On the basis of the Gibbs free energy profile, a ligand exchange is highly likely prior to the reductive elimination so as to generate an exoergic hetero-bimetallic species 7a. The conversion of 7a to 8a and then to the product precursor 9 provides a lower energy pathway for the catalytic cycle.
We have also analysed the overall Gibbs free energy profile using the energetic span model proposed.51 In this method, the catalytic efficiency determined by the turnover frequency (TOF). In a catalytic cycle, the TOF is determined by only one transition state and one intermediate known as the TOF-determining transition state (TDTS) and TOF-determining intermediate (TDI) respectively. The TDI is the lowest energy intermediate in the overall Gibbs free energy profile and TDTS is the transition state which gives maximum energy span (δE). In the Gibbs free energy profile diagram (Fig. 7), the intermediate 5a′s is the TDI and (8a–9)‡3 is the TDTS. It can be noted that the energetic span (δE) for the Caryl–N bond formation in the presence of ZnCl2 is 33.4 kcal mol−1 whereas in the absence of ZnCl2 the span is 34.8 kcal mol−1.51b Although the computed energetic span is moderately higher than expected, the role of the Lewis acid additive is clearly established that it improves the catalytic efficiency through its favorable role in the reductive elimination step of the reaction.
Conclusions
Molecular insights on the role of the Lewis acid additive (ZnCl2) and a protic additive (pivalic acid) has been established by using DFT(M06) computational tools. Different modes of ZnCl2 participation in the C–H activation and the reductive elimination steps in the palladium catalyzed reaction between two molecules of benzohydroxamic acid leading to isoxazolone has been examined in this study. The coordination of ZnCl2·DMA to the carbonyl oxygen of the amido directing group has been found to be lower in energy for the cyclometallation deprotonation step. However, the corresponding mode of Lewis acid–substrate interaction led to a less favorable reductive elimination as compared to an alternative pathway involving a direct Pd–Zn hetero-bimetallic species obtained via a chloride to acetic acid ligand exchange process between palladium and zinc. The computed energetics is comparable with the reported experimental conditions for this reaction. With a Pd–Zn hetero-bimetallic species, the zinc serves as an acceptor of the palladium electrons and offers additional stabilization to the reductive elimination transition state. Fine-tuning of the ligands around the metals could offer interesting variations to the reactivity of hetero-bimetallic catalytic systems. The insights presented here could help perceive the role of additives as going beyond being a passive species and would help exploit the latent potential of hetero-bimetallic catalytic systems for C–H functionalization reactions.Acknowledgements
We are grateful to IIT Bombay supercomputing for the computational facilities. C. A. acknowledges a senior research fellowship from the Council for Scientific and Industrial Research (CSIR-New Delhi). We acknowledge Dr Chandan Patel for helpful discussions during the course of revising this manuscript.References
-
(a) J. Yamaguchi, A. D. Yamaguchi and K. Itami, Angew. Chem., Int. Ed., 2012, 51, 8960–9009 CrossRef CAS PubMed
; (b) D. Y.-K. Chen and S. W. Youn, Chem – Eur. J., 2012, 18, 9452–9474 CrossRef CAS PubMed
.
-
(a) S. R. Neufeldt and M. S. Sanford, Acc. Chem. Res., 2012, 45, 936–946 CrossRef CAS PubMed
; (b) G. B. Shul'pin, Org. Biomol. Chem., 2010, 8, 4217–4228 RSC
.
-
(a) L. Ackreman, Acc. Chem. Res., 2014, 47, 281–295 CrossRef PubMed
; (b) J. Karthikeyan and C.-H. Cheng, Angew. Chem., Int. Ed., 2011, 50, 9880–9883 CrossRef CAS PubMed
; (c) T. Wu, X. Mu and G. Liu, Angew. Chem., Int. Ed., 2011, 50, 12578–12581 CrossRef CAS PubMed
; (d) T. W. Lyons and M. S. Sanford, Chem. Rev., 2010, 110, 1147–1169 CrossRef CAS PubMed
.
-
(a) L.-C. Campeau, D. J. Schipper and K. Fagnou, J. Am. Chem. Soc., 2008, 130, 3266–3267 CrossRef CAS PubMed
; (b) M. H. Emmert, A. K. Cook, Y. J. Xie and M. S. Sanford, Angew. Chem., Int. Ed., 2011, 50, 9409–9412 CrossRef CAS PubMed
.
-
(a) T. Matsubara, S. Asako, L. Ilies and E. Nakamura, J. Am. Chem. Soc., 2014, 136, 646–649 CrossRef CAS PubMed
; (b) X.-C. Wang, Y. Hu, S. Bonacorsi, Y. Hong, R. Burrell and J.-Q. Yu, J. Am. Chem. Soc., 2013, 135, 10326–10329 CrossRef CAS PubMed
; (c) F. J. Chen, S. Zhao, F. Hu, K. Chen, Q. Zhang, S. Q. Zhanga and B. F. Shi, Chem. Sci., 2013, 4, 4187–4192 RSC
.
-
(a) T. Wu, X. Mu and G. Liu, Angew. Chem., Int. Ed., 2011, 50, 12578–12581 CrossRef CAS PubMed
; (b) Z. Ren, F. Mo and G. Dong, J. Am. Chem. Soc., 2012, 134, 16991–16994 CrossRef CAS PubMed
.
-
(a) M. Albrecht, Chem. Rev., 2010, 110, 576–623 CrossRef CAS PubMed
; (b) M. Zhang, Y. Zhang, X. Jie, H. Zhao, G. Li and W. Su, Org. Chem. Front., 2014, 1, 843–895 RSC
.
- L V. Desai, K. J. Stowers and M. S. Sanford, J. Am. Chem. Soc., 2008, 130, 13285–13293 CrossRef CAS PubMed
.
-
(a) M. V. De Almeida, D. H. R. Barton, I. Bytheway, J. A. Ferreira, M. B. Hall, W. Liu, D. K. Taylor and L. Thomson, J. Am. Chem. Soc., 1995, 117, 4870–4874 CrossRef CAS
; (b) C. Zhu, R. Wang and J. R. Falck, Chem. – Asian J., 2012, 7, 1502–1514 CrossRef CAS PubMed
.
-
(a) S. Rousseaux, S. I. Gorelsky, B. K. W. Chung and K. Fagnou, J. Am. Chem. Soc., 2010, 132, 10692–10705 CrossRef CAS PubMed
; (b) X.-G. Zhang, H.-X. Dai, M. Wasa and J.-Q. Yu, J. Am. Chem. Soc., 2012, 134, 11948–11951 CrossRef CAS PubMed
.
-
(a) J. Kim, S.-W. Park, M.-H. Baik and S. Chang, J. Am. Chem. Soc., 2015, 137, 13448–13451 CrossRef CAS PubMed
; (b) G. Li, L. Wan, G. Zhang, D. Leow, J. Spangler and J.-Q. Yu, J. Am. Chem. Soc., 2015, 137, 4391–4397 CrossRef CAS PubMed
; (c) A. K. Cook and M. S. Sanford, J. Am. Chem. Soc., 2015, 137, 9022–9031 CrossRef PubMed
; (d) B. E. Haines and D. G. Musaev, ACS Catal., 2015, 5, 830–840 CrossRef CAS
; (e) D. G. Musaev, A. Kaledinm, B.-F. Shi and J.-Q. Yu, J. Am. Chem. Soc., 2012, 134, 1690–1698 CrossRef CAS PubMed
; (f) D. G. Musaev, T. M. Figg and A. L. Kaledin, Chem. Soc. Rev., 2014, 43, 5009–5031 RSC
.
-
(a) S. Asako, L. Ilies and E. Nakamura, J. Am. Chem. Soc., 2013, 135, 17755–17757 CrossRef CAS PubMed
; (b) K. S. L. Chan, M. Wasa, L. Chu, B. N. Laforteza, M. Miura and J.-Q. Yu, Nature, 2014, 6, 146–150 CAS
; (c) G. Jindal and R. B. Sunoj, J. Am. Chem. Soc., 2014, 136, 15998–16008 CrossRef CAS PubMed
; (d) T. M. Figg, M. Wasa, J.-Q. Yu and D. J. Musaev, J. Am. Chem. Soc., 2013, 135, 14206–14214 CrossRef CAS PubMed
; (e) H. Xu, K. Muto, J. Yamaguchi, C. Zhao, K. Itami and D. G. Musaev, J. Am. Chem. Soc., 2014, 136, 14834–14844 CrossRef CAS PubMed
; (f) K. Muto, J. Yamaguchi, D. G. Musaev and K. Itami, Nat. Commun., 2015, 6, 7508–7515 CrossRef PubMed
.
-
(a) M. Anand, R. B. Sunoj and H. F. Schaefer, J. Am. Chem. Soc., 2014, 136, 5535–5538 CrossRef CAS PubMed
; (b) S. Kamijo and Y. Yamamoto, J. Org. Chem., 2003, 68, 4764–4771 CrossRef CAS PubMed
; (c) P. Buchwalter, J. Jacky Rose and P. Braunstein, Chem. Rev., 2015, 115, 28–126 CrossRef CAS PubMed
; (d) Y.-Y. Jiang, Q. Zang, H.-Z. Yu and Y. Fu, ACS Catal., 2015, 5, 1414–1423 CrossRef CAS
; (e) W. K. Walker, B. M. Kay, S. A. Michaelis, D. L. Anderson, S. J. Smith, D. H. Ess and D. J. Michaelis, J. Am. Chem. Soc., 2015, 137, 7371–7378 CrossRef CAS PubMed
; (f) M. Anand, R. B. Sunoj and H. F. Schaefer, ACS Catal., 2016, 6, 696–708 CrossRef CAS
; (g) Y.-F. Yang, G.-J. Cheng, P. Liu, D. Leow, T. Y. Sun, P. Chen, X. Zhang, J.-Q. Yu, Y.-D. Wu and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 344–355 CrossRef CAS PubMed
; (h) D. G. Musaev and L. S. Liebeskind, Organometallics, 2009, 28, 4639–4642 CrossRef CAS PubMed
.
- L. Ackermann and S. Fenner, Org. Lett., 2011, 13, 6548–6551 CrossRef CAS PubMed
.
- Benzisoxazolones are known to exhibit antimicrobial, antileukemic, and antidepressant activities, see
(a) V. Varshney, N. N. Mishra, P. K. Shukla and D. P. Sahu, Bioorg. Med. Chem. Lett., 2009, 19, 3573–3576 CrossRef CAS PubMed
; (b) Q. Zhou and B. B. Snider, Org. Lett., 2009, 11, 2936–2939 CrossRef CAS PubMed
; (c) N. Nishiwaki, K. Kobiro, H. Kiyoto, S. Hirao, J. Sawayama, K. Saigo, K. Okajima, T. Uehara, A. Maki and M. Ariga, Org. Biomol. Chem., 2011, 9, 2832–2839 RSC
.
- X.-A. Gao, R.-U. Yan, X.-X. Wang, H. Yan, J. Li, H. Guo and G.-S. Huang, J. Org. Chem., 2012, 77, 7700–7705 CrossRef CAS PubMed
.
- Role of zinc salts in palladium(0) catalyzed C–H bond functionalization in the presence of a base is recently reported in the literature. See
(a) A. Millet, D. Dailler, P. Larini and O. Baudoin, Angew. Chem., Int. Ed., 2014, 53, 2678–2682 CrossRef CAS PubMed
.
-
(a) Y. Zhu, R. G. Cornwall, H. Du, B. Zhao and Y. Shi, Acc. Chem. Res., 2014, 47, 3665–3678 CrossRef CAS PubMed
; (b) E. M. Beccalli, G. Broggini, M. Martinelli and S. Sottocornola, Chem. Rev., 2007, 107, 5318–5365 CrossRef CAS PubMed
.
- All computations were performed using.
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven Jr., J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed
.
-
(a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS
; (b) Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101–194118 CrossRef PubMed
; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS
; (d) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS
.
-
(a) C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS
; (b) C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS
.
-
(a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6397 CrossRef CAS PubMed
; (b) J. Ho, Phys. Chem. Chem. Phys., 2015, 17, 2859–2868 RSC
; (c) J. Ho and M. Z. Ertem, J. Phys. Chem. B, 2016, 120, 1319–1329 CrossRef CAS PubMed
.
-
(a) D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chem. Acc., 1990, 77, 123–141 CrossRef CAS
; (b) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS
. M06 functional with an SMD solvation model is effectively used to study transition metal catalysis. See (c) T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed
; (d) R. V. Hoveln, B. M. Hudson, H. B. Wedler, D. M. Bates, G. L. Gros, D. J. Tantillo and J. M. Schomaker, J. Am. Chem. Soc., 2015, 137, 5346–5354 CrossRef PubMed
; (e) Y. Y. Jiang, H.-Z. Yu and Y. Fu, Organometallics, 2014, 33, 6577–6584 CrossRef CAS
; (f) J. Delpozo, D. Carrasco, M. H. Pérez-Temprano, M. García-Melchor, R. Álvarez, J. Casares and P. Espinet, Angew. Chem., Int. Ed., 2013, 52, 2189–2193 CrossRef CAS PubMed
.
-
C. J. Cramer, Essentials of Computational Chemistry- Theories and Models, John Wiley & Sons Ltd., England, 2002, pp. 341–342 Search PubMed
. We have calculated the standard state corrections by taking the solvent into consideration (10.75 M N,N-dimethyl acetamide) and the correction factor of 1.5 kcal mol−1 per N,N-dimethyl acetamide at 318 K is added to the electronic energies on the final Gibbs free energy profile diagram. See ESI, Fig. S20.†.
-
(a) J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS
; (b) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS
; (c) A. E. Reed and F. Weinhold, J. Chem. Phys., 1983, 78, 4066–4073 CrossRef CAS
; (d) J. E. Carpenter and F. Weinhold, J. Mol. Struct. (THEOCHEM), 1988, 46, 41–50 CrossRef CAS
; (e) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS
; (f) F. Weinhold and J. E. Carpenter, in The Structure of Small Molecules and Ions, ed. R. Naaman and Z. Vager, Plenum, 1988, p. 227 Search PubMed
.
-
(a) A. C. Skapski and M. L. Smart, J. Chem. Soc. D, 1970, 658b–6659 RSC
; (b) V. M. Nosova, Y. A. Ustynyuk, L. G. Bruk, O. N. Temkin, A. V. Kisin and P. A. Storozhenko, Inorg. Chem., 2011, 50, 9300–9310 CrossRef CAS PubMed
; (c) T. A. Stephensons, S. M. Morehousae, R. Powell, J. P. Heffer and G. Wilkinson, J. Chem. Soc., 1965, 3632–3640 RSC
; (d) E. S. Stoyanov, J. Struct. Chem., 2000, 41, 440–445 CrossRef CAS
.
-
(a) J. Evans, L. O'Neill, V. L. Kambhampati, G. Rayner, S. Turin, A. Genge, A. J. Dent and T. Neisius, J. Chem. Soc., Dalton Trans., 2002, 2207–2212 RSC
; (b) W. Raufa and J. M. Brown, Chem. Commun., 2013, 49, 8430–8440 RSC
; (c) L. A. Adrio, B. N. Nguyen, G. Guilera, A. G. Livingston and K. K. Hii, Catal. Sci. Technol., 2012, 2, 316–323 RSC
; (d) D. P. Bancroft, F. A. Cotton, L. R. Falvello and W. Schowtzer, Polyhedron, 1988, 7, 615–621 CrossRef CAS
; (e) R. N. Pandey and P. Henry, Can. J. Chem., 1974, 52, 1241–1247 CrossRef CAS
.
-
(a) K. J. Donald, M. Hargittai and R. Hoffmann, Chem – Eur. J., 2009, 15, 158–164 CrossRef CAS PubMed
; (b) M. Hargittai, Chem. Rev., 2000, 100, 2233–2302 CrossRef CAS PubMed
.
-
(a) C.-Y. Niu, H. Su, L. Meng and C.-H. Kou, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, m869 CAS
; (b) F. J. Barros-Garcıa, A. Bernalte-Garcıa, F. L. Cumbrera, A. M. Lozano-Vila, F. Luna-Giles, J. Melendez-Martınez and A. L. Ortiz, Polyhedron, 2005, 24, 1975–1982 CrossRef
; (c) S. Tepavitcharova, D. Havlicek, I. Nemec, P. Vojtišek, D. Rabadjieva and J. Plocek, J. Mol. Struct., 2009, 918, 55–63 CrossRef CAS
.
-
(a) O. N. Ventura, J. B. Rema, L. Turi and J. J. Dannenberg, J. Am. Chem. Soc., 1993, 115, 5754–5761 CrossRef CAS
; (b) B. Garcıa, S. Ibeas, J. M. Leal, F. Secco, M. Venturini, M. L. Senent, A. Nino and C. Munoz, Inorg. Chem., 2005, 44, 2908–2919 CrossRef PubMed
; (c) C. J. Marmion, D. Griffith and K. B. Nolan, Eur. J. Inorg. Chem., 2004, 15, 3003–3016 CrossRef
; (d) M. M. Khalil and R. K. Mahmoud, J. Chem. Eng. Data, 2008, 53, 2318–2327 CrossRef CAS
; (e) A. K. Agrawal and S. K. Tandon, J. Inorg. Nucl. Chem., 1974, 36, 869–873 CrossRef
; (f) B. Kurzak, H. Koziowski and E. Farkas, Coord. Chem. Rev., 1992, 114, 169–200 CrossRef CAS
.
-
(a) M. Lafrance and K. Fagnou, J. Am. Chem. Soc., 2006, 128, 16496–16497 CrossRef CAS PubMed
; (b) D. P. Bancroft, F. A. Cotton, L. R. Falvello and W. Schowtzer, Polyhedron, 1988, 7, 615–621 CrossRef CAS
.
- Similar catalyst–substrate complexes have been noted earlier.
(a) L. Xu, Q. Zhu, G. Huang, B. Cheng and Y. Xia, J. Org. Chem., 2012, 77, 3017–3024 CrossRef CAS PubMed
; (b) M. Anand and R. B. Sunoj, Org. Lett., 2011, 13, 4802–4805 CrossRef CAS PubMed
; (c) M. Anand and R. B. Sunoj, Organometallics, 2012, 31, 6466–6481 CrossRef CAS
.
- (a) In an alternative Pd–N coordination with the second molecule of hydroxamic acid, the deprotonation is found to be higher in energy than that in Pd–O coordination. See Fig. S2, Tables S5 and S6 in the ESI.†; (b) The detailed scheme and associated energetics describing the role of the protic additive in N–H deprotonation are given in Fig. S3, Tables S7 and S8 in the ESI.†.
- A detailed scheme and associated energetics are given in Fig. S13–S16, and in Tables S20–S25 in the ESI.†.
-
(a) The detailed scheme and energetics for deprotonation of hydroxamic acid is given in Fig. S1–S3 and S10 and in Tables S1, S2 and S5–S8 in the ESI.†;
(b) J. R. Murdoch, J. Chem. Educ., 1981, 58, 32–36 CrossRef CAS
See Fig. S17–S19 and Table S26 in the ESI† for the free energy profile for the formation of product precursor 9 (without ZnCl2 and with a strained chelated binding mode of ZnCl2).
- A reversal of role wherein a palladium-bound pivalate acts as a ligand in the C–H activation while the acetic acid helps in proton shuttle, is found to be of higher energy. See Table S3 in the ESI.†.
- Similar donor–acceptor properties of Brønsted acids in catalysis can be found in
(a) J. Monot, P. Brunel, C. E. Kefalidis, N. E. Espinosa-Jalapa, L. Maron, B. Martin-Vaca and D. Bourissou, Chem. Sci., 2016, 7, 2179–2187 RSC
; (b) R. D. Bach, J. Org. Chem., 2012, 77, 6801–6815 CrossRef CAS PubMed
; (c) I. Coric, J. H. Kim, T. Vlaar, M. Patil, W. Thiel and B. List, Angew. Chem., Int. Ed., 2013, 52, 3490–3493 CrossRef CAS PubMed
; (d) Y. Y. Khomutnyk, A. J. Arguelles, G. A. Winschel, Z. Sun, P. M. Zimmerman and P. Nagorny, J. Am. Chem. Soc., 2016, 138, 444–456 CrossRef CAS PubMed
; (e) J. Ma, K. Chen, H. Fu, L. Zhang, W. Wu, H. Jiang and S. Zhu, Org. Lett., 2016, 18, 1322–1325 CrossRef CAS PubMed
; (f) M. Anand and R. B. Sunoj, Phys. Chem. Chem. Phys., 2012, 14, 12715 RSC
.
- The effect of hydrogen bonding in the CMD transition states ((3a–4a)6‡, (3a–4a)8‡, (3a–4a)10‡) the case of pivalate as the ligand is provided in ESI Table S4.† We have considered different hydrogen bonding interactions of the pivalic acid with (a) the carboxylate ligand, (b) the acetic acid additive, or (c) the directing group.
-
(a) B.-H. Xia, H.-X. Zhang, C.-M. Che, K.-H. Leung, D. L. Phillips, N. Zhu and Z.-Y. Zhou, J. Am. Chem. Soc., 2003, 125, 10362–10374 CrossRef CAS PubMed
; (b) D. C. Powers, D. Benitez, E. Tkatchouk, W. A. Goddard III and T. Ritter, J. Am. Chem. Soc., 2010, 132, 14092–14103 CrossRef CAS PubMed
; (c) A. Laguna, O. Crespo, J. M. Lopez-de-Luzuriaga, E. J. Fernandez, P. G. Jones, M. Teichert, M. Monge, P. Pyykko1, N. Runeberg, M. Schu1tz and H.-J. Werner, Inorg. Chem., 2000, 39, 4786–4792 CrossRef
; (d) T. J. Steiman and C. Uyeda, J. Am. Chem. Soc., 2015, 137, 6104–6110 CrossRef CAS PubMed
; (e) T. J. Mazzacano and N. P. Mankad, J. Am. Chem. Soc., 2013, 135, 17258–17261 CrossRef CAS PubMed
; (f) W. K. Walker, B. M. Kay, S. A. Michaelis, D. L. Anderson, S. J. Smith, D. H. Ess and D. J. Michaelis, J. Am. Chem. Soc., 2015, 137, 6104–6110 CrossRef PubMed
.
-
(a) It is important to recollect that several Pd–Zn heterobimetallic species are reported, including some examples in Suzuki cross coupling reactions;
(b) N. S. Akhmadullina, N. V. Cherkashina, N. Y. Kozitsyna, I. P. Stolarov, E. V. Perova, A. E. Gekhman, S. E. Nefedov, M. N. Vargaftik and I. I. Moiseev, Inorg. Chim. Acta, 2009, 362, 1943–1951 CrossRef CAS
; (c) B. Fuentes, M. G. Melchor, A. Lledos, F. Maseras, J. A. Casares, G. Ujaque and P. Espinet, Chem. – Eur. J., 2010, 16, 8596–8599 CrossRef CAS PubMed
; (d) A. B. G. Perez, R. Álvarez, O. N. Faza, A. L. de Lera and J. M. Aurrecoechea, Organometallics, 2012, 31, 2053–2058 CrossRef
.
- See Fig. S5, Tables S11 and S12 in the ESI† for the other Pd–Zn bridged hetero-bimetallic alternatives as well as the energetics associated with their formation. The O-coordination of the substrate is found to be 3.5 kcal mol−1 lower in energy than the N-coordination. See Fig. S6 in the ESI.†.
- A detailed mechanistic description of the effect of Pd–Zn hetero-bimetallic species is given in Scheme S1 in the ESI.†.
- (a) A larger number of configurational possibilities are examined. See Fig. S7 and Tables S13 and S14 in the ESI.†; (b) The CMD transition state with N-coordination is 1.4 kcal mol−1 higher in energy than the O-coordinated one.
- The reductive elimination via a five-membered ring transition state is found to be higher in energy than the conventional three-membered transition state. See Fig. S4, Tables S9 and S10 in the ESI.†.
- The elementary step barrier is found to be as low as 0.1 kcal mol−1 for the transition state (6a1–7a)‡ with pivalate as the ligand.
- The relative Gibbs free energy of the transition state for the formation of intermediate 7a when pivalate acts as the ligand is found to be 2.6 kcal mol−1. Elementary step barrier for this process is only 0.1 kcal mol−1.
- Similar ligand exchanges leading to bimetallic interaction are reported in A. B. G. Perez, R. Álvarez, O. N. Faza, A. L. de Lera and J. M. Aurrecoechea, Organometallics, 2012, 31, 2053–2058 CrossRef
.
- A larger number of configurational possibilities are examined for reductive elimination involving a Pd–Zn heterobimetallic species. See Fig. S11, Tables S17 and S18 in the ESI.†.
- See Fig. S12 and Table S19 in the ESI† for more details on the second order perturbative stabilization energies.
- A summary of the effect of ZnCl2 on relative free energy and activation barrier on various catalytically important steps is provided in Table S26 in the ESI.†.
-
(a) S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed
; (b) The details of the energetic span model are provided in Table S27.†.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized geometries, additional schemes, figures, and tables. See DOI: 10.1039/c6ob02318e |
| This journal is © The Royal Society of Chemistry 2017 |