Tuning quantum tunnelling of magnetization through 3d–4f magnetic interactions: an alternative approach for manipulating single-molecule magnetism†
Jing
Li
a,
Rong-Min
Wei
a,
Tian-Cheng
Pu
b,
Fan
Cao
a,
Li
Yang
a,
Yuan
Han
a,
Yi-Quan
Zhang
*c,
Jing-Lin
Zuo
 *a and
You
Song
*a
*a and
You
Song
*a
aState Key Laboratory of Coordination Chemistry, Collaborative Innovation Center of Advanced Microstructures, School of Chemistry and Chemical Engineering, Nanjing University, Xianlin Road 163, Nanjing 210023, P. R. China. E-mail: yousong@nju.edu.cn; zuojl@nju.edu.cn
bMaterial Science and Chemical Engineering Department, Stony Brook University, Stony Brook, NY, 11794 USA
cJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology Department, Nanjing Normal University, Wenyuan Road 1, Nanjing 210046, P. R. China. E-mail: zhangyiquan@njnu.edu.cn
First published on 3rd November 2016
Abstract
The magnetic relaxation and magnetization blocking barriers of butterfly complexes, [Dy2Zn2(L)4(NO3)2(CH3OH)2] (1), [Dy2Mn2(L)4(NO3)2(DMF)2] (2) and [Dy2Co2(L)4(NO3)2(DMF)2]·2DMF (3) (H2L = (E)-2-ethoxy-6-(((2-hydroxyphenyl)imino)methyl)phenol), were systematically investigated. The change of SMM behavior originating from the purposeful replacement of two ZnII sites in 1 with MnII and CoII was elucidated by a combined experimental and theoretical study. The quantum tunnelling of magnetization (QTM) was observed in 1. Contrarily, it was quenched in 2 and 3 by spin–spin exchange. A detailed comparative study on these closely-related model complexes reveals the remarkable changes of the ligand field splitting, anisotropy of the Dy-coordinated moiety and the total exchange spectrum due to the replacement of ZnII with CoII and MnII.
Introduction
As an attractive property of molecular materials, single-molecule magnet1 (SMM) behaviour displays slow relaxation and quantum tunnelling of magnetization (QTM) because of its molecule-based blocking anisotropy. In 2003, Ishikawa et al.2 discovered the first mononuclear lanthanide SMM, [Pc2Tb]−TBA+. Since then designing SMMs with lanthanide ions has been applied as a possible strategy in generating large barriers due to the presence of significant magnetic anisotropy arising from the prominent spin–orbital coupling. Over the past few years, lots of mono- and polynuclear complexes with large energy barriers have been synthesized.3 For example, Tong et al.4 reported a mononuclear lanthanide SMM with a record energy barrier up to 1000 K, ten times larger than that of the [Mn12] complex (60 K).1 Song et al. discovered that the idiosyncrasy of inherent anisotropy within the DyIII ion is the main reason leading to the slow relaxation rather than any other coupling interaction.5 Hence, the DyIII ion has become a good choice for designing and synthesizing SMMs. However, most of the mononuclear DyIII complexes are field-induced SMMs due to the QTM effect under zero magnetic field, which limits their range of application. Suppressing the QTM effect poses a new challenge to chemists. In the previous reports, it has been believed that spin–spin exchange effects in clusters6a–h and a special crystal field or/and local symmetry around individual lanthanide ions6i have been the successful strategies to suppress the QTM effect. Nevertheless, there has been no direct and clear evidence reported about the former so far. Several years ago, Powell's group7a reported a butterfly complex [Co2Dy2(L′)4(NO3)2(THF)2]·4THF (H2L′ = (E)-2-methoxy-6-(((2-hydroxyphenyl)imino)methyl)phenol) with extraordinary SMM properties. Owing to its magnetization hysteresis loop up to 4 K, this complex can be a good candidate for achieving a thorough understanding on how the spin–spin exchange interaction between 3d–4f ions disturbs the DyIII ion energy levels and reduces zero-field QTM. Based on this strategy, three complexes, [Dy2Zn2(L)4(NO3)2(CH3OH)2] (1), [Dy2Mn2(L)4(NO3)2(DMF)2] (2) and [Dy2Co2(L)4(NO3)2(DMF)2]·2DMF (3), were synthesized after the modification of ligands. Quite obviously and surprisingly, different from the typical lanthanide-based SMM behaviour of 1, the 3d–4f magnetic interaction quenches the SMM properties in 2, but enhances the SMM properties in 3. Herein, we report the synthesis, structure and magnetostructural correlation of complexes 1, 2 and 3.Results and discussion
Through adjusting the reference method,7 three complexes 1, 2 and 3 with similar construction were synthesized (Fig. 1). Complex 1 crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z = 1, which is a heterometallic 3d–4f tetranuclear cluster with the metallic core displaying a butterfly-type topology. The asymmetric unit consists of a half component of the cluster, and the whole molecule is grown by an inversion centre. The two ZnII ions are found at the “body” sites of the butterfly, whereas the DyIII ions occupy the outer “wing” position. The eight-coordinated DyIII ion can be seen as a hula-hoop configuration. One of the two L2− ligands chelates Dy1 through its two phenolate O atoms (O1 and O2) and an imine N atom (N1), while the other one chelates through one phenolate and one ether oxygen atom (O5 and O6, respectively). Therefore, five ligand atoms on the equatorial plane construct a distorted hoop with a mean deviation of 0.1731 Å. Two nitrate O atoms (O7 and O8) and phenolate O4i (symmetry code: i, −x, −y, −z) coordinate to the DyIII ion and complete the eight-coordinated environment. The ZnII ion is located in the centre of a slightly distorted octahedron. In the equatorial plane, two phenolate O atoms (O4 and O5) and an imine N one (N2) are all provided by the same ligand, and the residual oxygen atom (O1) is from the other ligand. One MeOH molecule and phenolate O1i (symmetry code: i, −x, −y, −z) occupy the axial positions, respectively. All the atoms in the two equatorial planes are approximately coplanar with Dy1 and Zn1 bridged by two phenolate O atoms (O1 and O5) from two ligands, respectively. The cluster molecule is further formed via the axial coordination of a μ3-O (O1, bridging Dy1, Zn1 and Zn1i, symmetry code: i, −x, −y, −z) and a μ2-O (O4, bridging Zn1 and Dy1i, symmetry code: i, −x, −y, −z). Complex 3 also crystallizes in the triclinic space group P
with Z = 1, which is a heterometallic 3d–4f tetranuclear cluster with the metallic core displaying a butterfly-type topology. The asymmetric unit consists of a half component of the cluster, and the whole molecule is grown by an inversion centre. The two ZnII ions are found at the “body” sites of the butterfly, whereas the DyIII ions occupy the outer “wing” position. The eight-coordinated DyIII ion can be seen as a hula-hoop configuration. One of the two L2− ligands chelates Dy1 through its two phenolate O atoms (O1 and O2) and an imine N atom (N1), while the other one chelates through one phenolate and one ether oxygen atom (O5 and O6, respectively). Therefore, five ligand atoms on the equatorial plane construct a distorted hoop with a mean deviation of 0.1731 Å. Two nitrate O atoms (O7 and O8) and phenolate O4i (symmetry code: i, −x, −y, −z) coordinate to the DyIII ion and complete the eight-coordinated environment. The ZnII ion is located in the centre of a slightly distorted octahedron. In the equatorial plane, two phenolate O atoms (O4 and O5) and an imine N one (N2) are all provided by the same ligand, and the residual oxygen atom (O1) is from the other ligand. One MeOH molecule and phenolate O1i (symmetry code: i, −x, −y, −z) occupy the axial positions, respectively. All the atoms in the two equatorial planes are approximately coplanar with Dy1 and Zn1 bridged by two phenolate O atoms (O1 and O5) from two ligands, respectively. The cluster molecule is further formed via the axial coordination of a μ3-O (O1, bridging Dy1, Zn1 and Zn1i, symmetry code: i, −x, −y, −z) and a μ2-O (O4, bridging Zn1 and Dy1i, symmetry code: i, −x, −y, −z). Complex 3 also crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with Z = 1, while complex 2 in the monoclinic space group P21/c with Z = 2 (Table S1†). The molecular structures of 2 and 3 are similar to 1 except that the solvent molecule coordinating to Mn or Co is DMF instead of MeOH, and there are two additional DMF molecules found in the lattice of 3. In 2, the MnII ion is located in the centre of a more distorted octahedron, which is unusual for a d5 ion (Table S2†). A THF coordinating to the CoII ions of the [Co2Dy2] complex reported in ref. 7a is replaced by a DMF molecule in 3. The bond lengths and angles of the fragment surrounded DyIII ions in two [Co2Dy2] complexes are basically consistent, except the Co–O bond linked with THF is 2.197 Å, much longer than that (2.060 Å) with DMF in 3 (Fig. S16 and Table S7†).
with Z = 1, while complex 2 in the monoclinic space group P21/c with Z = 2 (Table S1†). The molecular structures of 2 and 3 are similar to 1 except that the solvent molecule coordinating to Mn or Co is DMF instead of MeOH, and there are two additional DMF molecules found in the lattice of 3. In 2, the MnII ion is located in the centre of a more distorted octahedron, which is unusual for a d5 ion (Table S2†). A THF coordinating to the CoII ions of the [Co2Dy2] complex reported in ref. 7a is replaced by a DMF molecule in 3. The bond lengths and angles of the fragment surrounded DyIII ions in two [Co2Dy2] complexes are basically consistent, except the Co–O bond linked with THF is 2.197 Å, much longer than that (2.060 Å) with DMF in 3 (Fig. S16 and Table S7†).
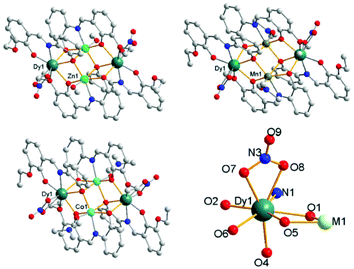 | ||
| Fig. 1 Molecular structures of the coordination clusters in 1 (up, left), 2 (up, right), 3 (down, left) and ligand atoms linked to DyIII (down, right). | ||
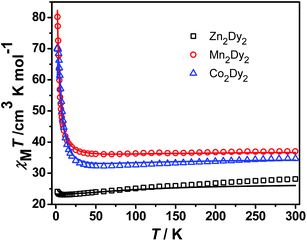
Direct current (dc) magnetic susceptibility measurements of 1, 2 and 3 were performed in the temperature range 1.9–300 K in a field of 100 Oe on a polycrystalline sample. The χMT versus T plots for three complexes are shown in Fig. 2. The room-temperature χMT value of 28.13 cm3 K mol−1 for 1 is in good agreement with the value of the two isolated DyIII (S = 5/2, L = 5, 6H15/2, gJ = 4/3, C = 14.17 cm3 K mol−1) ions. The χMT value gradually decreases with cooling due to the thermal depopulation of the excited mJ states of the DyIII ions until reaching a minimum of 23.1 cm3 K mol−1 at ca. 9.5 K, below which it increases to 24.1 cm3 K mol−1 at 2 K. This anomaly can be modelled by using the effective g values (gx = 0.006, gy = 0.008 and gz = 19.05) of the ground Kramers doublet obtained from CASSCF/RASSI calculations, taking into consideration the anisotropic dipole interaction between the two effective spins of Seff = 1/2 (J = +2.8 cm−1 for a Hamiltonian function S1), which is in agreement with a ferromagnetic dipolar interaction observed for the reported dimeric lanthanide systems.8 Complexes 2 and 3 show similar plots of χMT–T except a peak was observed at 2.5 K for 3. The room-temperature χMT products are 37.01 and 34.71 cm3 K mol−1 for 2 and 3, respectively, corresponding to the value of two non-interacting MnII (S = 5/2, g = 2) or CoII (S = 3/2, g > 2) and DyIII (C = 14.17 cm3 K mol−1) ions. The higher χMT value of 3 is ascribed to the unquenched orbital contribution from the CoII ions.7a,9 Upon cooling, χMT gradually decreases and reaches the minimum at 70 K for 2 and 60 K for 3, resulting from the thermal depopulation of the Starks levels of the DyIII ions and the additional orbital contribution of the CoII ions in 3. As expected, owing to the total contribution of both DyIII and CoII ions, complex 3 shows a lower temperature with a minimum χMT value than 2, but the latter is only due to the effect of DyIII ions. And then, χMT begins to increase and increases steeply below 18 K (2) and 25 K (3). This behaviour suggests the presence of weak intramolecular ferromagnetic interactions between the metal centres, which, however, is strong enough to overwhelm the contribution of the thermal depopulation of the Starks levels of the DyIII ions leading to the decrease of χMT, even including the unquenched orbital effect of the CoII ions in 3.
The magnetizations of three complexes from zero dc field to 7 T at different temperatures are shown in Fig. S1.† The field dependence of their magnetization at 1.9 K exhibits an abrupt increase at low fields below 1 T for 1 and 0.5 T for 2 and 3, respectively, providing evidence for the ferromagnetic interaction. At higher fields, the magnetization increases slightly and reaches 10.48 (1), 22.5 (2) and 13.6NμB (3) up to 7 T. These values are lower than the expected saturation value of 20 (1), 30 (2) and 26NμB (3) for two non-interaction DyIII ions (gJJ = 4/3 × 15/2 = 10NμB per DyIII ion), two isolated MnII (gS = 2 × 5/2 = 5NμB per Mn II ion) or CoII (gS = 2 × 3/2 = 3NμB per CoII ion) and two DyIII ions, respectively. Such a phenomenon arises most likely from magnetic anisotropy,10 proved by the non-superposition of the M vs. H/T data (Fig. S2†) on a single master curve.11
AC susceptibility measurements in a 2 Oe AC field oscillating at 1–999 Hz were performed on 1, 2 and 3 (Fig. 3 and S3†). For 1, the temperature dependence of both in-phase (χ′M) and out-of-phase (χ′′M) susceptibility shows strong frequency dependence under zero dc field. The maximum of χ′′M is observed at 22 K for 999 Hz, while below 125 Hz no peak is found in the χ′′Mversus T curve due to the quantum tunnelling effect (Fig. S4(a)†). All of these feature the SMM behaviour. A plot of ln(τ) versus T−1 based on variable-frequency susceptibility data is linear between 17 K and 22 K (Fig. 4). Fitting the data with the Arrhenius law τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(ΔE/kBT) poses a thermal energy barrier to the relaxation of magnetization ΔE = 78 K (54.1 cm−1) with τ0 = 4.59 × 10−6 s. At lower temperatures, ln(τ) increases much more slowly with cooling, which shows the onset of a quantum regime, contrary to what is often observed for the majority of Ln-based SMMs where the QTM is fast.11b,12 The Cole–Cole plots of χ′′Mversus χ′M between 10 and 30 K (Fig. S5†) reveal semicircular profiles, and are fitted by the CCFIT program13 to a generalized Debye model with α parameters in the range of 0–0.13, indicating a narrow distribution of relaxation times in 1 (Table S3†).6e,f Given the coexistence of multiple relaxations under zero dc field, the relaxation data can be modelled with QTM, Raman and Orbach relaxation processes. A fit with eqn (1) (where τQTM is the quantum tunnelling of the magnetization relaxation time, C is the coefficient of the Raman process, Ueff is the energy barrier to magnetization reversal, and kB is the Boltzmann constant) is in good agreement with the data over the whole temperature regime (Fig. 4) with parameters of τQTM−1 = 108.39 s−1, C = 0.116 s−1 K−3.26n = 3.26, τ0 = 2.35 × 10−6 s, and Ueff = 115 K (79.8 cm−1) (detailed information can be seen in Table S6†). Theoretically, the parameter n in the Raman relaxation pathway is equal to 9 for Kramers ions,14 and lower values would be allowed due to the optical phonons taken into account.10b,15 To study the properties of a single DyIII ion without QTM, we searched dc fields from 200 to 2000 Oe, and found an appropriate dc field of 1000 Oe to hinder the QTM effect (Fig. S6†). The maximum of χ′′M is observed at 24 K for 999 Hz and it varies at different frequencies (Fig. S7†). The thermal energy barrier for the relaxation of magnetization is 96 K (66.6 cm−1) with τ0 = 3.79 × 10−6 s (Fig. 4). The Cole–Cole plots, fitted between 10 and 30 K, give the parameters of 0–0.095, which shows that QTM was hindered by the extra dc field effectively (Fig. S8 and Table S4†).10a,12a
exp(ΔE/kBT) poses a thermal energy barrier to the relaxation of magnetization ΔE = 78 K (54.1 cm−1) with τ0 = 4.59 × 10−6 s. At lower temperatures, ln(τ) increases much more slowly with cooling, which shows the onset of a quantum regime, contrary to what is often observed for the majority of Ln-based SMMs where the QTM is fast.11b,12 The Cole–Cole plots of χ′′Mversus χ′M between 10 and 30 K (Fig. S5†) reveal semicircular profiles, and are fitted by the CCFIT program13 to a generalized Debye model with α parameters in the range of 0–0.13, indicating a narrow distribution of relaxation times in 1 (Table S3†).6e,f Given the coexistence of multiple relaxations under zero dc field, the relaxation data can be modelled with QTM, Raman and Orbach relaxation processes. A fit with eqn (1) (where τQTM is the quantum tunnelling of the magnetization relaxation time, C is the coefficient of the Raman process, Ueff is the energy barrier to magnetization reversal, and kB is the Boltzmann constant) is in good agreement with the data over the whole temperature regime (Fig. 4) with parameters of τQTM−1 = 108.39 s−1, C = 0.116 s−1 K−3.26n = 3.26, τ0 = 2.35 × 10−6 s, and Ueff = 115 K (79.8 cm−1) (detailed information can be seen in Table S6†). Theoretically, the parameter n in the Raman relaxation pathway is equal to 9 for Kramers ions,14 and lower values would be allowed due to the optical phonons taken into account.10b,15 To study the properties of a single DyIII ion without QTM, we searched dc fields from 200 to 2000 Oe, and found an appropriate dc field of 1000 Oe to hinder the QTM effect (Fig. S6†). The maximum of χ′′M is observed at 24 K for 999 Hz and it varies at different frequencies (Fig. S7†). The thermal energy barrier for the relaxation of magnetization is 96 K (66.6 cm−1) with τ0 = 3.79 × 10−6 s (Fig. 4). The Cole–Cole plots, fitted between 10 and 30 K, give the parameters of 0–0.095, which shows that QTM was hindered by the extra dc field effectively (Fig. S8 and Table S4†).10a,12a
τ−1 = τQTM−1 + CTn + τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ueff/kBT) exp(−Ueff/kBT) | (1) |
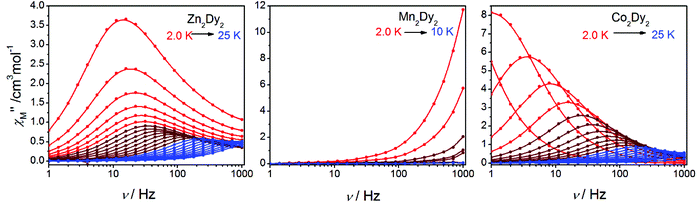 | ||
| Fig. 3 Frequency dependence of out-of-phase (χ′′M) AC susceptibilities under zero dc field (1–999 Hz, by MPMS Squid VSM) at indicated temperatures for 1, 2 and 3. | ||
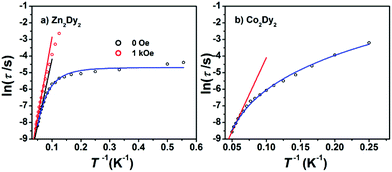 | ||
Fig. 4 (a) Magnetization relaxation time, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ, versus T−1 for 1: the black solid line (under zero dc field) and the red line (under 1000 Oe dc field) are fitted with the Arrhenius law; (b) ln(τ) versus T−1 for 3 under zero dc field: the red solid line is fitted in the temperature range 16–20 K with the Arrhenius law (see the text). The blue lines in both plots are fitted with eqn (1) over the whole temperature regime. τ, versus T−1 for 1: the black solid line (under zero dc field) and the red line (under 1000 Oe dc field) are fitted with the Arrhenius law; (b) ln(τ) versus T−1 for 3 under zero dc field: the red solid line is fitted in the temperature range 16–20 K with the Arrhenius law (see the text). The blue lines in both plots are fitted with eqn (1) over the whole temperature regime. | ||
For 2, the temperature dependence of susceptibility also shows the frequency dependence under zero dc field but without a peak in both χ′M and χ′′M (Fig. S4(b)†). Fitting to ln(χ′′M/χ′M) = ln(ωτ0) + Ea/kBT (ref. 16) allows us to evaluate roughly Ea and τ0, giving the energy barrier ca. Ea = 11 K (7.6 cm−1) and τ0 = 1 × 10−8 s (Fig. S9†). Under Hdc = 1000 Oe (Fig. S10†), the curves of χ′M and χ′′Mversus T show a slight change compared with those under Hdc = 0. The result indicates that there is no QTM influence on the magnetic properties, and the signal under zero fields is an intrinsic character of 2.7b,17
For 3, the strong temperature and frequency dependence of AC susceptibility under Hdc = 0 illustrate the characteristic of SMM (Fig. 3, S3 and S4(c)†). Compared with 1, the maximum of χ′′M even can be observed at 2.6 K at the lowest 1 Hz, indicating that the magnetic interaction between CoII and DyIII has suppressed QTM effectively. The deduced plots of ln(τ ) − T−1 (Fig. 4) can be fitted with ΔE = 88.8 K (61.6 cm−1) and τ0 = 2.29 × 10−6 s in the range of 16–20 K through the Arrhenius law. A fit employing eqn (1) obtained τQTM−1 = 0.001 s−1, C = 0.301 s−1 K−3.16, n = 3.16, τ0 = 2.67 × 10−6 s, and Ueff = 125.1 K (86.8 cm−1) (detailed information can be seen in Table S6†). The Cole–Cole plots were fitted with the generalized Debye model (Fig. S11 and Table S5†). The α values are in the range of 0–0.18(2), suggesting the coexistence of multiple relaxation pathways, which is discovered in several examples.7a,12a The AC susceptibilities were also measured under 1000 Oe external dc field (Fig. S12†). A plot of ln(τ) versus T−1 based on variable-frequency susceptibility data shows a slight change compared with those under Hdc = 0 (Fig. S13 and Table S6†), indicating that the magnetic interaction between CoII and DyIII dominates the Zeeman effect.
To confirm the SMM behaviour, hysteresis loops were recorded at low temperatures. Below 4 K, butterfly-like hysteresis can be clearly observed for 1 (Fig. S14†). However, for 2 and 3, no hysteresis loop was observed even at 1.8 K (Fig. S15†). Interestingly, Powell et al.7a reported a [Co2Dy2] complex with a THF coordinating to CoII ions, showing large hysteresis loops below 4 K. However, the difference of the environment between CoII ions (Fig. S16 and Table S7†) directly influences the molecular magnetic properties. Compared with the calculating results, the g values of DyIII ions in two complexes are almost equal (gx = 0.005 (0.004), gy = 0.008 (0.006), gz = 19.53 (19.68) for reported [Co2Dy2] (and 3)), while the g values of CoII are much different (gx = 1.89 (1.60), gy = 3.24 (2.333), gz = 6.74 (7.599), respectively). The magnetic axes on all magnetic central ions for 3 are parallel to each other, while those on the reported [Co2Dy2] complex are interlaced. The difference of the uniaxial magnetic anisotropy of CoII influences the magnetic interaction between CoII and DyIII, and further impacts on the magnetic properties of the whole complexes. As a result, complex 3 shows a stronger interaction between ions (JDy–Co = 11.7 cm−1 and JCo–Co = 6.8 cm−1) than the reported [Co2Dy2] complex7a (JDy–Co = 1.6 cm−1 and JCo–Co = 2.0 cm−1). In the reference complex, it is believed that the properties of single ion DyIII were retained due to the weak interaction, and some single ion DyIII complexes show large hysteresis loops.6d Nevertheless, the stronger interaction in complex 3 destroyed the properties of the single ion DyIII, which yielded the properties of the entire molecule [Dy2Co2]. For clarifying the effect of 3d–4f magnetic interactions on the difference between complex 3 and the reference complex in hysteresis loops, perhaps, more examples are necessary for obtaining more information in regularity.
The temperature dependence of susceptibility for 2 and 3 shows similar intramolecular ferromagnetic interactions between the metal centres. Interestingly, in complex 1, two DyIII ions separated by two diamagnetic ZnII ions also show weak ferromagnetic dipole–dipole interactions at a low temperature. But in the AC susceptibility aspect, the three complexes represent much different behaviours. In order to understand the strikingly different properties of 3d–4f mixed complexes with different 3d metal ions and the origin of their magnetic properties, we performed ab initio calculations on 1–3, which are very appropriate for the interpretation of lanthanide complexes.6b–d,7a,12a,18
Complete-active-space self-consistent field (CASSCF) calculations on individual DyIII, MnII and CoII fragments of 1, 2 and 3 on the basis of X-ray determined geometries have been carried out with MOLCAS 7.818i and SINGLE_ANISO18d,g,m programs. The lowest Kramers doublets and the g tensors of DyIII, MnII and CoII ions of three complexes are shown in Table S8,† where the energy separations between the ground and the first-excited doublets for the DyIII fragments19 of 1, 2 and 3 are 229.1, 202.4 and 206.6 cm−1, respectively, which indicates that the Dy–Dy, Dy–Mn and Dy–Co exchange interactions can be approximately regarded as the Ising type. Moreover, the MnII in 2 from Table S8† is almost isotropic, but the CoII in 3 is strongly anisotropic. The magnetic susceptibilities of 1, 2 and 3 were simulated with the program POLY_ANISO18 (Fig. 2) using the exchange parameters shown in Table 1. All parameters from Table 1 were calculated with respect to the pseudospin = 1/2 of the Dy ions. For CoII with strong anisotropy in 3, we also approximately regard the pseudospin as 1/2. For the three complexes, the total coupling parameters J (dipolar and exchange) were included when fitting the magnetic susceptibilities. The calculated and experimental χMT versus T plots of the three complexes are shown in Fig. 2, where a slight discrepancy of the fit to the experimental data for 1 is found above 100 K.6h From Table 1, the fitted DyIII–MnII, DyIII–DyIII, DyIII–CoII and CoII–CoII couplings in three complexes within the Lines model20 are all ferromagnetic. The main magnetic axes on the magnetic ions of the three complexes are indicated in Fig. S17† where the magnetic axes on all magnetic centre ions for each complex are parallel to each other.
| J (1) | J (2) | J (3) | |
|---|---|---|---|
| Dy–Dy | 2.8 | 5.5 | 2.0 |
| Dy–Mn | 4.8 | ||
| Mn–Mn | 0.2 | ||
| Co–Dy | 11.7 | ||
| Co–Co | 6.8 |
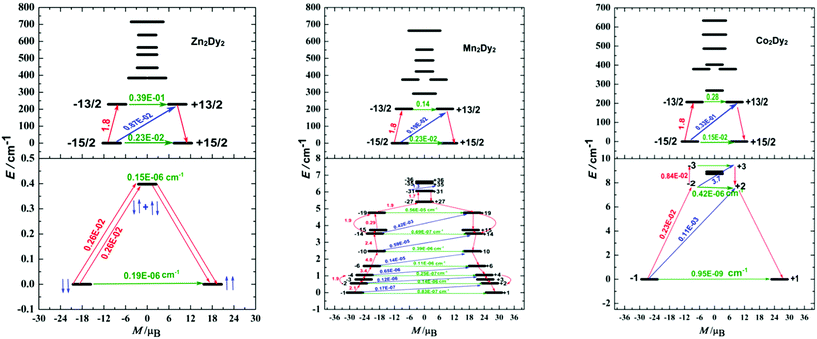
The calculated exchange spectrum and the corresponding tunnelling gaps and gz values are given in Table S9.† Considering that those three complexes are not isostructural, we therefore demonstrate the magnetization blocking barriers and the corresponding tunnelling gaps of individual DyIII ions with the electrostatics generated by the ligands as shown in Fig. 5 (top), which was very important for the discussion between QTM and the magnetic exchange interaction. According to a recent proposal by Ungur and co-workers,21 the relaxation path can be related to the tunnelling gaps. Then, the blocking barrier may be defined by the shortest paths, where these quantities are the largest. For 1, the energy barrier cannot be associated with the exchange states since the highest of four exchange states (0.4 cm−1) lies much lower than the experimental barrier (79.8 cm−1), and the order of magnitude of the magnetic moment matrix element connecting the four exchange states is 10−6 cm−1, so that the corresponding tunnelling transition between these states are efficient. Thus, the energy barrier of 1 should be associated with relaxation through the excited KDs of individual Dy ions. This phenomenon is also observed in the reference complex [Co2Dy2].7a
The energy barrier of 2 is very small given the fact that the energy separations between the exchange states split by the weak Dy–Mn exchange coupling are quite small (the highest exchange state is only 12.3 cm−1). According to the relaxation path indicated in Fig. 5, we deduced that the blocking barrier of 2 corresponding to the magnetic relaxation from −31 to +35 is 6.5 cm−1, which is very close to the experimental fitting value (Fig. S9†). For 3, the high excited state (15 cm−1, see Table S9†) is much smaller than the energy barrier (86.8 cm−1), which is associated with the relaxation through the excited KDs of the magnetic centre ions rather with the exchange states. Although the height of this barrier matches well with that in the complex 1 (79.8 cm−1), we note that these two quantities are not directly related. For the difference between complexes 2 and 3 in the magnetic behaviours, we try giving some possible reasons here. In our opinion, the main difference of their energy barriers is originated from the tunnelling gaps between the low-lying exchange states and the temperature disturbing. From Table S9,† complex 2 has 72 low-lying exchange states and there are a lot of magnetic relaxation pathways. Although higher energy states would be populated at higher temperatures, the large tunnelling gaps between the 72 low-lying non-Kramers doublet exchange states will destroy the probable magnetic relaxation of 2 to a higher energy state. Compared to complex 2, complex 3 only has 8 low-lying non-Kramers doublet exchange states, and the magnetic relaxation will not happen between 8 exchange states. The thermally assisted QTM is another choice for 3 under this situation. At higher temperatures, higher energy states will be populated for 3.
From the relaxation path indicated in Fig. 5 top, a conclusion can be made is that their low-lying state energies are close. Particularly, the energy gaps are 229.1, 202.4 and 206.6 cm−1 for complexes 1, 2 and 3, respectively (Table S8†). Additionally, the ground state in individual Dy ions without magnetic interaction displays much larger tunnelling splitting (of 10−2 cm−1, Fig. 5 top), indicating that the slight difference in the structure and space group did not influence the tunnelling splitting gaps of individual Dy ions obviously, and the discussion between the three complexes based on the isostructure is acceptable. For 1, the Dy–Dy anisotropic dipole interaction changed the ground state tunnelling splitting (from 10−2 cm−1 to 10−6 cm−1), and should have hindered the QTM. However, the highest one of the four exchange states (0.4 cm−1) is still small when confronting with thermal disturbance. As a result, the dipole interaction between Dy ions can be ignored in the relaxation process which is in good agreement with the experimental data (Fig. 3 and 4). For 2 and 3, after bringing in the 3d–4f magnetic exchange coupling interaction, the tunnelling gaps in the ground state become very small (on the order of 10−7 to 10−9 cm−1), indicating that QTM is quenched largely in the process.
The calculated energy gaps between the ground and the first excited states for the individual Dy ions of complexes 1 and 3 are much larger than the experimental one, while the latter is much larger than the energy gaps of the exchange splitting state. Considering the large error of the fitted parameters with eqn (1), we infer that the above-mentioned phenomenon could result from the Raman process instead of the Orbach one. The effective energy barriers extracted from the experiment may not be the “real barrier”. As a result, we fit the relaxation times with two processes (Raman + QTM) (Fig. 6):
| τ−1 = τQTM−1 + CTn | (2) |
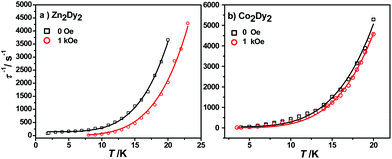 | ||
| Fig. 6 Magnetization relaxation time, τ−1, versus T for 1 (a) and 3 (b), respectively. The black solid line (under zero dc field) and the red line (under 1 kOe dc field) are fitted with eqn (2). | ||
The best fit parameters obtained were n ≥ 4 for both complexes under different fields which is in accordance with the expected values for Kramers ion SMMs.15 All parameters and standard error can be seen in Table S10.†
Conclusions
A series of butterfly [M2Dy2] complexes have been successfully developed to probe into the magnetic relaxation mechanism of 3d–4f complexes systematically. Single-crystal X-ray diffraction shows that the molecular structures of 1, 2 and 3 are comparable. Complex 1 with two diamagnetic ZnII ions shows typical SMM behaviour with a blocking energy (ΔE) of 54.1 cm−1 under zero dc field with an obvious QTM effect in the low temperature region. However, with two CoII ions instead of ZnII ions, complex 3 undergoes a relaxation process with ΔE = 61.6 cm−1 without the QTM effect, and complex 2, with two MnII ions, shows the same magnetic behaviour under both Hdc = 0 and 1000 Oe, indicating that the 3d–4f spin–spin exchange effects can reduce the zero-field QTM. Unexpectedly, complexes 2 and 3 undergo two totally different relaxation processes. Through a detailed comparative study of these closely-related model complexes, the structure and magnetic properties, especially the total exchange spectrum due to the replacement of ZnII with CoII and MnII, were investigated. Finally, the blocking barriers in these two complexes were rationalized, which explains their different blocking behaviours.This analysis was made possible through a deliberate design of butterfly model complexes with purposeful metal replacement. Our study gives direct and clear evidence that spin–spin exchange effects can reduce the zero-field QTM and enhance our understanding of magnetic interactions in elucidating the relaxation dynamics of the 3d–4f mixed metal system. However, the results indicate that the spin–spin interaction can improve the SMM properties in some lanthanide-based systems, but also weakens the magnetic properties in another system. Thus, the selected 3d ions play a key role in designing 3d–4f SMM. Accordingly, 3d ions, not all, with strong spin–orbital coupling contribution, might provide an alternative pathway for the rational design of new 3d–4f SMMs with high performance.
Experimental
General methods
All the reagents and solvents were purchased from commercial sources without any purification. The compound (E)-2-ethoxy-6-(((2-hydroxyphenyl)imino)methyl)phenol (H2L) was prepared by reported procedures.7bPhysical measurement
Elemental analyses of C, H, and N were performed on a PerkinElmer 240C elemental analyser. IR spectra were obtained with a Nexus 870 FT-IR spectrometer using KBr pellets in the range from 400 to 4000 cm−1. Magnetic data were collected on a Quantum Design VSM SQUID magnetometer. Static magnetic measurements were performed in the temperature range 1.9–300 K in a field of 100 Oe on a polycrystalline sample. The alternating-current (AC) susceptibility measurements were performed under an oscillating field of 2 Oe with the frequency ranging from 1 to 999 Hz. Due to the air-sensitivity of complex 3, the magnetic data were obtained under paraffin oil protection. Experimental susceptibilities were corrected for the diamagnetism estimated Pascal's tables22 and for the sample holder by previous calibration.Ab initio calculations for complexes 1, 2 and 3
Complete-active-space self-consistent field (CASSCF) calculations on individual lanthanide DyIII, MnII (S = 5/2) and CoII (S = 3/2) fragments of complexes 1, 2 and 3 on the basis of the X-ray determined geometry have been carried out with the MOLCAS 7.8 program package.18i During the calculations, the other DyIII, MnII and CoII ions were replaced by diamagnetic LuIII, ZnII and ZnII, respectively. The basis sets for all atoms are atomic natural orbitals from the MOLCAS ANO-RCC library: ANO-RCC-VTZP for DyIII, MnII and CoII ions; VTZ for close O and N; VDZ for distant atoms. The calculations employed the second order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set and the spin–orbit couplings were handled separately in the restricted active space state interaction (RASSI-SO) procedure. For the fragment of DyIII, active electrons in 7 active spaces include all f electrons CAS (9 in 7) in the CASSCF calculation. For MnII, CAS (5 in 5) was used. For CoII, CAS (7 in 10) was used. To exclude all the doubts, we calculated all the roots in the active space. We have mixed the maximum number of spin-free states which was possible with our hardware (all from 21 sextets, 128 from 224 quadruplets, 130 from 490 doublets for the DyIII fragment; all from 1 sextet, 24 quadruplets and 75 doublets for the MnII fragment; all from 10 quadruplets, all from 40 doublets for the CoII fragment).Crystallographic data collection and refinement
The crystallographic data of complexes 1 and 2 were collected on a Bruker Smart CCD area-detector diffractometer with Mo-Kα radiation (λ = 0.71073 Å) by using an ω scan mode at 296 K, and of complex 3 were collected on a PHOTON100 CMOS detector with Mo-Kα radiation (λ = 0.71073 Å) by using the ω scan mode at 173 K. The diffraction data were treated using SAINT,23a and all absorption corrections were applied by using SADABS.23b All non-hydrogen atoms were located by the Patterson method23c using the SHELXS programs of the SHELXTL package and subsequent difference Fourier syntheses. Hydrogen atoms bonded to carbon were determined theoretically and refined with isotropic thermal parameters riding on their parents. The H-atoms of methanol were first located by difference Fourier E-maps and then treated isotropically as riding. All non-hydrogen atoms were refined by full-matrix least-squares on F2. All calculations were performed by using SHELXTL-97.23d Complex 3 is a non-merohedral twin, which has two Rint values (0.0519 and 0.0551) corresponding to two crystal domains. The value of 0.0000 in the CIF was automatically generated during refinement. CCDC 1430222–1430224 contain the supplementary crystallographic data for this paper.Acknowledgements
This work was supported by the Major State Basic Research Development Program (2013CB922102), the National Natural Science Foundation of China (21571097 and 21171089), the Natural Science Foundation of Jiangsu Province of China (BK20130054 and BK20151542), the Specialized Research Fund for the Doctoral Program of Higher Education and a Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.Notes and references
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141 CrossRef CAS
.
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed
.
-
(a) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328 CrossRef CAS
; (b) D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed
; (c) L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092 RSC
; (d) H. L. C. Feltham and S. Brooker, Coord. Chem. Rev., 2014, 276, 1 CrossRef CAS
.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer, S. Gao, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef CAS PubMed
.
- Y. Wang, X.-L. Li, T.-W. Wang, Y. Song and X.-Z. You, Inorg. Chem., 2010, 49, 969 CrossRef CAS PubMed
.
-
(a) W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406 CrossRef PubMed
; (b) Y. N. Guo, G. F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H. J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948 CrossRef CAS PubMed
; (c) F. Habib, P. H. Lin, J. Long, I. Korobkov, W. Wernsdorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830 CrossRef CAS PubMed
; (d) S. K. Langley, D. P. Wielechowski, V. Vieru, N. F. Chilton, B. Moubaraki, B. F. Abrahams, L. F. Chibotaru and K. S. Murray, Angew. Chem., Int. Ed., 2013, 52, 12014 CrossRef CAS PubMed
; (e) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed
; (f) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed
; (g) J. L. Liu, J. Y. Wu, Y. C. Chen, V. Mereacre, A. K. Powell, L. Ungur, L. F. Chibotaru, X. M. Chen and M. L. Tong, Angew. Chem., Int. Ed., 2014, 53, 12966 CrossRef CAS PubMed
; (h) L. E. Rosaleny and A. G. Arino, Inorg. Chem. Front., 2016, 3, 61 RSC
; (i) C. Görller-Walrand, K. Binnemans, K. A. Gschneidner and L. Eyring, Handbook on the Physics and Chemistry of Rare Earths, 1996 Search PubMed
.
-
(a) K. C. Mondal, A. Sundt, Y. Lan, G. E. Kostakis, O. Waldmann, L. Ungur, L. F. Chibotaru, C. E. Anson and A. K. Powell, Angew. Chem., Int. Ed., 2012, 51, 7550 CrossRef CAS PubMed
; (b) K. C. Mondal, G. E. Kostakis, Y. Lan, W. Wernsdorfer, C. E. Anson and A. K. Powell, Inorg. Chem., 2011, 50, 11604 CrossRef CAS PubMed
.
- E. Moreno Pineda, N. F. Chilton, F. Tuna, R. E. Winpenny and E. J. McInnes, Inorg. Chem., 2015, 54, 5930 CrossRef CAS PubMed
.
-
(a) X.-Q. Zhao, Y. Lan, B. Zhao, P. Cheng, C. E. Anson and A. K. Powell, Dalton Trans., 2010, 39, 4911 RSC
; (b) S. M. Abtab, M. C. Majee, M. Maity, J. Titis, R. Boca and M. Chaudhury, Inorg. Chem., 2014, 53, 1295 CrossRef CAS PubMed
; (c) S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Inorg. Chem., 2014, 53, 4303 CrossRef CAS PubMed
.
-
(a) J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572 CrossRef CAS PubMed
; (b) C. Benelli and D. Gatteschi, Chem. Rev., 2002, 102, 2369 CrossRef CAS PubMed
.
-
(a) N. F. Chilton, S. K. Langley, B. Moubaraki and K. S. Murray, Chem. Commun., 2010, 46, 7787 RSC
; (b) F. Cao, S. Wang, D. Li, S. Zeng, M. Niu, Y. Song and J. Dou, Inorg. Chem., 2013, 52, 10747 CrossRef CAS PubMed
.
-
(a) F. Gao, L. Cui, Y. Song, Y.-Z. Li and J.-L. Zuo, Inorg. Chem., 2014, 53, 562 CrossRef CAS PubMed
; (b) F. Gao, M.-X. Yao, Y.-Y. Li, Y.-Z. Li, Y. Song and J.-L. Zuo, Inorg. Chem., 2013, 52, 6407 CrossRef CAS PubMed
; (c) F. Gao, L. Cui, W. Liu, L. Hu, Y.-W. Zhong, Y.-Z. Li and J.-L. Zuo, Inorg. Chem., 2013, 52, 11164 CrossRef CAS PubMed
; (d) R. J. Blagg, C. A. Muryn, E. J. McInnes, F. Tuna and R. E. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 6530 CrossRef CAS PubMed
; (e) S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448 CrossRef CAS PubMed
; (f) A. Yamashita, A. Watanabe, S. Akine, T. Nabeshima, M. Nakano, T. Yamamura and T. Kajiwara, Angew. Chem., Int. Ed., 2011, 50, 4016 CrossRef CAS PubMed
.
- Y. N. Guo, G. F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953 RSC
.
-
A. Abragam and B. Bleaney, in Electron paramagnetic resonance of transition ions, Oxford University Press, 2012 Search PubMed
.
-
(a) K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437 CrossRef CAS
; (b) A. Singh and K. Shrivastava, Phys. Status Solidi B, 1979, 95, 273 CrossRef CAS
.
-
(a) J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Phys. Rev. B: Condens. Matter, 2009, 80, 014430 CrossRef
; (b) S. K. Langley, L. Ungur, N. F. Chilton, B. Moubaraki, L. F. Chibotaru and K. S. Murray, Chem. – Eur. J., 2011, 17, 9209 CrossRef CAS PubMed
; (c) S. Y. Lin, G. F. Xu, L. Zhao, Y. N. Guo, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 8213 RSC
.
- J.-Y. Ge, J. Ru, F. Gao, Y. Song, X.-H. Zhou and J.-L. Zuo, Dalton Trans., 2015, 44, 15481 RSC
.
-
(a) P. H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489 CrossRef CAS PubMed
; (b) F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P. A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. S. Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224 CrossRef CAS PubMed
; (c) L. Ungur, W. V. Heuvel and L. F. Chibotaru, New J. Chem., 2009, 33, 1224 RSC
; (d) J. J. Le Roy, M. Jeletic, S. I. Gorelsky, I. Korobkov, L. Ungur, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 3502 CrossRef CAS PubMed
; (e) J. J. Le Roy, L. Ungur, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2014, 136, 8003 CrossRef CAS PubMed
; (f) L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086 RSC
; (g) L. Ungur, J. J. Le Roy, I. Korobkov, M. Murugesu and L. F. Chibotaru, Angew. Chem., Int. Ed., 2014, 53, 4413 CrossRef CAS PubMed
; (h) J. D. Leng, J. L. Liu, Y. Z. Zheng, L. Ungur, L. F. Chibotaru, F. S. Guo and M. L. Tong, Chem. Commun., 2013, 49, 158 RSC
; (i) M. E. Boulon, G. Cucinotta, S. S. Liu, S. D. Jiang, L. Ungur, L. F. Chibotaru, S. Gao and R. Sessoli, Chem. – Eur. J., 2013, 19, 13726 CrossRef CAS PubMed
; (j) P. H. Guo, J. L. Liu, Z. M. Zhang, L. Ungur, L. F. Chibotaru, J. D. Leng, F. S. Guo and M. L. Tong, Inorg. Chem., 2012, 51, 1233 CrossRef CAS PubMed
; (k) F. Habib, G. Brunet, V. Vieru, I. Korobkov, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2013, 135, 13242 CrossRef CAS PubMed
; (l) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126 CrossRef CAS PubMed
; (m) G. Karlstrom, R. Lindh, P. A. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222 CrossRef
.
-
(a) S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701 RSC
; (b) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125 RSC
; (c) N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 RSC
; (d) E. M. Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. V. Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef PubMed
; (e) D. Aravena and E. Ruiz, Inorg. Chem., 2013, 52, 13770 CrossRef CAS PubMed
.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977 CrossRef CAS
.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328 CrossRef CAS PubMed
.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS
.
-
(a)
W. Madison, SAINT v5.0–6.01, Bruker Analytical X-ray Systems Inc, 1998 Search PubMed
; (b) G. M. Sheldrick, SADABSs: An Empirical Absorption Correction Program, 1996 Search PubMed
; (c) A. L. Patterson, Phys. Rev., 1934, 46, 372 CrossRef CAS
; (d) G. M. Sheldrick, SHELXS-97, PC version, University of Göttingen, Göttingen, Germany, 1997 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Auxiliary magnetic data and the methods for ab initio calculation. CCDC 1430222–1430224. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6qi00407e |
| This journal is © the Partner Organisations 2017 |