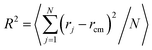Role of chain ends in coil deformation of driven single polymer†
Huachen
Tao
,
Huanhuan
Gao
and
Wenbing
Hu
*
Department of Polymer Science and Engineering, State Key Laboratory of Coordination Chemistry, School of Chemistry and Chemical Engineering, Nanjing University, 210023 Nanjing, China. E-mail: wbhu@nju.edu.cn
First published on 7th February 2017
Abstract
Nonlinear elasticity of coil deformation is profound in polymer rheology. The structural asymmetry between the middle part of the chain and the chain end is supposed to be the origin of internal tension for coil deformation of driven single linear polymers. We performed dynamic Monte Carlo simulations on driven single ring polymers without the abovementioned asymmetry, and compared their deformation behavior to that of the linear counterparts of the same chain length. The comparison proved that the chain ends are not the cause of internal tension for coil deformation, and rather, their relatively high mobility suppresses the coil–stretch transition upon large coil deformation. Therefore, the “cracking-the-whip” effect, as an integration of local acceleration caused by dynamic heterogeneity of nearby monomers on the polymer chain, is the sole origin of internal tension for the observed coil deformation of driven single linear and ring polymers. This study opens an extensive investigation on the intramolecular source of nonlinearity for nonequilibrium polymer dynamics.
Introduction
Chain-connectivity of chemical units endows macromolecules or polymers with numerous unique properties. For instance, the large conformational entropy and the chain entanglement separately raise a high elasticity and a high viscosity of polymer coils in fluids, which determine the processing techniques of polymeric materials. Currently, the non-Newtonian-fluid behaviours of polymer under shear flows, such as shear thinning, are discussed with orientation alignments or disentanglements of polymer chains,1 while the nonlinear elasticity of coil deformation, although fundamentally important, has been overlooked. Under shear flow, coil deformation is commonly attributed to the internal tension raised by the monomer distribution of each coil over several layers of velocity gradient, but its implication to the nonlinear dynamics of polymers has not yet been seriously investigated. Recently, Brownian Dynamics simulations of driven single linear polymer revealed that even without the velocity gradient, the uniformly driven forces, i.e. the uniform shear stress imposed onto all the monomers, could raise coil deformation as well, provided by the local acceleration of dynamic heterogeneity of monomer motions on the chain.2 Dynamic Monte Carlo simulations of driven single linear polymer3 and bulk polymer4 inherited local dynamic heterogeneity by performing random updating of monomers in the short-time scale and reproduced some type of non-Newton-fluid behaviours of polymer under shear flows upon such coil deformation. Therefore, the stress-induced coil deformation in shear flow brings a fresh and complemental intramolecular viewpoint to the fundamental aspect of polymer rheology, in particular, to Oldroyd-B model.Dynamic heterogeneity has been an important topic in the field of glass transition at low temperatures.5 At high temperatures, dynamic heterogeneity appears rather local in high frequencies, even within the scale of single polymer coils.6 In principle, the dynamic heterogeneity of nearby monomers on the chain will raise a local acceleration between these monomer motions, raising a nonlinear effect beyond the linear elastic connection of monomers adopted by the classical Rouse model. Such an intramolecular origin of nonlinearity has been overlooked because in the quiescent fluid, the local acceleration will be neutralized by random Brownian motions of monomers. However, in the driven polymer flow, the situation will be changed by biased Brownian motions of monomers. Recently, the so-called “cracking-the-whip” effect has been proposed as an integration of local acceleration, raised by dynamic heterogeneity of nearby monomers on the chain, and the asymmetry of this effect between chain middle and chain end on the linear polymer chain was supposed to raise the internal tension for the observed coil deformation.2 As a matter of fact, a single macromolecule with one chain end under pinning and another end subjected to a flow field has been well investigated by both experiments and simulations, demonstrating an extreme case of dynamic heterogeneity on coil deformation.7
The dynamic behaviours of linear polymers have often been compared to their ring counterparts of similar chain lengths.8 In this sense, the validity of the above supposition on the structure asymmetry of linear polymers raising coil deformation can be examined by the parallel simulations of driving single ring polymer holding no more chain end. In this study, we perform dynamic Monte Carlo simulations of driven single ring polymers in comparison to their linear counterparts of the same chain lengths. To our surprise, the results showed that structural asymmetry is actually not a prerequisite for coil deformation of driven single polymers, and rather, the high mobility of chain ends significantly suppresses the coil–stretch transition upon large coil deformation. We therefore draw the conclusion that the “cracking-the-whip” effect is the sole origin of internal tension for the observed coil deformation of driven single polymers.
Technical details
Our dynamic Monte Carlo simulations of single linear and ring polymers were based on a phantom free-jointed bead-stick lattice-chain model. The single chain occupied a group of consecutive lattice sites varying from 32 to 128 in a box of 643 cubic lattice cells with periodic boundary conditions. In the sampling method, which reflected dynamic heterogeneity in the short time scale, we randomly selected a monomer to make a trial move for micro-relaxation with the monomer hopping into its vacancy neighbour if available or sometimes accompanied with local sliding diffusion along the chain to maintain the unit of bond lengths as the lattice spacing.9 In the large-scale integration of sequential moves, Rouse dynamics of polymer coils can be reproduced well by this approach.10 The random coils of single linear and ring polymers holding various numbers of monomers were prepared via a long-term athermal relaxation.A constant driven-force field was imposed along the X-axis onto all the monomers of the polymer coils, presumably raised due to the shear stress as a result of the momentum exchange with surrounding solvents, exempting the hydrodynamic drag forces beyond the monomer scale. The Metropolis importance sampling was employed in each trial move of micro-relaxation.11 The driving-force potential F was given by
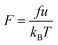 | (1) |
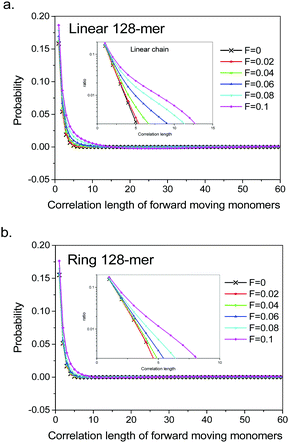
We imposed various driving forces F from 0.001 to 2, and at each force, we made a long-term relaxation of 108 Monte Carlo cycles (each Monte Carlo cycle was defined as the number of trial moves equal to the number of monomers, and the characteristic Rouse relaxation periods for present polymers are around 103 Monte Carlo cycles). The coil deformation was monitored by the dimensional fractions of mean square radius of gyration R2 according to
Results and discussion
We started with the reproduction of coil deformation of linear polymers with variable chain lengths under various driving forces and then compared the results to the ring counterparts under parallel situations. Fig. 1a reproduces the coil deformation of the linear polymers with variable chain lengths as denoted at large driving forces. The raise of normal-stress differences appears as gradual and saturated at larger driving forces, consistent with our previous simulation results.3 To our surprise, Fig. 1b demonstrates that under parallel situations, the ring polymers of the same chain lengths still exhibit coil deformation. The observation that deformation remains in driven single ring polymers proves that the asymmetry between the chain middle and chain end is not a prerequisite of the observed coil deformation. Therefore, the supposition on the asymmetry mechanism of coil deformation appears to be invalid. In comparison to that of linear polymers, ring polymers deform much more abruptly and are saturated to a larger extent of deformation at larger driving forces.The probability of monomer sequences occurring at the very front of moving coils reveals any structural asymmetry for the origin of internal tension of coil deformation. Fig. 2a compares the distributions of monomer sequences at the very front of the moving coils of linear 128-mer under different strengths of driving forces. As usual, the chain-ends of linear polymers have the highest probability of occurring at the very front of the moving coil, reflecting their relatively high mobility. The larger driving forces that raise coil deformation do not appear to change the sequence distribution in the front. The observation did not reproduce the previous observation on a slightly enhanced probability of middle part of 32-mers once deformed2,3 which drew our attention to the asymmetry between chain middle and chain end. In contrast to the linear counterpart, Fig. 2b shows that there is no evident priority for the monomers to occur at the very front of moving ring 128-mers. In other words, all monomers have equal chance of occurring at the very front. This observation implies that the ring polymer is moving in a tank-treading mode. We have provided a movie in the online ESI† to demonstrate the tank-treading motion of the driven ring polymers (look the red monomer). Such a mode of motion could effectively remove the knotting on the polymer chain, although the latter may affect the coil shape in zero-shear states when the chain length becomes much larger than our that in present cases.15 In this sense, the internal tension for coil deformation of ring polymers must be raised by the local “cracking-the-whip” acceleration effect along the polymer chain.
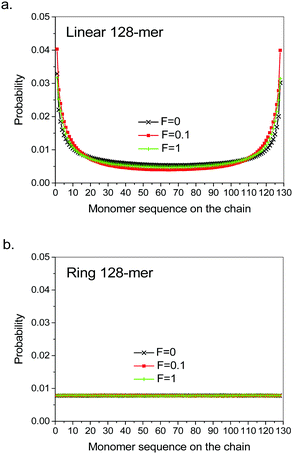 | ||
| Fig. 2 Monomer sequence distributions at the moving front of the coil along X-axis for (a) linear 128-mer and (b) ring 128-mer under three different strengths of driving forces. | ||
The abrupt change in coil sizes upon coil deformation of driven single ring polymers implies a first-order coil–stretch transition, as theoretically described by a free energy barrier between coil and stretch states in the de Gennes’ classic book.16 To confirm the first-order transition behaviour, we made observations on the coil size distribution in the force region of abrupt change from F = 0.1 to 0.38, and compared the results between linear and ring polymers. Fig. 3a demonstrates a gradual shift of single peak upon coil deformation of linear 128-mer, while Fig. 3b shows double peak shifting in their separate weights upon coil deformation of ring 128-mer. Since the coil-size distribution represents the state distribution over coil sizes or according to the Boltzmann's relation, the corresponding free energy curve, the double peak implies the coexistence of two favourite states (two free energy minima) with a free energy barrier lower than the thermal energy level for the free transitions between them, demonstrating the typical first-order coil–stretch transition. The similar all-or-none coexistence behaviour has been observed in the reversible melting of single chain single crystal.17 In comparison, linear polymers make only limited deviations from the coil states, which implies that the coil–stretch transition is suppressed by the highly mobile chain ends. Therefore, the gradual and limited deformation of driven single linear polymer is resulted, as shown in Fig. 1a.
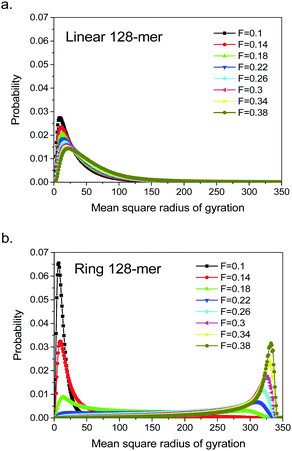 | ||
| Fig. 3 Coil-size distribution curves of (a) linear 128-mer and (b) ring 128-mer at different driving forces as labelled upon significant coil deformation. | ||
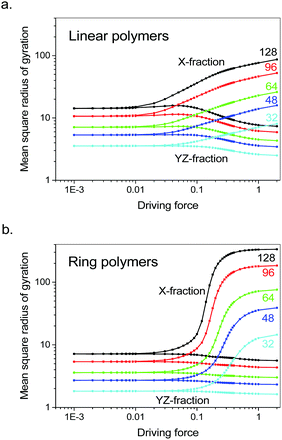
The shifting weights between two states of ring polymers are caused by their free energy differences. We observed the time evolution of fractional sizes for the stretched ring 128-mer at F = 0.2, as shown in Fig. 4. One can clearly see a fast jumping between the coil and stretch states. The much smaller variation of the sectional sizes indicates that the coil–stretch transition looks like spring expansion. One can also see the movie that demonstrates such the expansion process in the online ESI.†
The coil–stretch transition is just a consequence of large coil deformation. The deformation actually starts much earlier before the driving force has reached F = 0.1. Fig. 5 demonstrates that both linear and ring 128-mers start coil deformation as soon as the driving forces have been launched, implying no threshold for coil deformation. In the logarithmic scale of driving forces, for instance in Fig. 1, the divergence in each pair of size fractions looks like launched at a certain critical force as discussed in previous publications,3,4 but this is not evident when one checks them in the linear scale of driving forces. It is interesting to note that the ring 128-mer behaves very similar to the linear 64-mer, except for its X-fraction trend at large forces. The similarity indicates that coil deformation originates in the local chain connection. Therefore, the ring 128-mer behaves like two linear 64-mers bonded to each other at their chain ends. The difference of their X-fraction trends at large forces reflects the early-stage suppression of coil–stretch transition owing to highly mobile chain ends, as already demonstrated in Fig. 3a.
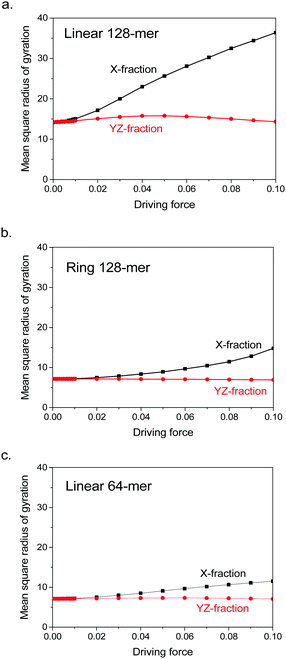 | ||
| Fig. 5 Parallel fraction (squares) and perpendicular fraction (spheres, averaged over two dimensions) of mean square radius of gyration for (a) linear 128-mer, (b) ring 128-mer and (c) linear 64-mer at driving forces smaller than F = 0.1. The data are adopted from Fig. 1. | ||
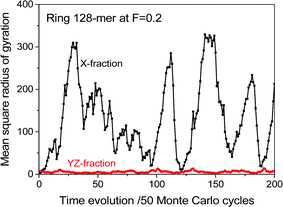
The “cracking-the-whip” effect of a driven single polymer can be evaluated by the correlation length of forward moving monomers along the chain. Fig. 6 shows the calculation results separately for linear and ring 128-mers at various driving forces. The strong correlation of forward moving monomers decays quickly along the polymer chain. However, if we enlarge the small logarithmic length scale for the positive correlation probabilities, we can clearly see the increase of correlation length with the increase of driving forces at very beginning of launching driving forces, indicating the emergence of “cracking-the-whip” effect along the chain connection of driven monomers.
Conclusions
We performed dynamic Monte Carlo simulations of driven single ring polymers in order to compare their deformation behaviours to driven single linear polymers. The results show that ring polymers without chain ends still exhibit coil deformation, proving the “cracking-the-whip” effect as the sole origin of internal tension for coil deformation under uniform driving forces on all the monomers. At strong driving forces for significant coil deformation, ring polymers show a clear coil–stretch transition, while their linear counterparts exhibit no clear transition as it has been suppressed by the highly mobile chain ends. We calculated the correlation lengths of forward moving monomers along the chain to confirm the “cracking-the-whip” effect upon launching driving forces. Our present simulations demonstrate that the chain ends of driven single linear polymers are not the origin of internal tension of coil deformation, but rather they suppress large coil-deformation under large driving forces. The new insights expand our fundamental understanding on the nonlinear elasticity in the driven flows of polymeric materials.Acknowledgements
The financial support of National Natural Science Foundation of China (Grant No. 21474050) and Program for Changjiang Scholars and Innovative Research Team in University is appreciated.Notes and references
- W.-B. Hu, Polymer Physics: A Molecular Approach, Springer, Vienna, 2013 Search PubMed.
- J. Li and W.-B. Hu, Polym. Int., 2015, 64, 49–53 CrossRef CAS.
- J. Li, Y. Ma and W.-B. Hu, Mol. Simul., 2015, 42, 321–327 CrossRef.
- J. Li, Y.-J. Nie, Y. Ma and W.-B. Hu, Chin. J. Polym. Sci., 2013, 31, 1590–1598 CrossRef CAS.
- M. D. Ediger, Annu. Rev. Phys. Chem., 2000, 51, 99–128 CrossRef CAS PubMed; E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627–631 CrossRef PubMed; J. Eaves and D. Reichman, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15171–15175 CrossRef PubMed; H. Tanaka, T. Kawasaki, H. Shintani and K. Watanabe, Nat. Mater., 2010, 9, 324–331 CrossRef PubMed.
- W. W. Graessley, J. Chem. Phys., 2009, 130, 164502 CrossRef PubMed.
- A. Buguin and F. Brochard-Wyart, Macromolecules, 1996, 29, 4937–4943 CrossRef CAS; T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef PubMed; K. Avramova, V. Yamakov and A. Milchev, Macromol. Theory Simul., 2000, 9, 516–522 CrossRef.
- R. Pasquino, T. C. Vasilakopoulos and Y. C. Jeong, et al. , ACS Macro Lett., 2013, 2, 874–878 CrossRef CAS PubMed.
- W.-B. Hu, J. Chem. Phys., 1998, 109, 3686–3690 CrossRef CAS.
- I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823 CrossRef CAS; W.-B. Hu and D. Frenkel, Adv. Polym. Sci., 2005, 191, 1–35 CrossRef.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1095 CrossRef CAS.
- S. Katz, J. L. Lebowitz and H. Spohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1655–1658 CrossRef CAS; R. K. P. Zia, J. Stat. Phys., 2010, 138, 20–28 CrossRef.
- J. Baschnagel and K. Binder, Macromol. Theory Simul., 1996, 5, 417–448 CrossRef CAS; G. Q. Xu, J. D. Ding and Y. L. Yang, J. Chem. Phys., 1997, 107, 4070–4084 CrossRef; S. Gleiman and J. Dorgan, J. Chem. Phys., 2000, 112, 6073–6083 CrossRef; J. K. Jeszka and T. Pakula, Polymer, 2006, 47, 7289–7301 CrossRef; P. Romiszowski and A. Sikorski, Comput. Mater. Sci., 2008, 43, 127–131 CrossRef.
- Y. Ma, X.-H. Zhang and W.-B. Hu, Chin. J. Polym. Sci., 2013, 31, 1463–1469 CrossRef CAS.
- E. J. Rawdon, J. C. Kern, M. Piatek, P. Plunkett, A. Stasiak and K. C. Millettin, Macromolecules, 2008, 41, 8281–8287 CrossRef CAS; R. Matthews, A. A. Louis and C. N. Likos, ACS Macro Letters, 2012, 1, 1352–1356 CrossRef PubMed.
- P. G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, NY, Ch. VIII, 1979 Search PubMed.
- W.-B. Hu, D. Frenkel and V. B. F. Mathot, Macromolecules, 2003, 36, 8178–8183 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Clip at F = 0.2. avi. See DOI: 10.1039/c6qm00369a |
| This journal is © the Partner Organisations 2017 |