Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effects of structural changes of new organophosphorus cationic exchangers on a solvent extraction of cobalt, nickel and manganese from acidic chloride media†
Kateryna Omelchuka,
Piotr Szczepańskic,
Akhilesh Shrotrea,
Mansour Haddada and
Alexandre Chagnes *ab
*ab
aPSL Research University, Chimie ParisTech – CNRS, Institut de Recherche de Chimie Paris, 11 rue Pierre et Marie Curie, 75005 Paris, France
bGéoRessources – UMR CNRS 7359-CREGU-Université de Lorraine, 2 Rue du Doyen Roubault, 54518 Vandoeuvre les Nancy Cedex, France. E-mail: alexandre.chagnes@univ-lorraine.fr
cNicolaus Copernicus University in Toruń, Faculty of Chemistry, Gagarina 7, 87-100 Toruń, Poland
First published on 21st December 2016
Abstract
The effects of structural changes of organophosphorus cationic exchangers on metal-distribution curves (extraction efficiency vs. pH) have been investigated for the recovery of cobalt(II), nickel(II) and manganese(II) from acidic chloride solutions. By using alkyl groups with different branching and hydrophobicity and by including oxygen atoms in the hydrophobic chains of the cationic exchangers, it has been shown that the change of the chemical structure in the hydrophobic chains plays an important role in the extraction behaviours and causes more specifically a shift of the extraction curves to higher or lower pH depending on pKa values of extracting agents (evaluated by using QSPR calculations), distribution constants of metal–ligand complexes between organic and aqueous phases and the formation constant of the metal–ligand complexes. Based on the present results, interest in the new cationic exchangers synthesized in the present work for cobalt(II), nickel(II) and manganese(II) separation is also discussed.
Introduction
Cobalt, nickel and manganese are the main components of the positive electrodes used in lithium-ion batteries (LiBs). Demand will likely strongly increase in the next few decades due to the emergence of electric vehicles since LiBs are considered to be the best choice for high energy density applications such as electric vehicles. In order to meet the world demand for cobalt, manganese and nickel, it is mandatory to exploit new primary deposits such as laterites, sulphide ores and sea nodules or to develop processes to recover these metals from secondary wastes such as spent LiBs.1,2 However, these raw materials contain manganese, nickel and cobalt at various concentrations and their valorisation relies on the development of processes capable to perform efficient separation of these metals in spite of their very close extraction properties.3–5 For this goal, liquid–liquid extraction appears as the best and the most appropriate technology. Many papers report the use of cationic exchangers such as Cyanex 272, D2EHPA, Cyanex 301 or Ionquest 801 alone or in mixture with other cationic exchangers, anionic exchangers or solvating agents.6,7 Their extraction efficiency is quite dependent on the nature of the metal and their speciation in aqueous phase. Metal speciation depends on the nature of the inorganic acid used for leaching the ore. For instance, hydrochloric acid is preferred instead of sulphuric acid when ores are difficult to leach because chloride ions have stronger tendency to form metal complexes than sulphate ions.8The most frequently used extracting agent for cobalt–nickel separation is Cyanex 272 (bis-(2,4,4-trimethylpentyl)phosphinic acid). However, this extractant exhibits a low separation factor between cobalt(II) and manganese(II) both from acidic sulphate and chloride media. Conversely, D2EHPA (bis-(2-ethyl-hexyl-phosphoric acid) is a suitable extractant for Co(II)–Mn(II) separation from acidic chloride media.9 The pH1/2 (pH for which the extraction efficiency is equal to 50%) for Mn(II), Co(II) and Ni(II) extraction from acidic chloride media are equal to 3.95, 4.30 and 6.65 when Cyanex 272 is used as extractant diluted in kerosene and 2.20, 3.30 and 3.83 when D2EHPA is employed instead of Cyanex 272, respectively (vide infra). Therefore, a large amount of alkaline solution such as sodium hydroxide must be added in the leach solution to adjust the pH so that a selective extraction could be achieved, especially when Cyanex 272 is used to separate Co(II) and Ni(II). In order to decrease the operational expenditure, the design of new extracting agents capable to recover and separate cobalt, nickel and manganese at low pH and in few stages is highly required.
Metal extraction by cationic exchangers usually occurs according to the following equation:10
| Maq2+ + 2{HL}org = {ML2}org + 2Haq+ | (1) |
The extraction constant (Kex) of the previous equilibrium is defined as:
| Kex = [{ML2}org][Haq+]2/([Maq2+][{HL}org]2) | (2) |
The following chemical equilibria can be written to describe the system:
| 2{HL}org = {(HL)2}org Kdim = [{(HL)2}org]/[{HL}org]2 | (3) |
| {HL}aq = Haq+ + Laq− Ka = [Haq+][Laq−]/[{HL}aq] | (4) |
| Maq2+ + 2Laq− = {ML2}aq β = [{ML2}aq]/([Maq2+][Laq−]2) | (5) |
| {ML2}aq = {ML2}org KD,ML2 = [{ML2}org]/[{ML2}aq] | (6) |
The distribution coefficient D = [{ML2}org]/[Maq2+] can be expressed by using eqn (2)–(6) as follows:
log(D) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD,ML2 + log KD,ML2 + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β − 2pKa + 2 β − 2pKa + 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[{HL}org] + 2pH log[{HL}org] + 2pH
| (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ka.
Ka.
Thus, eqn (7) shows the extraction efficiency at constant pH of the aqueous phase and constant concentration of extractant in the organic phase is improved provided that: (i) the metal–ligand complex is very stable in the organic phase (high value of β), (ii) the metal–ligand complex is highly soluble in the organic phase (high value of KD,ML2) and (iii) the pKa of the organophosphorus acid is as low as possible. The chemical structure of the extractants is particularly important as it influences its pKa value, its affinity toward metals (steric hindrance, complexing properties) and its partition between organic and aqueous phases (hydrophobicity).
Therefore, the pKa value is one of the main factors influencing the distribution coefficient (D) as illustrated in eqn (7). For new extracting agents, the experimental determination of pKa is frequently cumbersome and complicated because of their low solubility in water. On the other hand, in order to estimate pKa values (as well as distribution coefficients or dimerization constants), various regression models based on the linear free energy relationship (LFER) can be applied.11–17 For example, these models were applied to predict or estimate a distribution constant of non-ionizable crown ethers and their benzo-derivatives in the organic/water system,18 to describe selectivity towards alkali metal cations in the bulk liquid membrane19 as well as to correlate the distribution, dimerization, and dissociation constants of dialkylorganophosphorous acidic extractants with the properties of solutes and solvents.20,21 However, some values of the descriptors used in the model construction should be determined experimentally22,23 or predicted from other regression models.24–27 Moreover, for new substances (e.g. extractants), the descriptor values prediction can be associated with the extrapolation outside the range of the model space (applicability domain) and can result in an error in estimating these values.
Alternatively, for the pKa values estimation, the quantitative structure–property relationships (QSPR) models based on molecular descriptors as the independent variables have been used.28,29 In the 2D-QSPR models over 1200 molecular descriptors, derived from a two-dimensional graph representation of a molecule, can be calculated30 and applied in the model formulation, whereas in the LFER models, a small set of descriptors (e.g. 5 or 6 Abraham solvation parameters) were used. However, in the QSPR modelling, the application of appropriate variable selection methods results in a significant reduction in the number of descriptors. Additionally, it enables also the prediction of a given physicochemical property inside the applicability domain.
In the present paper, 2D-QSPR models based on multiple linear regression (MLR) and partial least square (PLS) methods31 has been applied to predict pKa values of new and commercial organophosphorus cationic exchangers in order to discuss the influence of their chemical structure on the extraction efficiency of Co(II), Ni(II) and Mn(II) vs. pH. In particular, the influence of branching, hydrophobicity and the presence of oxygen atoms in the hydrophobic chains has been investigated.
Experimental section
Synthesis of organophosphorus acids
Phosphorus trichloride (Fisher Scientific, purity 99%), pyridine (Fisher Scientific, purity 99%), 1-octanol (Fisher Scientific, purity 99%), 2-methyl-1-propanol (Fisher Scientific, purity 99%), 1-butanol (Fisher Scientific, purity 99.5%), lithium aluminium hydride (Fisher Scientific, purity 95%, powder), iodine (Fisher Scientific, purity 99%), sodium (Sigma Aldrich purity ≥ 99.8%), ethylene glycol butyl ether (Sigma Aldrich, purity ≥ 99%), 6-undecanone (TCI, purity > 98%), 2-ethyl-1-hexanol (TCI, purity > 99.5%) and 1,3-dichloro-2-propanol (TCI, purity > 98%) were used as delivered.The synthesis of BiDiBOPP was performed according to the procedure previously published by Beltrami et al.32 (Scheme 1).
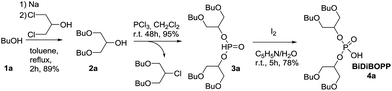 | ||
| Scheme 1 Synthesis route to BiDiBOPP as a sake of illustration of the general synthesis route of organophosphorus compounds synthesized in the present paper. | ||
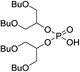
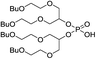
The 1,3-dibutoxy-2-propanol (2a) was synthesized by reaction of n-butanol and 1,3-dichloro-2-propanol in the presence of sodium metal. The reaction of 2a with phosphorus trichloride (PCl3) at room temperature led to bis(1,3-dibutoxypropan-2-yl)phosphite (3a) in a 78% yield. After purification, 3a was oxidized by I2 in pyridine–water mixture to form bis(1,3-dibutoxypropan-2-yl)phosphoric acid (BiDiBOPP, 4a) (Scheme 1).
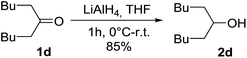
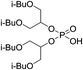
The cationic exchangers were synthesized by using the same procedure as for BiDiBOPP except for the synthesis of bis(undecan-6-yl)phosphoric acid (4d) (Table 1). Indeed, the corresponding alcohol 2d used for the synthesis of 4d was synthesized by reduction of undecan-6-on with lithium aluminium hydride LiAlH4 at 0 °C in anhydrous THF according to the following reaction:
The reaction yield and the product purity determined by 1H, 13C, 31P NMR spectroscopy are gathered in Table 1. The synthesized molecules were used in liquid–liquid extraction without any further purification.
Liquid–liquid extraction procedure
Feed solutions of Ni(II), Co(II) and Mn(II) at 1.17 g L−1 (0.02 mol L−1), 1.18 g L−1 (0.02 mol L−1) and 1.1 g L−1 (0.02 mol L−1) were prepared by dissolving the required amount of salts in 1 M hydrochloric acid solution.
Metal-distribution curves (metal extraction efficiency vs. pH)
The extraction properties of the organophosphorus acids towards Co(II), Ni(II) and Mn(II) in acidic chloride media were evaluated by plotting the metal distribution curves (extraction efficiency %E vs. pH). Extraction efficiency was calculated as follows.
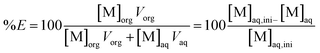 | (8) |
In order to plot the metal-distribution curves, the pH values of the aqueous phases were adjusted by using NaOH and HCl (standard solution, Alfa Aesar). Batch experiments were conducted at 25 °C in a flask containing equal volumes of aqueous and organic phases (10 mL; Vorg/Vaq = 1). The biphasic system was shaken with a Thermoshaker (Gerhardt) at 100 rpm for 15 minutes. Preliminary experiments on the kinetics of extraction of Ni(II), Co(II) and Mn(II) showed that equilibrium was reached in all cases within 5 minutes of contact. After phase separation, the aqueous phase was filtered on nylon filter (VWR, Sartorius®, 0.20 μm) and the equilibrium pH of the aqueous phase was measured. Metal concentrations in aqueous solutions were determined by ICP-OES (ICAP 6000 Series, Thermo Scientific) at 243.7 nm for nickel, 237 nm for cobalt and 257 nm for manganese after diluting the sample in hydrochloric acid (ICP standard solution, 37%, VWR). Metal ion concentration transferred from the aqueous phase into the organic phase was then deduced by mass balance in order to calculate the extraction efficiency defined in eqn (8). Experiments were duplicated and the experimental error on the distribution coefficients of metals was estimated to be within 5%.
Quantitative structure–properties relationships
Quantitative Structure–Activity Relationship (QSAR) and Quantitative Structure–Property Relationship (QSPR) studies are the typical areas of chemical research in which the chemical properties of a compound are related with the structure of molecules represented by the molecular descriptors. The term molecular descriptor indicates a characterization of a molecule by a number (or numbers) that primarily is (are) “the final result of a logical and mathematical procedure which transforms chemical information encoded within a symbolic representation of a molecule”.33 QSPR methods were successfully applied for e.g. prediction of acidity constants of some anthraquinone derivatives in binary methanol–water systems,34 octanol–water partition coefficient35, design of ligands for the separation of lanthanides and actinides36 or prediction of pKa for benzoic acids in different solvents.37 In this paper, the QSPR method for estimating pKa values of the investigated cationic exchangers was applied. Molecular descriptors were calculated using the Parameter Client software (VCCLAB).38,39The Multiple Linear Regression (MLR) and Partial Least Square (PLS) analyses were performed using MATLAB and Statistics Toolbox (Release 2010b, The MathWorks, Inc., Natick, Massachusetts, USA) as well as PS Imago 3 (IBM SPSS Statistics 23, IBM Corporation, Armonk, NY, USA) software. The stepwise procedure in MLR was applied to remove the insignificant coefficients from the regression model. Alternatively, the optimum number of descriptors (among 1309 calculated) in MLR was selected according to the procedure described in ref. 40. Statistical validity of the correlation was estimated using the values of determination coefficient (R2) and test function F of Snedecor–Fisher (F-statistics). In order to evaluate the predictive accuracy of the model, the cross-validation procedure was applied.
Results and discussion
As mentioned previously, metal extraction properties of extracting agents are related to the thermodynamic parameters such as pKa value (eqn (7)). The present section investigates the extraction properties of six new and four commercial cationic exchangers. These properties are analysed in the light of pKa deduced from QSPR model since no pKa values are available in the literature for the six new molecules.QSPR model for determining pKa values
In order to perform QSPR calculations for evaluating pKa values of the investigated cationic exchangers, two different training data sets were applied. In the first part of the study, a training data set of 55 dissociation constants was used (see ESI,† data set I = molecules from 1 to 55). The set of data was carefully selected from experimental data reported in literature by potentiometric titration in water. In particular, we paid attention to select pKa values determined under very close experimental conditions in terms of media, ionic strength, temperature, etc. This database and the corresponding references are reported in ESI.†The calculated molecular descriptors (1309 MDs) for these compounds were linearly correlated with the dissociation constants. After performing the regression analysis with the forward variable selection method (to remove the insignificant coefficient from the regression model), the following relationship was obtained:
| pKa = 0.910(0.037)Jhetv − 10.8(2.7)R4p + − 1.18(0.18)MATS2v + 4.05(0.78)RBF | (9) |
| R2 = 0.989, S.D. = 0.28, F = 1114, N = 55, Qcv2 = 0.921 |
| pKa = −22.9(1.6) + 0.910(0.45)BEHp1 + 0.181(0.030)C-003 − 0.429(0.074)Mor15e + 0.53(0.14)MATS2m + 0.213(0.054)Jhetp | (10) |
| R2 = 0.984, S.D. = 0.12, F = 377, N = 36, Qcv2 = 0.978 |
| No. | Acid | pKa values | ||||
|---|---|---|---|---|---|---|
| Exp. | M1 | M2 | M3 | M4 | ||
| 1 | Cyanex 301 C5H10(C2H5)CH2– | 2.80 | — | — | — | — |
| 2 | Cyanex 272 C5H10(C2H5)CH2– | 3.73 | 4.17 | 3.91 | 3.85 | 3.72 |
| 3 | Ionquest 801 C5H10(C2H5)CH2–C5H10(C2H5)CH2O– | 3.3 | 3.26 | 3.37 | 3.5 | 3.33 |
| 4 | D2EHPA C5H10(C2H5)CH2O– | 2.75 | 2.3 | 2.59 | 2.71 | 2.76 |
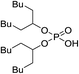
| 5 | BiDiBOPP (C4H9OCH2)2CHO– | — | 3.58 | 4.04 | 1.65 | 2.35 |
| 6 | IPA (i-C4H9OCH2)2CHO– | — | 3.43 | 4.24 | 2.43 | 2.42 |
| 7 | TPA (C4H9OC2H4OCH2)2CHO– | — | 4.01 | 5.53 | 1.80 | 1.66 |
| 8 | UPA (C5H11)2CHO– | — | 2.99 | 3.45 | 2.88 | 2.85 |
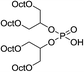
| 9 | OPA (C8H17OCH2)2CHO– | — | 3.83 | 5.65 | 2.09 | 3.07 |
| 10 | EHPA (C4H9CH(C2H5)CH2OCH2)2CHO– | — | 3.98 | 6.90 | 3.79 | 4.02 |
In the PLS model analysis the highest cross-validation coefficient (Qcv2 = 0.928) was obtained for 9 latent variables, with the determination coefficient (R2) equals to 0.998.
The calculated pKa values by means of the MLR and PLS methods are reported in Table 2 (Models 3 and 4, respectively).
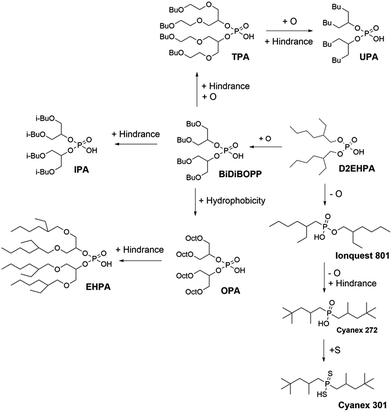
The calculated pKa values are quite different from one model to another. The pKa values estimated by Models 3 and 4 are in the best accordance with experimental values of pKa of Cyanex 272, D2EHPA and Ionquest 801 (Table 2). Furthermore, it is worth noting that the pKa values calculated with these models follow the same general trends as in the literature (see ESI†), i.e. an increase of the number of oxygen atoms in the hydrophobic chains of organophosphorus acids leads to a decrease of pKa values due to attractive inductive effects (extractants 4 and 7 in Table 2).
Model 3 predicts that the pKa values of the extractants 4 and 5 are different while their chemical structures are very close. The difference between these two molecules arises only for the branching of the hydrophobic chains. Conversely, Model 4 predicts branching does not influence significantly the pKa values of extractants 4 and 5. Therefore, models 4 seems to be more relevant to calculate pKa values since it was expected that branching in the hydrophobic chains may influence pKa values very slightly.
Extraction properties of new cationic exchangers
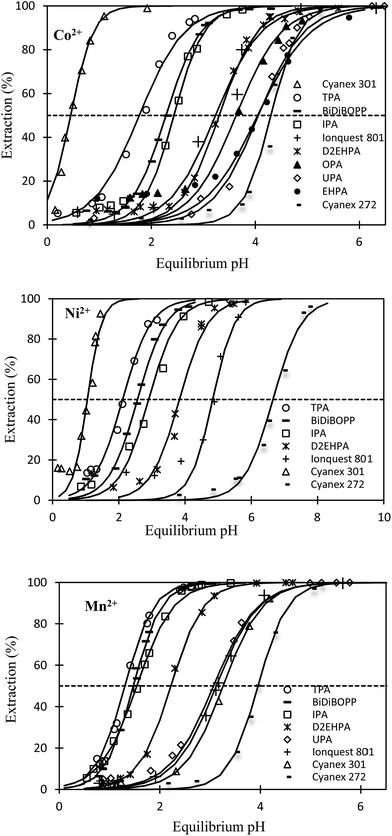
Fig. 1 shows the extraction efficiencies of Co(II), Ni(II) and Mn(II) vs. pH for Cyanex 301, Cyanex 272, Ionquest 801 and D2EHPA as well as for the 6 new cationic exchangers synthesized in the laboratory (see Table 2). The pH values at half extraction (pH for which 50% of metals are extracted, pH1/2) are reported in Table 3. All investigated extracting agents can recover Ni(II), Mn(II) and Co(II) from acidic chloride solution. In certain cases, the extraction efficiency is not equal to zero under very acidic conditions likely because of the presence of impurities, which can extract metals even at very low pH because impurities might be solvating agents (extraction efficiency of metals by solvating agents does not depend on pH).| No. | Name | pKa | pH1/2 | |||
|---|---|---|---|---|---|---|
| Exp. | Calc. | Mn(II) | Co(II) | Ni(II) | ||
| 1 | Cyanex 301 | 2.80 | — | 3.2 | 0.5 | 1.0 |
| 2 | Cyanex 272 | 3.73 | 3.72 | 3.9 | 4.3 | 6.6 |
| 3 | Ionquest 801 | 3.30 | 3.33 | 3.1 | 3.2 | 4.8 |
| 4 | D2EHPA | 2.75 | 2.76 | 2.2 | 3.3 | 3.8 |
| 5 | BiDiBOPP | — | 2.35 | 1.5 | 2.3 | 2.6 |
| 6 | IPA | — | 2.42 | 1.5 | 2.4 | 2.9 |
| 7 | TPA | — | 1.66 | 1.3 | 2.0 | 2.1 |
| 8 | UPA | — | 2.85 | 3.0 | 4.0 | — |
| 9 | OPA | — | 3.07 | — | 3.6 | — |
| 10 | EHPA | — | 4.02 | — | 4.0 | — |
The value of pH1/2 can be derived from eqn (7) as follows:
pH1/2 = pKa − ½(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD,ML2 + log KD,ML2 + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β + log(ν) − log[{HL}org]) β + log(ν) − log[{HL}org])
| (11) |
This equation shows that pH1/2 values are influenced by (i) the hydrophobicity of the cationic exchanger (an increase of the hydrophobicity, i.e. an increase of KD,ML2, is responsible for a decrease of pH1/2), (ii) the pKa values (a decrease of pKa is responsible for a decrease of pH1/2) and (iii) the affinity of the cationic exchanger towards metals (an increase of β is responsible for a decrease of pH1/2). Therefore, it is expected that alkyl chain branching at the vicinity of the acidic group is responsible for a decrease of β due to steric hindrance, and thus, an increase of pH1/2. Likewise, the presence of oxygen or sulphur atoms in the acidic group of the extracting agents may change β (as predicted by the Hard–Soft–Acid–Base Theory) and consequently, the value of pH1/2.
Such influences of branching, hydrophobicity of the alkyl chains and the presence of oxygen or sulphur atoms in the acidic function of the cationic exchangers have been studied in the present paper by investigating the extraction properties of several cationic exchangers (Fig. 2).
Table 3 shows pKa and pH1/2 values increase as follows:
- pKa: TPA < BiDiBOPP ≤ IPA < D2EHPA ≤ UPA < OPA < Ionquest 801 < Cyanex 272 < EHPA.
- pH1/2 for Mn(II): TPA ≤ BiDiBOPP = IPA < D2EHPA < UPA ≤ Ionquest 801 < Cyanex 301 < Cyanex 272.
- pH1/2 for Co(II): Cyanex 301 ≪ TPA < BiDiBOPP ≤ IPA ≪ Ionquest 801 ≤ D2EHPA < OPA < UPA = EHPA < Cyanex 272.
- pH1/2 for Ni(II): Cyanex 301 < TPA < BiDiBOPP < IPA < D2EHPA < Ionquest 801 < Cyanex 272.
It is interesting to notice that Mn(II) extraction from acidic chloride media by the investigated cationic exchangers is mainly governed by the pKa probably because the sum of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and log
β and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD,ML2 does not vary so much from a cationic exchanger to another one (the variation of β may compensate the variation of KD,ML2). Therefore, more the cationic exchanger is hydrophobic, more the affinity between Mn(II) and the cationic exchanger is weakened and log
KD,ML2 does not vary so much from a cationic exchanger to another one (the variation of β may compensate the variation of KD,ML2). Therefore, more the cationic exchanger is hydrophobic, more the affinity between Mn(II) and the cationic exchanger is weakened and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β + log
β + log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD,ML2 remains close to zero (see eqn (12)).
KD,ML2 remains close to zero (see eqn (12)).
Regarding Ni(II) and Co(II) extraction, the behaviour of these two metals is similar as pH1/2 values vary in the same order. This is not surprising as these two metals are known to have the same behaviour in solvent extraction. However, the trend is completely different for Ni(II) and Co(II) compared to Mn(II) as pH1/2 values do not follow the variation of pKa. Therefore, unlike Mn(II), the sum of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β and log
β and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KD,ML2 is not the same from a cationic extractant to another one. In particular, it is interesting to notice that Cyanex 301 exhibits the lowest pH1/2 (for Ni and Co) whereas its pKa value is not very low, i.e. pKa = 2.80 given that all investigated cationic exchangers exhibit pKa values between 1.6 and 4.0. The low value of pH1/2 can be explained by the presence of sulphur atoms instead of oxygen atoms in the complexing group (Cyanex 301 and Cyanex 272 have the same alkyl chains). These results are in agreement with the Hard–Soft–Acid–Base theory (HSAB), which indicates that soft atoms such as sulphur have more affinity with soft acids or borderline hard acids like Ni(II) and Co(II) rather than with hard acids like Mn(II). Therefore, the value of β may be much greater than the value of pKa, resulting in low value of pH1/2 for Co(II) and Ni(II) extraction by Cyanex 301.
KD,ML2 is not the same from a cationic extractant to another one. In particular, it is interesting to notice that Cyanex 301 exhibits the lowest pH1/2 (for Ni and Co) whereas its pKa value is not very low, i.e. pKa = 2.80 given that all investigated cationic exchangers exhibit pKa values between 1.6 and 4.0. The low value of pH1/2 can be explained by the presence of sulphur atoms instead of oxygen atoms in the complexing group (Cyanex 301 and Cyanex 272 have the same alkyl chains). These results are in agreement with the Hard–Soft–Acid–Base theory (HSAB), which indicates that soft atoms such as sulphur have more affinity with soft acids or borderline hard acids like Ni(II) and Co(II) rather than with hard acids like Mn(II). Therefore, the value of β may be much greater than the value of pKa, resulting in low value of pH1/2 for Co(II) and Ni(II) extraction by Cyanex 301.
Despite the high pKa value of EHPA, pH1/2 is not so high likely because EHPA–metal complexes exhibit low value of β due to steric hindrance and high value of KD,ML2 resulting from the presence of long alkyl chains in the chemical structure of EHPA.
More generally, the presence of oxygen atoms in the hydrophobic chains of the cationic exchangers decreases the pH1/2 values. Unfortunately, oxygen atoms in the hydrophobic chains are also responsible for a decrease of the selectivity (the difference in pH1/2 between Ni(II), Co(II) and Mn(II) for the same cationic exchanger is lowered when oxygen atoms are inserted in the hydrophobic chains as illustrated in Table 3). Likewise, steric hindrance may play a negative role by disfavouring the metal–ligand interactions leading to an increase of the pH1/2 values provided that the steric hindrance factor would be more important than the hydrophobic factor.
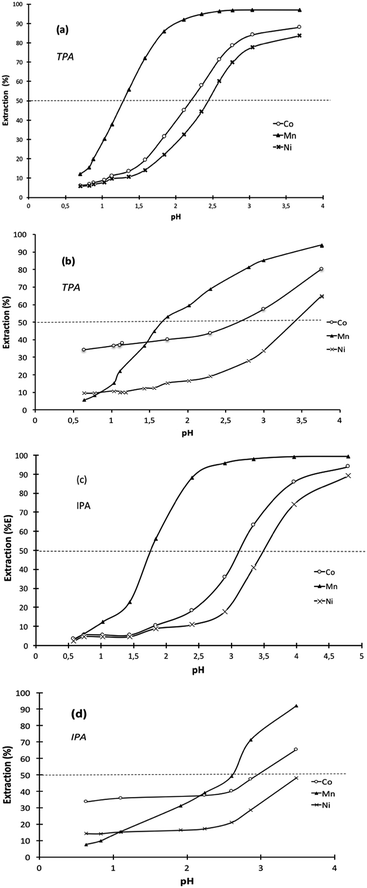
Comparison of pH1/2 values of the cationic exchangers for the extraction of Co(II), Ni(II) and Mn(II) shows the decrease of pH1/2 is accompanied by a loss in selectivity, which gets difficult Co–Ni–Mn separation (Table 3). For instance, TPA exhibits the lowest pH1/2 values (1.3–2.1) but the difference in pH1/2 is too low for allowing efficient Ni–Mn–Co separation. As a sake of illustration, Fig. 3 shows extraction curves vs. pH of Co(II), Ni(II) and Mn(II) from acidic chloride media by using TPA and IPA in kerosene (these two extractants are the most interesting molecules among those synthesized in the present paper). The acidic chloride solutions containing Co(II), Ni(II) and Mn(II) simulate leaching solutions of cathode from spent lithium-ion batteries (Li1/3Ni1/3Mn1/3O2) or leaching solution of sea nodules.1,41–43 Mn(II) can be easily separated towards Ni(II) and Co(II) by controlling the pH of simulated leaching solutions of cathodes at 1.1 (Fig. 3a) and 1.6 (Fig. 3c) when the extractant is TPA and IPA, respectively. Less than 10% of Ni(II) and Co(II) are co-extracted but the use of multi-stage solvent extraction equipment such as mixers-settlers will permit full separation of Mn(II) towards Co(II) and Ni(II). However, separation of Co(II) and Ni(II) cannot be achieved by using TPA or IPA as pH1/2 values are too close. Change in composition of the aqueous solution affects strongly the metal separation. For instance, the ability of TPA or IPA to separate Mn(II) towards Co(II) and Ni(II) is strongly reduced when the extraction solvent is contacted with an aqueous phase simulating a leaching solution of sea nodules instead of a leaching solution of cathodes from spent lithium-ion batteries (Fig. 3b and d). The high Co(II) extraction at low pH might be due to the presence of 6% and 8% of impurities in IPA and TPA, respectively. These impurities are likely solvating agents because such molecules can extract metals even at low pH. The high affinity of the impurities for Co(II) and the low Co(II) concentration in aqueous phase, like in the case of leaching solutions of cathodes, exalts Co(II) extraction efficiency and no selectivity can be achieved even at low pH values.
Conclusion
The pH1/2 values of the metal distribution curves for cationic exchangers depends on the hydrophobicity of the cationic exchanger (an increase of the hydrophobicity, i.e. an increase of the distribution constant between the organic and the aqueous phase is responsible for a decrease of pH1/2), the pKa value of the cationic exchanger (a decrease of pKa is responsible for a decrease of pH1/2) and the affinity of the cationic exchanger towards metals (an increase of the complexation constant is responsible for a decrease of pH1/2).In the case of Ni(II) and Co(II) extraction, the pH1/2 follows the variation of pKa unlike Mn(II). For the latter, it appears that the more hydrophobic the cationic exchanger is, the more weakened the affinity between Mn(II) and the cationic exchanger is. Furthermore, the presence of oxygen atoms in the hydrophobic chains of the cationic exchangers decreases the pH1/2 values and reduces the selectivity in Co–Ni–Mn extraction. Obviously, the nature of the atoms in the complexing group influences the extraction properties in accordance with the Hard–Soft–Acid–Base theory (HSAB). More generally, it appears that a decrease of pKa values of organophosphorus cationic exchangers by adding oxygen atoms in the hydrophobic chains is responsible for an important loss of selectivity towards cobalt, nickel and manganese.
References
- A. Chagnes and B. Pospiech, J. Chem. Technol. Biotechnol., 2013, 88, 1191 CrossRef CAS.
- Lithium Process Chemistry : Resources, Extractions, Batteries and Recycling, ed. A. Chagnes and J. Swiatowska, Elsevier, 2015, p. 313, ISBN: 978-0-12-801417-2 Search PubMed.
- Extractive metallurgy of nickel, cobalt and platinum-group materials, ed. F. K. Crundwell and M. S. Moats, Elsevier, 2011, p. 610, ISBN: 978-0-08-096809-4 Search PubMed.
- P. K. Parhi, S. Panigrahi, K. Sarangi and K. C. Nathsarma, Sep. Purif. Technol., 2008, 59, 310 CrossRef CAS.
- K. Sarangi, B. R. Reddy and R. P. Das, Hydrometallurgy, 1999, 52, 253 CrossRef CAS.
- H. Nadimi, A. Amirjani, D. H. Fatmehsari, S. Firoozi and A. Azadmehr, Miner. Eng., 2014, 69, 177 CrossRef CAS.
- D. Darvishi, D. F. Haghshenas, E. K. Alamdari, S. K. Sadrnezhaad and M. Halali, Hydrometallurgy, 2005, 77, 238 CrossRef.
- Y. Liu, S.-H. Nam and M.-S. Lee, Bull. Korean Chem. Soc., 2015, 36, 2646 CrossRef CAS.
- J. M. Zhao, X. Y. Shen, F. L. Deng, F. C. Wang, Y. Wu and H. Z. Liu, Sep. Purif. Technol., 2011, 78, 345 CrossRef CAS.
- A. Chagnes and G. Cote, Séparation du Cobalt et du Nickel à l’aide du Cyanex® 272 par extraction liquide-liquide, L’Actualité Chimique, 2010, 346, 29–347 CAS.
- M. H. Abraham, Pure Appl. Chem., 1993, 65, 2503 CrossRef CAS.
- M. H. Abraham, J. Phys. Org. Chem., 1993, 6, 660 CrossRef CAS.
- T. A. Mastryukova and M. I. Kabachnik, Russ. Chem. Rev., 1969, 38, 795 CrossRef.
- T. A. Mastryukova and M. I. Kabachnik, J. Org. Chem., 1971, 36, 1201 CrossRef CAS.
- R. W. Taft, J.-L. Abboud, M. J. Kamlet and M. H. Abraham, J. Solution Chem., 1985, 14, 186 CrossRef.
- D. C. Leggett, J. Solution Chem., 1993, 22, 289 CrossRef CAS.
- D. C. Leggett, Anal. Chem., 1993, 65, 2907 CrossRef CAS.
- W. Robak, W. Apostoluk and P. Maciejewski, Anal. Chim. Acta, 2006, 569, 119 CrossRef CAS.
- R. A. Bartsch, E.-G. Jeon, W. Walkowiak and W. Apostoluk, J. Membr. Sci., 1999, 159, 123 CrossRef CAS.
- W. Apostoluk, B. Gajda, J. Szymanowski and M. Mazurkiewicz, Anal. Chim. Acta, 2000, 405, 321 CrossRef CAS.
- W. Apostoluk and W. Robak, Anal. Chim. Acta, 2005, 548, 116 CrossRef CAS.
- M. H. Abraham, R. J. Abraham, J. Byren and L. Griffith, J. Org. Chem., 2006, 71, 3389 CrossRef CAS PubMed.
- C. F. Poole, S. N. Atapattu, S. K. Poole and A. K. Bell, Anal. Chim. Acta, 2009, 652, 32 CrossRef CAS PubMed.
- M. H. Abraham, R. E. Smith, R. Luchtefeld, A. J. Boorem, R. Luo and W. E. Acree Jr, J. Pharm. Sci., 2010, 99, 1500 CrossRef CAS PubMed.
- J. A. Platts, D. Butina, M. H. Abraham and A. Hersey, J. Chem. Inf. Comput. Sci., 1999, 39, 835 CrossRef CAS.
- J. Jover, R. Bosque and J. Sales, J. Chem. Inf. Comput. Sci., 2004, 44, 1098 CrossRef CAS PubMed.
- L. M. Sprunger, A. Proctor, W. E. Acree Jr and M. H. Abraham, Phys. Chem. Liq., 2008, 46, 574 CrossRef CAS.
- A. R. Katritzky, M. Kuanar, S. Slavov and C. D. Hall, Chem. Rev., 2010, 110, 5714 CrossRef CAS PubMed.
- Y. E. Zevatskii and D. V. Samoilov, Russ. J. Org. Chem., 2011, 47, 1445 CrossRef CAS.
- R. Todeschini and V. Consonni, Handbook of molecular descriptors, WILEY-VCH Verlag GmbH, Weinheim, 2000 Search PubMed.
- R. G. Brereton, Chemometrics. Data analysis for the laboratory and chemical plant, John Wiley & Sons, Ltd, Chichester, UK, 2003 Search PubMed.
- D. Beltrami, A. Chagnes, M. Haddad, H. Laureano, H. Mokhtari, B. Courtaud, S. Jugé and G. Cote, Sep. Sci. Technol., 2013, 48, 480 CrossRef CAS.
- R. Todeschini and V. Consonni, Handbook of Molecular Descriptors, Wiley-VCH, 2000 Search PubMed.
- M. Shamsipur, B. Hemmateenejad, M. Akhond and H. Sharghi, Talanta, 2001, 54, 1113 CrossRef CAS PubMed.
- Y. J. Xie, H. Liu, H. X. Liu, Z. C. Zhai and Z. Y. Wang, Bull. Environ. Contam. Toxicol., 2008, 80, 319 CrossRef CAS PubMed.
- M. G. B. Drew, M. J. Hudson and T. G. A. Youngs, J. Alloys Compd., 2004, 374, 408 CrossRef CAS.
- J. Jover, R. Bosque and J. Sales, QSAR Comb. Sci., 2008, 27, 563 CAS.
- VCCLAB, Virtual Computational Chemistry Laboratory, http://www.vcclab.org, 2005.
- I. V. Tetko, J. Gasteiger, R. Todeschini, A. Mauri, D. Livingstone, P. Ertl, V. A. Palyulin, E. V. Radchenko, N. S. Zefirov, A. S. Makarenko, V. Y. Tanchuk and V. V. Prokopenko, J. Comput.-Aided Mol. Des., 2005, 19, 453 CrossRef CAS PubMed.
- A. G. Mercader, M. Goodarzi, P. R. Duchowicz, F. M. Fernandez and E. A. Castro, Chem. Biol. Drug Des., 2010, 76, 433 Search PubMed.
- Extractive metallurgy of nickel, cobalt and platinum-group materials, ed. F. K. Crundwell, Amsterdam, Boston, Elsevier, 2011 Search PubMed.
- G. Senanayake, Miner. Eng., 2011, 24(13), 1379 CrossRef CAS.
- J. R. Hein, K. Mizell, A. Koschinsky and T. A. Conrad, Ore Geol. Rev., 2013, 51, 1 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra21695a |
| This journal is © The Royal Society of Chemistry 2017 |