Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shear effects on the diffusive movement of oil in triacylglycerol networks
Nuria C. Acevedo*a,
Bryce MacMillanb,
Benedict Newlingb and
Alejandro G. Marangonic
aDepartment of Food Science and Human Nutrition, Iowa State University, 2312 Food Sciences Building, Ames, IA 50011-1054, USA. E-mail: nacevedo@iastate.edu; Tel: +1-515-294-3011 Tel: +1-515-294-5962
bMRI Centre, Department of Physics, University of New Brunswick, Fredericton, NB, Canada E3B 5A3. E-mail: bnewling@unb.ca; bryce@unb.ca
cGuelph-Waterloo Physics Institute, Centre for Food & Soft Materials Science, Department of Food Science, University of Guelph, 50 Stone Road East, Guelph, Ontario, Canada N1G 2W1. E-mail: amarango@uoguelph.ca
First published on 9th January 2017
Abstract
Oil migration is the foremost contributor to the quality loss of many high fat food products; thus, developing an understanding on how this phenomenon takes place in food systems is crucial for the food industry. Diffusion of triacylglycerols (TAG) through the fat network has often been modeled using simplified solutions to Fick's second law. However, a drawback of the use of diffusion models is the lack of sensitivity toward some microstructural characteristics of the matrix. This work reports the study of molecular and macroscopic oil diffusion coefficients of fat crystal networks using nuclear magnetic resonance measurements and from gravimetric determinations of oil loss, respectively. Blends of fully hydrogenated soybean oil (FHSO) in soybean oil (SO) were crystallized statically, under laminar shear rates of 30 and 240 s−1 at different wall temperatures (−10, 0, 20 °C). Another batch of similar blends prepared with and without emulsifier was crystallized in a scraped surface heat exchanger. The results showed a good correlation between diffusion coefficients obtained using both methodologies only when samples exhibited low oil loss, particularly in blends crystallized statically or under mild-shearing conditions. This work suggests that although the Ziegleder model has great advantages and provides valuable insight into the oil migration in fat matrices, there remains a large need for further evaluating its suitability, principally in cases where crystalline structure is severely affected by processing conditions and where oil migration mechanisms other than diffusion may be involved.
1 Introduction
In confectionary and many other high fat products, oil migration is a key contributor to product quality loss. Controlling the migration of liquid oil in a fat rich product is critical for maintaining an acceptable quality. Models that predict fat migration can be very useful to optimize manufacturing processes and guarantee the best quality of the final product for consumers. Diffusive transport is usually described using Fick's law, which relates the diffusive solute flux to the difference in liquid phase solute concentration between adjacent regions by means of a diffusion coefficient. In the last few years, several attempts have been made to model fat migration using simplified solutions to this Fick's second law.1,2 However, a major concern regarding the use of diffusion models has been the lack of sensitivity toward other microstructural aspects of the matrix.3 Many findings have suggested that a capillary flow mechanism may play a role on the migration of oil in high fat products.3 For instance, Ziegler et al.4 reported that oil migration is not well described by Fickean diffusion at all temperatures. Marty et al.5 suggested that both diffusion and capillary rise mechanisms might be active during oil migration through cocoa butter. However, it has recently been proposed that diffusion is the prevalent mechanism of oil migration: Ziegler6 reported that capillary action is too fast; within the order of seconds and hours to be considered in the timescale of oil migration wish is in the range of days or months. Furthermore, Altimiras et al.7 after solving Lucas–Washburn equation that describes the kinetics of capillary rise, obtained capillary curves which predicted oil migration with times 800 shorter than those observed experimentally, therefore indicating little role of capillary forces in oil migration. Thus, current simplified models are not adequate to reproduce experimental data because simplifying assumptions are not satisfied. Today, there is still the need to understand the exact mechanism of fat and oil migration through a crystallized network of lipids in order to aid the modelling of the structuring process and therefore allow the design of fat products with predictable and desirable oil binding capacity.This paper addresses changes in molecular and macroscopic diffusion of oil in fat crystal networks crystallized under different conditions and attempts to evaluate the transport mechanism that determine these changes as well as their relationship with the physical and structural properties of the systems. Diffusivities were measured at both, the molecular and macroscopic level using two different approaches. Coefficients of diffusion measured by nuclear magnetic resonance (Dmol) were compared to those calculated using the Fickean-based diffusion model (Deff) fitted to macroscopic oil loss data.
2 Experimental
Materials
Fully hydrogenated soybean oil (FHSO) and soybean oil (SO) were generously provided by Bunge Canada (Toronto, Canada). All chemicals and organic solvents were purchased from Fisher Scientific and Sigma-Aldrich (ON, Canada).Blend preparation
Blends of FHSO and SO were prepared as reported by Acevedo et al.8 Briefly, binary FHSO:SO blends were mixed in 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 (w/w) proportions. The mixtures were melted and held at 80 °C for 30 min to erase crystal memory. Then, the samples were crystallized for 30 minutes in a shear cell with a Searle configuration at 3 different wall temperatures (−10 °C, 0 °C and 20 °C), and laminar shear rates (0, 30 and 240 s−1). After crystallization, the mixtures were kept at 20 °C for 48 hours to allow the material setting and subsequently stored at 4 °C until the moment of analysis.
55 (w/w) proportions. The mixtures were melted and held at 80 °C for 30 min to erase crystal memory. Then, the samples were crystallized for 30 minutes in a shear cell with a Searle configuration at 3 different wall temperatures (−10 °C, 0 °C and 20 °C), and laminar shear rates (0, 30 and 240 s−1). After crystallization, the mixtures were kept at 20 °C for 48 hours to allow the material setting and subsequently stored at 4 °C until the moment of analysis.
Another set of FHSO:SO blends were prepared according to Acevedo and Marangoni.9 FHSO and SO were mixed at different ratios in order to formulate 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60; 30
60; 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70; and 20
70; and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 w/w FHSO:SO blends. Additionally, different emulsifiers in a concentration of 1% w/w were incorporated to 30
80 w/w FHSO:SO blends. Additionally, different emulsifiers in a concentration of 1% w/w were incorporated to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 FHSO:SO blends. The emulsifiers added to the mixtures were Glyceryl Monostearate (GMS), Polyethylene Glycol Sorbitan Monostearate -Tween 60- (PGMS), Glyceryl Monopalmitate (GMP); Sorbitan Monopalmitate (SMP), Sodium Stearoyl Lactylate (SSL), phosphatidylcholine (P-CHOLINE), 75 BFP – mono and di glycerides from hydrogenated palm fat (BFP-75). Fat blends were crystallized in a pilot plant scale scraped surface heat exchanger or votator. After melted in the vessel and kept at 80 °C for 30 min, fat blends were cooled down to 70 °C. The molten mixture was pumped at a flow rate of 0.65 kg min−1 (39 kg h−1) through the votator line. The tubing system between each unit and the outlets were well-insulated to avoid heat loss. In all experiments, the wall temperature of each unit was set to reach ∼−2 °C in unit A, ∼15 °C in unit B and ∼10 °C in unit C. Fat blends were collected after passing through 2 scraped-surface chiller (A and C units) and the agitated working unit (unit B) in a configuration ABC. After crystallization the samples were held at 20 °C for 2 days to allow crystallization completion and subsequently stored at a refrigerator temperature (4 °C) until the moment of characterization.
70 FHSO:SO blends. The emulsifiers added to the mixtures were Glyceryl Monostearate (GMS), Polyethylene Glycol Sorbitan Monostearate -Tween 60- (PGMS), Glyceryl Monopalmitate (GMP); Sorbitan Monopalmitate (SMP), Sodium Stearoyl Lactylate (SSL), phosphatidylcholine (P-CHOLINE), 75 BFP – mono and di glycerides from hydrogenated palm fat (BFP-75). Fat blends were crystallized in a pilot plant scale scraped surface heat exchanger or votator. After melted in the vessel and kept at 80 °C for 30 min, fat blends were cooled down to 70 °C. The molten mixture was pumped at a flow rate of 0.65 kg min−1 (39 kg h−1) through the votator line. The tubing system between each unit and the outlets were well-insulated to avoid heat loss. In all experiments, the wall temperature of each unit was set to reach ∼−2 °C in unit A, ∼15 °C in unit B and ∼10 °C in unit C. Fat blends were collected after passing through 2 scraped-surface chiller (A and C units) and the agitated working unit (unit B) in a configuration ABC. After crystallization the samples were held at 20 °C for 2 days to allow crystallization completion and subsequently stored at a refrigerator temperature (4 °C) until the moment of characterization.
Solid fat content determination
Crystallized samples were introduced into NMR glass tubes and stored for 24 hours at 4 °C. Then, the tubes were incubated at the desired temperature for 30 min to allow a homogeneous distribution of temperature at the moment of measurement. Solid fat content (SFC) was measured by pulse nuclear magnetic resonance (p-NMR) using a Bruker Minispec spectrometer, (Bruker Optics Ltd., Milton, ON, Canada). The reported data corresponds to the average of at least five individual measurements.Polarized light microscopy
Polarized light microscopy (PLM) was used to observe fat microstructure as described previously.9 Briefly, a definite amount of the crystallized sample plus soybean oil was weighed on a slide in order to maintain a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 proportion; then the mixture was homogeneously spread in all directions and a cover glass was carefully laid over the fat to remove air and complete spreading the fat. Samples were imaged using a Leica DM RXA2 microscope with polarized light (Leica Microsystems, Richmond Hill, Canada) and equipped with a CCD camera (Q Imaging Retiga 1300, Burnaby, BC, Canada). All images were acquired using a 40× objective lens (Leica, Germany). The camera was set for autoexposure. Openlab 6.5.0 software (Improvision, Waltham, MA, USA) was used to acquire images. Focused images were stored as uncompressed 8 bit (256 grays) grayscale TIFF files with a 1280 × 1024 spatial resolution. Five images were captured from each of the five replicates prepared.
1 proportion; then the mixture was homogeneously spread in all directions and a cover glass was carefully laid over the fat to remove air and complete spreading the fat. Samples were imaged using a Leica DM RXA2 microscope with polarized light (Leica Microsystems, Richmond Hill, Canada) and equipped with a CCD camera (Q Imaging Retiga 1300, Burnaby, BC, Canada). All images were acquired using a 40× objective lens (Leica, Germany). The camera was set for autoexposure. Openlab 6.5.0 software (Improvision, Waltham, MA, USA) was used to acquire images. Focused images were stored as uncompressed 8 bit (256 grays) grayscale TIFF files with a 1280 × 1024 spatial resolution. Five images were captured from each of the five replicates prepared.
Microstructural analysis was carried out by image analysis employing the Adobe Photoshop CS 3 software (Adobe Systems Inc., San Jose, California, USA) and filters from the Fovea Pro 4.0 software (Reindeer Graphics, Inc., Asheville, NC, USA). A manual threshold was applied to all the pictures to convert the grayscale images to binary images, in order to discriminate between features and background and to measure the features sizes. The microstructural elements were determined using the filter tools included in the Fovea Pro software.
Cryogenic transmission electron microscopy (Cryo-TEM)
In order to discard oil fraction and favor single crystals observation, fat blends were treated as reported previously by Acevedo and Marangoni.10,11 Five microliters of the obtained dispersion were placed on a copper grid with perforated carbon film (Canemco-Marivac, Quebec, Canada), and excess liquid was blotted automatically for 2 s using filter paper. A staining aqueous solution of 2% of uranyl acetate was used to enhance contrast. Subsequently, the sample was transferred to a Cryo holder (Gatan Inc., Pleasanton, CA, USA) for direct observation at −176 °C in a FEI Tecnai G2 F20 Cryo-TEM operated at 200 kV in low dose mode (Eidhoven, The Netherlands). Images were taken using a Gatan 4k CCD camera. Micrographs were stored and analyzed using DigitalMicrograph™ software (USA). Image J 1.42q software (USA) was employed for a semiautomatic analysis procedure.Oil loss determination
Oil migration studies were performed according with the technique described previously by Dibildox-Alvarado et al.12 Once crystallized, fat blends were molded in discs of 22 mm diameter and 3.2 mm of thickness using polyvinyl chloride (PVC) molds and then transferred to filter papers (Whatman # 5, 110 mm diameter). The amount of oil that each sample (prepared as discs) lost to filter papers was determined by the difference in weight of the filter papers before and after placing the fat disc on the paper for 24 hours at 20 °C. A “blank” filter paper was included in all experiments to account for the effects of the treatments on the paper itself such as the influence of the humidity of storage environment. Filter papers must be large enough in order to avoid the paper saturation with oil during the period of measurement. An average and standard deviation of at least five replicates (five separate disks on individual filter papers) is reported. Oil migration (%) was calculated as:
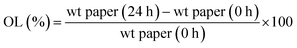 | (1) |
Nuclear magnetic resonance
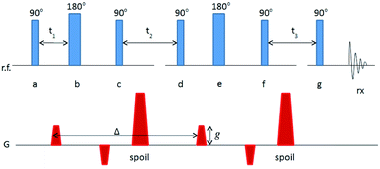
Nuclear magnetic resonance (NMR) experiments were performed on a Tecmag (Houston, TX, USA) Apollo console equipped with a Nalorac 2.4-T 32-cm i.d. horizontal bore superconducting magnet (Nalorac Cryogenics, Martinez, CA, USA). Sample excitation and signal detection were both accomplished with a homebuilt radiofrequency (RF) sensor (an eight-rung birdcage coil13), 4 cm in diameter and 10 cm in length, driven by a 2 kW 3445 RF amplifier (American Microwave Technology, Brea, CA, USA). Magnetic field gradients for diffusion sensitization were generated by supplying current to a 200 mm-i.d. homebuilt coil winding14 from a Techron (Elkhart, IN, USA) 8710 amplifier, providing for maximum gradient strengths of 900 mT m−1.The series of RF and magnetic field gradient applications (the NMR pulse sequence) used to measure a diffusion coefficient is illustrated in Fig. 1. In the diagram, each line indicates the history of magnetic field gradient application (G) or RF application (r.f.) and detection (rx). The fat sample becomes magnetized when it is placed in the superconducting magnet, with the net sample magnetization aligned along the main magnetic field (conventionally designated the z-axis). Pulses of RF labeled 90° or 180° have sufficient amplitude and duration to rotate the sample magnetization, about the applied RF field, through the angle shown. The two pairs of magnetic field gradients of amplitude g sensitize the net sample magnetization (and, hence, the amplitude of detected signal) to diffusion during the interval Δ. Broadly, the greater the diffusion coefficient, the greater the attenuation of detected signal for a given g. This particular use of up-down pairs of magnetic field gradient, combined with 180° RF pulses (known as the Cotts 13-interval sequence) eliminates any incidental signal attenuation caused by heterogeneities in the magnetic properties of the sample.15 The magnetic field gradient pulses labeled “spoil” destroy unwanted sample magnetization, which can be generated by the sequence of RF pulses. Unwanted magnetization is further suppressed by variation of the relative phases of the RF pulses (phase cycling) according to the cogwheel scheme.16
For each fat sample, the amplitude of g was varied in 20 steps from 0 to a maximum of 600 or 900 mT m−1. The decay of the ratio, SN = S/S0, of detected signal to that at g = 0 was fit, using SigmaPlot (Systat Software Inc., San Jose, CA, USA) with:
| SN = exp(−γ2δ2g2[4t2 + 6t1 − 2δ/3]D | (2) |
A variety of more complex models for the signal were assessed for non-exponential decays (see results), but the consistently best and most stable fit was to the function:
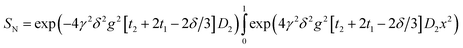 | (3) |
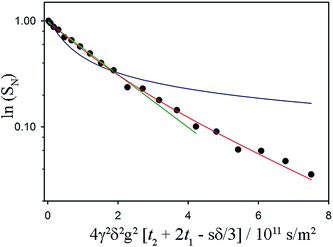 | ||
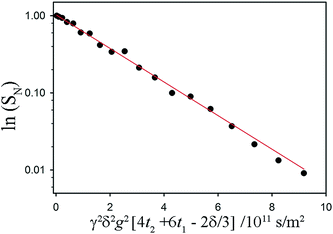
Fig. 3 Sample fits to a non-exponential NMR signal decay associated with restricted diffusion of the mobile 1H in a fat sample. The acquisition time for these data was 13 minutes (with 16 coadded scans to improve signal-to-noise ratio). Referring to the timings indicated in the pulse sequence diagram, δ = 7.6 ms, t2 + 2t1 = Δ = 60 ms. The maximum value of g was 900 mT m−1. The fat sample was 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 (laminar shear crystallizer), shear rate = 200 s−1, wall temperature = 20 °C and the data were taken at 18 °C. The green and the blue lines are attempted fits using a free diffusion model (like that used in Fig. 2) and a one-dimensional diffusion model (diffusion confined to randomly oriented tubes) respectively. Clearly preferable is the red fit line, which models diffusion restricted to two dimensions in a sample consisting of many randomly oriented lamellar domains. 55 (laminar shear crystallizer), shear rate = 200 s−1, wall temperature = 20 °C and the data were taken at 18 °C. The green and the blue lines are attempted fits using a free diffusion model (like that used in Fig. 2) and a one-dimensional diffusion model (diffusion confined to randomly oriented tubes) respectively. Clearly preferable is the red fit line, which models diffusion restricted to two dimensions in a sample consisting of many randomly oriented lamellar domains. | ||
Statistical analysis
Data were processed using GraphPad Prism 5 software (GraphPad Software, Inc., San Diego, CA, USA). Reported values correspond to means and standard errors of the determinations. Statistical analysis was performed by one-way ANOVA (p < 0.001) using Tukey's multiple comparisons as post-test (p < 0.005).3 Results and discussion
The macroscopic and functional properties of fats, such as mechanical strength, texture, mouthfeel, and other sensory characteristics strongly depend on the structural organization at the nano- and meso-scale.18,19 It was recently discovered that crystalline nanoplatelets (CNP) with a characteristic length scale of approximately 100 nm represent the fundamental structural unit of fat crystal networks.10 Thus, a bulk fat as we know it, is comprised by a spherulitic colloidal network of polycrystals (Fig. 4A and B) at the microstructural level, which is in turn the result of CNP assembled from crystalline lamellae of triglycerides (Fig. 4C).20 Furthermore, fat crystalline networks contain liquid oil trapped within. The distribution of liquid oil within a fat crystal network and the ability of the matrix to entrap and bind liquid oil are essential for its stability, as well as for its mechanical and thermal properties. Liquid oil is distributed in the space between crystals and crystal aggregates, thus the surface of the CNP and aggregates is in complete contact with the oil (Fig. 4C).The mechanisms controlling oil migration throughout fat crystal networks are still uncertain, thus its study is a topic of continuous debate. Furthermore, it is worth discussing the fact that the amount of oil lost from the fat matrix is the result of both, local and global oil migration, in other words, the result of molecular and macroscopic oil diffusion. This raises doubts not only on the contribution of strongly and loosely bound and free oil to the overall mechanism of oil migration but also on the relationship, if any, between both types of oil movement and the system properties. Ziegleder et al.1,21 proposed an equation to model oil migration in fats, based on Fickean diffusion and that can be simplified for a slab as:
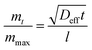 | (4) |
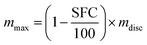 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 FHSO:SO blends subjected to a laminar shear crystallization at 0, 30 and 240 s−1 using wall temperatures of −10, 0 and 20 °C are represented in Fig. 5A and B, respectively. As expected, both Deff values and OL increased significantly as the laminar shear rate used during crystallization was greater, signifying that shear affects the structure of the system in such a way that oil loss (diffusion of liquid oil from the crystal network) is enhanced. Furthermore, at each determined shear rate, the increase in wall temperature led to higher values of Deff and OL, however the temperature influence was found to be not as important as the laminar shear rate. For instance, at 30 s−1 there was a two fold increase in Deff when changing the wall temperature from 0 to 20 °C; whereas at 0 °C Deff was at least 3 orders of magnitude higher when changing the shear rate from 0 s−1 to 30 s−1 and 240 s−1. It is also interesting to note that the Deff values are in line with values existing in the literature for similar fat systems.1,5,22–25 Nevertheless, the results obtained in this work are opposite to those reported by Maleky et al.25 when samples were subjected to shearing process; these authors described a reduction of oil migration in a cocoa butter matrix crystallized in a laminar shear fashion. Nonetheless, they worked with a significantly more complex system in composition and with a significantly higher shear rate (340 s−1) which translates into a different crystalline network organization and therefore a different oil movement within the sample.
55 FHSO:SO blends subjected to a laminar shear crystallization at 0, 30 and 240 s−1 using wall temperatures of −10, 0 and 20 °C are represented in Fig. 5A and B, respectively. As expected, both Deff values and OL increased significantly as the laminar shear rate used during crystallization was greater, signifying that shear affects the structure of the system in such a way that oil loss (diffusion of liquid oil from the crystal network) is enhanced. Furthermore, at each determined shear rate, the increase in wall temperature led to higher values of Deff and OL, however the temperature influence was found to be not as important as the laminar shear rate. For instance, at 30 s−1 there was a two fold increase in Deff when changing the wall temperature from 0 to 20 °C; whereas at 0 °C Deff was at least 3 orders of magnitude higher when changing the shear rate from 0 s−1 to 30 s−1 and 240 s−1. It is also interesting to note that the Deff values are in line with values existing in the literature for similar fat systems.1,5,22–25 Nevertheless, the results obtained in this work are opposite to those reported by Maleky et al.25 when samples were subjected to shearing process; these authors described a reduction of oil migration in a cocoa butter matrix crystallized in a laminar shear fashion. Nonetheless, they worked with a significantly more complex system in composition and with a significantly higher shear rate (340 s−1) which translates into a different crystalline network organization and therefore a different oil movement within the sample.
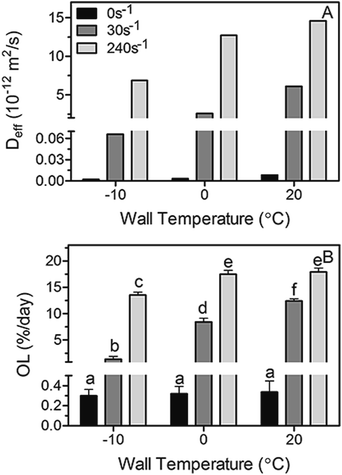 | ||
Fig. 5 Diffusion coefficients ((A), Deff) calculated using the simplified model of Ziegleder et al.1 and oil loss (OL) values (B) obtained for non-sheared and sheared blends of 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 Fully Hydrogenated Soybean Oil (FHCO) and Soybean Oil (SO). Bars and error bars represent mean and standard deviation values. Different letters represent statistically significant different between values (p < 0.05). 55 Fully Hydrogenated Soybean Oil (FHCO) and Soybean Oil (SO). Bars and error bars represent mean and standard deviation values. Different letters represent statistically significant different between values (p < 0.05). | ||
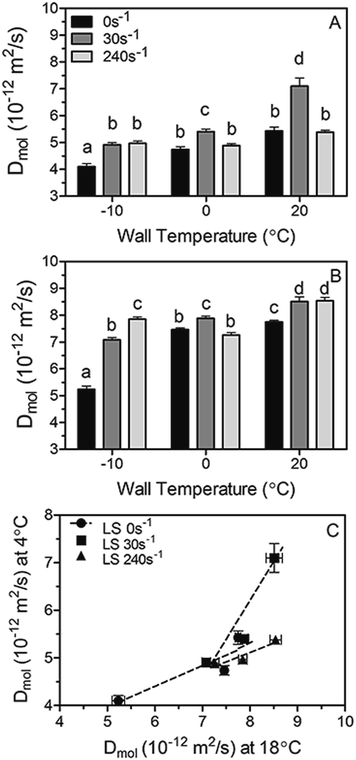
Diffusion coefficients (Dmol) measured at 4 °C and 18 °C by NMR for the same fat blends, as well as the relationship between them are plotted in Fig. 6A–C, respectively. Not surprisingly, Dmol measured at 18 °C are higher than those obtained at 4 °C owed to the increase in molecular mobility and the amount of energy available for diffusion. However, although minor differences between Dmol magnitudes exist at both temperatures, similar trends with high correlations (Fig. 6C) can be observed at the studied shear rates-wall temperatures combinations. The results clearly demonstrate that similar assumptions can be made at both measured temperatures, thus only diffusion coefficient determined by NMR at 18 °C will be considered and discussed in the following sections of this work.
Overall, Dmol is found to increase when increasing the shear rate and wall temperature during crystallization. Exceptions to this tendency can be observed upon shearing at 240 s−1, in particular at 0 and 20 °C where the diffusivity (Dmol) showed to be similar or inferior to the one observed at 30 s−1. Interestingly, the different trends observed between Deff (Fig. 5) and Dmol (Fig. 6) at the highest shear rate studied can be explained by the fact that the diffusion coefficients obtained by both methods are a measure of essentially different phenomena occurring at different structural length scales. Deff is determined from the measurement of the macroscopic amount of oil lost by the fat sample; meanwhile Dmol is related to the molecular mobility of oil within the fat matrix. It is most likely that a laminar shear rate of 240 s−1 with wall temperatures of 0 and 20 °C, where shearing can affect more severely the crystallizing sample, induced a large change in the architecture of the matrix which resulted in the macroscopic loss of oil; nevertheless molecular and local oil mobility within the matrix is not affected in the same way. It is evident that perhaps in intensely sheared fat crystal networks other phenomena besides diffusion come into play which leads to high values of oil loss and therefore an overestimation of the diffusion coefficient Deff.
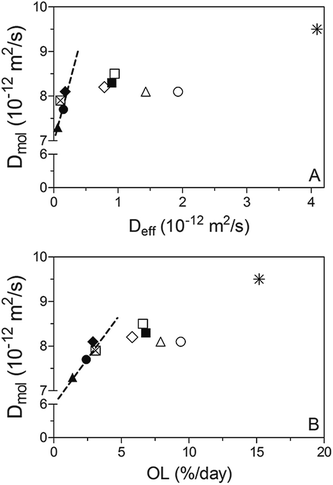
An attempt was made to correlate Deff and Dmol, as displayed in Fig. 7. While both diffusivities were within the 10−15 to 10−11 m2 s−1 range and therefore comparable to previous reported values;1,5,22–25 much higher Dmol values (up to 3 orders of magnitude) were observed for samples processed under static conditions compared to Deff. This is probably because there is a limit on the sensitivity of the method used to obtain Deff when OL values are very low, as occurs in the case of samples crystallized statically.
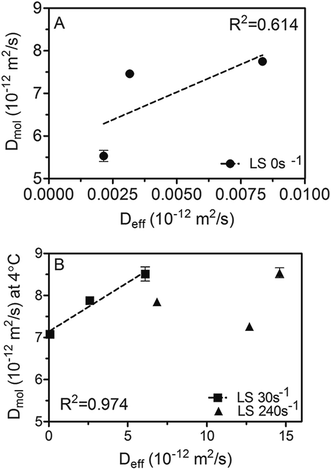 | ||
Fig. 7 Correlation between diffusion coefficients measured by NMR at 18 °C (Dmol) and those calculated using the simplified model of Ziegleder et al.1 (Deff). 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 Fully Hydrogenated Soybean Oil (FHCO) and Soybean Oil (SO) non-sheared samples (A) and blends crystallized under laminar shear (B). 55 Fully Hydrogenated Soybean Oil (FHCO) and Soybean Oil (SO) non-sheared samples (A) and blends crystallized under laminar shear (B). | ||
Furthermore, based on the obtained linear correlation coefficients values (R2) Deff and Dmol appear to be well correlated to each other under static and mild shearing conditions, with R2 of 0.613 and 0.974, respectively. As expected, an exception was found for crystallization under a laminar shear rate of 240 s−1 where no relationship can be detected between both diffusion coefficients. As discussed previously, these results probably denote a change on the crystal network structure induced by high shear forces that reflects on the macroscopic diffusivity which in turn encompasses not only mechanistic but also microstructural effects. Hence, previous results point out that in spite of the fact that the Ziegleder's expression is a simple formula to model the oil migration process,1 it is fairly well correlated with the molecular approach to oil mobility determined by NMR. However, special considerations should be taken into account in circumstances where oil movement though the matrix may not be strictly diffusive, such as when structural features are severely altered by processing conditions.
To confirm the above conjecture, similar fat blends crystallized in a scraped surface heat exchanger, where turbulent high shear fields are applied, were analyzed on purpose for comparison. As expected, the plot Dmol vs. Deff for the samples exhibited a random dispersion, particularly at high values as shown in Fig. 8A. As previously discussed and observed in Fig. 5, high Deff correspond to high OL values. The possible reasons for the discrepancy between D values are the severe processing conditions the samples were exposed to during crystallization which led to a significant breakage of the structural features and thus, an oil movement in the matrix that is not merely diffusive. Both D values exhibit a linear correlation only at low magnitudes. It should be noted that the diffusive regime is observed up to a specific value of OL. From approximately 3% OL and above the movement of oil is not only driven by diffusion (Fig. 8B). Instead, it is possible that oil transport within the fat matrix is mediated by convection currents. Thus, analysis of additional factors should be considered when a quantitative Deff determination is required in highly sheared samples.
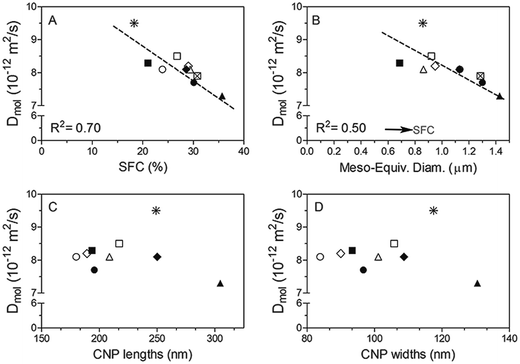
In order to further examine the correlation between structural properties and oil transport, we plotted Dmol as a function of SFC and crystal size (Fig. 9A and B). Dmol obtained for all the samples show an inverse linear relationship (with relatively high correlation coefficients) with the SFC (%) and the equivalent diameter of the mesocrystals present (Fig. 9A and B, respectively). Not surprisingly, the higher the amount of solid material in the network, the lower the oil movement, which in general translates into an increase in the ability of the fat matrix to bind liquid oil. Similarly, Ziegleder et al.1 reported a strong inverse dependence of D with the amount of solid fat in chocolate. Acevedo et al.,8 observed the same tendency when working with similar fat blends subjected to laminar shearing during crystallization.
It has been stated that low solid fat contents provide a reduced viscosity appropriate for crystal growth and development26 and hence, the formation of large crystals in samples crystallized at low supersaturations is expected. Surprisingly, according to Fig. 9B, meso-crystal dimensions observed by PLM are smaller when supersaturation, defined by the SFC, decreases. The possible reason for this effect may be the high shear forces applied to the samples during crystallization cause shear-heating, which effectively translates to crystallization at higher temperatures, thus resulting in the formation of large crystals. It has been discussed elsewhere that high shear fields can exceed van der Waals attractive forces between crystals producing breakage and/or preventing their further aggregation.8,27,28 Thus, it is not surprising the observation of small crystal in these samples. Furthermore, it is possible that this effect is more significant at low SFC since system's viscosity is low, and therefore, the effect of strong shear fields, more effective.
As depicted in Fig. 9B molecular diffusivity is higher when meso-crystal dimensions are reduced. The results of this work are opposite to those previously reported when studying similar fat crystal networks; the formation of small crystals in the network is responsible for the high oil binding capacity in the system which is attributed to the large specific surface area and thus, enhanced solid–oil interaction.8,29,30 While the different results may reflect inherent differences between the fat matrices analysed caused by the high shearing process; it is also important to emphasise that the Dmol obtained in this study does not encompass large scale movement of oil which is the parameter determined by the mentioned authors; furthermore Dmol and Deff are not well correlated in many of the analysed samples as previously stated.
For further assessment of the relationship between diffusivity and system's structural properties, Dmol values were plotted as a function of crystal nano-platelets (CNP) lengths (Fig. 9C) and widths (Fig. 9D) obtained by Cryo-TEM analysis. No significant correlation between CNP sizes and Dmol was found. These results clearly show that fat crystal nanostructure, i.e. platelet sizes, do not seem to play a governing role in the mechanism of liquid TAG diffusion through a crystalline fat matrix; at least at the local or molecular level. Structural features, not only at the nanoscale but also at higher length scales are most likely strongly affected by processing conditions in the scraped surface heat exchanger. Additionally, the fact that an inverse correlation was observed between mesocrystal size and diffusivity leads us to hypothesize that other factors not considered yet are at play to explain oil migration in fat crystal networks.
Based on these findings, it is not surprising that a lack of correlation between D values calculated using the Ziegleder approach1 and NMR were found, particularly in highly sheared materials. It is likely that strong alterations in the structure and permeability of the fat matrix occurred upon crystallization under laminar shear rates of 240 s−1 and in a scraped surface heat exchanger are responsible for the observed discrepancies. As mentioned earlier, perhaps the macroscopic oil leakage from the crystal network involves an additional contribution to that of molecular diffusion.
4 Conclusions
Two different approaches have been used to obtain diffusion coefficients and evaluate their relationship with each other and with physical and structural parameters of fat crystal networks. Interestingly, a significant correlation between Deff, obtained through the Ziegleder model and Dmol measured by NMR was observed only at low OL values; i.e. under static of mild shearing conditions during crystallization of the fat blends. On the contrary, no correlation between Dmol vs. Deff was found upon crystallization under high shear fields. This can be attributed in part to the contribution of other factors, particularly in cases where crystalline structure is drastically affected by processing conditions.The results reported in this study are important since it has been verified that oil migration in highly sheared fat samples is not fully diffusive in nature. The assumption that the mechanism of oil migration is purely diffusive should be re-considered. It is evident that further work needs to be carried out to fully describe and understand the behaviour of oil as it migrates through the a crystalline mass.
Acknowledgements
The authors acknowledge The Natural Sciences and Engineering Research Council of Canada and Advanced Foods and Materials network for the financial support.References
- G. Ziegleder, C. Moser and J. Geier-Greguska, Fett/Lipid, 1996a, 98, 196–199 Search PubMed.
- Y. J. Choi, K. L. McCarthy, M. J. McCarthy and M. H. Kim, Appl. Magn. Reson., 2007, 32, 205–220 CrossRef CAS.
- J. M. Aguilera, M. Michel and G. Mayor, J. Food Sci., 2004, 69, 167–174 CrossRef.
- G. R. Ziegler, A. Shetty and R. C. Anantheswaran, Manuf. Confect., 2004, 84, 118–226 Search PubMed.
- S. Marty, K. Baker, E. D. Alvarado and A. G. Marangoni, Food Res. Int., 2005, 38, 1189–1197 CrossRef CAS.
- G. R. Ziegler, Science and Technology of Enrobed and Filled Chocolate, Confectionary and Bakery Products, CRC Press, Boca Raton, FL, 2009 Search PubMed.
- P. Altimiras, L. Pyle and P. Bouchon, J. Food Eng., 2007, 80, 600–610 CrossRef.
- N. C. Acevedo, J. M. Block and A. G. Marangoni, Faraday Discuss., 2012, 158, 171–194 RSC.
- N. C. Acevedo and A. G. Marangoni, Food Biophys., 2014, 9, 368–379 CrossRef.
- N. C. Acevedo and A. G. Marangoni, Cryst. Growth Des., 2010, 10, 3327–3333 CAS.
- N. C. Acevedo and A. G. Marangoni, Cryst. Growth Des., 2010, 10, 3334–3339 CAS.
- E. Dibildox-Alvarado, J. Neves Rodrigues, L. A. Gioielli, J. F. Toro-Vazquez and A. G. Marangoni, Cryst. Growth Des., 2004, 4, 731–736 CAS.
- C. E. Hayes, W. A. Edelstein, J. F. Schenck, O. M. Mueller and M. Eash, J. Magn. Reson., 1985, 63, 622–628 CAS.
- K. Deka, M. B. MacMillan, A. V. Ouriadov, I. V. Mastikhin, J. J. Young, P. M. Glover, G. R. Ziegler and B. J. Balcom, J. Magn. Reson., 2006, 178, 25–32 CrossRef CAS PubMed.
- R. M. Cotts, M. J. R. Hoch, T. Sun and J. T. Marker, J. Magn. Reson., 1989, 83, 252–266 CAS.
- M. H. Levitt, P. K. Madhu and C. E. Hughes, J. Magn. Reson., 2002, 155, 300–306 CrossRef CAS PubMed.
- P. T. Callaghan, Principles of Nuclear Magnetic Resonance Microscopy, Clarendon Press, Oxford, 1991 Search PubMed.
- D. Rousseau and A. G. Marangoni, Food Res. Int., 1999, 31, 381–388 CrossRef.
- J. M. deMan and A. M. Beers, J. Texture Stud., 1987, 18, 303–318 CrossRef.
- N. C. Acevedo, F. Peyronel and A. G. Marangoni, Curr. Opin. Colloid Interface Sci., 2011, 16, 374–383 CrossRef CAS.
- G. Ziegleder, C. Moser and J. Geier-Greguska, Fett/Lipid, 1996b, 98(7–8), 253–256 Search PubMed.
- M. E. Miquel, S. Carli, P. J. Couzens, H. J. Wille and L. D. Hall, Food Res. Int., 2001, 34(9), 773–781 CrossRef CAS.
- R. S. Khan and D. Rousseau, Eur. J. Lipid Sci. Technol., 2006, 108, 434–443 CrossRef CAS.
- N. L. Green and D. Rousseau, Soft Matter, 2015, 11, 5523–5530 RSC.
- F. Maleky, A. Smith and A. G. Marangoni, Cryst. Growth Des., 2011, 11, 2335–2345 CAS.
- J. Garside and R. J. Davey, Chem. Eng. Commun., 1980, 4, 393–424 CrossRef CAS.
- S. Sonwai and M. R. Mackley, J. Am. Oil Chem. Soc., 2006, 83, 583–596 CrossRef CAS.
- P. Walstra, W. Kloek and T. van Vliet, Crystallization Processes in Fats and Lipid Systems, Marcel Dekker Inc., New York, USA, 2006 Search PubMed.
- T. S. Omonov, L. Bouzidi and S. S. Narine, Chem. Phys. Lipids, 2010, 163, 728–740 CrossRef CAS PubMed.
- A. Bot, Y. S. J. Veldhuizen, R. den Adel and E. C. Roijers, Food Hydrocolloids, 2009, 23, 1184–1189 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |