Ion-specific ice propagation behavior on polyelectrolyte brush surfaces

Abstract

Ice propagation is an essential step when freezing happens on hydrated surfaces. In this work, we choose polyelectrolyte brushes (PB), whose hydration ability can be controlled by simply exchanging the counterions, to demonstrate the distinct ice propagation mechanism on differently hydrated surfaces.

---

Undesired ice formation on solid surfaces, such as wind turbine blades, power network towers and transmission lines, heat exchanger surfaces and wings of aircraft, causes serious property losses and safety risks for human beings.^1–3 Therefore, there has been continuous interest in the design and construction of effective and low-cost anti-icing and anti-frost materials. Recently some icephobic surfaces have been proposed in avoiding/retarding undesired ice formation.^4–11 In particular, numerous hydrated surface materials have been utilized for fighting against icing, e.g., surfaces with a delayed freezing time of water droplets and surfaces with lowered adhesion to formed ice.^12–15

The ice formation on solid surface always goes through several processes: ice nucleation, growth and propagation.^16–21 In real-world conditions, even if the ice nucleation can be avoided effectively, the runaway ice propagation will result in failure of anti-icing coatings. Actually, the ice propagation control is crucial for the anti-icing strategies due to the unavoidable ice nucleation arising from the ambient contaminants like impurities or dusts. Though the control of ice propagation has been reported on the lubricant-infused surfaces and superhydrophobic surfaces with different structures, few studies have been performed on the hydrated surfaces.^10,22 Unlike most of inorganic or metallic surfaces, the hydrated surfaces contain a high content of interfacial water. The different states of hydration will play an important role on the ice propagation on the hydrated surfaces other than the well-studied effect like thermal conductivity, humidity and pressure.^5,23,24 Therefore, it is highly desired to study the ice propagation on various hydrated surfaces as well as the underlying mechanism.

Polyelectrolyte brush (PB) surfaces, whose hydration state can be controlled simply by exchanging the counterions, were utilized as the research platform.^25–29 Previously, we have studied the ion-specific effect on heterogeneous ice nucleation on polyelectrolyte brush (PB) surfaces.³⁰ Herein, we find that the ice propagation can also be tuned on the PB surfaces by changing their hydration state. Ice propagation rates were observed to be five orders of magnitude faster on the highly hydrated PB surfaces with hydrophilic counterions than that on the dehydrated PB surfaces with hydrophobic counterions. Owing to the ubiquity of ice formation on hydrated surfaces in biological and climate fields, our findings can shed new light upon the anti-icing studies.

Results and discussion

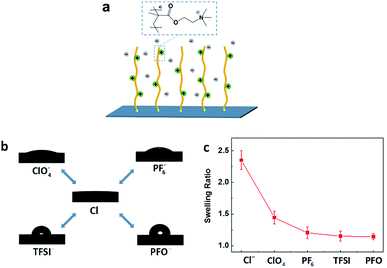
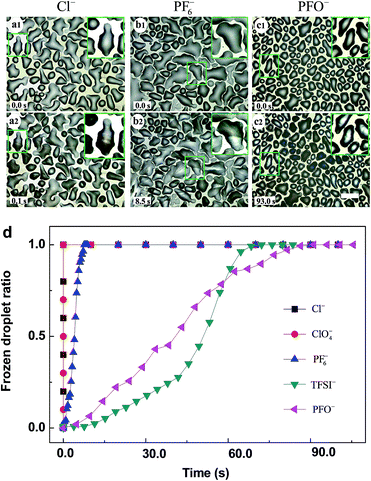
The as-prepared PMETA–Cl brush underwent a transition from a hydrophilic state to a hydrophobic state by exchanging Cl⁻ with ClO₄⁻, PF₆⁻, TFSI⁻ and PFO⁻ as shown in Fig. 1a and b. According to X-ray photoelectron spectroscopy (XPS) results, all the counterions were successfully exchanged in PMETA brushes as shown in Fig. S1.† The value of contact angles (CA) of water drops on the PMETA brush surfaces increased from 5° to 19°, 36°, 87°, 96° following the counterion order of Cl⁻ < ClO₄⁻ < PF₆⁻ < TFSI⁻ < PFO⁻. The thickness of PMETA brush with different counterions was measured by spectroscopic ellipsometer in both the ‘dry’ state in air and the ‘wet’ state in water. The heights of the PB in the ‘dry’ state with different counterions were all about 38 nm. It is interesting to note that the thickness of PMETA–Cl brush in water was ∼90 nm and was 2.4 times of that in the ‘dry’ state. As shown in Fig. 1c, the large thickness ratio of 2.4 (h_water/h_dry) implies that the PMETA–Cl brush is fully swollen and traps a large amount of water. In contrast, the thickness of PMETA–PFO brush in water was almost the same as that in the ‘dry’ state (the ratio of h_water/h_dry is ∼1.1), suggesting that it is poorly swollen with water. This phenomenon was also observed by other groups and was termed as the hydrophobic collapsed state.³¹ The thickness ratio (h_water/h_dry) decreased following the counter-anion order: Cl⁻ > ClO₄⁻ > PF₆⁻ > TFSI⁻ > PFO⁻. According to the quartz crystal microbalance with the dissipation (QCM-D) study by Zhou et al., it was found that the amount of free water trapped in the PB decreases in the order of Cl⁻ > ClO₄⁻ > PF₆⁻ > TFSI⁻,³² which is consistent with our experimental observations. The PMETA brush with Cl⁻, ClO₄⁻, PF₆⁻ and TFSI⁻ as the counterion exhibited swollen (highly hydrated), partially collapsed (hydrated) and completely collapsed (dehydrated) state, respectively. The surface morphology investigated by atomic force microscopy (AFM) displays no observable difference of the PB surfaces with these counterions as shown in Fig. S3.†³³ It is worth mentioning that such a counterion-driven ‘hydrophobic collapse’ of the PB in pure water is different from the ‘electrostatic driven collapse’ in salt solutions, since it is just induced by the chemical nature of counterions. In this report, PB serves as a research platform to investigate distinct ice propagation behaviors on differently hydrated surfaces.

Fig. 1 (a) Schematic illustration of the PMETA brush. Variation of (b) the surface wettability, (c) the swelling ratio in water of PMETA brushes with different counterions (Cl⁻, ClO₄⁻, PF₆⁻, TFSI⁻, PFO⁻). The grafting density of all the PB samples is 0.50 chain nm⁻².

The freezing measurements were examined by using the method and apparatus previously reported (details in Fig. S2†). As shown in Fig. 2a–c, the detailed ice propagation process of condensed microdroplets on the PB surface was studied by optical microscope coupled with a high speed camera at 300 frames per second. The microdroplets of water formed atop of the PB surfaces with different counterions through a controlled evaporation and condensation process.³⁴ We defined the “time zero” to be the acquisition time of the frame right before the freezing (the time interval of frames recorded by the high speed camera was 3.3 ms) to exclusively study the effect of counterions on ice propagation. The morphology of the condensed water drops at time zero and details of ice propagation at −20.0 °C were displayed in Fig. 2a1–c1 and a2–c2, respectively. Fig. 2d and S4† presents the evolution of the fraction of frozen condensed water droplets in the observation window on the PB surfaces with different counterions. For the highly hydrated brush surface of PMETA–Cl and PMETA–ClO₄, ice propagated rapidly across the entire observation window when freezing occurred as shown in Fig. 2a and d, that is, all condensed drops were frozen within 3.3 ms. In contrast, much longer time was needed for all condensed drops to be frozen as shown in Fig. 2b–d, i.e., ∼8.5 s, 70.0 s and 93.0 s were needed on the PB surface with counterions of PF₆⁻, TFSI⁻ and PFO⁻, respectively. The corresponding ice propagation rate for the freezing of condensed water on the PB surface with counterions of Cl⁻, PF₆⁻, TFSI⁻, and PFO⁻ are ∼63 000 ± 5000, 26 ± 4, 3 ± 1 and 2 ± 1 s⁻¹ cm⁻², respectively. Ice propagation rate on the PMETA–Cl surface was more than 30 000 times faster than that on the PMETA–PFO surface.

Fig. 2 Optical microscopic images of condensed water microdroplets on the PMETA brush surfaces with counterions of (a) Cl⁻, (b) PF₆⁻ and (c) PFO⁻ (1) before and (2) after freezing. The inset magnified images in the dotted square show the details before and after freezing. (d) Evolution of the fraction of frozen condensed water droplets with time on the PB surfaces carrying different counterions at −20.0 °C. The relative humidity of the experimental environment was kept at 100%. The scale bar is 100 μm.

The details of ice propagation between the frozen droplet (ice) and neighbouring liquid droplets on PMETA–Cl and PMETA–PFO brush surfaces were also characterized. In magnified images of Fig. 2a, it was obvious that no ice bridge could be observed on the PMETA–Cl brush surface, but all ice formed almost at the same time, which indicated that the condensed droplets were all linked with freezable water. In contrast, most of the neighbouring frozen droplets were connected by ice bridges on the PMETA–PFO brush surface in Fig. 2c and S4.† The ice propagation on the PMETA–PFO brush surface via ice bridges indicated that the condensed water droplets were not connected with each other by freezable water.

In the above condensed water experiment, we employed the same amount of water (0.4 μL) for the evaporation and condensation process, which made the water surface coverage and the distance between microdroplets different due to the different wettability of the PB. It was reported that the possibility of ice propagation via ice bridging for neighbouring independent droplets is determined by the competition between distance “L” of the frozen and unfrozen droplets and their diameter “D”. Chen et al. have suggested the parameter of S = L/D to evaluate if ice propagate via the ice bridging.⁵ When S < 1, it is favourable to form ice bridges and promotes ice propagation on solid surfaces. On the other hand, when S > 1, water droplets tend to evaporate or freeze independently without triggered by other frozen droplets. In order to further explore how hydration of the PB control the ice propagation process and eliminate the influencing factor of wettability, we next systematically studied the freezing of two macroscopic droplets on the PMETA brush with counterions of Cl⁻ and PFO⁻ as shown in Fig. 3a and b. In our case, the distance L (∼3 mm) between two water droplets was controlled larger than the diameter D (∼1.8 mm) of individual water droplets on the PB surface with two different counterions, in other words, S > 1 (Fig. 3). Then we could focus on the effect of hydration on ice propagation by eliminating the uncontrollable influence of the ice bridging effect.^5,23

Fig. 3 Optical images of two water macroscopic droplets frozen at −20.0 °C on brush surfaces of (a) PMETA–Cl for (1) 0 s, (2) 0.1 s, (3) 2.0 s, (4) 8.0 s and (b) PMETA–PFO for (1) 0 s, (2) 0.1 s, (3) 3600.0 s, (4) 4513.0 s. Here 100 ms before the onset time of freezing was defined as “time zero”. The scale bar is 1.0 mm. Correlation plots of freezing temperatures (T₁ and T₂) of two neighbouring macroscopic water droplets (S = L/D > 1) on the (c) PMETA–Cl and (d) PMETA–PFO brush surfaces when the surface temperature decreased at a rate of 5.0 °C min⁻¹.

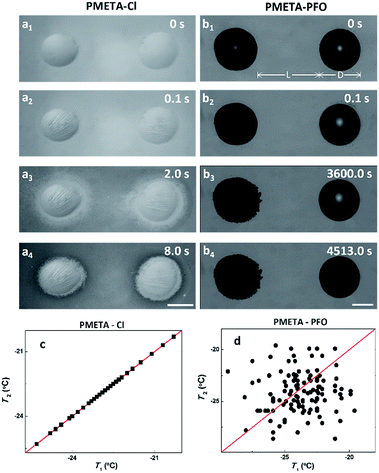
Similarly, the two macroscopic water droplets on PMETA–Cl brush froze almost simultaneously (within 100 ms as shown in Fig. 3a3 and a4), which is consistent with the freeze of condensed microdroplets on the same surface. It can be seen that an ice film formed around the two macroscopic droplets which might act as the propagation media (ESI Movie†). In strong contrast, two water droplets froze independently on the PMETA–PFO brush surface as shown in Fig. 3b3 and b4. ‘Dendrimer-like’ ice structures formed on the frozen drop (left) as time went by because of the desublimation of vapour. Due to the mechanism of Wegener–Bergeron–Findeisen that ice crystals grow at the expense of liquid water droplets, the unfrozen water droplet was observed to decrease in size (more obvious observations are given in Fig. S5†).^35,36 Furthermore, ‘Depletion region of water’ between water droplets was formed due to the devoid of freezable water trapped inside the PMETA–PFO brush as well as the movement of water molecules from the PB surface towards the ice growth front. Such water depletion region impeded ice propagation between frozen and unfrozen droplets. The droplet finally froze 4513.0 s later. To further verify the distinct ice propagation behaviour on the PB surface with different counterions, we gave a correlation of freezing temperatures (T) of two neighbouring droplets on the PB surface as shown in Fig. 3a and b. We measured the T of two water neighbouring droplets on PMETA–Cl and PMETA–PFO brush surfaces with S > 1. The correlation diagram of T₁ and T₂ was plotted during cooling runs.³⁷ As shown in Fig. 3c, freezing temperatures of T₁ and T₂ on the PMETA–Cl brush surface are well correlated, and all data points lay on the line with a slope of 1. However, the T₁ and T₂ of two droplets on the PMETA–PFO brush surface are independent from each other, resulting in randomly scattered data points in the correlation plot as shown in Fig. 3d.

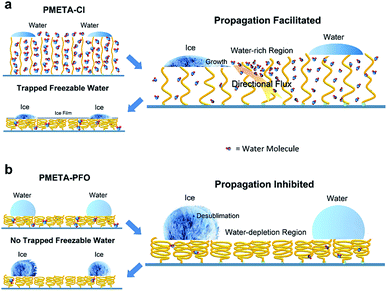
Fig. 4 illustrates the mechanism for differently hydrated PB in tuning ice propagation. It was reported that the PB could trap a large amount of water and swelled ∼1.5 times even in air of 100% relative humidity.³⁸ The uniqueness of the PB surface is that the amount of water can be reversibly controlled simply by changing its counterions.^39,40 When freezing occurs, the highly ionic circumstance inside PB inhibits ice growth inside the brush. Ice nucleation in the water droplets started at the water/brush interface, followed by the upward ice growth. In order to supply the ice growth, a directional flow of water molecules in the PB may move outwards to the ice growth front. It is expected that the dehydration during ice propagation process would cause the PB to shrink. Although the speculation is reasonable, the change of PB material is hardly to be detected in experiment until now due to the low temperature and specific micro environments. This consequently promoted ice propagation, which was totally different from the classical ice bridging effect. As the hydrophobicity of counterions increased, the total amounts of freezable water within the brush reduced significantly because of the ‘hydrophobic collapse’ of the PB. Therefore, the increased hydrophobicity and devoid of freezable water inside the brush caused the formation of ‘water depletion region’ during freezing process, and then ice propagation was suppressed.

Fig. 4 Mechanisms of ice propagation on (a) PMETA–Cl and (b) PMETA–PFO brush surfaces.

Conclusion

In this work, we employed PB surfaces to study the effect of hydration on ice propagation. On highly hydrated PB surfaces with the hydrophilic counterions, ice propagation is facilitated due to the directional movement of the trapped freezable water molecules towards the ice growth front. This is in strong contrast with that on the dehydrated PB surfaces with hydrophobic counterions, where ice propagation is inhibited due to the formation of the ‘water depletion region’ between droplets. The experimental results show that the difference in ice propagation rate is up to five orders of magnitude.

Acknowledgements

We gratefully acknowledge the financial support from the 973 Program (2012CB933801) and the National Natural Science Foundation of China (51436004, 21421061, 21503240).

References

1. P. Eberle, M. K. Tiwari, T. Maitra and D. Poulikakos, Nanoscale, 2014, 6, 4874.
2. L. Huang, Z. Liu, Y. Liu and Y. Gou, Int. J. Therm. Sci., 2011, 50, 432.
3. K. Manabe, S. Nishizawa, K.-H. Kyung and S. Shiratori, ACS Appl. Mater. Interfaces, 2014, 6, 13985.
4. V. Hejazi, K. Sobolev and M. Nosonovsky, Sci. Rep., 2013, 3, 2194.
5. X. Chen, R. Ma, H. Zhou, X. Zhou, L. Che, S. Yao and Z. Wang, Sci. Rep., 2013, 3, 2515.
6. J. B. Boreyko and C. P. Collier, ACS Nano, 2013, 7, 1618.
7. P. Tourkine, M. Le Merrer and D. Quéré, Langmuir, 2009, 25, 7214.
8. L. Cao, A. K. Jones, V. K. Sikka, J. Wu and D. Gao, Langmuir, 2009, 25, 12444.
9. P. Guo, Y. Zheng, M. Wen, C. Song, Y. Lin and L. Jiang, Adv. Mater., 2012, 24, 2642.
10. M. J. Kreder, J. Alvarenga, P. Kim and J. Aizenberg, Nat. Rev. Mater., 2016, 1, 15003.
11. K. Golovin, S. P. R. Kobaku, D. H. Lee, E. T. DiLoreto, J. M. Mabry and A. Tuteja, Sci. Adv., 2016, 2(3), e1501496.
12. J. Chen, Z. Luo, Q. Fan, J. Lv and J. Wang, Small, 2014, 10, 4693.
13. J. Chen, R. Dou, D. Cui, Q. Zhang, Y. Zhang, F. Xu, X. Zhou, J. Wang, Y. Song and L. Jiang, ACS Appl. Mater. Interfaces, 2013, 5, 4026.
14. R. Dou, J. Chen, Y. Zhang, X. Wang, D. Cui, Y. Song, L. Jiang and J. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 6998.
15. L. Boinovich, A. M. Emelyanenko, V. V. Korolev and A. S. Pashinin, Langmuir, 2014, 30, 1659.
16. N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2012, 13, 179.
17. S. Jung, M. K. Tiwari, N. V. Doan and D. Poulikakos, Nat. Commun., 2012, 3, 615.
18. J. M. Campbell, F. C. Meldrum and H. K. Christenson, J. Phys. Chem. C, 2015, 119, 1164.
19. P. Hao, C. Lv and X. Zhang, Appl. Phys. Lett., 2014, 104, 161609.
20. A. J. Meuler, G. H. McKinley and R. E. Cohen, ACS Nano, 2010, 4, 7048.
21. J. Lv, Y. Song, L. Jiang and J. Wang, ACS Nano, 2014, 8, 3152.
22. K. Rykaczewski, S. Anand, S. B. Subramanyam and K. K. Varanasi, Langmuir, 2013, 29, 5230.
23. S. Jung, M. K. Tiwari and D. Poulikakos, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16073.
24. P. Kim, T.-S. Wong, J. Alvarenga, M. J. Kreder, W. E. Adorno-Martinez and J. Aizenberg, ACS Nano, 2012, 6, 6569.
25. S. E. Moya, A. A. Brown, O. Azzaroni and W. T. S. Huck, Macromol. Rapid Commun., 2005, 26, 1117.
26. X. Chu, J. Yang, G. Liu and J. Zhao, Soft Matter, 2014, 10, 5568.
27. Y. Tran, P. Auroy and L. T. Lee, Macromolecules, 1999, 32, 8952.
28. Y. Tran, P. Auroy, L. T. Lee and M. Stamm, Phys. Rev. E, 1999, 60, 6984.
29. S. E. Moya, O. Azzaroni, T. Kelby, E. Donath and W. T. S. Huck, J. Phys. Chem. B, 2007, 111, 7034.
30. Z. He, W. J. Xie, Z. Liu, G. Liu, Z. Wang, Y. Q. Gao and J. Wang, Sci. Adv., 2016, 2(6), e1600345.
31. O. Azzaroni, S. Moya, T. Farhan, A. A. Brown and W. T. S. Huck, Macromolecules, 2005, 38, 10192.
32. Q. Wei, M. Cai, F. Zhou and W. Liu, Macromolecules, 2013, 46, 9368.
33. T. Farhan, O. Azzaroni and W. T. S. Huck, Soft Matter, 2005, 1, 66.
34. K. Li, S. Xu, W. Shi, M. He, H. Li, S. Li, X. Zhou, J. Wang and Y. Song, Langmuir, 2012, 28, 10749.
35. A. Korolev, J. Atmos. Sci., 2007, 64, 3372.
36. A. V. Korolev and I. P. Mazin, J. Atmos. Sci., 2003, 60, 2957.
37. J. L. Carvalho and K. Dalnoki-Veress, Phys. Rev. Lett., 2010, 105, 237801.
38. C. J. Galvin, M. D. Dimitriou, S. K. Satija and J. Genzer, J. Am. Chem. Soc., 2014, 136, 12737.
39. J. J. I. Ramos and S. E. Moya, Macromol. Rapid Commun., 2011, 32, 1972.
40. S. Moya, O. Azzaroni, T. Farhan, V. L. Osborne and W. T. S. Huck, Angew. Chem., Int. Ed., 2005, 44, 4578.

---

Footnote

† Electronic supplementary information (ESI) available: XPS data, experimental apparatus, AFM topologies, ice front growth and Wegener–Bergeron–Findeisen behavior on PMETA–PFO (PDF), the full movie for ice propagation on PMETA–Cl (AVI). See DOI: 10.1039/c6ra24847k

---