Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rate effect of liquid infiltration into mesoporous materials
Yueting Suna,
Chengliang Xua,
Weiyi Lub and
Yibing Li*a
aState Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing, 100084, P. R. China. E-mail: syt@tsinghua.edu.cn; liyb@tsinghua.edu.cn
bDepartment of Civil and Environmental Engineering, Michigan State University, East Lansing, MI 48824, USA
First published on 4th January 2017
Abstract
Rate effect is observed during the pressurized liquid infiltration into mesoporous materials. The infiltration pressure increases with loading rate, which is associated with liquid viscosity. Through parametric experiments on liquid composition and temperature, the mesoscale fluid is shown to retain some characteristics of laminar flow, influenced by the shear liquid viscosity force, as well as the nanoscale solid–liquid interfacial properties. The effective viscosity at the mesoscale increases with its bulk counterpart in a power law, but due to the mesoscale boundary condition, it is much lower than the bulk value, and their gap becomes larger for more viscous liquids.
Introduction
Nanofluidic systems enable a wide range of engineering applications, owing to their small scale and large surface areas.1,2 For instance, the nanoporous material functionalized (NMF) liquid has drawn increasing attention in recent years, which is composed of lyophobic nanoporous materials and liquids.3,4 It's regarded as a novel and efficient candidate for energy conversion and absorption. Due to its ultra-large surface area (usually in the range of 100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m2 g−1), a huge amount of mechanical energy can be converted into interfacial and thermal energy once the liquid is pushed into nanopores upon external loading, contributing to an energy absorption efficiency higher than conventional values by orders of magnitude. Extensive studies have been carried out on this nanoscale infiltration and transport phenomena under quasi-static condition, however, little research has been conducted on its rate effect, which remains a critical challenge for its applications.5–7
000 m2 g−1), a huge amount of mechanical energy can be converted into interfacial and thermal energy once the liquid is pushed into nanopores upon external loading, contributing to an energy absorption efficiency higher than conventional values by orders of magnitude. Extensive studies have been carried out on this nanoscale infiltration and transport phenomena under quasi-static condition, however, little research has been conducted on its rate effect, which remains a critical challenge for its applications.5–7
Several experiments have been reported concerning the rate effect, but obtained inconsistent or contradictory results. The infiltration of saturated sodium chloride solution into microporous silica MCM-41 was found to be rate insensitive,8 while its infiltration pressure into microporous zeolite ZSM-5 increased with loading rate.9 Such rate effect has also been observed for the infiltration of pure glycerol into mesoporous silica and carbon.10,11 Despite these experimental advances, the effects of liquid and solid properties as well as their interactions on the rate effect still remain blank, which is a critical part for the elucidation of its intrinsic mechanism.
To bridge this gap, in this paper we carry out comprehensive experiments to study the pressurized liquid infiltration phenomenon into mesoporous materials, with varying loading rates, liquid compositions and temperatures. In this way, the mechanism of nanofluidic rate effect is elucidated in detail. Based on our experimental results, the rate effect of mesoscale liquid infiltration proves to be a combined contribution from the velocity slip phenomenon unique to nanofluid,12,13 and the shear viscosity force peculiar to conventional laminar flow.14 That is, both the liquid viscosity and solid–liquid interaction should be taken into consideration. An effective viscosity at mesoscale is quantitatively investigated and compared with its bulk value. The influence of temperature is also analysed as a support for the conclusions.
Experimental
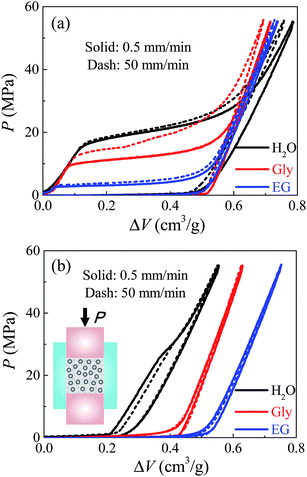
The mesoporous material employed here was Fluka 100 C8 reversed phase silica (Sigma-Aldrich 60755), with an average nanopore size of 7.8 nm. The specific surface area was 287 m2 g−1 and the specific pore volume was 0.55 cm3 g−1. The particle size ranged from 15–35 μm. 0.2 g silica was immersed in 2 ml liquid, then sealed in a stainless steel chamber with precisely-fitted sealing rings. Based on the Instron 8872, a piston (with a diameter of 12.7 mm) was compressed into the chamber at a constant loading rate. Once the system pressure reached 56 MPa, the piston moved back at the same rate for unloading. Three kinds of liquid were investigated here, including deionized water, glycerol, and ethylene glycol. Two different loading rates were selected, being v = 0.5 and 50 mm min−1 respectively. Note that 0.5 mm min−1 can be regarded as quasi-static, since further lowering the loading rate would not make any significant difference.Fig. 1 shows the P–ΔV curves of these three systems at quasi-static and dynamic loading conditions. The specific volume change ΔV is defined as the volume occupied by piston per unit mass of silica, and the pressure P is the reaction force on piston divided by its cross-sectional area A. For the first loading–unloading cycle in Fig. 1a, the overall trends of these curves are quite similar. Initially, the pressure changes linearly with system volume, indicating that the nanopore surfaces are lyophobic so that the liquid phase cannot enter the non-wettable nanopores. Once the pressure goes sufficiently high and overcomes the capillary effect, infiltration starts and a plateau region is formed with a considerably increased compressibility. When all nanopores are filled, the system compressibility reduces abruptly. The unloading curves are quite linear like elastic recovery, indicating that most of the intruded liquid will be retained inside the nanopores without outflow. This is validated by their second loading–unloading cycles in Fig. 1b where almost no further infiltration can be found. Otherwise, if there's considerable liquid outflow upon unloading, the 1st cycle should have nonlinear unloading curves with defiltration plateaus and the 2nd cycles should also exhibit infiltration plateaus since some nanopores become accessible for liquid to intrude again. Subsequent cycles are not shown here because they have exactly the same curves with the second cycle.
Results and discussion
By comparing the first-cycle infiltration performance of these three kinds of systems, one meaningful observation is the distinct infiltration pressure Pin. Under quasi-static condition, water, glycerol, and ethylene glycol contribute to a quasi-static infiltration pressure Pstin = 21 MPa, 12 MPa and 3 MPa respectively, which results from their different polarity and surface tension. Here Pin is calculated as the midpoint of infiltration plateau for self comparison. At room temperature (20 °C), deionized water has the highest polarity (with its dielectric constant being 80.4) and surface tension 72.80 mN m−1, while ethylene glycol has the lowest dielectric constant 37.0 and surface tension 47.70 mN m−1.15 According to the classic Young's equation,16 Pstin = (k/r)γ|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ|, where k is a section factor which equals 2 for circular channels, r is the pore radius, γ is the liquid surface tension and θ is the contact angle. Note that the silica nanopore surface is very hydrophobic, so the most polar liquid tends to form the highest contact angle. Consequently, the highest Pstin goes to the water based system while the lowest goes to the ethylene glycol based system. The glycerol based system obtains a moderate infiltration pressure since both its dielectric constant and surface tension lie in between those of water and ethylene glycol.15 This also explains why after the system is unloaded, small amount of water molecules will flow out indicated by the remaining infiltration plateau in its 2nd and following loading cycles, while glycerol and ethylene glycol molecules do not evidenced by its linear compressive behavior after the 1st cycle. This is because the nanopore surface is relatively more wettable by glycerol or ethylene glycol. The discussions on interfacial properties here will help our analysis on the rate effect in following parts.
θ|, where k is a section factor which equals 2 for circular channels, r is the pore radius, γ is the liquid surface tension and θ is the contact angle. Note that the silica nanopore surface is very hydrophobic, so the most polar liquid tends to form the highest contact angle. Consequently, the highest Pstin goes to the water based system while the lowest goes to the ethylene glycol based system. The glycerol based system obtains a moderate infiltration pressure since both its dielectric constant and surface tension lie in between those of water and ethylene glycol.15 This also explains why after the system is unloaded, small amount of water molecules will flow out indicated by the remaining infiltration plateau in its 2nd and following loading cycles, while glycerol and ethylene glycol molecules do not evidenced by its linear compressive behavior after the 1st cycle. This is because the nanopore surface is relatively more wettable by glycerol or ethylene glycol. The discussions on interfacial properties here will help our analysis on the rate effect in following parts.
As the loading rate increases, different liquids lead to various degrees of rate effect. Water based system is nearly insensitive to loading rate, while glycerol based system obtains a much higher dynamic infiltration plateau Pdyin compared with its quasi-static result Pstin. Given that these three liquids have very different viscosities at room temperature, with water being 1 mPa s, ethylene glycol being 19.9 mPa s, and glycerol being 1412 mPa s,17,18 this rate effect may be attributed to some kind of flow resistance related to their viscosities. According to the classic Poiseuille flow solution,14 the additional infiltration pressure caused by the rate effect can be expressed as ΔPin = (8ηQL)/(πr4), with η being the effective viscosity of liquid in nanopores, Q being the flux, and L being the effective nanopore depth. This equation is based on continuum theory, but it is employed here for the purpose of self-comparison, to allow the analysis on effective viscosity and the comparison with its bulk counterpart H.
In order to provide a deeper insight on this issue, glycerol–water solutions of different volume concentrations were prepared and investigated. Fig. 2a shows the infiltration pressures of these systems at both 0.5 mm min−1 and 50 mm min−1. Under quasi-static condition, Pstin decreases gradually with the glycerol concentration C, which can be explained by its declining polarity and surface tension. While under dynamic condition, Pdyin firstly declines when C < 0.85, but grows up afterwards, because the rate effect becomes stronger and prevents the decrease of infiltration pressure. Consequently, ΔPin is shown to increase with C.
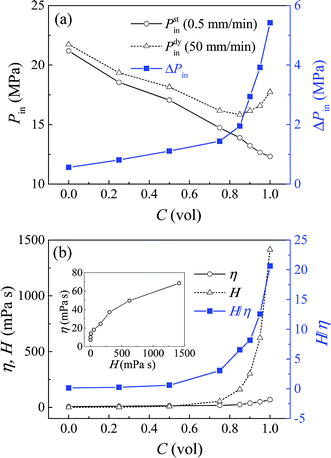 | ||
| Fig. 2 Liquid infiltration testing results at different glycerol concentrations: (a) Pin and ΔPin; (b) H, η and H/η. | ||
The effective viscosity can be calculated by η = ΔPin(πr4)/(8QL), in which Q = (vA)/N, and the number of nanopores N = Vp/(πr2L), with Vp being the gross pore volume. Note that this calculation is under the assumption of uniform pore size, since the infiltration plateaus are nearly flat. So we have η = ΔPin(r2Vp)/(8vAL2), with r = 3.9 nm, Vp = 0.11 cm3, v = 50 mm min−1, A = 127 mm2, and L = 12.5 μm (taken as one-half of the average particle size 25 μm). Fig. 2b shows the value of η and H, and their ratio H/η at various glycerol concentrations. The inset shows the effective viscosity increasing with its bulk counterpart in power law, indicating that liquid viscosity may have the same impact on mesoscale fluids as it does for bulk liquid. But this effective viscosity proves to be orders lower than its bulk value, and their ratio H/η increases sharply with glycerol concentration. So the loading rate effect of NMF liquid is much less pronounced than the prediction of continuum fluid mechanics, which may be associated with the nanoscale confinement.
The above findings are in agreement with previous simulation and experimental results about the ultra-fast transport rate of nanoconfined liquid, which is typically higher than the prediction of classic continuum theory by more than one magnitude.12,13,19,20 The low effective viscosity found here, and this high flux phenomenon should be caused by the velocity slip unique to the nanoenvironment. Nonslip boundary condition is a common assumption for continuum fluid, but no longer holds true at nanoscale.12,13 Liquid molecules can move along the nanopore wall, subject to solid–liquid interaction force as its flow resistance. In lyophobic nanopores, due to the weak solid–liquid attraction, the liquid flow becomes nearly frictionless and thus rapid, with a significant velocity slip at the interface.21 In that case, ideally, a plug flow profile can be formed, with no velocity variation and shear stress among liquid molecules. Therefore, the effective viscosity becomes much lower than its bulk value.
In this study, the nanopores are at mesoscale, so the liquid flow inside should still remain some patterns of laminar flow, instead of a perfect plug flow.22 Conventional viscosity force in a laminar flow is caused by the inherent dissipation of bulk liquid, with a velocity profile of parabolic shape. Therefore, the flow resistance here comprises of two parts: the boundary force at the solid–liquid interface, and the shear viscosity force among liquid molecules. Furthermore, the solid–liquid interface serves as a boundary condition of the viscosity force, which cannot form without enough interfacial attraction. As the glycerol concentration increases, the surface wettability is slightly enhanced, proved by the decrease of infiltration pressure. This allows a limited increase of both the boundary force and viscosity force. Their combined effect increases the effective viscosity, up to nearly 70 mPa s for a pure glycerol. However, this turns out to be a trivial growth compared with the change of its bulk value under the same condition. For a nonslip hydrodynamic flow without nanoconfinement, the viscosity force can increase without restraint, up to 1400 mPa s for the pure glycerol. This explains why η seems to have an upper limit, and H/η increases sharply with glycerol concentration in Fig. 2b.
The above analysis is also in consistence with the testing results of ethylene glycol in Fig. 1. Compared with glycerol, ethylene glycol is distinguished by its higher wettability (proved by its low infiltration pressure), as well as its extremely lower viscosity, which is close to the value of water. Therefore, although enough interfacial attraction is provided, its viscosity force cannot obtain a meaningful growth. This results in its low effective viscosity, which accounts for its trivial rate effect.
The testing results at different temperatures will further support the above analysis. Fig. 3 shows the infiltration pressures and effective viscosities of pure glycerol based system at a temperature ranging from 20 °C to 140 °C, obtained by liquid infiltration tests conducted in an environmental control chamber. The quasi-static results are insensitive to temperature, with a constant infiltration pressure around 12.5 MPa, while the infiltration pressure under dynamic loading decreases significantly with temperature. So the rate effect weakens gradually and becomes trivial at temperatures over 100 °C. The constant quasi-static infiltration pressure reflects that the solid–liquid interfacial properties remain unchanged at different temperatures. So the decline of rate effect results exclusively from the variation of viscosity. This to a great extent, demonstrates the existence of viscosity force in mesoscale channels. Fig. 3b presented the effective viscosity, which increases with its bulk value, and both of them decrease with temperature. As expected, η is much lower than H, and their ratio H/η decreases sharply with temperature. It is worth mention that for the non-outflow NMF liquid investigated here, its energy absorption density is proportional to infiltration pressure, so it is also sensitive to loading rate, and influenced by temperature and glycerol concentration. For instance, the pure glycerol based system has an energy absorption density around 6.8 J g−1 under quasi-static condition, independent of temperature. However, this value can reach 9.5 J g−1 under dynamic loading (50 mm min−1) at 20 °C, but decreases to 6.8 J g−1 at 140 °C.
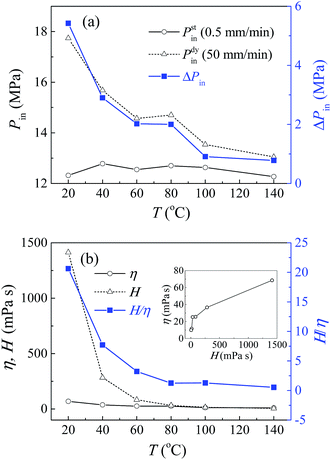 | ||
| Fig. 3 Liquid infiltration testing results of pure glycerol based system at different temperatures: (a) Pin and ΔPin; (b) H, η and H/η. | ||
Conclusions
In summary, we provided experimental results on the rate effect of pressurized liquid infiltration into mesoporous materials. With liquid composition and temperature varied, its detailed mechanism is elucidated. Results show that rate effect of mesoscale infiltration is associated with both the solid–liquid interfacial property and liquid viscosity. Due to the lyophobic nature of mesopore surface in this study, the effective viscosity at mesoscale is orders lower than its bulk counterpart. A higher bulk viscosity can increase this effective viscosity, but subject to a constraint from the interfacial interaction. These findings are unique to mesoscale fluids, which lie between the nanoscale transport and continuum fluid, characterized by the coexistence of velocity slip and viscosity force.Acknowledgements
The work is supported by the Tsinghua University under Grant No. 20121080050 and the National Natural Science Foundation of China under Grant No. 11372164.References
- A. Srivastava, O. Srivastava, S. Talapatra, R. Vajtai and P. Ajayan, Nat. Mater., 2004, 3, 610–614 CrossRef CAS PubMed.
- C. R. Martin and P. Kohli, Nat. Rev. Drug Discovery, 2003, 2, 29–37 CrossRef CAS PubMed.
- Y. Qiao, L. Liu and X. Chen, Nano Lett., 2009, 9, 984–988 CrossRef CAS PubMed.
- Y. Sun, J. Xu, Y. B. Li, B. Liu, Y. Wang, C. Liu and X. Chen, Adv. Eng. Mater., 2013, 15, 740–746 CrossRef CAS.
- Y. Sun, P. Li, Y. Qiao and Y. Li, Sci. Rep., 2014, 4, 6547 CrossRef CAS PubMed.
- Y. Sun, Z. Guo, J. Xu, X. Xu, C. Liu and Y. Li, Mater. Des., 2015, 66, 545–551 CrossRef CAS.
- Y. Sun, W. Lu and Y. Li, Appl. Phys. Lett., 2014, 105, 121609 CrossRef.
- A. Han, W. Lu, V. K. Punyamurtula, T. Kim and Y. Qiao, J. Appl. Phys., 2009, 105, 024309 CrossRef.
- J. Zhao, P. J. Culligan, J. T. Germaine and X. Chen, Langmuir, 2009, 25, 12687–12696 CrossRef CAS PubMed.
- A. Han, W. Lu, V. K. Punyamurtula, X. Chen, F. B. Surani, T. Kim and Y. Qiao, J. Appl. Phys., 2008, 104, 124908 CrossRef.
- X. Chen, G. Cao, A. Han, V. K. Punyamurtula, L. Liu, P. J. Culligan, T. Kim and Y. Qiao, Nano Lett., 2008, 8, 2988–2992 CrossRef CAS PubMed.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Nature, 2005, 438, 44 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- J. A. Fay, Introduction to fluid mechanics, MIT press, 1994 Search PubMed.
- T. E. ToolBox, The Engineering ToolBox.
- H. Ibach, Physics of surfaces and interfaces, Springer, Berlin, 2006 Search PubMed.
- H. D. Gesser, Applied chemistry: a textbook for engineers and technologists, Springer, 2002 Search PubMed.
- N.-S. Cheng, Ind. Eng. Chem. Res., 2008, 47, 3285–3288 CrossRef CAS.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190 CrossRef CAS PubMed.
- A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180 CrossRef CAS PubMed.
- G. Nagayama and P. Cheng, Int. J. Heat Mass Transfer, 2004, 47, 501–513 CrossRef CAS.
- J. Li, D. Liao and S. Yip, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 7259 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |