Third- and high-order nonlinear optical properties of an intramolecular charge-transfer compound

Abstract

An oligo(phenylenevinylene) bridged intramolecular charge-transfer (ICT) compound, (TCNQ)₂OPV₃, has been synthesized and its third- and fifth-order nonlinear optical refraction indexes have been determined by measurement with the 4f system with a phase-object, under near-infrared excitation.

---

Organic π-conjugated molecules have been extensively studied and applied in diverse fields ranging from field-effect transistors (FETs),^1,2 organic light-emitting diodes (OLEDs),^3,4 and organic photovoltaic cells (OPVs),^5–7 thanks to their attractive optoelectronic properties. π-Conjugated compounds with electron donors (D) and electron acceptors (A) typically feature a intramolecular charge transfer (ICT) process. In the solid state, the properties of ICT compounds are determined not only by the intrinsic features of their component moieties but also by their molecular packing modes. Control over the relative orientation of the component parts and subtle modulation of intermolecular overlap are very important aspects for ensuring desired functions. These compounds are of particular importance for applications in material science such as nonlinear optical (NLO) materials,^8–10 electrogenerated chemiluminescence materials,¹¹ fluorescence probes¹² and dye-sensitized solar cells.^13–17 Libraries of electron donors and acceptors have been explored for constructing such materials systems in the past decades.¹⁸ Recently a series of novel D–π–A molecular systems of donor-substituted tetracyanoethylene (TCNE) and 7,7,8,8-tetracyanoquinodimethane (TCNQ) adducts have been explored by Diederich et al.^19–23 and other groups,^24–31 by taking advantage of the “click-type” near-quantitative [2 + 2] cycloadditions with appropriately activated alkynes, followed by retro-electrocyclizations. These naturally stable, nonplanar chromophores are ideal platforms for efficient intramolecular charge-transfer (ICT) processes and are regarded as promising nonlinear optical materials.^{19–22,32–36}

In this work, we have designed and synthesized an oligo(phenylenevinylene) (OPV) bridged ICT compound, (TCNQ)₂OPV₃, and studied its third- and fifth-order optical nonlinearities by a nonlinear optical imaging technique with the phase-object (NIT-PO) at the entry of a 4f coherent imaging system.³⁷ The method is based on a 4f system with top-hat beams and its theoretical model is simple Fourier optics, which leads to many advantages such as simple optical alignment, very high sensitivity and insensitivity to statistical fluctuations of the laser beam.³⁸ The improved technique of greater signal sensibility can be used to measure the nonlinear absorption and refraction at the same time. Another vital advantage of the technique is that it can extract information about both the magnitude and the sign of the nonlinear coefficients simultaneously with only one-laser-shot³⁹ without the necessarity of scanning of the sample as that of the Z-scan method.⁴⁰ Although the method was initially developed to measure the nonlinear refraction index of the materials, it can simultaneously measure the nonlinear refraction index and nonlinear absorption coefficient of materials conveniently from the analysis of three experiment images.⁴¹ Moreover, the results of different sensitivity of nonlinear absorption and refraction are given by choosing different phase shift of the phase object.⁴² As an efficient method, the technique of measurement has successfully utilized to study the kinetics of photo-induced effects by shot-by-shot measurements.⁴³

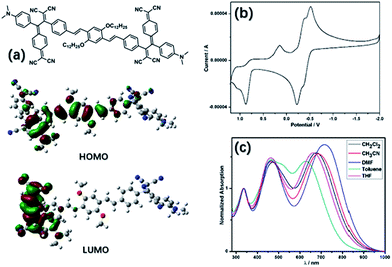
The ICT compound (TCNQ)₂OPV₃ has been synthesized following the [2 + 2] cycloaddition and the subsequent retro-electrocyclization of TCNQ with the OPV bridged alkynes which have been activated by electronic donating groups (Fig. 1a and Scheme S1 in the ESI†). The compound displays two charge-transfer (CT) bands at 470 nm and 677 nm, respectively, in CH₂Cl₂ in the UV-vis absorbance spectra, resulting from the two different D–A transitions of the compound (Fig. 1c and S1 in the ESI†). A distinct solvatochromic effect of (TCNQ)₂OPV₃ has been observed in varied solvents, which was a characteristic behavior of the dipolar ICT molecules.^19–22,44 The major CT band at 677 nm (1.83 eV) in CH₂Cl₂ red-shifts to 687 nm (1.80 eV) in CH₃CN and 718 nm (1.73 eV) in DMF, and blue-shifts to 658 nm (1.88 eV) in THF and 625 nm (1.98 eV) in toluene. The solvent effect of the CT band generally follows the reported tendency of red shift of such ICT compounds when increasing the solvent polarity.²⁵ Cyclic voltammetry (CV) curves of (TCNQ)₂OPV₃ collected in CH₂Cl₂ with nBu₄NPF₆ (0.1 M) give the information on the redox properties (Fig. 1b). The compound shows two well-defined reversible one-electron reduction steps with the first electron transfer occurring at −0.51 V to −0.35 V and the second one at −0.38 V to −0.22 V (using the Ag/Ag⁺ electrode couple as the internal standard), occurring on the C=(CN)₂ moieties of the molecule.^20–22 The oxidation steps occurring on the aniline moieties are irreversible, as shown in the CV curves. Optimized geometry of the compound calculated from the B3LYP functional 6-31G(d,p) within the DFT level^45–48 shows the greatly twisted configuration of the charge-transfer moieties and the slight distortion in the OPV₃ bridge. The HOMO and LUMO obtained from DFT calculations show the electrons of HOMO are relatively homogeneous and a clear electron transfer while the electrons of LUMO are mainly distributed in the TCNQ derivative moieties.

Fig. 1 (a) Chemical structure of (TCNQ)₂OPV₃ (top) and LUMO and HOMO orbital plots (down) calculated from the B3LYP functional 6-31G(d,p) optimized geometry. The dodecyl substitutes were replaced by methyl substitutes for ease of calculation and hydrogen atoms were omitted for clarity. (b) Cyclic voltammogram of (TCNQ)₂OPV₃ measured in CH₂Cl₂ (+0.1 M nBu₄PF₆ at a scan rate of 0.2 V s⁻¹). (c) Normalized linear UV-vis absorption spectra of (TCNQ)₂OPV₃ in different solvents.

To study the NLO property of the compound, we use the shunt-wound double 4f system‡ to overcome the instability of energy and space distributing of the beam from OPG (optical parameter generator).⁴⁹ The monitor branch is replaced by another 4f system. The theoretical model of the developed system is the same as the traditional ones. The shunt-wound double 4f system without material acquisition³⁷ is only used to calculate the linear transmittance of the material if the linear transmittance of the material is known. This leads to simple calculation and easy data processing processes. The main difference between the developed 4f coherent imaging system and the traditional one is that the reference facula is used in the nonlinear acquisition instead of the main facula in the linear acquisition as the incident beam to fit the main facula in the nonlinear acquisition.

In a typical experiment, the excitation beam at 800 nm with 21 picoseconds (ps) pulse width (FWHM) which is emitted from the OPG pumped by a Q-switched, frequency-doubled Nd:YAG laser (Ekspla) is expanded to 40 mm in diameter and subsequently pass through the aperture with a phase-object (PO) (Scheme S2 in the ESI†). The radii of the aperture and PO are R_n = 1.70 mm and L_n = 0.5 mm respectively. The phase shift of the PO is φ_L = 0.266π. The 4f system of the main branch consists of two lenses L₁ and L₂ with the same focal length f₁ = f₂ = 100 mm, and the monitor branch consists of lenses L₁ and L₂ with the same focal length f₁ = f₂ = 100 mm. The airy radius at the focal plane of lens L₁ is ω₀ = 1.22λf₁/(2R_a) = 28.7 μm, giving a Rayleigh range z₀ = πω₀²/λ = 3.2 mm. This satisfies the thin sample approximation (2 mm-thick fused silica cell). The detecting system is a cooled charge-coupled device (CCD) camera with (1040 × 1376) pixels. The camera pixels have 4095 gray levels, and the size of each pixel is 6.4 × 6.4 μm². Neutral filters (tf) are used to keep the CCD with its linear response range.

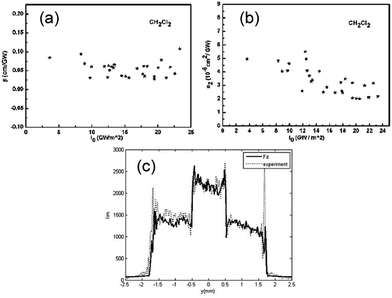
The nonlinear optical property of (TCNQ)₂OPV₃ has been deduced by subtracting nonlinear index of the solvent (CH₂Cl₂) from its solution for picoseconds excitation at 800 nm with the sample concentration of 8 × 10⁻⁵ M (see Fig. S2 in the ESI†). The values of third-order nonlinear absorption index β and third-order nonlinear refraction index n₂ measured at different peak-on-axis intensity in the sample are shown in Fig. 2a and b, respectively. The average value of β is 0.0546 cm GW⁻¹ with a standard error of ±13%, and the average value of n₂ is 3.33 × 10⁻¹⁹ m² W⁻¹ with a standard error of ±6% (Fig. 2a and b). The comparison between the two profiles of experimental nonlinear image (in dots) and the calculated nonlinear image (in bold) shows a very good agreement between experimental result and numerical simulation (Fig. 2c).

Fig. 2 (a) The nonlinear absorption index of CH₂Cl₂ for different peak-on-axis intensity. (b) The nonlinear refraction index of CH₂Cl₂ for different peak-on-axis intensity. (c) The result of the numerical simulation. The comparison of profiles (in dots) and (in bold) shows a very good agreement between experimental acquisition and numerical simulation.

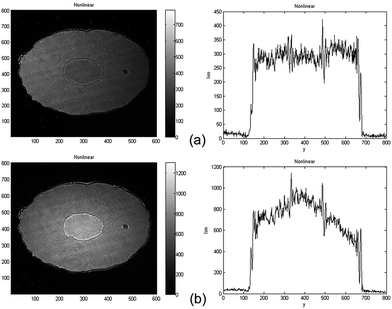
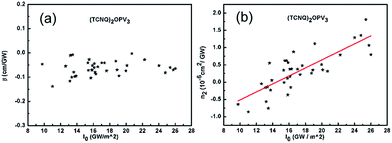
The optical nonlinearity of the solution has been measured under the same operation conditions as those for measuring the solvent. The two different main faculae of nonlinear image and its corresponding fluence distribution at x = 300 indicating two different sign of nonlinearity (Fig. 3). The values of β and n₂ measured at different peak-on-axis intensity in the sample from 9.76 to 26 GW cm⁻² are shown in Fig. 4a and b respectively. The change tendency of nonlinear absorption index β with peak-on-axis intensity is small with an average value of [small beta, Greek, macron] = −0.0638 cm GW⁻¹, showing a good reproducibility of the measurements (Fig. 4a). The nonlinear absorption is mainly produced by the two-photon process (a third-order NLO).^50,51 From Fig. 4b, a linear dependence of nonlinear refraction index n₂ with peak-on-axis intensity has been noticed. One can clearly see that the solution exhibits negative nonlinearity as the peak-on-axis intensity is small (Fig. 3a), while it changes to positive when the peak-on-axis intensity is large enough (Fig. 3b). Because the nonlinear refraction index of the solvent is a little smaller as the peak-on-axis intensity is large enough, this indicates the existence of high-order nonlinearity besides the cubic term of the solute. High order terms with opposite sign are required to compensate the cubic term and to generate a sign change of the whole nonlinear refraction index of the solution. This is similar to what have been observed from quantum dot-polymer nanocomposite films,^50,51 as determined by the Z-scan technique. We use the cubic/quintic model given by G. Boudebs et al.^52–54 Let n₂ and n₄ represent the third-order and fifth-order nonlinear refraction indexes, respectively. The whole nonlinear refraction index measured is an effective refraction index and can be written as

n^eff₂ = n₂ + n₄I_m (1)

Fig. 3 (a) The main facula of nonlinear image at high peak-on-axis intensity and its corresponding fluence distribution at x = 300. (b) The main facula of nonlinear image at low peak-on-axis intensity and its corresponding fluence distribution at x = 300.

Fig. 4 (a) The nonlinear absorption index of (TCNQ)₂OPV₃ solution for different peak-on-axis intensities. (b) The nonlinear optical refraction indexes of (TCNQ)₂OPV₃ solution for different peak-on-axis intensities. The solid line is the theoretical fitting by the use of high-order nonlinear model.

For α = 3.08 cm⁻¹ (linear absorption index) and [small beta, Greek, macron] = −0.06382 cm GW⁻¹, we obtain I_m ≈ 0.9103I₀ (see Fig. 4a), so eqn (1) becomes

n^eff₂ = n₂ + 0.9103n₄I₀ (2)

At the same time, we obtain eqn (3) by linear fit to the experimental result.

n^eff₂ (1 × 10⁻¹⁹ m² W⁻¹) = 0.1159I₀ (GW m⁻²) − 1.6755 (3)

By comparing eqn (2) and (3), we obtain the two nonlinear refraction indexes n₂ = −1.676 × 10⁻¹⁹ m² W⁻¹ and n₄ = 1.273 × 10⁻³³ m⁴ W⁻². So the nonlinear refraction index of solute can be deduced by subtracting nonlinear refraction index of solvent from the solution. The third- and fifth-order refraction indexes have been deduced to be n^solute₂ = −5.01 × 10⁻¹⁹ m² W⁻¹ and n^solute₄ = −1.273 × 10⁻³³ m⁴ W⁻² respectively.

In conclusion, the nonlinear optical properties of an ICT compound (TCNQ)₂OPV₃ in the near infrared have been investigated by using a nonlinear-imaging technique with phase-object at the entry of a 4f coherent imaging system. The third-order and fifth-order nonlinear refraction indexes have been deduced to be n₂ = −1.676 × 10⁻¹⁹ m² W⁻¹ and n₄ = −1.273 × 10⁻³³ m⁴ W⁻² by subtracting nonlinear refraction index of the solvent from its solution for picoseconds excitation at 800 nm. The picosecond third- and fifth-nonlinear optical properties of the compound in the near-infrared and the new technique of 4f coherent nonlinear-imaging system with phase-object for determining NLO properties of the D–π–A organic molecular systems indicate potential applications both in the basic research field of nonlinear optical theory and the fields of photonic device fabrications.

Acknowledgements

We are grateful for the fruitful discussions with Prof. Yuliang Li from the Institute of Chemistry, Chinese Academy of Sciences (ICCAS). This work was supported by the National Nature Science Foundation of China (NSFC, Project No. 51503143 and 21476162), the Tianjin Natural Science Foundation (Project No. 16JCQNJC05000), the China International Science and Technology Projects (Project No. 2012DFG41980 and S2016G3413), the Innovation Foundation of Tianjin University (Project No. 2016XRX-0017), the Tianjin Science and Technology Innovation Platform Program (Project No. 14TXGCCX00017), the Netherlands Organization for Scientific Research (NWO) with the Veni Grant (Project no. 680-47-437), and the Tianjin 1000 Youth Talents Plan.

Notes and references

1. C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267.
2. Y. Ie, A. Uchida, N. Kawaguchi, M. Nitani, H. Tada, F. Kakiuchi and Y. Aso, Org. Lett., 2016, 18, 4320–4323.
3. M. M. Rothmann, S. Haneder, E. D. Como, C. Lennartz, C. Schildknecht and P. Strohriegl, Chem. Mater., 2010, 22, 2403–2410.
4. L. Yao, S. Zhang, R. Wang, W. Li, F. Shen, B. Yang and Y. Ma, Angew. Chem., Int. Ed., 2014, 53, 2119–2123.
5. Z. Li, G. He, X. Wan, Y. Liu, J. Zhou, G. Long, Y. Zuo, M. Zhang and Y. Chen, Adv. Energy Mater., 2012, 2, 74–77.
6. A. Facchetti, Chem. Mater., 2011, 23, 733–758.
7. J. Zhou, Y. Zuo, X. Wan, G. Long, Q. Zhang, W. Ni, Y. Liu, Z. Li, G. He, C. Li, B. Kan, M. Li and Y. Chen, J. Am. Chem. Soc., 2013, 135, 8484–8487.
8. H. Meier, Angew. Chem., Int. Ed., 2005, 44, 2482–2506.
9. S. R. Marder, Chem. Commun., 2006, 131–134.
10. T. Michinobu, J. C. May, J. H. Lim, C. Boudon, J. P. Gisselbrecht, P. Seiler, M. Gross, I. Biaggio and F. Diederich, Chem. Commun., 2005, 737–739.
11. R. Y. Lai, X. Kong, S. A. Jenekhe and A. J. Bard, J. Am. Chem. Soc., 2003, 125, 12631–12639.
12. A. W. Czarnik, Acc. Chem. Res., 1994, 27, 302–308.
13. Y. Liang, X. Xue, W. Zhang, C. Fan, Y. Li, B. Zhang and Y. Feng, Dyes Pigm., 2015, 115, 7–16.
14. C. Fan, B. Zhang, Y. Li, Y. Liang, X. Xue and Y. Feng, Phys. Chem. Chem. Phys., 2015, 17, 30624–30631.
15. F. Lu, L. Qian, J. Cao, Y. Feng, B. Du and L. Ding, Polym. Chem., 2015, 6, 7373–7376.
16. F. Lu, J. Zhang, Y. Zhou, Y. Zhao, B. Zhang and Y. Feng, Dyes Pigm., 2016, 125, 116–123.
17. Y. Zhou, N. A. Lee, K. T. Ngo, X. Peng, Y. Feng and J. Rochford, RSC Adv., 2015, 5, 41193–41202.
18. M. Bendikov, F. Wudl and D. F. Perepichka, Chem. Rev., 2004, 104, 4891–4946.
19. B. Esembeson, M. L. Scimeca, T. Michinobu, F. Diederich and I. Biaggio, Adv. Mater., 2008, 20, 4584–4587.
20. M. Kivala and F. Diederich, Acc. Chem. Res., 2009, 42, 235–248.
21. M. Kivala, C. Boudon, J. P. Gisselbrecht, B. Enko, P. Seiler, I. B. Muller, N. Langer, P. D. Jarowski, G. Gescheidt and F. Diederich, Chem.–Eur. J., 2009, 15, 4111–4123.
22. T. Michinobu, C. Boudon, J. P. Gisselbrecht, P. Seiler, B. Frank, N. N. Moonen, M. Gross and F. Diederich, Chem.–Eur. J., 2006, 12, 1889–1905.
23. M. Kivala, C. Boudon, J. P. Gisselbrecht, P. Seiler, M. Gross and F. Diederich, Angew. Chem., Int. Ed., 2007, 46, 6357–6360.
24. W. Zhou, J. Xu, H. Zheng, X. Yin, Z. Zuo, H. Liu and Y. Li, Adv. Funct. Mater., 2009, 19, 141–149.
25. J. Xu, L. Wen, W. Zhou, J. Lv, Y. Guo, M. Zhu, H. Liu, Y. Li and L. Jiang, J. Phys. Chem. C, 2009, 113, 5924–5932.
26. J. Xu, H. Zheng, H. Liu, C. Zhou, Y. Zhao, Y. Li and Y. Li, J. Phys. Chem. C, 2010, 114, 2925–2931.
27. Y. Li, T. Liu, H. Liu, M. Z. Tian and Y. Li, Acc. Chem. Res., 2014, 47, 1186–1198.
28. T. Shoji, S. Ito, K. Toyota, M. Yasunami and N. Morita, Chem.–Eur. J., 2008, 14, 8398–8408.
29. J. Xu, X. Liu, J. Lv, M. Zhu, C. Huang, W. Zhou, X. Yin, H. Liu, Y. Li and J. Ye, Langmuir, 2008, 24, 4231–4237.
30. T. Michinobu, J. Am. Chem. Soc., 2008, 130, 14074–14075.
31. K. Tahara, T. Fujita, M. Sonoda, M. Shiro and Y. Tobe, J. Am. Chem. Soc., 2008, 130, 14339–14345.
32. J. Xu, S. Semin, D. Niedzialek, P. H. Kouwer, E. Fron, E. Coutino, M. Savoini, Y. Li, J. Hofkens, H. Uji-I, D. Beljonne, T. Rasing and A. E. Rowan, Adv. Mater., 2013, 25, 2084–2089.
33. M. Torres, S. Semin, I. Razdolski, J. Xu, J. A. W. Elemans, T. Rasing, A. E. Rowan and R. J. M. Nolte, Chem. Commun., 2015, 51, 2855–2858.
34. J. Xu, S. Semin, J. Cremers, L. Wang, M. Savoini, E. Fron, E. Coutino, T. Chervy, C. Wang, Y. Li, H. Liu, Y. Li, P. Tinnemans, P. H. J. Kouwer, T. W. Ebbesen, J. Hofkens, D. Beljonne, A. E. Rowan and T. Rasing, Adv. Opt. Mater., 2015, 3, 948–956.
35. J. Xu, S. Semin, T. Rasing and A. E. Rowan, Small, 2015, 11, 1113–1129.
36. Y. Duan, C. Ju, G. Yang, E. Fron, E. Coutino-Gonzalez, S. Semin, C. Fan, R. S. Balok, J. Cremers, P. Tinnemans, Y. Feng, Y. Li, J. Hofkens, A. E. Rowan, T. Rasing and J. Xu, Adv. Funct. Mater., 2016, 26, 8968–8977.
37. G. Boudebs and S. Cherukulappurath, Phys. Rev. A, 2004, 69, 053813.
38. M. Sheik-Bahae, A. A. Sald, T. H. Wei, D. J. Hagan and E. W. V. Strylang, IEEE J. Quantum Electron., 1990, 26, 760–769.
39. C. B. de Araújo, A. S. L. Gomes and G. Boudebs, Rep. Prog. Phys., 2016, 79, 036401.
40. Y. Li, K. Yang, X. Zhang, Q. Chang, Y. Wang and Y. Song, Opt. Commun., 2008, 281, 3913–3918.
41. Y. Li, Y. Song, Y. Wang, X. Zhang, J. Sun, J. Yang, G. Shi and Y. Wang, Sci. China, Ser. E: Technol. Sci., 2008, 51, 1483–1490.
42. Y. Li, K. Yang, X. Zhang, Q. Chang, Y. Wang and Y. Song, Opt. Commun., 2008, 281, 3913–3918.
43. G. Boudebs and C. B. de Araújo, Appl. Phys. Lett., 2004, 85, 3740–3742.
44. P. Suppan and N. Ghoneim, Solvatochromism, Royal Society of Chemistry Cambridge, Cambridge, 1997.
45. W. Y. Paul, W. Ayers and A. L. J. Bartolotti, in Chemical Reactivity Theory: A Density Functional View, ed. P. K. Chattaraj, CRC Press, 2009, vol. 18, pp. 255–267.
46. A. Y. Tolbin, A. V. Dzuban, V. I. Shestow, Y. I. Gudkova, V. K. Brel, L. G. Tomilova and N. S. Zefirov, RSC Adv., 2015, 5, 8239–8247.
47. Y. Zhang, Y. Shi and Y. Li, J. Mater. Sci.: Mater. Electron., 2016, 27, 7132–7140.
48. Y. Li, D. Qi, P. Song and F. Ma, Mater, 2015, 8, 42–56.
49. Y.-L. Song, J. Yang, Y. Li, J. Gu and Y. Wang, CN101308091, 2008, vol. 19.
50. X. Liu and Y. Tomita, Phys. Res. Int., 2012, 2012, 161572.
51. X. Liu, Y. Adachi, J. Oshima, T. Nakashima and T. Kawai, Opt. Express, 2012, 20, 13457.
52. G. Boudebs, S. Cherukulappurath, H. Leblond, J. Troles, F. Smektala and F. Sanchez, Opt. Commun., 2003, 219, 427–433.
53. S. Cherukulappurath, M. Guignard, C. Marchand, F. Smektala and G. Boudebs, Opt. Commun., 2004, 242, 313–319.
54. G. Boudebs and S. Cherukulappurath, Opt. Commun., 2005, 250, 416–420.
55. Y. Li, Y. Song, T. Wei, C. He, X. Zhang, Y. Wang, K. Yang, M. Shen and J. Yang, Appl. Phys. B, 2008, 91, 119–122.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed synthesis and characterization of (TCNQ)₂OPV₃ and NLO measurement of the solvent. See DOI: 10.1039/c6ra25408j

‡ This new system is not propitious to measure films materials with surface inhomogeneities because the reference facula does not include the imperfect information of the materials.⁵⁵

---