The influence of process parameters on needle punched nonwovens investigated using image analysis

Abstract

The influence of process parameters including punch frequency, needle penetration depth and punch times on the fiber distribution and straight segment fiber length of needle punched nonwovens was investigated using the Hough transform method. The results show that punch frequency and punch times have more significant influence on the samples than needle penetration depth. When combining the experimental results with image analysis, the optimum process parameters to prepare needle punched nonwovens based on preoxidized polyacrylonitrile were obtained.

---

Introduction

Nonwovens are polymer-based engineered textiles manufactured from a set of randomly distributed fibers consolidated together by thermal, mechanical or chemical techniques. Simple entanglement of fibers is also possible through mechanical puncture with steel or water needles.^1–3 Owing to their excellent properties, such as high porosity and low cost, nonwovens and their composites with other materials can be used for a range of applications, including geotextiles for soil reinforcement, medical applications, filtration, and in the automobile and aerospace industries.^4–6 It is generally known that the properties of nonwovens mainly depend on the properties of the individual fibers and the microstructure of the fabrics. In the past two decades many researchers have investigated the microstructure of nonwovens, including the arrangement of fibers and fiber entanglement, based on image analysis.^7,8

The arrangement of fibers in nonwovens is represented by the orientation distribution function (ODF). The ODF is a histogram defining the angle of fibers with respect to a reference direction. This is a significant parameter for nonwovens because it affects the property distribution of nonwoven materials, such as permeability and absorbance of liquids, especially the anisotropic mechanical properties. For example, if there are more fibers oriented in a particular direction, the nonwoven will be stronger in that direction.⁹ Various methods have been developed to estimate fiber orientation distribution in nonwovens, such as direct tracking, flow field analysis, Fourier transform (FT) and Hough transform (HT) techniques.^10–14 Of these methods, FT and HT are the most widely used to compute the ODF via the nonwoven images. An image of a nonwoven structure contains spatial details in the form of brightness transitions cycling from light to dark and from dark to light. The spatial frequencies in a nonwoven image are related to the fiber orientation. FT transforms a gray intensity domain to a frequency spectrum with appropriate magnitude and phase values; if the fibers are mainly oriented in a given direction in a nonwoven fabric, the spatial frequencies in that direction will be low and the spatial frequencies in the perpendicular direction will be high. We can use this property of the FT to obtain the ODF of nonwovens.^15,16 The brightness of the image and density of the structure for nonwovens will affect the efficiency of the FT method. However, the HT method can directly detect the straight segments of fibers, obtaining the information for their orientation and length, and tolerate gaps at the object edges. It is reported that when used to obtain the ODF of spunlance fabrics, the results of HT were more close to the experimental results than those of FT.¹⁷

Polyacrylonitrile (PAN) fibers are heated in air atmosphere to between 180 and 300 °C to form preoxidized polyacrylonitrile (OPAN) fibers, which are the most suitable precursors to produce excellent carbon fibers.^18,19 In addition, owing to their excellent thermostability, OPAN fibers are usually used for nonwovens for various thermal insulation materials and filter materials. As far as we know, nothing has been reported on the influence of process punch parameters on the microstructure of fabrics through image analysis. In this research, we have investigated the effect of particular technological parameters on ODF and fiber entanglement of needle punched nonwoven fabrics based on OPAN fibers using the HT method.

Materials and methods

The samples utilized for this study were obtained from Wedo Technology (Tianjin) Co. Ltd, China. Properties of the OPAN fibers used to produce the samples of nonwovens are listed in Table 1. Carded webs of about 300 g cm⁻² were prepared by a series of processes: opening, carding and parallel lapping. Then, the carded batts were needle punched using a needling machine. Process parameters such as punch frequency, needle penetration depth and punch times were selected for consideration, and the other parameters were consistent. Parameters of seven needle punched samples are detailed in Table 2.

Table 1 Properties of the OPAN fibers

Length (mm)	Linear density (dtex)	Diameter (μm)	Breaking strength (cN dtex^−1)	Elongation (%)	Crimp frequency (crimp per cm)
51.00	1.66	12.40	1.53	18.29	1.40

---

Table 2 Parameters of the controlled samples

Samples	A1	A2	A3	B1	B2	C1	C2
Punch frequency (strokes per min)	100	240	380	240	240	240	240
Needle penetration depth (mm)	9	9	9	6	12	9	9
Punch times	2	2	2	2	2	1	3
Breaking strength in MD (MPa)	0.68	0.88	0.43	0.81	0.68	0.51	0.18
Breaking strength in CD (MPa)	0.25	0.28	0.13	0.30	0.13	0.09	0.06

---

The images of needle punched nonwovens were obtained using scanning electron microscopy (SEM, TM-1000). Tensile tests were carried out on a universal testing machine (INSTRON 3369) to investigate the breaking strength of the nonwovens. The sample size was 50 × 200 mm and there were five of each sample. The actual length of fibers in the nonwovens was also measured, to assess the damage of fibers affected by the needle punch process. The number of effective specimens in each case was five hundred. The ODF and straight segments’ fiber lengths were obtained via the HT method in MATLAB software.

The HT method is most commonly used to simplify the task of detecting regular lines such as curves, circles, and ellipses – especially straight-line segments in binary images.²⁰ The HT is also widely used for various applications in real life. Combining HT and the vanishing point, Jiang Guoquan proposes a simple and effective method to detect rows of wheat at the early growth stage.²¹ Mehdi Fatan uses edge detection and classification for cable lines exploration. The edge points belonging to the cable lines are retained and later the HT is used for the cable’s detection.²² Wang Yafei introduced a powerful method using gradient-based Hough transform to automatically recognize corrosion pits in microscopic images, making the statistical analysis of pit size and pit location easier and more efficient.²³ In addition, the HT has been shown to be effective for track initiator techniques and detection of loosened bolts.^24,25

In this research, the HT method is used to recognize straight segments of fibers in the nonwoven fabrics. A straight line in the Cartesian space can be expressed with two parameters in polar coordinates as r = x cos θ + y sin θ, where r is the normal distance from the origin to the line and θ is the angle of the normal line with respect to the x axis. With this method, points (x_i, y_i) of a line are transformed into sinusoidal curves r = x_i cos θ + y_i sin θ in the Hough space, which intersect at one point (r, θ). For a certain range of parameters r and θ, each (x_i, y_i) is mapped onto the Hough space and the points mapped onto the locations (r_m, θ_m) are accumulated in the 2D histogram. Therefore, the local peaks in the Hough space are considered to be straight-line segments in the original image space.^8,26

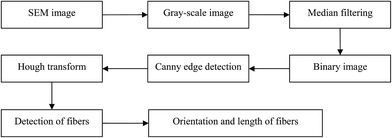
The fiber detection algorithm in the MATLAB software that we used is summarized in Fig. 1. Before beginning the process, the original SEM image was divided into four subdomains to decrease the influence of local brightness and increase distinguishability of individual fibers.¹⁷ Each subdomain processed followed Fig. 1 according to its own noise and brightness, and then the results of all four subdomains were combined to give the final result of the complete image.

Fig. 1 Steps of image analysis to detect fibers in nonwovens.

An image including eleven artificial black lines with random orientation is used to verify the image analysis algorithm (Fig. 2a). In the image there are green lines drawn on the black ones by the code indicating their detection, and their two ends are marked by a red and yellow “x” respectively. The distance between the coordinates of two end points of a line is named the line length. The ODF and length of lines in Fig. 2a are given in Fig. 2b and c respectively. In Fig. 2b, the frequency of lines for an angle refers to the ratio of the amount of lines aligned along the direction with an angle from the respective range to the total amount of lines. In Fig. 2c, length index is employed, as the values on the horizontal axis do not show the actual line length but are proportional to the line length.

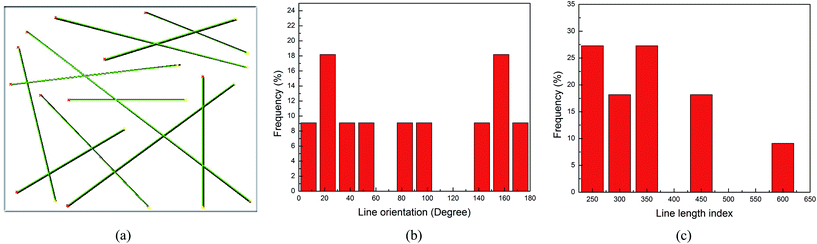Fig. 2 Image containing eleven randomly oriented lines (a), their ODF (b), and the distribution of length (c) computed with the image analysis algorithm.

Needle punched nonwovens based on OPAN fibers

Needle punching is a purely mechanical bonding method used for nonwoven production. When the carded web is fed into the machine, the barbed needles impact the web and penetrate into its inner planes, resulting in the fibers captured by the barbs moving from the horizontal plane to the vertical plane, even the bottom surface. After the needles return, the displaced fibers remain displaced, forming fiber bundles, leading to the mechanical entanglement of fibers in the web. Meanwhile, the movement of fibers always causes a change of fiber orientation and fiber damage for the nonwovens.^27,28

Fig. 3 shows SEM images of samples A1 and A3, which have different punch frequencies. We can see from the figure that the needle punched nonwovens consist of interconnecting OPAN fibers forming a porous network structure. Because the nonwovens are formed from a parallel lapping web, the fibers distribute mainly along the approximate machine direction, i.e. 90°. However, compared to A3, there are more fibers distributed along the machine direction in A1. This is because the higher punch frequency leads to more impacts per unit area, which means more fibers take part in migration and change their orientations. Due to the low fiber breaking strength, more impacts mean more damage to the OPAN fibers. Although A3 has more entanglement points per unit area, the breaking strength in the machine direction (MD) and cross direction (CD) of A3 is 0.43 MPa and 0.13 MPa, which is much less than 0.68 MPa and 0.25 MPa for A1 (Table 2). We also observed that there is some fiber breakage in A3, which can explain the above phenomenon.

Fig. 3 SEM images of A1 and A3.

Fiber damage caused by barbed needles is mechanical, mainly stretching and cutting, resulting in fiber weakening and fiber breakage.²⁹ The breaking strength of OPAN fiber is 1.53 cN dtex⁻¹ (Table 1), which is much less than other commonly used fibers for needle punched nonwovens, for example polypropylene. Fiber breakage was found to be the main form of fiber damage for the investigated samples, caused by needling. Fig. 4 shows the distribution of actual fiber lengths in the nonwoven fabrics, for various parameters of needle punching. It can be seen from Fig. 4a and c that with the increase of punch frequency and punch times, the length of fibers decreases significantly. Higher punch frequency and punch times mean higher punch density, which leads to more fibers being stroked and transformed per unit area, causing more serious fiber damage. In Fig. 4b, comparing to B1, the fiber length of A2 has a little variation, but the fiber length of B2 decreases significantly. Fibers twist around each other, and some of them are matted by their surrounding fibers. Increasing the needle penetration depth enhances the migration distance of fibers in the thickness direction of the fabric, which will increase the degree of fiber damage. On the other hand, when the depth is increased to a certain value, the force of the barbs to the fibers will increase significantly, resulting in more fiber breakage. On consideration of the strength of nonwovens based on OPAN fibers, a punch penetration depth of 9 mm was chosen as the optimum.

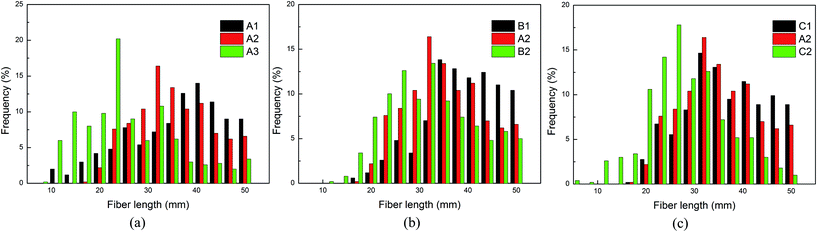Fig. 4 Distribution of accurate fiber length: affected by punch frequency (a), needle penetration depth (b) and punch times (c).

The ODF affected by the process parameters

In this study, SEM images were used to obtain fiber information for the samples. Compared to optical microscopy, SEM has a high depth of field even at high magnifications, which allows for a greater area of fibers in the viewing area to be focused.³⁰ In the previous report, the effects of sample magnification, uniformity of image brightness and shape of the image frame on image analysis were discussed.⁸ In order to obtain information on the individual fibers and more microstructure, an image magnification of 60× was selected. Also, the image was divided into four non-overlapped small, square images to reduce the influence of uniformity of brightness. The ODF of samples obtained by the HT method is shown in Fig. 5. In these figures, 90° and 0° (180°) indicate machine direction and cross-direction respectively.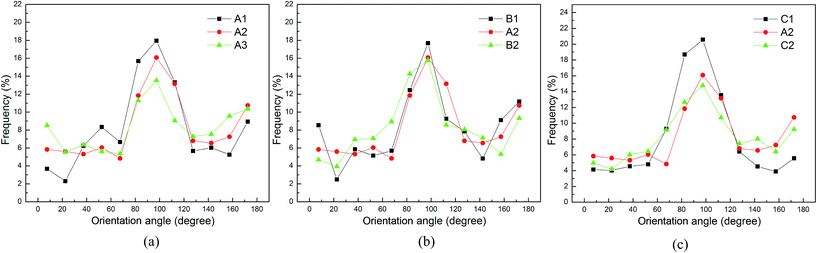

Fig. 5 ODF of samples affected by various parameters: punch frequency (a), needle penetration depth (b) and punch times (c).

The fiber ODFs estimated using the HT method for samples with various punch frequencies are compared in Fig. 5a. The predominant orientation of the fibers is in the MD (90°), because the fabric consists of a parallel-laid web. From A1 to A2 to A3, a decrease in fiber distribution in the MD is observed with an increase in punch frequency. A higher punch frequency means more fibers are transformed by the barbed needle, and the orientation distribution of these migration fibers changes in both the horizontal and vertical directions. With the increase in the relative number of fibers in the other direction and the fiber entanglement, the mechanical anisotropy of the fabric is improved. However, if the punch frequency is too great then serious fiber damage, and even fiber breakage, can occur. Therefore, optimum punch frequency is important for needle punched nonwoven fabrics to achieve excellent mechanical properties.

Fig. 5b shows the fiber distribution of samples tested with varying needle penetration depth. The three solid lines show a similar tendency; most of the fibers are oriented in the MD. When the punch depth increases from 6 mm to 9 mm and 12 mm, A2 and B2 have a more uniform distribution compared with B1, but any observed variation is not very prominent. Increasing the punch penetration depth contributes to fiber migration, because more barbs take part in displacing fibers and the displacement of fibers increases. As a result, reorientation of fibers occurs in the process of fiber migration. However, the number of fibers captured by a barb is a certain value. The influence of punch penetration depth on fiber distribution is limited. On the other hand, extreme punch penetration depth will permit the barbs to carry the fibers to migrate from the bottom of the fabric and cause fiber damage and even breakage.

The influence of punch times on the fiber distribution measured with the HT method is shown in Fig. 5c. The ratio of fibers oriented in the MD for A2 and C2 is significantly decreased compared to C1. This is because a higher punch density is obtained with an increase in punch times, which means more fibers have the chance to reorient per unit area of fabric. However, the variation in the orientation distribution from C1 to A2 is more significant than the variation from A2 to C2. In the process of preparation of A2 from C1, there are fewer initial fiber bundles in C1 and the fibers can be reoriented with less effort. In the process of preparation of C2 based on A2, the number of bonds between the fibers within A2 is more than the number of entanglement points within C1, which makes fiber migration more difficult. When the punch times exceed a certain value, there will be holes within the fabric due to extreme punch density. Therefore, when the other parameters are fixed, the optimum punch time is very important to obtain the desired fabrics and avoid energy waste.

The effect of the process parameters on the straight fiber length

The mechanics and attrition of the bulk structure are influenced by the entanglement of fibers within nonwovens, in the form of regulating the mechanical interactions between the fibers.³¹ In the process of entanglement, fibers with barbed needles transferred from the horizontal to the vertical plane, meanwhile, the fibers bend, curl and one part of them remains in the thickness direction. This results in a reduction in the straight segment fiber length within the horizontal plane, therefore the straight segment fiber length can give an indication of the fiber entanglement. The shorter the most frequent fiber length, the higher the degree of fiber entanglement.³² Based on this principle, the influence of various parameters on fiber entanglement within needle punched nonwovens was evaluated using image analysis by the HT method.

The distribution of the straight segment fiber length within samples with various process parameters, obtained from the HT method, is shown in Fig. 6. In this figure, a fiber length index is employed, as the values on the horizontal axis do not show the actual fiber length but are proportional to the fiber length. Fig. 6a shows the straight segment fiber lengths of samples with different punch frequencies. The straight segment fiber lengths corresponding to the maximum ratio for A1, A2 and A3 are 240–270, 180–210 and 120–150 respectively. On the whole, with increasing punch frequency, the straight segment fiber length decreases. While keeping other parameters constant, a higher punch frequency results in the formation of more fiber bundles per unit area, and therefore more fibers taking part in migration remain in the thickness direction. As a result, the degree of fiber entanglement increases, and the strength of the fabric is improved. However, higher punch frequency adversely affects the structure of the web, which results in serious damage to the fibers (as shown in Fig. 3a) and weakens the strength of the fabrics. As listed in Table 2, in order to obtain excellent tensile properties, an optimum punch frequency of 240 strokes per min was selected.

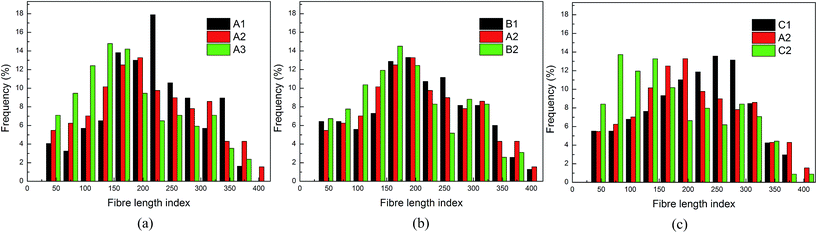Fig. 6 Distribution of straight segment of fiber length: affected by punch frequency (a), needle penetration depth (b) and punch times (c).

Fig. 6b shows the influence of needle penetration depth on the straight segment fiber distribution. We found that the values of length corresponding to the maximum ratio for B1 and B2 are both in the range from 150 to 210, however, the value of short straight segment fiber length increases slightly from B1 to A2 to B2. Increasing the needle penetration depth enhances the migration distance of fibers in the thickness direction of the fabric, which decreases the straight segment fiber length. However, the fibers carried in the horizontal plane by a barbed needle are limited without significant variation as the punch penetration depth increases. At the same time, the fibers recognized by the HT method are mostly in the plane of the web. Therefore, the distribution of straight segment fiber length with different punch penetration depths, assessed by the HT method, has only a slight variation.

The influence of punch times on the distribution of straight segment fiber length is shown in Fig. 6c. As the length distribution for these fibers verifies, the straight segment length of the fibers decreases significantly from C1 to A2 to C2, as indicated by the length index. It can be concluded that increasing the punch times of the fabric decreases the length of the fiber straight segments or enhances the entanglement of fibers within the web. With increasing punch times, the punch density increases and more fibers transform from the horizontal to the vertical plane. These fibers bend, curl and one part of them remains in the thickness direction, which enhances the fiber entanglement and decreases the straight segment fiber length within the horizontal plane of the web. When combining the influence of fiber entanglement and fiber damage, the breaking strength of the fabric increases from C1 to A2 and reduces from A2 to C2 as listed in Table 2. Therefore, a punch time of 2 is the appropriate option here.

Conclusions

Image analysis by Hough transform was used to investigate the arrangement of fibers within needle punched nonwovens, based on preoxidized polyacrylonitrile, prepared using various process parameters. The fiber orientation distribution and straight segment fiber length as affected by punch frequency, needle penetration depth and punch times were evaluated. With an increase in punch frequency and punch times, the quantity of fibers oriented in the MD decreases significantly, and the influence of needle penetration depth on fiber orientation distribution was limited. These parameters have the same influence on the straight segment fiber length; the length decreases with an increase in these parameters.

The breaking strength of nonwoven fabrics and actual fiber length within the fabrics were measured using ordinary experiments. Combining the results of experimental and image analyses, optimum process parameters were obtained: punch frequency of 240 strokes per min, needle penetration depth of 9 mm and punch times of 2. Although there are some deficiencies, for example the fiber orientation distribution in the thickness direction has not been investigated, this study is helpful to understand the influence of processing on the microstructure of nonwovens and to select optimum parameters for preparation of the fabrics.

Acknowledgements

This work was supported by the Natural Science Foundation of China (No. 51206122), and the Tianjin Research Program of Application Foundation and Advanced Technology (15JCQNJC06300; 13JCYBJC37900).

References

1. F. Farukh, E. Demirci, B. Sabuncuoglu, M. Acar, B. Pourdeyhimi and V. V. Silberschmidt, Comput. Mater. Sci., 2014, 94, 8–16.
2. E. Demirci, M. Acar, B. Pourdeyhimi and V. V. Silberschmidt, Comput. Mater. Sci., 2012, 52, 157–163.
3. F. Farukh, E. Demirci, M. Acar, B. Pourdeyhimi and V. V. Silberschmidt, J. Mater. Sci., 2013, 48, 2334–2345.
4. S. H. S. Yousfani, R. H. Gong and I. Porat, Polym. Polym. Compos., 2015, 23, 351.
5. K. Dharshika, F. Javad, G. Sanjeev, M. Spinks and G. Wallace, RSC Adv., 2016, 6, 73203–73209.
6. N. Prorokova, V. Istratkin, T. Kumeeva, S. Vavilova, A. Kharitonov and V. Bouznik, RSC Adv., 2015, 5, 44545–44549.
7. F. Farukh, E. Demirci, B. Sabuncuoglu, M. Acar, B. Pourdeyhimi and V. V. Silberschmidt, Composites, Part B, 2015, 68, 327–335.
8. E. Ghassemieh, M. Acar and H. Versteeg, Proc. Inst. Mech. Eng., Part L, 2002, 216, 199–207.
9. S. H. S. Yousfani, R. H. Gong and I. Porat, Fibres Text. East. Eur., 2012, 91, 61–67.
10. B. Pourdeyhimi and R. Ramanathan, Text. Res. J., 1996, 66, 747–753.
11. R. H. Gong and A. Newton, J. Text. Inst., Part 1, 1996, 87, 371–388.
12. B. Pourdeyhimi and R. Dent, Text. Res. J., 1997, 67, 181–187.
13. A. A. Jeddi, H. S. Kim and B. Pourdeyhimi, Int. Nonwovens J., 2001, 10, 10–16.
14. X. Gao and L. Wang, Autex Res. J., 2015, 15, 48–53.
15. B. Pourdeyhimi, R. Dent and H. Davis, Text. Res. J., 1997, 67, 143–151.
16. M. Tunak, J. Antoch, J. Kula and J. Chvojka, Text. Res. J., 2014, 84, 989–1006.
17. E. Demirci, Mechanical behaviour of thermally bonded bicomponent fibre nonwovens: experimental analysis and numerical modelling, Loughborough University, 2011.
18. J. Chang, M. He, H. Niu, G. Sui and D. Wu, Polymer, 2016, 89, 102–111.
19. E. N. Sabet, P. Nourpanah and S. Arbab, Polymer, 2016, 90, 138–146.
20. B. Pourdeyhimi and H. S. Kim, Text. Res. J., 2002, 72, 803–809.
21. G. Jiang, X. Wang, Z. Wang and H. Liu, Comput. Electron. Agr., 2016, 123, 211–223.
22. M. Fatan, M. R. Daliri and A. Mohammad Shahri, Measurement, 2016, 91, 309–317.
23. Y. Wang and G. Cheng, Appl. Surf. Sci., 2016, 366, 9–18.
24. Y. Cha, K. You and W. Choi, Autom. Construct., 2016, 71, 181–188.
25. H. Benoudnine, A. Meche, M. Keche, A. Ouamri and M. S. Woolfson, Inf. Sci., 2016, 337–338, 82–92.
26. B. Xu and Y. Ling, Text. Res. J., 1997, 67, 563.
27. F. Martínez-Hergueta, A. Ridruejo, C. González and J. LLorca, Int. J. Solids Struct., 2015, 64–65, 120–131.
28. M. Miao, Text. Res. J., 2004, 74, 394–398.
29. M. Miao, H. E. Glassey and M. Rastogi, Text. Res. J., 2004, 74, 485–490.
30. R. Wang, B. Xu and C. Li, Text. Res. J., 2014, 84, 115–124.
31. S. Grishanov, M. Tausif and S. J. Russell, Compos. Sci. Technol., 2012, 72, 1318–1323.
32. S. Grishanov, M. Tausif and S. J. Russell, Compos. Sci. Technol., 2012, 72, 1331–1337.

---