DOI:
10.1039/C6RA25478K
(Paper)
RSC Adv., 2017,
7, 642-650
Spirooxazine molecular switches with nonlinear optical responses as selective cation sensors†
Received
20th October 2016
, Accepted 14th November 2016
First published on 3rd January 2017
Abstract
Spirooxazine, a photochromic material, can transform into metallic open-form merocyanine by molecular switching, giving rise to large contrasts in its second-order nonlinear optical (NLO) properties. The switching properties are particularly large when various metal ions (Li+, Na+, K+, Mg2+, Ca2+, Fe2+, Zn2+, and Ag+) are introduced, as evidenced by density functional theory calculations, which show that the spirooxazine undergoes a pronounced change in geometry accompanied by formation of a larger π-conjugated system. The resultant merocyanine derivatives have 10–21-fold higher static second-order NLO responses. Spirooxazine can therefore be used as a powerful and multi-use detection tool. The large first hyperpolarizability (βtot) is shown to rely on the alkaline earth metal, causing βtot values to increase nearly 21-fold, as evidenced by the larger charge distribution, lower transition energy, and separate distribution of first hyperpolarizability density. In contrast, variation of βtot in the Fe2+ derivative is not obvious, owing to stronger complexation, a larger amount of charge transferred from the napthoxazine moiety to the metal, and the reduction in N⋯O distance between the ligand heads. Therefore, spiropyran-to-merocyanine molecular switching can be used to distinguish alkaline earth metals and determine the efficiency of cation detection.
1. Introduction
Cation detection techniques are of extensive interest because of their widespread application in various fields, including biology, chemistry, clinical biochemistry, and environmental sciences.1,2 Conventional cation detection techniques are based on changes in light absorption, which results in color changes or fluorescence induction/modification. Spirooxazine (SP) responds to different external stimuli, such as light,3,4 temperature,5,6 and metal ions, to undergo reversible structural interconversion accompanied by changes in its photophysical properties. Therefore, it is of interest in optoelectronic applications to optical memories with data storage,7–9 molecular switches,10–14 and metal ion detection.15–17 In particular, the introduction of different metal ions causes the closed-form spirooxazine to transform into the open-form metallic merocyanine (MC*Mn+), which is always accompanied by a major change in geometric structure or π-electron conjugation, resulting in a significant switching effect in nonlinear optical response properties.18
Spirooxazines have been utilized extensively in the development of optical probes and molecular switches because their molecular architecture is easily tuned. Previous studies, which focused on coupling the changes in electronic structure and open-ring reaction mechanism of spirooxazine, have allowed an in-depth understanding of its optical properties in metal ion detection. A systematic study of highly sensitive and selective metal ion detection through optical signals using a spirooxazine derivative has been reported.19–29 As spirooxazine and its derivatives have strong fluorescence signals, complexes of spirooxazine and transition metal cations (Fe2+, Zn2+, and Ag+) have been fully reported at the molecular level.19,20 Recently, Huang et al. reported that spirooxazine combined with earth metal cations (Mg2+ and Ca2+) can show the superior metallochromic properties.19,21 Using the same rationale, alkali metals (Li+, Na+, and K+) with spirooxazine were calculated to produce similar molecular switches. In this work, we demonstrate that selective cation recognition can be performed using molecular NLO switches. Indeed, this property is associated with the important first hyperpolarizability (βtot) contrast, when the merocyanine form complexes a series of alkaline, alkaline earth, and transition metal cations. In addition, the large NLO contrast is demonstrated to depend strongly on the nature of the metal, providing selective cation sensing.
2. Computational details
Geometry optimizations were carried out using the B3LYP30,31 functional as implemented in the Gaussian 09W32 program. The 6-31G(d) basis set and the LanL2DZ effective core potential (ECP) basis set for transition metal cations (Fe2+, Zn2+, and Ag+) were applied to the complexes studied. The B3LYP functional, a combination of Becke's three-parameter hybrid exchange functional and the Lee–Yang–Parr correlation functional, has been widely used in geometrical optimizations.33–35 Harmonic vibrational frequency calculations were used to confirm that the optimized structures were minima, as characterized by positive vibrational frequencies.
The total first hyperpolarizabilities, βtot, for the studied complexes are defined as:
| |
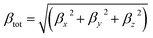 | (1) |
where
βi is defined as:
| |
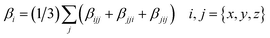 | (2) |
Choosing an appropriate method for the evolution of hyperpolarizability is crucial for hyperpolarizability calculations. High-level ab initio methods, such as the second-order Møller–Plesset perturbation method (MP2), coupled cluster methods (CCSD, CCSD(T), or even higher CCSD(T)) are known to be generally reliable for calculating molecular system hyperpolarizabilities.36 However, the high scaling order of the ab initio methods requires tremendous computational resources with increasing system size.37 Therefore, density functional theory (DFT) offers an attractive alternative to the demanding high-level ab initio methods. Four functionals, the BHandHLYP hybrid exchange–correlation functional, the M06-2X functional with a high percentage of HF exchange, and two long-range corrected functionals, CAM-B3LYP and ωB97XD, were chosen to check that our calculations were consistent.38,39 Moreover, studies have shown that basis sets must be chosen with due consideration of the calculation of optical properties, especially in hyperpolarizability calculations.40,41 Therefore, five Pople's basis sets (6-31+G(d), 6-31++G(d), 6-31+G(d,p), 6-31++G(d,p), and 6-311++G(d,p)) were chosen to evaluate the effect of the basis set. Due to the high computational cost, MC*Ca2+ was chosen to assess the basis set effects at the CAM-B3LYP level in this work.
In order to further explain the second-order NLO behaviors of this series of complexes, time-dependent density functional theory (TD-DFT) is a useful tool for computing linear and nonlinear molecular properties, because of its desirable compromise between computational efficiency and accuracy.42,43 The ωB97XD functional was found to be suitable for large π-systems.44 Therefore, the absorption spectra of complexes were simulated using the ωB97XD functional with the 6-31+G(d) basis set (LanL2DZ ECP basis set for transition metal ions).
All DFT and TD-DFT calculations were carried out using the Gaussian 09W program package, with the results analyzed by Multiwfn 3.3.8 software.45
3. Results and discussion
3.1 Molecular structures
The photochromic molecules in this study originate from the combination of metal ions with spirooxazine, which can be converted into the corresponding open-form merocyanine after the introduction of the metal ions (Scheme 1). The geometric structures of the studied complexes were optimized without any symmetry constraint at the B3LYP/6-31G(d)/LanL2DZ level. Typically, the closed spirooxazine consists of an indoline fragment and a napthoxazine moiety, which are kept almost orthogonal by a chiral “spiro” carbon atom. When metal ions are added, two isolated π-conjugated portions in the spirooxazine become extensively conjugated as a large coplanar structure (MC*Mn+). The O1–N1–C1–C2 dihedral angle of SP was shown to be 7.7°, while that of MC*Ca2+ was 92.6°. Unlike other derivatives, the Ca2+ cation lead to C1, C2, and C3 atoms becoming out of the plane (C1–C2–C3–Ca2+ dihedral angle of 46.0°), suggesting that it caused the largest structural distortion. The O1–C2 bond length of the SP was 1.428 Å, which was very close to the corresponding value (1.454 Å) previously reported by Sahoo et al.,20 suggesting that the geometrical calculations were reliable. Selected bond lengths and dihedral angles are listed in Table 1. The O1–N1 bond length of SP was found to be 2.825 Å (Table 1). In the metal cation derivatives, the O1–N1 distances became smaller (ranging from 2.549 to 2.798 Å), which was easily explained by the metal cations having strong interactions with napthoxazine. Moreover, calculation results showed that metal ions were located near the center of the coplanar structure in the complexes, but slightly closer to the O side, probably because of the stronger interaction of O⋯Mn+ relative to N⋯Mn+. In these complexes, the distances between the different metal ions and the oxygen and nitrogen atoms were 1.792–2.422 Å and 1.924–3.886 Å, respectively. These data not only revealed strong O⋯Mn+ and N⋯Mn+ charge transfer interactions, but also indicated the metal ion location in the complexes. The bond length alternation (BLA) value, defined as the absolute value of the difference between the average length of single and double bonds, is a quantitative tool to evaluate the degree of π-conjugation in a molecule with conjugated bonds. Smaller BLA values imply greater π-conjugation in the system. Compared with monovalent cations, complexation with divalent cations sharply decreased the BLA value of the napthoxazine moiety (∼0.001 Å vs. ∼0.056 Å, as shown in Table 1), indicating greater π-conjugation in the system and further demonstrating that the two isolated π-conjugated parts in spirooxazine can become extensively conjugated upon the introduction of metal ions, which is associated with large hyperpolarizability NLO responses.
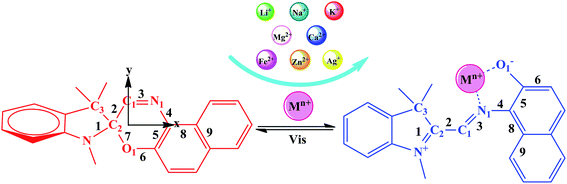 |
| | Scheme 1 Equilibrium between the spiropyran form and the cation-complexed merocyanine form. | |
Table 1 Important geometrical parameters and NBO charges of metal cations at the B3LYP/6-31G(d)/LanL2DZ level
| Compound |
Mn+–O1 (Å) |
Mn+–N1 (Å) |
O1–N1 (Å) |
Anglea (°) |
Angleb (°) |
Qc (M) |
BLAd (Å) |
| O1–N1–C1–C2 dihedral angle. C1–C2–C3–M dihedral angle. Natural bond orbital (NBO)46,47 charge on the metal atom in e. Bond length alternation (BLA) in the conjugated bridge between the indoline and napthoxazine rings, defined as BLA = |(R1 + R3 + R8)/3 − (R2 + R4 + R9)/3| (Scheme 1). |
| SP |
— |
— |
2.825 |
−7.7 |
— |
— |
0.056 |
| MC*Li+ |
1.792 |
2.022 |
2.670 |
−37.4 |
4.2 |
0.78 |
0.013 |
| MC*Na+ |
2.123 |
2.482 |
2.752 |
−60.8 |
3.9 |
0.89 |
0.022 |
| MC*K+ |
2.422 |
3.886 |
2.706 |
−39.9 |
2.6 |
0.96 |
0.020 |
| MC*Mg2+ |
1.877 |
2.059 |
2.686 |
−32.9 |
6.9 |
1.59 |
0.001 |
| MC*Ca2+ |
2.179 |
2.449 |
2.701 |
−92.6 |
46.0 |
1.83 |
0.005 |
| MC*Fe2+ |
1.789 |
1.924 |
2.549 |
−37.1 |
−3.0 |
0.84 |
0.017 |
| MC*Zn2+ |
1.888 |
2.032 |
2.728 |
−37.9 |
6.5 |
1.47 |
0.003 |
| MC*Ag+ |
2.209 |
2.452 |
2.798 |
−70.3 |
4.3 |
0.77 |
0.017 |
3.2 NBO analysis
The NBO charges of the metal cations are listed in Table 1. For the alkali and alkaline-earth metal cation derivatives (Li+, Na+, K+, Mg2+, and Ca2+), the metal charges decreased slowly with respect to the free metal cations. However, for transition metal cation compounds, the metal charge decreased moderately for Zn2+ and Ag+, but significantly for Fe2+. This large decrease was attributed to stronger Fe2+ complexation with the napthoxazine moiety, as evidenced by analysis of the NBO second-order interaction energies, which provide a further interpretation of the stabilizing effect of the metal ions, as calculated using the following equation:| |
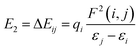 | (3) |
where qi is the donor orbital occupancy, εi and εj are the diagonal elements (orbital energies) of the Fock matrix, and F(i,j) is the off-diagonal NBO Fock matrix element. The stabilization energy, E2, indicates the strength of donor–acceptor interactions, as summarized in Table S1.† The calculated results showed that the interaction energies, E2, of most MC*Mn+ species were mainly attributed to the lone pair electrons (LP) of oxygen atoms and partial nitrogen atoms, and the LP* (one-center valence antibonding lone pair) of the metal cations (Li+, Na+, K+, Mg2+, Ca2+, and Ag+). Interactions between the lone pair electrons of the electron-donating oxygen atom and the LP* orbitals of Mn+ were much stronger than those between the nitrogen atom lone pairs and the Mn+LP*, except for compounds containing metal cations with strong interactions with oxygen and nitrogen atoms (Fe2+ and Zn2+), as indicated by their stabilization energies, E2 (Table S1†). Larger stabilization interaction energies, E2, are known to cause stronger interactions between the bonds.48–52 Therefore, the results suggested that Fe2+ complexation was stronger, which was in good agreement with the reduced N⋯O distance between the ligand heads (from 2.825 Å in uncomplexed merocyanine to 2.549 Å in the Fe2+ complex). Furthermore, the E2 value would increase with decreasing metal center charge. As shown in Tables 1 and S1,† the calculated E2 values increased in the order MC*K+ < MC*Na+ < MC*Li+ < MC*Ag+ for monovalent metal complexes and MC*Ca2+ < MC*Mg2+ < MC*Zn2+ < MC*Fe2+ for divalent metal complexes. Meanwhile, the charge on the metal was in the order MC*K+ < MC*Na+ < MC*Li+ < MC*Ag+ for monovalent metal complexes and MC*Ca2+ < MC*Mg2+ < MC*Zn2+ < MC*Fe2+ for divalent metal complexes.
3.3 First hyperpolarizability
Quantum chemistry calculations can aid understanding of the relationship between molecular structure and NLO properties, and prescreen molecules with large NLO responses.53–55 As no experimental or theoretical βtot values were available for the studied compounds, a comparative discussion of the results obtained using different DFT methods (see Table 3) was useful. Here, four DFT functionals (CAM-B3LYP, BHandHLYP, M06-2X, and ωB97XD), were used to assess the effect of DFT functionals on the first hyperpolarizability. Notably, the β value of the four functionals varied within a small margin for SP and the monovalent metal complexes (Table S2† and Fig. 1). However, BHandHLYP can give relatively large β values, while M06-2X underestimates β values, which seem to be comparable with the CAM-B3LYP result, providing a consistent first hyperpolarizability picture with respect to the method ωB97XD for divalent metal complexes. Moreover, recent studies show that the first hyperpolarizabilities predicted by CAM-B3LYP are similar to those obtained by MP2.56–58 Therefore, we used the CAM-B3LYP results as an example to assess the multistate second-order NLO behaviors of the complexes studied. Moreover, five Pople's basis sets (6-31+G(d), 6-31++G(d), 6-31+G(d,p), 6-31++G(d,p), and 6-311++G(d,p)) were chosen to evaluate the effect of the basis set at the CAM-B3LYP level for MC*Ca2+ (Table S3†). Compared with the 6-31+G(d) basis set, using the slightly extended basis set with an added p polarization function led to a slight decrease in βx, resulting in a smaller βtot. Likewise, using the more diffuse 6-31++G(d) basis set, βx decreased slightly, along with an increase in βz values. However, for the triple split valence basis set 6-311++G(d,p), adding diffuse and polarization functions resulted in an overestimation of βx, βy, βz, and βtot values from their 6-31+G(d) values. Therefore, we used only the 6-31+G(d) basis set as an example to shed light on changes in the first hyperpolarizabilities of the complexes studied (except for transition metals). The solvent effect is known to be important for first hyperpolarizability calculations. As typical examples, βtot values for SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+ were calculated using the different functionals (CAM-B3LYP, BHandHLYP, M06-2X, and ωB97XD) and basis sets (6-31+G(d) and LanL2DZ), via the PCM model, which simulated the solvent effect (with methanol as the solvent). We chose methanol as the solvent because it was used in related experiments. The results are listed in Table S4,† and clearly show that the βtot values in methanol solvent are larger than those in the gas phase, but variation tendencies remaining the same, with βtot values 10–21 times higher after the metal ions were added. The regularity of the βtot values remained the same in gas-phase and methanol-solvent conditions. The calculation in the gas phase can be proved to be reasonable. Therefore, we used the gas phase results to discuss the second-order NLO behaviors of the complexes studied.
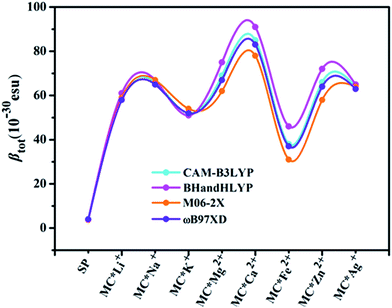 |
| | Fig. 1 Relationships between complex βtot values computed at various levels of theory. | |
The calculated first hyperpolarizability (βtot) values of the studied compounds at the 6-31+G(d) (LanL2DZ basis set for the transition metal ion) level are given in Table 3. For these compounds, the origin of the Cartesian coordinate system was located in the middle of the C1–C2 bond in the metal complexes (Fig. 2), and in the xy-plane with the central C1–O1 bonds, and x-axis along with napthoxazine moiety in SP (Scheme 1). Before discussing the first hyperpolarizabilities, it is worth studying the dipole moments. The dipole moments of the metal cation complexes were obviously larger than that of SP. This meant that the complexation of SP with metal cations significantly enhanced the dipole moment, due to the strong positive charge of the metal cation. The principal component of dipole moment was μy for all the compounds studied (except for MC*Li+, for which it was μx) and its sign was positive. The orientation of the dipole moment remained in the positive direction of the y-axis and was aligned with the center of indoline and naphthoxazine in the metal axis (Fig. 2). The size of the dipole moment and the positive metal cation charge separation was clearly implied by the total electrostatic potentials. As typical examples, the total electrostatic potentials of SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+ are plotted in Fig. 3. As shown, the important region of positive charge is the metal cation fragment. In contrast, the net negative charge is mostly located on the oxygen atom of the naphthoxazine fragment. This charge distribution led to large dipole moments in the complexes studied.
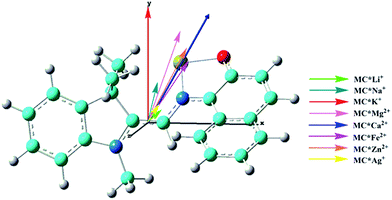 |
| | Fig. 2 Components of dipole moment (scale = 0.5) of the metal cation complexes MC*Mn+. Carbon (light blue), hydrogen (white), nitrogen (blue), oxygen (red), and the cation (yellow). | |
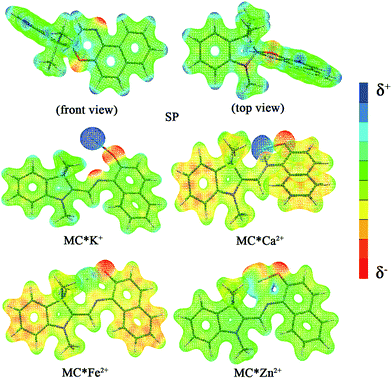 |
| | Fig. 3 Electrostatic potentials of SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+. | |
As mentioned above, the separation of charges is large, inevitably leading to a large first hyperpolarizability. For SP, the calculated βtot value was only 4.1 × 10−30 esu. With the introduction of metal ions, prominent reinforcement of second-order NLO responses was obtained with enhanced βtot values (38.4 × 10−30 esu for MC*Fe2+ and 84.6 × 10−30 esu for MC*Ca2+), which were about 10–21 times larger than that of SP. Consequently, these improved βtot values for MC*Mn+ were also due to the formation of larger π-conjugated system with the aid of metal ions, which, as is mentioned previously regarding BLA values, also play a vital and predominant role in the selection of metal cations. Therefore, SP can be used for selective sensing or NLO-based detection of cations.
For all compounds, the βx component was dominant (except for SP and MC*Fe2+, for which βy was dominant) in describing the βtot responses, compared with βy and βz components, suggesting that, during polarization, electronic charge transfer is expected along the x-axis. However, intramolecular charge transfer of naphthoxazine along the y-axis occurs in SP, and a small amount of charge transfer from the naphthoxazine fragment to metal remains in MC*Fe2+.
We also examined the spatial contributions of different molecular regions to the static first hyperpolarizability using the hyperpolarizability density59,60 in the finite field (FF). As is well known, the dipole moment μ(![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ) can be Taylor expanded in powers of the external field,
) can be Taylor expanded in powers of the external field, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) , as
, as
| |
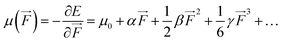 | (4) |
Similarly, Taylor expansion of the electron density function
ρ(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
,
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif)
) can also be conducted as
| |
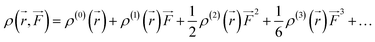 | (5) |
From
eqn (4) and
(5), static
β can thus be expressed as
| |
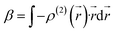 | (6) |
where
| |
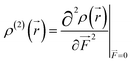 | (7) |
This second-order derivative of electron density with respect to the applied electric field is referred to as the
β density. In this study, we confine our attention to the
β density
ρ(2)(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
)(
ρ(2)xx(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
)) corresponding to
βxxx, which is the most crucial component of
β in the metal cation complexes, except for MC*Fe
2+ (
Table 2). In this section, we focus on the MC*Ca
2+ complex because it has electronic distributions similar to those of MC*Li
+, MC*Na
+, MC*K
+, MC*Mg
2+, MC*Zn
2+, and MC*Ag
+ along the
x-axis. Moreover,
ρ(2)yy(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) is related to
βyyy and is the most significant component for SP and MC*Fe
2+. These
ρ(2)xx(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) and
ρ(2)yy(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
) can be calculated at each spatial point in discretized space using the following second-order numerical differentiation formulas:
| |
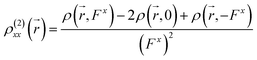 | (8) |
| |
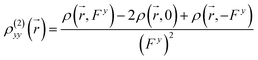 | (9) |
where
ρ(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
,
Fx) or
ρ(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
,
Fy) represent the electron density at spatial point
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif)
in the presence of electric field
Fx or
Fy, respectively. The applied electric fields along the
x-axis and
y-axis were 0.003 a.u. The electron densities over a three-dimensional grid of points were evaluated using the CAM-B3LYP functional with 6-31+G(d) (LanL2DZ for transition metal ion) from the Gaussian 09 program package.
Table 2 Dipole moments (Debye), individual components of first hyperpolarizabilities (a.u.), and total first hyperpolarizabilities (10−30 esu) computed at the CAM-B3LYP/6-31+G(d)/LanL2DZ level of theory
| Compound |
μx |
μy |
μtot |
βx |
βy |
βz |
βtot |
| SP |
−0.26 |
−0.67 |
0.77 |
0.5 |
−3.9 |
−1.0 |
4.0 |
| MC*Li+ |
1.25 |
1.03 |
1.62 |
−50.0 |
−31.9 |
1.4 |
59.3 |
| MC*Na+ |
0.83 |
3.54 |
3.67 |
−58.2 |
−30.9 |
5.5 |
66.1 |
| MC*K+ |
−0.07 |
10.56 |
10.57 |
−41.3 |
−31.8 |
3.1 |
52.3 |
| MC*Mg2+ |
2.96 |
8.11 |
8.67 |
−55.9 |
−39.5 |
6.5 |
68.7 |
| MC*Ca2+ |
4.39 |
8.64 |
12.11 |
−75.3 |
−33.8 |
18.9 |
84.6 |
| MC*Fe2+ |
3.66 |
5.28 |
6.52 |
−20.0 |
−32.8 |
0.3 |
38.4 |
| MC*Zn2+ |
3.60 |
6.52 |
7.45 |
−50.6 |
−41.6 |
6.1 |
65.8 |
| MC*Ag+ |
1.07 |
1.68 |
2.14 |
−53.4 |
−34.0 |
4.6 |
63.5 |
In this work, the visualized results of the −xρ(2)xx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) function, together with βxxx values of the studied MC*Ca2+ system, and the −yρ(2)yy(
) function, together with βxxx values of the studied MC*Ca2+ system, and the −yρ(2)yy(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) function, together with βyyy values of the studied SP and MC*Fe2+ systems, at the CAM-B3LYP/6-31G(d)/LanL2DZ level, are illustrated in Fig. 4. The total magnitudes of βxxx and βyyy are decomposed into positive (yellow) and negative (blue) parts. For SP, negative contributions were primarily distributed on the indoline side, compared with the sparse positive contributions distributed on the naphthoxazine side. It was not surprising that SP provided a rather small negative βyyy value (−3.9 × 10−30 esu). In contrast, relatively large negative contributions were present on the naphthoxazine side in MC*Fe2+. MC*Ca2+ contained remarkably large negative contributions, principally distributed in the naphthoxazine fragment and the inner regions of the indoline fragment, and, hence, gave a considerably large negative βxxx value (−75.3 × 10−30 esu).
) function, together with βyyy values of the studied SP and MC*Fe2+ systems, at the CAM-B3LYP/6-31G(d)/LanL2DZ level, are illustrated in Fig. 4. The total magnitudes of βxxx and βyyy are decomposed into positive (yellow) and negative (blue) parts. For SP, negative contributions were primarily distributed on the indoline side, compared with the sparse positive contributions distributed on the naphthoxazine side. It was not surprising that SP provided a rather small negative βyyy value (−3.9 × 10−30 esu). In contrast, relatively large negative contributions were present on the naphthoxazine side in MC*Fe2+. MC*Ca2+ contained remarkably large negative contributions, principally distributed in the naphthoxazine fragment and the inner regions of the indoline fragment, and, hence, gave a considerably large negative βxxx value (−75.3 × 10−30 esu).
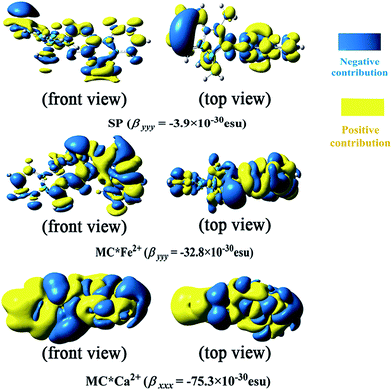 |
| | Fig. 4 Electronic density (isovalue = 7) of first hyperpolarizability at the CAM-B3LYP/6-31+G(d)/LanL2DZ level. | |
3.4 TDDFT studies
To understand the first hyperpolarizability values, TD-DFT calculations of the studied complexes were carried out at the ωB97XD/6-31+G(d)/LanL2DZ level. In SP, the napthoxazine moiety serving as an electron donor contained the majority of occupied molecular orbitals. The orthogonality of the indoline and napthoxazine moieties led to little overlap between the orbital pairs, resulting in the generation of a weak CT transition between the napthoxazine moieties. Meanwhile, the transition energy of SP was rather large (5.53 eV), as observed via electron density difference plots (Fig. 5). For MC*Fe2+, the crucial excited state was formed by the orbits of the HOMO−1 → LUMO and HOMO → LUMO+1 transitions. The HOMO and HOMO−1 were found to be localized on the whole merocyanine molecule and napthoxazine unit, respectively, while the LUMO and LUMO+1 were localized on the metal center and napthoxazine unit, respectively. A partial area of overlap between these transitions would generate a charge transfer from the napthoxazine unit to the metal center, and thus this excited state contained the ligand-to-metal charge-transfer (LMCT) transition. From the electron density difference plot of MC*Fe2+, we also noted that there were some π–π* and π–d contributions, and slightly weak CT transitions over the MC*Fe2+. However, for MC*K+, MC*Ca2+, and MC*Zn2+, there were no contributions from these molecular orbitals to the metal center. These first transitions were dominated by HOMO-to-LUMO singly excited electronic configurations, and were assigned as π–π* transitions displaying better charge transfer character from the indoline to the napthoxazine moiety (see Fig. 6). It was also noted that the direction of charge transfer in the coplanar MC series (MC*K+, MC*Ca2+, and MC*Zn2+) was along the x-axis, inevitably resulting in negative βx values. Furthermore, these complexes with larger π-conjugation, lower excited energy, and stronger oscillator strength might be promising for generating a large increase in static first hyperpolarizability.
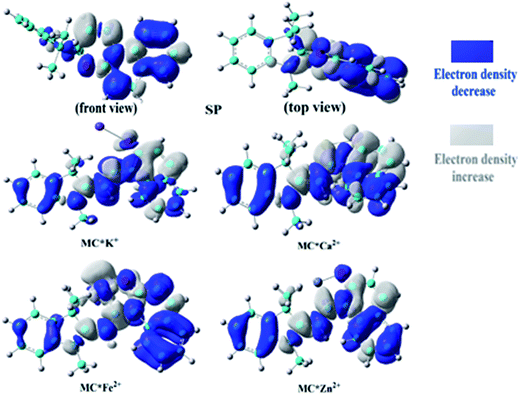 |
| | Fig. 5 Electron density differences in SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+ from the ground state to the crucial excited state, calculated at the ωB97XD/6-31+G(d)/LanL2DZ level. | |
 |
| | Fig. 6 Molecular orbitals involved in the main excited states contributing to the βtot values. | |
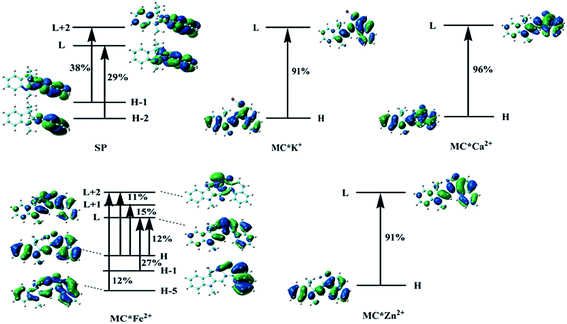
Molecular NLO properties are closely related to electronic absorption characteristics. Therefore, the static first hyperpolarizability can be elucidated from the electronic absorption characteristics using the two-level model established by Oudar and Chemla,61,62 with relevant parameters shown in Table 3 and visualized in Fig. 7. The ΔE values of crucial transition states that made that largest contribution to the hyperpolarizabilities are listed in Table 3. The ΔE values increased in the order MC*Ca2+ (2.01 eV) < MC*Zn2+ (2.11 eV) < MC*Fe2+ (2.37 eV) < MC*K+ (2.53 eV) < SP (5.53 eV). However, the ΔE value of MC*K+ was larger than that of MC*Fe2+, indicating that the sequence of βtot values could not be determined only in terms of ΔE values. Therefore, we focused on another factor controlling βtot values, namely, oscillator strength. Intriguingly, the oscillator strength of MC*Fe2+ was particularly small, which was mainly attributed to charge transfer from the napthoxazine unit to the metal center of HOMO−1 and LUMO (because the major CT at this state arises from HOMO−1-to-LUMO). The f/ΔE3 values of the SP and the metal cation complex varied after the introduction of metal ions, to give the following order SP (0.0032) < MC*Fe2+ (0.0196) < MC*K+ (0.0397) < MC*Zn2+ (0.0648) < MC*Ca2+ (0.0723). The βtot values of these complexes were in good agreement.
Table 3 Energies, oscillator strengths, and major contributions of SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+ at the ωB97XD/6-31+G(d)/LanL2DZ level
| Compound |
State |
Wavelength (nm) |
ΔE (eV) |
Oscillator (fos) |
MO transition |
| H = HOMO, H−1 = HOMO−1, L = LUMO, L+1 = LUMO+1, etc. |
| SP |
S8 |
224 |
5.53 |
0.55 |
Ha−2 → L (29%), H−1 → L+2 (38%) |
| MC*K+ |
S1 |
490 |
2.53 |
0.64 |
H → L (91%) |
| MC*Ca2+ |
S1 |
615 |
2.01 |
0.60 |
H → L (96%) |
| MC*Fe2+ |
S7 |
523 |
2.37 |
0.26 |
H−5 → L+2 (12%) |
| H−1 → L (27%) |
| H → L (12%) |
| H → L+1 (15%) |
| H → L+2 (11%) |
| MC*Zn2+ |
S1 |
587 |
2.11 |
0.61 |
H → L (91%) |
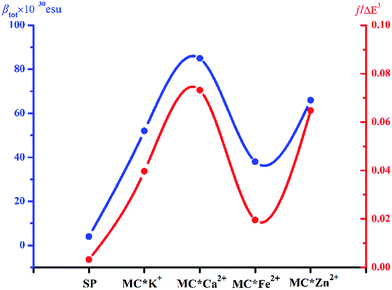 |
| | Fig. 7 Relationship between the βtot values (blue curve) and corresponding f/ΔE3 values (red curve) of complexes SP, MC*K+, MC*Ca2+, MC*Fe2+, and MC*Zn2+. | |
4. Conclusions
Prototypical SP and MC complexes containing various metals (MC*Ca2+, MC*Mg2+, MC*Fe2+, MC*Zn2+, and MC*Ag+) were synthesized, and DFT calculations were employed, along with three additional reference MC compounds (MC*Li+, MC*Na+ and MC*K+), to theoretically investigate electronic absorption characteristics and predict static second-order NLO responses. Using various functionals, DFT calculations showed that the introduction of various metals into spirooxazine can drastically enhance second-order NLO switches. For the large conjugated MC*Ca2+ compound, the first hyperpolarizability (βtot) increased significantly, due to the obvious charge transfer from the indoline unit to the napthoxazine unit, large charge distribution, and lower transition energy. In contrast, the βtot values of the Fe2+ derivative increased moderately due to the larger amount of charge transferred from the napthoxazine unit to the metal and the shorter N⋯O distance between the ligand heads. Consequently, the performances of both prototypical and additional metal compounds in this study showed them to be excellent candidates for optical molecular switches, and further verified the ability of spirooxazine/merocyanine systems to selectively detect alkali, alkaline earth, and transition metal cations.
Acknowledgements
The authors gratefully acknowledge financial support from the “12th Five-Year” Science and Technology Research Project of the Education Department of Jilin Province ([2016] 494) and the National Natural Science Foundation of China (No. 21173035).
References
- B. Valeur and I. Leray, Coord. Chem. Rev., 2000, 205, 3–40 CrossRef CAS.
- A. P. de Silva, T. P. Vance, M. E. S. West and G. D. Wright, Org. Biomol. Chem., 2008, 6, 2468–2481 CAS.
- S. Houbrechts, K. Clays, A. Persoons, Z. Pikramenou and J. M. Lehn, Chem. Phys. Lett., 1996, 258, 485–489 CrossRef CAS.
- M. Sliwa, S. Letard, I. Malfant, M. Nierlich, P. G. Lacroix, T. Asahi, H. Masuhara, P. Yu and K. Nakatani, Chem. Mater., 2005, 17, 4727–4735 CrossRef CAS.
- Y. C. Liang, A. S. Dvornikov and P. M. Rentzepis, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 8109–8112 CrossRef CAS PubMed.
- N. S. Makarov, A. Rebane, M. Drobizhev, H. Wolleb and H. J. Spahni, J. Opt. Soc. Am. B, 2007, 24, 1874–1885 CrossRef CAS.
- S. Kawata and Y. Kawata, Chem. Rev., 2000, 100, 1777–1788 CrossRef CAS PubMed.
- M. Q. Zhu, L. Y. Zhu, J. J. Han, W. W. Wu, J. K. Hurst and A. D. Q. Li, J. Am. Chem. Soc., 2006, 128, 4303–4309 CrossRef CAS PubMed.
- W. Yuan, L. Sun, W. Huang, H. Tang, Y. Wen, G. Jiang, L. Jiang, Y. Song, H. Tian and D. B. Zhu, Adv. Mater., 2005, 17, 156–160 CrossRef CAS.
- H. Tian, B. Qin, R. X. Yao, X. L. Zhao and S. J. Yang, Adv. Mater., 2003, 15, 2104–2107 CrossRef CAS.
- J. L. Bahr, G. Kodis, L. de la Garza, S. Lin, A. L. Moore, T. A. Moore and D. Gust, J. Am. Chem. Soc., 2001, 123, 7124–7133 CrossRef CAS PubMed.
- G. Berkovic, V. Krongauz and V. Weiss, Chem. Rev., 2000, 100, 1741–1753 CrossRef CAS PubMed.
- J. A. Delaire and K. Nakatani, Chem. Rev., 2000, 100, 1817–1845 CrossRef CAS PubMed.
- N. Y. C. Chu, Can. J. Chem., 1983, 61, 300 CrossRef CAS.
- L. R. Dalton, P. A. Sullivan and D. H. Bale, Chem. Rev., 2010, 110, 25–55 CrossRef CAS PubMed.
- K. A. Green, M. P. Cifuentes, T. C. Corkery, M. Samoc and M. G. Humphrey, Angew. Chem., Int. Ed., 2009, 48, 7867–7870 CrossRef CAS PubMed.
- K. Szaciłowski, Chem. Rev., 2008, 108, 3481–3548 CrossRef PubMed.
- N. Tamai and H. Miyasaka, Chem. Rev., 2000, 100, 1875–1890 CrossRef CAS PubMed.
- Y. Huang, F. Li, C. Ye, M. Qin, W. Ran and Y. Song, Sci. Rep., 2015, 5, 9724 CrossRef CAS PubMed.
- P. R. Sahoo and S. Kumar, Sens. Actuators, B, 2016, 226, 548–552 CrossRef CAS.
- H. Nishikiori, R. Sasai, N. Arai and K. Takaoki, Chem. Lett., 2000, 10, 1142 CrossRef.
- J. Ren and H. Tian, Sensors, 2007, 7, 3166–3178 CrossRef CAS.
- M. Natali and S. Giordani, Org. Biomol. Chem., 2012, 10, 1162–1171 CAS.
- M. I. Zakharova, C. Coudret, V. Pimienta, J. C. Micheau, S. Delbaere, G. Vermeersch, A. V. Metelitsa, N. Voloshin and V. I. Minkin, Photochem. Photobiol. Sci., 2010, 9, 199–207 CAS.
- K. H. Fries, J. D. Driskell, S. Samanta and J. Locklin, Anal. Chem., 2010, 82, 3306–3314 CrossRef CAS PubMed.
- K. H. Fries, J. D. Driskell, G. R. Sheppard and J. Locklin, Langmuir, 2011, 27, 12253–12260 CrossRef CAS PubMed.
- H. Nishikiori, T. Takamura, S. Shimamura and T. Fujii, J. Photochem. Photobiol., A, 2011, 222, 236–240 CrossRef CAS.
- M. I. Zakharova, V. Pimienta, A. V. Metelitsa, V. I. Minkin and J. C. Micheaua, Russ. Chem. Bull., 2009, 58, 1329–1337 CrossRef CAS.
- H. Zhang, X. Guo, J. Hui, S. Hu, W. Xu and D. Zhu, Nano Lett., 2011, 11, 4939 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al., Gaussian 09W, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- D. Herebian, K. E. Wieghardt and F. Neese, J. Am. Chem. Soc., 2003, 125, 10997–11005 CrossRef CAS PubMed.
- D. Espa, L. Pilia, L. Marchio, F. Artizzu, A. Serpe, M. L. Mercuri, D. Simao, M. Almeida, M. Pizzotti, F. Tessore and P. Deplano, Dalton Trans., 2012, 41, 3485–3493 RSC.
- W. Y. Wang, L. Wang, N. N. Ma, C. L. Zhu and Y. Q. Qiu, Dalton Trans., 2015, 44, 10078–10088 RSC.
- W. Chen, Z. R. Li, D. Wu, R. Y. Li and C. C. Sun, J. Phys. Chem. B, 2004, 109, 601–608 CrossRef PubMed.
- J. Y. Yuan, Y. Z. Yuan, X. H. Tian, J. Y. Sun and Y. Ge, J. Phys. Chem. C, 2016, 120, 14840–14853 CAS.
- M. Torrent-Sucarrat, J. M. Anglada and J. M. Luis, J. Chem. Theory Comput., 2011, 7, 3935–3943 CrossRef CAS PubMed.
- L. Wang, W. Y. Wang, X. Y. Fang, C. L. Zhu and Y. Q. Qiu, RSC Adv., 2015, 5, 79783–79791 RSC.
- C. G. Liu, M. L. Gao, S. Liu and D. F. Zhang, RSC Adv., 2015, 5, 42311–42321 RSC.
- W. Y. Wang, Y. H. Kan, L. Wang, S. L. Sun and Y. Q. Qiu, J. Phys. Chem. C, 2014, 118, 28746–28756 CAS.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 302, 375–382 CrossRef CAS.
- U. Salzner and A. Aydin, J. Chem. Theory Comput., 2011, 7, 2568–2583 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 10, 27211–27218 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- K. Paredes-Gil and P. Jaque, Chem. Phys. Lett., 2015, 618, 174–181 CrossRef CAS.
- M. Iwaoka, H. Komatsu, T. Katsuda and S. Tomoda, J. Am. Chem. Soc., 2004, 126, 5309–5317 CrossRef CAS PubMed.
- K. J. de Almeida, T. C. Ramalho, J. L. Neto, R. T. Santiago, V. C. Felicissimo and H. A. Duarte, Organometallics, 2013, 32, 989–999 CrossRef CAS.
- D. Chakraborty and P. K. Chattaraj, Phys. Chem. Chem. Phys., 2016, 18, 18811–18827 RSC.
- Y. Xia, Z. J. Qi, Y. M. Sun, D. Cao, H. H. Ling, F. Yang and X. Ji, J. Mol. Model., 2014, 20, 2243 CrossRef PubMed.
- L. Wang, W. Y. Wang, Y. Q. Qiu and H. Z. Lu, J. Phys. Chem. C, 2015, 119, 24965–24975 CAS.
- B. Champagne, A. Plaquet, J. L. Pozzo, V. Rodriguez and F. Castet, J. Am. Chem. Soc., 2012, 134, 8101–8103 CrossRef CAS PubMed.
- H. Q. Wang, W. Y. Wang, X. Y. Fang, L. Wang, C. L. Zhu, Z. Z. Chen, H. Chen and Y. Q. Qiu, J. Mol. Graphics Modell., 2016, 67, 111–118 CrossRef CAS PubMed.
- K. Y. Suponitsky, S. Tafur and A. E. Masunov, J. Chem. Phys., 2008, 129, 044109 CrossRef PubMed.
- B. Champagne, F. A. Bulat, W. T. Yang, S. Bonness and B. Kirtman, J. Chem. Phys., 2006, 125, 194114 CrossRef PubMed.
- K. Y. Suponitsky, Y. Liao and A. E. Masunov, J. Phys. Chem. A, 2009, 113, 10994–11002 CrossRef CAS PubMed.
- M. Nakano, S. Yamada and K. Yamaguchi, Chem. Phys. Lett., 1999, 306, 187–196 CrossRef CAS.
- S. Yamada, M. Nakano, I. Shigemoto and K. Yamaguchi, Chem. Phys. Lett., 1996, 254, 158–164 CrossRef CAS.
- J. L. Oudar, J. Chem. Phys., 1977, 67, 446–457 CrossRef CAS.
- J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664–2668 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25478k |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
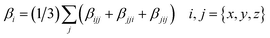
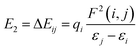

![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ) can be Taylor expanded in powers of the external field,
) can be Taylor expanded in powers of the external field, ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) , as
, as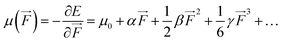
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,
,![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ) can also be conducted as
) can also be conducted as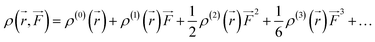
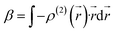
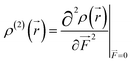
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )(ρ(2)xx(
)(ρ(2)xx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )) corresponding to βxxx, which is the most crucial component of β in the metal cation complexes, except for MC*Fe2+ (Table 2). In this section, we focus on the MC*Ca2+ complex because it has electronic distributions similar to those of MC*Li+, MC*Na+, MC*K+, MC*Mg2+, MC*Zn2+, and MC*Ag+ along the x-axis. Moreover, ρ(2)yy(
)) corresponding to βxxx, which is the most crucial component of β in the metal cation complexes, except for MC*Fe2+ (Table 2). In this section, we focus on the MC*Ca2+ complex because it has electronic distributions similar to those of MC*Li+, MC*Na+, MC*K+, MC*Mg2+, MC*Zn2+, and MC*Ag+ along the x-axis. Moreover, ρ(2)yy(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is related to βyyy and is the most significant component for SP and MC*Fe2+. These ρ(2)xx(
) is related to βyyy and is the most significant component for SP and MC*Fe2+. These ρ(2)xx(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and ρ(2)yy(
) and ρ(2)yy(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) can be calculated at each spatial point in discretized space using the following second-order numerical differentiation formulas:
) can be calculated at each spatial point in discretized space using the following second-order numerical differentiation formulas: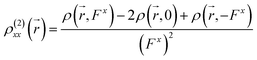
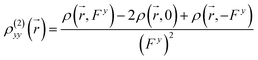
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Fx) or ρ(
,Fx) or ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,Fy) represent the electron density at spatial point
,Fy) represent the electron density at spatial point ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) in the presence of electric field Fx or Fy, respectively. The applied electric fields along the x-axis and y-axis were 0.003 a.u. The electron densities over a three-dimensional grid of points were evaluated using the CAM-B3LYP functional with 6-31+G(d) (LanL2DZ for transition metal ion) from the Gaussian 09 program package.
in the presence of electric field Fx or Fy, respectively. The applied electric fields along the x-axis and y-axis were 0.003 a.u. The electron densities over a three-dimensional grid of points were evaluated using the CAM-B3LYP functional with 6-31+G(d) (LanL2DZ for transition metal ion) from the Gaussian 09 program package.
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) function, together with βxxx values of the studied MC*Ca2+ system, and the −yρ(2)yy(
) function, together with βxxx values of the studied MC*Ca2+ system, and the −yρ(2)yy(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) function, together with βyyy values of the studied SP and MC*Fe2+ systems, at the CAM-B3LYP/6-31G(d)/LanL2DZ level, are illustrated in Fig. 4. The total magnitudes of βxxx and βyyy are decomposed into positive (yellow) and negative (blue) parts. For SP, negative contributions were primarily distributed on the indoline side, compared with the sparse positive contributions distributed on the naphthoxazine side. It was not surprising that SP provided a rather small negative βyyy value (−3.9 × 10−30 esu). In contrast, relatively large negative contributions were present on the naphthoxazine side in MC*Fe2+. MC*Ca2+ contained remarkably large negative contributions, principally distributed in the naphthoxazine fragment and the inner regions of the indoline fragment, and, hence, gave a considerably large negative βxxx value (−75.3 × 10−30 esu).
) function, together with βyyy values of the studied SP and MC*Fe2+ systems, at the CAM-B3LYP/6-31G(d)/LanL2DZ level, are illustrated in Fig. 4. The total magnitudes of βxxx and βyyy are decomposed into positive (yellow) and negative (blue) parts. For SP, negative contributions were primarily distributed on the indoline side, compared with the sparse positive contributions distributed on the naphthoxazine side. It was not surprising that SP provided a rather small negative βyyy value (−3.9 × 10−30 esu). In contrast, relatively large negative contributions were present on the naphthoxazine side in MC*Fe2+. MC*Ca2+ contained remarkably large negative contributions, principally distributed in the naphthoxazine fragment and the inner regions of the indoline fragment, and, hence, gave a considerably large negative βxxx value (−75.3 × 10−30 esu).






