High mechanical strength in Zn₄B₆O₁₃ with an unique sodalite-cage structure

Abstract

Recently, a borate crystal Zn₄B₆O₁₃ (ZBO) has been focused on since it exhibits novel isotropic near-zero thermal expansion behavior in a wide temperature range. In this work, the mechanical properties in ZBO are studied by high-pressure X-ray diffraction and first-principles calculations. It is found that ZBO possesses the highest mechanical hardness in all known borates whose mechanical properties have been measured. The very high mechanical strength in ZBO mainly originates from the resistance of strong Zn–O bonds to the rotation among BO₄ tetrahedra in the unique sodalite-cage structure. Moreover, ZBO shows relatively high mechanical resistance to the axial and shear stress and exhibits high optical transparence in the ultraviolet spectral region under high pressure. Benefitting from these good properties, ZBO may find potential applications in high-precision optical facilities used at extreme conditions under complex environments.

---

Introduction

Structural mechanical materials have attracted much research attention for centuries due to their crucial role in many scientific and technology fields, including aeronautics, architecture engineering, geological machines, medical apparatus, precise instruments, and so on.^1–3 In particular, materials with superior mechanical performances and good optical properties are widely applied in high-precision optical instruments, such as space telescopes, deep-sea cables and acoustic-optics devices.^4,5 Therefore, the exploration of these functional materials has become an advanced topic in materials science. It is well known that the borate crystals often exhibit good optical transmission in the ultraviolet (UV) spectral region, and quite a few good optical crystals have been discovered in this material system, e.g., nonlinear optical crystals β-BaB₂O₄ (BBO),⁶ LiB₃O₅ (LBO)⁷ and KBe₂BO₃F₂ (KBBF),⁸ and birefringent crystals Ca₃(BO₃)₂ (ref. 9 and 10) and Ba₂Mg(B₃O₆)₂ (ref. 11). The good optical properties in these borate crystals are originated from the boron–oxygen groups which are either triangle-shaped or tetrahedral-shaped.¹² In fact, the strong covalent interaction between boron and oxygen atoms can also result in the good mechanical properties. Owing to the rigid characteristic, the B–O groups mainly rotate with each other when experiencing pressure fluctuation.¹³ This pressure-responding mechanism would bring interesting mechanical behaviors in borates, as demonstrated by the discovery of anomalous negative compressibility in BiB₃O₆,^14,15 BPO₄ (ref. 16) and KBe₂BO₃F₂.¹⁷

Very recently, our group discovered rare isotropic near-zero thermal expansion over a wide temperature range from 13 to 270 K in the cubic borate crystal Zn₄B₆O₁₃ (ZBO).¹⁸ Phonon analysis based on first-principles calculations revealed that the low thermal expansion in ZBO is resulted from its unique [B₂₄O₄₈] sodalite cage structure fixed by the strong covalent Zn–O bonds. Meanwhile, this crystal exhibits high UV transparency down to the wavelength of 218 nm. All these observations demonstrated that this crystal may have important applications in the ultrahigh precision optical instruments especially those operated at low temperature environment. Since the effect of temperature action on materials usually could be considered as the reverse to that of pressure,¹⁹ it is anticipated that the unique structural feature in ZBO is very likely to generate some interesting mechanical behaviors. However, till now the mechanical properties which have been measured in ZBO were just the elastic constants by ultrasonic resonance under low pressures with the resonance frequencies in the range from 5–40 MHz.²⁰ In this work, we investigate the mechanical property of ZBO in depth by high-pressure X-ray diffraction (XRD) experiments combined with first-principles calculations. Our study revealed that ZBO possesses very large bulk modulus, even comparable to that of α-Al₂O₃. Moreover, the other important mechanical performance indices for practical applications, including Young's modulus, Shear modulus and Poisson's ratio, are discussed. The variation of optical properties in ZBO under high-pressure is also studied.

Experimental and computational methods

Polycrystalline powder synthesis

Polycrystalline was synthesized through traditional solid-state techniques. Stoichiometric amounts of Zn(CH₃COO)₂·2H₂O and B₂O₃ were ground thoroughly, packed in a platinum crucible, then gradually heated to 800 °C and kept at that temperature in the air for 3 days with several intermittent grindings at 300 °C, 500 °C, 700 °C and 800 °C. The phase purity was confirmed by powder X-ray diffraction (Fig. S1†).

High-pressure X-ray diffraction

The high-pressure XRD experiments were performed at the 4W2 beam line of Beijing Synchrotron Radiation Facility (BSRF). The X-ray beam at the wavelength 0.6199 Å was focused into a 36 × 12 μm² spot using Kirkpatrick–Baez mirrors. The hydrostatic pressure was exerted by the systematic diamond anvil cells (DAC) with the culet diameter of 400 μm. The samples in well grinded powder were placed in a hole of about 100 μm diameter in a pre-indented stainless steel gasket with the thickness of 40 μm. The mixture of methanol and ethanol was adopted to act as the pressure-transmitting medium and ruby chips were mixed for pressure calibration by measuring the fluorescence shift as the function of pressure.²¹ The diffraction patterns were recorded by a Pilatus image plate and integrated with the FIT2D software package.²² The cell parameters under different pressure were refined by Lebail method²³ using general structure analysis system (GSAS) program.²⁴

First-principles calculation

Since ZBO possesses very large bulk modulus (>240 GPa) and the structural modification is very tiny with respect to hydrostatic pressure. So it is a great challenge to determine the very small modification of bond lengths and angles, which is a common problem for powder XRD studies. We have tried to elongate the X-ray exposure time at each pressure point (more than 15 minutes per point), but it was still very difficult to accurately determine the structural modification in ZBO partly due to the weak beam intensity in Beijing Synchrotron Radiation Facility (a first-generation synchrotron radiation facility). At the same time, it is expected that the modification of positions of boron atoms would be crucial to the response of ZBO to external pressure. However, boron is among the lightest element and their positions are difficult to be determined by powder XRD, because most of the diffraction intensity of ZBO is concentrated on the much heavier zinc atoms. Under this situation, the accurate first-principles calculations became a powerful and complementary tool to probe the mechanism of structural evolution in ZBO under high-pressure.

The mechanical properties in ZBO under high pressures were theoretically investigated by CASTEP,²⁵ a total energy package based on plane-wave pseudopotential density functional theory (DFT).²⁶ The functionals developed by Perdew, Burke and Ernzerhof (PBE) in generalized gradient approximation (GGA)^27,28 form were adopted to describe the exchange–correlation (XC) energy. Optimized norm-conserving pseudopotentials²⁹ in the Kleinman–Bylander form³⁰ for all the elements were used to model the effective interaction between atom cores and valence electrons. Zn 3d¹⁰4s², O 2s²2p⁴ and B 2s²2p¹ electrons were treated as valence electrons, which allows us to adopt a relatively small plane-wave basis set without compromising the computational accuracy. The kinetic energy cutoff of 660 eV and the Monkhorst–Pack³¹ k-point mesh spanning less than 0.03 Å⁻¹ were chosen. To account for the deviation between the experimental and theoretical data, the cell parameters were fixed at the experimental values in the atomic position optimizations.

The finite strain technology³² was adopted to calculate the elastic constants, which were determined by the second derivative of the ground energies with respect to the varied strains. For each strain the energy were optimized by the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme.³³ The convergence criteria for the structure optimization were set to 5.0 × 10⁻⁵ eV per atom, 0.1 eV Å⁻¹, 0.2 GPa and 5.0 × 10⁻³ Å for energy, maximum force, maximum stress and maximum displacement, respectively. After obtaining the calculated elastic constants, the analysis of Young's modulus, Shear modulus and Poisson's ratio were performed using EIAM program.³⁴ On the other hand, the energy band gaps in ZBO at various pressures were determined by hybridized PBE0 XC functionals.³⁵ Our previous studies have demonstrated that the theoretical band gaps predicted by this type of XC functionals are in very good agreement with experimental values for UV borates (with relative error less than 5%).^36,37

Results and discussion

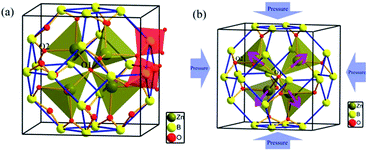
ZBO crystallizes in cubic space group I4̄3m and possesses an unique sodalite cage structure in borates.^38,39 As shown in Fig. 1a, in an unit cell 24 [BO₄] tetrahedra construct a closed [B₂₄O₄₈] truncated octahedron by sharing the corner oxygen atoms (O2 atoms), so forming the sodalite-cage. In each sodalite cage, four [ZnO₄] tetrahedra form a radial [Zn₄O₁₃] cluster by sharing the same oxygen atom at the center of the cage (O1 atom). The [B₂₄O₄₈] sodalite cage is fixed by relatively strong Zn–O bonds in the [Zn₄O₁₃] clusters.

Fig. 1 (a) The crystal structure of ZBO, (b) schematic of large bulk modulus in ZBO under pressure: the shrink of sodalite cage under pressure is resisted by [Zn₄O₁₃] cluster. Zinc, boron, and oxygen atoms are represented by taupe, yellow and red balls, and ZnO₄ and BO₄ group are represented by red and olivine tetrahedra, respectively.

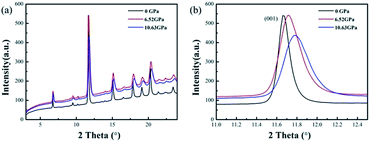
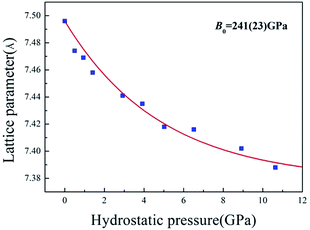
The high-pressure XRD experiments were performed on ZBO with the hydrostatic pressure ranged from 0 to 10.63 GPa. There is no new XRD peak appearing in the XRD spectra (see Fig. 2a, S2 and S3†), indicating that no phase-transition occurs during the pressure-exerting process. Although the peaks are broadened with the increasing pressure, the crystallinity is well kept in the whole pressure range up to 10.63 GPa, manifesting the high mechanical stability of ZBO. With the increase of pressure, all diffraction peaks gradually move to the higher angles (Fig. 2b shows the shift of the strongest (001) peak of sample as an example), which means that the unit cell shrinks three-dimensionally with respect to the pressure. The refined lattice parameters at various pressures are plotted in Fig. 3 (also in Fig. S4 and Table S1†). From 0 to 10.63 GPa, the volume only shrink about 3.5% and the bulk modulus fitted by the second-order Birch–Murnaghan method⁴⁰ is 241(23) GPa, slightly larger than the value (196 GPa) deduced from the elastic constants previously measured.²⁰

Fig. 2 (a) The XRD patterns and (b) diffraction peak (001) of ZBO at 0, 6.52 and 10.63 GPa.

Fig. 3 The variation of lattice parameter in ZBO as a function of applied hydrostatic pressure.

The value difference between this work and previous work is mainly attributed to the fact that the elastic constant measurements only considered the linear terms and ignored the nonlinear terms to the bulk modulus as the pressure increases. The high-pressure XRD data demonstrate that ZBO is very difficult to be compressed, and its rigidity under high pressure is consistent with the high mechanical hardness.¹⁸ The bulk modulus of ZBO is much larger than that of α-quartz (37 GPa of the Fd3̄m phase).⁴¹ ZBO exhibits the highest mechanical hardness in all known borate crystals whose mechanical properties have been measured. The high mechanical strength would be very beneficial to the practical applications of ZBO.

To investigate the microscopic mechanism of the high bulk modulus in ZBO, we performed first-principles simulations on the variation of the crystal structure as the hydrostatic pressure increase from 0 to 10.63 GPa. The structural analysis shows that the volume of ZBO unit cell is not directly related with [Zn₄O₁₃] cluster, but exclusively determined by the [B₂₄O₄₈] sodalite cage. Fig. 4 plots the variations of the bond lengths and angles in the cage structure with respect to the pressure (the data are also listed in Table S2†). When the pressure increases from 0 GPa to 10.63 GPa, the B–O bond lengths are slightly contracted by about 1.0% (from 1.472 Å to 1.457 Å), and the ∠B–O2–B angles are decreased by just about 0.7% (from 128.301° to 127.346°). Since the shape of sodalite-cage is tightly associated with the Zn–O2 bonds, we focus on Zn–O2 bonds to elaborate the mechanism of mechanical behavior in ZBO. The very tiny rotation among rigid BO₄ tetrahedra during the pressure rise is mainly attributed to the restricting effect by the inside [Zn₄O₁₃] cluster, due to the relatively strong covalent Zn–O interaction (the shrinkage of Zn–O2 bond is about 1.6%, from 1.979 Å to 1.948 Å). Therefore, it is the special sodalite-cage structure that results in the large bulk modulus in ZBO: the distortion of the [B₂₄O₄₈] cage with increasing pressure is hindered by the strong Zn–O bonds, as schematically depicted in Fig. 1b.

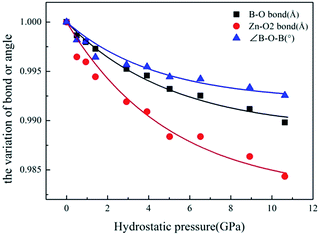Fig. 4 The relative variation of B–O bond length, Zn–O2 bond length and ∠B–O–B angles with respect to pressure.

Bulk modulus is very important to characterize the mechanical properties in a crystal, but it is not enough to just determine this parameter from the viewpoint of practical applications. In order to more comprehensively understand the elastic properties, the full elastic tensors of ZBO were calculated by the first-principles method. Under the cubic space group I4̄3m, ZBO has three independent elastic constants (C₁₁, C₁₂, C₄₄), and the mechanical stability criterion of C₄₄ > 0, C₁₁ > |C₁₂|, C₁₁ + 2C₁₂ > 0 (ref. 42) is satisfied. The calculated elastic constants are listed in Table 1, in very good agreement with the measured ones²⁰ with the relative error less than ∼5%. The excellence of the first-principles calculations ensures the good accuracy for the further determination and analysis on other mechanical properties in ZBO.

Table 1 The calculated and measured elastic constants (GPa)

Elastic constant	C11	C12	C44
Calculated	322.9	146.1	104.2
Measured^20	312.2(2)	137.6(4)	102.3(1)

---

The Young's modulus (E), Shear modulus (G), and Poisson's ratio (ν) of ZBO were also calculated by the first-principles calculations. The Young's modulus of ZBO (>230 GPa) are significantly larger than that of the α-quartz (72.95 GPa),⁴³ indicating the very high rigidity of ZBO to axial stress.

The 3D and 2D representations of the Young's modulus are shown in Fig. 5a and b, respectively. Clearly, the Young's modulus shows slight anisotropy in ZBO. The contours are distorted from the axial 〈001〉 directions to the body diagonal 〈111〉 directions: the Young's modulus has the minimum value of 231.88 GPa along the 〈001〉 directions, and it reaches the maximum value of 267.31 GPa along the 〈111〉 directions. This indicates that ZBO is more difficult to be stretched along the body diagonal directions than the axial directions. The orientational distribution difference of the Young's modulus mainly originates from the anisotropic spatial distribution of the [ZnO₄] groups in the crystal lattice. In the sodalite-cage, each of the four [ZnO₄] groups in the radial [Zn₄O₁₃] cluster is exactly aligned along one of the 〈111〉 directions (see Fig. 1b). The restriction of the [Zn₄O₁₃] cluster to the [B₂₄O₄₈] sodalite-cage thus make ZBO exhibit the largest mechanical strength along 〈111〉 directions.

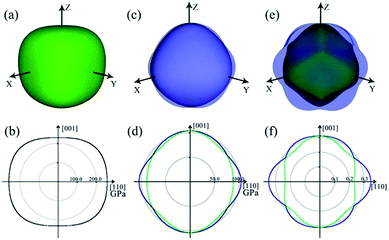Fig. 5 3D and 2D representations of Young's modulus E (a and b), shear modulus G (c and d) and Poisson's ratio ν (e and f) for ZBO. Color scheme: maximum (blue), minimum positive (green).

The 3D and 2D representation for the shear modulus of ZBO are shown in Fig. 5c and d, respectively. The maximum shear modulus (G) is 104.20 GPa along the 〈001〉 axial direction and the minimum shear modulus (G) is 88.40 GPa along the face diagonal 〈110〉 direction. The shear modulus of ZBO is also much larger than that of α-quartz (41 GPa). Thus, ZBO exhibits a high rigidity against structural deformation, so it would be convenient for industrial manufacture.

Moreover, the 3D and 2D representations of the Poisson's ratio (ν) for the ZBO crystal are shown in Fig. 5e and f, respectively. The Poisson's ratio of the crystal ZBO is maximized (ν = 0.35) when the stretching along the 〈110〉 directions induces the lateral contraction along 〈001〉 directions. However, it reaches the minimum (ν = 0.24) with the same loading conditions accompanied by a lateral contraction along the 〈1−10〉 directions. According to the Frantsevich's definition,⁴⁴ the materials with ν < 1/3 and ν > 1/3 are considered as the brittle and ductile materials, respectively. The Poisson's ratio of ZBO is located near the boundary (ν = 1/3), and hence ZBO may have good mechanical process ability, which is not very brittle and not very ductile.

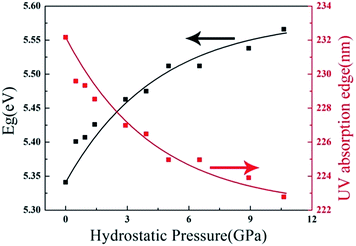
The above studies clearly demonstrate that ZBO has a very good mechanical property, which is very favorable to its practical applications in harsh environments. As ZBO exhibits high ultraviolet transparency at ambient pressure,¹⁸ one may inquire about the light-transmitting property in ZBO at the pressure-fluctuating environments. In order to answer this question, the variation of its energy band gap with respect to the applied hydrostatic pressure was theoretically determined by the first-principles calculations. The results show that the energy band gap in ZBO increases from 5.34 eV to 5.57 eV as the pressure increases from 0 to 10.63 GPa (Fig. 6). The detailed electronic structure analysis reveals that the contraction of chemical bonds responding to the applied pressure results in a stronger hybridization between the electronic states at the top of valence band (VB), which lowers the energy of the VB and enlarges the energy band gap in ZBO (see the discussion in Fig. S5†). Therefore, the high UV transparency in ZBO can be well kept when subjected to pressure fluctuation, which is very favourable to keep the performance stability at complex circumstances.

Fig. 6 The variation of energy band gap and optical absorption edge in ZBO as function of pressure.

Conclusion

The mechanical properties of ZBO were comprehensively investigated by the high-pressure XRD and first-principles calculations. The high-pressure XRD revealed that no phase-transition occurs in ZBO over wide pressure range from 0 to 10.63 GPa, manifesting the high mechanical stability. Meanwhile, ZBO exhibits a very large bulk modulus (even comparable to that of Al₂O₃) and the largest mechanical hardness in all known borate crystals, and hence it has a high rigidity to the large pressure fluctuation. First-principles calculations revealed that this is mainly due to the resistance of strong Zn–O bonds in the radial [Zn₄O₁₃] cluster to the rotation among [BO₄] tetrahedra in the [B₂₄O₄₈] sodalite cage. The studies on Young's modulus (E), shear modulus (G) and Poisson's ratios (ν) further confirmed that ZBO possesses very high mechanical strength. Furthermore, the high optical transmittance in the UV region in ZBO can be well kept under high pressure. Since ZBO has been demonstrated to have an isotropic near-zero thermal expansion behavior, the high mechanical strength combined with good transmitting property strongly suggests that this crystal would find many important applications in high-precision optical instrument operated at complex environments.

Acknowledgements

The authors acknowledge Dr Siyang Luo for useful discussion. This work is supported by the National Scientific Foundations of China (Grant 11474292), the Special Foundation of the Director of Technical Institute of Physics and Chemistry (TIPC), and China “863” project (No. 2015AA034203).

References

1. R. H. Wentorf, R. C. Devries and F. P. Bundy, Science, 1980, 208, 873–880.
2. M. Bhatnagar and B. J. Baliga, IEEE Trans. Electron Devices, 1993, 40, 645–655.
3. I. A. Ibrahim, F. A. Mohamed and E. J. Lavernia, J. Mater. Sci., 1991, 26, 1137–1156.
4. L. S. Wohn, B. Joshi, Z. Y. Fu and K. Niihara, Korean J. Mater. Res., 2010, 20, 444–449.
5. J. Sun, X. Cui, C. Zhang, C. Zhang, R. Ding and Y. Xu, J. Mater. Chem. C, 2015, 3, 7187–7194.
6. C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. Sin., Ser. B, 1985, 28, 235–243.
7. C. T. Chen, Y. C. Wu, A. D. Jiang, B. C. Wu, G. M. You, R. K. Li and S. J. Lin, J. Opt. Soc. Am. B, 1989, 6, 616–621.
8. C. T. Chen, Y. B. Wang, Y. N. Xia, B. C. Wu, D. Y. Tang, K. C. Wu, W. R. Zeng, L. H. Yu and L. F. Mei, J. Appl. Phys., 1995, 77, 2268–2272.
9. X. Lu, Z. Y. You, J. F. Li, Z. J. Zhu, G. H. Jia, Y. Wang, B. C. Wu and C. Y. Tu, J. Cryst. Growth, 2005, 281, 416–425.
10. A. Kato and H. Rikukawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 041101.
11. R. K. Li and Y. Ma, CrystEngComm, 2012, 14, 5421–5424.
12. Y. N. Xia, C. T. Chen, D. Y. Tang and B. C. Wu, Adv. Mater., 1995, 7, 79–81.
13. R. M. Hazen, R. T. Downs and C. T. Prewitt, Rev. Mineral. Geochem., 2000, 41, 1–33.
14. B. Teng, Z. P. Wang, H. D. Jiang, X. F. Cheng, H. Liu, X. B. Hu, S. M. Dong, J. Y. Wang and Z. S. Shao, J. Appl. Phys., 2002, 91, 3618–3620.
15. L. Kang, X. Jiang, S. Luo, P. Gong, W. Li, X. Wu, Y. Li, X. Li, C. Chen and Z. Lin, Sci. Rep., 2015, 5, 13432.
16. J. Haines, C. Chateau, J. M. Leger, C. Bogicevic, S. Hull, D. D. Klug and J. S. Tse, Phys. Rev. Lett., 2003, 91, 015503.
17. X. Jiang, S. Luo, L. Kang, P. Gong, W. Yao, H. Huang, W. Li, R. Huang, W. Wang, Y. Li, X. Li, X. Wu, P. Lu, L. Li, C. Chen and Z. Lin, Adv. Mater., 2015, 27, 4851–4857.
18. X. Jiang, M. S. Molokeev, P. Gong, Y. Yang, W. Wang, S. Wang, S. Wu, Y. Wang, R. Huang, L. Li, Y. Wu, X. Xing and Z. Lin, Adv. Mater., 2016, 28, 7936–7940.
19. A. L. Goodwin, D. A. Keen and M. G. Tucker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18708–18713.
20. L. Bohaty, S. Haussuhl, J. Liebertz and S. Stahr, Z. Kristallogr., 1982, 161, 157–158.
21. H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., 1986, 91, 4673–4676.
22. J. Hammersley, Fit2d User Manual, 1996.
23. A. Lebail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452.
24. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
25. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
26. M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097.
27. D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569.
28. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079.
29. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230.
30. L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428.
31. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
32. V. B. Deyirmenjian, V. Heine, M. C. Payne, V. Milman, R. M. LyndenBell and M. W. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15191–15207.
33. B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240.
34. A. Marmier, Z. A. D. Lethbridge, R. I. Walton, C. W. Smith, S. C. Parker and K. E. Evans, Comput. Phys. Commun., 2010, 181, 2102–2115.
35. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
36. R. He, H. Huang, L. Kang, W. Yao, X. Jiang, Z. Lin, J. Qin and C. Chen, Appl. Phys. Lett., 2013, 102, 231904.
37. Z. S. Lin, L. Kang, T. Zheng, R. He, H. Huang and C. T. Chen, Comput. Mater. Sci., 2012, 60, 99–104.
38. P. Smith, L. Rivoir and S. Garciablanco, An. R. Soc. Esp. Fis. Quim., Ser. A, 1961, 57, 263.
39. P. Smithverdier and S. Garciablanco, J. Appl. Phys., 1980, 151, 175–177.
40. O. Ermakova, J. Lopez-Solano, R. Minikayev, S. Carlson, A. Kaminska, M. Glowacki, M. Berkowski, A. Mujica, A. Munoz and W. Paszkowicz, Acta Crystallogr., Sect. B: Struct. Sci., 2014, 70, 533–538.
41. P. Hess, J. Appl. Phys., 2012, 111, 051101.
42. J. F. Nye, Physical Properties of Crystals, Clarendon press, Oxford, 1985.
43. W. Martienssen and H. Warlimont, Handbook Springer of Condensed Matter and Materials Data, 2004.
44. I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1982.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1519591–1519600. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra25752f

---