Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxygen adsorption and CO desorption behavior of B- and N-doped vacancy defected nuclear graphite by DFT study
Juan Liua,
Tongxiang Liang *b,
Chen Wang*a and
Wenzheng Laic
*b,
Chen Wang*a and
Wenzheng Laic
aState Key Laboratory of New Ceramics and Fine Processing, Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing, 100084, China. E-mail: 9120160073@jxust.edu.cn
bSchool of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou, 341000, China
cSchool of Materials Science and Engineering, Tsinghua University, Beijing, 100084, China
First published on 13th January 2017
Abstract
Oxygen adsorption and desorption of gasification products are two factors that influence graphite oxidation behavior. Whether the catalytic or inhibiting effect occurs after B and N doping still remains controversial. In this paper, the activation energies for the adsorption of oxygen and desorption of CO on a modified nuclear graphite surface, combining vacancy and dopants, are studied by density functional theory (DFT). Vacancy defected graphite is more sensitive to O2 adsorption because of the unpaired electron on the dangling carbon atom. However, substitution with B or N makes the adsorption more difficult, since substituting C by a B or N atom eliminates the effect of the unpaired electron, which means that these dopants can be applied to improve oxidation resistance of nuclear graphite or other carbon materials. Desorption calculation of adsorbed radical (C–O) indicates that substitutional B or N atoms in graphite facilitate CO desorption, in this respect B or N dopants play a role of catalyst for graphite oxidation. Introduction of dopants such as B, N results in weaker O2 adsorption capability on vacancy defected graphite while they help desorption of oxidation products such as CO. Both the inhibiting and catalytic effects of these dopants are an example of the compensation effect.
Introduction
Nuclear graphite is the key material for High Temperature Gas Cooled Reactor (HTR) cores and fuel elements. Knowledge of its oxidative behavior is of importance in design and operation procedures. Graphite oxidation reaction is influenced by many factors including microstructure, temperature, oxygen partial pressure as well as surface defects. All these factors ultimately lead to different levels of O2 adsorption and CO/CO2 desorption.Defect investigations in graphite and related materials have attracted considerable attention by the desire to investigate irradiation damage taking place in a HTR.1 Vacancy defects are proved to be more prevalent in irradiated materials and are considered as the primary defects in irradiated graphite or nanotubes.2 The effect of neutron irradiation in nuclear graphite leads to the change of volume, mechanical and thermal physical properties, meanwhile to the happening of radiolytic oxidation, all these changes are associated with the defect of graphite. Reactive species such as oxygen can easily react with defective graphite surfaces thus resulting in enhanced carbon erosion yields. DFT study shows that adsorption energy of O2 on monovacancy defected graphite is approximately 10 times stronger than that on defect-free graphite surface.3 Theoretical and experimental investigations have proved that O2 tends to physically adsorb on perfect graphite surface.4,5 It is the extensive conjugate π bonding among carbon atoms that makes the graphite sheet chemically inert. However, the displacement of C atoms in graphite layers by neutron irradiation causes electronic redistribution and behaves as active sites that promote dissociation, transformation and activation of adsorbed gases.6,7 Besides oxygen, other gas molecule such as CO2 on monovacancy surface is also found to be more active than that on pure graphene layer.8 These studies suggest that graphite plane with vacancy defect is active enough to interact with reaction species.
Based on the reactivity of vacancy defected graphite, it is of significant importance to find a way to reduce oxidation. The use of boron as doping element for carbon-based materials has been proved to improve oxidation resistance. Previous studies have found that oxidation rate of graphite decreases 3–6 times owing to boron substitution.9,10 Boron is one electron less compared with carbon, and the substitution is expected to modify electronic and physicochemical properties.11,12 Boron substitution has also been applied in Li ion batteries to improve carbon's capacity.13 Furthermore, boron has also been introduced in carbon nanotubes and diamond electrodes to modify electronic structure as well as electrochemical performance.14,15 Other impurity atoms (such as N, S, Al) are also applied into graphitic materials to affect sensitivity for gas adsorption.18 Peng et al. has investigated the improvement of sensor devices by substitutional doping of impurity N atoms into pure single-walled carbon nanotubes (SWCNTs). It is found that CNx nanotube is more efficient to detect toxic species than pristine CNTs probably because of the existence of highly reactive pyridine-like composition in tube walls.16,17
Improving oxidation resistance of nuclear graphite is critical to security operation of HTR reactor. Even though the observation of catalytic oxidation19,20 of boron at low concentration makes the role of substitutional boron more mysterious, we expect to understand the mechanism of B or N doping on the behavior of O2 adsorption and CO desorption. In the present study, the effect of substitutional boron and nitrogen on the structure and electronic states of vacancy defected graphite surface is investigated by using DFT method. Adsorption of O2 molecule on impurity doped systems is compared with that on un-doped one. Meanwhile, desorption of adsorbed radical for CO formation is also studied by nudged elastic band method.
Calculation methods
In the framework of Vienna ab initio simulation package (VASP) code, all calculations are carried out by using density functional theory (DFT) formalism.21 The application of projected augmented wave (PAW) method is performed.22 In the description of exchange-correlation term, Perdew–Burke–Ernzerhof (PBE) gradient corrected functional within the frame of generalized gradient approximation (GGA) is applied.23 An energy cutoff of 680 eV is set to a more accurate calculation to describe the valence electrons.24 During electronic relaxation, an energy convergence of 10−4 eV is set by employing blocked Davidson iteration scheme along with the residual minimization method with direct inversion in iterative subspace (RMMDIIS). In the ionic relaxations Hellmann–Feynman forces is minimized by the conjugate gradient method. Spin-polarization is considered in all calculations due to the presence of unpaired electrons in some of these systems.In our calculation basal plane is chosen because of its least reactive property than zigzag and armchair surfaces. A 4 × 2 × 1 supercell containing 32 atoms (without vacancy) is set within a single graphite layer. Periodic boundary condition is set in two spatial directions. The vacancy defected graphite is created by removing one carbon atom and then fully optimized. One layer model is used by the reason that van der Waals interactions between layers are relatively weaker than the planar bonding, and consequently the impact on the surface processes is not important.25,26 To further confirm the accuracy of one layer model, we have compared the vacancy formation energy, chemisorption energy of O2 and desorption energy barrier of CO on one layer and four layer vacancy defected graphite surfaces. The details are listed in Table 1. The energy values are almost the same for these two models. Therefore one layer model is selected in this work by computational resource limitation. The optimized lattice constants of the planar structure are a = b = 2.46 Å, that is agree with theoretical and experimental reports.27,28 Our supercell is working within a box in which three lattice vectors are perpendicular to each other. The graphite layers are separated to have a vacuum of ∼16 Å to avoid the influence of neighboring slabs although the fact that an 11 Å vacuum layer is large enough to reduce the periodic neighbor interaction.29,30 The same supercells are applied for the systems with O2 interaction as for the isolated graphite species. The k-point is set to 5 × 5 × 1 for structure optimization, which increases to 12 × 12 × 1 for more accurate electronic calculation including density of states (DOS) and charge density difference (CDD). All atoms in the supercell are relaxed to reach the equilibrium configurations, and the calculations of reaction energy barriers are performed by employing the nudged elastic band (NEB) method.
| Type | Ef_v (eV) | Eads_O2 (eV) | Edes_CO (eV) |
|---|---|---|---|
| 1 layer | 7.76 | −3.85 | 5.94 |
| 4 layer | 7.58 | −3.82 | 6.01 |
The adsorption energy during the interaction between oxygen molecule and graphite is defined by following formula:
| Eads = Egra+O2 − Egra − EO2 | (1) |
The charge density difference (CDD) is defined as:
| Δρ = ρ(graphite + O2) − ρ(graphite) − ρ(O2) | (2) |
Results and discussion
VG and B or N doped VG
First of all, the optimized geometries of bare vacancy-defected graphite (VG) are considered along with B or N dopant substituted vacancy-defected graphite (BVG and NVG). Following earlier work on the monovacancy structure, it is indicated that the reconstruction configuration gives a lower energy than the ideal symmetric one.3,31 As can be seen in Fig. 1(a), under a John–Teller distortion, the ideal symmetric vacancy tends to the configuration of bonding between two dangling atoms (C2 and C3) which lead to the formation of a pentagon and an enneagon. This distortion induces an energy lowering about 0.17 eV due to the in-plane and out-of-plane displacement. The value is consistent with the result by El-Barbary et al. indicating that the energy of the reconstructed structure is around 0.2 eV lower than that of the symmetric one.31 Therefore the reconstructed monovacancy structure is further considered in our work. The weak reconstructed bond between C2 and C3 atoms is 2.11 Å, shorter than that in the perfect graphite (2.46 Å). Moreover, the third dangling carbon atom C1 is displaced out of atomic layers by the distortion. One qualitative explanation of the out-of-plane displacement is that the paired electrons formed in the new bond tend to repel the electron on the third dangling atom. While an out-of-plane displacement is the easiest direction for movement.31 Furthermore, the vacancy-defected graphite (VG) exhibits a magnetic moment of 1.37 μB since the presence of the unpaired sp2 dangling bond. The value is in agreement with Faccio's report that the magnetic moment of monovacancy is 1.34 μB.32 In their results, the dangling sp2-orbital contributes with 1.0 μB and the rest of 0.34 μB comes from the unbalance between spin polarized π-orbitals. In Fig. 2(a), the unpaired electron is indicated by the unsymmetrical density of states (DOS) distribution near Fermi level. It points out clearly that the asymmetrical spin-up states in the valence band and spin-down states in conductive band are mainly contributed by the dangling carbon atom (C1). The large DOS overlap for C2 and C3 demonstrates the newly formed chemical bond.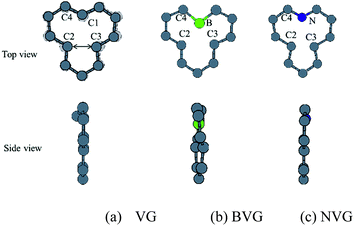 | ||
| Fig. 1 Relaxed structures of graphite with or without dopants. (a) Graphite with vacancy defect (VG), (b) boron doped and (c) nitrogen doped vacancy-defected graphite. | ||
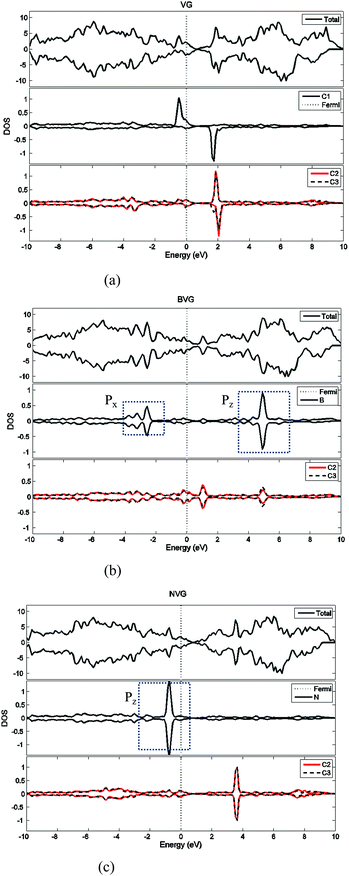 | ||
| Fig. 2 Density of state (DOS) analysis for (a) vacancy-defected graphite, (b) B-doped vacancy-defected graphite and (c) N-doped vacancy-defected graphite. | ||
For dopant defected graphite, a single impurity atom is inserted in the defect region. Three doping sites (C1, C2 and C4) are considered after taking into account the symmetry of the vacancy. It is found that C1 substitution exhibits lower energy and higher stability in comparison with C2 and C4 sites for B, N dopants. Therefore substitutions at C1 site are mainly considered in further study upon O2 adsorption. Fig. 1 shows the structures of B- and N-doped vacancy-defected graphite after optimization, named as BVG and NVG. For BVG, substitution of B causes small distortion of C2 and C3 atom and makes them move out of the original plane. The substitution in this case causes a larger B–C distance, which elongates from 1.37 Å in VG to 1.61 Å. Meanwhile, the distance between C2 and C3 is elongated from 2.11 Å in VG to 2.55 Å, while the distance between B–C2 is changed from 2.56 Å in VG to 2.16 Å. The structure modification is mainly contributed by the introduction of C–B bond. As we know, the covalent radius of boron (0.88 Å) is slightly larger than that of carbon (0.77 Å).33 A C–B bond cannot replace a C–C bond in equal length thus resulting in structure modification. In order to have a deeper insight into the effect of dopants in vacancy graphite (VG), the obtained DOS of impurity-doped graphite are also illustrated in Fig. 2. It is learned that the defected graphite types are metallic with a zero band gap which is different from perfect graphite.34 Substitution of B leads to more symmetrical DOS distribution near the Fermi level as performed in Fig. 2(b). This result is different from Zhou's work which gives the DOS for BVG with asymmetric disposition.35 In our opinion, the symmetrical DOS of BVG is more convincing. As we know, the existence of unpaired electron in VG causes asymmetrical spin-up and spin-down DOS. The valance electron configuration of B is 2s22p1, one electron less than C. Substituting a C atom located at the vacancy site by a B atom would eliminate the effect of the unpaired electron thus leading to symmetrical DOS. Faccio's work has also proved the symmetric DOS distribution by substitution of the dangling C atom.32 Large DOS overlap of C2 and C3 demonstrates the interaction of two carbon atoms. The BVG exhibited a slight magnetic moment of −0.002 μB.
In the case of N-doped VG (NVG), the bond length of N–C is shortened to 1.33 Å along with the distance between C2 and C3 (1.87 Å), which is shorter than that of VG (2.11 Å). The substitution of N makes all atoms locate in the graphene plane and no out-of-plane atomic displacement is discovered. According to Fig. 2(c), it shows that the DOS distribution for spin-up and spin-down are completely symmetric. Based on the valence bond theory, two N-2s electrons are pairing and the remaining three electrons named 2px, 2py and 2pz are unpaired. The newly formed C–C bond is attributed to the interaction of unpaired electrons in C2 and C3. Two unpaired electrons of N atom interact with neighbouring C atoms and the rest unpaired electron contributes to the π electron system, which results in the NVG presented non-magnetic state.36 In general, the dopants mostly affect the valence electrons around Fermi energy. Considering the symmetrical or asymmetrical distribution of DOS peaks near Fermi energy, we suspect the VG with B, N impurity are more inert than VG itself. The relationship between symmetrical property of DOS distribution and reactivity of graphite will be studied in detail in our next paper. In the present work, we anticipate that the introduction of dopants will improve oxidation resistance of graphite. In following sections, interaction of molecular oxygen with VG and dopant induced VG will be analysed.
Adsorption of O2 molecule on VG, BVG and NVG
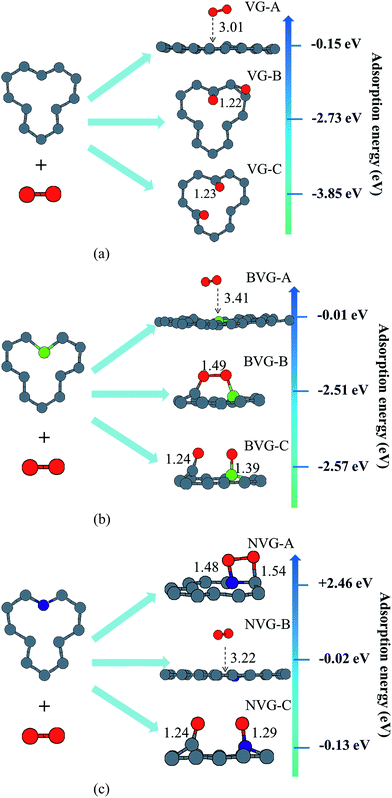
In this section, the adsorption of a O2 molecule on vacancy-defected graphite with and without B, N dopants are investigated. For each type of graphenes, we consider four possible adsorption sites, i.e. top site of C, B and N atom, on the top of the center of the vacancy, on the bridge site of C–C, B–C and N–C bond, and on the top of C-V (vacancy), B-V or N-V site, respectively. Different initial configurations are simulated and the total energies are calculated. As shown in Fig. 3, the fully relaxed structures and corresponding energies are listed for this three graphitic types. Three optimized geometries are found for each type. One is a physical adsorption structure and the others are chemisorbed configurations. For physical adsorption structures, O2 is away from graphite surface in a distance of more than 3 Å, and O–O bond keeps a length of 1.24 Å which is in accordance with the bond length of O2 molecule. Adsorption energies are −0.15 eV for VG, −0.01 eV for BVG and −0.02 eV for NVG, respectively. It seems that physisorption on doped systems are much weaker than that on the undoped one from the view of distance and energy. For two chemisorbed structures, both oxygen atoms in O2 interact with graphite surface strongly. In the case of VG-B with an adsorption energy of −2.73 eV, one atomic oxygen connects the dangling carbon atom to form a new C–O bond (1.22 Å) while the other combines with the nearby atoms to form a triangle. For VG-C, the O–O bond breaks to form two O–C bonds (1.23 Å) with dangling C atoms. The newly formed C–O bond is a little longer than the bond length of a CO molecule in gas phase (1.14 Å). The adsorption energy during this process is −3.85 eV. This indicates that the most stable interaction structure is the breaking of O–O bond and forming two dangling C–O bonds. Two chemisorbed structures of BVG are much different from that of VG. As depicted in Fig. 3(b), it can be obtained that the adsorbed O2 may interact with the dangling atoms near the vacancy to form a bridge (BVG-B) or separate as atomic oxygen to bond with the dangling B or C and form a more stable structure (BVG-C). It takes an activation energy barrier of 0.24 eV for BVG-B to break the O–O bond to form a BVG-C structure. For BVG-C, the adsorption pulls the B and C atoms out slightly from the surface. The length of C–O bond is similar to that of VG-C. However, the length of B–O bond in BVG-C (1.39 Å) is relatively longer compared with the C–O bond in VG-C (1.23 Å). The adsorption energy is −2.57 eV, which is 1.28 eV higher than that of VG-C structure (−3.85 eV). In the case of NVG, an unexpected unstable chemical adsorption configuration named NVG-A is found with extraordinary positive adsorption energy of +2.46 eV. Compared with the physisorption structure NVG-B, the charge density difference (CDD) in Fig. 4 proved that it is a chemical adsorption with the increasing charge states at the newly formed N–O and C–O bond. The other structure NVG-C is similar to that of VG-C or BVG-C in which O–O bond breaks spontaneously to form two chemical bonds with the dangling C or B atoms. However, the absolute value of adsorption energy in NVG-C is more than ten times smaller than that of VG. All these results indicate that the introduction of dopants such as B and N inhibits the interaction between graphite and oxygen molecule significantly.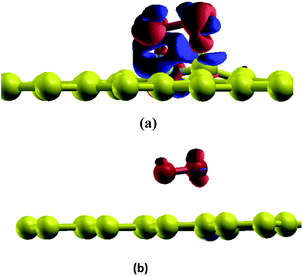 | ||
| Fig. 4 CDD for adsorption structures of O2 on graphite (a) NVG-A and (b) NVG-B. Orange area indicates a positive value while blue colour indicates the negative value of electron transfer. | ||
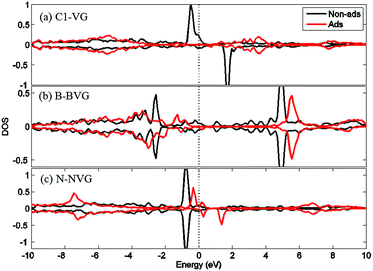
For a better understanding of the mechanism, DOS of the dopants before and after O2 interaction is calculated. The most stable adsorption configuration in each graphitic type (VG-C, BVG-C or NVG-C) is chosen for DOS calculation. As performed in Fig. 5, local density of states (LDOS) of the dangling atoms (C1, B and N) before and after O2 adsorption is depicted. It is found that the intensive peaks in valance states near the Fermi level largely decrease after bonding with O atom. Especially for C1 in VG (Fig. 5(a)), the adsorption produces the disappearance of electronic spin-up states above the Fermi energy as well as the spin-down states below the Fermi level. The change of electronic properties is due to the changing of distribution of unpaired electrons by orbital interaction. The charge distribution of systems is also examined by using Bader charge analysis. As summarized in Table 2, O2 molecule behaves as an accepter capturing charge from graphite. This is due to the stronger ability of O atom to grab charge, which is also observed by other studies.25,37 The charge transfer between oxygen and graphite surface is much larger in VG-C (−0.96e) than that of BVG-C (−0.78e) and NVG-C (−0.38e). The results indicate that the presence of dopants such as B or N inhibits the interaction between O2 molecule and vacancy defected graphite surface. Fig. 5(b) and (c) plot the LDOS of dopants (B, N) with and without adsorption of O2. It shows that interaction with B or N leads to unsymmetrical spin-up and spin-down state due to the orbital interaction changing the original structures of paired electrons. Meanwhile, spin polarization is introduced to the system during adsorption on BVG or NVG, with a magnetic moment of 0.84 μB for BVG-C and 1.09 μB for NVG-C. Furthermore, partial electronic density of states (LDOS) of the dangling atoms in these three graphite systems is analysed (Fig. 6). Compared to the un-doped systems, there is rather larger overlap between the doped atom and C3 which implies the existence of strong hybridization between the dopant and the C atoms around the vacancy. This is in accordance with Qin's results that the combination of defect-dopant affects the adsorption mechanism to some extent due to the orbital hybridization between C atoms and the dopants.38
| Type | VG-C | BVG-C | NVG-C |
| Ead (eV) | −3.85 | −2.57 | −0.13 |
| d(Å) | C–O: 1.23 | B–O: 1.39 | N–O: 1.29 |
| Q(e) | C: +0.91 | B: +0.33 | N: +0.84 |
| O: −0.96 | O: −0.78 | O: −0.38 |
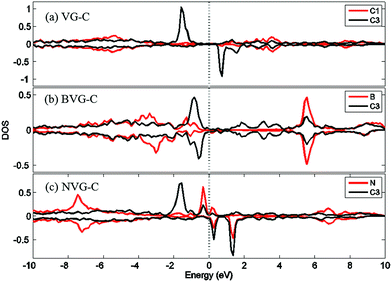 | ||
| Fig. 6 Partial electronic density of states (LDOS) of the dangling atoms in (a) VG-C, (b) BVG-C and (c) NVG-C after O2 adsorption. | ||
Desorption of CO on VG, BVG and NVG
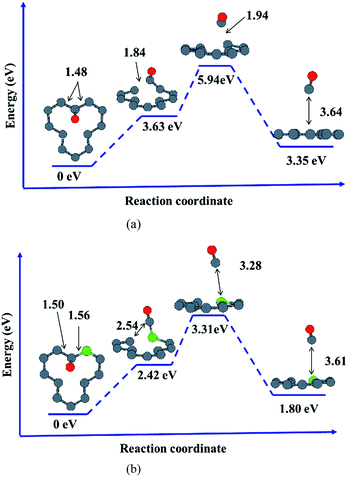
In order to further understand the effects of dopants upon oxidation behavior of vacancy-defected graphite, desorption of oxidation products such as carbonic oxide, is investigated on graphite with or without B, N dopants. It is important to note that the energy values calculated in our work only give the correct trends owing to the small size of our models. Based on the NEB calculation in the present work, it is found that substitutional B or N atom in graphite facilitates CO desorption because of the lower activation energy taking for B–C/N–C breaking than that for C–C bond.As shown in Fig. 7, desorption paths for CO on VG and BVG are displayed. The diffusion path on NVG is similar to that on BVG and thus will not be presented here. The initial situations are those with the adsorbed oxygen atom bonding to the dangling C atom with C–O length of 1.23 Å, and the dopant is located at the position neighbor to the dangling carbon. The substitution of B leads to much longer C–C (1.50 Å) and B–C (1.56 Å) bond compared to the corresponding C–C (1.48 Å) bond in VG system. To some extent, the substitution weakens C–C bond. NEB calculation shows that desorption of CO takes place step by step on these graphitic surfaces. The C–O radical tends to break a C–C bond in the first step. During the second stage, the other C–C (C–B or C–N) bond is elongated for preparation of bond breaking. As the process continues, the C–O radical move off the surface and ultimately a CO molecule desorbs. The formation of CO on doped graphite surface takes place with much lower activation energies. For instance, the energy barrier for VG is 5.94 eV, which is 2.63 eV higher than BVG (3.31 eV) and 2.32 eV higher than NVG (3.62 eV). This implies that substitutional B or N facilitates CO formation and finally results in the elimination of carbon in graphite.
In fact, the lowering of activation energy barrier for oxidation of B-doped graphite has been observed by Allardice et al.20 Thus substitutional boron is considered to anticipate the catalytic effect even though this effect is masked by inhibitory action of B2O3 in their study. Based on experimental and theoretical evidence, Radovic provides an effect that the redistribution of π electrons in the presence of substitutional boron results not in weaker C–O bonds and stronger C–C bonds,11 but in exactly the opposite effect that as π electron acceptor, boron is to both reduce the π electron density and accept additional electron density into its vacant 2pz orbital. By accepting electrons from the graphene layer, the substitution ultimately results in the weakening of C–C bonds along with strengthening of C–O bonds.19
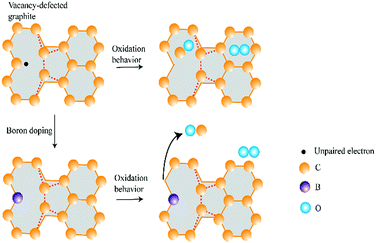
Our investigation shows that under conditions favouring desorption control boron appears to be a catalyst, while under conditions favouring adsorption control boron behaves as an inhibitor. This phenomenon indicates another example of the compensation effect, which is interpreted as a “macroscopic complementarity principle” by Radovic.19
In summary, as shown in Fig. 8, the effect of B or N doping on graphite oxidation is two-fold. Dopants of B and N induce a weaker O2 adsorption capability and they behave as an inhibitor to graphite oxidation. On the other hand, the removal of CO gasification product becomes easier after B or N doping. At this point, dopants behave as catalyst to graphite oxidation.
Conclusions
The interaction of O2 on B- and N-doped vacancy defected graphite has been investigated by means of density functional theory. The results have been compared to undoped defective system. Dopant (B or N) induces a weaker O2 adsorption capability on vacancy defected graphite while it makes easier desorption of oxidation product such as CO. Smaller adsorption energies of O2 on B- and N-doped vacancy defected graphite suggest an improvement of oxidation resistance of graphite by B, N substitution. DOS calculation indicates that the introduction of dopants eliminates effect of the unpaired electron, which results in less active interaction with O2. However, reaction path of CO desorption implies that substitutional B, N facilitates CO formation, in this respect B or N dopants plays a role of catalyst for graphite oxidation. The phenomenon of both inhibiting and catalytic effects of the dopants indicates another example of the compensation effect.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grand No. 21271114 and No. 91326203); Tsinghua University independent research and development fund (20111080982) and Program for Changjiang Scholars and Innovative Research Team in University (IRT13026).Notes and references
- F. Banhart, Irradiation effects in carbon nanostructures, Rep. Prog. Phys., 1991, 62, 1181 CrossRef.
- J. R. Hahn and H. Kang, Vacancy and interstitial defects at graphite surfaces: Scanning tunneling microscopic study of the structure, electronic property, and yield for ion-induced defect creation, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 6007 CrossRef CAS.
- J. Liu, L. Dong, C. Wang, T. X. Liang and W. Lai, First principles study of oxidation behavior of irradiated graphite, Nucl. Instrum. Methods Phys. Res., Sect. B, 2015, 352, 160–166 CrossRef CAS.
- C. Thierfelder, M. Witte, S. Blankenburg, E. Rauls and W. G. Schmidt, Methane adsorption on graphite from first principles including dispersion interaction, Surf. Sci., 2011, 605, 746 CrossRef CAS.
- Y. J. Xu and J. Q. Li, The interaction of molecular oxygen with active sites of graphite: a theoretical study, Chem. Phys. Lett., 2004, 400, 406–412 CrossRef CAS.
- J. F. Espinal, A. Montoya, F. Mondragon and T. N. Truong, A DFT study of interaction of carbon monoxide with carbonaceous materials, J. Phys. Chem. B, 2004, 108, 1003–1008 CrossRef CAS.
- M. Terrones, A. R. Botello-Méndez, J. Campos-Delgado, F. López-Urías, Y. I. Vega-Cantú and F. J. Rodríguez-Macías, et al., Graphene and graphite nanoribbons: Morphology, properties, synthesis, defects and applications, Nano Today, 2010, 5, 351–372 CrossRef.
- Y. Liu and J. Wilcox, CO2 adsorption on carbon models of organic constituents of gas shale and coal, Environ. Sci. Technol., 2011, 45, 809–814 CrossRef CAS PubMed.
- W. Kowbel, Y. Huang and H. Tsou, Effect of boron ion implantation on the oxidation behavior of a three-dimensional carbon–carbon composite, Carbon, 1993, 31, 355–363 CrossRef CAS.
- J. Y. Howe and L. E. Jones, Influence of boron on structure and oxidation behavior of graphite fiber, P120, Carbon, 2004, 42, 461–467 CrossRef CAS.
- L. E. Jones and P. A. Thrower, Influence of boron on carbon fiber microstructure, physical properties, and oxidation behavior, Carbon, 1991, 29, 251 CrossRef CAS.
- J. Liu, C. Wang, T. X. Liang and W. S. Lai, Interaction of boron with graphite: A van der Waals density functional study, Appl. Surf. Sci., 2016, 379, 402–410 CrossRef CAS.
- G. Luo, J. Zhao and B. Wang, A theoretical evaluation of the effect of interlayer spacing and boron doping on lithium storage in graphite, Comput. Mater. Sci., 2013, 68, 212–217 CrossRef CAS.
- X. Wu and L. R. Radovic, Ab initio molecular orbital study on the electronic structures and reactivity of boron-substituted carbon, J. Phys. Chem. A, 2004, 108, 9180–9187 CrossRef CAS.
- M. Jafari, M. Asadpour, N. A. Majelan and M. Faghihnasiri, Effect of boron and nitrogen doping on electro-optical properties of armchair and zigzag graphene nanoribbons, Comput. Mater. Sci., 2014, 82, 391–398 CrossRef CAS.
- L. Bai and Z. Zhou, Computational study of B- or N-doped single-walled carbon nanotubes as NH3 and NO2 sensors, Carbon, 2007, 45, 2105–2110 CrossRef CAS.
- S. Peng and K. Cho, Ab initio study of doped carbon nanotube sensors, Nano Lett., 2003, 3, 513–517 CrossRef CAS.
- J. Dai, J. Yuan and P. Giannozzi, Gas adsorption on graphene doped with B, N, Al and S: A theoretical study, Appl. Phys. Lett., 2009, 95, 232105 CrossRef.
- L. R. Radovic, M. Karra, K. Skokova and P. A. Thrower, The role of substitutional boron in carbon oxidation, Carbon, 1998, 36, 1841–1854 CrossRef CAS.
- D. J. Allardice and P. L. Walker Jr, The effect of substitutional boron on the kinetics of the carbon–oxygen reaction, Carbon, 1970, 8, 375 CrossRef CAS.
- G. Kresse and J. Hafner, Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal-Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- T. Bjorkman, A. Gulans, A. V. Krasheninnikov and R. M. Nieminen, van der Waals bonding in layered compounds from advanced density-functional first-principles calculations, Phys. Rev. Lett., 2012, 108, 235502 CrossRef CAS PubMed.
- Q. Hu, Q. Wu, G. Sun, X. Luo, Z. Liu and B. Xu, et al., First-principles study of atomic oxygen adsorption on boron-substituted graphite, Surf. Sci., 2008, 602, 37–45 CrossRef CAS.
- Y. Ferro, F. Marinelli and A. Allouche, Density functional theory investigation of H adsorption and H2 recombination on the basal plane and in the bulk of graphite: connection between slab and cluster model, J. Chem. Phys., 2002, 116, 8124–8131 CrossRef CAS.
- V. Morón, P. Gamallo and R. Sayós, DFT and kinetics study of O/O2 mixtures reacting over a graphite (0001) basal surface, Theor. Chem. Acc., 2011, 128, 683–694 CrossRef.
- J. Fayos, Possible 3D carbon structures as progressive intermediates in graphite to diamond phase transition, J. Solid State Chem., 1999, 148, 278–285 CrossRef CAS.
- J. Liu, L. Dong, W. Guo, T. X. Liang and W. Lai, CO adsorption and oxidation on N-doped TiO2 nanoparticles, J. Phys. Chem. C, 2013, 117, 13037–13044 CAS.
- J. Liu, Q. Liu, P. Fang, C. Pan and W. Xiao, First principles study of the adsorption of a NO molecule on N-doped anatase nanoparticles, Appl. Surf. Sci., 2012, 258, 8312–8313 CrossRef CAS.
- A. A. El-Barbary, R. H. Telling and C. P. Ewels, et al., Structure and energetics of the vacancy in graphite, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144107 CrossRef.
- R. Faccio, L. Fernández-Werner, H. Pardo, C. Goyenola, O. N. Ventura and Á. W. Mombrú, Electronic and structure distortions in graphene induced by carbon vacancies and boron doping, J. Phys. Chem. C, 2010, 114, 18961–18971 CAS.
- Y. Ferro, F. Marinelli and A. Allouche, Density functional theory investigation of H adsorption on the basal plane of boron-doped graphite, J. Chem. Phys., 2003, 118, 5650–5656 CrossRef CAS.
- J. Liu, C. Wang, T. X. Liang and W. S. Lai, Density functional theory investigation of oxygen interaction with boron-doped graphite, Appl. Surf. Sci., 2016, 390, 273–282 CrossRef CAS.
- Q. Zhou, L. Yuan, X. Yang, Z. Fu, Y. Tang and C. Wang, et al., DFT study of formaldehyde adsorption on vacancy defected graphene doped with B, N, and S, Chem. Phys., 2014, 440, 80–86 CrossRef CAS.
- S. Casolo, O. M. Lovvik, R. Martinazzo and G. F. Tantardini, Understanding adsorption of hydrogen atoms on graphene, J. Chem. Phys., 2009, 130, 054704 CrossRef PubMed.
- Y. Ferro, A. Allouche, F. Marinelli and C. Brosset, Theoretical study of oxygen adsorption on boron-doped graphite, Surf. Sci., 2004, 559, 158–168 CrossRef CAS.
- X. Qin, Q. Meng and W. Zhao, Effects of Stone-Wales defect upon adsorption of formaldehyde on graphene sheet with or without Al dopant: A first principle study, Surf. Sci., 2011, 605, 930–933 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |