Open Access Article
Open Access ArticleBinding mechanism of uranyl to transferrin implicated by density functional theory study†
Meng Wang a,
Wanjian Ding*a and
Dongqi Wang*bc
a,
Wanjian Ding*a and
Dongqi Wang*bc
aKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, China. E-mail: dingwanjian@bnu.edu.cn
bCAS Key Laboratory of Nuclear Radiation and Nuclear Energy Techniques, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China. E-mail: dwang@ihep.ac.cn
cThe State Key Laboratory of Molecular Reaction Dynamics in DICP, CAS, Dalian, China
First published on 13th January 2017
Abstract
Transferrins have been proposed to be responsible for the in vivo transportation of uranyl. In this work, the binding mechanism of uranyl to transferrin has been studied using density functional theory method. Three possible stepwise pathways have been investigated and compared, differing in the sequence of the three residues to bind with uranyl, i.e. Tyr* → Tyr* → Asp* (YYD) and Tyr* → Asp* → Tyr* (YDY) and Asp* → Tyr* → Tyr* (DYY). Compared with the activation energies and the reaction heat of these three possible mechanisms, it is concluded that the YYD pathway is a more plausible description for the binding of uranyl. According to the calculations, the binding process is described as a ligand exchange process assisted by the hydrolysis of uranyl tricarbonate complex, and the role of carbonate ligand which determines the optimal pathway is identified. The QTAIM analysis was used to compare the bond nature of uranyl complexes in its free form and its complex with the amino acid residues. The results are expected to benefit our understanding of the uptake of uranyl by serum transferrins, and have implications on protein engineering and the development of decorporation agents towards improved binding kinetics and thermodynamics of uranyl in a specific pH range.
Introduction
Uranium is a toxic and radioactive heavy metal. It is naturally available in the earth's crust, and can be found in, e.g. food, groundwater, and mineral resources.1 Uranium distributed in the environment may enter the human body via various ways. In vivo uranium is toxic to bones, kidneys, lungs, and the brain,2–6 and can even cause cancer in the human body. In serum, uranium predominantly exists in the uranyl (UO22+) form,7–10 and displays an affinity constant in the range of 107 to 1013 to combine with serum transferrin (sTf),9,11,12 and the uranyl–sTf complex can form a weak interaction with the sTf receptor to constitute a potential channel for the transportation of uranyl from serum to cell.13Serum transferrin is a glycoprotein of about 80 kDa, and its major function is to transport Fe3+ in human cells.14 It exists in the form of a single chain with two lobes, C and N lobes, consisting of 700 amino acid residues. Each lobe has an iron-binding site constituted by four residues, including two tyrosines (Tyr), one histidine (His), and one aspartate (Asp).15 The N-lobe of transferrin in its holo state has been crystallized16 and its binding site with ferric cation bound is shown in Fig. 1 to highlight how the key residues assembly to accommodate the ferric cation. When the transferrin is in its apo state, the four ligands open up in the aqueous medium.17–19 The apo state can also form complex with other metals besides iron, such as aluminum, titanium, bismuth, gallium, cobalt, uranium, and so on.20–22
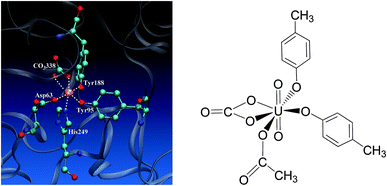 | ||
| Fig. 1 The binding site of the N-lobe of the human serum transferrin with Fe3+ bound (PDB ID 1a8e16) (left) and the schematic elucidation of its possible binding conformation with uranyl considered in the present work (right), where the Tyr and Asp residues are simplified as p-cresol and acetate, respectively. | ||
Uranyl differs from Fe3+ in its linear geometry with two Oyl atoms at the axial coordination sites. When coordinating with sTf, since the axial positions of uranyl are occupied by Oyl groups only three ligands may bind with uranyl in the equatorial plane in addition to a synergistic bidentate ligand, and the binding region of the complex is semi-closed.10 In a previous study, Vidaud et al. obtained the FTIR spectra of the uranyl–transferrin complex, which showed the His249 does not connect to the uranyl ion.23 This was later supported by a B3LYP study of the vibrational frequencies of potential QM models.24 The stronger interaction between O and U than that between N and U was also observed in a survey of crystal structures of proteins with uranyl bound deposited in the databases.25 In the work of Vidaud et al.,23 the binding of uranyl has been compared to that of Fe3+, and a structural model was proposed to illustrate the semi-open conformation of uranyl–sTf complex which may be responsible to its weaker interaction with the sTf receptor than that of Fe3+–sTf. In that work, the Asp63 and the synergistic anion CO32− were identified to interact with uranyl differently compared to Fe3+, while lack of details at the molecular level in their interaction modes with uranyl.
The burgeoning application of fission energy in civilian use raises serious concerns on the environmental and health consequences. The insufficient knowledge on the in vivo migration mechanism of uranyl leaves the public in fear on the operation of nuclear plant, but also makes it difficult to implement a rescue strategy to cope with unexpected situations. This motivated the current work, in which we employed density functional theory method to investigate the binding process of uranyl to sTf in serum. Based on previous work from both experimental15 and computational24,26,27 sides, we assumed a stepwise pathway started from uranyl tricarbonate, during which the U atom remains in hexa- or penta-coordinated. This work is expected to shed light on our understanding of the in vivo behavior of uranyl and has implications on protein engineering targeting at improved binding kinetics and thermodynamics of uranyl and biomolecules or at the development of decorporation agents.
Computational details
Density functional theory (DFT) methods have been used28–31 in the studies of actinide chemistry. In this work, B3LYP functional,32–35 as implemented in Gaussian 09 package,36 was employed to conduct the calculations. Uranium was described by a quasi-relativistic pseudopotential according to Dolg, et al.,37–39 denoted as ECP60MWB, which treats inner 60 electrons in the core shells, together with the optimized basis set for the valence shells. For the other atoms, a triple-ζ-quality basis set with diffuse and polarization functions, denoted as 6-311++G(d,p), was used. All stationary points were fully optimized, followed by vibrational frequency calculations to identify the nature of each structure to be a minimum or a transition state. Intrinsic reaction coordinate (IRC)40 calculations were carried out to guarantee that the transition states are in the right reaction paths. Correction to the Gibbs free energy of solvation was done by a THERMO program according to Fang.41 All discussions about the thermodynamics of the reaction pathways are based on the corrected Gibbs free energies.Simplified models cultivated from the binding site of sTf were used to study the binding mechanism of uranyl. Only the functional groups of the residues that are responsible for the binding of uranyl to sTf were considered, and the solvent environment was handled by using the polarizable continuum model (PCM)42,43 with a dielectric permittivity of 78.3553 (water). In the models, the Tyr was mimicked by p-cresol (HTyr*) and Asp by acetate (HAsp*). The protonation states of the residues were determined according to their pKa values, which are 9.84 ± 0.11 for Tyr and 3.67 ± 0.04 for Asp, respectively,44 thus at pH = 7, the Tyr exists in its protonated state while Asp in its deprotonated state.
Results and discussion
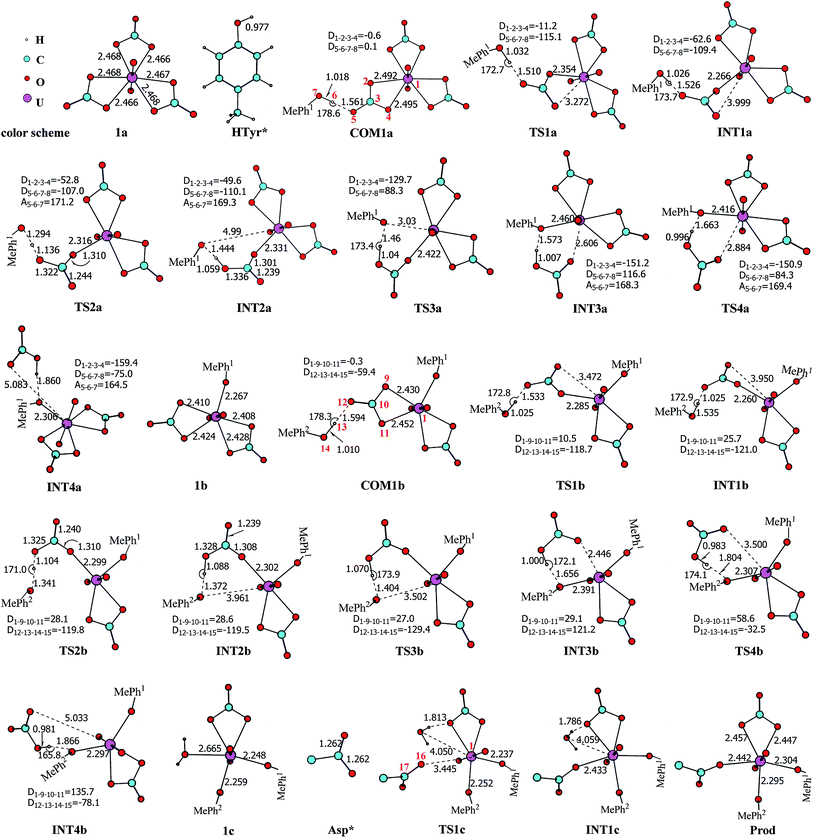
Previous studies45,46 show that the in vivo uranyl may exist in the free form, or binding with target proteins, e.g. transferrins, or deposited in bones. The general form of free uranyl in serum appears as uranyl tricarbonate complex (UO2(CO3)34−), which was used as the starting material in the present study. In the holo form of transferrins, the uranyl interacts with the protein via the coordination with three amino acid residues, i.e. two tyrosine and one aspartic acid. We consider the binding process of one lobe of transferrins. Assuming the binding of uranyl to the transferrin proceeds in a stepwise manner, three pathways were investigated, differing in the sequence of the residues to coordinate to uranyl: Tyr* → Tyr* → Asp* (denoted as YYD), Tyr* → Asp* → Tyr* (YDY) or Asp* → Tyr* → Tyr* (DYY). In the following, these three pathways will be analyzed and compared.I. Pathway YYD: Tyr* → Tyr* → Asp*
Along this pathway, the whole reaction starts two sequential ligand exchange steps of carbonate by HTyr*. The released excess coordination site of uranyl is then occupied by an Asp* residue nearby. Initially, the exchange of carbonate by the first Tyr* may happen in three channels, i.e. either by a direct ligand exchange between the two groups (channel I, eqn (1)), or assisted by a hydronium ion in aqueous phase (channel II, eqn (2) and (3)), or a direct ligand exchange between hydrolyzed uranyl tricarbonate species and Tyr* (channel III, eqn (4) and (5)). These three channels are elucidated as below:Channel I:
| UO2(CO3)34− (1a) + HTyr* → UO2(CO3)2(Tyr*)3− (1b) + HCO3− | (1) |
Channel II:
| UO2(CO3)34− (1a) + H3O+ → UO2(CO3)2(H2O)2− (U-H2O) + HCO3− | (2) |
| UO2(CO3)2(H2O)2− (U-H2O) + HTyr* → UO2(CO3)2(Tyr*)3− (1b) + H3O+ | (3) |
Channel III:
| UO2(CO3)34− (1a) + H2O → UO2(CO3)2(OH)3− (U-OH) + HCO3− | (4) |
| UO2(CO3)2(OH)3− (U-OH) + HTyr* → UO2(CO3)2(Tyr*)3− (1b) + H2O | (5) |
According to the calculations, the direct ligand exchange reaction (channel I) is an exothermic process with a free energy change of −8.0 kcal mol−1 (Table S1†). The channel II mimics an acidic environment and the hydration of uranyl tricarbonate complex 1a is strongly exothermic by 53.2 kcal mol−1. However, the highly stable hydrated intermediate UO2(CO3)2(H2O)2− (U-H2O) is inert to the ligand exchange of H2O by HTyr* thermodynamically and the reaction is endothermic by 45.2 kcal mol−1. This suggests that in acidic environment, the uranyl species may be trapped in its UO2(CO3)2(H2O)2− state, which hammers its binding with the HTyr* ligand. The channel III is a ligand exchange reaction assisted by the participation of water. The reaction of eqn (4) is moderately endothermic by 2.2 kcal mol−1. The HTyr* then approaches the uranyl to replace the hydroxide anion (eqn (5)). This reaction is thermodynamically favorable in view of its exothermicity of −10.2 kcal mol−1. Based on the above data, below we consider the reaction initialized by the channel I. The channel III was also investigated and the data are provided in ESI.†
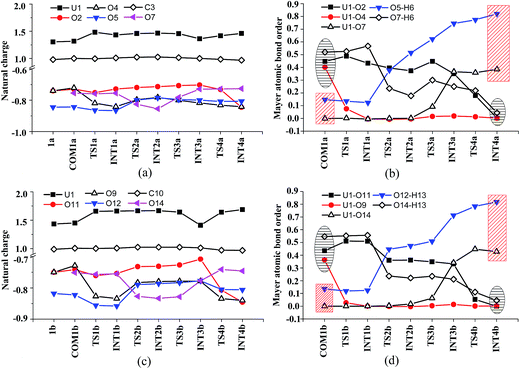
Along the channel I, starting from 1a and HTyr*, the first ligand exchange reaction is described as a four-step process, including the breakage of U–O4 bond (TS1a), the proton transfer from HTyr* to O5 (TS2a), the ligand exchange of HCO3− by Tyr* (TS3a), and the HCO3− release (TS4a), as shown in Fig. 2. The free energy profile is plotted in Fig. 3. When approaching 1a, HTyr* may first form a hydrogen bond (H-bond) with one carbonate group (COM1a), which is thermodynamically favorable by 7.4 kcal mol−1. In COM1a, the HTyr* interacts with the carbonate group via an H-bond between H6 (HTyr*) and O5 (carbonate). We have also checked the possibility for an H-bond between H6 and O2/O4, which is given in Fig. S4,† and found that the complex is less stable than COM1a by about 1.6 kcal mol−1. This is because O5 (−0.84e) is more negatively charged than O2/O4 (−0.74e/−0.74e), leading to stronger interaction between H6 and O5 than that between H6 and O2/O4. Below we consider the COM1a as a key species on the pathway of the ligand exchange reaction.
The H-bond interaction between HTyr* and CO32− may perturb the dative bond between the carbonate group and uranyl, and induce a transition of the coordination mode of CO32− from κ2 in COM1a to η1 in INT1a via a transition state TS1a by overcoming a free energy barrier of 4.9 kcal mol−1. The highly nucleophilic CO32− group may abstract the proton H6 from the Tyr* group, as indicated by the variation of the Mayer atomic bond orders (MBO) of H6–O5, which is to be formed, and H6–O7, which is to be broken, from 0.123 and 0.568 in INT1a to 0.378 and 0.235 in TS2a to 0.515 and 0.177 in INT2a, respectively (Fig. 4b).
The protonated carbonate group is easily replaced by the Tyr* anion via TS3a. In TS3a, the imaginary vibration frequency corresponds to the asymmetric stretching mode of the U–O7 (Tyr*) and U–O2 (carbonate), suggesting the coordination of Tyr* and the dissociation of bicarbonate happened simultaneously. The free energy barrier to this process is 13.1 kcal mol−1 and this step is endothermic by 9.4 kcal mol−1. The detached HCO3− group then leaves, and gives the penta-coordinated UO2(CO3)2(Tyr*)3− complex (INT4a). In INT4a, the Tyr* is coordinated to U in a η1-manner, with a U–O7 bond length of 2.306 Å. Note that, the coordination of the second deprotonated phenolate ligand (INT2b → TS3b → INT3b) is exothermic, which is in contrast to that of the first one (INT2a → TS3a → INT3a). This is because that INT2b is less negatively charged than INT2a. In the meantime, uranyl has coordination site ready to receive the deprotonated phenolate ligand. This leads to a thermodynamically more favorable formation of INT3b than INT3a.
In Fig. 4, the fluctuations of the natural charges of U and the coordinating O atoms of the ligands and the MBO of key bonds along the channel I are monitored, which are consistent with the structural evolution along the reaction. Considering the proton transfer step as an example, it can be seen that accompanying the proton transfer from HTyr* (O7) to one carbonate ligand (O5), there is marginal change in the atomic charges residing on these two atoms and the O4 atom. For the other atoms, the atomic charges remain roughly constant during the reaction. This suggests that the complex may adapt to the new chemical environment during the ligand exchange and reach its equilibrium state quickly. The monitoring of the MBO clearly shows the cleavage of U1–O2, U1–O4, and O7–H6 bonds, whose MBO values evolve from 0.4–0.6 to around 0.0, and the formation of O5–H6 and U1–O7 bonds.
The newly formed INT4a may experience a second ligand exchange reaction to have one of the rest two carbonate groups replaced by another HTyr* ligand. A process similar to the first ligand exchange reaction was identified, as shown in Fig. 2.
Similar to the binding of the first Tyr*, along the binding of the second Tyr* ligand, there is also no significant charge transfer (within 0.28e) during the reaction, as seen in Fig. 4c, and the evolution of the Mayer atomic bond order of key bonds (Fig. 4d) clearly shows that the proton transfer from O14 (HTyr*) to O12 (CO32−) happens prior to the U–O14 bond formation and the U–O11 bond cleavage.
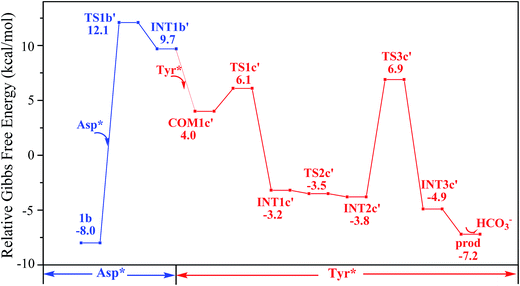
Upon the dissociation of O14⋯H13–O12 hydrogen bond in INT4b, a water molecule close to uranyl may attach to U to keep it penta-coordinated in its equatorial plane. This gives the intermediate UO2(CO3)(H2O)(Tyr*)22− (1c, Fig. 2). It may interact to the neighboring Asp carboxylate group, which is modelled by Asp* ligand here. The reaction is a thermoneutral process with the free energy of Prod being 1.1 kcal mol−1 lower than 1c. The free energy profile of this whole process of YYD is plotted in Fig. 3.
In summary, following the pathway YYD starting with channel I, the rate-determining step is the coordination of the first Tyr* ligand (TS3a) with a relative free energy of 8.2 kcal mol−1, and the entire reaction is exothermic by 7.2 kcal mol−1. This suggests that the whole reaction can happen easily under the physiological condition.
II. Pathway YDY: Tyr* → Asp* → Tyr*
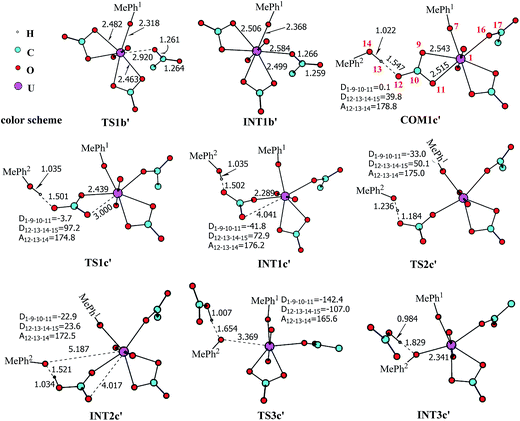
The pathway YDY differs from the YYD in the second ligand exchange step, where in the former case a negatively charged Asp* ligand, instead of Tyr* in the latter case, reacts with UO2(CO3)2(Tyr*)3− (1b). Here starting from UO2(CO3)2(Tyr*)3−, we located the stationary points of the second and the third ligand exchange steps in the pathway YDY. The optimized structures are shown in Fig. 5 for the two sequential steps, and the free energy profile of process YDY is plotted in Fig. 6.For the coordination of Asp*, as the carboxylate group is in its deprotonated state, we did not consider the release of one carbonate group upon its coordination, but considered a direct coordination to U atom at the site between Tyr* and a carbonate group. This process faces a high free energy barrier of up to 20.1 kcal mol−1 (TS1b′) and is strongly endothermic by 17.7 kcal mol−1 (INT1b′). In the transition state TS1b′, the interaction between U and the original three ligands is weakened in view of the longer U–O distances, and the U–O16 (Asp*) bond which is going to form is calculated to have a distance of 2.92 Å. The imaginary frequency is −84.2 cm−1, corresponding to the vibrational mode of U–O16 (Asp*) stretching. The binding of Asp* gives a hexa-coordinated complex INT1b′.
As in INT1b′ the U atom is hexa-coordinated in its equatorial plane, the binding of the third ligand Tyr* requires the release of at least one coordination site. Concerning the binding mode of uranyl in sTf, here we consider the replacement of one of the two carbonate groups by a second Tyr* ligand. Similar to the coordination of the first Tyr* ligand shown in Fig. 2, the HTyr* ligand first builds an H-bond interaction with the leaving CO32− group. The hydrogen bond between O12 (carbonate) and H13 (Tyr*) stabilizes COM1c′ by 5.7 kcal mol−1. The following cleavage of the U–O9 coordination bond, which releases one coordination site, is a facile process with a free energy barrier of 2.1 kcal mol−1 (TS1c′) and an exothermicity of 7.2 kcal mol−1 (INT1c′). The η1-coordinated carbonate group is highly nucleophilic, and can easily abstract a proton (H13) from the HTyr* (TS2c′). The formation of a dative bond between U and O14 (Tyr*) gives the product via TS3c′, at the cost of the break of U–O11 (carbonate) bond with a free energy barrier of 10.7 kcal mol−1. The whole reaction of the pathway YDY is exothermic by 7.2 kcal mol−1.
III. Pathway DYY: Asp* → Tyr* → Tyr*
In principle, there exists a third potential pathway for the binding of UO2(CO3)34− to sTf in a sequential manner. Along this pathway, the uptake of uranyl by sTf starts from its coordination to a negatively charged Asp residue followed by the binding of two Tyr residues nearby. With the models employed here, this pathway is denoted as Asp* → Tyr* → Tyr* (DYY). We first considered the formation of the intermediate UO2(CO3)3(Asp*)5− (U-3CO3-Asp*, Fig. 7) via the reaction below:| UO2(CO3)34− (1a) + Asp* → UO2(CO3)3(Asp*)5− (U-3CO3-Asp*) | (6) |
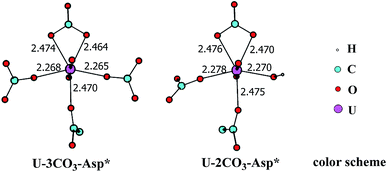 | ||
| Fig. 7 The schematic structures of U-3CO3-Asp* and U-2CO3-Asp* with key geometrical parameters (bond lengths in Å). | ||
Thermodynamically this reaction is unfavorable and the Gibbs free energy change was calculated to be 16.2 kcal mol−1 (Table S1†). This means that an activation free energy more than 16.2 kcal mol−1 is inherent to the binding of Asp* to the UO2(CO3)34− complex. It is conceivable that the negatively charged Asp* feels strong repulsive interaction when approaching to the negatively charged UO2(CO3)34− complex which blocks this channel. This suggests that the direct exchange of CO32− by Asp* is hard to happen.
There exists another possibility with the exchange mediated by a water molecule, which may thus alleviate the electrostatic repulsion. It involves two reactions below:
| UO2(CO3)34− (1a) + H2O → UO2(CO3)2(OH)3− (U-OH) + HCO3− | (4) |
| UO2(CO3)2(OH)3− (U-OH) + Asp*− → UO2(CO3)2(OH)(Asp*)4− (U-2CO3-Asp*) | (7) |
This clears space in the surrounding of U atom to allow Asp* to approach uranyl. The ΔG of eqn (7) is calculated to be 11.3 kcal mol−1. These data suggest that the DYY pathway cannot compete against the YYD pathway under physiological conditions.
IV. Discussion
We note that in an earlier B3LYP study,24 an uranyl complex was constructed with the equatorial plane of U atom tetra-coordinated, where the Asp and the carbonate groups coordinate with uranyl as monodentate ligands. In a well confined and limited space, such a conformation may represent a special case for uranyl to adapt to the chemical environment constructed by protein due to the constraints of protein backbone. In recent years, it is established knowledge that in aqueous phase, uranyl prefers to adopt a penta-coordinated conformation in its equatorial plane. In the case of sTf, the uptake of the uranyl triggers a domain rotation of the protein around an axis crossing the hinge site. This means that the binding site is not uniquely defined prior to the binding of uranyl, and the flexible residues may adjust their orientations to reach an optimal binding state with uranyl. Thus, in this work, we have considered a hexa- or penta-coordinated conformation of the uranyl in its equatorial plane,1 where the synergistic anion binds to uranyl in a κ2 manner. According to our calculations, the whole reaction is exothermic, suggesting such a treatment is reasonable in view of thermodynamics.As mentioned above, the free energy barrier to the rate-determining step of pathway YYD is 13.1 kcal mol−1 which corresponds to the ligand exchange of the first Tyr* with HCO3−. For the pathway YDY, the binding of the Asp* ligand costs more energy of 20.1 kcal mol−1 (Asp*) and appears as the rate-determining step. These data show that when loading to sTf, the uranyl tricarbonate favors to coordinate to two Tyr residues sequentially first prior to its interaction with Asp, although Asp is ready to interact with uranyl while Tyr requires to be deprotonated before coordinating to uranyl. Note that, in serum, uranyl exists mainly in its tricarbonate complex form, and any ligand exchange process requires the release of one or two of its carbonate ligands. Keeping this in mind, the proton on the phenol group offers a “dragging force” to weaken the interaction between the coordinated carbonate ligand and uranyl and facilitate its leaving to trigger the ligand exchange reaction, in Chinese idiom, mislead a tiger (carbonate) to leave the mountains it based (uranyl) by a plot (proton) in order to conquer its territory (the coordination site). This benefits the Tyr residue to grab uranyl nearby. The deprotonated Asp residue does not have this “bait”, and cannot compete against Tyr residue in their coordinating with uranyl which is under the protection of the negatively charged carbonate ligands. In other words, the approach of Asp to uranyl is posterior to the binding of two Tyr residues, and the YYD pathway is the most plausible mechanism for the ligand exchange of uranium tricarbonate. An overview of the YYD pathway is shown in Fig. 8.
According to our calculations, the whole process is exothermic, either along the YYD or the YDY pathway, by −7.2 kcal mol−1. This suggests that the capture of uranyl by sTf is a thermodynamically favorable process. To understand the bonding nature of the starting material UO2(CO3)34− and the product UO2(CO3)(Tyr*)2(Asp*)3−, we analyzed the bonding properties of the coordination bonds using QTAIM topological analysis technique. Four descriptors are used to compare the coordination bonds in the two complexes, and these include the electronic density ρb and its Laplacian ∇2ρb, the energy density Hb(r) at the bond critical point, and the delocalization index between two atoms δ(A,B). These values are collected in Table 1.
| UO2(CO3)34− | UO2(CO3)(Tyr*)2(Asp*)3− | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Bonda | ρb | ∇2ρb | Hb(r) | δ | Bonda | ρb | ∇2ρb | Hb(r) | δ |
| a Oia and Oib (i = 1, 2, 3) represent the two coordinating O atoms of the i-th CO32−; OY, OY′ and OD are the coordinating O atoms of the two Tyr* (Y, Y′) and the Asp* (D) ligands, respectively. | |||||||||
| U–O1a | 0.0592 | 0.1856 | −0.0045 | 1.12 | U–O1a | 0.0623 | 0.1964 | −0.0053 | 1.16 |
| U–O1b | 0.0595 | 0.1863 | −0.0046 | 1.12 | U–O1b | 0.0609 | 0.1920 | −0.0050 | 1.14 |
| U–O2a | 0.0594 | 0.1863 | −0.0046 | 1.12 | U–OY | 0.0763 | 0.3021 | −0.0084 | 1.39 |
| U–O2b | 0.0592 | 0.1858 | −0.0045 | 1.12 | U–OY′ | 0.0776 | 0.3070 | −0.0090 | 1.42 |
| U–O3a | 0.0593 | 0.1859 | −0.0045 | 1.12 | U–OD | 0.0557 | 0.2168 | −0.0017 | 1.13 |
| U–O3b | 0.0596 | 0.1867 | −0.0046 | 1.12 | |||||
As seen in Table 1, in UO2(CO3)34− (1a), the six U–O (carbonate) bonds have almost same nature with a ρb of 0.06 e bohr−3 and a ∇2ρb of 0.19 e bohr−5, suggesting a depleted feature for the interaction between the two atoms in each pair. Upon the substitution of two CO32− ligands by two Tyr* and one Asp* ligands to form UO2(CO3)(Tyr*)2(Asp*)3− (prod), as the coordination number decreases from 6 to 5, the values of δ(A,B) for all of the five dative bonds increase marginally compared to those in the reactant with the largest values for U–O (Tyr*) bonds which are 1.39 and 1.42, respectively. We note that the U–η1-O (Asp*) has a smaller ρb while a larger ∇2ρb than the U–κ2-O (carbonate), suggesting different bond ellipticity between them. The larger ρb of U–O (Tyr*) than the other coordination bonds indicates its more covalent feature due to its stronger nucleophilicity.
Conclusion
The binding process of uranium to transferrin has been investigated by density functional theory method, and three stepwise pathways have been compared, differing in the sequence of the three amino acid residues, which are simplified as two HTyr* and an Asp*, in a series of ligand exchange reactions. The calculations identified the Tyr* → Tyr* → Asp* (YYD) pathway as the optimal pathway. Along this pathway, the HTyr* residues may grab the free UO2(CO3)34− aqueous species, and the proton transferred from HTyr* to the bound CO32− ligand triggers the ligand exchange reactions. The Asp* residue builds interaction with uranyl in the end to anchor the uranyl in the binding site. This is also consistent with the experimental hypothesis that the Asp is relevant to the semi-open conformation of the uranyl–sTf complex.The other two pathways, i.e. Tyr* → Asp* → Tyr* (YDY) and Asp* → Tyr* → Tyr* (DYY), in which the negatively charged Asp* coordinates to uranyl prior to the binding of one or both neutral HTyr* ligands, suggests that the excess ligands CO32− to be replaced play a key role in determining the uptake mechanism of uranyl by sTf. The deprotonated Asp* does not have a proton to perturb the strong interaction between CO32− and uranyl, which makes it energy demanding to repel one of the CO32− ligands in order to release coordination site. In addition, in its carbonate complex, the positive charge of uranyl is already neutralized by the carbonate ligands, and the approaching of Asp* also brings electrostatic repulsive interaction, which disfavor its binding when uranyl is tri- or di-carbonated.
In summary, this work identified an optimal pathway for the uptake of uranyl by sTf at around pH = 7.0, and clarified that this is determined by synergistic ligands CO32−. This shows that at low pH, due to the strong preference of carbonate to be protonated, the UO2(CO3)34− is no longer the predominant species,47 and the YYD mechanism may no longer dominate. This work thus helps improve our understanding on the in vivo migration of uranyl by providing detailed mechanism at the molecular level, and sheds light on the protein engineering and the design of decorporation reagents toward the enhanced capture of uranyl in specific pH range.
Acknowledgements
The authors gratefully acknowledge the National Natural Science Foundation of China (21573021, 21073013, 21473206, and 91226105) and the CAS Hundred Talents Program (Y2291810S3) for financial support.References
- J. Grenthe, J. Drożdżyński, T. Fujino, E. C. Buck, T. E. Albrecht-Schmitt and S. F. Wolf, in The Chemistry of The Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein, J. Fuger and J. J. Katz, Springer, Dordrecht, The Netherlands, 2006 Search PubMed.
- M. Hada and A. G. Georgakilas, J. Radiat. Res., 2008, 49, 203–210 CrossRef CAS PubMed.
- Y. Knöbel, M. Glei, A. Weise, K. Osswald, A. Schäferhenrich, K. K. Richter, U. Claussen and B. L. Pool-Zobel, Toxicol. Sci., 2006, 93, 286–297 CrossRef PubMed.
- S. S. Wise, W. D. Thompson, A. M. Aboueissa, M. D. Mason and J. P. Wise, Chem. Res. Toxicol., 2007, 20, 815–820 CrossRef CAS PubMed.
- P. Lestaevel, P. Houpert, C. Bussy, B. Dhieux, P. Gourmelon and F. Paquet, Toxicology, 2005, 212, 219–226 CrossRef CAS PubMed.
- P. Lestaevel, E. Romero, B. Dhieux, H. B. Soussan, H. Berradi, I. Dublineau, P. Voisin and P. Gourmelon, Toxicology, 2009, 258, 1–9 CrossRef CAS PubMed.
- O. Averseng, A. Hagege, F. Taran and C. Vidaud, Anal. Chem., 2010, 82, 9797–9802 CrossRef CAS PubMed.
- M. G. Benavides-Garcia and K. Balasubramanian, Chem. Res. Toxicol., 2009, 22, 1613–1621 CrossRef CAS PubMed.
- M. Sutton and S. R. Burastero, Chem. Res. Toxicol., 2004, 17, 1468–1480 CrossRef CAS PubMed.
- J. D. Van Horn and H. Huang, Coord. Chem. Rev., 2006, 250, 765–775 CrossRef CAS.
- G. Montavon, C. Apostolidis, F. Bruchertseifer, U. Repinc and A. Morgenstern, J. Inorg. Biochem., 2009, 103, 1609–1616 CrossRef CAS PubMed.
- S. Scapolan, E. Ansorborlo, C. Moulin and C. Madic, Radiat. Prot. Dosim., 1998, 79, 505–508 CrossRef CAS.
- M. Hémadi, N. T. Haduong, S. Plantevin, C. Vidaud and J. M. Chahine, J. Biol. Inorg. Chem., 2010, 15, 497–504 CrossRef PubMed.
- H. Sun, H. Li and P. J. Sadler, Chem. Rev., 1999, 99, 2817–2842 CrossRef CAS PubMed.
- M. Hémadi, N. T. Haduong and J. M. Chahine, J. Phys. Chem. B, 2011, 115, 4206–4215 CrossRef PubMed.
- R. T. Mac-Gillivray, S. A. Moore, J. Chen, B. F. Anderson, H. Baker, Y. Luo, M. Bewley, C. A. Smith, M. E. Murphy and Y. Wang, Biochemistry, 1998, 37, 7919–7928 CrossRef CAS PubMed.
- H. M. Baker, Q. He, S. K. Briggs, A. B. Mason and E. N. Baker, Biochemistry, 2003, 42, 7084–7089 CrossRef CAS PubMed.
- J. Wally, P. J. Halbrooks, C. Vonrhein, M. A. Rould, S. J. Everse, A. B. Mason and S. K. Buchanan, J. Biol. Chem., 2006, 281, 24934–24944 CrossRef CAS PubMed.
- F. B. Abdallah and J. M. Chahine, J. Mol. Biol., 2000, 303, 255–266 CrossRef CAS PubMed.
- Z. Chikh, N. T. Haduong, G. Miquel and J. M. Chahine, J. Biol. Inorg. Chem., 2007, 12, 90–100 CrossRef CAS PubMed.
- Z. Chikh, M. Hémadi, G. Miquel, N. T. Haduong and J. M. Chahine, J. Mol. Biol., 2008, 380, 900–916 CrossRef CAS PubMed.
- N. T. Haduong, M. Hémadi, Z. Chikh and J. M. Chahine, Biochem. Soc. Trans., 2008, 36, 1422–1426 CrossRef CAS PubMed.
- C. Vidaud, S. Gourion-Arsiquaud, F. Rollin-Genetet, C. Torne-Celer, S. Plantevin, O. Pible, C. Berthomieu and E. Quéméneur, Biochemistry, 2007, 46, 2215–2226 CrossRef CAS PubMed.
- M. G. Benavidesgarcia and K. Balasubramanian, Chem. Res. Toxicol., 2009, 22, 1613–1621 CrossRef CAS PubMed.
- O. Pible, P. Guilbaud, J. L. Pellequer, C. Vidaud and E. Quéméneur, Biochimie, 2006, 88, 1631–1638 CrossRef CAS PubMed.
- M. Bühl, H. Kabrede, R. Diss and G. Wipff, J. Am. Chem. Soc., 2006, 128, 6357–6368 CrossRef PubMed.
- S. O. Odoh, S. M. Walker, M. Meier, J. Stetefeld and G. Schreckenbach, Inorg. Chem., 2011, 50, 3141–3152 CrossRef CAS PubMed.
- N. Kaltsoyannis, Chem. Soc. Rev., 2003, 32, 9–16 RSC.
- D. Wang and Z. Chai, Chem. Soc. Rev., 2012, 41, 5836–5865 RSC.
- W. Ding, W. Fang, Z. Chai and D. Wang, J. Chem. Theory Comput., 2012, 8, 3605–3617 CrossRef CAS PubMed.
- W. Ding, W. Fang, Z. Chai and D. Wang, Acta Phys.-Chim. Sin., 2015, 31, 1283–1301 CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789 CrossRef CAS.
- B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- W. Küchle, M. Dolg, H. Stoll and H. Preuss, J. Chem. Phys., 1994, 100, 7535–7542 CrossRef.
- X. Cao, M. Dolg and H. Stoll, J. Chem. Phys., 2003, 118, 487–496 CrossRef CAS.
- X. Cao and M. Dolg, J. Mol. Struct., 2004, 673, 203–209 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- D.-C. Fang, Beijing Normal University, Beijing 100875, People's Republic of China, free of charge for academic users. Solution-phase free energy has been obtained from the THERMO program by using solution-phase translational entropy, which is different from that of the Gaussian 09 output based on gas-phase translational entropy.
- M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- G. R. Grimsley, J. M. Scholtz and C. N. Pace, Protein Sci., 2006, 15, 1214–1218 CrossRef PubMed.
- A. O. Tirler and T. S. Hofer, J. Phys. Chem. B, 2014, 118, 12938–12951 CrossRef CAS PubMed.
- S. Tsushima, Y. Uchida and T. Reich, Chem. Phys. Lett., 2002, 357, 73–77 CrossRef CAS.
- T. Lan, Z. Liu and D. Wang, Chin. J. Inorg. Chem., 2015, 31, 1774–1784 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The full citation of Gaussian 09; discussion on channel III of the first HTyr* binding to UO2(CO3)34− along pathway YYD; the energy, entropy, and free energy of each stationary point involved in eqn (1)–(7) and the relative energy, entropy, and free energy of eqn (1)–(7); the schematic structures of stationary points involved in the present work while not included in the main text along with key geometrical parameters; the natural charges of key atoms and the Mayer atomic bond order of key bond along the reaction coordination of Tyr* binding toward uranyl; the coordinates and energies of stationary points. See DOI: 10.1039/c6ra26109d |
| This journal is © The Royal Society of Chemistry 2017 |