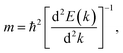The electronic properties of the stanene/MoS₂ heterostructure under strain

Abstract

The effect of a MoS₂ substrate on the structural and electronic properties of stanene were systematically investigated by first-principles calculations. The Brillouin zone of isolated stanene has a Dirac cone at the K point. MoS₂ helps to open an energy gap at the K point, whereas contributes no additional transport channels near the Fermi level. Our results suggest that the carrier mobility remains large, which makes the stanene/MoS₂ heterostructure a competitive material for electronic applications. Subsequently, strain engineering study by changing the interlayer spacing between stanene and MoS₂ layer and changing lattice constants indicates that the energy gap at K point can be effectively tuned to meet the demands of experiments and device design in nanoelectronics. Moreover, a large enough strain leads to a metal–semiconductor phase transition to make the intrinsic semiconductor turn into self-doping phase. Our study indicates that MoS₂ is a good substrate to promote the development of Sn-based nanoelectronics.

---

I. Introduction

Graphene, a two-dimensional (2D) honeycomb-like carbon network, has attracted significant interest since its discovery, leading to a boom in the development of 2D materials.^1–4 In the low-energy regime, the excited carriers can be described as massless Dirac fermions, which lead to various remarkable electronic properties.^1,5 One unique property is the high carrier mobility (200 000 cm² V⁻¹ s⁻¹),^6,7 which allows the electrons to freely move while experiencing low scattering from the defects and impurities. However, graphene still faces many challenges, such as toxicity, incompatibility with the current silicon-based electronic technology, and the lack of an intrinsic band gap, which impedes its application in electric devices.⁸ Hence, great efforts have been devoted to either opening an appropriate band gap in graphene or searching for other 2D materials that have honeycomb-like structures similar to that of graphene but with buckled structure to open an energy gap.^9,10

Stanene is a honeycomb-like monolayer of tin atoms. It may be a competitive candidate of graphene because of the high conductivity of stanene;¹¹ moreover, its electric structure can be easily tuned.¹² Recently, it is commonly used to tune graphene-like structure by applying electric field, strain or extra functional group. In the case of stanene, external strain tends to open an energy gap, as predicted by M. Modarresi.¹³ Li et al.¹⁴ tuned the electronic structure and magnetic properties of 2D stanene by hydrogenation. Ethynyl derivative-functionalized stanene (SnC₂X: X = H, F, Br, and I) has been studied by Zhang et al.¹⁵ Recently, it was found that the strong interaction with the substrate can disturb the Dirac cones.¹⁶ The H-BN¹⁷ and Ge (1 1 1) substrates¹⁸ will induce a band gap in stanene, transforming it into a quantum spin Hall phase.

In this study, the properties of stanene on a MoS₂ monolayer substrate with an interlayer spacing of −1.0 to 1.0 Å and applied strain of −6 to 6% were investigated by first-principles calculations. Our results revealed that MoS₂ is a good substrate and induces a band gap in stanene, whereas contributes no additional transport channels near the Fermi level. The interlayer spacing and extra strain were found to effectively tune the band gap. These findings indicate that the stanene/MoS₂ heterostructure is a good platform to realize the Sn-based nanoelectronic device design.

II. Methods

All calculations were performed by the density functional theory (DFT) method as implemented in the Vienna ab initio Simulation Package (VASP).^18,19 We applied the Perdew–Burke–Ernzerhof (PBE)²⁰ and generalized gradient approximation (GGA)^18,21 functional to describe the exchange correlation energy. A plane-wave basis with a kinetic energy cut-off of 500 eV was employed and a supercell with a 20 Å vacuum layer was used to simulate the isolated sheet. In addition, the electron–ion interactions were represented by the projector augmented wave (PAW) method.²² The van der Waals (vdW) interactions were properly considered, which have been demonstrated to reliably describe the 2D heterostructures (HTSs). With the optimized structure, the more sophisticated HSE06 hybrid functional^23,24 was used to check the corresponding results for the systems. The Brillouin zone was sampled using a 9 × 9 × 1 gamma-centered Monkhorst–Pack (MP)²⁵ grid. Herein, the convergence criterion of self-consistent calculations for ionic relaxations was 10⁻⁵ eV between two consecutive steps. Using the conjugate gradient method, all atomic positions and the size of the unit cell were optimized until the atomic forces were less than 0.01 eV Å⁻¹ m.

III. Results and discussion

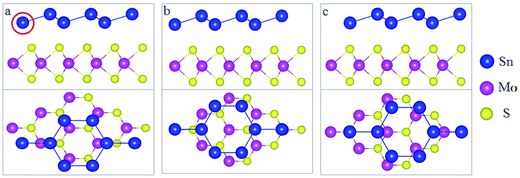
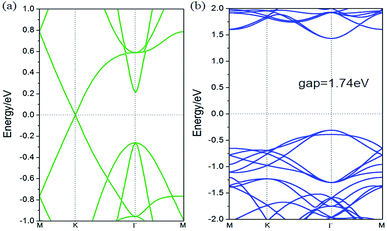
In this study, we selected MoS₂ as the substrate to form a stanene/MoS₂ heterostructure (HTS). The relaxed lattice constants were 9.36 and 9.48 for 2 × 2 lateral periodicity of stanene and 3 × 3 lateral periodicity of MoS₂, respectively.^26,27 In this study, it exhibited a small lattice mismatch (∼1.28%), showing that it was feasible to grow stanene on the MoS₂ substrate and completely achieve the required preparation conditions. Stanene and MoS₂ all exhibit hexagonal honeycomb structure,^12,28 as shown in Fig. 1. Herein, we considered three patterns for the arrangement of stanene on the MoS₂ substrate: (I) reference Sn atoms in the centre of MoS₂ hexagon (hollow) [Fig. 1(a)]; (II) reference Sn atoms on top of one of the Mo atoms (Mo) [Fig. 1(b)]; and (III) reference Sn atoms on top of one of the S atoms (S) [Fig. 1(c)].

Fig. 1 Side and top views of the three patterns of stanene/MoS₂ HTS: (a) hollow pattern, (b) Mo pattern, and (c) S pattern. The blue, pink-purple, and yellow spheres represent Sn, Mo, and S atoms, respectively.

The electronic properties of the isolated stanene and MoS₂ monolayers have been discussed. Fig. 2(a) shows the energy band structure of stanene. There is a Dirac cone at the K point and an optical gap at the Γ point, consistent with the results obtained by Wang et al.²⁹ and Zhu et al.³⁰ It is clear that stanene is a gapless semiconductor and it has a large carrier mobility due to the Dirac cone, which is beneficial for potential applications in electric devices. However, for practical applications, a good substrate is necessary. Moreover, further orbital analyses suggest that the energy bands at the K point are composed of 5P_z hybrid orbitals of the Sn atoms, which ensures the stability of stanene by forming π-bonding. Fig. 2(b) shows the energy band structure of MoS₂. MoS₂ exhibits a semiconducting behavior with a direct band gap of 1.74 eV, which agrees well with previous studies,³¹ and the gap nearly covers the Dirac cone region of stanene. We expected that MoS₂ may be an ideal substrate to tune the electric structure of stanene while contributing no additional transport channels near the Fermi surface. Based on these considerations, we investigated the electric properties of the stanene/MoS₂ heterostructure in this study.

Fig. 2 Band structure of (a) 2D stanene and (b) MoS₂ monolayer.

To determine the stabilities for the three patterns of stanene/MoS₂ HTSs, we calculated the binding energy, which is defined as follows:

E_b = [E(stanene/MoS₂) − E(stanene) − E(MoS₂)]/N,

where E(stanene/MoS₂), E(stanene), and E(MoS₂) are the energies of the stanene/MoS₂ HTS, isolated stanene, and MoS₂ monolayer, respectively. N is the number of Sn atoms for stanene. These values are listed in Table 1. The binding energy values are −39.63 meV, −39.38 meV, and −39.75 meV for the hollow, Mo, and S patterns, respectively, indicating weak physical interactions in the HTS interface. To further ensure the stability of the structure, we also investigated the interlayer spacing for all patterns. The interlayer spacing was 3.12, 3.21, and 3.20 Å for the hollow, Mo, and S patterns, respectively. These results are clearly consistent with those obtained by the Grimme's method and the values are appropriate for realizing the HTS, which suggests that our results are reliable and the stanene/MoS₂ HTS is feasible.

Table 1 Detailed structural and electronic information for stanene/MoS₂, including binding energies (E_b) (per Sn atoms), optical band gap (E_g), interlayer distance (d), as well as the effective masses of electrons (m_e) and holes (m_h) for the three configurations at the K point along the K–M and K–Γ directions. Herein, m₀ is the free electron mass

Configuration	Eb (meV)	Eg (meV)	d (Å)	me^KM	me^KΓ	mh^KM	mh^KΓ
Stanene/hollow	−39.63	76.5	3.26	0.0517m0	0.0566m0	0.0517m0	0.0568m0
Stanene/Mo	−39.38	71.9	3.36	0.0481m0	0.0531m0	0.0479m0	0.0531m0
Stanene/S	−39.75	73.2	3.34	0.0506m0	0.0554m0	0.0506m0	0.0555m0

---

To explore how the electronic structure of stanene can be affected by the MoS₂ substrate, we examined the band structures of the stanene/MoS₂ HTSs, as shown in Fig. 3. For the hollow pattern, due to the strong interaction between stanene and the MoS₂ substrate, the high symmetry of the honeycomb-like structure of stanene is broken, and stanene undergoes a slight deformation that leads to opening a 76.5 meV band gap at the K point. However, the linear Dirac dispersion is nearly well-preserved, slightly away from the K point, suggesting that there is still a high carrier mobility for stanene grown on the MoS₂ substrate. On the other hand, the binding energy of stanene/MoS₂ (hollow) is −39.63 meV, as shown in Table 1. Therefore, it was easy to prepare stanene on a MoS₂ substrate via the existing fabrication process such as high-speed centrifugation. It provides a possible way to prepare semiconductors with high carrier mobility for electronic applications. Compared with the hollow pattern, the Mo and S patterns presented similar results. Therefore, MoS₂ is a good substrate for all three patterns considered herein.

Fig. 3 Band structures of stanene/MoS₂ HTSs: (a) hollow pattern, (b) Mo pattern, and (c) S pattern. The red dots represent the contribution from Sn atoms, the blue dots represent the contribution from MoS₂ and the black line represents the band structure of stanene/MoS₂.

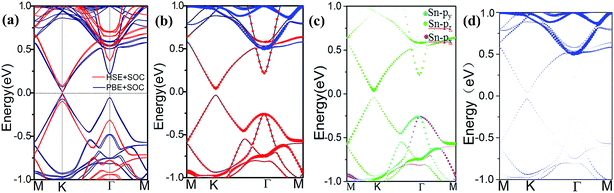
The spin–orbit coupling (SOC) opened a band gap at the Dirac point, however, the associated gap due to rather weak second-order effective SOC was too small (∼10⁻³ meV), which makes the quantum spin Hall (QSH) effect in silicene and germanene only appear at an unrealistically low temperature.^32,33 In addition, the GGA method usually underestimates the band gap. Therefore, we conducted calculations based on the hybrid HSE06 functional to assess the robustness of the results obtained herein with the PBE functional. Fig. 4(a) shows the DFT- and HSE-fitted band structures with SOC. It can be observed that the effect of SOC can change the value of the band gap but can not induce a band gap inversion in all systems. The band structure calculation at the PBE level reports a band gap of 11.9 meV, and HSE06 calculated results are essentially identical to the PBE results except for the increased band gap of 20.1 meV. We took the hollow pattern as an example to analyze the orbital components of the energy bands near the Fermi level. As shown in Fig. 4(b) and (d), we can find that the band gap at the K point is mainly due to the stanene layer, whereas orbitals due to MoS₂ are mainly distributed in the energy region from 0.6 eV to 1.0 eV. As shown in Fig. 4(c), to further analyze the orbit components, we extracted and plotted the orbitals due to stanene by projecting the bands on different atomic orbitals. We found that the valence band maximum (VBM) and the conduction band minimum (CBM) near the Fermi level was two-fold degenerated with the features of binding states of P_z orbitals from the Sn atoms. At the Γ point, the VBM is formed by the P_x and P_z orbitals of the Sn atoms, whereas the CBM contains the anti-bonding state features of P_z orbital. Overall, for the band structure, the main feature is the P_z orbital from the Sn atoms, which is similar to the band structure of isolated stanene. In isolated stanene, the Dirac point is protected by crystal symmetry. However, the match between stanene and the MoS₂ substrate will break this symmetry, leading to the opening of a direct band gap. However, the MoS₂ orbitals do not hybridize with the stanene orbitals at the K point near the Fermi level, and the only effect of the substrate is to tune the electronic structure at the K point, which suggests that MoS₂ is an ideal substrate and electric carriers will transport through the stanene layer only.

Fig. 4 Band structure for the hollow pattern of the stanene/MoS₂ HTS: (a) electronic band structure obtained based on PBE/HSE06 functional for the hollow-pattern stanene/MoS₂ HTS including SOC; (b) orbital-resolved band structure for stanene/MoS₂; (c) orbital-resolved band structure for stanene; and (d) orbital-resolved band structure for MoS₂. The red dots represent the contribution from Sn atoms, the blue dots represent the contribution from MoS₂, and the black line represents the band structure of stanene/MoS₂.

A high carrier mobility is essential for practical applications in field-effect-transistors.³⁴ We estimated the carrier mobility of the stanene/MoS₂ HTS by calculating the effective mass of electrons (m_e) and holes (m_h) in the valence and conduction bands at the Dirac point of stanene/MoS₂ for the three patterns of the HTSs, respectively. The effective particle mass is expressed as follows:^35,36

where k is the wave vector, ħ is the reduced Planck constant, and E(k) is the dispersion relation. Table 1 lists m_e and m_h along the K–M and K–Γ directions. The calculated effective mass of electrons (m_e) and holes (m_h) were found to be very small, in the range of 0.0479–0.0568m_e. These values are higher than the previously reported values for graphene and silicene HTSs.^37,38 Based on the relationship between carrier mobility (μ) and effective mass, the carrier mobility can be calculated as μ = eτ/m, where τ is the scattering time.^35,39 Assuming that stanene has the same scattering time as graphene or silicene (∼10⁻¹³ s),^35,39 the carrier mobility of the HTS is estimated to be of the order of ∼10⁵ cm² V⁻¹ s⁻¹, which is similar to that of germanene as obtained by organic molecule adsorption (∼10⁵ cm² V⁻¹ s⁻¹)³⁹ and silicene (∼10⁵ cm² V⁻¹ s⁻¹).³⁵ In addition, the carrier mobility is larger than that observed for pristine stanene.⁴⁰ As is known, carrier mobility can affect the conductivity of transistor and the working efficiency of the device.⁴¹ These results demonstrate that this HTS is an ideal material for FETs, with a high carrier mobility and tunable band gap (the band gap opening in stanene/MoS₂ can be effectively modulated by applying an external strain and changing the interlayer spacing, as has been described hereinafter). In addition, these results also shed light on its experimental applications.

By studying the structural stability, electric structure and carrier mobility, we found that MoS₂ is an ideal substrate for stanene since it opens a band gap at the original Dirac point of isolated stanene and contributes no additional transport channels near the Fermi level. The band gap makes stanene/MoS₂ HTS exhibit a large mobility and opening a band gap in this HTS will provide an ideal platform for potential applications in experiments and electronic devices. As it is known, external strain is a common method in the industry to tune the electric structure in semiconductors. In our material, we were tuned the interlayer spacing and the in-plane lattice constants of stanene and MoS₂ by applying an external strain. In the following section, we showed how these two parameters tune the energy gap at the K point.

First, we investigated the effect of the interlayer distance on the electronic structure of stanene/MoS₂. Our calculations indicate that there will always be an energy gap at the K point, which will maintain HTS as a semiconductor. In Fig. 5, we displayed the energy gap with respect to the spacing between the stanene and MoS₂ layers for the hollow, Mo, and S patterns. One can observe that the gap size will decrease upon increasing the interlayer spacing. This is due to the effect of the MoS₂ substrate on stanene layer that becomes weaker as the interlayer spacing increases, leading to the separation of two Sn–P_z bands from each other at the Fermi level. With respect to symmetry, as the interlayer spacing changes, the size of the induced band gap in stanene is related to symmetry breaking of the two stanene sublattices, which is due to the substrate (MoS₂) effect and the stanene layer tends to recover the original symmetry,^42–44 which preserves the Dirac point at the K point. In addition, with the decrease of interlayer spacing, the interactions between the stanene and MoS₂ monolayers become stronger due to a symmetry breaking potential, thus leading to a decrease in the energy gap, as we can see in Fig. 5. Remarkably, for the distance of −0.2 Å, the largest gap about 77.4 meV, 73.0 meV, and 75.4 meV for hollow, Mo, and S patterns, respectively, was observed. The stanene/MoS₂ still retains the semiconductor properties and the linear Dirac dispersion is nearly well-preserved, slightly away from the K point. The two layers would separate from each other when the interlayer spacing changes, which can cause a shift of the energy levels and thus a change in the band gap.

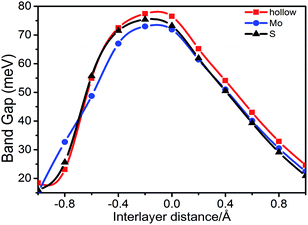Fig. 5 Band gap for the hollow, Mo, and S patterns, respectively, as a function of the spacing between the stanene and MoS₂ monolayer.

Elastic strain engineering is another route to continuously tune the energy gap. External strain will change the lattice constants measured by ε = (a − a₀)/a₀, where a (a₀) is the lattice constant with (without) strain and ε denotes the strength of the strain. Fig. 6 presents the variation in the band gap of stanene/MoS₂ for all three patterns under external strain ε. The strain has dramatic effects on the electronic properties of stanene/MoS₂. If we observe the hollow pattern [Fig. 6(a)], we can see that increasing the lattice constant will continuously decrease the energy gap. A straightforward explanation is that the hopping strength or bonding energy is weakened, leading to a narrower energy range. Upon increasing the strain applied on stanene/MoS₂, the lattice relaxes, the interactions between stanene and MoS₂ are weakened, and the Sn–Sn bonds are stretched, thus weakening π-bonding between Sn atoms, leading to a smaller band gap. This result is similar to the results obtained in previous studies with a tight-binding model.^45,46 Another effect of strain is to tune the Fermi level, with a metal–semiconductor phase transition occurring under a large enough strain. At a large enough tensile (compressive) strain, self-hole-doping (self-electron-doping) regime with hole (electron) carriers was observed.

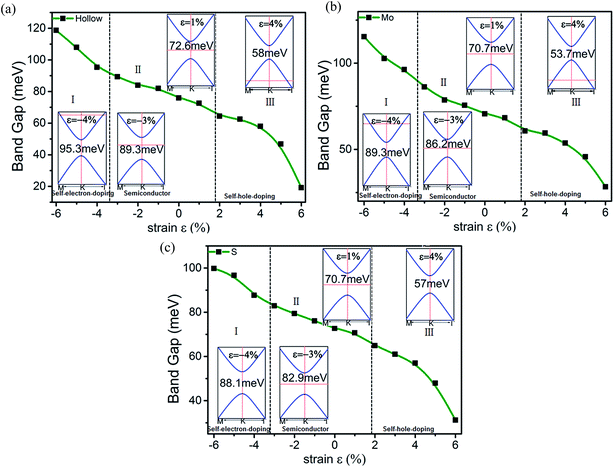Fig. 6 Changes in the band gap of the HTSs as a function of strain for the (a) hollow pattern, (b) Mo pattern, and (c) S pattern.

Herein, it is demonstrated that strain can cause a metal–semiconductor phase transition, which is consistent with the common pressure-induced metal–insulator phase transitions in three-dimensional materials. The stanene/MoS₂ heterostructure of Mo and S patterns under strain share properties qualitatively consistent with those of the hollow pattern and therefore a similar analysis applies as well, which has not been discussed herein. Our results show that the band gap in the stanene/MoS₂ HTS can be conveniently tuned by external strain, making it a promising platform for applications in experiments and electronic devices.

IV. Conclusion

In summary, we systematically investigated the electronic properties of the stanene/MoS₂ heterostructure by first-principles calculations. We calculated and determined the electronic structure for three different patterns of the free heterostructure, and then focused on the effect of an external strain, which would change the interlayer spacing and lattice constants in both the stanene and MoS₂ layers. The MoS₂ substrate induces an energy gap at the K point in stanene and preserves the linear Dirac dispersion slightly away from the K point while contributing no additional transport channels near the Fermi level. Our calculations suggest that the stanene/MoS₂ heterostructure has a high carrier mobility, which is beneficial for electronic applications. Our results indicate that the band gap of all these HTSs can be continuously modulated by external strain to meet the demands in experiments and device design. In our opinion, the MoS₂ substrate makes stanene a feasible platform to realize Sn-based nanostructures for applications in experiments and nanoelectronics.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 61571210, 61172028, 11274143, and 11304121).

References

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
2. M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2010, 110, 132–145.
3. Q. Tang and Z. Zhou, Prog. Mater. Sci., 2013, 58, 1244–1315.
4. A. K. Geim, Science, 2009, 324, 1530–1534.
5. G. G. Guzman-Verri and L. C. Lew Yan Voon, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 76, 12825–12834.
6. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang and Y. Zhang, Science, 2004, 306, 666–669.
7. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Doubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
8. D. L. Miller, K. D. Kubista, G. M. Rutter, M. Ruan, W. A. de Heer, P. N. First and J. A. Stroscio, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125427.
9. Y. Jing, X. Zhang, D. H. Wu, X. D. Zhao and Z. Z. Hou, J. Phys. Chem. Lett., 2015, 6, 4252.
10. R. W. Zhang, C. W. Zhang, W. X. Ji, S. S. Li and S. J. Hu, New J. Phys., 2015, 17, 083036.
11. F. F. Zhu, W. J. Chen, Y. Xu, C. L. Gao, D. D. Guan, C. H. Liu, D. Qian, S. C. Zhang and J. F. Jia, Nat. Mater., 2015, 14, 1020–1025.
12. B. Peng, H. Zhang, H. Z. Shao, Y. C. Xu, X. C. Zhang and H. Y. Zhu, Sci. Rep., 2016, 6, 20225.
13. M. Modarresi, A. Kakoee, Y. Mogulkoc and M. R. Roknabadi, Comput. Mater. Sci., 2015, 101, 164–167.
14. S. S. Li and C. W. Zhang, Mater. Chem. Phys., 2016, 173, 246–254.
15. R. W. Zhang, C. W. Zhang, W. X. Ji, S. S. Li, S. S. Yan, S. J. Hu, P. Li, P. Wang and F. Li, Sci. Rep., 2016, 6, 18879.
16. D. Wang, L. Chen, X. Wang, G. Cui and P. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 26979–26987.
17. Y. Fang, Z. Q. Huang, C. H. Hsu, X. Li, Y. Xu, Y. Zhou, F. Chuang and Z. Zhu, Sci. Rep., 2015, 5, 14196.
18. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
19. M. Houssa, B. van der Broek, E. Scalise, G. Pourtois, W. Afanas'ev and A. Stesmans, Phys. Chem. Chem. Phys., 2013, 15, 3702–3705.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
21. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
22. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
23. J. Heyd, G. E. Scuseria and M. J. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
24. J. Heyd, G. E. Scuseria and M. J. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
25. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
26. S. C. Wu, G. C. Shan and B. H. Yan, Phys. Rev. Lett., 2014, 113, 256401.
27. C. Ataca, H. Şahin, E. Aktürk and S. Ciraci, J. Phys. Chem. C, 2011, 115, 3934–3941.
28. K. F. Mak, K. L. He, C. G. Lee, G. H. Lee, J. Hone, T. F. Heinz and J. Shan, Nat. Mater., 2013, 12, 207–211.
29. H. Wang, S. T. Pi, J. Kim, Z. Wang and H. H. Fu, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 035112.
30. F. F. Zhu, W. J. Chen, Y. Xu, C. L. Gao and D. D. Guan, Nat. Mater., 2015, 14, 1020–1025.
31. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 474–479.
32. S. Cahangirov, M. Messer, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
33. C. C. Liu, W. X. Feng and Y. Q. Yao, Phys. Rev. Lett., 2011, 107, 076802.
34. R. Zhang, C. Zhang, H. Luan, W. Ji and P. Wang, RSC Adv., 2015, 5, 35377–35383.
35. R. W. Zhang, C. W. Zhang, W. X. Ji, S. J. Yan, S. S. Li, P. Li, P. J. Wang and Y. S. Liu, J. Phys. Chem. C, 2014, 118, 25278–25283.
36. S. S. Li, C. W. Zhang, S. S. Yan, S. J. Hu, W. X. Ji, P. J. Wang and P. Li, J. Phys.: Condens. Matter, 2014, 26, 395003.
37. R. Zhang, C. Zhang, W. Ji, F. Li, M. Ren, P. Li, M. Yuan and P. Wang, Phys. Chem. Chem. Phys., 2015, 17, 12194–12198.
38. K. Chen, X. Wan and J. Xu, J. Mater. Chem. C, 2013, 1, 4869–4878.
39. Y. P. Wang, W. X. Ji, C. W. Zhang, S. S. Li, F. Li, P. Li, M. J. Ren, X. L. Chen, M. Yuan and P. J. Wang, Mater. Chem. Phys., 2016, 173, 379–384.
40. S. S. Li, C. W. Zhang, W. X. Ji, F. Li, P. J. Wang and S. S. Yan, Phys. Chem. Chem. Phys., 2014, 16, 15968–15978.
41. M. V. Fischetti and S. E. Laux, J. Appl. Phys., 1996, 80, 2234–2252.
42. L. Li and M. Zhao, J. Phys. Chem. C, 2014, 118, 19129–19138.
43. L. Li, X. Wang, X. Zhao and M. Zhao, Phys. Lett. A, 2013, 377, 2628–2632.
44. L. Li and M. Zhao, Phys. Chem. Chem. Phys., 2013, 15, 16853–16863.
45. M. Zhao, X. Zhang and L. Li, Sci. Rep., 2015, 5, 16108.
46. M. Zhao, X. Chen, L. Li and X. Zhang, Sci. Rep., 2015, 5, 8441.

---