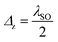Open Access Article
Open Access ArticleThe effect of Rashba spin–orbit coupling on the spin- and valley-dependent electronic heat capacity of silicene
Mohsen Yarmohammadi
Young Researchers and Elite Club, Kermanshah Branch, Islamic Azad University, Kermanshah, Iran. E-mail: m.yarmohammadi69@gmail.com
First published on 8th February 2017
Abstract
Through restructuring of the electronic spectrum of two-dimensional massive fermions in buckled silicene under an applied electric field and induced exchange field, we have studied how Rashba spin–orbit coupling enhances the electronic band structure and electronic heat capacity of the system. Special attention was given to investigate the spin- and valley-dependent electronic heat capacity. By variation of the electric field, system transitions occurred from the topological insulator phase to the band insulator phase. The Kane–Mele Hamiltonian model and the Green’s function technique were used in this work. The first remarkable point is the unchanged (changed) subband gap size (effective mass of fermions) with Rashba coupling for all phases. We have found a critical Dirac-like point which affects the effective mass of the carriers in the band insulator phase. And finally, we found that variation in the Hall conductivity with Rashba coupling leads to quantized Hall conductivity, which was the main result of the current study: a new quantum anomalous Hall effect at large Rashba coupling strengths. The presented methodology may be extended to other two-dimensional materials, like germanene and stanene.
1 Introduction
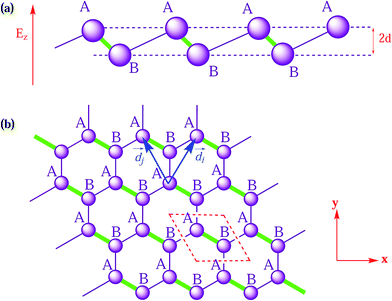
In the past decade, after the revolutionary breakthrough of honeycomb graphene,1 great interest in novel two-dimensional (2D) materials has continuously grown. Their interesting physics and diverse applications have been extensively studied both theoretically and experimentally.1–6 In particular, the possibility of obtaining new semiconducting materials has been studied. In graphene, the low-energy carriers near the two nodal (“Dirac”) points in the first Brillouin zone (FBZ) posses linear energy spectra and behave as Dirac massless relativistic fermions.7–9 This limits the use of graphene in electronic technology. In new materials, a band gap can be tuned using external electric bias which was first demonstrated for bilayer graphene.10 The creation of a band gap as a tunable semiconducting gap has its uses in tunable transistors.A close cousin of graphene is a graphene-like 2D honeycomb lattice of silicon atoms called silicene. Its important structural difference from graphene is that it consists of a puckered structure due to tetrahedral sp3 hybridization over sp2, leading to a band gap under normal-to-plane electric bias.11–13 Interest in silicene has soared due to its possible future applications in spintronics14–16 and valleytronics17–21 at room temperature. Sublattice A and B atoms in silicene are displaced from each other in the out-of-plane direction with a distance d ≃ 0.46 Å,22–24 as presented in Fig. 1. Additionally, the buckled lattice structure of silicene enables us to break the inversion symmetry of the sublattices by applying an external perpendicular electric field which induces an energy gap of 2Δz (Δz is the characteristic energy of the electric field).11,25–27 On the other hand, this inversion symmetry breaking causes significant intrinsic spin–orbit coupling (SOC) at the Dirac points which may reach a value of about 2λSO = 1.55–7.9 meV (λSO is the characteristic energy of SOC).28
The SOC is predicted to bring about many intriguing physical properties, such as the quantum spin Hall effect12,29,30 which exhibits a new quantum state of matter with non-trivial topological properties. SOC provides a mass to the Dirac points, the effective mass of which could be controlled to undergo a topological phase transition from a quantum spin Hall state (|Δz| < |λSO|) to a band insulator state (|Δz| > |λSO|).31–33 It is necessary to mention that the on-site energies of the different sublattices separate the spin-up and spin-down bands.25 Furthermore, a wealth of fascinating features of silicene have been investigated and reported theoretically, including the quantum anomalous Hall (QAH) effect and valley-polarized quantum Hall effect in the presence of an external electric field.
Internal magnetization can also break the time reversal symmetry of a system without the need for an external magnetic field. When coupled with the special band structures and SOC of the system, it can generate the so-called QAH effect, which was first proposed by Haldane.9 The topology of a QAH state is characterized by the appearance of quantized Hall conductivity in the absence of an external magnetic field. To acquire QAH insulators, the following four conditions should be satisfied simultaneously; they must be 2D systems, insulators, have long-range ferromagnetic order, and special band structures with a finite Chern number. To obtain the QAH effect, the system must satisfy two conditions: (i) the state with one kind of spin is in the inverted regime while the other is in the normal regime, and (ii) the entire system is still in the insulating state with a bulk band gap.
Generally, the extrinsic Rashba SOC (RSOC) of pristine silicene is zero because of its structure inversion symmetry. Also, extrinsic RSOC induced by an external electric field is negligible,33 but strong extrinsic RSOC may arise due to metal-atom adsorption or for substrates, as it dramatically breaks the structure inversion symmetry of the system, as has been discussed for graphene.34–37 Recently, first-principles calculations have shown that a strong extrinsic SOC effect in silicene with adsorption of different transition metal atoms attributes ∼7–44 meV to the band gap,38 which is much larger than the gap (1.55 meV) of pristine silicene. Ferromagnetic substrates and transition metal adatoms can also induce a sizable exchange field.39,40 One can also induce an exchange field M in silicene by putting a ferromagnet near its surface and further influence its spin properties. Combined with the spin and valley dependence of the gap and the fact that silicene has a longer spin-diffusion time15,41 and spin-coherence length42 than graphene,43 this makes silicene an excellent candidate for applications in spintronics and valleytronics.
Beside its electronic properties, the thermal properties of silicene are still not well studied. Due to the specific lattice of monolayer silicene, the investigation of the thermal conductivity and thermodynamic properties is interesting. A lot of work has been done to investigate this case, for example the thermal conductivity of silicene is predicted to be around 20–65 W mK−1 in ref. 44–48. The thermal properties of the materials could be reflected in their heat capacity (HC) and thermal conductivity (TC). The HC of a system is defined as the ratio of the heat added to (or removed from) the matter to the resulting temperature change.49 Generally, there exist two mechanisms governing the thermal behavior of the matter, phonons and electrons, from which the latter has been shown to have a much smaller contribution.50–52 However, in cases of high electron concentration and decreased phonon mean free path, the electronic role could also be important. Furthermore, the electronic contribution to the HC depends directly on the electronic structure and basically reflects the details of the excitation spectrum. So it is better to take it into account to achieve a more accurate figure. In this respect, the electronic HC (EHC), defined as the ratio of the portion of heat used by the electrons to the rise in temperature, could easily be extracted.52
In this work, we have reproduced and investigated the effect of the electric field and RSOC on the electronic band structure (EBS) and EHC of a ferromagnetic silicene material in three phases at Dirac points. Green’s function approach is carried out in addition to the Kane–Mele Hamiltonian to study the dynamics of massive carriers. The outline of this paper is as follows: Section 2 describes the Hamiltonian and calculation details, Section 3 shows the calculated Berry curvature, Chern number and Hall conductivity, in Section 4 the numerical results are explained, and the conclusions are given in Section 5.
2 The effective Hamiltonian model, spin- and valley-dependent energy dispersions and electronic heat capacity
The low-energy excitation of the fermions in the silicene system, which is considered as a monolayer sheet consisting of two sublattices A and B, can be described by a four bands second-nearest neighbor tight-binding model as follows:33,53
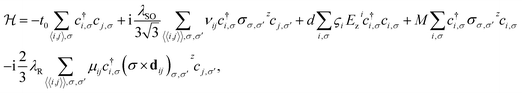 | (1) |
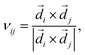 with the two nearest bonds
with the two nearest bonds ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i and
i and ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) j connecting the next-nearest neighbors dij, and μij = ±1 for the A(B) sites, as shown in Fig. 1. The third term is the staggered sublattice potential, where ςi = ±1 for the A(B) sites. The fourth term is for the magnetic ordering where an exchange interaction with strength M is induced by the magnetic insulator substrates. Finally, the RSOC term is denoted by the last term λR ≃ 0.7 meV. By performing a Fourier transformation in the continuum model, the low-energy effective Hamiltonian in the vicinity of the K and K′ points is
j connecting the next-nearest neighbors dij, and μij = ±1 for the A(B) sites, as shown in Fig. 1. The third term is the staggered sublattice potential, where ςi = ±1 for the A(B) sites. The fourth term is for the magnetic ordering where an exchange interaction with strength M is induced by the magnetic insulator substrates. Finally, the RSOC term is denoted by the last term λR ≃ 0.7 meV. By performing a Fourier transformation in the continuum model, the low-energy effective Hamiltonian in the vicinity of the K and K′ points is
![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) η(k) = ℏνF(kx η(k) = ℏνF(kx![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) x − ηky x − ηky![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) y) − ηλSO y) − ηλSO![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) z z![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z + ηaλR z + ηaλR![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) z(kx z(kx![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y − ky y − ky![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x) + Δz x) + Δz![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) z − M z − M![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z, z,
| (2) |
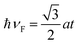 with the lattice constant a = 3.86 Å. The Green’s function matrix of the system can be readily obtained using the following equation:
with the lattice constant a = 3.86 Å. The Green’s function matrix of the system can be readily obtained using the following equation:
Gη−1(k,iωn) = iωnÎ − ![[script letter H]](https://www.rsc.org/images/entities/i_char_e142.gif) η(k). η(k).
| (3) |
Having substituted eqn (2) into (3), the explicit form of the Green’s function matrix has been found but has not been written here because it is quite lengthy.
The DOS can be calculated by the trace of the imaginary part of the Green’s function matrix, 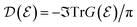 .54 Taking the trace over the quantum numbers which label the Hamiltonian, using eqn (2) and (3) along with setting iωn → ε + i0+ as an analytical continuation (0+ being a very small real number), the total DOS would become
.54 Taking the trace over the quantum numbers which label the Hamiltonian, using eqn (2) and (3) along with setting iωn → ε + i0+ as an analytical continuation (0+ being a very small real number), the total DOS would become
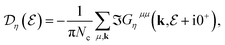 | (4) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/i_char_e140.gif) (k) of eqn (2) which give the EBS as follows:
(k) of eqn (2) which give the EBS as follows:
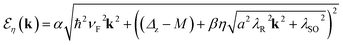 | (5) |
| ψηn(k) = (ψη1n(k), ψη2n(k), ψη3n(k), ψη4n(k))T |
 | (6) |
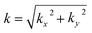 .
.
The DOS and EBS have the same meaning for studying band gaps. The EHC could be introduced using the following expression:55
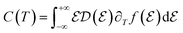 | (7) |
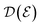 is calculated using eqn (4) and f(
is calculated using eqn (4) and f(![[scr E, script letter E]](https://www.rsc.org/images/entities/i_char_e140.gif) ) = 1/[e
) = 1/[e![[scr E, script letter E]](https://www.rsc.org/images/entities/i_char_e140.gif) /kBT + 1] (kB is the Boltzmann constant) represents the Fermi–Dirac distribution function. By using eqn (4) and (7), the EHC would be obtained as
/kBT + 1] (kB is the Boltzmann constant) represents the Fermi–Dirac distribution function. By using eqn (4) and (7), the EHC would be obtained as
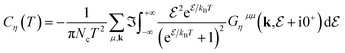 | (8) |
3 Berry curvature, Chern number and Hall conductivity
The SOC-induced insulating state is topologically nontrivial and exhibits quantized charge Hall conductivity, which can be identified by calculating the Berry curvature and Chern number. The Berry curvature Ωηn(k) is calculated as follows:56–58
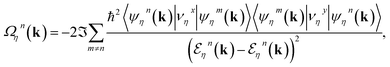 | (9) |
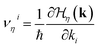 are the velocity operators. By integrating the Berry curvature over the FBZ, the Chern number C and Hall conductivity σxy can be obtained as
are the velocity operators. By integrating the Berry curvature over the FBZ, the Chern number C and Hall conductivity σxy can be obtained as
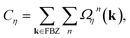 | (10) |
and
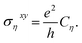 | (11) |
The absolute value of the Chern number corresponds to the number of gapless chiral edge states along each side of the sample.
4 Numerical results and discussions
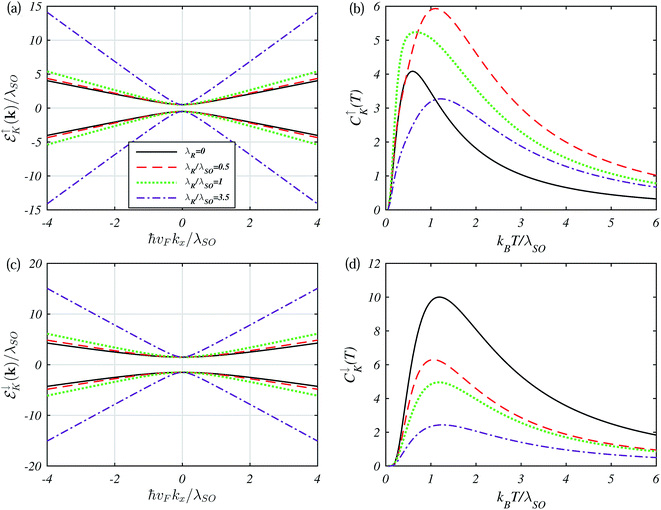
As far as we know, there is symmetry behavior between two Dirac points, K and K′, and also both spins. Here, we consider only the K point because at the K′ point the spin labels only switch. The presented panels in Fig. 2 of the electronic spectrum in silicene within the framework of the Kane–Mele Hamiltonian model for external electric field perturbation show a variety of restructuring processes with different dynamics for its particular spin subbands. At Δz = dEz = 0, all the spin-dependent EBSs have the same absolute values as the spin degeneracy of the bands. As dEz increases, the spin-up band gap decreases until Δz = λSO while the spin-down band gap increases gradually. At Δz = λSO, the spin-up band gap closes, forming a Dirac-like point and then reopens as Δz continues to increase. The Dirac nature of the fermions in silicene makes a topological insulator (TI) phase which for Δz = λSO the system is referred to as a valley-spin-polarized metal (VSPM) phase. For Δz > λSO, a transition from the TI phase to the band insulator (BI) phase is found, in agreement with ref. 11, 25 and 26. Likewise, one can further prove the behaviors based on perturbation induced by an electric field. For spin-down (up) electrons from valley K (K′), the transport gap is symmetric about the Fermi energy, while such electron–hole symmetry cannot drive a non-zero current. Actually, it is the electron–hole symmetry of the spin bands. An exchange field of M = λSO/2, on the order of meV, can be fully achieved in silicene using an appropriate ferromagnetic insulating substrate (for instance, EuS) without inducing external Rashba-type interactions. This is according to the latest experimental report on graphene59 where such a strength of M (depending critically on the sample quality) was realized.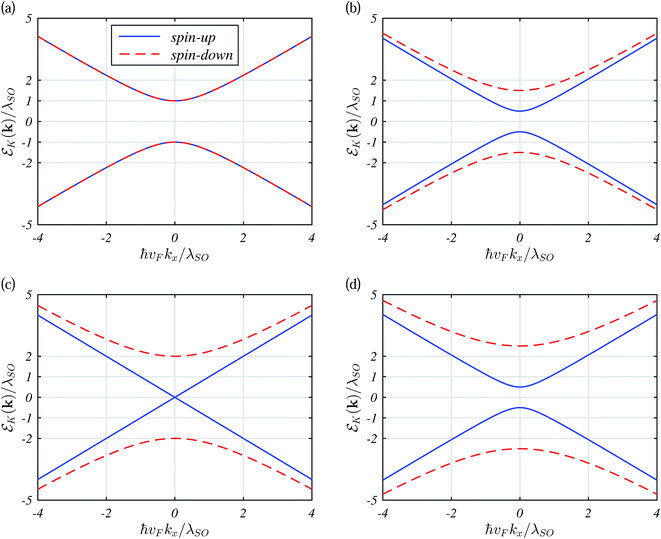 | ||
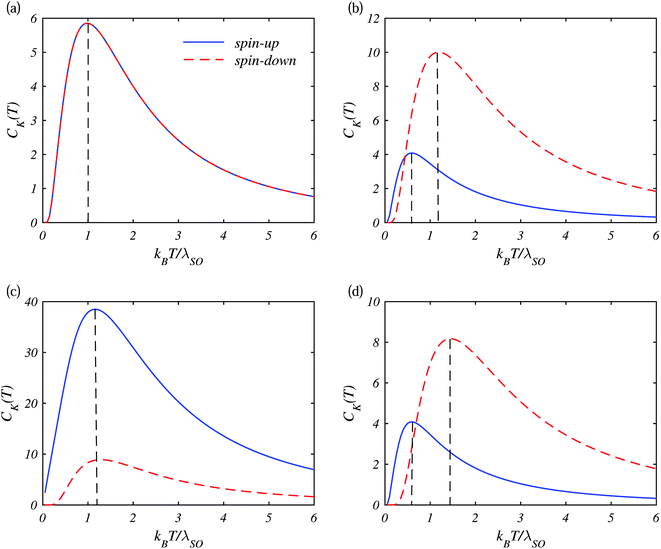
Fig. 2 Dispersion curves for silicene for both spin-up and spin-down subbands by increasing the electric field Δz as (a) Δz = 0 (TI), (b) 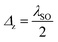 (TI), (c) Δz = λSO (VSPM) and (d) (TI), (c) Δz = λSO (VSPM) and (d) 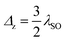 (BI). (BI). | ||
It is well-known that the EHC of semiconductors at low temperatures can be written as C(T) ∝ e−Δ/kBT.49,55,60 The Schottky anomaly as an interesting effect can be explained with the change of entropy of a system. As we know, at zero temperature only the lowest energy level is occupied and the entropy is zero. In this regard, there is very little probability of a transition to a higher energy level but as the temperature increases, entropy increases and therefore the probability of a transition goes up. As the change in temperature closes the difference between the energy levels in the system, there is a broad peak corresponding to a large change in the entropy for a small change in the temperature. At high temperatures, all levels are occupied and there is again a little change in the entropy for small changes in the temperature and thus a lower EHC is obtained.61 Here, Δ is the combined electric field and RSOC potentials. The corresponding curves for the EHC in the TI, VSPM and BI regimes are presented in Fig. 3. TSchottky (≃ΔSO/kB) is constant for each spin in panel (a). The reason why the heat capacity can be tuned by the electric field is related to the band gap sizes in Fig. 2 based on eqn (8). By decreasing (increasing) the band gaps, the EHC moves towards lower (higher) temperatures due to the above mentioned relationship. At Δz = λSO, the corresponding case for the VSPM phase, the spin-up EHC has a larger value than the spin-down EHC due to spin polarization.62 In our analysis, we have considered only the electronic contribution in the EHC and neglect the phonon contribution.
 | ||
| Fig. 3 Temperature dependence of the electronic heat capacity in the TI, VSPM and BT phase for both spins. | ||
In Fig. 4, we show how the spin-dependent EBS and EHC behave as a function of RSOC at the given values of Δz = 0 and 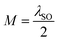 . Panels (a) and (b) show the calculated energy eigenvalues and EHC of silicene corresponding to valley K within a continuous model. For silicene, λR is small compared to λSO.26 The low-energy band gap spectrum of silicene is independent of λR for both spins, as shown in panels (a) and (c). Only the slope of the curves is changed with λR, leading to a change in the effective mass of the fermions,
. Panels (a) and (b) show the calculated energy eigenvalues and EHC of silicene corresponding to valley K within a continuous model. For silicene, λR is small compared to λSO.26 The low-energy band gap spectrum of silicene is independent of λR for both spins, as shown in panels (a) and (c). Only the slope of the curves is changed with λR, leading to a change in the effective mass of the fermions, 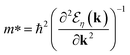 . Therefore, by increasing λR, m* decreases which causes the transport of small carriers. Qualitatively, from a scattering point of view, the presence of small λR introduces a small scattering rate, resulting in a lower EHC. Because of the symmetry behaviors of the spin-up and spin-down subbands, our analyses are the same for panels (c) and (d) and there is no difference between the cases of spin-up and spin-down subbands.
. Therefore, by increasing λR, m* decreases which causes the transport of small carriers. Qualitatively, from a scattering point of view, the presence of small λR introduces a small scattering rate, resulting in a lower EHC. Because of the symmetry behaviors of the spin-up and spin-down subbands, our analyses are the same for panels (c) and (d) and there is no difference between the cases of spin-up and spin-down subbands.
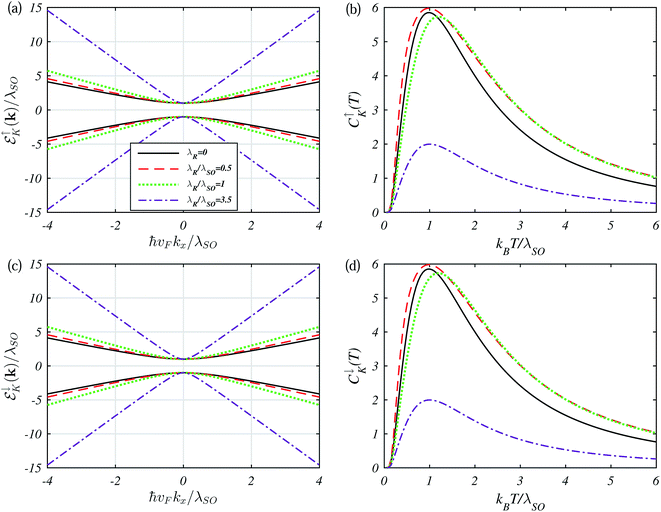 | ||
Fig. 4 Band structure of (a) spin-up and (c) spin-down subbands. (b) and (d) are the corresponding electronic heat capacities as a function of temperature for the TI regime at Δz = 0 and 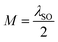 . . | ||
The previous analysis for the behavior of the subband slopes with λR is valid here in the case of 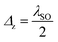 , as illustrated in Fig. 5(a) and (c), in agreement with ref. 20 and 33. For Δz < λSO, the system is in the TI phase, but the difference between Fig. 4 and 5 is the relocation of the Schottky peak in the presence of an external electric field. When both the electric field and RSOC are present in the system, their interplay leads to interesting and particular behavior of the EHC. By increasing λR, the entropy of the system increases, leading to a larger thermal energy requirement for the transition to the higher energy levels. For this reason, the Schottky anomaly is shifted to higher temperatures, which is more evident for spin-up subbands. We have found that EHC↑max occurs at
, as illustrated in Fig. 5(a) and (c), in agreement with ref. 20 and 33. For Δz < λSO, the system is in the TI phase, but the difference between Fig. 4 and 5 is the relocation of the Schottky peak in the presence of an external electric field. When both the electric field and RSOC are present in the system, their interplay leads to interesting and particular behavior of the EHC. By increasing λR, the entropy of the system increases, leading to a larger thermal energy requirement for the transition to the higher energy levels. For this reason, the Schottky anomaly is shifted to higher temperatures, which is more evident for spin-up subbands. We have found that EHC↑max occurs at 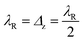 for spin-up subbands while EHC↓max appears at λR = 0 due to the large spin-down subband gap. EHC↓ decreases slightly with RSOC.
for spin-up subbands while EHC↓max appears at λR = 0 due to the large spin-down subband gap. EHC↓ decreases slightly with RSOC.
Based on the above discussions of the slopes of the EBSs and subband gap sizes, interesting behavior is found for the VSPM phase and also λR > λSO. It is necessary to say that in all the phases, λR > λSO shows this behavior more considerably than in the other cases. This scenario can be more suitably presented in the VSPM and BI phases. One can see that the linear curves in the VSPM regime convert to parabolic curves at large RSOC strengths (λR ≥ λSO), as presented in Fig. 6(a) for the spin-up subband. The corresponding EHC (panel (b)) denotes that in this phase, λR < λSO has a fluctuation in the Schottky anomaly peak and λR ≥ λSO shows double Schottky anomalies. In fact, the actual reason for the double peak is that the difference between the form of the bands due to the RSOC results in parabolic curves for each spin, thus resulting in two peaks in the EHC. For spin-down subbands, similar to when 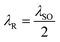 , the EHC decreases with λSO gradually.
, the EHC decreases with λSO gradually.
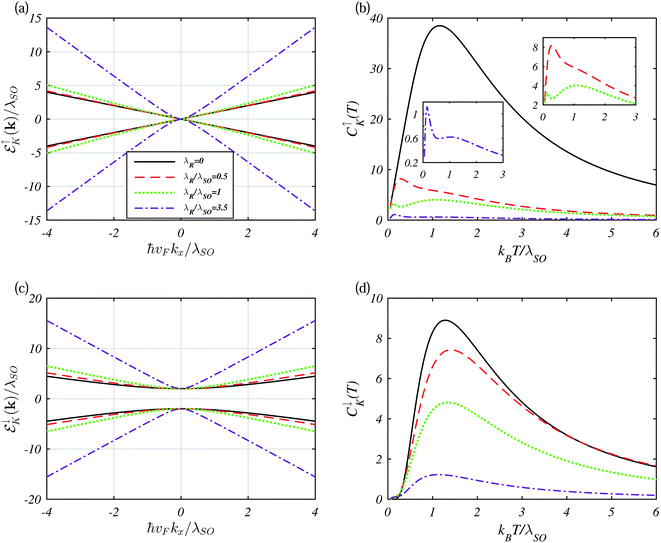 | ||
| Fig. 6 Like Fig. 5 but at Δz = λSO (VSPM). | ||
Finally, a note about the possible consequences if the SOC is superimposed on the BI phase is needed. The corresponding EBS and EHC for the BI phase, i.e., Δz > λSO, are shown in Fig. 7. For λR < λSO, the EBS slopes do not change and behave as in the previous cases, but at λR = λSO the EBS passes from λR < λSO and so curves at ![[scr E, script letter E]](https://www.rsc.org/images/entities/i_char_e140.gif) ↑K(k)/λSO = ±2 and also ħνFkx/λSO = ±2, which are the critical points for the effective mass of carriers in the BI phase (the arrows in panel (a)). After that, the spin-up subbands show two massive Dirac points at
↑K(k)/λSO = ±2 and also ħνFkx/λSO = ±2, which are the critical points for the effective mass of carriers in the BI phase (the arrows in panel (a)). After that, the spin-up subbands show two massive Dirac points at 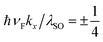 as a new quantum anomalous state. One can understand the behavior of the dotted curves for the spin-up subband in the EHC curves at very low temperatures. In this case,
as a new quantum anomalous state. One can understand the behavior of the dotted curves for the spin-up subband in the EHC curves at very low temperatures. In this case, 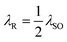 corresponds to EHC↑max and EHC↓max while EHC↑,↓min appears for λR > λSO.
corresponds to EHC↑max and EHC↓max while EHC↑,↓min appears for λR > λSO.
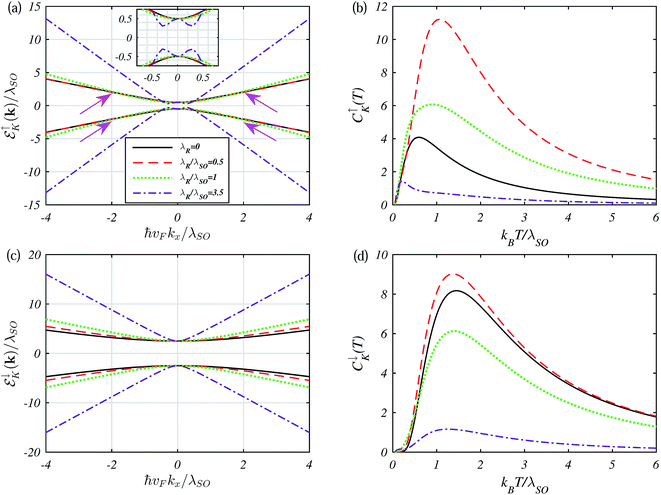 | ||
Fig. 7 Like Fig. 6 but at 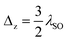 (BI). (BI). | ||
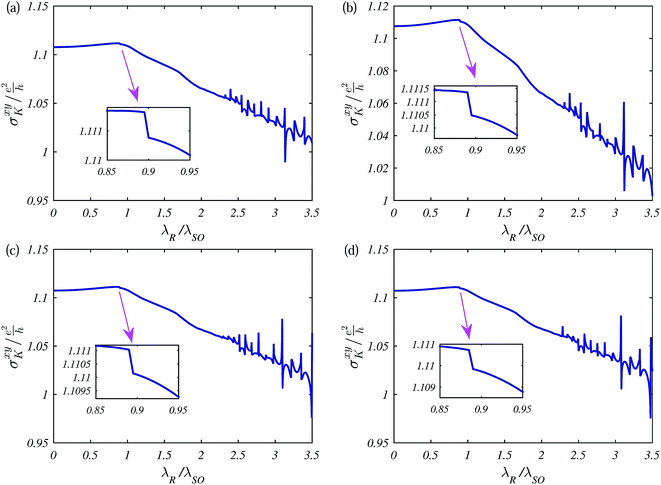
Now the time is to show how RSOC enhances the system based on the Hall conductivity plateau. Consider first the situation when λR is smaller than λSO. The corresponding Hall conductivity is shown in Fig. 8 for various λR and four different values of Δz. The general shape of the curve shows an increase of the Hall conductivity as a function of RSOC. However, the interplay of the intrinsic spin–orbit interaction and Rashba coupling leads to an interesting feature. More specifically, the conductivity increases slightly but a weak kink in the conductance appears at λR ≃ λSO. When λR increases and approaches λSO, the kink becomes more pronounced. The kink is associated with the splitting of the valence band by the Rashba interaction. Variation in the Hall conductivity with RSOC becomes more complex when both λSO and λR are comparable. Some simple analytical results, however, can be obtained for when λR = λSO. For this particular case, the bottom edges of the two conduction bands coincide with the top edge. Let us now consider the opposite case when λR is significantly larger than λSO. In this case, the conductivity is determined only by the Rashba coupling and diverges more than before, leading to an increase in the quantized Hall conductivity kinks, and resulting in a new quantum anomalous Hall state without the need for an external magnetic field. This finding is in agreement with the behavior of Hall conductivity as a function of RSOC strength in ref. 63 and 64.
5 Conclusions
To summarize, in this paper, a generalized Kane–Mele model has been used to study the effects of extrinsic Rashba spin–orbit coupling on the electronic excitations and electronic heat capacity of monolayer ferromagnetic silicene. Here we have adopted Green’s function formalism to carry out our analysis. The excitation spectrum is efficiently solved using an exact diagonalization method. The spin-dependent electronic heat capacity for specific values of the electric field, corresponding to a topological insulator, valley-spin-polarized metal and band insulator phases, has been investigated by changing the Rashba coupling strength. It has been shown that the edge subbands are more highly sensitive to large Rashba couplings in the band insulator phase than to other values of Rashba coupling. Also, large Rashba couplings quantize the Hall conductivity. In fact, we have proposed a guideline for Rashba coupling that is suitable for a new quantum anomalous Hall state without the need for an external magnetic field.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- A. Castro Neto, F. Guinea, N. Peres, K. Novoselov and A. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- S. Das Sarma, S. Adam, E. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407–470 CrossRef CAS.
- D. N. Basov, M. M. Fogler, A. Lanzara, F. Wang and Y. Zhang, Rev. Mod. Phys., 2014, 86, 959–994 CrossRef CAS.
- P. Wallace, Phys. Rev., 1947, 71, 622–634 CrossRef CAS.
- G. W. Semenoff, Phys. Rev. Lett., 1984, 53, 2449–2452 CrossRef.
- F. D. M. Haldane, Phys. Rev. Lett., 1988, 61, 2015–2018 CrossRef CAS PubMed.
- E. V. Castro, K. S. Novoselov, S. V. Morozov, N. M. R. Peres, J. M. B. Lopes dos Santos, J. Nilsson, F. Guinea, A. K. Geim and A. H. Castro Neto, Phys. Rev. Lett., 2007, 99, 216802 CrossRef PubMed.
- Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113–118 CrossRef CAS PubMed.
- L. Stille, C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195405 CrossRef.
- R. Quhe, R. Fei, Q. Liu, J. Zheng, H. Li, C. Xu, Z. Ni, Y. Wang, D. Yu, Z. Gao and J. Lu, Sci. Rep., 2012, 2, 853–856 Search PubMed.
- I. Zutic, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef CAS.
- Y. Wang, J. Zheng, Z. Ni, R. Fei, Q. Liu, R. Quhe, C. Xu, J. Zhou, Z. Gao and J. Lu, Nano, 2012, 7, 1250037 CrossRef.
- S. Rachel and M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195303 CrossRef.
- M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155415 CrossRef.
- H. Pan, Z. Li, C.-C. Liu, G. Zhu, Z. Qiao and Y. Yao, Phys. Rev. Lett., 2014, 112, 106802 CrossRef PubMed.
- A. Kundu, H. A. Fertig and B. Seradjeh, Phys. Rev. Lett., 2016, 116, 016802 CrossRef PubMed.
- T. Yokoyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 241409(R) CrossRef.
- R. Saxena, A. Saha and S. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 245412 CrossRef.
- K. Takeda and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14916–14925 CrossRef CAS.
- E. Durgun, S. Tongay and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 075420 CrossRef.
- S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804 CrossRef CAS PubMed.
- N. D. Drummond, V. Zolyomi and V. I. Falko, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 075423 CrossRef.
- M. Ezawa, New J. Phys., 2012, 14, 033003 CrossRef.
- Y. Cai, C.-P. Chuu, C. M. Wei and M. Y. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245408 CrossRef.
- C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235426 CrossRef.
- M. Tahir and U. Schwingenschlgl, Sci. Rep., 2013, 3, 1075–1080 CAS.
- M. Tahir, A. Manchon, K. Sabeeh and U. Schwingenschlogl, Appl. Phys. Lett., 2013, 102, 162412 CrossRef.
- A. Dyrda and J. Barnas, Phys. Status Solidi RRL, 2012, 6, 340–343 CrossRef.
- V. Vargiamidis, P. Vasilopoulos and G.-Q. Hai, J. Phys.: Condens. Matter, 2014, 26, 345303 CrossRef CAS PubMed.
- M. Ezawa, Phys. Rev. Lett., 2012, 109, 055502 CrossRef PubMed.
- Y. S. Dedkov, M. Fonin, U. Rudiger and C. Laubschat, Phys. Rev. Lett., 2008, 100, 107602 CrossRef PubMed.
- W. K. Tse, Z. Qiao, Y. Yao, A. H. MacDonald and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155447 CrossRef.
- J. Ding, Z. Qiao, W. Feng, Y. Yao and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195444 CrossRef.
- Z. H. Qiao, S. A. Yang, W. X. Feng, W.-K. Tse, J. Ding, Y. G. Yao, J. Wang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161414 CrossRef.
- Z. Ni, H. Zhong, X. Jiang, R. Quhe, G. Luo, Y. Wang, M. Ye, J. Yang, J. Shi and J. Lu, Nanoscale, 2014, 6, 7609–7618 RSC.
- X.-L. Zhang, L.-F. Liu and W.-M. Liu, Sci. Rep., 2013, 3, 2908 Search PubMed.
- T. P. Kaloni, N. Singh and U. Schwingenschlogl, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035409 CrossRef.
- B. Huang, D. J. Monsma and I. Appelbaum, Phys. Rev. Lett., 2007, 99, 177209 CrossRef PubMed.
- S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. van Wees, Nature, 2007, 448, 571–574 CrossRef CAS PubMed.
- E. Scalise, M. Houssa, G. Pourtois, B. Broek, V. Afanasev and A. Stesmans, Nano Res., 2013, 6, 19–28 CrossRef CAS.
- H. P. Li and R. Q. Zhang, Europhys. Lett., 2012, 99, 36001 CrossRef.
- M. Hu, X. Zhang and D. Poulikakos, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195417 CrossRef.
- Q.-X. Pei, Y.-W. Zhang, Z.-D. Sha and V. B. Shenoy, J. Appl.Phys., 2013, 114, 033526 CrossRef.
- T. Y. Ng, J. Yeo and Z. Liu, Int. J. Mech. Mater. Des., 2013, 9, 105–114 CrossRef CAS.
- R. K. Pathria, Statistical Mechanics, Oxford Press, London, 1997 Search PubMed.
- S. Ghosh, I. Calizo, D. Teweldebrhan, E. P. Pokatilov, D. L. Nika, A. A. Balandin, W. Bao, F. Miao and C. Ning Lau, Appl. Phys. Lett., 2008, 92(15), 151911 CrossRef.
- A. A. Balandin, et al., Nat. Mater., 2011, 10, 569–581 CrossRef CAS PubMed.
- V. S. Katti and S. S. Kubakaddi, Physica E, 2013, 47, 188–192 CrossRef CAS.
- C.-C. Liu, H. Jiang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195430 CrossRef.
- M. Yarmohammadi, AIP Adv., 2016, 6, 085008 CrossRef.
- C. Kittle, Introduction to Solid State Physics, Wiley, New York, 8th edn, 2004 Search PubMed.
- D. J. Thouless, M. Kohmoto, M. P. Nightingale and M. Nijs den, Phys. Rev. Lett., 1982, 49, 405 CrossRef CAS.
- M. C. Chang and Q. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 7010–7023 CrossRef CAS.
- Y. G. Yao, L. Kleinman, A. H. MacDonald, J. Sinova, T. Jungwirth, D. S. Wang, E. Wang and Q. Niu, Phys. Rev. Lett., 2004, 92, 037204 CrossRef PubMed.
- P. Wei, S. Lee, F. Lemaitre, L. Pinel, D. Cutaia, W. Cha, F. Katmis, Y. Zhu, D. Heiman, J. Hone, J. S. Moodera and C.-T. Chen, Nat. Mater., 2016, 15, 711–716 CrossRef CAS PubMed.
- X. Xu, J. Chen and B. Li, J. Phys.: Condens. Matter, 2016, 28, 483001 CrossRef PubMed.
- A. Tari, The Specific Heat of Matter at Low Temperatures, Imperial College Press, 2003, p. 250 Search PubMed.
- M. Yarmohammadi, Solid State Commun., 2017, 250, 84–92 CrossRef CAS.
- C. P. Moca and D. C. Marinescu, New J. Phys., 2007, 9, 343 CrossRef.
- Z. Yu, H. Pan and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155419 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |