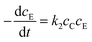Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics based on the base-catalyzed mechanism of a click reaction between glycol dimercaptoacetate and glycidyl phenyl ether†
Zhen Yaob,
Bo-en Daib,
Yun-fei Yub,
Hai-wei Jib,
Li-zhong Zhoub and
Kun Cao *ab
*ab
aState Key Laboratory of Chemical Engineering, College of Chemical and Biological Engineering, Zhejiang University, Hangzhou 310027, China. E-mail: kcao@che.zju.edu.cn; Fax: +86 0571 87951612; Tel: +86 0571 87951832
bInstitute of Polymerization and Polymer Engineering, Zhejiang University, Hangzhou 310027, China
First published on 10th February 2017
Abstract
The kinetics model of the thiol–epoxy reaction was built, and the parameters of elementary reactions were obtained according to the well-defined base-catalyzed mechanism. Through the comparison of rate constants, the rate-controlling step was proven to be the deprotonation of thiol by the base catalyst, instead of the nucleophilic attack of thiolate anion on the epoxy functional group, as previously commonly believed. Moreover, alkoxide anions tend to deprotonate unreacted thiol, rather than the conjugate acid of the base catalyst with increasing temperature. Finally, the kinetic model and its parameters have been validated using the experimental data with different initial concentrations of base catalyst, thiol and epoxy functional groups.
The concept of “Click Chemistry” has drawn intensive attention from worldwide researchers since it was raised by Sharpless and his colleagues in 2001.1 “Click Chemistry” is a collection of carbon-heteroatom bond-forming reactions that possess a fast reaction rate and high selectivity, under mild conditions. Thiol “Click Chemistry”, including thiol–ene, thiol–isocyanate, thiol–halogen and thiol–epoxy reactions, has attracted much attention in the last decade.2
While the thiol–epoxy reaction has been applied widely,3–9 the fundamental research has mainly focused on the efficiency of various base catalysts and the structure effects of thiols and epoxides. Inorganic bases like LiOH10 have strong basicity, leading to high catalytic efficiency in the thiol–epoxy reaction. However, inorganic bases cannot dissolve completely in organic solvents, which limits their application as homogeneous catalysts in thiol–epoxy reactions. Although having weaker basicity, organic bases such as 1,5,7-triazabicyclo[4.4.0]dec-5-ene (TBD),11 trimethylamine (TEA)12 and tetrabutylammonium fluoride (TBAF)13 are also frequently used in thiol–epoxy reactions due to their excellent solubility in organic solvents. To widen the application fields of the thiol–epoxy reaction, it is necessary to undertake a thorough investigation of its mechanism.
The well-acknowledged base-catalyzed mechanism of the thiol–epoxy reaction is a simple nucleophilic ring-opening reaction.2,14,15 In this mechanism, the thiol group is deprotonated by the base catalyst to form thiolate anion. Under the nucleophilic attack of the thiolate anion, the epoxy functional group is ring-opened to generate the alkoxide anion, which has strong basicity and forms the final product after proton transfer. The first step is an acid–base reaction that is usually considered to be a fast reaction.16,17 Therefore, the nucleophilic attack of the thiolate anion on the epoxy functional group is assumed to be the rate-controlling step of the thiol–epoxy reaction, resulting in a second-order reaction mechanism.18
In this study, 1,8-naphthalenediamine was selected as the base catalyst to avoid the influence of the nucleophile-initiated mechanism19 because it is a well-known non-nucleophilic organic base.20 Moreover, 1,8-naphthalenediamine is an organic base with strong basicity and it is expected to trigger the thiol–epoxy reaction at a fast rate in the acid–base step. Kinetic parameters of elementary reactions involved in the base-catalyzed mechanism of the thiol–epoxy reaction were obtained by fitting experimental data. Rate constants were compared to determine the rate-controlling step of the thiol–epoxy reaction.
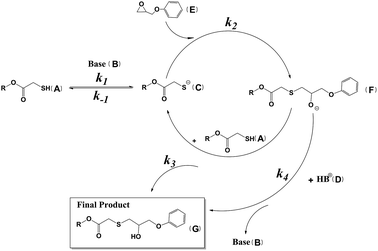
Even though the epoxy functional group is very active with its structure of a strained three-membered ring, it cannot react with thiol directly. In the well-established base-catalyzed mechanism of the thiol–epoxy reaction, thiol is deprotonated by the base catalyst and loses its active hydrogen ion to generate the thiolate anion, which is an acid–base reaction in a broad sense. The thiolate anion has much stronger nucleophilicity than that of thiol. The epoxy functional group is opened under the nucleophilic attack of the thiolate anion. The thiolate anion prefers to attack the less sterically hindered carbon of the epoxy functional group to form the alkoxide anion. Alkoxide anion has high basicity, with a pKa of around 17. It can deprotonate all hydrogen sources in the reaction system, including the conjugate acid of the catalyst and unreacted thiol to generate the final product of the thiol–epoxy reaction.14,15 The base-catalyzed mechanism of the thiol–epoxy reaction is illustrated in Scheme 1.
According to the abovementioned mechanism, there are a total of five elementary reactions involved. These are as follows: (1) deprotonation of thiol by the base catalyst to form the thiolate anion and the conjugate acid of the catalyst (Reaction 1); (2) the reverse of Reaction 1 (Reaction −1); (3) nucleophilic attack of the thiolate anion on the epoxy functional group to generate the alkoxide anion (Reaction 3); (4) deprotonation of unreacted thiol by alkoxide anion to generate the final product and the thiolate anion (Reaction 4); (5) deprotonation of unreacted thiol by the alkoxide anion to generate the final product and base catalyst (Reaction 5). The rate constants of these five elementary reactions are set as k1, k−1, k2, k3 and k4. There are seven substances or functional groups appearing in the mechanism; they are the thiol functional group, the base catalyst, the thiolate anion, the conjugated acid of the catalyst, the epoxy functional group, the alkoxide anion and the final product. All of the elementary reactions are bimolecular ones. The differential equations of consumption or generation rates of the substances can be obtained according to the mechanism (see ESI†). The kinetic model has been built combining the differential equations and initial concentrations of substances. Kinetic experiments were carried out under different conditions to obtain epoxy concentration curves. Experimental data with a molar ratio fixed at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of thiol and epoxy functional group was fitted using this model to obtain kinetic parameters.
1 of thiol and epoxy functional group was fitted using this model to obtain kinetic parameters.
The experimental points and fitting curves are compared in Fig. 1. It can be seen that the fitting curves at every reaction temperature from 60–130 °C match the experimental points well. The rate constants of the five elementary reactions at each temperature were obtained and are listed in Table 1. The ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k–1/T curves of each rate constant show fine linearity, which means that all elementary reactions satisfy Arrhenius' equation well in this temperature range (Fig. S1 in ESI†). The activation energies and pre-exponential factors have been obtained by the intercepts and slopes of the fitting lines according to Arrhenius' equation. The results are listed in Table 2.
k–1/T curves of each rate constant show fine linearity, which means that all elementary reactions satisfy Arrhenius' equation well in this temperature range (Fig. S1 in ESI†). The activation energies and pre-exponential factors have been obtained by the intercepts and slopes of the fitting lines according to Arrhenius' equation. The results are listed in Table 2.
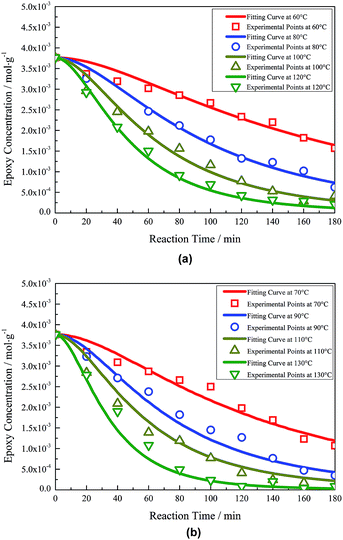 | ||
| Fig. 1 Experimental points and fitting curves of thiol–epoxy reaction under different temperatures: (a) 60/80/100/120 °C (b) 70/90/110/130 °C. | ||
| Temperature/°C | k1 | k−1 | k2 | k3 | k4 |
|---|---|---|---|---|---|
| a The unit of each rate constant is g mol−1 min−1. | |||||
| 60 | 4.746 | 0.04001 | 257.6 | 1398 | 1176 |
| 70 | 5.591 | 0.04242 | 327.6 | 2454 | 1464 |
| 80 | 6.614 | 0.04555 | 442.1 | 3757 | 1478 |
| 90 | 7.777 | 0.04775 | 591.8 | 5649 | 1990 |
| 100 | 8.906 | 0.04882 | 646.9 | 8150 | 2356 |
| 110 | 10.23 | 0.05216 | 739.5 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
3141 |
| 120 | 11.68 | 0.05347 | 884.3 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 390 390 |
3709 |
| 130 | 15.58 | 0.05408 | 1233 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540 540 |
3950 |
| Reaction i | i = 1 | i = −1 | i = 2 | i = 3 | i = 4 |
|---|---|---|---|---|---|
| Eai/kJ mol−1 | 17.8 | 4.95 | 23.4 | 42.6 | 22.4 |
| A0i/g·(mol min)−1 | 2.88 × 103 | 0.242 | 1.24 × 106 | 7.24 × 109 | 3.29 × 106 |
The value of the rate constant k1 reflects the deprotonation rate of thiol by base catalyst 1,8-naphthalenediamine, whereas the value of rate constant k−1 corresponds to the rate of the reverse reaction of this acid–base reaction. The organic base 1,8-naphthalene-diamine is a strong base with a pKa of 12.1.20 From the comparison between k1 and k−1 listed in Table 1, it can be found that k1 is two orders of magnitude greater than k−1. This means that reaction −1, namely the reverse reaction of the acid–base reaction, hardly takes place in the entire mechanism. This is also in agreement with the high basicity of the catalyst. In addition, the activation energy of reaction 1 (Ea1) is 17.8 kJ mol−1 while Ea−1 is only 4.95 kJ mol−1, indicating that Reaction 1 is more sensitive to temperature changes compared to Reaction −1. The values of k−1 in this temperature range stay in the low values, while k1 increases noticeably with increased temperature.
Therefore increasing temperature can be employed as a way to increase the concentration of the thiolate anion, which is deprotonated by the base catalyst.
Reaction 2 is the ring-opening reaction of the epoxy functional group. The epoxy functional group is opened under nucleophilic attack of thiolate anion and the alkoxide anion is generated in this step. The values of the rate constant k2 presented in Table 1 are much greater than those of k1, according to the simulation. This comparison indicates that the nucleophilic attack step is neither the slowest step in the base-catalyzed mechanism of the thiol–epoxy reaction nor the rate-controlling step. Moreover, the value of Ea2 is 23.4 kJ mol−1, while that of Ea1 is 17.8 kJ mol−1, which suggests that Reaction 2 is more sensitive to temperature changes than Reaction 1. Seen from Table 1, the gap between k1 and k2 becomes wider with the increasing temperature; high temperature is beneficial to nucleophilic attack.
The product of Reaction 2 is alkoxide anions whose basicity is so strong that they could capture the potential hydrogen ions in the reaction system, including unreacted thiol and conjugate acid of the base catalyst, and form the final products of the thiol–epoxy reaction, namely Reaction 3 and Reaction 4. Because the base catalyst can deprotonate thiol in Reaction 1, the acidity of thiol is stronger than that of the conjugate acid of the base catalyst. Therefore, Reaction 3 proceeds preferentially to Reaction 4 in this mechanism. The values of rate constants k3 and k4 are much greater than those of k1, k−1 and k2, indicating that Reaction 3 and Reaction 4 proceed much more rapidly than Reaction 1, −1 and 2, which is in agreement with the strong basicity of alkoxide anions. At different temperatures, k3 is always greater than k4, which also fits the fact that the acidity of thiols is stronger than that of the conjugate acid of the base catalyst. However, more importantly, Reaction 3 and Reaction 4 are competing reactions. There is a huge gap between their activation energies. Ea3 is 42.6 kJ mol−1, whereas Ea4 is 22.4 kJ mol−1. From the values presented in Table 1, it is seen that k3 (1398) is only 20% greater than k4 (1176) at 60 °C, whereas k3 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 540) is almost 6 times k4 (3950) at 130 °C. That is to say, alkoxide anions tend to deprotonate unreacted thiol rather than conjugate acid of the base catalyst with increasing temperature. If at a certain temperature, k3 is far greater than k4, alkoxide anions will hardly capture the hydrogen ions of the conjugate acid of the base catalyst, indicating that Reaction 4 hardly takes place in the mechanism. Therefore, the base catalyst is only playing the role of triggering the thiol–epoxy reaction under these conditions. After Reaction 1, the base catalyst only exists in the form of conjugate acid in the reaction system and will not react further in the thiol–epoxy reaction.
540) is almost 6 times k4 (3950) at 130 °C. That is to say, alkoxide anions tend to deprotonate unreacted thiol rather than conjugate acid of the base catalyst with increasing temperature. If at a certain temperature, k3 is far greater than k4, alkoxide anions will hardly capture the hydrogen ions of the conjugate acid of the base catalyst, indicating that Reaction 4 hardly takes place in the mechanism. Therefore, the base catalyst is only playing the role of triggering the thiol–epoxy reaction under these conditions. After Reaction 1, the base catalyst only exists in the form of conjugate acid in the reaction system and will not react further in the thiol–epoxy reaction.
The traditional simplified kinetic equation of the thiol–epoxy reaction was raised on the condition that the nucleophilic attack was the slowest step in the entire mechanism.18 Then, the apparent kinetic equation could be written in the following form:
However, the condition mentioned here is not always corrected in every reaction system. Taking our reaction system as an example, the rate-controlling step of the entire mechanism is the deprotonation step of thiol and not the nucleophilic attack step. Then, the kinetic equations could not be simplified to one in the form of a second order reaction.
In other reaction systems using more active thiol and a catalyst with stronger basicity, the rate of Reaction 1 may be fast at certain temperatures and the acid–base equilibrium can be reached in a short time as well. Moreover, if the k3 is far greater than k4, then Reaction 4 could be neglected in the mechanism. Therefore, the base-catalyzed mechanism could be simplified and presented in the following form, as shown in Scheme 2, under these two assumptions.
Only under this condition will the nucleophilic attack be the rate-controlling step of the entire mechanism and will the thiol–epoxy reaction satisfy the requirements of a second order reaction. However, according to the analysis of elementary reactions involved in the mechanism, not all reaction systems will satisfy these two assumptions at an arbitrary temperature.
Due to the strong basicity of the alkoxide anion, the reaction rates of Reaction 3 and Reaction 4 are both rapid. Therefore, the concentration of the alkoxide anion remains very low in the reaction system throughout the reaction time (Fig. S2 in ESI†). The low concentration of the alkoxide anion also explains the absence of epoxy homopolymerization in the reaction system and confirms the thiol–epoxy reaction as a click reaction.21
According to the analysis mentioned above, the concentration of the base catalyst can directly influence the initiation rate of the thiol–epoxy reaction, namely the rate of Reaction 1. Kinetic experiments with different base catalyst concentrations were carried out to obtain the epoxy concentration points. In addition to the experimental points, the predicted epoxy concentration curves were obtained from the kinetic model using the parameters shown in Table 1. Both the experimental results and predicted curves are presented in Fig. 2. The predicted epoxy concentration curves given by the kinetic model fit the experimental points well. It can be concluded that the kinetic model and parameters obtained above could predict kinetic curves well within a base catalyst concentration range of 1–5 mol%.
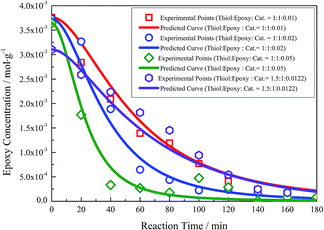 | ||
| Fig. 2 Experimental points and fitting curves of thiol–epoxy reaction under different catalyst concentrations. | ||
Moreover, kinetic experiments with a different initial molar ratio of functional groups were carried out to validate the kinetic model. Similarly, it can be concluded that the kinetic model and parameters obtained herein can predict the kinetic curves well in the range of molar ratios of thiol and epoxy functional groups from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 1.5
1 to 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The present study establishes the kinetic model of the thiol–epoxy reaction according to the well-acknowledged base-catalyzed mechanism. Experimental points are fitted in the kinetic model to obtain kinetic parameters of elementary reactions including rate constants at different temperatures, activation energies and pre-exponential factors. Through the analysis of kinetic parameters of each elementary reaction, the slowest reaction in the mechanism is proven to be the deprotonation reaction of thiol by base catalyst, instead of the nucleophilic attack of thiolate anion on the epoxy functional group. Under certain conditions, the nucleophilic attack step will be the rate-controlling step of the thiol–epoxy reaction, and the entire reaction will satisfy the requirements of a second order reaction. Kinetic experiments with different initial concentrations of base catalyst, thiol and epoxy functional group were carried out. All the predicted epoxy concentration curves fit the experimental points well, validating the kinetic model and its parameters.
Acknowledgements
This study was supported by the National Natural Science Foundation of China (No. 51473146). In the year 2017, it is dedicated to celebrate the 120th anniversary of the most prestigious Zhejiang University and the 90th anniversary of the oldest chemical engineering in China.Notes and references
- H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004 CrossRef CAS PubMed.
- C. E. Hoyle, A. B. Lowe and C. N. Bowman, Chem. Soc. Rev., 2010, 39, 1355 RSC.
- K. J. Shaw, J. R. Luly and H. Rapoport, J. Org. Chem., 1985, 50, 4515 CrossRef CAS.
- P. J. Maurer, C. G. Knudsen, A. D. Palkowitz and H. Rapoport, J. Org. Chem., 1985, 50, 325 CrossRef CAS.
- S. Y. Ko, H. Masamune and K. B. Sharpless, J. Org. Chem., 1987, 52, 667 CrossRef CAS.
- J. R. Luly, N. Yi, J. Soderquist, H. Steni, J. Cohen, T. J. Perun and J. J. Plattner, J. Med. Chem., 1987, 30, 1609 CrossRef CAS PubMed.
- P. N. Guivisdalsky and R. Bittman, J. Am. Chem. Soc., 1989, 111, 3077 CrossRef CAS.
- W. R. Roush and B. B. Brown, J. Org. Chem., 1992, 57, 3380 CrossRef CAS.
- M. J. Kim and Y. K. Choi, J. Org. Chem., 1992, 57, 1605 CrossRef CAS.
- N. Azizi, A. Khajeh-Amiri, H. Ghafuri and M. Bolourtchian, Phosphorus, Sulfur Silicon Relat. Elem., 2010, 185, 1550 CrossRef CAS.
- F. Fringuelli, F. Pizzo, C. Vittoriani and L. Vaccaro, Eur. J. Org. Chem., 2006, 2006, 1231 CrossRef.
- F. Fringuelli, F. Pizzo, S. Tortololi and L. Vaccaro, Tetrahedron Lett., 2003, 44, 6785 CrossRef CAS.
- D. Albanese, D. Landini and M. Penso, Synthesis, 1994, 34 CrossRef CAS.
- M. C. Stuparu and A. Khan, Adv. Polym. Sci., 2015, 269, 87 CrossRef CAS.
- I. Gadwal, M. C. Stuparu and A. Khan, Polym. Chem., 2015, 6, 1393 RSC.
- B. D. Mather, K. Viswanathan, K. M. Miller and T. E. Long, Prog. Polym. Sci., 2006, 31, 487 CrossRef CAS.
- D. P. Nair, M. Podgorski, S. Chatani, T. Gong, W. Xi, C. R. Fenoli and C. N. Bowman, Chem. Mater., 2014, 26, 724 CrossRef CAS.
- K. Jin, W. H. Heath and J. M. Torkelson, Polymer, 2015, 81, 70 CrossRef CAS.
- J. A. Carioscia, J. W. Stansbury and C. N. Bowman, Polymer, 2007, 48, 1526 CrossRef CAS PubMed.
- J. W. Chan, C. E. Hoyle, A. B. Lowe and M. Bowman, Macromolecules, 2010, 43, 6381 CrossRef CAS.
- R. Meizoso Loureiro, T. Carballeira Amarelo, S. Paz Abuin, E. R. Soule and R. J. J. Williams, Thermochim. Acta, 2015, 616, 79 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental procedures. See DOI: 10.1039/c6ra26477h |
| This journal is © The Royal Society of Chemistry 2017 |