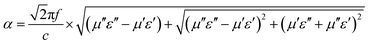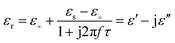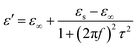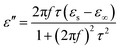DOI:
10.1039/C6RA26489A
(Paper)
RSC Adv., 2017,
7, 3907-3913
Achieving rough sphere-shaped ZnS with superior attenuation electromagnetic absorption performance
Received
8th November 2016
, Accepted 19th December 2016
First published on 16th January 2017
Abstract
ZnS micrometer spheres were prepared via a facile hydrothermal route. Polyvinyl pyrrolidone (PVP) was used as the surfactant. By controlling the PVP content, the smooth surface of ZnS sphere was converted to a rough surface, which led to a stronger electromagnetic wave scattering intensity when used as an electromagnetic absorption absorber. ZnS microspheres with the roughest surface showed the best electromagnetic absorption property. The absorption frequency of this product at 2.0 mm was 4.2 GHz. The minimum reflection loss was nearly −35.0 dB, indicating excellent attenuation ability. The attenuation mechanism is discussed in detail and was attributed to the scattering effect.
1. Introduction
Recently, the application of an electromagnetic absorber to treat the increasing electromagnetic wave interference (EMI) has attracted considerable attention.1,2 This functional material can make the electromagnetic wave incident on the absorption layer and convert it to thermal energy, depending on its intrinsic attenuation ability.3 To achieve a good electromagnetic absorption performance, better impedance matching behavior is the key to ensure less reflection of electromagnetic wave from the interface of the absorption layer. The incoming electromagnetic wave can then be attenuated because of the intrinsic physic loss features. Currently, metal oxides have are the desired absorbers owing to the impedance matching and attenuation ability.4,5 Currently, representative metal oxides, such as Fe3O4,6 CoFe2O4,7 NiO,8 and CuO,9 have been widely applied in electromagnetic absorption studies. For example, the optimal reflection loss of CoO nanoparticles prepared by Li et al. was estimated to be −37.0 dB.10 The minimum reflection loss (RLmin) for the CoxFe3−xO4 was up to −41.089 dB at a thickness of 2.0 mm, according to the Ji's report.11 The binary NiCo2O4/CoNiO2 sample also showed a RLmin value less than −40 dB with a thickness of 1.5 mm.12 Compared to metal oxides, recent research has shown that metal sulfides presented better dielectric loss ability if used in the electromagnetic absorber field.12,13 The primary reason is the improved conductive ability.14 According to the electromagnetic absorption mechanism, the improved conductive ability can lead to an increase in permittivity. In this case, the dielectric loss ability of metal sulfides is prominently stronger than those of the corresponding metal oxides notwithstanding a slight decrease in impedance matching performance.15 For example, Lv and co-workers developed the Fe0.5Ni0.5Co2S4 composite and obtained a RLmin value of −14.0 dB with a thin coating thickness of 1.5 mm. At the same time, the frequency region of RL <−10 dB was nearly 6.2 GHz.16 Through a simple top-down exfoliation method, few-layer MoS2 was achieved, the RLmin value was approximately −38.42 dB and the frequency bandwidth was 4.1 GHz with a thickness of 2.4 mm.17 In addition, the Fe3S4 introduced by Liu et al. had a minimum reflection loss of −36.03 dB with a thickness of 3.0 mm.18
Owing to the advantages of easy production and low-cost, considerable efforts have been focused on the ZnS absorber.19 In addition to these merits, ZnS also presents moderate conductive behavior and results in impedance matching and dielectric loss ability. Therefore, the development of ZnS is considered to be another efficient strategy to gain the desired electromagnetic absorber. In this study, sphere-like ZnS was obtained using a simple hydrothermal strategy. By controlling the contents of the surfactant, the ZnS surface was becoming increasingly rough. The electromagnetic absorption properties of these ZnS spheres were studied.
2. Experiment
2.1 Synthesis of ZnS sphere
Sphere-like ZnS was prepared via a facile hydrothermal process. Typically, 0.1 g zinc acetate (Zn(Ac)2) and 0.5 g thiourea (TA) were dispersed in 60 mL of distilled water (DI) for 30 min ultrasonic treatment to form a clear solution. A certain amount of pyrrolidone polyvinyl (PVP) was dispersed into the abovementioned solution to serve as the surfactant. After another 10 min of ultrasonic treatment, the abovementioned solution was transferred to a 100 mL autoclave and heated at 150 °C for 12 hours. After natural cooling, the precipitate was collected via centrifugation and washed several times with ethanol and distilled water. Finally, sphere-like ZnS was achieved after drying the precipitate at 60 °C for one day. The ZnS spheres obtained with the addition of 0, 10, 20, and 30 mg of PVP are denoted as ZS-1, ZS-2, ZS-3 and ZS-4, respectively.
2.2 Measurement
X-ray diffraction (XRD, Rigaku Desktop X-ray diffractometer, Cu Kα radiation) was employed to test the crystalline phase of the ZnS samples: (test region: 20–70°, wavenumber λ = 0.15418 nm; scanning voltage = 40 keV). The morphology of the samples was observed via Field Emission Scanning Electron Microscopy (FE-SEM, JEOL JSM-7100F) and equipped with Electron Energy Disperse Spectroscopy (EDS). The X-ray photoelectron spectrum was obtained on a PHI 5000 VersaProbe systems, in which an Al Kα X-ray source was operated at 150 W. At the same time, a TEM image was obtained on a Tecnai G220 S-Twin. The complex permittivity and permeability parameters were measured on an Agilent 8722ES network analyzer. The cylindrical sample (inner diameter of 3.04 mm and outer diameter of 7.0 mm) was fabricated by uniformly mixing a paraffin matrix with 60 wt% absorbents, and the composite was then pressed into a cylindrical mold. Transmission line theory was used to calculate the reflection loss.
3. Results and discussion
The morphology of ZnS sample (ZS-1) was characterized by FE-SEM. A sphere-structure can be observed in Fig. 1a. These ZnS spheres without adding PVP presented a smooth surface (in Fig. 2b). According to Fig. 1c, this ZnS sphere has a solid structure. Through EDS, only Zn and S signals were detected and the corresponding atomic ratio of Zn/S was 52.1 to 48.9, which is approximately 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (seen Fig. 1e). Fig. 1f also showed that the diameters of these ZnS spheres were primarily distributed in the range 5–7 μm. In addition, a small part of the ZnS spheres was smaller than 1.0 μm, indicating that the size of these ZnS sphere is not uniform. Fig. 1f presents the XRD pattern of the sample. These diffraction peaks were matched to the standard XRD card (JCPDS card no: 75-1534) without other impurity peaks. X-ray photoelectron spectroscopy (XPS) revealed the binding energy values of Zn at 1022 and 1045 eV, which were attributed to 2p3/2 and 2p1/2 of Zn2+. At the same time, the binding energy of S 2p was 162 eV, corresponding to S2−.20
50 (seen Fig. 1e). Fig. 1f also showed that the diameters of these ZnS spheres were primarily distributed in the range 5–7 μm. In addition, a small part of the ZnS spheres was smaller than 1.0 μm, indicating that the size of these ZnS sphere is not uniform. Fig. 1f presents the XRD pattern of the sample. These diffraction peaks were matched to the standard XRD card (JCPDS card no: 75-1534) without other impurity peaks. X-ray photoelectron spectroscopy (XPS) revealed the binding energy values of Zn at 1022 and 1045 eV, which were attributed to 2p3/2 and 2p1/2 of Zn2+. At the same time, the binding energy of S 2p was 162 eV, corresponding to S2−.20
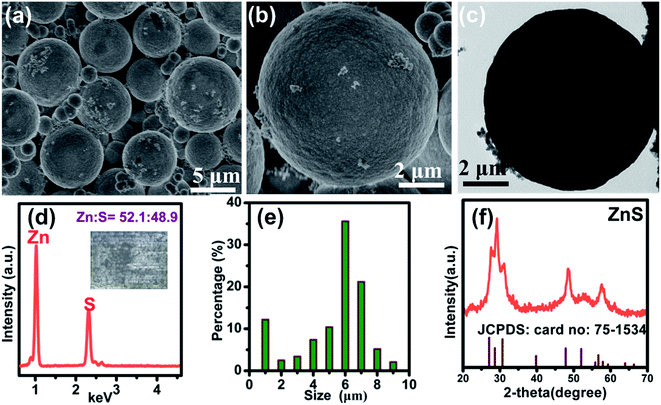 |
| | Fig. 1 (a and b) FE-SEM images (c) the TEM image of the ZnS prepared without PVP; (d) EDS spectrum (e) and size distribution of these ZnS micrometer spheres without the addition of PVP. (f) XRD patterns of the ZnS without PVP. | |
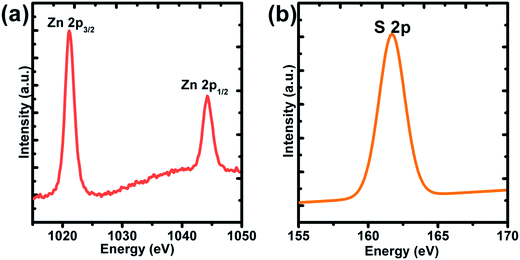 |
| | Fig. 2 XPS spectrum of the ZnS spheres prepared without the addition of PVP. (a) Zn 2p; (b) S 2p. | |
In this study, the initial content of PVP plays a key role in the final structure. Fig. 3a–c show the ZnS obtained with a mass of 10, 20 and 30 mg. Through the FE-SEM images, the ZnS with varying content of PVP still showed a spherical structure. However, the surface of the ZnS spheres became more rugged with increasing PVP content.
 |
| | Fig. 3 FE-SEM images of the ZnS spheres with various amounts of PVP: (a) 10 mg; (b) 20 mg; (c) 30 mg. | |
The electromagnetic absorption properties of these ZnS samples were tested using a coaxial-line method. The electromagnetic parameters, including real/imaginary part of permittivity (ε′/ε′′) as well as the permeability (μ′/μ′′) were also obtained. The reflection loss at 2–18 GHz was calculated using the following equations:21,22
| |
Zin = Zo(μr/εr)1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh[j(2πfd(μrεr)1/2/c)] tanh[j(2πfd(μrεr)1/2/c)]
| (1) |
| |
RL (dB) = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log|(Zin − Zo)/(Zin + Zo)| log|(Zin − Zo)/(Zin + Zo)|
| (2) |
where
Zin is the input impedance of the absorber;
Zo accounts for the characteristic impedance of free space (377 Ω);
f is the frequency of electromagnetic wave;
d is the coating thickness of the absorber;
c is the velocity of the light and
μr and
εr are the complex permeability and permittivity values. For a desired electromagnetic absorber, the minimum reflection loss should be less than −10 dB (corresponding to 90% of absorption and attenuation). The frequency region of RL <−10 dB is better when it is as broad as possible (denoted as the qualified frequency region). The reflection loss
vs. frequency curves are given in
Fig. 4. The qualified frequency bandwidth of ZS-1 was approximately 2.0 GHz (14–16 GHz) with a coating thickness of 2.0 mm. At other thicknesses (
d = 2.5 or 3.0 mm), the qualified frequency bandwidth was smaller than 2.0 GHz and the corresponding minimum reflection loss was larger than −15.0 dB. For ZS-2, however, the qualified frequency bandwidth was narrow and not more than 1.0 GHz at 2.0 mm, indicating a poor microwave absorption ability. For other thicknesses, the reflection loss of ZS-2 was even larger than −10 dB, as shown in
Fig. 4b. In
Fig. 4c, the qualified frequency bandwidth for ZS-3 was estimated to be 3.8 GHz (14.2–18 GHz) at 2.0 mm. In addition, the optimal reflection loss increased in the range from −15 to −20 dB. Further enhancement was observed for the ZS-4 sample, in which the frequency bandwidth at 2.0 mm was larger than 4.0 GHz (13.8–18 GHz). The electromagnetic absorption properties of ZS-4 are better than those of the similar products, as listed in
Table 1.
23–28 Most importantly, the RL
min value at 2.5 mm was below −35 dB, which was highest of these samples. Therefore, it can be concluded that ZS-4 achieved the strongest electromagnetic absorption ability while that of ZS-2 was poor.
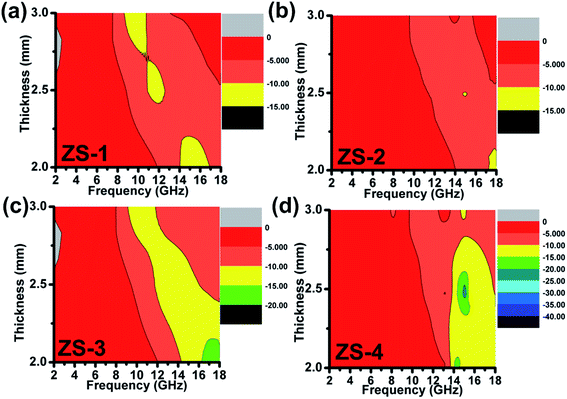 |
| | Fig. 4 Electromagnetic absorption spectrum of the ZnS samples: (a) ZS-1; (b) ZS-2; (c) ZS-3; (d) ZS-4. | |
Table 1 Electromagnetic absorption properties of similar metal sulfides
| Sample |
fE (GHz) |
RLmin (dB) |
Filled ratio (wt%) |
Thickness (mm) |
Ref. |
| ZnS |
<2.0 |
−11.02 |
70 |
2.5 |
23 |
| CuS |
∼3.0 |
−25.0 |
10 |
2.0 |
24 |
| CoS |
0.0 |
<−10.0 |
40 |
2.0 |
25 |
| MoS2 |
0.0 |
<−10.0 |
10 |
2.0 |
26 |
| MnS |
0.0 |
<−10.0 |
40 |
3.0 |
27 |
| CuS/ZnS |
0 GHz |
<−10 dB |
N.A |
2.0 |
28 |
| ZnS |
4.2 GHz |
−18 dB |
60 |
2.0 |
In this work |
To analyze the electromagnetic attenuation mechanism, the real and imaginary parts of permittivity are listed in Fig. 5a and b (for the nonmagnetic material, the real part of permeability was a constant value of 1.0 and the imaginary part of the permeability value was almost 0).29 Based on the electromagnetic absorption mechanism, the role of impedance matching and attenuation (including the dielectric and magnetic loss ability) is to determine the final electromagnetic absorption ability. In Fig. 4a, these ε′ values follow the order ZS-1 < ZS-2 < ZS-3 < ZS-4. Generally, a larger ε′ value indicates the better storage electrical ability but damages to the impedance matching performance.30 The ε′′ value refers to the dielectric loss ability. For these nonmagnetic ZnS samples, the attenuation ability resulted was only from the dielectric loss. As shown in Fig. 5b, ZS-4 showed the largest ε′′ value (1.8–2.0), whereas ZS-1 showed the smallest value over the entire frequency region (1.2–0.8). Several peaks could be observed at a higher frequency region for the ZS-1, ZS-2 and ZS-3 products. Generally, these peaks could be assigned to the dipolar polarization effect.31,32 The ε′′ value cannot fully stand for the attenuation ability. If one absorber has a smaller ε′ value, the larger ε′′ value does not contribute to the final dielectric loss ability. Therefore, the effective attenuation ability generally can be calculated based on the following equation:33,34
| |
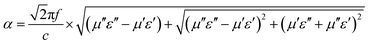 | (5) |
where
α is the effective attenuation constant. A bigger
α value generally indicates stronger effective attenuation ability. Among these samples, ZS-4 presented the largest
α value, whereas ZS-1 showed the smallest, as indicated in
Fig. 6. For the electromagnetic absorption properties, the ZS-1 sample was better than ZS-2, which could be explained by the improved impedance matching behavior (
Fig. 7).
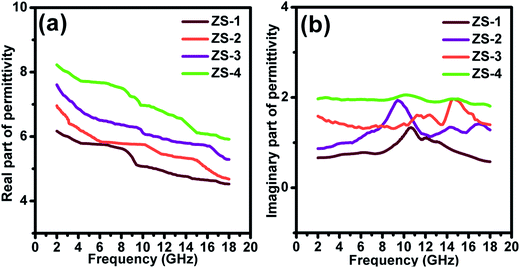 |
| | Fig. 5 Real (a) and imaginary (b) part of permittivity ZnS samples. | |
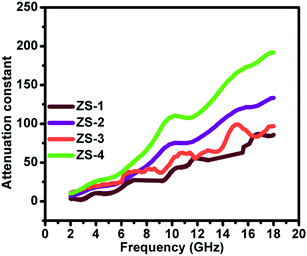 |
| | Fig. 6 Attenuation constant of the ZnS samples. | |
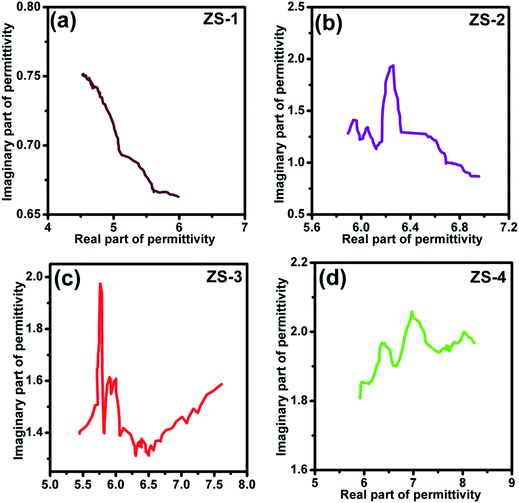 |
| | Fig. 7 Cole–Cole curves of the ZnS samples. | |
The dielectric loss is composed mainly of the conductive and polarization forms. Generally, conductive loss occurs in a highly conductive material, which should be ruled out for these ZnS materials.35 Considering the polarization effect, it generally involves the relaxation process, which can be expressed by the Cole–Cole semicircle. The relative complex permittivity can be described by the following equation:36,37
| |
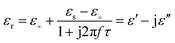 | (6) |
where
εs,
ε∞, and
τ are static permittivity, relative dielectric permittivity at high-frequency limit, and polarization relaxation time, respectively. Therefore,
ε′ and
ε′′ can be calculated using the following equations.
| |
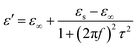 | (7) |
| |
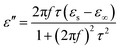 | (8) |
Based on eqn (7) and (8), the ε′ − ε′′ can be expressed as
| | |
(ε′ − ε∞)2 + (ε′′)2 = (εs − ε∞)2
| (9) |
Therefore, a plot of ε′ − ε′′ should be a semicircle, which is generally called the Cole–Cole semicircle. Each Cole–Cole semicircle indicates one Debye relaxation process. The Debye relaxation process is related to the polarization forms, such as an electron, atomic, dipolar as well interface polarization. On the other hand, these samples do not present the Cole–Cole semicircle, indicating a weak polarization effect. This result is not consistent with the ε′′ curve, as mentioned above. In other words, dipolar polarization is not stronger, and hence the Cole–Cole curve could be reflected.
The electromagnetic wave scattering effect plays an important role in the attenuation of an electromagnetic wave. The detailed attenuation mechanism can be understood easily from Fig. 8. Generally, the incident electromagnetic wave (E0) can be divided into the following parts. One part of the electromagnetic wave will reflect directly from the absorber interface (E1). Subsequently, the entered electromagnetic wave can be attenuated (E2) or transmitted (E3) to the absorber. Commonly, a stronger scattering intensity results in a decrease in E3. According to the literature, a larger sized (generally larger than a micron) polyhedron structure as well as a rough surface influences the scattering intensity.38 In this study, the ZS-4 sample with the roughest surface showed the best electromagnetic absorption performance, which may be caused by the stronger scattering effect.
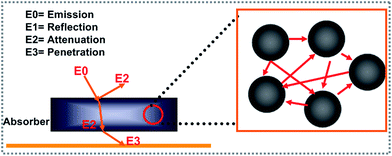 |
| | Fig. 8 Illustration of the scattering effect mechanism. | |
4. Conclusion
Through a simple hydrothermal process, rough spherical ZnS was achieved. Interestingly, the surface of ZnS sphere could be roughened by adding PVP as a surfactant. An analysis of the electromagnetic absorption properties showed that spherical ZnS with the roughest surface presented the stronger dielectric loss ability and electromagnetic absorption properties. In detail, the qualified absorption frequency of the optimal sample at 2.0 mm was up to 4.2 GHz. At the same time, the reflection loss was also less than −30 dB. A study of the attenuation mechanism suggested that these results were due to an electromagnetic scattering effect.
Acknowledgements
This study was supported financially by the Special Scientific Research Funds for Central Non-profit Institutes, Heilongjiang River Fishery Research Institute (HSY201402) and the Special Scientific Research Funds for Central Non-profit Institutes, Chinese Academy of Fishery Sciences (2016HY-ZD1205).
References
- Y. Zhang, Y. Huang, T. F. Zhang, H. C. Chang, P. S. Xiao, H. H. Chen, Z. Y. Huang and Y. S. Chen, Adv. Mater., 2015, 27, 2049–2053 CrossRef CAS PubMed.
- X. F. Zhang, Y. X. Li, R. G. Liu, Y. Rao, H. W. Rong and G. W. Qin, ACS Appl. Mater. Interfaces, 2016, 8, 3494–3498 CAS.
- H. L. Lv, H. Q. Zhang and G. B. Ji, Part. Part. Syst. Charact., 2016, 33, 656–663 CrossRef CAS.
- L. Saini, Y. Janu, M. K. Patra, R. K. Jani, G. K. Gupta and S. R. Vadera, J. Am. Ceram. Soc., 2016, 99, 3002–3007 CrossRef CAS.
- M. Zhou, F. Lu, B. T. Liu, J. Yang and X. H. Zeng, J. Phys. D: Appl. Phys., 2015, 48, 495303–495311 CrossRef.
- H. L. Lv, G. B. Ji, W. Liu, H. Q. Zhang and Y. W. Du, J. Mater. Chem. C, 2015, 3, 10232–10241 RSC.
- D. Moitra, M. Chandel, B. K. Ghosh, R. Jani, M. K. Patra, S. Vaderab and N. N. Ghosh, RSC. Adv., 2016, 6, 76759–76772 RSC.
- T. Liu, Y. Pang, X. B. Xie, W. Qi, Y. Wu, S. Kobayashi, J. Zheng and X. G. Li, J. Alloys Compd., 2016, 667, 287–296 CrossRef CAS.
- Y. Z. Wan, T. Cui, J. Xiao, G. Y. Xiong, R. S. Guo and H. L. Luo, J. Alloys Compd., 2016, 687, 334–341 CrossRef CAS.
- Y. Li, J. Zhang, Z. W. Liu, M. M. Liu, H. J. Lin and R. C. Che, J. Mater. Chem. C, 2014, 2, 5216–5222 RSC.
- R. L. Ji, C. B. Cao, Z. Chen, H. Z. Zhai and J. Bai, J. Mater. Chem. C, 2014, 2, 5944–5953 RSC.
- H. J. Wu, G. L. Wu, Y. Y. Ren, L. Yang, L. D. Wang and X. H. Li, J. Mater. Chem. C, 2015, 3, 7677–7690 RSC.
- J. C. Park and Y. S. Nam, J. Colloid Interface Sci., 2015, 460, 177–180 CrossRef PubMed.
- X. J. Xu, L. F. Hu, N. Gao, S. X. Liu, S. Wageh, A. Ghamdi, A. Alshahire and X. S. Feng, Adv. Funct. Mater., 2015, 21, 445–454 CrossRef.
- X. Z. Lin, A. Ennaoui, S. Levcenko, T. Dittrich, J. Kavalakkatt and S. Kretzschmar, Appl. Phys. Lett., 2015, 106, 013903–013907 CrossRef.
- H. L. Lv, H. Q. Zhang, B. S. Zhang, G. B. Ji, Y. He and Q. Lin, J. Mater. Chem. C, 2016, 4, 5476–5482 RSC.
- M. Q. Ning, M. M. Lu, J. B. Li, Z. Chen, Y. K. Dou, C. Z. Wang, F. Rehman, M. S. Cao and H. B. Jin, Nanoscale, 2015, 7, 15734–15740 RSC.
- X. G. Liu, C. Feng, N. N. Bi, Y. P. Sun, J. C. Fan, Y. H. Lv, C. G. Jin, Y. R. Wang and C. T. Li, Ceram. Int., 2014, 40, 9917–9922 CrossRef CAS.
- Y. H. Zhang, N. Zhang, Z. R. Tang and Y. J. Xu, ACS Nano, 2012, 6, 9777–9789 CrossRef CAS PubMed.
- J. Y. Park, S. J. Park, J. H. Lee, C. H. Hwang, K. J. Hwang, S. H. Jin, D. Y. Choi, S. D. Yoon and I. H. Lee, Mater. Lett., 2014, 121, 97–100 CrossRef CAS.
- H. L. Lv, G. B. Ji, X. H. Liang, H. Q. Zhang and Y. W. Du, J. Mater. Chem. C, 2015, 3, 5056–5064 RSC.
- M. Zhou, X. Zhang, J. M. Wei, S. L. Zhao, L. Wang and B. X. Feng, J. Phys. Chem. C, 2011, 115, 1398–1402 CAS.
- B. Zhao, G. Shao, B. B. Fan, W. Y. Zhao, Y. J. Xie and R. Zhang, RSC Adv., 2014, 4, 61219–61225 CAS.
- S. He, G. S. Wang, C. Lu, X. Luo, B. Wen, L. Guo and M. S. Cao, ChemPlusChem, 2013, 78, 250–258 CrossRef CAS.
- T. Y. Huang, M. He, Y. M. Zhou, S. W. Li, B. B. Ding, W. L. Pan, S. Huang and Y. Tong, RSC Adv., 2016, 6, 100392–100400 RSC.
- X. Ding, Y. Huang, S. P. Li, N. Zhang and J. G. Wang, Composites, Part A, 2016, 90, 424–432 CrossRef CAS.
- D. Z. Chen, H. Y. Quan, G. S. Wang and L. Guo, ChemPlusChem, 2013, 78, 843–851 CrossRef CAS.
- X. H. Guan, P. Gu and G. S. Wang, RSC Adv., 2014, 4, 15579–15585 RSC.
- H. L. Lv, Y. H. Guo, Y. Zhao, H. Q. Zhao, B. S. Zhang, G. B. Ji and Z. C. J. Xu, Carbon, 2016, 110, 130–137 CrossRef CAS.
- M. Fu, Q. Z. Jiao, Y. Zhao and H. S. Li, J. Mater. Chem. A, 2014, 2, 735–744 CAS.
- H. L. Lv, H. Q. Zhang, G. B. Ji and Z. C. Xu, ACS Appl. Mater. Interfaces, 2016, 8, 6529–6538 CAS.
- M. Zhou, F. Lu, B. Chen, X. Y. Zhu, X. S. Shen, W. W. Xia, H. He and X. H. Zeng, Mater. Lett., 2015, 159, 498–501 CrossRef CAS.
- G. Wang, X. Peng, L. Yu, G. Wan, S. Lin and Y. Qin, J. Mater. Chem. A, 2015, 3, 2734–2740 CAS.
- Y. Liu, X. X. Liu, R. Liu, W. Wu and X. J. Wang, RSC Adv., 2015, 5, 8713–8720 RSC.
- Y. P. Duan, Z. Liu, H. Jing, Y. H. Zhang and S. Q. Li, J. Mater. Chem. A, 2012, 22, 18291–18299 RSC.
- G. P. Wan, L. Yu, X. G. Peng, G. Z. Wang, X. Q. Huang, H. N. Zhao and Y. Qin, RSC Adv., 2015, 5, 77443–77448 RSC.
- M. Zhou, F. Lu, T. Y. Lv, X. Yang, W. W. Xia, X. S. Shen, H. He and X. H. Zeng, J. Phys. D: Appl. Phys., 2014, 48, 215305–215311 CrossRef.
- H. L. Lv, H. Q. Zhang, J. Zhao, G. B. Ji and Y. W. Du, Nano Res., 2016, 6, 1813–1822 CrossRef.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Yi Song*d
*a and
Yi Song*d
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (seen Fig. 1e). Fig. 1f also showed that the diameters of these ZnS spheres were primarily distributed in the range 5–7 μm. In addition, a small part of the ZnS spheres was smaller than 1.0 μm, indicating that the size of these ZnS sphere is not uniform. Fig. 1f presents the XRD pattern of the sample. These diffraction peaks were matched to the standard XRD card (JCPDS card no: 75-1534) without other impurity peaks. X-ray photoelectron spectroscopy (XPS) revealed the binding energy values of Zn at 1022 and 1045 eV, which were attributed to 2p3/2 and 2p1/2 of Zn2+. At the same time, the binding energy of S 2p was 162 eV, corresponding to S2−.20
50 (seen Fig. 1e). Fig. 1f also showed that the diameters of these ZnS spheres were primarily distributed in the range 5–7 μm. In addition, a small part of the ZnS spheres was smaller than 1.0 μm, indicating that the size of these ZnS sphere is not uniform. Fig. 1f presents the XRD pattern of the sample. These diffraction peaks were matched to the standard XRD card (JCPDS card no: 75-1534) without other impurity peaks. X-ray photoelectron spectroscopy (XPS) revealed the binding energy values of Zn at 1022 and 1045 eV, which were attributed to 2p3/2 and 2p1/2 of Zn2+. At the same time, the binding energy of S 2p was 162 eV, corresponding to S2−.20

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh[j(2πfd(μrεr)1/2/c)]
tanh[j(2πfd(μrεr)1/2/c)]
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log|(Zin − Zo)/(Zin + Zo)|
log|(Zin − Zo)/(Zin + Zo)|