Utilizing super-atom orbital ideas to understand properties of silver clusters inside ZSM-5 zeolite

Abstract

The energetic properties of Ag_n clusters in ZSM-5 zeolite were investigated using density functional theory (DFT) calculations with the B3PW91 functional. Several optimized geometries (Ag_n–ZSM-5(Al_m), 3 ≤ n ≤ 6 and 1 ≤ m ≤ 5) were obtained using this method, where m is the number of Al atoms substituted for Si atoms of a ten-membered ring of ZSM-5. DFT calculations found that an Ag_n cluster is well stabilized within a ZSM-5(Al_m) cavity at n = m + 2. The stabilization conditions can be explained by frontier orbital theory because the HOMO of Ag_m+2–ZSM-5(Al_m) zeolites is composed by totally symmetric 5s-based orbitals on silver atoms. The totally symmetric 5s-based orbital corresponds to a superatom S-orbital in cluster chemistry. Accordingly, the Ag_m+2–ZSM-5(Al_m) zeolites have an S² electronic configuration, being similar to magic-number silver clusters in the gas phase. Time-dependent DFT calculations found significant oscillator strength at the electronic transition between 5s-based orbitals from the totally symmetric orbital (S-orbital) to that with one node (P-orbital). The S → P electronic transitions in Ag_m+2–ZSM-5(Al_m) follow the selection rule of electronic transitions of bare clusters. Because the excitation energies (λ_max) change with an increase in the number of contained silver atoms, the S → P electronic transitions of Ag_m+2–ZSM-5(Al_m) could be used to identify the state of the inner silver atoms.

---

Introduction

When silver atoms with an electronic configuration of 4d¹⁰5s¹ aggregate to form clusters, the resulting clusters exhibit unique electronic properties dependent on the number of contained atoms and their shapes. In general, their electronic properties are due to frontier orbitals composed of a linear combination of 5s orbitals on silver atoms. These 5s-based orbitals with different numbers of nodes can be categorized by utilizing “superatom orbitals” such as S, P, and D orbitals.^1–5 The superatom orbitals, analogous to orbitals in hydrogen-like atoms, have an angular momentum quantum number (L) (L = 0, 1, and 2 for the S, P, and D orbitals, respectively) corresponding to the number of nodes of the 5s-based orbitals. Using superatom orbital ideas, the magic number of bare silver clusters and the selection rule in their electronic transitions (ΔL = ±1) can be determined.^1–5

To modulate the electronic properties of silver clusters, one needs to control the size of silver clusters, and the use of nanometre-sized cavities of zeolites is promising for the stabilization of relatively small silver clusters.^6–47 Zeolite cavities have been shown to encapsulate silver clusters from 2 to 8 atoms in size.^6–47 For example, Faujasite and Linde-type A (LTA) zeolites contain Ag₃ and Ag₆ clusters in their cavities, respectively.⁴⁷ Previously, we combined UV-vis measurements with density functional theory (DFT) calculations to elucidate the state of silver atoms within ZSM-5 zeolites, whose ten-membered rings cavities are on the nanometre scale.^48,49 UV-vis measurements in previous studies found maximum peaks ranging from 300–320 nm.^43,49 These peaks can be assigned by electronic transitions of triangle Ag₃ and butterfly Ag₄ clusters inside ZSM-5, whose structures were optimized by DFT calculations (Fig. S1 (ESI†)).

Furthermore, DFT calculations^48,49 revealed that structures of Ag₃ or Ag₄ clusters within a ten-membered ring of ZSM-5 zeolite are influenced by the degree of substitution of Al atoms for Si atoms in SiO₂ frameworks located within the ten-membered ring. The Si → Al substitution in zeolites creates negative charges on framework oxygen atoms and positive charges on silver atoms contained within clusters. The oppositely charged silver clusters and framework oxygen atoms interact through electrostatic attraction, stabilizing the inner cluster. In addition, the Si → Al substitution is directly linked to the number of 5s electrons in silver clusters within a ZSM-5 cavity based on simple electron count arguments.^48,49 Accordingly, the Si → Al substitution is the dominant factor in the strength of the orbital interactions between adjacent Ag cations, which is in turn responsible for determining the cluster structures within a zeolite cavity.

Although previous studies provided preliminary insight, knowledge is still lacking on the structural properties of ZSM-5 zeolites containing silver clusters larger than Ag₃ and Ag₄ clusters, which are experimentally proposed to be responsible for the UV-vis peaks at higher wavelengths. This study extends previous works to obtain atomistic information on the contained silver clusters and to examine the structural features of larger silver clusters inside a ZSM-5 cavity. This extension can allow us to find out conditions of stabilizing silver clusters inside a ZSM-5 cavity with the Si → Al substitution. Moreover, the present paper newly applies superatom orbital ideas^1–5 to interpret the properties of silver clusters inside a ZSM-5 cavity with particular focus on the role of the substituted Al atoms in determining stability of inner silver clusters.

Computational methods

The current study employed DFT calculations with the B3PW91 functional⁵⁰ to elucidate the properties of silver clusters inside a nanometre-sized cavity of ZSM-5 zeolite. Several previous computational studies,^51–57 including ours,^48,49 indicated that the B3PW91 functional can reproduce results obtained from more reliable calculations using coupled-cluster singlet double (CCSD)⁵⁸ methods for the stability of neutral Ag₃ isomers. Following our previous studies, periodic ZSM-5 structure was modelled using an aluminium-free ZSM-5 cluster (Si₉₂O₁₅₁H₆₆).^59–65 Si atoms within a ten-membered ring of ZSM-5 zeolite were then substituted by Al atoms, where the number of the Al atoms is m. The ZSM-5 cavity containing the substituted Al atoms is denoted as ZSM-5(Al_m). Using the finite-size model, the initial structures were constructed by placing an Ag_n cluster into a ten-membered ring of ZSM-5(Al_m) zeolite. Then, we fully optimized initial structures for an Ag_n cluster contained within a ZSM-5(Al_m) cavity, designated by Ag_n–ZSM-5(Al_m). Note that the formal charge of an Ag_n cluster inside a ZSM-5(Al_m) is m, and therefore the inner Ag_n cluster has n–m 5s electrons. In our calculations, we considered the Ag_n–ZSM-5(Al_m) structure with n–m being even (odd) in the singlet (doublet) state during the B3PW91 optimization.

During the optimization, we used Gaussian 09 code⁶⁶ instead of Gaussian 03 code⁶⁷ used in the previous studies.^48,49 This study re-optimized Ag₃–ZSM-5(Al_m) and Ag₄–ZSM-5(Al_m) geometries in Gaussian 09 code, although both codes yielded almost same results in terms of the energetics and geometrical features. The CEP-121G basis set was used for Ag atoms,^68,69 the 6-31G* basis set for substituted Al atoms and for the two O atoms bound to a substituted Al atom,^70–72 and the 3-21G basis set for all other atoms,^73–78 due to computational resource limitations. For example, Ag₅–ZSM-5(Al₁) and Ag₆–ZSM-5(Al₁) involve the 2857 and 2888 contracted basis functions, respectively. First, we checked reliability of the cluster-model calculations by comparing them with QM/MM ONIOM calculations⁷⁹ of a triangle Ag₃ cluster inside a ZSM-5(Al₁) cavity. As shown in Fig. S2 (ESI†), optimized silver separations of the inner Ag₃ cluster in the cluster-model calculations are consistent with those in QM/MM ONIOM calculations, indicating accuracy in our cluster-model calculations. Furthermore, time-dependent DFT calculations were performed to investigate electronic transitions of silver cluster inside a ZSM-5 cavity, where the number of states was considered to be 50.

Results and discussion

Super-atom orbital ideas on bare small silver clusters

Let us first apply super-atom orbital ideas to understand frontier orbitals of a triangle Ag₃ cluster and square and tetragonal Ag₄ clusters. Fig. 1 displays frontier orbitals of prototype cluster structures: a triangle Ag₃ cluster and square and tetragonal Ag₄ clusters. Irrespective of the cluster structure, the most stable 5s-based orbital does not possess any nodes (totally symmetric). 5s-based orbitals with nodes have greater energy above the totally symmetric orbital. Based on superatom orbital ideas,^1–5 these 5s-based orbitals can be distinguished by the number of nodes; the orbital without any node corresponds to the S-orbital, and those with one and two nodes correspond to the P- and D-orbitals. When two electrons occupy the symmetric 5s-based orbital (S-orbital), their in-phase interaction makes adjacent silver atoms have attractive interactions, stabilizing the cluster structure. In fact, we optimized structures for Ag₃⁺, and Ag₄²⁺ clusters, where the S orbital is doubly occupied.^48,49 As the number of 5s electrons in a silver cluster increases beyond two, 5s-based orbitals with some nodes are occupied. Because of the presence of some nodes, the electron occupation in the orbitals leads to a partial weakening of Ag–Ag interactions, distorting the symmetric cluster.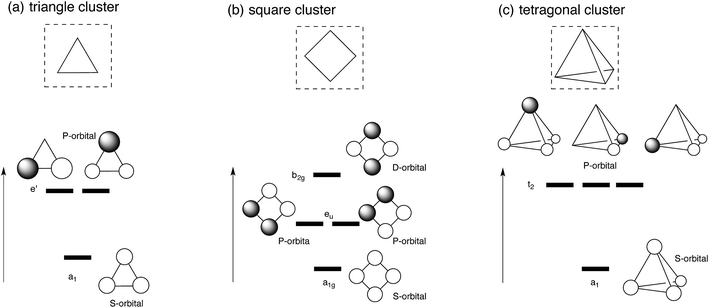

Fig. 1 Schematic view of frontier orbitals of prototype silver clusters: (a) triangle Ag₃ cluster (b) square Ag₄ cluster, and (c) tetragonal Ag₄ cluster.

Situations are more complicated in Ag₅ and Ag₆ clusters. We tried to obtain local minima of bare Ag₅^m+ and Ag₆^m+ clusters. As a result of computation, we obtained only Ag₅, Ag₅⁺, and Ag₅²⁺ clusters as well as Ag₆, Ag₆⁺, and Ag₆²⁺ clusters (Fig. 2). Optimization of Ag₅³⁺ and Ag₆⁴⁺ clusters, which would have doubly occupied S orbital, resulted in decomposition into small fragments such as Ag₃³⁺ and Ag₄²⁺ clusters plus single Ag⁺ cations.⁸⁰ These results indicate that Ag₅^m+ and Ag₆^m+ clusters at m being large cannot exist in the gas-phase. Thus, not only attractive interactions from 5s-based orbital interactions, but also repulsive electrostatic interactions between silver cations are important in determining the structure of small silver clusters.

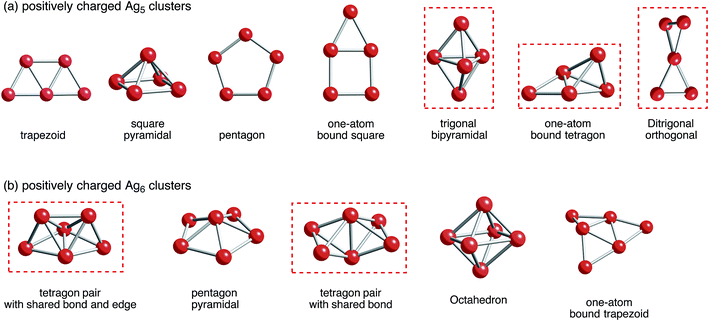Fig. 2 B3PW91 optimized geometries for (a) Ag₅ and (b) Ag₆ clusters charged positively. The cut-off length used to indicate formation of Ag–Ag bonds is 3 Å. Detailed information can be found in Tables 1 and 2. Clusters that correspond to a ZSM-5 pore and at the same time are energetically stable are marked in red.

With respect to the optimized structures in Fig. 2, we found seven types of Ag₅ clusters and five types of Ag₆ cluster. Detailed information on geometrical features of silver clusters is listed in Tables 1 and 2. As shown in Fig. 2, Tables 1 and 2, DFT calculations found different optimized geometries for positive charged Ag₅ clusters. For Ag₅⁺, a ditrigonal orthogonal cluster is the most energetically stable. The next stable clusters take one-atom bound tetragon and trigonal bipyramidal forms. We obtained three energetically comparable Ag₅²⁺ clusters; one-atom bound tetragon, trigonal bipyramidal, and ditrigonal orthogonal forms. Similarly, there are two energetically comparable Ag₆⁺ clusters: a tetragon pair with a shared bond and edge and a pair with shared bonds.

Table 1 Key parameters in optimized positively charged Ag₅ geometries^a

	Spin state	Shape^a	Silver separations^b	ΔE^c
a Optimized structures can be seen in Fig. 2(a).b Separations between adjacent silver atoms less than 3 Å are listed.c ΔE: relative energies of Ag5^m+ are in kcal mol^−1. The most stable cluster is given by 0.
Ag5	Doublet	Trapezoid	2.72, 2.72, 2.74, 2.74, 2.79, 2.79, 2.79	0
	Doublet	Trigonal bipyramidal	2.70, 2.70, 2.80, 2.80, 2.85, 2.85, 2.85, 2.85	12.4
Ag5^+	Singlet	Ditrigonal orthogonal	2.65, 2.65, 2.78, 2.78, 2.78, 2.78	0
	Singlet	One-atom bound tetragon	2.63, 2.65, 2.75, 2.75, 2.99, 2.99	6.7
	Singlet	Trigonal bipyramidal	2.73, 2.73, 2.73, 2.86, 2.86, 2.86, 2.86, 2.87, 2.87	12.2
	Triplet	Square pyramidal	2.77, 2.77, 2.77, 2.77, 2.87, 2.87, 2.87, 2.87	22.5
	Triplet	Pentagon	2.73, 2.73, 2.73, 2.73, 2.73	38.3
Ag5^2+	Doublet	One-atom bound tetragon	2.71, 2.76, 2.93, 2.93, 2.94, 2.94, 2.94, 2.94	0
	Doublet	Trigonal bipyramidal	2.80, 2.80, 2.80, 2.93, 2.93, 2.94, 2.94, 2.95, 2.95	1.7
	Doublet	Ditrigonal orthogonal	2.81, 2.81, 2.83, 2.83, 2.83, 2.83	3.5
	Doublet	One-atom bound square	2.68, 2.74, 2.88, 2.88, 2.88, 2.88	11.6

---

Table 2 Key parameters in optimized positively charged Ag₆ geometries^a

	Spin state	Shape^a	Silver separations^b	ΔE^c
a Optimized structures can be seen in Fig. 2(b).b Separations between adjacent silver atoms less than 3 Å are listed.c ΔE: relative energies of Ag6^m+ are in kcal mol^−1. The most stable cluster is given by 0.
Ag6	Singlet	One-atom bound trapezoid	2.72, 2.72, 2.72, 2.72, 2.72, 2.73, 2.82, 2.82, 2.82	0.0
	Singlet	Pentagon pyramidal	2.72, 2.72, 2.72, 2.72, 2.72, 2.86, 2.86, 2.86, 2.86, 2.87	5.3
	Singlet	Tetragon pair with shared bond and edge	2.66, 2.73, 2.78, 2.78, 2.78, 2.78, 2.91, 2.91, 2.91, 2.91, 2.92, 2.92	16.0
	Singlet	Octahedron	2.69, 2.69, 2.69, 2.69, 2.69, 2.69	26.4
Ag6^+	Doublet	Tetragon pair with shared bond and edge	2.67, 2.78, 2.78, 2.85, 2.85, 2.85, 2.85, 2.88, 2.90, 2.90, 2.90, 2.90	0
	Doublet	Tetragon pair with shared bond	2.72, 2.74, 2.74, 2.75, 2.75, 2.75, 2.75	3.7
	Doublet	One-atom bound trapezoid	2.73, 2.73, 2.73, 2.73, 2.73, 2.84, 2.84, 2.88, 2.88	5.6
Ag6^2+	Triplet	Pentagon pyramidal	2.80, 2.80, 2.80, 2.80, 2.80, 2.95, 2.95, 2.95, 2.95, 2.95	0
	Triplet	Octahedron	2.78, 2.78, 2.79, 2.79, 2.79, 2.79	8.2

---

Optimized geometries for Ag₅ or Ag₆ clusters inside a ZSM-5 cavity

Following the previous studies,^48,49 which are summarized in Fig. S1,† Ag₅ and Ag₆ clusters that are formed from single-atom and double-atom additions to the tetragonal or butterfly Ag₄ cluster, respectively (Fig. S3 (ESI†)), can be encapsulated into a ten-membered ring of ZSM-5 zeolites. Using these criteria, we chose energetically stable Ag₅ and Ag₆ clusters marked by red colour in Fig. 2 as candidates suitable to be encapsulated into a ZSM-5 cavity. To obtain optimized structures for Ag₅ or Ag₆ clusters inside a ZSM-5 cavity, clusters coloured red in Fig. 2 were put into the cavity to construct initial geometries, and their initial structures were fully optimized. Then, the Al atoms were substituted for Si atoms of zeolite SiO₂ frameworks (m) over the range of 1 to 5. Among configurations considered in this study (Fig. S4 and S5, ESI†), the most stable optimized structures for Ag₅ and Ag₆ clusters inside a ZSM-5 cavity (Ag₅–ZSM-5(Al_m) and Ag₆–ZSM-5(Al_m)) are displayed in Fig. 3 and 4, respectively. Their key parameters of inner silver clusters are listed in Tables 3 and 4, respectively.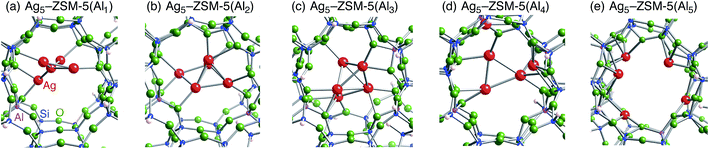

Fig. 3 Energetically stable B3PW91 optimized geometries for Ag₅–ZSM-5(Al_m). (a) m = 1, (b) m = 2, (c) m = 3, (d) m = 4, and (e) m = 5. The cut-off length used to indicate formation of Ag–Ag bonds is 3 Å. Other local minima are displayed in Fig. S4.† Key parameters are listed in Table 3.

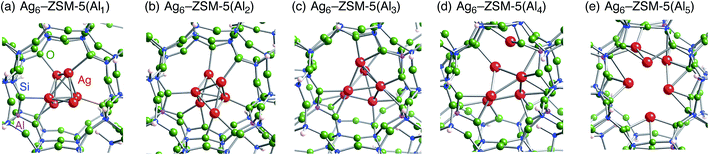Fig. 4 Energetically stable B3PW91 optimized geometries for Ag₆–ZSM-5(Al_m). (a) m = 1, (b) m = 2, (c) m = 3, (d) m = 4, and (e) m = 5. The cut-off length used to indicate formation of Ag–Ag bonds is 3 Å. Other local minima are displayed in Fig. S5.† Key parameters are listed in Table 4.

Table 3 Key parameters in optimized Ag₅–ZSM-(Al_m) geometries^a

m	Structure label^b	Silver separations^c	ΔE^d
a Optimized structures for Ag5–ZSM-(Alm) can be seen in Fig. S4.b Structure labels are displayed in Fig. S4.c Separations between adjacent silver atoms less than 3 Å are listed.d ΔE: relative energies of Ag5–ZSM-(Alm) are in kcal mol^−1. The most stable structure is given by 0.
1	a (i)	2.62, 2.68, 2.73, 2.78, 2.80, 2.80	0
1	a (ii)	2.73, 2.76, 2.77, 2.79, 2.82, 2.83, 2.86, 2.88, 2.93	1.6
1	a (iii)	2.66, 2.72, 2.72, 2.73, 2.78, 2.83, 2.84, 2.98	2.7
2	b (i)	2.74, 2.74, 2.76, 2.80, 2.86, 2.89, 2.91	0
2	b (ii)	2.68, 2.80, 2.80, 2.80, 2.82, 2.82, 2.87, 2.96	10.0
2	b (iii)	2.78, 2.80, 2.80, 2.86, 2.86, 2.87, 2.90, 2.90, 2.91	11.2
3	c (i)	2.79, 2.80, 2.81, 2.85, 2.87, 2.90, 2.92, 2.96	0
3	c (ii)	2.71, 2.76, 2.81, 2.82, 2.87, 2.89, 2.96	6.4
3	c (iii)	2.73, 2.76, 2.81, 2.84, 2.84, 2.85, 2.86, 2.88, 2.91, 2.92	8.2
4	d (i)	2.86, 2.97, 2.98	0
4	d (ii)	2.84, 2.87, 2.94	5.7
4	d (iii)	2.74, 2.81, 2.82, 2.84, 2.88, 2.90, 2.97	34.7
5	e	—	—

---

Table 4 Key parameters in optimized Ag₆–ZSM-(Al_m) geometries^a

m	Structure label^b	Silver separations^c	ΔE^d
a Optimized structures for Ag6–ZSM-(Alm) can be seen in Fig. S5.b Structure labels are displayed in Fig. S5.c Separations between adjacent silver atoms less than 3 Å are listed.d ΔE: relative energies of Ag6–ZSM-(Alm) are in kcal mol^−1. The most stable structure is given by 0.
1	a (i)	2.73, 2.78, 2.78 2.79, 2.79, 2.79, 2.82, 2.85, 2.90, 2.90, 2.91, 2.91	0
1	a (ii)	2.70, 2.75, 2.79, 2.81, 2.81, 2.81, 2.84, 2.84, 2.86, 2.87, 2.89, 2.94	8.7
2	b (i)	2.71, 2.72, 2.77, 2.83, 2.83, 2.86, 2.87, 2.89, 2.90, 2.91, 2.95	0
2	b (ii)	2.70, 2.70, 2.79, 2.79, 2.81, 2.83, 2.84, 2.87, 2.88, 2.88, 2.99	10.7
3	c (i)	2.73, 2.76, 2.81, 2.84, 2.84, 2.85, 2.86, 2.88, 2.90, 2.92	0
3	c (ii)	2.75, 2.79, 2.81, 2.81, 2.82, 2.83, 2.83, 2.85, 2.90, 2.96, 2.98	10.4
4	d (i)	2.70, 2.77, 2.78, 2.81, 2.90, 2.94	0
4	d (ii)	2.77, 2.77, 2.80, 2.84, 2.87, 2.87, 2.87, 2.87, 2.90	5.3
5	e (i)	2.78, 2.84, 2.91	0
5	e (ii)	2.76, 2.78, 2.84, 2.88, 2.91, 2.91, 2.91, 2.92, 2.99	22.6

---

Fig. S4 and S5† show that the different structures of Ag₅ or Ag₆ clusters are dependent on the number of substituted Al atoms. Within ZSM-5(Al₁) and ZSM-5(Al₂) cavities, the most stable Ag₅ clusters take ditrigonal-orthogonal and one-atom bound tetragon forms, respectively. Their structures are similar to those of the stable Ag₅⁺ and Ag₅²⁺ clusters without ZSM-5 surroundings in terms of silver separations (Tables 1 and 3), although slight distortions were found. The inner silver clusters are bound to adjacent framework oxygen atoms near the substituted Al atoms, whose separations are listed in Table S1 (ESI†). As shown in Table S1,† the shortest distance between a silver atom and a framework oxygen atom is ∼2.3 Å. Similarly, Ag₆ clusters inside ZSM-5(Al₁) and ZSM-5(Al₂) cavities take a stable shape where the tetragon pair with share a bond and edge. Orientation of the Ag₆ cluster with respect to the ZSM-5 cavity is important; the cluster oriented along the straight channel is energetically stable relative to that perpendicular to the straight channel, as shown in Fig. S5.† Between the two structures, different interactions between inner silver cations and framework oxygen atoms are expected from Table S2 (ESI†) to stabilize an inner cluster along the straight channel.

With an increase in m, the clusters are deformed by lengthening the Ag–Ag bond lengths, as shown in Tables 3 and 4. Although the ZSM-5(Al₃) cavity still contains a one-atom bound tetragonal Ag₅ cluster (Fig. 3(c)) (Ag₆ cluster taking a shape with the tetragonal pair with shared bond (Fig. 4(c))), separations between silver atoms increase (Tables 3 and 4). Containing Ag₅ cluster inside a restricted cavity of ZSM-5(Al₃) is unique, because an Ag₅³⁺ cluster, which cannot exist in the gas-phase, can be stabilized by the electrostatic interactions with framework oxygen atoms, as seen from Table S1.† When the number of Al atoms is 4, the number of Ag–Ag bonds less than 3 Å decreases.⁸¹ As a result, smaller clusters exist on the inside of ZSM-5(Al₄) instead of forming Ag₅ or Ag₆ clusters. Further increase of the number of Al atom leads silver atoms to exist as isolated cations. These single cations strongly coordinate to three or two oxygen atoms within the framework, which are separated by less than 2.2 Å. See Tables S1 and S2.†

Recently, Cuong et al. reported optical properties of hydrated charged silver tetramer and hexamer clusters inside the sodalite cavity of LTA-type zeolite models ((H₂O)₄Na₄Al₈Si₁₆O₃₆H₂₄, (H₂O)₅Na₃Al₇Si₁₇O₃₆H₂₄, and (H₂O)₆Na₂Al₆Si₁₈O₃₆H₂₄).^82,83 Their B3LYP calculations found that butterfly Ag₄ or O_h-like Ag₆ clusters inside four- and six-membered cavities of the LTA models.^82,83 Silver atoms on the inner Ag₆ clusters are not directly bound to framework oxygen atoms in LTA zeolite models, whose separations are larger than ∼2.6 Å. Note that these separation ranges are larger than our ZSM-5 cases. Instead, the clusters are bound to OH⁻ groups formed from water molecules near Al atoms of (H₂O)₅Na₃Al₇Si₁₇H₂₄O₃₆, and (H₂O)₆Na₂Al₆Si₁₈H₂₄O₃₆.^82,83 Reflecting from different coordination environment of inner silver atoms between LTA and our ZSM-5 models, the two types of zeolite contain different Ag₆ clusters. More interestingly, the structures of O_h-like Ag₆ clusters in LTA models remain almost unchanged irrespective of various number of contained Al atoms (m = 6–8). In terms of dependences of m on inner Ag₆ structures, their results are different from our results, due to weaker interactions between inner silver atoms and LTA framework oxygen atoms than ZSM-5 cases. These results indicate that zeolite surroundings, including the presence or absence of water molecules, have a strong impact on determining inner cluster structures and their properties.

Stability of Ag_n–ZSM-5(Al_m) dependent on the number of substituted Al atoms

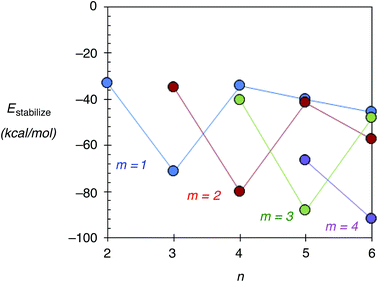
In this section, the stability of Ag_n–ZSM-5(Al_m) using E_stabilize values defined as E_total[Ag_n–ZSM-5(Al_m)] − E_total[Ag_n−1–ZSM-5(Al_m)] − E_total[Ag] is discussed. Here, E_total[Ag_n–ZSM-5(Al_m)], E_total[Ag_n−1–ZSM-5(Al_m)], and E_total[Ag] are the total energies of Ag_n–ZSM-5(Al_m), Ag_n−1–ZSM-5(Al_m), and the single silver atom, respectively. Fig. 5 shows the E_stabilize values plotted as a function of the number of silver atoms (n). See also Fig. S6 (ESI†), including Tables S3 and S4.† From Fig. 5 and S6,† we found negative E_stabilize values for Ag_n–ZSM-5(Al_m). These negative E_stabilize values indicate that Ag_n–ZSM-5(Al_m) is energetically stable relative to the dissociation limit towards Ag_n−1–ZSM-5(Al_m) and the single silver atom.

Fig. 5 E_stabilize values, defined in the main text, as a function of the number of atoms in silver clusters within ZSM-5(Al_m): m = 1 (blue), m = 2 (red), m = 3 (green) and m = 4 (purple). Lines are provided for visual assistance.

More interestingly, the E_stabilize values depend on the number of substituted Al atoms (m) and silver atoms (n). When m = 1, 2, and 3, the most significant E_stabilize values were found at n = 3, 4, and 5. The DFT results indicate that a ZSM-5(Al_m) cavity stabilizes an Ag_m+2 cluster (m ≤ 3). The stabilization conditions (n = m + 2) can be explained by applying the superatom orbital ideas of Ag_n–ZSM-5(Al_m). As previously mentioned, an Ag_n cluster inside a ZSM-5(Al_m) cavity has n–m 5s electrons. Thus, an Ag_m+2 cluster inside a ZSM-5(Al_m) cavity has two 5s electrons. The two electrons are occupied in the totally symmetric 5s-based orbital (S-orbital), indicating that the S-based orbital is the HOMO in Ag_m+2–ZSM-5(Al_m), as confirmed by ref. 48 and 49 and Fig. S7 and S8 (ESI†). Doubly occupation of an S-orbital can be also found in the formation of magic-number silver clusters in the gas phase.^1–5

The stabilization conditions can be validated only at m ≤ 3, when the 5s-orbital interactions are mainly responsible for determining the inner cluster structures. When 4 ≤ m, electrostatic interactions between silver cations and negatively charged framework oxygen atoms become more important in determining inner cluster structures, in addition to the 5s-orbital interactions. Although a significant E_stabilize value was found at n = 6 and m = 4, the optimized structure does not contain an Ag₆ cluster inside a ZSM-5 cavity. Instead, the optimized geometry can be viewed as constructed by the smaller silver clusters in the following manner: an Ag₅ cluster near three substituted Al atoms, together with a single silver cation near one Al atom, which separates from the cluster by larger than 3.00 Å. Therefore, our extension study suggests that Ag₅ clusters can exist within a ZSM-5(Al_m) cavity at m = 3 and 4.

Electronic absorption of stable Ag_m+2–ZSM-5(Al_m) structures

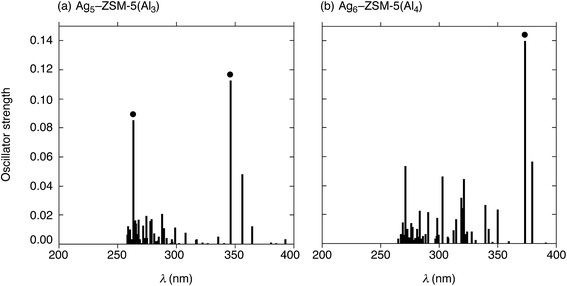
Next, we performed TD-DFT calculations to investigate the electronic transitions of energetically stable Ag_m+2–ZSM-5(Al_m) structures. For TD-DFT calculations, we used smaller Ag_m+2–ZSM-5(Al_m) models constructed by removing atoms far from the ten-membered ring containing the cluster (Fig. S9, ESI†). Note that the small models have frontier 5s-based orbitals whose energies are close to those in the whole Ag_m+2–ZSM-5(Al_m) models, as shown in Fig. S7 and S8.† The use of the smaller models is sufficient to reproduce TD-DFT results of the whole Ag_m+2–ZSM-5(Al_m) model because of the energetic similarity. Fig. 6 shows oscillator strengths (f) of the Ag₅–ZSM-5(Al₃) and Ag₆–ZSM-5(Al₄) structures as a function of excitation energy (λ in nm). Fig. 6(a) shows two strong peaks of the oscillator strength at 346 and 263 nm due to the 5s-based orbital excitations from totally symmetric orbital to an orbital with one node. Using the definition of the surperatom orbitals, this electronic excitation occurs from an S-orbital to a P-orbital, where ΔL increases by 1 (ΔL = +1). Similarly, the Ag₆–ZSM-5(Al₄) structure, composed of Ag₅–ZSM-5(Al₃) plus Ag₁–ZSM-5(Al₁), has a maximum oscillator strength value at 374 nm, as shown in Fig. 6(b). The electronic excitation behaviours are different from O_h-like Ag₆ clusters in LTA models that have maximum peaks around 530 nm judging from their oscillator strengths, as seen from Table S5 (ESI†).

Fig. 6 Electronic transitions of truncated Ag_m+2–ZSM-5(Al_m) structures obtained from time-dependent DFT (TD-DFT) calculations with the B3PW91 functional. (a) Ag₅–ZSM-5(Al₃) and (b) Ag₆–ZSM-5(Al₄). The oscillatory strengths (f) of Ag_m+2–ZSM-5(Al_m) are plotted as a function of the excitation energies (λ in nm). The black dots indicate fingerprint absorptions originating from electronic transitions between 5s-based orbitals: from the completely symmetric occupied orbital (S-orbital) to an unoccupied orbital with one node (P-orbital).

Combining the current and previous TD-DFT studies, we compared the Ag_m+2–ZSM-5(Al_m) structures in terms of excitation energies at the electronic transition with the strongest oscillator strength (λ_max), as listed in Table 5. Independent of m, the maximum absorption in Ag_m+2–ZSM-5(Al_m) comes from the S → P electronic transition, whose selection rule is ΔL = +1. The λ_max values increase from 303 nm to 374 nm, when m increases from 1 to 4 in Ag_m+2–ZSM-5(Al_m). Note that the zeolite at m = 4 containing a Ag₅ cluster plus a single silver cation has a larger λ_max value than that at Ag₅–ZSM-5(Al₃), due to slight interactions between the cluster and cation at m = 4. The DFT findings suggest that measurement of the absorptions due to the S → P electronic transition is a potential tool for identification of cluster sizes and structures.

Table 5 Electronic transition with the strongest oscillator strength in the most stable Ag_m+2–ZSM-5(Al_m) structures

m	1	2	3	4
a λmax: excitation energy (in nm) at the electronic transition with the largest oscillator strength of Agm+2–ZSM-5(Alm).b f: oscillator strength at a certain electronic transition.
λmax^a	303.4	324.5	346.2	373.6
f^b	0.31	0.29	0.11	0.14

---

Conclusions

Using density functional theory (DFT) calculations with the B3PW91 functional, we investigated the properties of Ag₅ and Ag₆ clusters inside a ZSM-5 zeolite whose ten-membered ring contains different numbers of Al atoms substituted for Si atoms of the SiO₂ framework (m) (Ag_n–ZSM-5(Al_m)). The current study achieved several optimized geometries for Ag₅–ZSM-5(Al_m) and Ag₆–ZSM-5(Al_m), and the results were compared with those of Ag_n–ZSM-5(Al_m) where n ≤ 3 in terms of energetics. DFT calculations found that a ZSM-5(Al_m) cavity stabilizes an Ag_m+2 cluster (m ≤ 3). The stabilization conditions (n = m + 2) can be understood through electron counting arguments based on 5s-based frontier orbitals in Ag_n–ZSM-5(Al_m), in which the number of 5s electrons in a cluster is n–m. When an Ag_m+2 cluster is on the inside of a ZSM-5(Al_m) cavity, the cluster has two 5s electrons populating the totally symmetric frontier orbitals, which effectively stabilize the cluster structure. The totally symmetric 5s-based orbital corresponds to a superatom S-orbital. Accordingly, the Ag_m+2–ZSM-5(Al_m) zeolites have an S² electronic configuration, being similar to magic-numbered silver clusters in the gas phase. Furthermore, time-dependent (TD) DFT calculations were performed to examine the electronic transition of Ag_m+2–ZSM-5(Al_m). Ag_m+2–ZSM-5(Al_m) zeolites were found to exhibit maximum absorption peaks due to electronic transitions based on 5s-based orbitals from the totally symmetric occupied orbital (S-orbital) to an unoccupied orbital with one node (P-orbital). The S → P electronic transitions follow the selection rule in bare cluster cases. In the case of maximum absorption, the excitation energies (λ_max) in Ag_m+2–ZSM-5(Al_m) increase from 303 to 374 nm when m increases from 1 to 4. DFT calculations revealed that the S → P electronic transitions of Ag_m+2–ZSM-5(Al_m) are a potential fingerprint for identifying the state of inner silver atoms.

Acknowledgements

This work was partly supported by a Grant-in-Aid for Young Scientists (B) (T. Y., No. 26790001) from the Japan Society for the Promotion of Science (JSPS), as well as by a Grant-in-Aid for Scientific Research on the Innovative Area “Stimuli-responsive Chemical Species for the Creation of Fundamental Molecules (No. 2408)” (JSPS KAKENHI Grant Number JP15H00941 for T. Y.).

References

1. W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Electronic shell structure and abundances of sodium clusters, Phys. Rev. Lett., 1984, 52, 2141–2143.
2. S. N. Khanna and P. Jena, Assembling crystals from clusters, Phys. Rev. Lett., 1992, 69, 1664–1667.
3. W. A. de Heer, The physics of simple metal clusters: experimental aspects and simple models, Rev. Mod. Phys., 1993, 65, 611–676.
4. D. M. P. Mingos, Structural and bonding patterns in gold clusters, Dalton Trans., 2015, 44, 6680–6695.
5. E. B. Guidez and C. M. Aikens, Quantum mechanical origin of the plasmon: from molecular systems to nanoparticles, Nanoscale, 2014, 6, 11512–11527.
6. H. Beyer, P. A. Jacobs and J. B. Uytterhoeven, Redox behaviour of transition metal ions in zeolites. Part 2—Kinetic study of the reduction and reoxidation of silver-Y zeolites, J. Chem. Soc., Faraday Trans. 1, 1976, 72, 674–685.
7. P. A. Jacobs, J. B. Uytterhoeven and K. H. Beyer, redox behaviour of transition metal ions in zeolites. Part 6—Reversibility of the reduction reaction in silver zeolites, J. Chem. Soc., Faraday Trans. 1, 1977, 73, 1755–1762.
8. P. A. Jacobs, J. B. Uytterhoeven and K. H. Beyer, some unusual properties of activated and reduced AgNaA zeolites, J. Chem. Soc., Faraday Trans. 1, 1979, 75, 56–64.
9. Y. Kim and K. Seff, The octahedral hexasilver molecule. Seven crystal structures of variously cacuum-dehydrated fully Ag⁺-exchanged zeolite A, J. Am. Chem. Soc., 1978, 100, 6989–6997.
10. T. Sun and K. Seff, Silver clusters and chemistry in zeolites, Chem. Rev., 1994, 94, 857–870.
11. S. Y. Kim, Y. Kim and K. Seff, Two crystal structures of fully dehydrated, fully Ag⁺-exchanged zeolite X. Dehydration in oxygen prevents Ag⁺ reduction. Without oxygen, Ag₈ⁿ⁺ (T_d) and cyclo-Ag₄^m+ (near S₄), form, J. Phys. Chem. B, 2003, 107, 6938–6945.
12. L. R. Gellens, W. J. Mortier, R. A. Schoonheydt and J. B. Uytterhoeven, The nature of the charged silver clusters in dehydrated zeolites of type A, J. Phys. Chem., 1981, 85, 2783–2788.
13. R. A. Schoonheydt and H. Leeman, Formation of the silver hexameric (Ag₆^x+) cluster in zeolite A, J. Phys. Chem., 1989, 93, 2048–2053.
14. G. A. Ozin and F. Hugues, Selective photoactivation of carbon–hydrogen bonds in paraffinic hydrocarbons. Dimerization of alkanes, J. Phys. Chem., 1982, 86, 5174–5179.
15. G. A. Ozin and F. Hugues, Silver atoms and small silver clusters stabilized in zeolite Y: optical spectroscopy, J. Phys. Chem., 1983, 87, 94–97.
16. G. A. Ozin, F. Hugues, S. M. Mattar and D. F. McIntosh, Low nuclearity silver clusters in faujasite-type zeolites: optical spectroscopy, photochemistry and relationship to the photodimerization of alkanes, J. Phys. Chem., 1983, 87, 3445–3450.
17. M. D. Baker, G. A. Ozin and J. Godber, Direct observation of the reversible redox couple Ag₃²⁺ ↔ Ag₃⁰ in silver zeolite A by Fourier transform far-infrared spectroscopy, J. Phys. Chem., 1984, 88, 4902–4904.
18. M. D. Baker, G. A. Ozin and J. Godber, Far-infrared studies of silver atoms, silver ions, and silver clusters in zeolites A and Y, J. Phys. Chem., 1985, 89, 305–311.
19. D. R. Brown and L. Kevan, Comparative electron spin resonance and optical absorption studies of silver-exchanged sodium Y zeolites: silver centers formed on dehydration, oxidation, and subsequent γ-irradiation, J. Phys. Chem., 1986, 90, 1129–1133.
20. B. Xu and L. Kevan, Formation of silver ionic clusters and silver metal particles in zeolite rho studied by electron spin resonance and far-infrared spectroscopies, J. Phys. Chem., 1991, 95, 1147–1151.
21. J. Texter, R. Kellerman and T. Gonsiorowski, Formation of charged silver clusters and their reversible silver ion desorption in zeolite A, J. Phys. Chem., 1986, 90, 2118–2122.
22. E. Gachard, J. Belloni and M. A. Subramanian, Optical and epr spectroscopic studies of silver clusters in Ag, Na-Y zeolite by γ-irradiation, J. Mater. Chem., 1996, 6, 867–870.
23. H. Yahiro, K. Manabe, Y. Itagaki and M. Shiotani, Epr of silver-ammonia adducts in γ-irradiation AgNa-A zeolite with low silver content, J. Chem. Soc., Faraday Trans., 1998, 94, 805–808.
24. J. Sadlo, M. Danilczuk and J. Michalik, Interaction of tetrameric silver with ammonia in AgCs-rho zeolite, Phys. Chem. Chem. Phys., 2001, 3, 1717–1720.
25. J. Sadlo, J. Michalik and L. Kevan, EPR and ESEEM study of silver clusters in ZK-4 molecular sieves, Nukleonika, 2006, 51, S49–S454.
26. J. Michalik, M. Danilczuk, J. Turek and J. Sadlo, Stabilisation of reactive intermediates in molecular sieves, Res. Chem. Intermed., 2007, 33, 793–806.
27. W. X. Zhang, H. Yahiro, N. Mizuno, M. Iwamoto and J. Izumi, Silver ion-exchanged zeolites as highly effective adsorbents for removal of NO_x by pressure swing adsorption, J. Mater. Sci. Lett., 1993, 12, 1197–1198.
28. M. Anpo, M. Matsuoka and H. Yamashita, In situ investigations of the photocatalytic decomposition of NO_x on ion-exchanged silver(I) ZSM-5 catalysts, Catal. Today, 1997, 35, 177–181.
29. M. Anpo, S. G. Zhang, H. Mishima, M. Matsuoka and H. Yamashita, Design of photocatalysts encapsulated within the zeolite framework and cavities for the decomposition of NO into N₂ and O₂ at normal temperature, Catal. Today, 1997, 39, 159–168.
30. S. M. Kanan, M. A. Omary, H. H. Patterson, M. Matsuoka and M. Anpo, Characterization of the excited states responsible for the action of silver(I)-Doped ZSM-5 zeolites as photocatalysts for nitric oxide decomposition, J. Phys. Chem. B, 2000, 104, 3507–3517.
31. W.-S. Ju, M. Matsuoka, K. Iino, H. Yamashita and M. Anpo, the local structures of silver(I) ion catalysts anchored within zeolite cavities and their photocatalytic reactivities for the elimination of N₂O into N₂ and O₂, J. Phys. Chem. B, 2004, 108, 2128–2133.
32. S. M. Kanan, M. C. Kanan and H. H. Patterson, Photophysical properties of Ag(I)-exchanged zeolite A and the photoassisted degradation of malathion, J. Phys. Chem. B, 2001, 105, 7508–7516.
33. J. Shibata, Y. Takada, A. Shichi, S. Satokawa, A. Satsuma and T. Hattori, Ag cluster as active species for SCR of NO by propane in the presence of hydrogen over Ag-MFI, J. Catal., 2004, 222, 368–376.
34. J. Shibata, K. Shimizu, Y. Takada, A. Shichi, H. Yoshida, S. Satokawa, A. Satsuma and T. Hattori, Structure of active Ag clusters in Ag zeolites for SCR of NO by propane in the presence of hydrogen, J. Catal., 2004, 227, 367–374.
35. K. Shimizu, K. Sugino, K. Kato, S. Yokota, K. Okumura and A. Satsuma, Formation and redispersion of silver clusters in Ag-MFI zeolite as investigated by time-resolved QXAFS and UV-vis, J. Phys. Chem. C, 2007, 111, 1683–1688.
36. K. Sawabe, T. Hiro, K. Shimizu and A. Satsuma, Density functional theory calculation on the promotion effect of H₂ in the selective catalytic reduction of NO_x over Ag–MFI zeolite, Catal. Today, 2010, 153, 90–94.
37. K. Shimizu, K. Sawabe and A. Satsuma, Unique catalytic features of Ag nanoclusters for selective NOx reduction and green chemical reactions, Catal. Sci. Technol., 2011, 1, 331–341.
38. T. Baba, N. Komatsu, H. Sawada, Y. Yamaguchi, T. Takahashi, H. Sugisawa and Y. Ono, ¹H magic angle spinning NMR evidence for dissociative adsorption of hydrogen on Ag⁺-exchanged A- and Y-zeolites, Langmuir, 1999, 15, 7894–7896.
39. T. Baba and H. Sawada, Conversion of methane into higher hydrocarbons in the presence of ethylene over H-ZSM-5 loaded with silver cations, Phys. Chem. Chem. Phys., 2002, 4, 3919–3923.
40. T. Baba, H. Sawada, T. Takahashi and M. Abe, Chemisorption study of hydrogen and methane by ¹H MAS NMR and conversion of methane in the presence of ethylene on Ag-Y zeolite, Appl. Catal., A, 2002, 231, 55–63.
41. H. Yoshida, T. Hamajima, Y. Kato, J. Shibata, A. Satsuma and T. Hattori, Active Ag Species in MFI zeolite for direct methane conversion in the light and dark, Res. Chem. Intermed., 2003, 29, 897–910.
42. S. Miao, Y. Wang, D. Ma, Q. Zhu, S. Zhou, L. Su, D. Tan and X. Bao, Effect of Ag⁺ cations on nonoxidative activation of methane to C₂-hydrocarbons, J. Phys. Chem. B, 2004, 108, 17866–17871.
43. Y. Kuroda, T. Mori, H. Sugiyama, Y. Uozumi, K. Ikeda, A. Itadani and M. Nagao, On the possibility of AgZSM-5 zeolite being a partial oxidation catalyst for methane, J. Colloid Interface Sci., 2009, 333, 294–299.
44. G. D. Cremer, Y. Antoku, M. B. J. Roeffaers, M. Sliwa, J. V. Noyen, S. Smout, J. Hofkens, D. E. D. Vos, B. F. Sels and T. Vosch, Photoactivation of silver-exchanged zeolite A, Angew. Chem., Int. Ed., 2008, 47, 2813–2816.
45. G. D. Cremer, E. Coutino-Gonzalez, M. B. J. Roeffaers, B. Moens, J. Ollevier, M. V. d. Auweraer, R. Schoonheydt, P. A. Jacobs, F. C. D. Schryver and J. Hofkens, et al., Characterization of fluorescence in heat-treated silver-exchanged zeolites, J. Am. Chem. Soc., 2009, 131, 3049–3056.
46. G. D. Cremer, B. F. Sels, J. Hotta, M. B. J. Roeffaers, E. Bartholomeeusen, E. Coutino-Gonzalez, V. Valtchev, D. E. D. Vos, T. Vosch and J. Hofkens, Optical encoding of silver zeolite microcarriers, Adv. Mater., 2010, 22, 957–960.
47. G. De Cremer, E. Coutiño-Gonzalez, M. B. J. Roeffaers, D. E. De Vos, J. Hofkens, T. Vosch and B. F. Sels, In situ Observation of the emission characteristics of zeolite-hosted silver species during heat treatment, ChemPhysChem, 2010, 11, 1627–1631.
48. T. Yumura, T. Nanba, H. Torigoe, Y. Kuroda and H. Kobayashi, Behavior of Ag₃ clusters inside a nanometer-sized space of ZSM-5 zeolite, Inorg. Chem., 2011, 50, 6533–6542.
49. T. Yumura, A. Oda, H. Torigoe, A. Itadani, Y. Kuroda, T. Wakasugi and H. Kobayashi, Combined experimental and computational approaches to to elucidate the structures of silver clusters inside the ZSM-5 cavity, J. Phys. Chem. C, 2014, 118, 23874–23877.
50. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
51. M. Muniz-Miranda and M. F. Ottaviani, Silver nanoclusters in mesoporous silica, as obtained by visible-laser irradiation, Laser Phys., 2004, 14, 1533–1538.
52. S. Yanagisawa, T. Tsuneda and H. Hirao, An investigation of density functionals: the first-row transition metal dimer calculations, J. Chem. Phys., 2000, 112, 545.
53. J. Yoon, K. S. Kim and K. K. Baeck, Ab initio study of the low-lying electronic states of Ag₃⁻, Ag₃, and Ag₃⁺: a coupled-cluster approach, J. Chem. Phys., 2000, 112, 9335.
54. R. Fournier, Theoretical study of the structure of silver clusters, J. Chem. Phys., 2001, 115, 2165.
55. H. M. Lee, M. Ge, B. R. Sahu, P. Tarakeshwar and K. S. Kim, Geometrical and electronic structures of gold, silver, and gold–silver binary clusters: origins of ductility of gold and gold–silver alloy formation, J. Phys. Chem. B, 2003, 107, 9994–10005.
56. S. Zhao, Z.-H. Li, W.-N. Wang, Z.-P. Liu, K.-N. Fan, Y. Xie and H. F. Schaefer III, Is the uniform electron gas limit important for small Ag clusters? assessment of different density functionals for Ag_n (n ≤ 4), J. Chem. Phys., 2006, 124, 184102.
57. G. N. Khairallah and R. A. J. O'Hair, Gas phase synthesis and reactivity of Ag_n⁺ and Ag_n−1H⁺ clyster cations, Dalton Trans., 2005, 2702–2712.
58. J. Cizek, Correlation problem in atomic and molecular systems. calculation of wave function components in ursell-type expansion using quantum-field theoretical methods, J. Chem. Phys., 1966, 45, 4256.
59. A. Itadani, H. Sugiyama, M. Tanaka, T. Ohkubo, T. Yumura, H. Kobayashi and Y. Kuroda, Potential for C–H activation in CH₄ utilizing a CuMFI-Type zeolite as a catalyst, J. Phys. Chem. C, 2009, 113, 7213–7222.
60. T. Yumura, H. Yamashita, H. Torigoe, H. Kobayashi and Y. Kuroda, Site-specific Xe additions into Cu–ZSM-5 zeolite, Phys. Chem. Chem. Phys., 2010, 12, 2392–2400.
61. A. Itadani, T. Yumura, T. Ohkubo, H. Kobayashi and Y. Kuroda, Existence of dual species composed of Cu⁺ in CuMFI being bridged by C₂H₂, Phys. Chem. Chem. Phys., 2010, 12, 6455–6465.
62. H. Torigoe, T. Mori, K. Fujie, T. Ohkubo, A. Itadani, K. Gotoh, H. Ishida, H. Yamashita, T. Yumura and H. Kobayashi, et al., Direct information on structure and energetic features of Cu⁺–Xe species formed in MFI-Type zeolite at room temperature, J. Phys. Chem. Lett., 2010, 1, 2642–2650.
63. T. Yumura, S. Hasegawa, A. Itadani, H. Kobayashi and Y. Kuroda, The variety of carbon-metal bonds inside Cu-ZSM-5 zeolites: a density functional theory study, Materials, 2010, 3, 2516–2535.
64. T. Yumura, M. Takeuchi, H. Kobayashi and Y. Kuroda, Effects of ZSM-5 zeolite confinement on reaction intermediates during dioxygen activation by enclosed dicopper cations, Inorg. Chem., 2009, 48, 508–517.
65. T. Yumura, Y. Hirose, T. Wakasugi, Y. Kuroda and H. Kobayashi, Roles of water molecules in modulating the reactivity of dioxygen-bound Cu-ZSM-5 toward methane: a theoretical prediction, ACS Catal., 2016, 6, 2487–2495.
66. M. J. Frisch, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
67. M. J. Frisch, et al., Gaussian 03, Gaussian, Inc., Pittsburgh, PA, 2003.
68. W. J. Stevens, H. Basch and M. Krauss, Compact effective potentials and efficient shared-exponent basis sets for the first- and second-row atoms, J. Chem. Phys., 1984, 81, 6026.
69. W. J. Stevens, M. Krauss, H. Basch and P. G. Jasien, Relativistic compact effective potentials and efficient, shared-exponent basis sets for the third-, fourth-, and fifth-row atoms, Can. J. Chem., 1992, 70, 612–630.
70. W. J. Hehre, R. Ditchfield and J. A. Pople, Self-consistent molecular orbital methods. xii. Further extensions of gaussian-type basis sets for use in molecular orbital studies of organic molecules, J. Chem. Phys., 1972, 56, 2257.
71. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77, 3654.
72. P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222.
73. J. S. Binkley, J. A. Pople and W. J. Hehre, Self-consistent molecular orbital methods. 21. Small split-valence basis sets for first-row elements, J. Am. Chem. Soc., 1980, 102, 939–947.
74. M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, Self-consistent molecular-orbital methods. 22. Small split-valence basis sets for second-row elements, J. Am. Chem. Soc., 1982, 104, 2797–2803.
75. W. J. Pietro, M. M. Francl, W. J. Hehre, D. J. DeFrees, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods. 24. Supplemented small split-valence basis sets for second-row elements, J. Am. Chem. Soc., 1982, 104, 5039–5048.
76. K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds 4. extended basis sets for third-and fourth-row, main-group elements, J. Comput. Chem., 1986, 7, 359–378.
77. K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds 5. Extended basis sets for first-row transition metals, J. Comput. Chem., 1987, 8, 861–879.
78. K. D. Dobbs and W. J. Hehre, Molecular orbital theory of the properties of inorganic and organometallic compounds. 6. Extended basis sets for second-row transition metals, J. Comput. Chem., 1987, 8, 880–893.
79. S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, A new oniom implementation in Gaussian 98. 1. The calculation of energies, gradients and vibrational frequencies and electric field derivatives, J. Mol. Struct.: THEOCHEM, 1999, 462, 1–21.
80. To obtain Ag₅³⁺ and Ag₆⁴⁺ clusters, which would have the HOMO composed of the S orbital, we tried to optimize their geometries by using initial geometries taken from the optimized geometries for Ag₅⁺ and Ag₆⁺ in Fig. 2. However, the initial geometries for Ag₅³⁺ clusters were decomposed into two Ag⁺ cations and one Ag₃⁺ cluster as well as two Ag⁺ cations and one Ag₄²⁺ cluster during the optimization. The decomposition into two Ag⁺ cations and one Ag₃⁺ cluster is about 200 kcal mol⁻¹ stable relative to initial Ag₅³⁺ clusters, and the decomposition into two Ag⁺ cations and one Ag₄²⁺ cluster is about 160 kcal mol⁻¹ stable. Similarly the optimization of Ag₆⁴⁺ clusters results in the decomposition into one Ag₄²⁺ cluster and two Ag⁺ cations. The decomposed form is about 390 kcal mol⁻¹ stable relative to the initial geometry.
81. Lengthening Ag–Ag separations are expected because electrostatic interactions between a silver ion and framework oxygen atoms become stronger than the 5s orbital interactions between silver atoms.
82. N. T. Cuong, H. M. T. Nguyen, M. P. Pham-Ho and M. T. Nguyen, Optical properties of the hydrated charged silver tetramer and silver hexamer encapsulated inside the sodalite cavity of an LTA-type zeolite, Phys. Chem. Chem. Phys., 2016, 18, 18128–18136.
83. N. T. Cuong, H. M. T. Nguyen and M. T. Nguyen, Theoretical modeling of optical properties of Ag₈ and Ag₁₄ silver clusters embedded in an LTA sodalite zeolite cavity, Phys. Chem. Chem. Phys., 2013, 15, 15404–15415.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized geometries for Ag₃–ZSM-5(Al_m) and Ag₄–ZSM-5(Al_m) obtained in ref. 48 and 49 (S1); QM/MM ONIOM calculations of Ag₃–ZSM-5(Al₁) (S2); selected Ag₅ and Ag₆ clusters that are could be formed by the single-atom and dual-atom additions into Ag₄ clusters (S3); optimized geometries for Ag₅–ZSM-5(Al_m) obtained in the current study (S4); optimized geometries for Ag₆–ZSM-5(Al_m) obtained in the current study (S5); E_stabilize values obtained from a different basis-set system (S6); frontier orbitals of Ag₅–ZSM-5(Al₃) and its truncated model (S7); frontier orbitals of Ag₆–ZSM-5(Al₃) and its truncated model (S8); models for time-dependent DFT calculations (S9); time-dependent B3PW91 DFT calculations of Ag₈ clusters inside LTA zeolites, whose geometries were taken from ref. 82 (S10); and full lists in ref. 66 and 67 (S11). See DOI: 10.1039/c6ra26492a

---