DOI:
10.1039/C6RA26555C
(Paper)
RSC Adv., 2017,
7, 16843-16853
First-principles study of structural stability, dynamical and mechanical properties of Li2FeSiO4 polymorphs†
Received
9th November 2016
, Accepted 23rd January 2017
First published on 17th March 2017
Abstract
Li2FeSiO4 is an important alternative cathode for next generation Li-ion batteries due to its high theoretical capacity (330 mA h g−1). However, its development has faced significant challenges arising from structural complexity and poor ionic conductivity. In the present work, the relative stability, electronic structure, thermodynamics, and mechanical properties of potential cathode material Li2FeSiO4 and its polymorphs have been studied by state-of-the-art density-functional calculations. Among the 11 structural arrangements considered for the structural optimization calculations, the experimentally known monoclinic P21 modification is found to be the ground state structure. The application of pressure originates a sequence of phase transitions according to P21 → Pmn21 → I222, and the estimated values of the critical pressure are found to be 0.38 and 1.93 GPa. The electronic structures reveal that all the considered polymorphs have a non-metallic character, with band gap values varying between 3.0 and 3.2 eV. The energy differences between different polymorphs are small, and most of these structures are dynamically stable. On the other hand, the calculation of single crystal elastic constants reveals that only few Li2FeSiO4 polymorphs are mechanically stable. At room temperature, the diffusion coefficient calculations of Li2FeSiO4 in different polymorphs reveal that the Li-ion conductivity of this material is poor.
Introduction
The research on polyanion cathodes for lithium-ion batteries has continued to gain momentum since Padhi et al. reported the electrochemical properties of LiFePO4 in 1997.1 The interest in polyanion cathodes comes from added safety and higher voltage values in comparison to the oxide analogues with the same M2+/3+ redox couples. The increased safety and higher voltage values have been attributed to strong covalent bonding within the polyanion units. Over the years, these inherent characteristics of polyanion cathodes have promoted the investigation of several series of polyanion compounds for use in lithium-ion batteries. For example: Li2MSiO4 silicates, Li2MP2O7 pyrophosphates, and LiMBO3 borates (M = Mn, Fe, Co, and Ni). Each of these compounds possesses additional favourable characteristics as cathode materials. The borates contain the lightest of the polyanion units (BO3) and, therefore, have a higher theoretical capacity (∼200 mA h g−1) than LiFePO4 (∼170 mA h g−1). The pyrophosphates and silicates offer the appealing possibility of extracting/inserting two lithium ions per transition metal ion in the material, further increasing the theoretical capacity, respectively, to ∼220 and 330 mA h g−1. Additionally, silicon is one of the most abundant elements on earth's crust, offering a reduction in cost for the silicates. Li2FeSiO4 (hereafter referred as LFS) is an attractive member of Li2MSiO4 group, which is built on inexpensive and abundant raw materials.2,3 In recent works, small particles of LFS and proper electrode engineering have yielded electrodes with good cycling stability close to the theoretical capacity.4 Experimental and theoretical studies on LFS have found stable structures where the cations are located in the tetrahedral interstitials of a nearly hexagonally close-packed framework of oxygen atoms.5–9 Depending on the crystal structure, the Li ions in transition metal silicates can either be arranged in layers,10 along lines, or in a three-dimensional network. Hence, the ionic conductivity might be strongly anisotropic.11,12 The most known polymorphs are Pmn21 (orthorhombic at low temperature), P21 (monoclinic at 700 °C), and Pmnb (orthorhombic at 900 °C).13 However, the monoclinic space group P21 is found to be the most stable polymorph by means of first-principles calculations.4,10,13,14 The stability of these polymorphs of LFS plays an important role in understanding the multi-electron process of LFS. However, to the best of our knowledge, the study of dynamical and mechanical stability of LFS is still missing to date. In the present study, we have investigated the structural phase stability, electronic, mechanical, and lattice dynamical properties of the of LFS polymorphs.
Computational details
Total energies have been calculated by the projected-augmented plane-wave (PAW) implementation of the Vienna ab initio simulation package (VASP).15,16 All these calculations were made using the Perdew, Burke, and Ernzerhof (PBE)17 exchange–correlation functional with the Hubbard parameter correction (GGA + U), following the rotationally invariant form.18,19 An effective U values of 5 eV (with J = 1 eV) was used for the Fe-d states. Ground-state geometries were determined by minimizing both the stresses and the Hellmann–Feynman forces using the conjugate-gradient algorithm with force convergence threshold of 10−3 eV Å−1. Brillouin zone integration was performed with a Gaussian broadening of 0.1 eV during all relaxations. From various sets of calculations, it was found that 512 k-points in the Brillouin zone for the structure with a 600 eV plane-wave cut-off are sufficient to ensure optimum accuracy in the computed results. The k-points mesh was generated using the Monkhorst–Pack method with a grid size of 8 × 8 × 8 for structural optimization. A similar density of k-points and energy cut-off were used to estimate total energy as a function of volume for all the structures considered in the present study. Iterative relaxation of atomic positions was stopped when the change in total energy between successive steps was smaller than 1 meV per cell. From our total-energy calculation for the LFS-Pmn21 phase, we have found that the antiferromagnetic (AFM; spins of electrons, align in a regular pattern with neighboring spins on different sub-lattices pointing in opposite directions) and ferromagnetic (FM; spins of electrons, align along the c axis) states are lower in energy compared to the paramagnetic (PM; non-magnetic) state. The energy difference between the AFM and FM states is found to be 2 meV per cell. (i.e., comparable with the convergence threshold), moreover, both states have a similar cell volume (see Fig. 1). Hence we have considered only the FM states in the rest of the other phases in the present work.
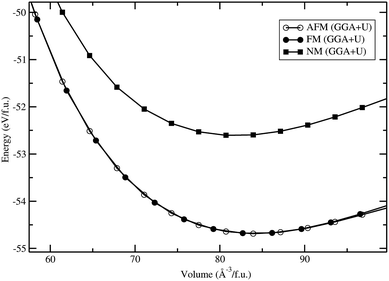 |
| | Fig. 1 Calculated unit cell volume vs. total energy (per formula unit; f.u.) for Li2FeSiO4 in Pmn21 symmetry with different magnetic configuration (anti ferro magnetic-AFM, ferro magnetic-FM, and nonmagnetic-NM ordering). | |
The calculated total energy as a function of volume has been fitted to the universal equation of state (EOS).20 The transition pressures are calculated from the pressure vs. Gibbs free energy curves. The Gibbs free energy (G = U + PV − TS where T = 0; G = total energy + pressure × volume) is calculated in the following way: the volume versus total energy curves calculated for two data sets were fitted to the universal EOS function. The pressure is defined as 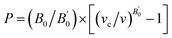 . The relation can be inverted to obtain the volume as
. The relation can be inverted to obtain the volume as 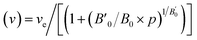 where ve, B0, and
where ve, B0, and 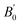 refers to the equilibrium volume, the bulk modulus, and its derivative with respect to pressure, respectively. The inverse is then calculated using the bisection method. From the scan over the pressures, the corresponding difference in the enthalpy between the two data sets was calculated.
refers to the equilibrium volume, the bulk modulus, and its derivative with respect to pressure, respectively. The inverse is then calculated using the bisection method. From the scan over the pressures, the corresponding difference in the enthalpy between the two data sets was calculated.
A frozen phonon calculation was performed on the supercells using the phonopy program to obtain the phonon dispersion curve and density of states.21 An atomic displacement of 0.0075 Å was used, with a symmetry consideration, to obtain the force constants for the phonon calculations. The displacements in opposite directions along all axes were incorporated in the calculations to improve the overall precision. The force calculations were made using the VASP code with the supercell approach (with GGA + U correction) and the resulting data were imported into the Phonopy program. The dynamical matrices were calculated from the force constants, and phonon DOS curves were computed using the Monkhorst–Pack scheme.22 The thermal properties, such as heat capacity, free energy and entropy, were obtained using the calculated phonon density of states (DOS).
The Li diffusion barrier height of the different polymorphs are investigated with the cNEB method using supercell approach.23,24 A large supercell (dimensions listed in Table 2) was used to ensure that the atoms are separated from their periodic images, providing a more accurate result for the activation barrier in the diluted limit. To determine the minimum energy path (MEP) through the climbing Nudged Elastic Band (cNEB) method, six replicas of the system were created, in each of which the diffusing Li atom was moved by equidistant steps to intermediate positions between the initial and final states, as obtained by linear interpolation of the path. A 1 × 2 × 1 supercell (for P21; the supercell sizes for the other phases are reported in Table 2) was used to ensure that the atoms are separated from their periodic image, providing a more accurate answer for the activation barrier in the diluted limit.
Result and discussions
Structure models considered
The crystal structure of LFS is quite ambiguous due to its rich polymorphism and hence to the difficulties encountered in obtaining single phase samples. The early studies by Tarte and Cahay,25 and Nyten et al.27 shows that the structure of LFS is isostructural with β-Li3PO4, that is, crystallizing in the orthorhombic structure with space group Pmn21. As noted by Quoirin et al.,26 the indexation given in ref. 27 was highly questionable, and it was found that LFS under goes a series of complex phase transformations. The Cmma space group with a = 10.66 Å, b = 12.54 Å, c = 5.02 Å was proposed for LFS annealed at 800 °C. Nishimura et al.9 determined the crystal structure of LFS (synthesized from a ceramic-type route at 800 °C) in monoclinic symmetry with a = 8.23 Å, b = 5.02 Å, c = 8.23 Å, β = 99.20°,9 which was confirmed by Sirisopanaporn et al. who discovered and calculated the crystal structure of a new metastable polymorph, obtained by rapid quenching at ambient temperature from 900 °C.14 In general, the structural models describing LFS are derived from Li3PO4-based structures, in which one-half of the tetrahedral sites, generated by a distorted hexagonal close packing of oxygen atoms, are occupied by cations. Li3PO4 itself crystallizes in two main groups of polymorphs (named as β and γ), which differ in their respective orientations of filled tetrahedral: all T+ (oriented upward) in the low-temperature β form, T+ and T− (oriented downward) for the high-temperature γ form.28 The structures of Li2MSiO4 analogues (M = Zn, Mn, Mg, and Co) have been reported to adopt “simple” β-type or γ-type structures or their distorted derivatives.7,29–32 The relative stability and electrochemical properties of various LFS polymorphs were very recently investigated from first-principles calculations.10,33 Quite recently the surface structures and energetics of the Pmn21 polymorph of the LFS were studied using DFT.34
In general, the equilibrium crystal structures predicted based on first principles calculations using the structural inputs from Inorganic crystal structure database (ICSD)35 mostly agree well with experimental structures. In our long experience (see ref. 36–38) on predicting structural properties of hydrides and oxides we found that the ICSD/guess-structure approach is more reliable when a number of existing structural information is used as a starting point. The reliability of the calculation depends upon the number of input structures considered in the calculations. Though it is a tedious process to select input structures from the 486 entries for the ABC2X4 composition in the ICSD database, which also involves extensive computations, several compounds/phases have the same structure type and some cases have only small variation in the positional parameters (only for certain atoms). Even though we used different positional parameters, these structures converted mostly to the similar type of structural arrangement during the full geometry optimization and hence these possibilities are omitted. For our theoretical simulations, we have chosen 11 structure types from the ABC2X4. The involved structure types are (space group and space group number are given in the parenthesis): Li2FeSiO4 (P21; 4), Li2BeSiO4 (Pc; 7), Li2FeSiO4 (P21/c; 14), Li2BeSiO4 (C2221; 20), Li2FeSiO4 (Pmn21; 31), Li2CoSiO4 (Pna21; 33), Li2FeSiO4 (Pnma; 62), Li2CaSiO4 (I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m; 121), EuLi2SiO4 (P3121; 152), Li2BaSiO4 (P63cm; 185), and Li2MnSiO4-modified-Pmn21 (Pmn21-modi). Among the considered structures for our structural optimization, the calculated total energy at the equilibrium volume for the P21 atomic arrangements occur at the lowest total energy (see Fig. 2). The calculated positional and lattice parameters (see Table 1) are found to be in good agreement with experimental findings9 and with the other theoretical calculations.10,33 It consists of a lattice built up from infinite conjugated layers of composite SiFeO4 linked through the LiO4 tetrahedra, with each Li, Fe, Si located in the centre of the tetrahedron formed by four oxygen atoms. Furthermore, the Li+ ions are occupying tetrahedral sites between the FeO4–SiO4 where the tetrahedra alternately point in opposite directions. It should be noted that this phase is stabilized when the particle size is reduced39 and, according to experimental findings, it is a thermodynamically less stable phase.9,40 The next energetically favourable phase is orthorhombic Pmn21. In this structure, chains of LiO4 tetrahedra run along the a direction, parallel to the chains of alternating FeO4 and SiO4 tetrahedra (see Fig. 3). The energy difference between this phase with P21 at the equilibrium volume is only ca. 4.6 meV f.u.−1 (see Fig. 2). The calculated structural parameters are found to be in good agreement (see Table 1) with the recent experimental finding9 and with other DFT studies.10,33 It is interesting to note that the energy difference between the P21/c, Pnma, Pc, Pna21 and Pmn21-modi is also very small, and hence, one can easily modify one polymorph into another by application of temperature or pressure; this explains the difficulties to control the synthesis of single phase samples of LFS polymorphs, also related to very similar electrochemical properties (voltage, volume variation, and electronic structure).10,41 One should also remember that the calculated results are valid only for defect-free ideal materials at low temperatures. However, the experimental findings show that, depending upon the synthesis route/conditions, one can stabilize different polymorphs of LFS and it is therefore difficult to get phase-pure materials from most synthesis processes.9,14,40
2m; 121), EuLi2SiO4 (P3121; 152), Li2BaSiO4 (P63cm; 185), and Li2MnSiO4-modified-Pmn21 (Pmn21-modi). Among the considered structures for our structural optimization, the calculated total energy at the equilibrium volume for the P21 atomic arrangements occur at the lowest total energy (see Fig. 2). The calculated positional and lattice parameters (see Table 1) are found to be in good agreement with experimental findings9 and with the other theoretical calculations.10,33 It consists of a lattice built up from infinite conjugated layers of composite SiFeO4 linked through the LiO4 tetrahedra, with each Li, Fe, Si located in the centre of the tetrahedron formed by four oxygen atoms. Furthermore, the Li+ ions are occupying tetrahedral sites between the FeO4–SiO4 where the tetrahedra alternately point in opposite directions. It should be noted that this phase is stabilized when the particle size is reduced39 and, according to experimental findings, it is a thermodynamically less stable phase.9,40 The next energetically favourable phase is orthorhombic Pmn21. In this structure, chains of LiO4 tetrahedra run along the a direction, parallel to the chains of alternating FeO4 and SiO4 tetrahedra (see Fig. 3). The energy difference between this phase with P21 at the equilibrium volume is only ca. 4.6 meV f.u.−1 (see Fig. 2). The calculated structural parameters are found to be in good agreement (see Table 1) with the recent experimental finding9 and with other DFT studies.10,33 It is interesting to note that the energy difference between the P21/c, Pnma, Pc, Pna21 and Pmn21-modi is also very small, and hence, one can easily modify one polymorph into another by application of temperature or pressure; this explains the difficulties to control the synthesis of single phase samples of LFS polymorphs, also related to very similar electrochemical properties (voltage, volume variation, and electronic structure).10,41 One should also remember that the calculated results are valid only for defect-free ideal materials at low temperatures. However, the experimental findings show that, depending upon the synthesis route/conditions, one can stabilize different polymorphs of LFS and it is therefore difficult to get phase-pure materials from most synthesis processes.9,14,40
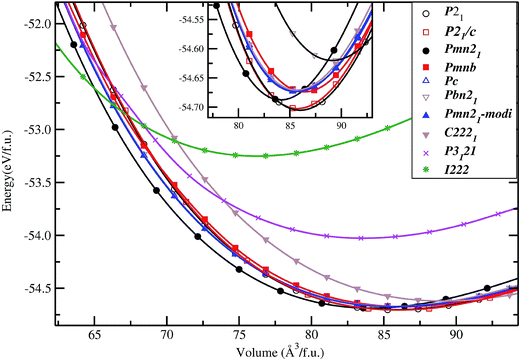 |
| | Fig. 2 Calculated unit cell volume vs. total energy (per formula unit; f.u.) for Li2FeSiO4 in actual and possible structural arrangements (structure types being labeled on the illustration). The magnified version around the low energy part of the cell volume vs. total energy is shown as an insert. | |
Table 1 The calculated equilibrium structural parameters (a, b and c are in Å) and bandgap (Eg in eV) values for Li2FeSiO4 polymorphs
| Phase |
Lattice parameter |
Eg (eV) |
| a |
b |
c |
β (deg) |
| From ref. 64. From ref. 9. From theoretical calculation by Saracibar et al.10 According to the structural analysis the modified Pmn21 structure (Pmn21-modi) can be described in monoclinic (space group Pc; space group number 7) structure. Structural parameters at the phase transition point. |
| Pmn21 |
6.3250(6.295)a |
5.3842(5.3454)a |
4.9731(4.9624)a |
90 |
3.2 |
| P21 |
8.313(8.2290)b |
5.084(5.0200)b |
8.282(8.2335)b |
99.15(99.20) |
3.2 |
| P21/c |
8.2320(8.231)a |
5.0168 (5.022)a |
8.2348(8.232)a |
99.18(99.27) |
3.15 |
| Pna21 |
6.2812(6.276)c |
10.9810(10.973)c |
5.0158(5.016)c |
90 |
3.06 |
| Pmn21-modi |
6.3743(6.271)c |
5.5755(5.485)c |
5.1002(5.017)c |
90.5(90.5)c |
3.07 |
| Pcd |
5.1002 |
5.5755 |
8.1311 |
128.4 |
| Pmna |
6.341(6.2853)a |
10.747(10.6592)a |
5.100 (5.0367)a |
86.89(84.36) |
3.11 |
| I222e |
4.7301 |
4.7237 |
5.5346 |
90 |
3.24 |
Table 2 Computational details for the phonon calculation, calculated zero-point energy (ZPE) from the phonon density of states, and dynamical stability (DS) for different Li2FeSiO4 polymorphsa
| Phase |
Supercell size |
Num. atoms |
ZPE (eV) |
DS |
| *According to the structural analysis the modified Pmn21 structure (Pmn21-modi) can be described in monoclinic (space group Pc; space group number 7) structure. **Stable at high pressure. |
| Pmn21 |
2 × 2 × 2 |
128 |
0.629 |
Stable |
| P21 |
1 × 2 × 1 |
64 |
0.626 |
Stable |
| P21/c |
1 × 2 × 1 |
64 |
0.644 |
Stable |
| Pna21 |
2 × 1 × 2 |
128 |
0.665 |
Unstable |
| Pmnb |
2 × 1 × 2 |
128 |
0.627 |
Stable |
| Pc* |
2 × 2 × 2 |
128 |
0.581 |
Stable |
| I222** |
3 × 3 × 3 |
216 |
0.730 |
Stable |
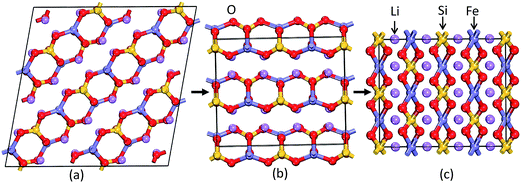 |
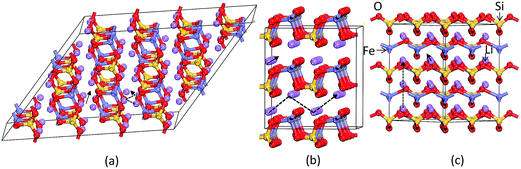
| | Fig. 3 Theoretically predicted low energy crystal structures for Li2FeSiO4: (a) P21 structure and (b) Pmn21 structure at equilibrium volume and (c) I222 structure at 1.93 GPa at T = 0 K. The legends for the different kinds of atoms are given in the illustration. | |
As discussed above, P21 is the ground-state structure, and it transforms into Pmn21 modification at 0.38 GPa (see Fig. 2 and 3). Further application of pressure on this Pmn21 modification transforms it into I222 modification at 1.9 GPa (see Fig. 4). It should be noted that the I222 structure is very close related to the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m (space group 121) and both modifications have similar energies (the variation is only 0.2 meV f.u.−1). The pressure induced Pmn21-to-I222 transition involves reconstructive rearrangements of the Li, Fe, Si, and O lattices with breaking and reconstruction of bonds. Usually, the application of pressure reduces the covalency in solids and makes the valence electrons more diffuse than at ambient condition. All these three polymorphs P21, Pmn21 and I222 are stabilized in layered structure type with a similar type of atomic arrangement. The main difference between the three polymorphs are both P21, Pmn21 polymorphs are having almost similar interlayer distances while in the I222 phase the interlayer distance become very narrow and the SiO4 and FeO4 tetrahedra become stretched along [011] (see Fig. 3).
2m (space group 121) and both modifications have similar energies (the variation is only 0.2 meV f.u.−1). The pressure induced Pmn21-to-I222 transition involves reconstructive rearrangements of the Li, Fe, Si, and O lattices with breaking and reconstruction of bonds. Usually, the application of pressure reduces the covalency in solids and makes the valence electrons more diffuse than at ambient condition. All these three polymorphs P21, Pmn21 and I222 are stabilized in layered structure type with a similar type of atomic arrangement. The main difference between the three polymorphs are both P21, Pmn21 polymorphs are having almost similar interlayer distances while in the I222 phase the interlayer distance become very narrow and the SiO4 and FeO4 tetrahedra become stretched along [011] (see Fig. 3).
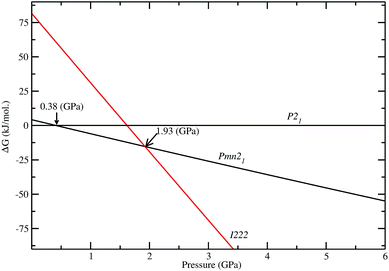 |
| | Fig. 4 Calculated stability diagram for Li2FeSiO4 phases (difference in Gibbs free energy ΔG) related to low energy P21 structure at T = 0 K. The transition points are marked by arrow with corresponding pressure. | |
The electronic up-spin and down-spin band structure calculated at the equilibrium volumes for all polymorphs considered in this study for LFS are displayed in Fig. S1–S8 (see ESI†). All modifications have finite energy gap (Eg; vary from 3.06 to 3.24 eV) between the valence band (VB) and the conduction band (CB), and hence, they have a non-metallic character. The magnitude of the Eg and band positions suggests that the LFS polymorphs are direct wide bandgap semiconductors. It is well known that the bandgap (Eg) values of solids obtained from usual DFT calculations are systematically underestimated due to the discontinuity in the exchange–correlation potential. Thus the calculated Eg values are commonly 30–50% smaller than those measured experimentally. Hence, LFS polymorphs are likely to have a much larger bandgap value than the one identified in this study.
The total phonon density of states (PDOS) is calculated at the equilibrium volumes for different polymorphs of LFS. For the I222 modifications, the PDOS are calculated both at equilibrium and at the phase transition point. The calculated PDOS of LFS polymorphs are displayed in Fig. 5. For all these polymorphs, no imaginary frequency was observed (except for Pbn21 and I222 phase), indicating that all the structures (except Pbn21 and I222) are stable or at least dynamically stable at ambient conditions. In the I222 phase the ambient condition phonon, soft modes disappear at pressures above 1.9 GPa (see Fig. 5). Hence, the predicted I222 phase is stable above the critical pressure. All the polymorphs of LFS (except Pbn21) including the high-pressure phase have a similar phonon density of states. Hence, we have displayed in Fig. 6 only the partial phonon DOS for Pmn21 polymorphs. In the Pmn21 phase, the partial phonon DOS is plotted along three directions x, y, and z. For Fe, Si, and Li atoms, the vibrational modes along the x, y, and z directions are almost identical. On the other hand, for the O atoms, the vibrational modes along the x, y, and z directions are considerably different at the high-frequency region (see Fig. 6).
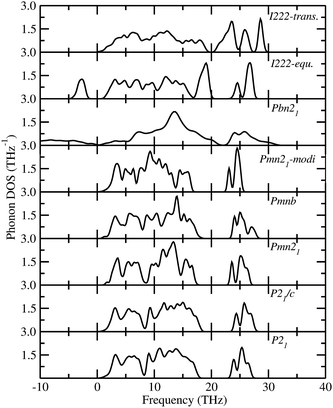 |
| | Fig. 5 Calculated total phonon density of states for Li2FeSiO4 in different modifications. The modifications are noted in the corresponding panel. | |
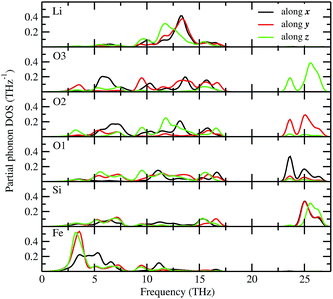 |
| | Fig. 6 Calculated site projected phonon density of states for Li2FeSiO4 in Pmn21 modification. The corresponding sites are noted in the panel and the phonon mode along different directions are marked with different color (black-along x; red-along y; and green-along z). | |
In addition to dynamical stability, some important thermodynamic properties of LFS polymorphs (such as, free energy, entropy, and lattice heat capacity; see Fig. S9†) at zero K, is calculated. Our calculated temperature-dependent lattice specific capacities for the different polymorphs of the LFS have similar values except for the high-pressure polymorph (see Fig. 7). This finding clearly demonstrates that all these polymorphs have similar thermodynamic properties. The specific heat coefficient increases rapidly below 600 K. Above this temperature the slope becomes gentler.
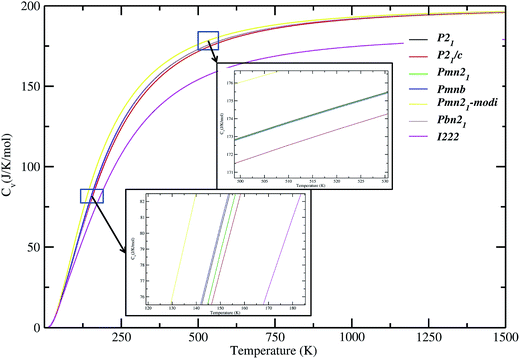 |
| | Fig. 7 Calculated lattice heat capacity verses temperature plot for Li2FeSiO4 polymorphs. The magnified version around the 100 K and 500 K part of the heat capacities curves are shown as an insert. | |
Single crystal elastic constants and mechanical stability
To understand the mechanical stability of the considered phases, we have computed the single-crystal elastic constants using the finite strain technique. The elastic constants of a material describe its response to an applied strain or, conversely, the stress required to maintain a given deformation. Both stress and strain have three tensile and three shear components. The linear elastic constants of a crystal can therefore be described using a 6 × 6 symmetric matrix, having 27 different components, 21 of which are independent. However, any symmetry present in the structure may reduce this number. Properties such as the bulk modulus (response to an isotropic compression), Poisson coefficient and Lame constants can be computed from the Cij matrix. Methods to determine the elastic constants from first principles usually involve setting either the stress or the strain to a finite value, re-optimizing any free parameters and calculating the other property (the strain or stress, respectively). Applying a given homogeneous deformation (strain) and calculating the resulting stress requires far less computational effort, since the unit cell is fixed and does not require optimization. The finite strain technique has been successfully used to study the elastic properties of a range of materials including simple metals (such as Al),42 super hard nitrides,43 borides,44,45 oxides,46 silicates,47 and semiconductors.48 The results of these studies show that the accuracy of DFT elastic constants is typically within 10% of the experiment. This allows us to predict elastic constants for LFS polymorphs.
For an orthorhombic crystal, the independent elastic stiffness tensor reduces to nine components C11, C22, C33, C44, C55, C66, C12, C13 and C23 in the Voigt notation.47 The well-known Born stability criteria49 for an orthorhombic system are
| | |
B1 = C11 + C22 + C33 + 2(C12 + C13 + C23) > 0,
| (1) |
| | |
B2 = C11 + C22 − 2C12 > 0,
| (2) |
| | |
B3 = C11 + C33 − 2C13 > 0, and
| (3) |
| | |
B4 = C22 + C33 − 2C23 > 0.
| (4) |
All the nine calculated independent single crystalline elastic stiffness constants for LFS in Pmn21, Pna21, Pmna, and I222 are given in Table 4. The computed B1, B2, B3, and B4 values for the LFS in Pmn21 is 811, 237, 236, 177 GPa, in Pna21 is 657, 161, 145, 186 GPa; in Pmna is 709, 205, 222, 139 GPa, and in I222 is 1032, −92, −89, 373 GPa. All the four conditions for mechanical stability given in eqn (1)–(4) are simultaneously satisfied for Pmn21, Pna21, and Pmna and this clearly indicates that these orthorhombic phases are mechanically stable. It should be noted that I222 polymorphs are unstable at equilibrium conditions and equations B2 (−92) and B3 (−89) are correspondingly not satisfied. On the other hand, above the phase transition point, the calculated Cij values simultaneously satisfy the equations B1 (1062), B2 (ref. 18), B3 (ref. 15), and B4 (360) and this phase is stable only at high pressure. This finding is consistent with the phonon calculations.
The mechanical stability criteria for the monoclinic phase are given by50
| | |
C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0,
| (5) |
| | |
[C11 + C22 + C33 + 2(C12 + C13 + C23)] > 0,
| (6) |
| | |
(C35C55 – C352) > 0, (C44C66 − C462) > 0, (C22 + C33 − 2C23) > 0,
| (7) |
| | |
[C22(C33C55 − C352) + 2C23(C25C35 − C232C55 − C252C33)] > 0,
| (8) |
| | |
{2[C15C25(C33C12 − C13C23) + C15C35(C22C13 − C12C23) + C25C35(C11C23 − C12C13)] − [C152(C22C33 − C232) + C252(C11C33 − C132) + C352(C11C22 − C122) + C55(C11C22C33 − C11C232 − C22C132 − C33C122 + 2C12C13C23)]}> 0,
| (9) |
The computed independent single crystalline elastic stiffness constants for LFS in P21, P21/c, Pc, and Pmn21-modi (Pc) at their equilibrium volume are shown in Table 4. In Pc monoclinic polymorph the largest component is C11, corresponding to the in-plane strain, and the second largest component, C33 is just a few tens of GPa smaller than it. On the other hand, in P21 and P21/c the largest component is C11. It is also evident that there is a large degree of elastic anisotropy among the three principal directions due to C11 ≠ C22 ≠ C33. The elastic constants C15, C23, C35 (for all monoclinic polymorphs) and C46 (except for Pc*) become negative and they are very sensitive to the relaxed structural parameters. All the three conditions given in eqn (7)–(9) are not simultaneously satisfied, and this clearly indicates that all these polymorphs are mechanically unstable phases. It should be noted that according to the phonon computation LFS in P21, P21/c, and Pc are found to be dynamically stable, but, according to the mechanical stability criteria they are mechanically unstable. In general, if a system is dynamically stable most of the time they are also mechanically stable. If a system is dynamically stable that indicates that this particular phase is either stable phase or that might be a possible metastable phase. The elastic constant is calculated from the different distortions in different orientations. In a particular distortion the structure is not stable that will reflect in the elastic constant. According to the mechanical stability point of view if a system is mechanically unstable but dynamically stable that might be a possible indication for a metastable phase. In this particular compound several polymorphs are identified experimentally and they are often changing structures during the charge/discharge cycling process. This might be the one of the possible reasons why the energetically favourable and dynamically stable structure P21 is a metastable phase in the experimental findings, and different polymorphs coexist during the charge/discharge cycles. The bulk modulus B, shear modulus G, Young's modulus E and Poisson's ratio ν can be assessed from these elastic stiffness moduli through the Voigt (V), Reuss (R) and Hill (H) approximations,51 and the V and R approximations usually give the upper and lower bounds, respectively, of these parameters as indicated in Table 4.
Like the elastic constant tensor, the bulk and shear moduli contain information regarding the hardness of a material on various types of deformation. Properties such as bulk moduli, shear moduli, Young's moduli and Poisson's ratio can be computed from the values of elastic constants and the calculated values are tabulated in Table 3. All these polymorphs are having almost similar Young's and shear modulus in x, y and z-direction. The compressibility value of these polymorphs suggested that these polymorphs of LFS are very soft materials. A parameter B/G is also introduced, in which B indicates the bulk modulus and G represent the shear modulus. The bulk and shear moduli are calculated from the Voigt–Reuss–Hill approximations.52–54 The high (low) B/G value is associated with ductility (brittleness) and the critical value which separates ductile and brittle materials is 1.75.55 The calculated B/G values of LFS polymorphs are larger than 1.75, implying the ductile characteristics of materials and the stable cycle performance. It is consistent with the electrochemical measurement that about 98.3% of the discharge capacity of LFS can be retained after 80 charge/discharge cycles.56
Table 3 Calculated barrier height (in eV), Li–Li migration distance (in Å), and diffusion coefficient (D; cm2 S−1) for different Li2FeSiO4 polymorphsa
| Phase |
Barrier height |
Li–Li distance |
Diffusion coefficient |
| Pathway A |
Pathway B |
| afrom present study; bfrom ref. 12; cfrom ref. 59; c1from ref. 40; dfrom ref. 41; efrom ref. 62; ffrom ref. 58; and gfrom ref. 61. |
| Pmn21 |
0.86a, 0.87b, 0.85c 0.79c1 |
0.98a, 0.97b, 1.0c |
3.7–3.74 |
10−14/10−13 |
| Pbn21 |
0.80a, 0.82b |
0.71a, 0.72b |
3.01, 3.02, 4.24 |
10−14/10−12 |
| P21 |
0.83a, 0.84d, 0.83e, 0.70c1 |
0.93a, 0.95d, 0.87e |
3.7–3.9, 4.236, 3.537 |
10−13/10−11 |
| Pmn21-cycl |
0.91f |
|
3.02, 3.23 |
|
| P21/c-cycl |
0.83/0.74/0.60g |
|
3.07, 3.56 |
10−14/10−12/10−10 |
| I222 |
1.23a |
1.64a |
3.53, 4.53 |
10−22/10−30 |
Table 4 The calculated single crystal elastic constants Cij (in GPa), bulk modulus B (in GPa), shear modulus G (in GPa), Possion's ratio ν, Young's modulus E (in GPa), and compressibility (GPa−1) for Li2FeSiO4 polymorphs. Subscript V indicates the Voigt bound, R indicates the Reuss bound and H indicates the Hill averagea
| Properties |
Phase |
| Pmn21 |
P21 |
P21/c |
Pna21 |
Pc |
Pc* |
Pmnb |
I222 |
| *According to the structural analysis the modified Pmn21 structure (Pmn21-modi) can be described in monoclinic (space group Pc; space group number 7) structure. |
| Cij |
C11 = 218 |
C11 = 149 |
C11 = 145 |
C11 = 119 |
C11 = 128 |
C11 = 127 |
C11 = 206 |
C11 = 85 |
| C12 = 58 |
C12 = 50 |
C12 = 44 |
C12 = 52 |
C12 = 53 |
C12 = 54 |
C12 = 61 |
C12 = 168 |
| C13 = 58 |
C13 = 81 |
C13 = 72 |
C13 = 46 |
C13 = 47 |
C13 = 56 |
C13 = 41 |
C13 = 169 |
| C22 = 135 |
C15 = −22 |
C15 = −14 |
C22 = 146 |
C15 = −5 |
C15 = 0.3 |
C22 = 121 |
C22 = 159 |
| C23 = 46 |
C22 = 125 |
C22 = 109 |
C23 = 39 |
C22 = 153 |
C22 = 170 |
C23 = 40 |
C23 = −25 |
| C33 = 134 |
C23 = 48 |
C23 = 38 |
C33 = 118 |
C23 = 54 |
C23 = 59 |
C33 = 98 |
C33 = 164 |
| C44 = 35 |
C25 = −5 |
C25 = −0.2 |
C44 = 38 |
C25 = −9 |
C25 = 1.8 |
C44 = 40 |
C44 = 28 |
| C55 = 41 |
C33 = 170 |
C33 = 146 |
C55 = 42 |
C33 = 121 |
C33 = 135 |
C55 = 53 |
C55 = 63 |
| C66 = 42 |
C35 = −25 |
C35 = −22 |
C66 = 36 |
C35 = −4 |
C35 = −7 |
C66 = 40 |
C66 = 58 |
| |
C44 = 41 |
C44 = 46 |
|
C44 = 34 |
C44 = 41 |
|
|
| |
C46 = −5 |
C46 = −4 |
|
C46 = −4 |
C46 = 2.9 |
|
|
| |
C55 = 55 |
C55 = 50 |
|
C55 = 38 |
C55 = 40 |
|
|
| |
C66 = 48 |
C66 = 39 |
|
C66 = 39 |
C66 = 42 |
|
|
| BV |
90 |
89 |
78 |
90 |
79 |
85 |
79 |
115 |
| BR |
85 |
82 |
73 |
84 |
78 |
84 |
71 |
123 |
| BH |
87 |
86 |
76 |
87 |
78 |
85 |
75 |
119 |
| GV |
46 |
46 |
44 |
46 |
39 |
42 |
46 |
36 |
| GR |
44 |
44 |
41 |
43 |
38 |
41 |
43 |
78 |
| GH |
45 |
45 |
43 |
45 |
38 |
42 |
44 |
57 |
| νxy |
0.32 |
0.25 |
0.26 |
0.32 |
0.24 |
0.20 |
0.42 |
1.25 |
| νyx |
0.20 |
0.26 |
0.23 |
0.20 |
0.24 |
0.28 |
0.23 |
−2.19 |
| νzx |
0.2 |
0.44 |
0.41 |
0.2 |
0.26 |
0.34 |
0.12 |
−2.10 |
| νxz |
0.33 |
0.38 |
0.41 |
0.33 |
0.29 |
0.33 |
0.25 |
1.22 |
| νyz |
0.25 |
0.17 |
0.16 |
0.25 |
0.35 |
0.33 |
0.31 |
2.09 |
| νzy |
0.25 |
0.20 |
0.18 |
0.25 |
0.28 |
0.24 |
0.27 |
2.07 |
| Ex |
180 |
101 |
103 |
91 |
101 |
98 |
171 |
−331 |
| Ey |
112 |
104 |
92 |
120 |
117 |
135 |
95 |
580 |
| Ez |
110 |
118 |
102 |
97 |
92 |
100 |
83 |
572 |
| Compressibility |
0.012 |
0.012 |
0.014 |
0.014 |
0.013 |
0.012 |
0.014 |
0.008 |
Diffusion coefficient
To identify the diffusion pathways and the activation energy for the Li+ transport of the different polymorphs of LiFeSiO4, we have calculated the diffusion constant D using the equation
where d is the hopping distance, Ea the activation energy, kB the Boltzmann constant, T the temperature and ν0 the attempt frequency (assumed as 1013 Hz).57 For the chosen structure, we have calculated two main Li migration paths with the Li–Li hop: pathway A, consisting of the linear diffusion of the lithium ions along a particular direction (see Fig. 8; for example in Pmn21 symmetry the Li hop along a-axis) and pathway B, consisting of lithium ions diffusion following a zig–zag trajectory (for example in Pmn21 symmetry the Li hop along c-axis). The Li activation energy (Ea) and estimated diffusion coefficients of various polymorphs of LFS along with other theoretical reports are summarized in Table 3. Our calculated activation barriers are in good agreement with other theoretical works,40,41,58–62 with the only exception of the HP phase. The calculated energy barrier for the low energy structure Pmn21 symmetry is 0.86 and 0.98 eV for pathways A and B respectively. In general, it can be seen in Table 3 that the activation energy ranges from 0.6 eV to 1.64 eV for the Li-ion diffusion in different polymorphs of LFS. The minimum value is observed for P21/c-cycl, and maximum one in the newly identified high-pressure polymorph I222. However, the values listed in Table 3 are much higher than that of ca. 0.30 eV typically reported for the LiFePO4 olivine cathode,63 which directly reflects on the poor ionic conductivity of LFS. Moreover, compared with the other LFS polymorphs, the P21/c-cycl structure has relatively greater activation energy, indicating better Li diffusion in it. This should be ascribed to the more opened 3D-framework structure of P21/c-cycl than the other LFS polymorphs. On the other hand in the high-pressure polymorph I222 the interlayer distances are very narrow, resulting in a larger value for the activation energy.
 |
| | Fig. 8 Schematic representation of Li ion transport in (a) P21, (b) Pmn21 and (c) I222 phases. The solid arrow indicates the Li-ion transport in linear path and dotted arrows represents the zig–zag trajectory. | |
Comparing both paths in the Pmn21 symmetry, it can be noticed that pathway B would be the most probable one. Fig. 9 summarizes the obtained results for the natural logarithm of the diffusion coefficient in the low energy structures of LFS as a function of 1/T. Note that the activation barrier is proportional to the slope of each straight line. In all these three polymorphs the diffusion coefficient follows the trend P21 > Pmn21> I222. The diffusion coefficient calculated in LFS polymorphs at room temperature, ranging from 10−30 cm2 s−1 up to 10−17 cm2 s−1 (lower value in I222 phase and higher value in P21 phase). On the other hand diffusion coefficient in currently used materials (e.g. LixCoO2) typically ranging from 10−13 cm2 s−1 to 10−7 cm2 s−1, it is seen clearly that LFS cannot provide at the moment better kinetics than the state-of-the-art materials. However, by tailoring the particle size of the LFS one can reduce the diffusion coefficient below 10−7 cm2 s−1. The result will be published in a forthcoming article.
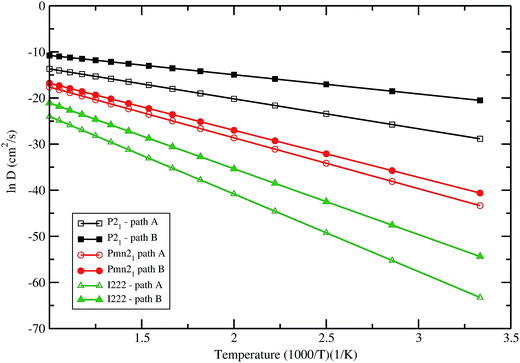 |
| | Fig. 9 Natural logarithm of the diffusion coefficient against 1/T for Li2FeSiO4 in different polymorphs with different possible pathways. | |
Conclusion
In summary, the relative stability of the LFS has been studied using density-functional total-energy calculations. At ambient condition, LFS stabilizes in the monoclinic (P21) structure. When an external pressure is applied, monoclinic LFS transforms into orthorhombic (Pmn21) at the critical load of 0.38 GPa. A further transformation (LFS into I222) is then observed at 1.9 GPa. The calculated structural data for modifications are in very good agreement with experimental and theoretical reports. At equilibrium, the energy difference between the P21/c, Pnma, Pc, Pna21 and Pmn21-modi modifications is very small and, as a result, depending upon the method of synthesis one can stabilize either of these phases at ambient conditions. The phonon calculations reveal that LFS is dynamically stable in P21/c, Pnma, Pc, and modified-Pmn21 structures; a larger pressure makes I222 modification become stable above the phase transition point. The calculated single crystal elastic constants indicate that Pnma, Pna21, modified-Pmn21, Pnmb, and I222 phases are mechanically stable. The low energy P21/c structure is a dynamically stable but mechanically unstable phase. This might explain why it is often experimentally observed as metastable. The diffusion coefficients in LFS at room temperature are calculated, their values ranging from 10−30 cm2 s−1 up to 10−21 cm2 s−1 and therefore suboptimal with respect to the current generation of state-of-the-art materials. More work is therefore required in order to improve the Li-ion diffusion in this class of materials.
Acknowledgements
The authors gratefully acknowledge the Research Council of Norway (Grant agreement no.: Nano-MILIB, 143732) project for financial support. PV acknowledges the Research Council of Norway for providing the computer time (under the project number NN2875k) at the Norwegian supercomputer.
References
- A. K. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, Phospho-olivines as positive-electrode materials for rechargeable lithium batteries, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- A. Manthiram and J. B. Goodenough, Lithium insertion into Fe2(MO4)3 frameworks: Comparison of M = W with M = Mo, J. Solid State Chem., 1987, 71, 349–360 CrossRef CAS.
- A. Manthiram and J. B. Goodenough, Lithium insertion into Fe2(SO4)3 frameworks, J. Power Sources, 1989, 26, 403–408 CrossRef CAS.
- A. Nyten, S. Kamali, L. Haggstrom, T. Gustafsson and J. O. Thomas, The lithium extraction/insertion mechanism in Li2FeSiO4, J. Mater. Chem., 2006, 16(23), 2266–2272 RSC.
- G. Zhong, Y. Li, P. Yan, Z. Liu, M. Xie and H. Q. Lin, Structural, Electronic, and Electrochemical Properties of Cathode Materials Li2MSiO4 (M = Mn, Fe, and Co): Density Functional Calculations, J. Phys. Chem. C, 2010, 114, 3693–3700 CAS.
- R. Dominko, M. Bele, M. Gaberscek, A. Meden, M. Remskar and J. Jamnik, Structure and electrochemical performance of Li2MnSiO4 and Li2FeSiO4 as potential Li-battery cathode materials, Electrochem. Commun., 2006, 8, 217–222 CrossRef CAS.
- M. Arroyo-de Dompablo, R. Dominko, J. Gallardo-Amores, L. Dupont, G. Mali and H. Ehrenberg, et al., On the Energetic Stability and Electrochemistry of Li2MnSiO4 Polymorphs, Chem. Mater., 2008, 20, 5574–5584 CrossRef CAS.
- D. M. Arroyo-de, J. Gallardo-Amores, J. García-Martínez, E. Morán, J. M. Tarascon and M. Armand, Is it possible to prepare olivine-type LiFeSiO4? A joint computational and experimental investigation, Solid State Ionics, 2008, 179, 1758–1762 CrossRef.
- S. Nishimura, S. Hayase, R. Kanno, M. Yashima, N. Nakayama and A. Yamada, Structure of Li2FeSiO4, J. Am. Chem. Soc., 2008, 130, 13212 CrossRef CAS PubMed.
- A. Saracibar and A. Van der Ven, Arroyo-de Dompablo ME. Crystal Structure, Energetics, And Electrochemistry of Li2FeSiO4 Polymorphs from First Principles Calculations, Chem. Mater., 2012, 24(3), 495–503 CrossRef CAS.
- A. R. Armstrong, N. Kuganathan, M. S. Islam and P. G. Bruce, Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries, J. Am. Chem. Soc., 2011, 133(33), 13031–13035 CrossRef CAS PubMed.
- A. Liivat and J. O. Thomas, Li-ion migration in Li2FeSiO4-related cathode materials: a DFT study, Solid State Ionics, 2011, 192, 58–64 CrossRef CAS.
- G. Mali, C. Sirisopanaporn, C. Masquelier, D. Hanzel and R. Dominko, Li2FeSiO4 polymorphs probed by 6Li MAS NMR and 57Fe Mossbauer spectroscopy, Chem. Mater., 2011, 23, 2735 CrossRef CAS.
- C. Sirisopanaporn, A. Boulineau, R. Dominko, D. Hanzel, A. R. Armstrong and P. Bruce, et al., Crystal Structure of a New Polymorph of Li2FeSiO4, Inorg. Chem., 2010, 49, 7446 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Density-functional theory and strong interactions: orbital ordering in Mott-Hubbard insulators, Phys. Rev. B:
Condens. Matter Mater. Phys., 1995, 52(8), R5467–R5470 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, Z. Szotek, W. M. Temmerman and A. P. Sutton, Electronic Structure and Elastic Properties of Strongly Correlated Metal Oxides from First Principles: LSDA + U, SIC-LSDA and EELS Study of UO2 and NiO, Phys. Status Solidi A, 1998, 166(1), 429–443 CrossRef CAS.
- P. Vinet, J. H. Rose, J. Ferrante and J. R. Smith, Temperature effects on the universal equation of state of solids, J. Phys.: Condens. Matter, 1989, 1, 1941–1963 CrossRef CAS.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(13), 134106 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188–5192 CrossRef.
- H. Jonsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, 2011, pp. 385–404 Search PubMed.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113(22), 9978–9985 CrossRef CAS.
- P. Tarte and R. Cahay, Synthesis and structure of a new family of Li2X(II)SiO4 and Li2X(II)GeO4 compounds structurally related to lithium phosphate, [X(II) = magnesium, zinc, manganese, cobalt, iron, and cadmium], C. R. Acad. Sci., 1970, 271, 777 CAS.
- G. Quoirin, F. Taulelle, L. Dupont and C. Masquelier, 211th ECS Meeting, 2007, p. 98 Search PubMed.
- A. Nyten, A. Abouimrane, M. Armand, T. Gustafsson and J. O. Thomas, Electrochemical performance of Li2FeSiO4 as a new Li-battery cathode material, Electrochem. Commun., 2005, 7, 156 CrossRef CAS.
- C. Frayret, C. Masquelier, A. Villesuzanne, M. Morcrette and J. M. Tarascon, Comparative Studies on the Phase Stability, Electronic Structure, and Topology of the Charge Density in the Li3XO4 (X = P, As, V) Lithium Orthosalt Polymorphs, Chem. Mater., 2009, 21, 1861 CrossRef CAS.
- L. D. Iskhakova and V. B. Rybakov, Crystal structure of Li2MgSiO4, Crystallogr. Rep., 2003, 48, 44 CrossRef.
- H. Yamaguchi and K. Akatsuka, Structure of dilithium zinc silicate γ II-Li2ZnSiO4, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 2678–2680 CrossRef CAS.
- C. Lyness, B. Delobel, A. R. Armstrong and P. G. Bruce, The lithium intercalation compound Li2CoSiO4 and its behaviour as a positive electrode for lithium batteries, Chem. Commun., 2007, 46, 4890–4892 RSC.
- V. V. Politaev, A. A. Petrenko, V. B. Nalbandyan, B. S. Medvedev and E. S. Shvetsova, Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4, J. Solid State Chem., 2007, 180(3), 1045–1050 CrossRef CAS.
- C. Eames, A. R. Armstrong, P. G. Bruce and M. S. Islam, Insights into Changes in Voltage and Structure of Li2FeSiO4 Polymorphs for Lithium-Ion Batteries, Chem. Mater., 2012, 24(11), 2155–2161 CrossRef CAS.
- N. G. Hörmann and A. Groß, Stability, composition and properties of Li2FeSiO4 surfaces studied by DFT, J. Solid State Electrochem., 2013, 8, 1401–1413 Search PubMed.
- Inorganic Crystal Structure Database (ICSD), Version 2011/2.
- P. Vajeeston, P. Ravindran, A. Kjekshus and H. Fjellvåg, Crystal structure of KAlH4 from first principle calculations, J. Alloys Compd., 2004, 363(1–2), L8–L12 CrossRef.
- P. Vajeeston, P. Ravindran, B. C. Hauback and H. Fjellvag, Prediction of crystal structure, lattice dynamical, and mechanical properties of CaB2H2, Int. J. Hydrogen Energy, 2011, 36(16), 10149–10158 CrossRef CAS.
- P. Vajeeston, P. Ravindran, A. Kjekshus and H. Fjellvåg, First-principles investigations of aluminum hydrides: M_{3}AlH_{6}(M = Na, K), Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(9), 092103 CrossRef.
- X. Lu, H.-C. Chiu, Z. Arthur, J. Zhou, J. Wang and N. Chen, et al., Li-ion storage dynamics in metastable nanostructured Li2FeSiO4 cathode: Antisite-induced phase transition and lattice oxygen participation, J. Power Sources, 2016, 329, 355–363 CrossRef CAS.
- X. Lu, H.-C. Chiu, K. H. Bevan, D.-T. Jiang, K. Zaghib and G. P. Demopoulos, Density functional theory insights into the structural stability and Li diffusion properties of monoclinic and orthorhombic Li2FeSiO4 cathodes, J. Power Sources, 2016, 318, 136–145 CrossRef CAS.
- R. B. Araujo, R. H. Scheicher, J. S. de Almeida, A. Ferreira da Silva and R. Ahuja, First-principles investigation of Li ion diffusion in Li2FeSiO4, Solid State Ionics, 2013, 247–248, 8–14 CrossRef CAS.
- V. B. Deyirmenjian, V. Heine, M. C. Payne, V. Milman, R. M. Lynden-Bell and M. W. Finnis, Ab Initio Atomistic Simulation of the Strength of Defective Aluminum and Tests of Empirical Force Models, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15191–15207 CrossRef CAS.
- M. Marlo and V. Milman, Density-functional study of bulk and surface properties of titanium nitride using different exchange–correlation functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2899–2907 CrossRef CAS.
- V. Milman and M. C. Warren, Elastic properties of TiB2 and MgB2, J. Phys.: Condens. Matter, 2001, 13, 5585–5595 CrossRef CAS.
- P. Ravindran, P. Vajeeston, R. Vidya, A. Kjekshus and H. Fjellvåg, Detailed electronic structure studies on superconducting MgB2 and related compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(22), 224509 CrossRef.
- A. de Vita, I. Manassidis, J. S. Lin and M. J. Gillan, The energetics of Frenkel defects in Li2O from 1st principles, Europhys. Lett., 1992, 19, 605–610 CrossRef CAS.
- P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2, J. Appl. Phys., 1998, 84(9), 4891–4904 CrossRef CAS.
- B. B. Karki, S. J. Clark, M. C. Warren, H. C. Hsueh, G. J. Ackland and J. Crain, Ab initio elasticity and lattice dynamics of AgGaSe2, J. Phys.: Condens. Matter, 1997, 9, 375–380 CrossRef CAS.
- F. I. Fedorov, Theory of Elastic Waves in Crystals, Plenum, New York, 1968, p. 33 Search PubMed.
- J. F. Nye, Physical Properties of Crystals, Oxford University Press, Oxford, 1985 Search PubMed.
- J. P. Watt, Hashin-Shtrikman bounds on the effective elastic moduli of polycrystals with orthorhombic symmetry, J. Appl. Phys., 1980, 51, 1520 CrossRef CAS.
- A. Reuss, Berechnung der Fließgrenze von Mischkristallen auf Grund der Plastizitätsbedingung für Einkristalle, Z. Angew. Math. Mech., 1929, 9(1), 49–58 CrossRef CAS.
- R. Hill, The Elastic Behaviour of a Crystalline Aggregate, Proc. Phys. Soc., London, 1952, 65, 350 Search PubMed.
- W. Voigt, Lehrbuch der Kristallphysik, Teubner, Leipzig, 1928, p. 1928 Search PubMed.
- S. F. Pugh, Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45, 823 CrossRef CAS.
- S. Zhang, C. Deng and S. Yang, Preparation of nano-Li2FeSiO4 as cathode material for lithium-ion batteries, Electrochem. Solid-State Lett., 2009, 12, A136–A139 CrossRef CAS.
- K. Kang, D. Morgan and G. Ceder, First principles study of Li diffusion in I-Li2NiO2 structure, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(1), 014305 CrossRef.
- A. R. Armstrong, N. Kuganathan, M. S. Islam and P. G. Bruce, Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries, J. Am. Chem. Soc., 2011, 133(33), 13031–13035 CrossRef CAS PubMed.
- R. B. Araujo, R. H. Scheicher, J. S. de Almeida, A. Ferreira da Silva and R. Ahuja, Lithium transport investigation in LixFeSiO4: a promising cathode material, Solid State Commun., 2013, 173, 9–13 CrossRef CAS.
- A. Liivat and J. O. Thomas, Li-ion migration in Li2FeSiO4-related cathode materials: a DFT study, Solid State Ionics, 2011, 192(1), 58–64 CrossRef CAS.
- P. Zhang, Y. Zheng, S. Yu, S. Q. Wu, Y. H. Wen and Z. Z. Zhu, et al., Insights into electrochemical performance of Li2FeSiO4 from first-principles calculations, Electrochim. Acta, 2013, 111, 172–178 CrossRef CAS.
- D. Su, H. Ahn and G. Wang, Ab initio calculations on Li-ion migration in Li2FeSiO4 cathode material with a P21 symmetry structure, Appl. Phys. Lett., 2011, 99(14), 141909 CrossRef.
- Y. Sun, X. Lu, R. Xiao, H. Li and X. Huang, Kinetically controlled lithium-staging in delithiated LiFePO4 driven by the Fe center mediated interlayer Li–Li interactions, Chem. Mater., 2012, 24(24), 4693–4703 CrossRef CAS.
- C. Sirisopanaporn, C. Masquelier, P. G. Bruce, A. R. Armstrong and R. Dominko, Dependence of Li2FeSiO4 Electrochemistry on Structure, J. Am. Chem. Soc., 2010, 133(5), 1263–1265 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26555c |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
H. Fjellvåg
* and
H. Fjellvåg
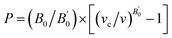 . The relation can be inverted to obtain the volume as
. The relation can be inverted to obtain the volume as 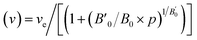 where ve, B0, and
where ve, B0, and 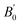 refers to the equilibrium volume, the bulk modulus, and its derivative with respect to pressure, respectively. The inverse is then calculated using the bisection method. From the scan over the pressures, the corresponding difference in the enthalpy between the two data sets was calculated.
refers to the equilibrium volume, the bulk modulus, and its derivative with respect to pressure, respectively. The inverse is then calculated using the bisection method. From the scan over the pressures, the corresponding difference in the enthalpy between the two data sets was calculated.![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m; 121), EuLi2SiO4 (P3121; 152), Li2BaSiO4 (P63cm; 185), and Li2MnSiO4-modified-Pmn21 (Pmn21-modi). Among the considered structures for our structural optimization, the calculated total energy at the equilibrium volume for the P21 atomic arrangements occur at the lowest total energy (see Fig. 2). The calculated positional and lattice parameters (see Table 1) are found to be in good agreement with experimental findings9 and with the other theoretical calculations.10,33 It consists of a lattice built up from infinite conjugated layers of composite SiFeO4 linked through the LiO4 tetrahedra, with each Li, Fe, Si located in the centre of the tetrahedron formed by four oxygen atoms. Furthermore, the Li+ ions are occupying tetrahedral sites between the FeO4–SiO4 where the tetrahedra alternately point in opposite directions. It should be noted that this phase is stabilized when the particle size is reduced39 and, according to experimental findings, it is a thermodynamically less stable phase.9,40 The next energetically favourable phase is orthorhombic Pmn21. In this structure, chains of LiO4 tetrahedra run along the a direction, parallel to the chains of alternating FeO4 and SiO4 tetrahedra (see Fig. 3). The energy difference between this phase with P21 at the equilibrium volume is only ca. 4.6 meV f.u.−1 (see Fig. 2). The calculated structural parameters are found to be in good agreement (see Table 1) with the recent experimental finding9 and with other DFT studies.10,33 It is interesting to note that the energy difference between the P21/c, Pnma, Pc, Pna21 and Pmn21-modi is also very small, and hence, one can easily modify one polymorph into another by application of temperature or pressure; this explains the difficulties to control the synthesis of single phase samples of LFS polymorphs, also related to very similar electrochemical properties (voltage, volume variation, and electronic structure).10,41 One should also remember that the calculated results are valid only for defect-free ideal materials at low temperatures. However, the experimental findings show that, depending upon the synthesis route/conditions, one can stabilize different polymorphs of LFS and it is therefore difficult to get phase-pure materials from most synthesis processes.9,14,40
2m; 121), EuLi2SiO4 (P3121; 152), Li2BaSiO4 (P63cm; 185), and Li2MnSiO4-modified-Pmn21 (Pmn21-modi). Among the considered structures for our structural optimization, the calculated total energy at the equilibrium volume for the P21 atomic arrangements occur at the lowest total energy (see Fig. 2). The calculated positional and lattice parameters (see Table 1) are found to be in good agreement with experimental findings9 and with the other theoretical calculations.10,33 It consists of a lattice built up from infinite conjugated layers of composite SiFeO4 linked through the LiO4 tetrahedra, with each Li, Fe, Si located in the centre of the tetrahedron formed by four oxygen atoms. Furthermore, the Li+ ions are occupying tetrahedral sites between the FeO4–SiO4 where the tetrahedra alternately point in opposite directions. It should be noted that this phase is stabilized when the particle size is reduced39 and, according to experimental findings, it is a thermodynamically less stable phase.9,40 The next energetically favourable phase is orthorhombic Pmn21. In this structure, chains of LiO4 tetrahedra run along the a direction, parallel to the chains of alternating FeO4 and SiO4 tetrahedra (see Fig. 3). The energy difference between this phase with P21 at the equilibrium volume is only ca. 4.6 meV f.u.−1 (see Fig. 2). The calculated structural parameters are found to be in good agreement (see Table 1) with the recent experimental finding9 and with other DFT studies.10,33 It is interesting to note that the energy difference between the P21/c, Pnma, Pc, Pna21 and Pmn21-modi is also very small, and hence, one can easily modify one polymorph into another by application of temperature or pressure; this explains the difficulties to control the synthesis of single phase samples of LFS polymorphs, also related to very similar electrochemical properties (voltage, volume variation, and electronic structure).10,41 One should also remember that the calculated results are valid only for defect-free ideal materials at low temperatures. However, the experimental findings show that, depending upon the synthesis route/conditions, one can stabilize different polymorphs of LFS and it is therefore difficult to get phase-pure materials from most synthesis processes.9,14,40![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m (space group 121) and both modifications have similar energies (the variation is only 0.2 meV f.u.−1). The pressure induced Pmn21-to-I222 transition involves reconstructive rearrangements of the Li, Fe, Si, and O lattices with breaking and reconstruction of bonds. Usually, the application of pressure reduces the covalency in solids and makes the valence electrons more diffuse than at ambient condition. All these three polymorphs P21, Pmn21 and I222 are stabilized in layered structure type with a similar type of atomic arrangement. The main difference between the three polymorphs are both P21, Pmn21 polymorphs are having almost similar interlayer distances while in the I222 phase the interlayer distance become very narrow and the SiO4 and FeO4 tetrahedra become stretched along [011] (see Fig. 3).
2m (space group 121) and both modifications have similar energies (the variation is only 0.2 meV f.u.−1). The pressure induced Pmn21-to-I222 transition involves reconstructive rearrangements of the Li, Fe, Si, and O lattices with breaking and reconstruction of bonds. Usually, the application of pressure reduces the covalency in solids and makes the valence electrons more diffuse than at ambient condition. All these three polymorphs P21, Pmn21 and I222 are stabilized in layered structure type with a similar type of atomic arrangement. The main difference between the three polymorphs are both P21, Pmn21 polymorphs are having almost similar interlayer distances while in the I222 phase the interlayer distance become very narrow and the SiO4 and FeO4 tetrahedra become stretched along [011] (see Fig. 3).








