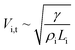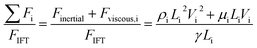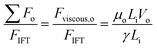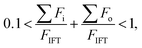Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The dripping-to-jetting transition in a co-axial flow of aqueous two-phase systems with low interfacial tension†
Sze Yi Mak ab,
Youchuang Chaoab and
Ho Cheung Shum*ab
ab,
Youchuang Chaoab and
Ho Cheung Shum*ab
aDepartment of Mechanical Engineering, The University of Hong Kong, Pokfulam Road, Hong Kong, China. E-mail: ashum@hku.hk
bHKU-Shenzhen Institute of Research and Innovation (HKU-SIRI), Shenzhen, Guangdong, China
First published on 13th January 2017
Abstract
The dripping-to-jetting transition of co-axial flow with high interfacial tension has been extensively studied; however, little is known about this with low interfacial tension. We use an aqueous two-phase system as a model to study the transition at low interfacial tension (<1 mN m−1). We identify a low critical jet velocity at which the transition occurs (V < 1 m s−1) when compared with the velocity in systems with high interfacial tension (V > 1 m s−1). The significant reduction in the critical jet velocity alters the relative importance of the inertial force (∝V2) and the viscous force (∝V). Counter-intuitively, even for systems with relatively low viscosities, the transition is no longer inertially-dominated. Therefore, we propose that all downstream forces, including inertial and viscous forces, contribute significantly in opposing the interfacial force. This comprehensive force balance accurately characterizes the dripping-to-jetting transition for a wide range of viscosities and low interfacial tension. The validity of this force balance is confirmed by the agreement in the interfacial tension values estimated by inputting the operating parameters of the flow into the force balance and that obtained by a commercial spinning drop tensiometer.
Introduction
Co-axial flow of two immiscible fluids exhibits dripping and jetting phenomena, which refer to the formation of drops and a jet at the nozzle respectively.1–3 The dynamics of the dripping-to-jetting transition in co-axial flow is of fundamental importance in industrial applications that involve droplets.4–6 Oil–water systems with a relatively high interfacial tension (γ = 0.1–40 mN m−1) are the main options to study the transition. Recently, some novel systems with a low interfacial tension, such as aqueous two-phase systems (ATPSs), are used to generate droplets and have great potential for applications in making bio- and cyto-compatible emulsion droplets.7–13 However, dripping is difficult to achieve spontaneously in aqueous two-phase flows, evidenced by the reliance on mechanical8,14 or electrical7,15 actuations to control the breakup of water–water jets, if not passively generated by hydrostatic flows.16 As a result, the dynamics of the dripping-to-jetting transition in these systems is rarely studied, despite lots of works reported for higher interfacial tension (γ = 0.1–40 mN m−1) using oil–water systems.17–21It is generally accepted that the dripping-to-jetting transition is typically achieved by the dominance of any of the downstream forces over the interfacial force. Strong inertial force of the inner phase (Finertial ∼ ρiLi2Vi2) and viscous forces of the inner and outer phases (Fviscous,i ∼ μiLiVi and Fviscous,o ∼ μoLiVo) can be achieved by a high velocities or high viscosities respectively.17,20,22,23 Inertial-dominated breakup is commonly characterized by the Weber number of the inner phase approaching unity (Wei ∼ 1), without considering the viscous force of the inner phase. Viscous-dominated breakup occurs only if the jet phase is highly viscous, such as in the case of glycerol or sucrose with viscosity on the order of 1–10 Pa s.24–26 However, water–water interfaces typically possess low interfacial tension ranging from O(10−3) to O(1) mN m−1.27 The lowering of interfacial tension by a thousand fold leads to a very small driving force for jet breakup, as well as a slow breakup dynamics.15 Therefore, to reveal the details of the dripping-to-jetting transition in low interfacial tension systems, a systematical view of the balanced forces is necessary.
In this work, we use aqueous two-phase systems (ATPSs) as a platform to study the dripping-to-jetting transition in the low interfacial tension system. We find that the jet velocity at the transition reduces by 1000-fold when the interfacial tension is low and viscosity is low. The relative importance of the inertial and viscous forces at the dripping-to-jetting transition is completely altered. Therefore, we propose a modified characterization of the dripping-to-jetting transition which is applicable even when the interfacial tension is low. Our results elucidate the underlying mechanism for the dripping-to-jetting transition in low-interfacial-tension systems, and thus provide a more representative phase diagram for the dripping-to-jetting transition in two-phase co-axial flow. The understanding of the roles of different hydrodynamic forces in the breakup of water–water jets not only has implications to controlled generation of bio- and cyto-compatible emulsions and particles,9,11,28–31 jets and fibers,10,14,32,33 but also has application to estimate low interfacial tension.
Experimental
Aqueous two phase systems
Immiscible aqueous phases are prepared by dissolving and phase-separating high concentrations of a polymer poly(ethylene glycol) MW 4000, or 8000 (10 wt% to 23.29 wt%),35 and a salt, sodium citrate (10 wt% to 12 wt%) or sodium carbonate (6.44 wt% to 10.27 wt%) in deionized water (see Fig. S1 in the ESI† for preparation of ATPSs). The interfacial tension is typically low and ranges from 0.02 mN m−1 to 3.2 mN m−1 (SITE100, KRÜSS) while the viscosity ratio varies between 0.04 and 45 (μVISC, RheoSense). The specific compositions and corresponding fluid properties of the ATPSs and oil–water system are listed in Table S1 in the ESI.†Microfluidics
A co-axial flow is formed in two aligned glass capillaries, one with a tip diameter Li ranging from 20 μm to 200 μm, as tapered by a micropipette puller (P-97, Sutter), inside another with a channel dimension Lo ranging from 400 μm to 2 mm. At this length scale, the Bond number Bo ∼ ΔρgLi2/γ, where g is the gravitational constant, is on the order of 10−3, indicating a negligible effect of gravity relative to the interfacial tension. The inner and outer phases are injected from the two inlets into the device using syringe pumps (LSP01-2A, Longer Pump) at flow rates Qi = 1–20 ml h−1 and Qo = 40–40 ml h−1, respectively (Fig. 1). Unless otherwise specified, we fix the outer flow rate and gradually increase the inner flow rate until a widening jet (Fig. 1b) is achieved.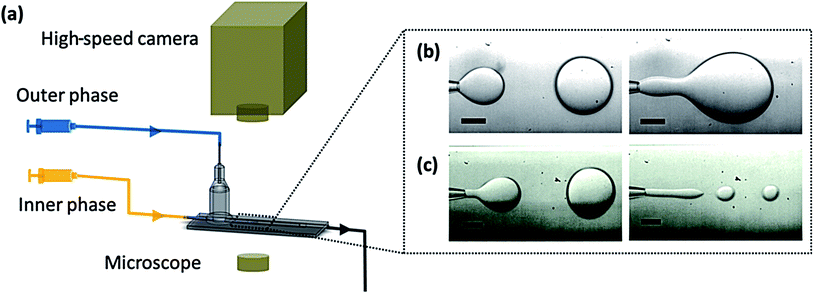 | ||
| Fig. 1 (a) Schematic diagram of the experimental setup. The phase-separated aqueous phases are fed, by syringe pumps, into the glass capillary device to form a co-flow, as shown in the subset of the figure. The breakup process is observed under an optical microscope and recorded using a high speed camera. Microscopic images of two different transitions. Scale bars are 100 μm. (b) Transition to a widening jet by increasing the flow rate of the inner phase: γ = 0.26 mN m−1, μi = 1.5 mPa s, Qo = 500 μl h−1. Dripping at Qi = 30 μl h−1, jetting at Qi = 100 μl h−1. (c) Transition to a narrowing jet by increasing the flow rate of the outer phase: γ = 0.99 mN m−1, μo = 47 mPa s, Qi = 100 μl h−1. Dripping at Qo = 1 ml h−1, jetting at Qo = 8 ml h−1. See Movies S1–S4 in ESI† for the dripping and jetting morphologies. | ||
Imaging and analysis
We capture high-speed videos of the breakup process using a high-speed camera (V9.1, Phantom; FASTCAM SA4, Photron) through an inverted microscope (AE2000, Motic). The mean velocity of the outer phase is Vo = 4Qo/(π(Lo2 − Li2)) or Qo/((Lo2 − πLi2/4)) for circular or square cross section of the outer channel while the mean velocity of the inner phase is Vi = 4Qi/(πLi2).Results and discussion
A low critical jet velocity at the dripping-to-jetting transition
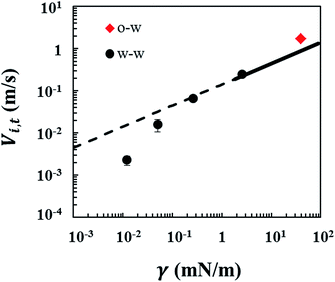
We monitor the critical jet velocity (Vi,t) at which the dripping-to-jetting transition takes place for different interfacial tensions. We observe that the dripping-to-jetting transitions in low interfacial tension systems always happen at a low critical jet velocity, on the order of mm s−1. However, for a typical oil–water system with a high interfacial tension of 40 mN m−1, this velocity is 1.7 m s−1. As the interfacial tension decreases from 2.6 mN m−1 to 0.012 mN m−1 while the viscosity of the jet phase is maintained at 1 mPa s to 3 mPa s, the critical jet velocity progressively reduces from 0.25 m s−1 to 0.002 m s−1 (Fig. 2). The extremely low critical jet velocity indicates a remarkably weak inertial force. From the literature,17 the breakup of systems with a high interfacial tension and a low viscosity of the jet phase falls into the inertial-dominated regime. In this regime, the inertial force dominates over the viscous force and is balanced by the interfacial force at the transition from dripping to jet widening, Finertial ∼ γLi. Hence we can estimate the jet velocity at the transition by the relation:The estimation, inferred from experimental studies on systems with higher interfacial tension, only serves well to predict Vi,t when the interfacial tension of the ATPS is higher than 1 mN m−1 but not lower (data points coincide with the solid line only when γ > 1 mN m−1 in Fig. 2). For interfacial tension lower than 1 mN m−1, the experimental jet velocity at the transition is lower than the extrapolated value and the deviation increases as the interfacial tension decreases further (data points deviate from the dotted line in Fig. 2).
The small interfacial force of ATPS
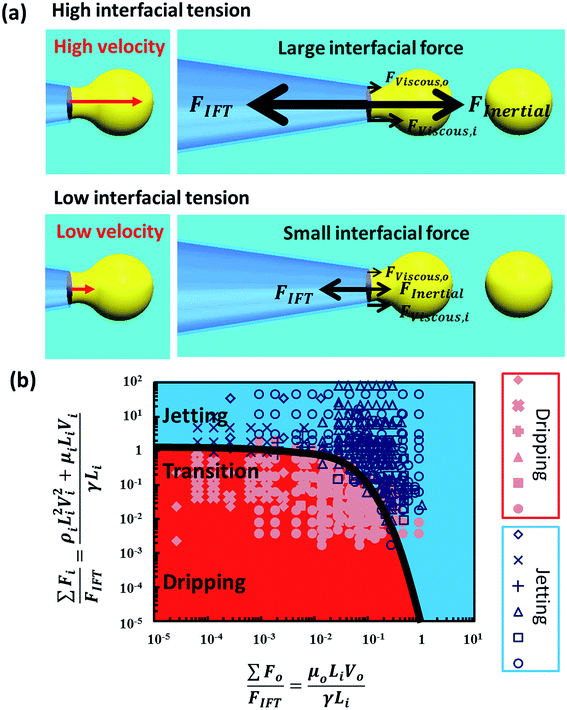
In fact, the critical jet velocity of the dripping-to-jetting transition is lowered by the small interfacial force of ATPSs. Specifically, for a jet ejected from a nozzle of 100 μm in diameter, the downstream force required to oppose the interfacial force of an ATPS is on the order of nanonewton. Due to a tremendous reduction in interfacial force, a jet with a very small velocity possesses sufficient downstream force to overcome the minute interfacial force and causes jetting. Hence, this small critical jet velocity results in an extremely small inertial force and viscous force, all of which possibly play important roles during the dripping-to-jetting transition.The relative importance of the forces at the transition
When the critical jet velocity is extremely low, (<1 m s−1), both the viscous and inertial forces of the inner phase are significantly smaller as they scale with the jet velocity (Fviscous,i ∼ μiLiVi) and the square of it (Finertial ∼ ρiLi2Vi2) respectively. Thus, the inertial force is reduced to a greater extent and becomes comparable to the viscous force of the inner phase, as illustrated in Fig. 3a. In the regime of low interfacial tension, the Reynolds number at the dripping-to-jetting transition Rei,t, which is the ratio of inertial force over viscous force, spans across three decades from O(10−3) to O(1) as the viscosity ratio μi/μo varies from 0.04 to 45. This range of Rei,t suggests that the transition is not inertial-dominated. Even if the viscosity of the inner phase is as low as that of water, the dripping-to-jetting transition is no longer sufficiently characterized by the Weber number of the inner phase (Fig. S2†), as in the case of high interfacial tension. Neglecting the viscous force in the characterization of the dripping-to-jetting transition, as is commonly done in low viscosity systems with high interfacial tension, is not appropriate in the case of low interfacial tension. However, given the wide span of Rei,t from O(10−3) to O(1), it is non-trivial whether the viscous force is dominant over or comparable to the inertial force.A new characterization of the transition based on force balance
Based on these results, we hypothesize the transition is influenced by both the inertial and viscous forces of the inner phase when the interfacial tension is low, regardless of the viscosity of the inner phase. We express the ratios of the total force contributed by the inner and outer phase over the interfacial tension force as below:Adopting these expressions, we propose a revised phase map that takes into account all the three downstream forces, namely the inertial force and viscous forces of the inner and outer phases, as well as the interfacial force. This new phase diagram captures the dripping-to-jetting transitions for low-interfacial tension aqueous two-phase systems with a wide range of viscosity (Fig. 3b). All the transitions of systems with different viscosity ratios collapse to the same order, where ∑Fi/FIFT approaches unity. The result illustrates a remarkable importance of viscous force of the jet in the breakup dynamics when the interfacial tension is low. When we increase the viscosity of the jet phase above 10 mPa s, the viscous effect is even more prominent. The transition to the jet-narrowing regime arises from increasing the speed of the continuous phase, such that the viscous force of the continuous phase overcomes the interfacial force. In general, jetting is achieved when the sum of the three downstream forces, namely the inertial force and viscous forces of the inner and outer phase, exceeds the interfacial force. The dripping-to-jetting transition can be characterized by the relation:
Implications to interfacial tension estimation
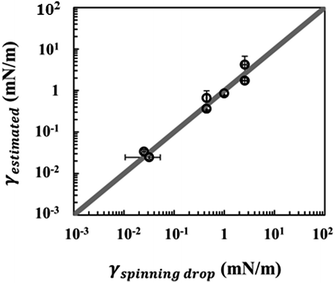
Our proposed characterization of dripping-to-jetting transition holds for a wide range of low interfacial tension and viscosity; hence it may be useful as a tool for estimating interfacial tension values.34 Based on the balance of the downstream and upstream forces at the dripping-to-jetting transition, the interfacial tension can be estimated by the following (see part 5 in the ESI†):| γestimated ∼ 5(ρiLiV2i,t + μiVi,t + μoVo,t) |
Over a wide range of relatively low interfacial tensions, the estimated values match well with those measured using a commercial spinning drop tensiometer (SITE100, KRÜSS), as shown in Fig. 4. These results provide further confirmation of our characterization of the dripping-to-jetting transition for an ATPS jet with low interfacial tension.
Conclusions
In conclusion, our results highlight the importance of the critical jet velocity in the dripping-to-jetting transition of co-axial flow with low interfacial tension. The low jet velocity at the dripping-to-jetting transition indicates an exceptionally small inertial force and hence a relatively important viscous force for ATPSs with low interfacial tension (γ < 1 mN m−1). The dripping-to-jetting transition is more properly characterized by the force balance between the interfacial force and the sum of downstream forces that does not neglect the viscous effect of the jet phase. Using this new characterization we also devise a method to estimate the low interfacial tension. By extending the understanding of the dripping-to-jetting transition to systems with low interfacial tension, our work lays a foundation to achieve control over formation of jets and drops in these systems.Acknowledgements
We thank Dr Tiantian Kong, Dr Yuan Liu, Dr Zhou Liu and Prof. Howard A. Stone for valuable discussions. This research was supported by the Early Career Scheme (No. HKU 707712P), the General Research Fund (No. HKU 719813E, 17304514 and 17306315) and the Collaborative Research Fund (C6004-14G) from the Research Grants Council of Hong Kong, the General Program (No. 21476189/B060201) and the Major Research Plan (No. 91434202) from the National Natural Science Foundation of China, as well as the Seed Funding Programme for Basic Research (No. 201411159038, 201511159280) from the University of Hong Kong.References
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- P. B. Umbanhowar, V. Prasad and D. A. Weitz, Langmuir, 2000, 16, 347–351 CrossRef CAS.
- P. Guillot, A. Colin and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 016307 CrossRef PubMed.
- S. Marre, C. Aymonier, P. Subra and E. Mignard, Appl. Phys. Lett., 2009, 95, 134105 CrossRef.
- J. J. Kaufman, G. Tao, S. Shabahang, E.-H. Banaei, D. S. Deng, X. Liang, S. G. Johnson, Y. Fink and A. F. Abouraddy, Nature, 2012, 487, 463–467 CrossRef CAS PubMed.
- Y. K. Li, G. T. Liu, J. H. Xu, K. Wang and G. S. Luo, RSC Adv., 2015, 5, 27356–27364 RSC.
- I. Ziemecka, V. van Steijn, G. J. M. Koper, M. T. Kreutzer and J. H. van Esch, Soft Matter, 2011, 7, 9878–9880 RSC.
- A. Sauret and H. C. Shum, Appl. Phys. Lett., 2012, 100, 154106 Search PubMed.
- Y. Song and H. C. Shum, Langmuir, 2012, 28, 12054–12059 CrossRef CAS PubMed.
- S. Hardt and T. Hahn, Lab Chip, 2012, 12, 434–442 RSC.
- Y. Song, Y. K. Chan, Q. Ma, Z. Liu and H. C. Shum, ACS Appl. Mater. Interfaces, 2015, 7, 13925–13933 CAS.
- B.-U. Moon, S. G. Jones, D. K. Hwang and S. S. H. Tsai, Lab Chip, 2015, 15, 2437–2444 RSC.
- H. C. Shum, J. Varnell and D. A. Weitz, Biomicrofluidics, 2012, 6, 012808 CrossRef PubMed.
- A. Sauret, C. Spandagos and H. C. Shum, Lab Chip, 2012, 12, 3380–3386 RSC.
- S. D. Geschiere, I. Ziemecka, V. van Steijn, G. J. M. Koper, J. H. V. Esch and M. T. Kreutzer, Biomicrofluidics, 2012, 6, 022007 CrossRef PubMed.
- B.-U. Moon, N. Abbasi, S. G. Jones, D. K. Hwang and S. S. H. Tsai, Anal. Chem., 2016, 88, 3982–3989 CrossRef CAS PubMed.
- A. S. Utada, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 094502 CrossRef PubMed.
- E. Castro-Hernández, V. Gundabala, A. Fernández-Nieves and J. M. Gordillo, New J. Phys., 2009, 11, 075021 CrossRef.
- M. L. Cordero, F. Gallaire and C. N. Baroud, Phys. Fluids, 2011, 23, 094111 CrossRef.
- J. K. Nunes, S. S. H. Tsai, J. Wan and H. A. Stone, J. Phys. D: Appl. Phys., 2013, 46, 114002 CrossRef PubMed.
- Y. Ren, Z. Liu and H. C. Shum, Lab Chip, 2015, 15, 121–134 RSC.
- A. S. Utada, A. Fernandez-Nieves, J. M. Gordillo and D. A. Weitz, Phys. Rev. Lett., 2008, 100, 014502 CrossRef PubMed.
- A. S. Utada, L. Y. Chu, A. Fernandez-Nieves, D. R. Link, C. Holtze and D. A. Weitz, MRS Bull., 2007, 32, 702–708 CrossRef CAS.
- E. C. Bingham and R. F. Jackson, Standard substances for the calibration of viscometers, US Government Printing Office, 1917 Search PubMed.
- J. R. Lister and H. A. Stone, Phys. Fluids, 1998, 10, 2758–2764 CrossRef CAS.
- T. Cubaud and T. G. Mason, Phys. Fluids, 2008, 20, 053302 CrossRef.
- Y. Song, A. Sauret and H. C. Shum, Biomicrofluidics, 2013, 7, 061301 CrossRef PubMed.
- I. Ziemecka, V. van Steijn, G. J. M. Koper, M. Rosso, A. M. Brizard, J. H. van Esch and M. T. Kreutzer, Lab Chip, 2011, 11, 620–624 RSC.
- J. Wu, T. Kong, K. W. K. Yeung, H. C. Shum, K. M. C. Cheung, L. Wang and M. K. T. To, Acta Biomater., 2013, 9, 7410–7419 CrossRef CAS PubMed.
- U. Shimanovich, Y. Song, J. Brujic, H. C. Shum and T. P. J. Knowles, Macromol. Biosci., 2015, 15, 501–508 CrossRef CAS PubMed.
- Q. Ma, Y. Song, G. Baier, C. Holtze and H. C. Shum, J. Mater. Chem. B, 2016, 4, 1213–1218 RSC.
- Y. Song, Z. Liu, T. Kong and H. Cheung Shum, Chem. Commun., 2013, 49, 1726–1728 RSC.
- S. Y. Mak, Z. Li, A. Frere, T. C. Chan and H. C. Shum, Sci. Rep., 2014, 4, 6675 CrossRef CAS PubMed.
- J. H. Xu, S. W. Li, W. J. Lan and G. S. Luo, Langmuir, 2008, 24, 11287–11292 CrossRef CAS PubMed.
- C. C. de Oliveira, J. S. D. R. Coimbra, A. D. G. Zuniga, J. P. Martins and A. M. D. O. Siqueira, J. Chem. Eng. Data, 2012, 57, 1648–1652 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Preparation of ATPSs, compositions and fluid properties of ATPSs, movies for dripping and jetting morphologies, and the figure of Wei against Cao for ATPSs. See DOI: 10.1039/c6ra26556a |
| This journal is © The Royal Society of Chemistry 2017 |