Open Access Article
Open Access ArticleCorrelation of natural muscovite exfoliation with interlayer and solvation forces†
Feifei
Jia
ab,
Lang
Yang
b,
Qingmiao
Wang
b and
Shaoxian
Song
*abc
aHubei Key Laboratory of Mineral Resources Processing and Environment, Wuhan University of Technology, Luoshi Road 122, Wuhan, Hubei 430070, China. E-mail: shaoxian@uaslp.mx; Tel: +86 27 87212127
bSchool of Resources and Environmental Engineering, Wuhan University of Technology, Luoshi Road 122, Wuhan, Hubei 430070, China
cHubei Provincial Collaborative Innovation Center for High Efficient Utilization of Vanadium Resources, Wuhan University of Technology, Luoshi Road 122, Wuhan, Hubei 430070, China
First published on 4th January 2017
Abstract
The correlation of natural muscovite exfoliation with interlayer and solvation forces was investigated in this work, respectively. The former was studied through exfoliating seven muscovite samples with different interlayer forces in 40% tert-butanol/water solvent, while the latter was performed by exfoliating a muscovite in various alcohol/water solvents. This study was implemented by means of measurements using a UV-VIS spectrophotometer, surface tension measurements, XRD, IR spectroscopy, and ICP-OES. The results indicated that the exfoliation degree of natural muscovite was strongly related to the interlayer and solvation forces. Weak interlayer forces facilitated the exfoliation of muscovite, which might be due to the fact that the interlayer structure was easily broken down. Solvents with a larger molecular size and similar surface energy to the muscovite (around 54.8 mJ m−2) were better for the exfoliation. This observation was attributed to the fact that the molecules of the solvents had stronger solvation forces to muscovite layers, leading them to intercalate into the adjacent layers to overcome the interlayer interactions and thus the exfoliation.
1. Introduction
Natural muscovite, with an ideal composition of KAl2(Si3AlO10)(OH)2, is a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 tetrahedral
1 tetrahedral![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) octahedral layered silicate.1 Si4+ and Al3+ in muscovite are commonly replaced by isomorphic low charge cations and alkali ions, mainly K+, are attracted in the interlayer to counterbalance the negative charge of the layers.2,3 Due to the serious charge deficiency of the layers and the presence of interlayer cations, there is a strong coulombic interaction operating between the adjacent layers of muscovite besides van der Waals forces, which are normally monotonically attractive and occur between all molecules.4,5 Despite the strong interlayer attraction, natural muscovite was successfully exfoliated into two dimensional nanosheets through weakening its layer attractions by enlarging the basal spacing and ultrasound-facilitated liquid exfoliation in our previous work.6 In this work some effect factors in the liquid exfoliation of muscovite will be investigated.
octahedral layered silicate.1 Si4+ and Al3+ in muscovite are commonly replaced by isomorphic low charge cations and alkali ions, mainly K+, are attracted in the interlayer to counterbalance the negative charge of the layers.2,3 Due to the serious charge deficiency of the layers and the presence of interlayer cations, there is a strong coulombic interaction operating between the adjacent layers of muscovite besides van der Waals forces, which are normally monotonically attractive and occur between all molecules.4,5 Despite the strong interlayer attraction, natural muscovite was successfully exfoliated into two dimensional nanosheets through weakening its layer attractions by enlarging the basal spacing and ultrasound-facilitated liquid exfoliation in our previous work.6 In this work some effect factors in the liquid exfoliation of muscovite will be investigated.
It was found that the surface energy or solution thermodynamics and Hansen solubility parameters of solvents determined the exfoliation degree and stability of 2D materials.7–9 All these findings were performed on liquid phase exfoliation of graphene analogues into individual atomic layers, in which these materials stack into three dimensional crystals by nanosheets through van der Waals interaction. Muscovite has strong coulombic interaction between the adjacent layers besides van der Waals, therefore the exfoliation of muscovite might be more complex. However, few results have been obtained about the liquid phase exfoliation of layered materials with strong interlayer forces, such as muscovite.
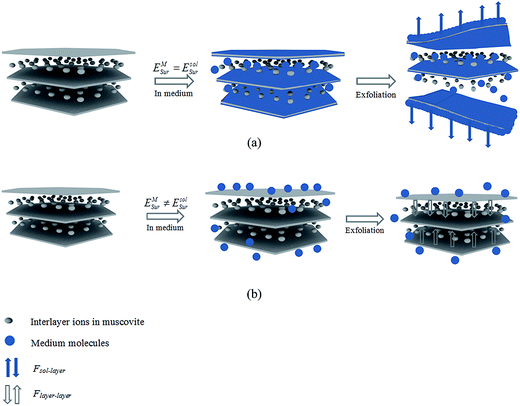
When a layered material was immersed in solvent during the exfoliation, the forces acting on each layer are mainly considered
| F = Flayer–layer + Fsol–layer | (1) |
In the present study, an attempt has been made to investigate the correlation between the exfoliation degree of muscovite and the interlayer attraction (Flayer–layer), solvent–layer interaction (Fsol–layer). The attraction between layers depended on the basal spacing.12,13 Therefore, to study the relation between Flayer–layer and the exfoliation of muscovite, experimental was performed through exfoliating muscovite samples with different basal spacing. While, another relationship between Fsol–layer and exfoliation of muscovite was explored through comparing the exfoliation degree of muscovite treated in water mixed with different alcohols and alcohol concentrations. To reveal the correlation, X-ray diffraction (XRD), infrared spectroscopy (IR), inductively coupled plasma atomic emission spectrometry (ICP-OES) and surface tensiometer were performed to characterize the properties of muscovite and solvent, ultraviolet-visible (UV-VIS) spectrophotometer was used to determine the exfoliation degree of muscovite. The objective was to obtain more understanding of the relation between the exfoliation degree of muscovite and Flayer–layer, Fsol–layer and to optimize the exfoliation. This study might provide a guidance in the exfoliation of layered materials because it opens a new idea in the exfoliation that Flayer–layer and Fsol–layer are complementary forces in the exfoliation and both of them should be considered in improving the exfoliation degree.
2. Experimental methods
2.1 Materials
The natural muscovite sample (termed as M) used in this work was collected from the Longqi mineral deposit located in Xinbin city, Liaoning province, China. The XRD pattern in Fig. S1† indicated that the main composition in the sample was monoclinic muscovite 2M1 and no other impurities were determined. The chemical composition of muscovite was given in Table S1† and the formula was (K1.02Na0.06)(Ca0.06Mg0.03Fe0.32)(Si2.77Al2.37Sn0.022Ti0.014)O10(OH)0.35. More details could be found in our previous work.6,14 All alcohols (methanol, ethanol, isopropanol, tert-butanol) were purchased from Sinopharm Chemical Reagent Co., Ltd, China and of analytical grade. Ultrapure Milli-Q water was used in all the experiments.2.2 Methods
Natural muscovite powder with a mass median diameter (d50) of 21.7 μm was first 750 °C heated, followed by ion exchange with LiNO3 and intercalation by octadecyl trimethyl ammonium chloride (OTAC), respectively, which was to increase the basal spacing and decrease the attraction force between layers of muscovite. The details were described in our previous work.14 The difference between the sample preconditioned in this study and our previous work was the LiNO3 treatment times. One period of LiNO3 treatment was that 750 °C heated muscovite was mixed with LiNO3 as a mass ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 and heated at 300 °C in muffle furnace for 48 h, followed by four series of washing-centrifugation using ultrapure water to remove the exchanged K+ and drying the sample in a freeze drying oven for 24 h. In this study, the 750 °C calcined muscovite was treated by LiNO3 for 1, 2, 3, 4, 5, 6, 7 times, respectively, to prepare muscovite with different layer charge and basal spacing. The resultant muscovite was named Li-M750-s with s = 1 to 7. After that, LiNO3 treated muscovite was intercalated by OTAC. The sample was named OTA-M750-s with s = 1 to 7. In the exfoliation, each of 50 mg OTA-M750-s was dispersed well into 35 ml 40% tert-butanol/water solvent, respectively. The dispersions were first exfoliated by a Cole-Parmer ultrasonic processor at 375 W for 15 min with an intermittent way (1 s on, 1 s off) and then 2 ml was taken and placed in a 10 mm cuvette to record their absorbance using an UV-VIS spectrophotometer at maximum absorption wavelength 650 nm for five times to determine the exfoliation degree. The blank solution in the absorbance test was 40% tert-butanol/water solution. After that a centrifugation (Thermo scientific Sorvall ST16) at 3856 × g for 30 min was executed for the ultrasonic treated dispersion. The top 10 ml of supernatant after centrifugation was decanted into a glass vial by pipette and then placed in a 10 mm cuvette to record their absorbance for three times. The exfoliation degree of muscovite was calculated through dividing the absorbance of supernatant after centrifugation at 3856 × g for 30 min by that before centrifugation because the particle concentration was considered related to the absorbance.15 The measured absorbance and exfoliation degree of OTA-M750-s was given in Table S2.†
60 and heated at 300 °C in muffle furnace for 48 h, followed by four series of washing-centrifugation using ultrapure water to remove the exchanged K+ and drying the sample in a freeze drying oven for 24 h. In this study, the 750 °C calcined muscovite was treated by LiNO3 for 1, 2, 3, 4, 5, 6, 7 times, respectively, to prepare muscovite with different layer charge and basal spacing. The resultant muscovite was named Li-M750-s with s = 1 to 7. After that, LiNO3 treated muscovite was intercalated by OTAC. The sample was named OTA-M750-s with s = 1 to 7. In the exfoliation, each of 50 mg OTA-M750-s was dispersed well into 35 ml 40% tert-butanol/water solvent, respectively. The dispersions were first exfoliated by a Cole-Parmer ultrasonic processor at 375 W for 15 min with an intermittent way (1 s on, 1 s off) and then 2 ml was taken and placed in a 10 mm cuvette to record their absorbance using an UV-VIS spectrophotometer at maximum absorption wavelength 650 nm for five times to determine the exfoliation degree. The blank solution in the absorbance test was 40% tert-butanol/water solution. After that a centrifugation (Thermo scientific Sorvall ST16) at 3856 × g for 30 min was executed for the ultrasonic treated dispersion. The top 10 ml of supernatant after centrifugation was decanted into a glass vial by pipette and then placed in a 10 mm cuvette to record their absorbance for three times. The exfoliation degree of muscovite was calculated through dividing the absorbance of supernatant after centrifugation at 3856 × g for 30 min by that before centrifugation because the particle concentration was considered related to the absorbance.15 The measured absorbance and exfoliation degree of OTA-M750-s was given in Table S2.†
When studying the correlation between exfoliation of muscovite and solvation force, the liquid phase exfoliation was similar with that in the above experimental, except that the exfoliation solvents were alcohol/water mixtures with different alcohol types (methanol, ethanol, isopropanol, tert-butanol) and alcohol concentrations (from 10% to 85%), and the sample was kept unchanged (here OTA-M750-7 was used because it exhibited the largest basal space compared with other samples). The exfoliation degree of OTA-M750-7 in different alcohol/water mixtures was given in Table S3.†
The surface free energy of OTA-M750-7 was determined using spectrophotometric method.15 Ten 45 ml ethanol/water mixtures with predefined ethanol concentrations (33% to 100%) were prepared. 0.2 g sample was dispersed into these solutions, respectively. The suspensions were centrifuged at 1000 rpm for 1 min, followed by transferring 10 ml supernatant of each suspension to a glass vial by pipette. Absorbance of these supernatants was measured with a UV-VIS spectrophotometer at 650 nm. Each measurement was repeated for 3 times and averaged.
2.3 Measurements
XRD patterns were recorded on a Bruker D8 Advance X-ray diffractometer with CuKα radiation. The diffraction patterns in the 2θ range from 1.5° to 8° were collected with a step-scanning speed of 0.01° s−1 to calculate the basal spacing of samples.The absorbance of muscovite suspension before and after exfoliation was determined by using a Thermo Scientific Orion AquaMate 8000 UV-VIS spectrophotometer with a quartz cell of 10 mm optical path. The absorbance was measured in the wavelength of 650 nm.
Middle-infrared spectra were collected with a Thermo Scientific Nicolet 6700 FT-IR spectrometer, for which 10 mg of muscovite sample were mixed with 200 mg of KBr in an agate mortar, and then the mixture was pressed at a pressure of 10 MPa for 3 min.
The K content of muscovite after different LiNO3 treatments was performed using the PerkinElmer Optima 4300DV ICP-OES. Before the determination, a given amount of powder was dissolved in 2 ml HCl, 1 ml HNO3 and 2 ml HF, and then heated to dry. After that, the sample was dispersed in 1 ml HCl and the suspension was diluted with deionized water.
Powereach JK99C tensiometer with Du Nouy ring method was used to determine the surface tension of alcohol–water mixtures at 15 °C.
3. Results and discussion
3.1 Effect of Flayer–layer on the exfoliation of muscovite
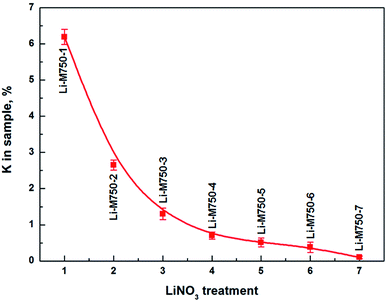
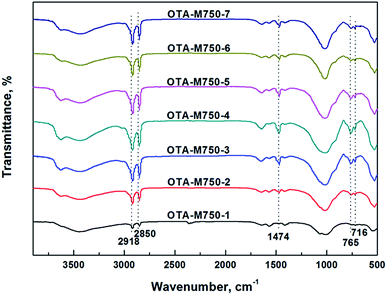
Fig. 1 shows the K in sample Li-M750-s. It indicated that K content decreased dramatically from 6.2% to 0.7% in the first four LiNO3 treatments. Bowers et al. suggested that muscovite layers had a strong affinity for K+, which was hard to be replaced by H3O+.16 White deemed that Li+ could exchange interlamellar K+ and stay in the muscovite in LiNO3 treatment.12 These previous findings interpreted that the desorption of K+ from muscovite was only due to the replacement of Li+ instead of H3O+ in the first four LiNO3 treatments in this experimental. Therefore, the great decrease of K+ indicated a huge increase of Li+ in muscovite. In addition, Li+ could migrate into the vacant octahedral positions of the muscovite layers,12 which meant that the adsorbed Li+ could stay in both the interlayers and layers. The affinity of muscovite to interlaminar Li+ was weak and Li+ in the interlayer could be exchanged with OTA+.5,17 Therefore, an increase of OTA+ and a decrease of Li+ in muscovite would occur in the subsequent OTAC treatment. As those Li+ migrated into the layers of muscovite will be discussed later.Fig. 2 illustrates the infrared spectroscopy of OTA-M750-s. The bands at 2918 and 2850 cm−1 corresponded to CH2 asymmetric and symmetric stretching vibration modes of alkyl chain, respectively.18 The bands around 1474 cm−1 and of 765, 716 cm−1 were due to the methylene scissoring and rocking mode, respectively. In other words, OTA+ replaced some interlayer cations and was detected in muscovite. It is well known that for highly ordered OTAC, the position of CH2 asymmetric and symmetric stretching vibration modes were at 2918 and 2850 cm−1, respectively. If conformational disorder was included in the chains, their wavenumbers shifted to higher values. In addition, less ordered arrangement was also reflected in broad bands.19 While all the CH2 stretching vibration positions of OTA-M750-s in Fig. 2 were exactly at 2918 and 2850 cm−1 and their shapes were sharp, therefore, the arrangements of OTA+ in all OTA-M750-s were well ordered. The organic content was related to the transmittance of the band, therefore the obvious increase of the transmittance of CH2 stretching vibration and especially scissoring and rocking bands (1474 and 765 cm−1) indicated the increase of OTA+ from OTA-M750-1 to OTA-M750-4. It should be pointed out that the band transmittance of OTA+ decreased when the samples treated in excess of 4 LiNO3 treatments, which will be explained in detail later.
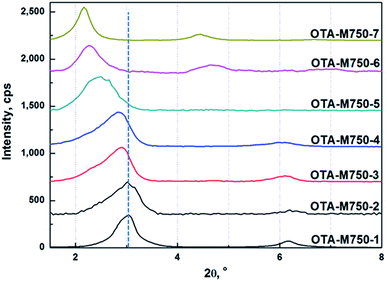
The XRD patterns of OTA-M750-s are shown in Fig. 3. The 2θ position of the first peak of OTA-M750-1 was marked by the dashed line. Fig. 3 clearly demonstrated that the characteristic peaks moved leftward slightly to lower angle region for sample OTA-M750-1 to OTA-M750-4, suggesting a little increase of the basal spacing. This was probably attributed to the increased OTA+ content between the layers. While a great leftward occurred on sample OTA-M750-5, OTA-M750-6, and OTA-M750-7, indicating a large increase of the basal spacing. The reason will be discussed below. It should be point out that the basal spacing of muscovite did not significantly increase when the LiNO3 treatment was beyond 7 cycles. Therefore, a maximum of 7 cycles LiNO3 treatment was performed in the experiment.
Fig. 1 shows that K+ decreased gradually after the fourth LiNO3 treatments, demonstrating the slow increase of Li+ in muscovite. While OTA+ from OTA-M750-4 to OTA-M750-7 decreased, as indicated by the decrease of the transmittance of CH2 stretching vibration and especially scissoring and rocking bands in Fig. 2. In addition the peaks in OTA-M750-5, OTA-M750-6 and OTA-M750-7 jumped to lower angle compared to those of other OTA-M750-s in Fig. 3, suggesting a large increase of the basal spacing. This was probably because that Li+ mainly stayed in interlayer in the first four LiNO3 treatments, while Li+ migrated into vacant octahedral positions of the layer with extending the LiNO3 treatments.20,21 According to previous study,17 only Li+ in interlayer could be exchanged with OTA+, therefore, the increase of Li+ in muscovite did not resulted in the increase of OTA+. However the migration of Li+ into muscovite layer could cause the partial neutralization of the negative charges in the layer and result in the lowering of the layer charge. As a consequence, the attraction force between layers weakened and the basal spacing increased. In addition, the arrangement and configuration of the OTA+ chains exhibited strong dependence on the crystal structure of muscovite, therefore the partial neutralization of the negative charges in muscovite might resulted in a better stretched conformation of OTA+, leading to an increase of the basal spacing.22
The attraction force between layers was dependent on the basal spacing, it decreased in strength with increasing the basal spacing.13 The basal spacing of sample OTA-M750-s was calculated according to Bragg's equation (eqn (S1)†) on the basis of the first peaks in Fig. 3 and the results were shown in Fig. S2 and Table S4.† It showed that the basal spacing had a slight increase from sample OTA-M750-1 to OTA-M750-4, while a dramatic increase in OTA-M750-5, OTA-M750-6 and OTA-M750-7. This indicated that the reduction of the layer charge might be the main reason for the increase of the basal spacing. As the basal spacing increased from OTA-M750-1 to OTA-M750-7, the interlayer force decreased. The exfoliation degree of muscovite as a function of basal spacing is illustrated in Fig. 4. Only six data were presented in the graph because values for OTA-M750-1 and OTA-M750-2 overlapped. The exfoliation degree increased linearly with increasing the basal spacing, indicating that the exfoliation degree was largely related to the basal spacing and further the interlayer forces. The exfoliation of the seven modified muscovite samples was carried out in the same solvent, and no significant differences on the surface energy of OTA-M750-s were observed, so Fsol–layer in eqn (1) was considered a constant. This means that the force acting on the layer of OTA-M750-s only differed in Flayer–layer. Therefore, it could be concluded from the above results that the exfoliation degree of muscovite largely related to Flayer–layer and the higher exfoliation degree achieved when Flayer–layer was weaker. This might be due to the fact that the interlayer structure of muscovite with weaker Flayer–layer was easier to be ruptured than those with stronger Flayer–layer.
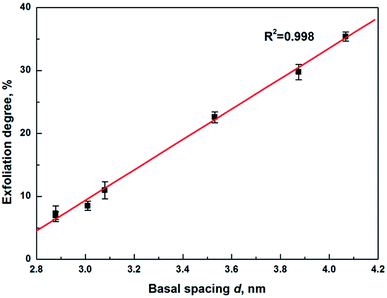 | ||
| Fig. 4 Exfoliation degree of muscovite as a function of basal spacing (error bars: one standard deviation). | ||
3.2 Effect of Fsol–layer on the exfoliation of muscovite
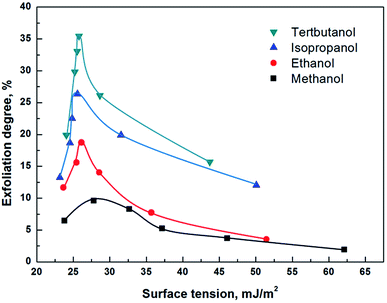
Fig. S3† shows the exfoliated OTA-M750-7 in twenty four alcohol/water solvents. As can be seen, the turbidity of the suspensions in methanol/water systems was limpid and became obviously more and more turbid when the solvents changed to ethanol, isopropanol and tert-butanol. In addition, the suspensions varied with the alcohol concentration. Because the concentration of the exfoliated particles was related to the turbidity, the above phenomenon illustrated that the solvent had a great effect on the exfoliation of muscovite.23,24 Fig. S4† gives exfoliation degree of OTA-M750-7 as a function of alcohol concentration. It was found that the exfoliation degree first increased and then decreased with the increase of alcohol concentration in all the alcohol/water solvents.The surface tensions of these solvents were measured and then related to the exfoliation of OTA-M750-7, as shown in Fig. 5. It was observed that the exfoliation degree appeared to reach a maximum value at 26 mJ m−2 for muscovite in ethanol/water, isopropanol/water and tert-butanol/water solvents, indicating that the three solvents with surface tension of 26 mJ m−2 tended to perform better in exfoliating muscovite. Too high or too low value resulted in low exfoliation degree. The surface energy of the solvent, ESolSur, is related to its surface tension, γ, expressed by:25
| ESolSur = γ + TSSolSur | (2) |
Fig. 6 shows the absorbance of OTA-M750-7 as a function of surface tension of ethanol/water liquid. It was clearly observed that the absorbance first increased to a maximum at around 27.2 mJ m−2 and then decreased with increasing the surface tension of ethanol/water mixture. According to the spectrophotometric method,15 the absorbance reached the maximum when the surface tension of the liquid and the surface free energy of the particles was equal to each other, indicating that the surface free energy of OTA-M750-7 was around 27.2 mJ m−2. Therefore, the surface energy of OTA-M750-7 was 54.4 mJ m−2, which was twice of the surface free energy due to the two free surfaces of particle.27 Combining the results of Fig. 5 and 6, it indicated that the good exfoliation occurred when the surface energy of solvent and OTA-M750-7 approached. It is worth mentioning that the best exfoliation of muscovite in methanol/water solvent occurred when the surface energy of solvent was 56.8 mJ m−2, which had a slight divergence from surface energy 54.8 mJ m−2. This phenomenon was probably attributed to the bad dispersion of the sample in the methanol/water solvent that was observed in the experimental. However, it did not go against to the fact that the best exfoliation occurred when the surface energy of sample and solvent matched, which will be explained below.
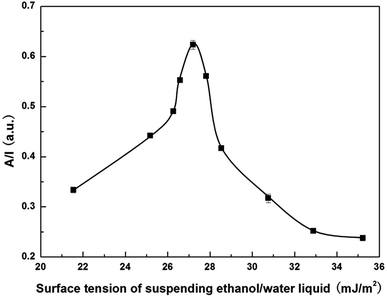 | ||
| Fig. 6 Surface free energy determination of OTA-M750-7 using spectrophotometric method (error bars: one standard deviation). | ||
The suspension of OTA-M-750-7 in alcohol/water solvents could be considered as a system, the enthalpy per unit volume of which could be expressed by7
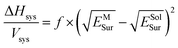 | (3) |
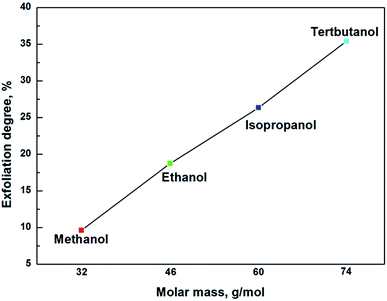
The highest exfoliation degree in each alcohol/water mixture as a function of alcohol molar mass was illustrated in Fig. 8. It was clearly shown that the exfoliation degree increased linearly with increasing the molar mass of alcohol, indicating that the exfoliation of muscovite had higher affinity for solvent with larger molar mass of alcohol. As it is known, the solvation force, Fsol–layer, is related to the molecular structure.28 Alcohol molecules with larger molar mass might favor stronger Fsol–layer. In addition, larger molar mass has bigger molecular size, which may open up a broader interlayer spacing in their intercalations, resulting in a weaker attraction from adjacent layers, facilitating the exfoliation of muscovite.
As discussed above, both the interlayer forces, Flayer–layer, and solvation force, Fsol–layer, determined the exfoliation degree of muscovite. Actually, the two forces were competitors. The correlation between the exfoliation of muscovite and Flayer–layer, Fsol–layer could be simplified into eqn (4) when other conditions are constants.
| E ∝ κ(Fsol–layer − Flayer–layer) | (4) |
4. Conclusions
The experimental results presented in this work had demonstrated that the exfoliation of muscovite was greatly related to the interlayer attraction and solvation force. A higher exfoliation degree was achieved for the muscovite with weaker interlayer attraction, which might be due to that the interlayer structure was more easily to be ruptured than those with stronger interlayer forces. Exfoliation results also illustrated that the exfoliation degree reached maximum in each alcohol/water mixture when the surface energy of solvent was around 54.8 mJ m−2, which was similar to that of muscovite. This might be resulted from that the solvation force was highest in this case, leading the solvent molecules to pull the layers away from the adjacent layers to overcome the attractions between them and thus the muscovite exfoliation. It was found that a better exfoliation was achieved in an alcohol with larger molar mass, which might be attributed to the fact that the solvation force was stronger and the intercalation of alcohol molecular could bring a broader interlayer spacing. This work placed emphasis on the importance of interlayer forces and solvation force in the exfoliation of layered materials and provided a guide for the exfoliation of layered materials.Acknowledgements
The financial supports to this work from the National Natural Science Foundation of China under the projects No. 51474167 and No. 51674183 were gratefully acknowledged.References
- S. W. Bailey, Classification and structures of the micas, Rev. Mineral. Geochem., 1984, 13(1), 1–12 CAS.
- G. L. Gaines Jr, The ion-exchange properties of muscovite mica, J. Phys. Chem., 1957, 61(10), 1408–1413 CrossRef.
- H. G. V. Reichenbach and C. I. Rich, Potassium release from muscovite as influenced by particle size, Clays Clay Miner., 1969, 17, 23–29 Search PubMed.
- M. A. Osman and U. W. Suter, Determination of the cation-exchange capacity of muscovite mica, J. Colloid Interface Sci., 2000, 224, 112–115 CrossRef CAS PubMed.
- M. A. Osman, C. Moor, W. R. Caseri and U. W. Suter, Alkali metals ion exchange on muscovite mica, J. Colloid Interface Sci., 1999, 209, 232–239 CrossRef CAS PubMed.
- F. Jia and S. Song, Preparation of monolayer muscovite through exfoliation of natural muscovite, RSC Adv., 2015, 5, 52882–52887 RSC.
- Y. Hernandez, V. Nicolosi, M. Lotya and F. M. Blighe, et al., High-yield production of graphene by liquid-phase exfoliation of graphite, Nat. Nanotechnol., 2008, 3, 563–568 CrossRef CAS PubMed.
- G. Cunningham, M. Lotya, C. S. Cucinotta, S. Sanvito, S. D. Bergin, R. Menzel, M. S. Shaffer and J. N. Coleman, Solvent exfoliation of transition metal dichalcogenides: dispersibility of exfoliated nanosheets varies only weakly between compounds, ACS Nano, 2012, 6, 3468–3480 CrossRef CAS PubMed.
- C. J. Shih, S. Lin, M. S. Strano and D. Blankschtein, Understanding the stabilization of liquid-phase-exfoliated graphene in polar solvents: molecular dynamics simulations and kinetic theory of colloid aggregation, J. Am. Chem. Soc., 2010, 132, 14638–14648 CrossRef CAS PubMed.
- J. Israelachvili, Solvation forces and liquid structure, as probed by direct force measurements, Acc. Chem. Res., 1987, 20(11), 415–421 CrossRef CAS.
- M. Patra and M. Karttunen, Systematic comparison of force fields for microscopic simulations of NaCl in aqueous solutions: diffusion, free energy of hydration, and structural properties, J. Comput. Chem., 2004, 25(5), 678–689 CrossRef CAS PubMed.
- J. L. White, Layer charge and interlamellar expansion in a muscovite, Clays Clay Miner., 1956, 5, 289–294 Search PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Elsevier press, 2011 Search PubMed.
- F. Jia, J. Su and S. Song, Can natural muscovite be expanded, Colloids Surf., A, 2015, 471, 19–25 CrossRef CAS.
- X. Zhang, Z. Jiang, M. Li, X. Zhang, G. Wang, A. Chou, L. Chen, H. Yan and Y. Y. Zuo, Rapid spectrophotometric method for determining surface free energy of microalgal cells, Anal. Chem., 2014, 86, 8751–8756 CrossRef CAS PubMed.
- G. M. Bowers, D. L. Bish and R. J. Kirkpatrick, Cation exchange at the mineral-water interface: H3O+/K+ competition at the surface of nano-muscovite, Langmuir, 2008, 24, 10240–10244 CrossRef CAS PubMed.
- X. Yu, L. Zhao, X. Gao, X. Zhang and N. Wu, The intercalation of cetyltrimethylammonium cations into muscovite by a two-step process: II. The intercalation of cetyltrimethylammonium cations into Li-muscovite, J. Solid State Chem., 2006, 179, 1525–1535 CrossRef CAS.
- R. A. Macphail, H. L. Strauss, R. G. Snyder and C. A. Elliger, Carbon–hydrogen stretching modes and the structure of n-alkyl chains. 2. long, all-trans chains, J. Phys. Chem., 1984, 15, 334–341 CrossRef.
- R. G. Snyder, H. L. Strauss and C. A. Elliger, Carbon–hydrogen stretching modes and the structure of n-alkyl chains. 1. Long, disordered chains, J. Phys. Chem., 2002, 86, 5145–5150 CrossRef.
- W. F. Jaynes, Charge reduction, octahedral charge, and lithium retention in heated, Li-saturated smectites, Clays Clay Miner., 1987, 35, 440–448 CAS.
- J. M. Trillo, M. D. Alba, R. Alvero and M. A. Castro, Reexpansion of collapsed Li-montmorillonites; evidence on the location of Li+ ions, Chem. Commun., 1993, 24, 1809–1811 RSC.
- X. Yu, The preparation and characterization of cetyltrimethylammonium intercalated muscovite, Microporous Mesoporous Mater., 2007, 98, 70–79 CrossRef CAS.
- G. Toennies and D. L. Gallant, The relation between photometric turbidity and bacterial concentration, Growth, 1949, 13(1), 7–20 CAS.
- H. Chanson, M. Takeuchi and M. Trevethan, Using turbidity and acoustic backscatter intensity as surrogate measures of suspended sediment concentration in a small subtropical estuary, J. Environ. Manage., 2008, 88(4), 1406–1416 CrossRef PubMed.
- J. Lyklema, The surface tension of pure liquids: Thermodynamic components and corresponding states, Colloids Surf., A, 1999, 156, 413–421 CrossRef CAS.
- K. L. Wolf, Physik und Chemie der Grenzflachen, ed. I. Band, Springer, Berlin, 1957 Search PubMed.
- D. P. Woodruff, The chemical physics of solid surfaces, Elsevier Press, 2002 Search PubMed.
- J. N. Coleman, Liquid-phase exfoliation of nanotubes and graphene, Adv. Funct. Mater., 2009, 19, 3680–3695 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26560j |
| This journal is © The Royal Society of Chemistry 2017 |