Accurate measurement of specific tensile strength of carbon nanotube fibers with hierarchical structures by vibroscopic method

Abstract

The specific strength of a carbon nanotube (CNT) fiber can be estimated to be much higher than its real value when the linear density of the fiber is measured using the vibroscopic method. This is because CNT fibers are not made of a single fiber, as assumed in the standard ASTM procedure, but rather have a hierarchical structure composed of CNTs and CNT bundles. Based on careful investigation, a new procedure using the vibroscopic method is proposed to drastically reduce the probability of erroneous results and provide a more reliable tool to investigate the mechanical properties of one-dimensional nanostructured fibers.

---

Introduction

Carbon nanotube (CNTs) fibers can be assembled by solution spinning,^1,2 forest spinning,^3,4 and direct spinning,^5,6 and have been evaluated as a next generation lightweight and strong material to replace carbon fibers. As the CNT fibers are made entirely of CNTs, potentially they can be as strong, and electrically and thermally conductive as individual CNTs. Even though the properties of CNT fibers are still much inferior to those of CNTs, a number of applications such as display,⁷ artificial muscle,⁸ supercapacitor,⁹ batteries,¹⁰ invisible material,¹¹ and strain sensor¹² have been demonstrated based on the current state of the electrical and thermal properties of CNT fibers, which are now comparable with conventional metals.¹³ However, very few applications have been demonstrated based on the mechanical strength of CNT fiber as a structural material. A specific strength of 9.8 N per tex for 1 mm length of the pristine CNT fiber,¹⁴ which is much higher than the highest specific strength of carbon fiber (Toray T1100, 3.7 N per tex),¹⁵ was reported in 2007; however, no specific strength of CNT fiber even close to those value has been shown in the literature in the past 10 years. The highest specific strength reported since then has been of about 1–2 N per tex.^16,17 Therefore, considerable research is still required into improving the mechanical properties of CNT fibers.

To efficiently improve the mechanical properties of CNT fibers, accurate measurements of their existing mechanical properties are required. Tensile strength (in GPa) is the principal mechanical property determined by the maximum tensile load divided by the cross-sectional area of a sample. However, it is difficult to define the cross-sectional area of one-dimensional fibers because of their irregular shapes. Thus, in many research articles, the tensile strength of one-dimensional fibers including CNT fibers has been reported using the value for specific strength determined by the maximum tensile load divided by the mass-per-unit length (linear density), rather than the cross-sectional area.^14,16–21 Specific strength has the unit of N per tex, where the linear density unit “tex” is defined as the mass in grams of 1 km length of fiber. The linear densities of the CNT fibers are reported in the 0.03–0.5 tex range.^14,22

According to the American Society for Testing and Materials (ASTM), the linear density of fibers can be determined by two methods: (1) weighing fibers with specific length (weighing method) and (2) calculating the linear density from the detected resonance frequency of oscillating fibers (vibroscopic method).²³ The vibroscopic method is faster and more convenient than the weighing method, because the vibroscopic method requires much shorter CNT fibers for the linear density measurement. However, during this study, it was noted that, sometimes, the measured linear density of CNT fibers by the vibroscopic method did not match with the linear density determined by the weighing method even though procedures were followed as written in the ASTM documents. The linear density of carbon fiber measured by the vibroscopic method also differs depending on the pre-tension values.²⁴ Therefore, when measuring the linear density of CNT fibers by the vibroscopic method, various factors that affect linear density measurement by the vibroscope should be taken into consideration. In this study, the mechanical behavior of CNT fibers is investigated by a vibroscope attached to a universal testing machine (UTM), and a new procedure is proposed for more accurate measurement of the linear density by the vibroscopic method.

Experimental section

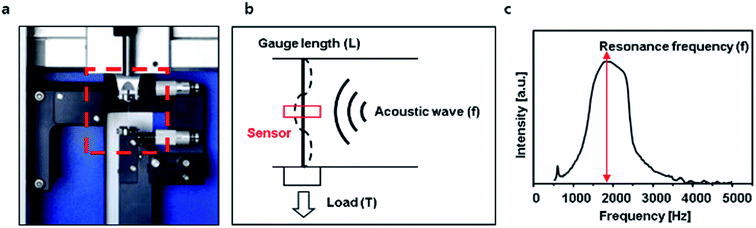
CNT fibers were produced by the direct spinning method, in which a CNT fiber is directly and continuously spun from CNT aerogel formed in a chemical vapor deposition (CVD) reactor (Fig. 1a).⁶ Acetone (carbon source), ferrocene (catalyst source) and thiophene (promoter) were injected into the gas phases along with hydrogen (carrier gas) through a controlled evaporation mixer (CEM, Bronkhorst W-102A, Netherlands) and a pre-heater. Injection lines were also heated to around 100 °C to prevent re-condensation of reactants. The reactant compositions (ESI Table S1†) were varied to control the linear densities of the obtained CNT fibers.

Fig. 1 (a) Photographs of synthesis equipment of CNT fiber by the direct spinning method. (b) Photograph of synthesized CNT fiber. (c) Table of the average linear densities and standard deviations for four CNT fiber samples.

The morphology of CNT fibers was analyzed by scanning electron microscopy (SEM, FEI Helios NanoLab650, operated at 10 kV). Cross-sectional SEM images of CNT fibers were acquired after cutting and polishing the fibers by focused ion beam (FIB) milling (operated at 30 kV Ga⁺ ion beam) using the same SEM equipment.

The linear densities of CNT fibers were measured via two methods following the ASTM D1577 procedure.²³ The first was to measure the weight of the CNT fiber of a specific length using a microbalance (Microbalance, Sartorius CPA2P, Germany). The weight of fiber (gauge length: 50 cm) was measured at least 10 times for each sample. The second was by mathematical calculation from the resonance frequency, which was measured by a vibroscope (frequency range: 500–5000 Hz). This vibroscope is attached to a universal testing machine (UTM, Textechno FAVIMAT+, Germany), which means the tensile loads on CNT fibers also could be measured. The resonance frequency of a CNT fiber (gauge length: 40 mm) was measured while increasing pre-tension from 0.05 cN in increments of 0.05 cN; each tension was incremented at least 40 times for each sample. The tension values for the strain values of each sample were converted based on tension–strain graphs created from tensile testing.

The linear density of an elastic fiber is calculated using Mersenne's law:

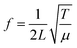where, f [Hz] is the resonance frequency of vibration, L [km] is the length of the vibrating string, T [N] is the tension applied to the string and μ [tex = g km⁻¹] is the linear density of the string. This equation also can be derived from the theory of vibrating strings and is explained in detail in the ESI.†

Results and discussion

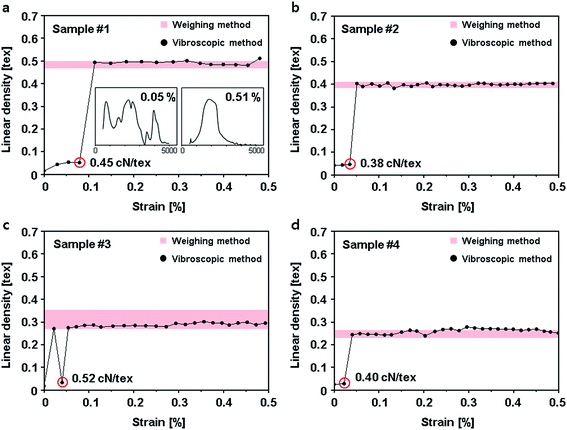
As-synthesized CNT fiber (Fig. 1b) was composed of CNTs with diameters of about 10–20 nm and I_G/I_D ratio about 3 (ESI Fig. S1†). CNT fiber samples #1 to #4 had differing linear densities from 0.47 to 0.24 tex but standard deviations of samples were less than 0.03 tex, which confirms that they had uniform linear densities along their longitudinal direction (Fig. 1c, ESI Fig. S2†). However, the cross-sectional shapes of as-synthesized CNT fibers are usually far from circular (ESI Fig. S3†); this is why it is difficult to accurately define the cross-sectional area of CNT fiber.

The vibroscopic method (Fig. 2) involves measuring the resonance vibration frequency, the sample should behave elastically during measurement. This specific frequency depends on the length of the vibrating string, the amount of tension on the string and the linear density of the string. The relation among these three factors that affect the resonance frequency is Mersenne's law (eqn (1)). During measurement of linear density by the vibroscopic method, external waves with various frequencies cause a fiber to vibrate (Fig. 2b) and the frequency at the highest vibration intensity is chosen as a resonance frequency (Fig. 2c).

Fig. 2 (a) Photograph of the vibroscope on UTM. (b) Graphical description of the vibroscopic method. (c) Plot of vibration intensity [a.u.] versus frequency [Hz] of a sample with a single peak, which corresponds to the resonance frequency of a sample. Using this resonance frequency, the linear density of a sample can be accurately estimated.

The linear density measured by the vibroscopic method was affected by strain induced by the applied tension during measurement. All graphs (Fig. 3(a)–(d)) have two regions. At the region above 0.05–0.1% strain, the linear density values (line with dots) are well matched with those measured by a microbalance (red block). However, at the region below 0.05–0.1% strain, the estimated linear density is much lower than that measured using a microbalance. The relationship of vibration intensity versus frequency for the same CNT fiber differed at strains of 0.05% and 0.51% (Fig 3a, inset; ESI Fig. S4 and S5†). In contrast to the graph for CNT fiber at a strain of 0.51%, the graph showing strain at 0.05% has multiple peaks without any numeric multiple relation, so a resonance frequency cannot be accurately determined. This means that if the linear density of a CNT fiber is measured by a vibroscopic method under a tension that generates strain below 0.05–0.1%, the linear density estimate can shows large errors. The intensity–frequency curves vary continuously with the strain values (ESI Movie S1†). For measurement of linear density of a fiber by a vibroscope, ASTM recommends tension values of 0.3–0.5 cN per tex.²³ Although tension was applied in the 0.3–0.5 cN per tex range (calculated by applied tension divided by a measured linear density of each CNT fiber) for measurements, the measured linear density values show large errors (Fig. 3). The linear density measurement of graphene oxide (GO) fiber with a hierarchical structure also shows similar results (ESI Fig. S6†). It appears that the vibroscopic method as described by the ASTM for measurement of linear density of hierarchically structured fibers, such as CNT and GO fibers, may not provide the optimum procedure.

Fig. 3 (a–d) Linear density versus strain graph of samples #1 to #4 measured by the vibroscopic method. The red block in each graph indicates the range of the linear density of each sample measured using a microbalance for comparison. Inset images in (a) show vibration intensity [a.u.] versus wave frequency [Hz] at 0.05% and 0.51% strain applied to sample #1.

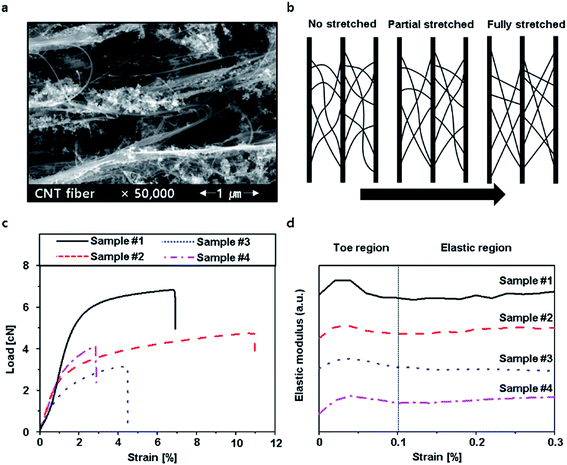
Whereas the ASTM procedures for measuring linear density of a fiber by a vibroscope are documented based on a single fiber, the CNT fiber is not a single fiber, rather it has a hierarchical structure composed of a large number of CNT bundles and CNTs of various sizes (Fig. 4a, ESI Fig. S7†). Baer et al. explained, using stress–strain curves, that the mechanical behavior of a fiber with a hierarchical structure is different from that of a single fiber.²⁵ Stress–strain curves have three regions: a toe region, a linear region and a plastic region. Compared with the stress–strain curve of a single fiber, in a hierarchically structured fiber, an additional toe region is present before the elastic region where each constituent bundle in the hierarchically structured fiber is fully stretched. The hierarchically structured fiber can therefore behave elastically only after all the bundles are fully stretched (Fig. 4b). When CNT fibers are partially stretched (toe region), the applied force is distributed preferentially on the fully stretched CNT bundles until the other CNT bundles are stretched, which increases the modulus of the CNT fiber. However, when the CNT fibers are fully stretched (elastic region), the force applied to the fibers is distributed among all the CNT bundles, and the modulus of the CNT fibers becomes stable.

Fig. 4 (a) SEM image of CNT fiber with hierarchical structure. (b) Illustration of behavior of the CNT fiber with hierarchical structure in the toe region. (c) Load–strain graph of each CNT fiber obtained by UTM. (d) Elastic modulus–strain graph of each CNT fiber at strain values below 0.3%.

The slope of the load–strain curve of each sample measured by UTM yield the modulus–strain curves which also show two distinguished regions (Fig. 4d). The load–strain curve of a single fiber usually shows two distinct regions: elastic and plastic. In the elastic region, the load–strain curve of a single fiber is linear, so the modulus–strain plot of a single elastic fiber should be invariable in contrast to the plot shown in Fig. 4d. The region showing variable modulus in Fig. 4d is characteristic of a fiber with hierarchical structures during tensile testing. Variations in the slope of the load–strain curves have been reported in various studies with different hierarchical structured materials^24–26 and also with CNT fibers.²⁷ Therefore, when the linear density of CNT fibers with hierarchical structures is measured by a vibroscope, reliable and accurate measurement is guaranteed only under appropriate tension, in which CNT fibers show an elastic response.

The gauge length also affects the accuracy of the linear density measurement. This influence is also related to the use of appropriate tension values and the detection range of vibroscope equipment for resonance frequencies. If gauge length is too long or too short, the fundamental resonance frequency is decreased or increased respectively, and can sometimes be out of the detection range. Based on Mersenne's law, a longer gauge length leads to a lower fundamental resonance frequency, which requires a higher tension on the CNT fibers to bring the fundamental resonance frequency into the detection range of the vibroscope. This increase in tension also causes the CNT fibers to respond in the elastic region; so increasing the gauge length reduces the probability of false measurement of linear density. However, very high applied tension may affect the actual measurement of the mechanical behavior of CNT fibers. Therefore, both gauge length and applied tension are critical experimental parameters that must be determined for accurate measurement of the mechanical properties of CNT fibers.

Based on careful investigation throughout this study, a new procedure is proposed to accurately measure the linear density of a hierarchically structured fiber such as a CNT fiber by a vibroscopic method (ESI Fig. S8†). The measurement consists of five steps: (1) obtain the load–strain curve using a universal testing machine (UTM) and draw the modulus–strain graph; (2) determine the appropriate strain value for which a hierarchical fiber behaves elastically; (3) determine the gauge length, at which the fundamental resonance frequency, calculated according to Mersenne's law, is within the detection range of a vibroscope; (4) measure the resonance frequency by applying the pre-determined tension to the hierarchical fiber with the pre-determined gauge length; and (5) calculate the linear density of the fiber based on Mersenne's law. Following such a procedure will drastically reduce the probability of an inaccurate measurement.

Conclusions

In conclusion, a new procedure is proposed for accurate measurement of the linear density of CNT fibers with hierarchical structures via a vibroscopic method. Since the vibroscopic method exploits the resonance phenomenon in a sample, the sample should behave elastically under the applied tension during the measurement. In their stress–strain curves, materials with hierarchical structures display a region called the “toe region” in which the individual components in the structure behave independently. Therefore, the linear density of CNT fibers in the toe region measured by the vibroscope can differ greatly from that measured using a microbalance. The determination of the appropriate tension to be applied to a hierarchically structured fiber is of critical significance to ensure accurate linear density measurement. In addition to intrinsic speed and convenience when combined with UTM, the proposed procedure for linear density measurement allows for more accurate and effective use of the vibroscopic method.

Acknowledgements

This study is supported by grants from the Korea Institute of Science and Technology (KIST) Institutional program and the Industrial Fundamental Technology Development program (10052838, Development of the direct spinning process for continuous carbon nanotube fiber) funded by the Ministry of Trade, Industry and Energy (MOTIE). This study is also supported by the Mid-career Researcher Program (Grant No. NRF-2014R1A2A1A01003266) and Nano-Material Technology Development Program (2016M3A7B4905619) through National Research Foundation (NRF) funded by the Ministry of Science, ICT and Future Planning (MSIP).

Notes and references

1. B. Vigolo, A. Pénicaud, C. Coulon, C. Sauder, R. Pailler, C. Journet, P. Bernier and P. Poulin, Science, 2000, 290, 1331–1334.
2. L. M. Ericson, H. Fan, H. Peng, V. A. Davis, W. Zhou, J. Sulpizio, Y. Wang, R. Booker, J. Vavro, C. Guthy, A. N. Parra-Vasquez, M. J. Kim, S. Ramesh, R. K. Saini, C. Kittrell, G. Lavin, H. Schmidt, W. W. Adams, W. E. Billups, M. Pasquali, W. F. Hwang, R. H. Hauge, J. E. Fischer and R. E. Smalley, Science, 2004, 305, 1447–1450.
3. K. Jiang, Q. Li and S. Fan, Nature, 2002, 419, 801.
4. M. Zhang, K. R. Atkinson and R. H. Baughman, Science, 2004, 306, 1358–1361.
5. Y. L. Li, I. A. Kinloch and A. H. Windle, Science, 2004, 304, 276–278.
6. S.-H. Lee, J. Park, H.-R. Kim, J. Lee and K.-H. Lee, RSC Adv., 2015, 5, 41894–41900.
7. P. Liu, D. Zhou, Y. Wei, K. Jiang, J. Wang, L. Zhang, Q. Li and S. Fan, ACS Nano, 2015, 9, 3753–3759.
8. J. Foroughi, G. M. Spinks, G. G. Wallace, J. Oh, M. E. Kozlov, S. L. Fang, T. Mirfakhrai, J. D. W. Madden, M. K. Shin, S. J. Kim and R. H. Baughman, Science, 2011, 334, 494–497.
9. C. Choi, J. A. Lee, A. Y. Choi, Y. T. Kim, X. Lepró, M. D. Lima, R. H. Baughman and S. J. Kim, Adv. Mater., 2014, 26, 2059–2065.
10. M. Li, Y. Wu, F. Zhao, Y. Wei, J. Wang, K. Jiang and S. Fan, Carbon, 2014, 69, 444–451.
11. A. E. Aliev, Y. N. Gartstein and R. H. Baughman, Nanotechnology, 2011, 22, 435704.
12. S. Ryu, P. Lee, J. B. Chou, R. Xu, R. Zhao, A. J. Hart and S.-G. Kim, ACS Nano, 2015, 9, 5929–5936.
13. N. Behabtu, C. C. Young, D. E. Tsentalovich, O. Kleinerman, X. Wang, A. W. K. Ma, E. A. Bengio, R. F. ter Waarbeek, J. J. de Jong, R. E. Hoogerwerf, S. B. Fairchild, J. B. Ferguson, B. Maruyama, J. Kono, Y. Talmon, Y. Cohen, M. J. Otto and M. Pasquali, Science, 2013, 339, 182–186.
14. K. Koziol, J. Vilatela, A. Moisala, M. Motta, P. Cunniff, M. Sennett and A. Windle, Science, 2007, 318, 1892–1895.
15. H. G. Chae, B. A. Newcomb, P. V. Gulgunje, Y. Liu, K. K. Gupta, M. G. Kamath, K. M. Lyons, S. Ghoshal, C. Pramanik, L. Giannuzzi, K. Şahin, I. Chasiotis and S. Kumar, Carbon, 2015, 93, 81–87.
16. T. S. Gspann, F. R. Smail and A. H. Windle, Faraday Discuss., 2014, 173, 47–65.
17. B. Alemán, V. Reguero, B. Mas and J. J. Vilatela, ACS Nano, 2015, 9, 7392–7398.
18. X. H. Zhong, Y. L. Li, Y. K. Liu, X. H. Qiao, Y. Feng, J. Liang, J. Jin, L. Zhu, F. Hou and J. Y. Li, Adv. Mater., 2010, 22, 692–696.
19. A. S. Wu, X. Nie, M. C. Hudspeth, W. W. Chen, T.-W. Chou, D. S. Lashmore, M. W. Schauer, E. Tolle and J. Rioux, Carbon, 2012, 50, 3876–3881.
20. Y. Jung, T. Kim and C. R. Park, Carbon, 2015, 88, 60–69.
21. M. Miao, Carbon, 2016, 96, 819–826.
22. V. Reguero, B. Alemán, B. Mas and J. J. Vilatela, Chem. Mater., 2014, 26, 3550–3557.
23. ASTM D1577-07(2012), Standard Test Methods for Linear Density of Textile Fibers ASTM International, West Conshohocken, PA, 2012,  DOI:10.1520/D1577-07R12.
24. K. M. Lyons, B. A. Newcomb, K. J. McDonald, H. G. Chae and S. Kumar, J. Compos. Mater., 2015, 49, 2231–2240.
25. E. Baer, A. Hiltner and D. Jarus, Macromol. Symp., 1999, 147, 37–61.
26. W. Yang, V. R. Sherman, B. Gludovatz, E. Schaible, P. Stewart, R. O. Ritchie and M. A. Meyers, Nat. Commun., 2015, 6, 6649.
27. Z.-J. Yang, Q.-S. Yang, X. Liu, X.-q. He and K.-M. Liew, Carbon, 2015, 94, 73–78.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26607j

---